1 Introduction

In the last few years, increasing efforts have been dedicated to the induced partial saturation (IPS) technology as a technique to increase the liquefaction resistance of granular soils. Although the ground improvement benefits of the technique have been widely investigated by several authors (e.g. [21, 33]), few results regarding a possible monitoring technique are available in the literature. The potential of the IPS lies in its non-invasive nature since a limited reduction in the degrees of saturation is required to achieve a significant improvement of the soil behaviour. Indeed, a degree of saturation (Sr) close to 85% is sufficient to provide to the soil a high value of Cyclic Resistance Ratio, CRR, [22, 40]. With such high Sr values, the presence of a more compressible fluid within the pores does not affect the intergranular forces, due to the air phase is not continuous, the gas bubbles are occluded and no suction is involved to change the mechanical behaviour of the soil [26, 34].

Several authors classified the non-saturated condition of a soil in “unsaturated” and “partially saturated” [15, 31]. In the former condition the gas phase is continuous, while in the latter gas is present in form of bubbles. When the soil is in unsaturated conditions, different Skempton’s B-parameters for the two fluids can be adopted: Ba = ∆ua/∆σ and Bw = ∆uw/∆σ, respectively for air and water [31]. When the degree of saturation is high enough that soil is not affected by suction, the surface tension of the bubble is negligible, and the air and pore water pressure can be approximately considered to be equal. Hence, a unique B-value can be adopted to investigate the integral response of a partially saturated specimen of sand subject to an isotropic confining pressure increment.

When IPS effectiveness evaluation is needed, measurements of the degree of saturation from B-values are inapplicable for both in situ-testing and advanced laboratory testing (i.e. shaking table or centrifuge tests). Therefore, alternative monitoring techniques to estimate the degree of saturation are required. One of the most promising techniques is the P-wave measurements, because they can be implemented for both in situ and laboratory testing. In laboratory tests, such as triaxial tests, the full saturation is typically assessed by measuring the Skempton’s B-value. In the literature, several studies are available to better understand the dependency of the Sr to Vp [17, 38]. Nishio [25] observed that a change of the B-value between 0.8 and 1 leads to a considerable variation in the P-wave velocity. Similar results were reported by Kokusho [16] after applying Biot’s poroelasticity theory [2]. This author stated when soil voids are completed fill with water, Vp should be almost equal to the pure water propagation velocity; that is, values of about 1482 m/s [28]. Therefore, correlations between Vp and B-value provide a reliable link between the field and laboratory measurements. Nevertheless, other authors pointed out that P-wave velocities are often less sensitive to the degree of saturation, at least, they are not as sensitive as the theory predicts [12]. Ishihara et al. [13] reported similar findings, highlighting a high discrepancy between the theoretical prediction and experimental data, particularly for B-values between 0.5 and 1. On the contrary, Lee et al. [18] observed a good agreement between the theoretical prediction and experimental data of these parameters. Clearly, different conclusions in both previous studies are inconsistent, as also documented by Gu et al. [10]. These discrepancies are because the dependency of the Vp to the B-value—or the degree of saturation—is affected by several variables, such as the type of pore gas and pore fluid [9], the distribution and homogeneity of occluded air bubbles, the solubility of the gas [30], and the morphology of soil grains. Hakanata et al. [11] showed that the size of soil particles influences the evolution of the relationship Vp and B-value. These authors observed that the discrepancy between the theory and the experimental data increases as the size of soil particles increases.

However, since the B-value is a very reliable parameter in laboratory tests, but clearly not applicable in field [32], in-situ measurement techniques have been developed to assess the degree of saturation on soil. Measurements of Vp are widely used in seismic non-destructive field tests and, at the same time, very sensitive to small changes in the Sr of the soil [20, 24, 30]. Hence, validating a relationship between these two Sr-depending parameters is useful to assess the Sr achieved with a ground improvement technique (e.g. IPS) in the field. Flora et al. [8] applied different methodologies during in situ tests, respectively measuring the velocity of compression waves Vp and the soil resistivity ρ (not discussed in this paper), both sensitive to a change in the saturation degree. Moreover, Okamura et al. [27] measured the P-wave velocity, in field trial tests, to ensure the initially fully saturation of the liquefiable soil.

The present study is based on the experimental results carried out in triaxial cells equipped with bender elements in order to investigate the correlation between the generated P-waves velocity (Vp) and the exhibited B-value of the specimen at different degrees of saturation. The data were processed to filter out the effects of interference among the generated waves, which can mask the real value of the degree of saturation (Sr). The processing procedure is described and discussed. As an outcome an experimental correlation between Vp and Sr is provided, which can be adopted to interpret the results of in-situ tests. Therefore, this paper aims to define an experimental relationship between the P-wave velocity and Skempton’s B-value, providing a final relationship linking Vp and Sr directly. The knowledge of such a relationship allows assessing Sr of partially saturated soils for both laboratory testing and in situ monitoring. In addition, some remarks on the signal interpretation are considered, defining a correction procedure to avoid any interferences due to technical issues.

2 Materials and methods

2.1 Bender element testing

The bender element (BE) is a piezoelectric transducer composed of two layers, which has two conductive outer electrodes, two piezoceramic sheets, and a conductive metal plate at the centre [19]. The use of BE in laboratory and field investigations has been widely used in geotechnical practice since they can induce an elastic stress–strain response in practically all soils without attaining the nonlinear behaviour of the material [4]. Due to the capability of BE to induce deformations in a very small-strain range, the elastic properties of the material can be measured and this enables non-destructively monitoring [37]. The most common methodologies for interpreting BE results are generally grouped into time-domain and frequency-domain methods [4]. In this study, a time-domain approach was initially adopted since it is more immediate and closer to the field geophysical testing especially [14]. Cross-correlation was not used to determine the travel time since its application supposes the input and output signals to be of the “same nature”. Indeed, such a procedure is not warranted in the case of multiple travel paths and diffraction effects [36], resulting in a more complex output signal.

Commonly, BE are used to induce S-wave. Figure 1a shows a schematic representation of the induced waves by bender elements. From this figure it can be observed that two P-wave side lobes normal to their plane, and an S-wave frontal lobe are generated. In the elastic range, the ratio between the Vp and Vs can be expressed as a function of the Poisson’s ratio:

$$\frac{{V_{{\text{p}}} }}{{V_{{\text{s}}} }} = \sqrt {\frac{{2\left( {1 - \upsilon } \right)}}{1 - 2\upsilon }}$$
(1)
Fig. 1
figure 1

Generated waves from bender elements (adapted from Lee and Santamarina [19]; Díaz-Durán [5]): a low input frequencies; b high input frequencies

Full size image

Ferreira et al. [7] demonstrated that BE can generate concurrent P- and S-waves by changing the frequency of the input signal. The results of these authors were validated by laser measurements, demonstrating that P-waves are generated by exciting the BE for high input frequencies (> 20 kHz) without using other configurations or piezoelectric transducers, such as extender elements or compressional plates. Laser results reported by these authors demonstrated that, for BE tests conducted at frequencies up to 20 kHz, polarised tip-to-tip movement induces vertical and horizontal displacements during BE testing, as also observed by Díaz-Durán [5]. Hence, S-wave is generated by input signals with frequencies between 1–15 kHz, while P-wave frontal lobe is caused by input signals with frequencies higher than 20 kHz (Fig. 1b). Besides, Ferreira et al. [7] validated the measured Vp by comparing experimental data against predicted values using Biot’s equations, showing an error below 1.5%. In this study, input signals with frequencies within a range of 1–100 kHz were covered, as discussed below.

In addition, during bender element testing, some interferences can affect either the S or P arrival time due to the complexity of piezoelectric distortion. Lee and Santamarina [19] showed that the P-wave reflected from the wall of cell triaxial can arrive earlier than the direct S-wave, and this is not supposed to be a near field effect. Since this paper deals with the dependency of the compression waves on the degree of saturation, the reflection of P-wave from the cell wall should be considered in the interpretation of the results, as far as it can alter the output signal, hiding the wave that propagates within the tri-phase material.

2.2 Experimental program and test procedures

In this study, two triaxial cells apparatus equipped with BE were used. The BE transmitter BE was excited by applying a sinusoidal pulse as an input signal [23]. Three input signals with frequencies between 1–8 kHz and 25–100 kHz were applied to generate S-wave and P-wave, respectively. The measurement of these three signals allowed minimise the uncertainty and subjectivity associated with the interpretation of BE test results; that is, misinterpretation of signals due to cross-talk or near-field effect [4]. The wave propagation travel time (tt) between the distance of the elements (Ltt) was obtained using the first arrival method [6]. The BE test set-up consists of a function generator (TTi TG1010), two input–output amplifiers (designed at the University of Western Australia), an oscilloscope (Tektronix TDS 220) and a computer with WaveStar software to acquire the wave signals. Figure 2 shows a scheme of the BE test configuration at the Geotechnical Laboratory of FEUP.

Fig. 2
figure 2

Schematic representation of BE test configuration

Full size image

Nine soil specimens of 50 mm and 70 mm diameter with an average relative density of about 40% were tested, corresponding to eight with 50 mm diameter and two with 70 mm diameter. The tests conducted in the specimens of 70 mm diameter involved the monitoring of volume change, using an automatic volume gauge instrumented with an electronic displacement transducer, to estimate the degree of saturation achieved in the specimen. These measurements were carried out for such a configuration because the greater volume of specimens allows a higher sensitivity to changes in the water content. All soil specimens were flushed with CO2 and partially saturated by flushing deaired water [35]. Afterwards, progressive increments of the backpressure (BP) were applied until achieving the full saturation condition. During this process, carried out under low effective confinement stress (\(\sigma^{\prime}_{c}\)) of 15 kPa, both Vp and B-value measurements were performed. Table 1 presents the experimental program performed in this study.

Table 1 Experimental program
Full size table

A preliminary calculation of the P-wave velocities was performed by measuring the time of wave using the procedure above referred. Moreover, the Fast Fourier Transformation (FFT) was implemented to investigate the frequency content of both input and output signals. Then, these data were associated with the B-values. Such an association is necessary to ensure a realistic interpretation of the first arrival time since the B-value measurement represents an integral response of the soil specimen, and it is the most reliable parameter to estimate the full saturation condition. As it will be shown below, a correction of the first arrival time is needed to neglect the P-waves cell wall interferences. Furthermore, a direct dependency between Vp and Sr has been performed by calibrating experimental data carried out in the 70 mm diameter triaxial cell.

2.3 Tested soil

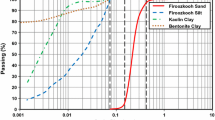
The tested soil is a silica monogranular clean sand. Figure 3 shows the grain size distribution of this soil. According to the unified soil classification system (USCS) the soil was classified as poorly-graded (SP). Table 2 summarises the physical properties measured in the laboratory of the tested soil, such as specific gravity of solid particles (Gs), mean diameter (D50), coefficient of uniformity (Cu), maximum and minimum void ratio (emax and emin).

Fig. 3
figure 3

Grain size distribution of the tested soil

Full size image
Table 2 Parameters of the tested soil
Full size table

To verify that the suction remains negligible during triaxial testing, tests on pressure plates were carried out to obtain the soil–water characteristic curve. Such tests were conducted by preparing the specimens in steel rings and fully saturating them by continuous imbibition of deaired water, following the ASTM D6836 standard [1]. Afterwards, specimens were arranged in the pressure plates. Thanks to a ceramic plate with high air entry pressure, it is possible to induce the desired suction by applying directly a specific air pressure. Hence, being the water pressure equal to the atmospheric one, the suction is easily imposed and equal to the air pressure inside the chamber (i.e. Ψ = ua − uw = ua).

The results presented in Fig. 4 confirmed that for the examined sand the suction is negligible, even a very low degree of saturation. Therefore, for the values of interest of Sr, is reasonable to consider that the gas phase distribution is discontinuous, indicating that bubbles are occluded and no-additional (suction-induced) normal forces are involved to significantly change the stiffness of the soil.

Fig. 4
figure 4

Pressure plate: experimental results

Full size image

3 Experimental results

3.1 Uncorrected output signals

The Vp values were calculated by measuring the first arrival time from the time histories of the output displacement measured at the receiving bender element in the time scale. Such a procedure considered the tip-to-tip distance between BE (specimen height of Hnominal = 110 mm). A delay of the BE system equal to 3.37E − 06 s was used for the estimation of the first arrival time. In all the tests, the BE transmitter was excited by a sinusoidal pulse with frequencies of 25, 50 and 75 kHz. These frequency values ensure that the movement of the bender can induce a compression strain in the specimen; thus, the first arrival to the receiving bender corresponds to the propagating P-wave [7]. Measurements of S-wave arrival times have been also performed by using lower input frequencies of 2, 4, 6 and 8 kHz. The results of S-wave velocity (Vs) ranged between 125 and 130 m/s in all BE tests, which correspond to lower than of the Vp results discussed below. This allowed computing the maximum shear modulus, G0, to be also determined avoiding any possible interferences with the P-wave propagation.

In Fig. 5 the time history of the output signals is shown for the ST1 test at different back-pressures (BP), as summarised in Table 3, for input frequencies of 25 and 50 kHz. It is easy to ascertain that the increase in the BP leads to a lower arrival time of the P wave, since it is increasing both the degree of saturation and the volumetric stiffness of the equivalent pore fluid. Furthermore, the first arrival time of about 70 µs, associated with a velocity of about 1360 m/s, is reached under a BP of 150 kPa, to remain quite constant afterwards, as shown in Table 3

Fig. 5
figure 5

ST1 test Normalised output signals

Full size image
Table 3 Values of ST1 Test, (Vp vs BP)
Full size table

Figure 6 shows the ST1 output signal measured for a BP of 200 kPa (Fig. 6a) and its frequency content (Fig. 6b) for an input frequency of 50 kHz. The presence of a peak is related to a frequency of about 75 kHz, higher than the input frequency of 50 kHz (dot line). The above has been interpreted as an interference of the propagated wave with possible refracted waves at the specimen boundaries or possibly of a coupled effect of the occluded air bubbles within the sample, resulting in propagation of the wave through a saturated path (i.e. no bubbles are crossed by the P-wave), as schematically shows in Fig. 7.

Fig. 6
figure 6

ST1 output signal and frequency content for BP = 200 kPa: a time-domain results; b frequency-domain results

Full size image
Fig. 7
figure 7

Schematic representation of P-wave propagation in partially saturated sands

Full size image

The experimental data are plotted in Fig. 8 to show the relation between Vp and B-value. Experimental data are contrasted against the theoretical prediction (see Sect. 3.3, Eq. 5). The interpretation of Fig. 8 allows verifying the consistency of the output data. It is clear that even for relatively low values of B-value (of about 0.70) the Vp measurements reach 1400–1500 m/s, which is the velocity of propagation of the P-wave in fully saturated soils (the well-known velocity of propagation through water). Since the B-test is an integral response of the specimen and a reliable parameter to ensure the complete saturation (i. e. B-value of about 0.95 to 0.98), such high values of Vp for B close to 0.70 are not realistic.

Fig. 8
figure 8

Correlation between Vp and B without signal correction

Full size image

Figure 8 shows higher results of measured Vp than the theoretical prediction for B-values ranging from 0.6 to 0.9, indicating that the waves propagated through a stiffer material than the unsaturated soil specimen. This might indicate that the P-waves are travelling along nearly saturated paths, randomly located within the sample, or as refracted waves along the interface between the latex membrane and the triaxial cell. The real travelled distance is not easy to be determined; however, if it is larger than the minimum tip-to-tip distance, a higher Vp would be computed. Therefore, the discrepancy between measured and predicted values of Vp in the figure does not depend on the assumption on the travel distance. Hence, the assessment of the arrival time was further investigated by inspecting the output signals in the frequency-domain.

Figure 9 presents the evolution of the P-wave in terms of frequency content for input signals of 25 and 50 kHz reported in ST1 tests (previously introduced in terms of time-domain in Fig. 5). For BP low enough to not fully saturated the specimen, the normalized FFT shows peaks higher than the nominal input frequencies, especially for output signals referred to BP of 150, 200 and 250 kPa, which correspond to B-values between 0.70 and 0.85. In these conditions, the specimen is not fully saturated yet, but occluded bubbles lie in the pore voids at approximately the same pressure of the water (i.e. high volumetric stiffness) easing the distortion and consequently the propagation of the generated P-wave through the water cell. On the contrary, when the specimen reaches the full saturation—for a BP of 400 kPa and B-value = 0.99—no occluded gas bubbles lie in the pore voids, indicating that the soil is fully saturated by water and no peaks higher than the nominal input frequencies are detected (see bold line in Fig. 9).

Fig. 9
figure 9

ST1 test Normalised output frequency spectra

Full size image

In detail, to provide further evidence of the effect of wave interference on the output signal, Fig. 10 compares the Fast Fourier Transformation (FFT) of the input signal (dashed line) to that of the output signal (solid line) for a BP of 150 kPa and 200 kPa. While the former showed a clear peak at 50 Hz—the nominal frequency of the input signal—in Fig. 10 two peaks can be observed, the first at about 50 kHz (which is comparable with the input frequency) and the second to a higher value of about 75 kHz. This second peak indicates that higher frequency content arises in the recorded signal, corresponding to the superimposition of wave fronts, as mentioned before. Therefore, a frequency content analysis of the output signal is needed to filter out spurious waves detected during the time-domain interpretation [3].

Fig. 10
figure 10

Fast Fourier transformation of the input (dashed line) and the entire output signal (solid line)

Full size image

3.2 Corrected output signals

Several output signals for different tests at different B-values are presented herewith for validating a procedure to correct the signal before carrying out data interpretation in the time-domain. Figure 11 shows the output signal referred to as an input sinusoidal wave of 50 kHz, respectively, for B-values equal to 0.701 and 0.785. These results were obtained for BP of 150 and 200 kPa, respectively. Equation (5) (see Sect. 3) provides the theoretical framework for interpreting the results of the test by correctly identifying the arrival of P-wave travelling along a truly unsaturated path. A theoretical value of the arrival time of direct P-wave travelling between the bender elements (tP), for each B-value, which is consistent with the value of Vp that corresponds to the measurement of B-value in the test can be assessed, according to the theoretical relationship of Eq. (5). Hence, for each test the starting point of the second branch of the output signal can be identified by looking at the inversion point closest to the assessed theoretical value tP (B-value). Successively, the frequency content analyses aim to validate the first arrival time of the unsaturated P-wave.

Fig. 11
figure 11

Output signal for ST1 test at BP = 150 and 200 kPa for sinusoidal input signal of 50 kHz

Full size image

In according with Gu et al. [9], for B-values higher than about 0.34, the first part of the output signal changes markedly, to further remain quite constant with increasing in the B-value. Indeed, from Fig. 11 two main branches of the signal can be observed. The above is consistent with the main findings reported in the previous section, in which two propagating wave fronts affect the receiver bender were identified. Only the second propagating wave front arises from the propagation within the partially saturated soil sample, while the first is affected either by refraction at the boundaries or by randomly distributed preferential saturated paths. Indeed, the first wave front would indicate Vp ≈ 1350 m/s, for a B-value ≈ 0.70 and 0.78 under a BP = 150–200 kPa, respectively, while the second indicates Vp = 545 m/s and Vp = 632 m/s. These results are consistent with the experimental B-value and the theoretical prediction.

Therefore, a subdivision of the signals was implemented by isolating the effect of the first wave fronts and considering the residual as the representative signals to identify the soil response (see Fig. 11). FFT has been applied to the two sub-signals, for each test. Figures 12 and 13 present the typical results in terms of frequency-domain. The spectrum of the first trains (dot lines) shows the same peaks at about 75 kHz, while no significant peaks are detected for lower frequencies. On the other hand, the frequency content of the residual signals (solid line) shows the peak for a frequency close to 50 kHz (i.e. the input frequency). A peak close to 75 kHz is still present because of the effect of the reflection induced by the surfaces waves that arrived at the BE receiver.

Fig. 12
figure 12

Fast Fourier transformation for the two sub-signals (ST1 Test, BP = 200 kPa)

Full size image
Fig. 13
figure 13

Fast Fourier transformation for the two sub-signals (ST1 Test, BP = 150 kPa)

Full size image

Furthermore, an analysis of signals referred to ST7 and ST2 tests is shown. Such tests were carried out during saturation stage for BP = 150 kPa and an input frequency of the signal of 75 kHz. Figures 14 and 15 present the output signals and their FFT, in which two events are still detected. For such tests, B-values equal to 0.83 (ST7) and 0.91 (ST2) were measured, ensuring the partially saturated condition of the specimens. As previously discussed, the first arrival time, close to 65 µs (first narrow in both tests), lead to a Vp ≈ 1490 m/s, so that the specimens should be fully saturated. If the first sub-signals are neglected and the second sub-signals showed in Figs. 14 and 15 are considered, the arrival time measured leads to a Vp ≈ 854 m/s and Vp ≈ 938 m/s—for ST7 and ST2 tests, respectively, in accordance with the measured B-value.

Fig. 14
figure 14

ST7 output signal and frequency content for BP = 150 kPa: a time-domain results; b frequency-domain results

Full size image
Fig. 15
figure 15

ST2 output signal and frequency content for BP = 150 kPa: a time-domain signal; b frequency-domain signal

Full size image

By applying the FFT for the entire signals, different peaks can be detected: the first, close to 50 kHz, and the second close to 100 kHz, higher than the input frequency applied. Therefore, a frequency content analysis was performed by dividing the output signals, isolating the interference waves that affects the interpretation. Figures 16 and 17 show the FFT results of two signals interpretation, one with the interference waves and the other with the corrected waves. If the first sub-signals are neglected, the frequency content of the residual signals show a peak close to 50 kHz, similar to the one shown in the ST1 test, while the interference waves present a peak close to 100 kHz. These results lead to an interesting consideration: the partially saturated soil response seems to be almost frequency independent and included between 30 and 50 kHz. Notwithstanding, a higher frequency content affects the signals, probably due to any interferences with the boundary conditions (e.g. membrane-water and triaxial chamber interfaces) or with randomly distributed preferential saturated paths.

Fig. 16
figure 16

Fast Fourier transformation for the two sub-signals (ST7 Test)

Full size image
Fig. 17
figure 17

Fast Fourier transformation for the two sub-signals (ST2 Test)

Full size image

This issue suggested individually investigating the role of the soil skeleton and the pore water by performing two different additional tests. Such tests were carried out for: (i) a dry specimen to assess the soil skeleton response, and (ii) a completely water-filled chamber without a sample to simulate the pore water response. Both tests are performed with an input frequency of 25 kHz, lower than the other ones, to investigate the frequency-independent response. Figure 18 shows these results in terms of FFT approach. For the dry sample, a peak was detected for a frequency between 10 and 20 kHz, which represents the soil skeleton response under the applied frequency input. On the other hand, for the test on the chamber filled with water, it is clear a higher frequency content included between 30 and 50 kHz regarding the water response under the applied input frequency. Such a response can be associated with the pore water response in a partially saturated sample test.

Fig. 18
figure 18

FFT for dry sample and chamber completely filled with water

Full size image

Figure 19 shows the comparison between the water and dry soil response—already reported in Fig. 18—and the fully and partially saturated soils. The FFT of the Partially saturated soils, performed for 25 50 and 75 kHz of input nominal frequency, confirm that the response in terms of frequency content, for the corrected signals, lie with a good approximation between the range discussed above—30 and 50 kHz—associated with the wave propagating within the three-phase material.

Fig. 19
figure 19

Frequency response for water, dry/fully/partially saturated soils

Full size image

The results in Figs. 18 and 19 confirm that there are two different responses, in terms of frequencies, of the soil skeleton and the pore water. When a partially saturated sample is subjected to BE distortion, the pore water response becomes predominant, and the most representative peak is due to the propagation of the wave through the bi-phase pore fluid. The soil skeleton response, at lower frequencies, is not appreciable (see Figs. 12 and 16). Such results also confirmed that the higher frequencies of 75 and 100 kHz obtained in the previous tests are due to an interference with the apparatus or to the water-membrane interface and they must be neglected during the signal manipulation.

Therefore, the subdivision of the signals in different branches and the respective analysis on the FFT can support the neglecting of interferences, resulting in frequency peaks higher than the input frequency content. The knowledge of the nominal frequency of the input signal and its frequency content is necessary to evaluate the output signals by deleting the wave fronts. This procedure was carried out to correct the experimental data of all tests, leading to higher frequency peaks in the FFT. Figure 20 shows the relationship between B-value and Vp after applying the data correction. These results show a good fitting with the theoretical values, calculated by applying the model proposed by Yang and Sato [39] (see Sect. 3.3, Eq. 5) and the parameters of Table 4—derived using the Vs measurements, obtained from BE tests at lower frequencies (between 1 and 8 kHz).

Fig. 20
figure 20

Correlation between Vp and B after frequency analysis correction

Full size image
Table 4 Elastic parameters
Full size table

3.3 Experimental correlation between P-wave velocity and degree of saturation

Two tests on the 70 mm triaxial cell equipped with bender elements were conducted to derive a direct relationship between the Vp and the degree of saturation. In such tests, the degree of saturation was experimentally estimated by considering a balance of the water flow during all triaxial testing—represented by the initial flushing and the saturation stages, under the increasing of the BP. On the other hand, for the tests in the 50 mm apparatus, the degree of saturation has been changed by increasing the BP values, allowing dissolving the occluded air bubbles in the water. The experimental data in terms of Sr were related to Vp to have a theoretical relationship to fit the experimental results with an equation that relates Vp − Sr.

It is well known that B-value is usually used to measure the full saturation condition in element testing (e.g. triaxial, resonant column or hollow cylinder). Its measurement, carried out in undrained condition, represents an integral response of the specimen under the increment of the total stresses, in radially symmetric conditions, and can be experimentally found as B = ∆u/∆σ easily. On the other hand, the B-value can be theoretically expressed as [29]:

$$B = \frac{1}{{1 + n\frac{{K_{{\text{b}}} }}{{K_{{\text{f}}} }}}}$$
(2)

where n is porosity, Kb is the bulk modulus of the soil skeleton and Kf is the bulk modulus of the pore fluid. When a specimen is considered to be partially saturated, as defined above, the equivalent pore fluid bulk modulus, Kf, can be expressed as a function of the degree of saturation as follows [39]:

$$K_{{\text{f}}} = \frac{1}{{\frac{1}{{K_{{\text{w}}} }} + \frac{{\left( {1 - S_{{\text{r}}} } \right)}}{{P_{{{\text{w}},{\text{abs}}}} }}}}$$
(3)

with Kw bulk modulus of water and Pw,abs absolute water pressure. With such basis, B is considered to be a linking parameter to the degree of saturation [38]:

$$B = \frac{1}{{1 + n\frac{{K_{{\text{b}}} }}{{K_{{\text{w}}} }} + n\frac{{K_{{\text{b}}} }}{{P_{{\text{w,abs}}} }}\left( {1 - S_{{\text{r}}} } \right)}}$$
(4)

Many authors have used a theoretical simplified relationship based on the P-waves velocity linked with the bi-phase nature of the pore fluid and the B-value [39]:

$$V_{{\text{p}}} = \left( {\frac{{\frac{4}{3}G_{0} + \frac{{K_{{{\text{b}},0}} }}{{\left( {1 - B} \right)}}}}{{\left( {1 - n} \right)\rho_{{\text{s}}} + n\rho_{{\text{f}}} }}} \right)^{1/2}$$
(5)

where (1 − n) ρs + n·ρf is the total density of the soil, ρ, and G0 the maximum shear modulus. Hence, since the equation relates Vp with B-value, and the latter is connected to Sr in turn, a direct link could be derived between Vp and Sr.

Therefore, a direct link between Vp and Sr is obtained by replacing Eq. (4) in Eq. (5). Note that both equations include the bulk modulus of the soil skeleton; that is, Kb and Kb,0 for Eqs. (4) and (5), respectively. The above is because B-tests are related to a strain level higher than one referred in the BE tests. Moreover, the BP increment during testing must be considered since it reduces the size of gas bubbles and then the response of the soil in terms of the B-value. Figure 21 shows an experimental relationship between the BP and B-value.

Fig. 21
figure 21

Experimental correlation between applied back pressures and achieved B-values

Full size image

The relationship between Vp with Sr is plotted in Fig. 22. This relationship was obtained using the parameters referred in Table 5, in which the compressibility, Kb, has been reasonably changed to obtain the best fitting with the experimental data. Note that the ratio between the Kb and Kb,0 is about 0.18 which is, as order of magnitude, the decrease in the stiffness from very low strain level, to higher ones.

Fig. 22
figure 22

Experimental fitting between Vp and Sr

Full size image
Table 5 Elastic properties for application of theoretical model
Full size table

Thanks to this calibration in terms of Kb, Sr values could be obtained from B-values, by using Eq. 6, in which the Pw,abs has been considered to be a function of the B-value itself, thanks to the experimental correlation shown in Fig. 21.

$$S_{{\text{r}}} = \frac{{\left\{ {B \cdot \left[ {1 + nK_{{\text{b}}} \cdot \left( {\frac{1}{{K_{{\text{w}}} }} + \frac{1}{{P_{{\text{w,abs}}} }}} \right)} \right] - 1} \right\}}}{{B \cdot n \cdot K_{{\text{b}}} }} \cdot P_{{\text{w,abs}}}$$
(6)

The results are shown in Fig. 23. For the purpose to underline the effect of the pore pressure (i. e. the compressibility of the air bubble) in Fig. 23 are also shown the trend of the theoretical curves for constant values of backpressure, ubp = 0 kPa and ubp = 300 kPa. As it is shown, by considering the real increments of the backpressure, the theoretical curve fit better the data, since it is considering the changes in the stiffness of the pore fluid—due to the incremental changes of the BP.

Fig. 23
figure 23

Final correlation between Vp and Sr for different backpressures

Full size image

4 Conclusions

The sensitivity of both B-value and P-wave velocity has been examined in this paper. B-value tests represent an integral response of the specimen, in terms of degree of saturation, while bender element tests, although they show a high sensitivity to the degree of saturation, need a carefully interpretation of the data. The stiffer path the wave propagates through, or apparatus-effects such surface waves across the water cell, can significantly affect the experimental data interpretation.

The frequency content analysis leads to a reasonable correction of the first arrival time, based on the neglecting of the wave trains at higher frequency content, probably due to an amplification of the frequency itself at the interface water cell-membrane or a stiffer-fully saturated path. Frequency content analysis on the dry soil and water cell tests also shows that the pore fluid response is predominant in BE tests (until a certain level of Sr is achieved) and almost frequency independent, demonstrating that higher frequency contents are related any interferences within the test apparatus. Such interferences seem to be highly related to the B-value and BP.

For B-values between approximately 0.7 and 0.9, corresponding to the partially saturated conditions, the higher volumetric stiffness—corresponding to the high BP required to saturate the soil specimen—facilitates the distortion and consequently the propagation of the generated P-wave through the water cell or the saturated path, randomly located within the soil. Hence, the knowledge of the input nominal frequency is fundamental to manipulate the output signal, avoiding any type of interference waves that could lead to a misleading elaboration of the output data.

The relationship between Vp and Sr must consider the nonlinear behaviour of the soil due to different strain levels induced in BE and B-value tests and the effects of the backpressure. For practical use of the Vp to check the degree of saturation in real scale problems, the results show that they are not able to verify the degree of saturation lower than 95%. This effect is due to the role of the soil skeleton becomes predominant compared to the equivalent pore fluid, in contrast to almost saturated conditions (95 < Sr < 100%).