1 Introduction

The hole erosion test (HET) was developed by Wan and Fell [21] to simulate piping erosion and to evaluate the erosion parameters of cohesive soil. The HET was confirmed to be an excellent tool in quantifying the rate of erosion in concentrated leak in a soil [3]. Over time, the HET was subjected to many modifications and improvements in the test setup and the test interpretation [4,5,6, 8, 11, 12, 14, 16, 23]. In the HET a soil is compacted inside a standard compaction test mould and an axial hole is drilled along the soil specimen. The flow through the hole in the specimen is driven by a head difference between a high-level tank upstream the specimen and a low-level tank downstream of it. The flow through the hole causes the hole diameter to increase with time due to the erosion process. The flow rate and the hydraulic head difference between upstream and downstream of the specimen are measured during the test. The final hole diameter is measured at the end of the test using, for example, a plaster cast of the hole.

By applying a force balance on a volume of fluid in a pipe in the direction of flow, the shear stress acting on the hole boundary can be expressed as shown in Eq. 1.

$${\uptau }_{\mathrm{b}}={\uprho }_{\mathrm{w}}\mathrm{g}\frac{\Phi }{4}\frac{\Delta \mathrm{h}}{\mathrm{L}}$$
(1)

where Tb is the hydraulic shear stress (N/m2), ϕ is the hole diameter (m), ∆h is the hydraulic head difference between upstream and downstream the specimen (m), L is the length of the specimen (m), ρw is the water density (kg/m3) and g is the acceleration of gravity (m/s2). Since the flow in the HET is turbulent [2], the hole diameter (ϕt) at time t during the test is estimated using Eq. 2 for turbulent flow condition [21].

$${\Phi }_{\mathrm{t}}={\left(\frac{64{\mathrm{Q}}_{\mathrm{t}}^{2}{\mathrm{f}}_{\mathrm{Tt}}}{{\uppi }^{2}{\uprho }_{\mathrm{w}}\mathrm{g}\frac{{\Delta \mathrm{h}}_{\mathrm{t}}}{\mathrm{L}}}\right)}^{1/5}$$
(2)

where Qt is the flow rate (m3/s), fTt (kg/m3) friction factors linking the shear stress to the mean flow velocity. The friction factor at the beginning and at the end of the test can be calculated since the initial hole diameter is known and the final hole diameter can be measured at the end of the test. During the test, the friction factor is assumed to vary linearly with time [21]. However, Lim [10] found that the friction factor does not vary linearly with time, rather with hole diameter and flow rate. Wahl et al. [20] found a linear relation between friction factor and hole diameter and a linear trend between friction factor and time but only with a low coefficient of determination R2. The linearity between friction factor and hole diameter according to Lim [10] was applied by Khoshghalb et al. [9] in the analysis of the HET. However, Lim [11] and Wahl et al. [20] carried out several HETs on different specimens, where they stopped the HETs at different flow rates and measured the hole diameter at the end of each test. They calculated the initial and final friction factors for each test and plotted them against, for example, the hole diameter. In this way, the friction factors were calculated for different specimens in which the preparation of the specimens could result in some differences in the specimen properties and the erosion process. In the present study, the friction factor was investigated in the same specimen using µCT-scan.

The erosion rate per unit surface area of the hole is calculated using Eq. 3.

$$\dot{\upvarepsilon }=\frac{{\uprho }_{\mathrm{d}}}{2}\frac{\mathrm{d\Phi }}{\mathrm{dt}}$$
(3)

where ϕ is the hole diameters (m), t is the time (s) and ρd is the dry density of the soil (kg/m3).

By plotting the erosion rates against the hydraulic shear stresses, a nearly linear relationship is obtained, which is used to determine the erosion characteristics of the soil [7, 21]. Wan and Fell [21] defined the slope of the line of best fit in the aforementioned relation as the coefficient of soil erosion Ce and proposed the erosion rate index I to be calculated as shown in Eq. 4.

$$\mathrm{I}=-\mathrm{log}\left({\mathrm{C}}_{\mathrm{e}}\right)$$
(4)

Wan and Fell [21] classified the soil based on the erosion rate index into six categories, from extremely rapid erodible soil at I < 2 to extremely low erodible soil for I > 6.

In this study, µCT was used to investigate the assumption regarding the friction factor, which is necessary to interpret the HET. Furthermore, based on the results of the µCT, a proposed method for interpreting the HET for high plastic clay is introduced. Finally, the proposed and previous interpretation methods were applied to a HET and the results were compared.

2 Experiments and methods

2.1 Hole Erosion test

2.1.1 Device setup

A modified hole erosion test developed at the German Federal Waterways Engineering and Research Institute [8] on the basis of HET-P [12] was used in this study (Fig. 1). The specimen cylinder is made of Plexiglas and has an internal diameter of 7.8 cm and a length of 12.8 cm. The length of the Plexiglas pipe upstream and downstream the specimen is 40 and 60 cm, respectively. The head difference between high-level tank and low-level tank is adjustable and can reach 2.9 m. The flow through the specimen is driven by a constant head difference between the high-level and the low-level tanks. A differential pressure sensor was used to measure the pressure difference between upstream (hu) and downstream (hd) the specimen. The flow rate was measured downstream the specimen using a magnetic-inductive flowmeter (MID). The vertical aligned of the device helps producing a symmetrical hole and prevent accumulation of the eroded material in the hole [5]

Fig. 1
figure 1

Hole erosion test device: a device setup; b device photo with a PVC specimen

Full size image

A collecting tank downstream the low-level tank was installed with a pump to recirculate the water back to the high-level tank and to collect the overflow from the high-level tank.

2.1.2 Test material

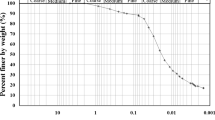
Two high plastic clays, namely Nottenkaemper (NTK) clay and Hohenwarsleben (HWL) clay, were used in the HETs. The grain size distribution of NTK and HWL is shown in Fig. 2. The characteristics of each clay type are shown in Tables 1 and 2. Both clay types are typically used as sealing material in the waterways in Germany, more specific for canals, which are built above the ground water level (Fig. 3). Due to ship-induced hydraulic actions on the sealing and possible damages caused by plant roots, the erosion resistance of the clay needs to be investigated.

Fig. 2
figure 2

Grain size distribution of NTK and HWL

Full size image
Table 1 Properties of Nottenkaemper (NTK) and Hohenwarsleben (HWL) clay samples
Full size table
Table 2 Clay mineral content [%]
Full size table
Fig. 3
figure 3

Installation of a sealing clay layer underwater condition (BAW Image archive)

Full size image

In addition, four PVC specimens (Fig. 1b) with different diameters (9, 12, 16 and 30 mm) were used to investigate the relationship between the hole diameter and the flow rate in the HET.

2.1.3 Specimen preparation

The soil was compacted inside the specimen cylinder. The specimen was prepared in three layers each one compacted using Proctor hammer (Fig. 4a).

Fig. 4
figure 4

Schematic representation of the specimen preparation: a layer compaction; b preparation of the hole; c anti-slip sup-port; d installation of the specimen cylinder in the test chamber

Full size image

The specimens were prepared at an undrained shear strength cu = 20 kPa which is required for the installation of the clay layers under water condition according to the guidelines of the Federal Waterways Engineering and Research Institute. A Laboratory vane shear apparatus was used to determine the water content required to arrive at cu = 20 kPa. The hole was introduced by inserting the copper pipe by hand through the soil. Two guide PVC plates were used to ensure the accuracy while inserting the copper pipe in the specimen (Fig. 4b). Before installing the specimen cylinder in the specimen chamber (Fig. 4d), a Plexiglas ring is installed beneath the specimen to avoid sliding of the specimen during the test (Fig. 4c).

2.1.4 Test programme and procedure

Two HETs were conducted to investigate the relationship between friction factor and hole diameter, flow rate and time as well as the relation between hole diameter and flow rate. Two specimens, one obtained from NTK clay and the other one from HWL clay, were used in the tests. The two HETs were combined with µCT for measuring the hole diameter several times during the test in an interrupted test run, i.e. the HET was paused after a preset time and the specimen cylinder was dismantled and transported to the µCT (Sec. 2.2.2) for measuring the hole diameter. After performing the µCT-scan, the specimen cylinder was installed again in the HET device and the test was continued to the next stop point. At the end of the HET gypsum was poured inside the hole to get the hole plaster cast, which was subsequently scanned using photogrammetry (Artec 3D Scanner, Sec. 2.2.1) to capture the hole geometry (Fig. 6). The results of the photogrammetry scan were compared with the µCT results (Sec. 2.2.2). To investigate further the relationship between the flow rate and the hole diameter, four HETs were carried out on the four PVC specimens (Sec. 2.1.2). The flow rate in each test was measured using a magnetic-inductive flowmeter (MID). Since the hole diameters of the PVC specimens are known, the relationship between the hole diameter and the flow rate was established (Sec. 3.4) and a proposed method for interpreting the HET was introduced. One HET on NTK clay was performed to compare the analysis of HET using the proposed and the previous interpretation methods. The boundary flow condition in all HETs was kept constant (head difference of 2.9 m).

2.1.5 Estimation of the friction factor

The estimation of the friction factor is essential for the interpretation of the HET. The friction factor is usually divided into skin friction (grain friction) and form friction [1, 2, 24]. The irregularities in the HET may increase the contribution of the form friction. However, the role of these two kinds of friction on cohesive soils as well as in pipe flow is not fully understood [2]. The investigations herein address how the friction factor develop during a HET test.

The friction factors fTt can be calculated using Eq. 2. Instead of ∆h, the effective hydraulic head difference ∆heff was used to account for the entrance and exit losses. Equation 5 is used to calculate the effective hydraulic head difference. Considering that the edge of the hole at the entrance is quickly rounded after the start of the test, the entrance losses coefficient KEnt can be taken as 0.05 [22]. The exit losses can be estimated using Eq. 6 [22]. The consideration of the local head losses was highlighted in different studies [2, 11, 13, 17]. Neglecting the local head losses results in significantly overestimating the hydraulic shear stress.

$${\Delta \mathrm{h}}_{\mathrm{eff}}={\mathrm{h}}_{\mathrm{u}}-{\mathrm{h}}_{\mathrm{d}}-\left[{\mathrm{K}}_{\mathrm{Ent}}\frac{{\mathrm{v}}^{2}}{2\cdot \mathrm{g}}+{\mathrm{K}}_{\mathrm{Ext}}\frac{{\mathrm{v}}^{2}}{2\cdot \mathrm{g}}\right]$$
(5)

where KEnt and KExt are the and the entrance and the exit losses coefficient, respectively, and hu and hd are the hydraulic head upstream and downstream the specimen, respectively.

$${\mathrm{K}}_{\mathrm{Ext}}={\left[1-\frac{{\mathrm{\varnothing }}_{\mathrm{h}}^{2}}{{\mathrm{\varnothing }}_{\mathrm{p}}^{2}}\right]}^{2}$$
(6)

where ϕh is the hole diameter [m] and ϕp is the pipe diameter downstream the specimen [m].

2.2 Measurement of the hole diameter

The determination of the final hole diameter is very important for the interpretation of the HET. However, difficulties in determining the hole diameter arise when the hole size is not uniform throughout the hole length. Different methods were applied to measure the final hole diameter. Lim [10] cut the specimen in three location and directly measured the hole diameter with a calliper. Using a plaster cast of the hole similar to that in Fig. 6a, more direct measurements of the hole diameter were taken with the calliper [11, 20]. The measurement of the hole diameter with the calliper may incorporate some inaccuracies, considering that the shape of the hole, in many cases, is not perfectly circular. Haghighi et al. [6] poured molten paraffin into the eroded hole and used the volume of the paraffin after it solidifies to calculate the hole diameter. In this paper, two methods were used to measure the hole geometry of the clay specimens, namely µCT-scan and photogrammetric 3D scanning of the hole plaster cast.

2.2.1 Micro-computed X-ray tomography (µCT)

The µCT-scans were performed on two clay specimens (4 scans on the NTK clay specimen and 5 scans on the HWL clay specimen). The samples were properly sealed with plastic foil and two plastic covers at both sides to avoid changes in the water content of the specimens (Fig. 5a). The µCT-scans were carried out using the YXLON CT Precision computed tomography system. The parameters of the µCT-scan are shown in Table 3. For the investigated specimen, the reflection tube head Y.FXE 225.48 with an acceleration voltage of 170 kV and a current of 0.2 mA was chosen. The specimen (Fig. 5a) was positioned on the rotatable plate between tube and detector with a focus-sample distance of 321.43 mm and a sample-detector distance of 578.57 mm. The resulting cubic voxel size of the reconstructed images is 71.43 µm. This allowed to fit the entire specimen in one image (Fig. 5b, c). At defined rotation angles, 2400 projection images were acquired by the detector. From these two-dimensional projection images, a volumetric image of the sample was reconstructed, which allows the visual inspection of the hole with sectional images.

Fig. 5
figure 5

µCT-scan No. 4 on NTK: a specimen photo; b µCT projection of the vertical cross section; c µCT projection of the horizontal cross section

Full size image
Table 3 µCT-scan parameters for the investigated sample
Full size table

The reconstructed sectional images of the specimen were evaluated using the open-source software ImageJ [18, 19]. Using this software, the images were segmented in order to subdivide the voxels in two areas: “hole” and “material”. For this purpose, the thresholding algorithm following Otsu [15] was applied. Afterwards, the acquired binary images were evaluated to determine the area of the hole over the height of the specimen at spacing of the voxel size. The equivalent hole diameter at each height ϕh was calculated over the specimen height from the determined hole area at each height Ah using Eq. 7.

$${\mathrm{\varnothing }}_{\mathrm{h}}= \sqrt{\frac{4{\mathrm{A}}_{\mathrm{h}}}{\uppi }}$$
(7)

The hole diameter was averaged over the specimen height to get hole diameter, which was used in the analysis of the HET.

2.2.2 Photogrammetric 3D scanning of the hole plaster cast

The hole diameter was measured at the end of the HET using a 3D scanner in order to confirm the accuracy of the µCT-scan.

The hole plaster cast was scanned using a professional handheld photogrammetric 3D scanner (Artec MHT 3D scanner). The plaster cast of the hole (Fig. 6a) was set on a rotating table and the 3D scanner (Fig. 6c) was oriented at the plaster cast and fixed while scanning. The photogrammetry scans were carried out from a distance of about 0.5 m to the plaster cast resulting in a nominal accuracy of about 0.1 mm.

Fig. 6
figure 6

Photogrammetric 3D scanning of the hole plaster cast: a photo of the plaster cast of the hole; b 3D model of the hole plaster cast; c Artec MHT 3D Scanner

Full size image

Using the 3D model of the hole (Fig. 6b), the cross-sectional area of the hole Ah at different heights was calculated with the scanner’s software. The hole diameter ϕh at height h of hole is calculated using the area Ah as shown in Eq. 7.

The final hole diameter is calculated as the average diameter over the height of the hole.

3 Results and discussion

3.1 Hole diameter

Using the µCT-scan, the hole diameter was determined at different time intervals for NKT clay and HWL clay. The hole diameter over the specimen height for different µCT-scans is shown in Fig. 7. The final hole diameter for each scan was calculated as the average diameter over the specimen height. The µCT-scan analysis allowed identifying some weak areas in the specimen, which causes irregularities in the geometry of the hole. Figure 8 shows trapped air in the specimen, i.e. voids in the first scan (µCT-scan 1) at a height of about 60 mm of the specimen. While the hole diameter increased in the HET, the voids were connected to the hole causing large local erosion and large hole diameter see µCT-scan 4 in Fig. 8. The large hole diameter at the weak areas was excluded when calculating the average hole diameter.

Fig. 7
figure 7

Hole diameter over the specimen height: a NTK clay specimen, to the right selected projection images for weak area in the specimen causing spikes in the hole diameter as the HET progresses; b HWL clay specimen

Full size image
Fig. 8
figure 8

Projection µCT-scan images for weak area in NTK specimen at height of approx. 60 mm at the begging and at the end of the HET

Full size image

To confirm the accuracy of the µCT-scans, the results of the µCT-scan at the end of the HET was compared with the results of the photogrammetric 3D Scanner (Fig. 9). A good agreement between the hole diameter measured using the µCT and the photogrammetric 3D Scanner was found. The average root mean square error was 0.55 mm and 0.28 mm for NTK and WHL specimens, respectively.

Fig. 9
figure 9

Final hole diameter over the height of the specimens measured using µCT-scan and the photogrammetric 3D scanner: a NTK clay specimen; b HWL clay specimen

Full size image

3.2 Relationship between friction factor and hole diameter in the HET

The µCT-scan measurements of the hole diameter at different time steps during the HET allowed calculating the friction factor using Eq. 2 and therefore investigating the evolution of the friction factor in the HET. The relationship between the friction factor and the hole diameter for the NTK clay and the HWL clay is shown in Fig. 10. The friction factor was calculated for two cases (i) considering the local head losses and (ii) without considering the local head losses according to Wan and Fell [21]. For both cases, the friction factor exhibited a linear correlation with the hole diameter with high coefficients of determination R2 (Fig. 10). However, the friction factor calculated without considering the local head losses was more than twice as high as the friction factor calculated considering local head losses.

Fig. 10
figure 10

Relationship between the friction factor and the hole diameter: a for NTK clay; b for HWL clay

Full size image

3.3 Relationship between friction factor and flow rate in the HET

Fitting a linear trendline for friction factor and flow rate, relatively high R2 can be obtained (Fig. 11). However, considering R2, the friction factor correlates linearly with the hole diameter better than the flow rate. These results agree well with the finding of Lim [10]. In fact, a logarithmic trendline with R2 of 0.96–0.98 fits the friction factor and the flow rate data better than a linear trendline (Fig. 11).

Fig. 11
figure 11

Correlations between the friction factor and the flow rate: a for NTK clay; b for HWL clay

Full size image

3.4 Relationship between friction factor and time in the HET

By plotting the friction factor versus time, an exponential trendline can be fitted with a high R2 (Fig. 12a, c). Fitting a linear trendline to the data showed slightly lower R2 than in the case of the exponential trendline (Fig. 12b, d). It is to be noted that there were no data around the first half duration of the test except at t = 0. In this period, there was a very small increase in the flow rate with time, therefore, no µCT-scans were carried out. Wahl et al. [20] found a general linear trend between friction factor and time but with a low R2. In contrast, Lim [10] found that the friction factor does not correlate with time at all. Both Lim [10] and Wahl et al. [20] used the initial and the final data of several HETs (different specimens) to study the relation between the friction factor and time. This results in a high scatter of the data as the erosion process in different specimens could be different due to, for example, the preparation of the specimens. The analysis of the HET analysis using exponential and linear relation between the friction factor and time is presented in Sect. 4. Analysing the HET using an exponential relation between friction factor and time showed significantly higher correlation between erosion rate and hydraulic shear stress than the analysis assuming that the friction factor varies linearly with time (Fig. 16).

Fig. 12
figure 12

Correlations between the friction factor and time: a, b for NTK clay specimen; c, d for HWL clay specimen

Full size image

3.5 Relationship between flow rate and hole diameter

The results of the HETs and the µCT-scans for both clay types showed a linear correlation between the flow rate and the hole diameter in the range of the measured diameters (Fig. 13). However, it can be noted that the first points in Fig. 13a, b are slightly below the line of best-fit, indicating a slightly higher flow rate than that estimated with the line of best-fit. This can be attributed to the smooth sidewalls of the hole at the beginning of the test due to the preparation of the hole with the copper pipe.

Fig. 13
figure 13

Variation of the hole diameter with the flow rate: a for NTK clay; b for HWL clay

Full size image

The relationship between the hole diameter and the flow rate was further investigated using the PVC specimens. The results of the HETs with the PVC specimens confirmed the linear variation of the flow rate with the hole diameter in the range of the tested hole diameters (Fig. 14).

Fig. 14
figure 14

Variation of the hole diameter with the flow rate for in the HETs with PVC specimens

Full size image

4 Proposed method for interpretation of the HET

A simplified interpretation method of the HET on high plastic clay is presented. The proposed interpretation method is based on the linear correlation between the hole diameter and the flow rate addressed in Sec. 3.4. Since the initial and final hole diameters in the HET are known, the hole diameter at time t (ϕt) can be calculated using the flow rate as given in Eq. 8.

$${\Phi }_{\mathrm{t}}={\Phi }_{\mathrm{i}}+\left(\frac{{\Phi }_{\mathrm{f}}-{\Phi }_{\mathrm{i}}}{{\mathrm{Q}}_{\mathrm{f}}-{\mathrm{Q}}_{\mathrm{i}}}\right)\left({\mathrm{Q}}_{\mathrm{t}}-{\mathrm{Q}}_{\mathrm{i}}\right)$$
(8)

The initial hole diameter ϕi is the diameter of the copper tube used to prepare the hole in the specimen (8 mm). The final hole diameter ϕf can be measured at the end of the test using a plaster cast of the hole. Since the flow rate Qt is measured continuously during the HET, the hole diameter ϕt can be calculated at any time during the test. Accordingly, the erosion rate \(\dot{\varepsilon }\) (m/s) can be calculated as the change of the hole diameter with time. Using the hole diameter, the local head losses can be calculated and therefore the effective hydraulic head difference can be obtained using Eq. 5. Ultimately, the hydraulic shear stress is calculated using Eq. 1 and the relationship between the erosion rate and the hydraulic shear stress can be established. In the proposed method there is no need to use Eq. 2 with the impeded assumptions regarding the relationship between the friction factor and hole diameter, flow rate or time.

To compare the results of the proposed analysis method and previous analysis methods of Wan and Fell [21] and Lim [10], one HET was carried out on NTK clay. The flow condition in the test was turbulent and the local head losses were considered in the analysis of the HET. The hydraulic head difference between upstream and downstream the specimen (∆h) and the flow rate (Qt) during the HET test are shown in Fig. 15. The erosion rate and the hydraulic shear stress calculated using the proposed method are shown in Fig. 16a. The results of the HET considering that the friction factor varies linearly with the flow rate or with the hole diameter are shown in Fig. 16b, c, respectively. The analysis using the assumption of Wan and Fell [21] that the friction factor varies linearly with time is shown in Fig. 13d. The correlation between the erosion rate and the hydraulic shear stress using exponential relation between the friction factor and time was higher than the one using the aforementioned assumption of Wan and Fell [21] and Lim [10].

Fig. 15
figure 15

Flow rate and hydraulic head difference in the HET

Full size image
Fig. 16
figure 16

Erosion rate and hydraulic shear stress using different HET analysis methods: a proposed method (ϕ varies linearly with Q); b fTt varies linearly with ϕ; c fTt varies linearly with Q; d fTt varies linearly with t, e fTt varies exponentially with t

Full size image

The proposed analysis method showed the highest R2 (Fig. 16a) and the lowest critical shear stress and erosion rate index (Table 4). Considering the investigation of the sealing clay resistance against erosion, the new analysis method is recommended, since it provides conservative erosion parameters of the soil, i.e. lowest critical shear stress and erosion rate index. All analysis methods resulted in almost the same erosion rate index and therefore the same classification of the soil as extremely low erodible according to the classification of Wan and Fell [21].

Table 4 Hole erosion test results using different analysis methods
Full size table

5 Conclusion

Micro-computed X-ray tomography (µCT) was successfully employed to measure the hole diameter inside the specimen at different time intervals during the HET. The results of the µCT-analysis directly at the specimen showed a good agreement with results on a plaster cast of the hole determined using a photogrammetric 3D scanner confirming the accuracy of capturing the hole geometry by the µCT-scan. HETs were combined with µCT-scans, to investigate the relations between the friction factor and the hole diameter, flow rate and time. The friction factor was calculated by combining the measured head difference and the flow rate measured in the HET together with the measured hole diameter from the µCT-scan. The friction factor during the HET correlates linearly with the hole diameter. A logarithmic trendline fits the friction factor and the flow rate data better than a linear trendline. Moreover, an exponential relation between friction factor and time was noted. Results of the µCT-scans and the HET data showed that the hole diameter correlates linearly with the flow rate in the range of the herein tested hole diameters. This allowed using the flow rate to estimate the hole diameter, given that the initial and the final hole diameters are known. Accordingly, a simplified method for interpreting the HET on high plastic clay was proposed. The results of the HET analysis using the proposed and previous analysis methods of Wan and Fell [21] and Lim [10] were compared. The proposed method showed the highest correlation between the erosion rate and the hydraulic shear stress and the lowest critical shear stress.