1 Introduction

Some rocks and soils tend to expand upon wetting due to their content of swellable clay minerals. They are commonly referred to as expansive geomaterials. Swelling can manifest itself in the form of swelling deformations or swelling stresses. While the tendency of a material to swell depends on its mineralogical composition, the swelling phenomenon (development of swelling strain or swelling stress) is largely dependent on the mechanical and hydraulic boundary conditions to which the material is subjected as well as the material properties. Reciprocally, the material properties are also affected by changes in water content. An adequate prediction of this hydro-mechanical coupled material behaviour, especially the maximum stresses or strains that can be reached during wetting, is essential for a reliable design of underground structures in contact with or embedded in expansive geomaterials.

In some practical cases, those predictions are obtained from semi-empirical extrapolations of results from laboratory tests following the Huder-Amberg-method [16] or similar according to the swelling law by Grob [13]. This law, however, focuses on the estimation of the expected deformation during unloading processes in the fully saturated state (i.e. a change in the mechanical boundary conditions) and does not consider any time effects. Further developments of this fundamental law have been implemented in several FE codes to analyze problems related to tunneling and swelling rocks and soils [3, 15]. At their basis, these models often consider a separate additional strain component for swelling in an elasto-plastic framework.

On the other hand, sophisticated constitutive models based on the Barcelona Basic Model (BBM) [1], which extends the capabilities of the CamClay model [34], have been used over the last decades to simulate the mechanical response of partially saturated soils during the installation of geotechnical constructions, e.g. by Toprak et al. [39].

The BBM can simulate the most prominent features of unsaturated soils like the apparent increase of the preconsolidation pressure due to partial saturation as well as the soil expansion or soil collapse upon changes in the degree of saturation. However, some important aspects of the behaviour of expansive soils could not be captured by the BBM as the model was not originally developed for materials with swellable clay minerals. Missing features are the influence of the loading history on the swelling strains and the swelling stresses, the reduction of the elastic stiffness with increasing saturation, and the strain accumulation upon wetting-drying cycles [2, 10, 12]. To improve the response of the BBM for expansive soils during wetting-drying cycles, Gens and Alonso [2, 12] introduced the concept of microstructure into the BExM model. The macrostructural deformation due to wetting of an expansive soil is assumed to be a mechanical response to reversible strains in the microstructure which manifests itself in the evolution of the pore structure from a bi- to a mono-modal distribution [2, 12]. Another approach extending the BBM was followed by Dieudonne et al. [10] amongst others [9, 33], who introduced the concept of microstructure in the hydraulic model instead of the mechanical model. Similar efforts for bi-modal soil water retention curves (SWRC) have also been recently introduced in other elasto-plastic frameworks, e.g. by Bosch et al. [6].

Although these extended models show promising simulation results, they require new material constants and initial state variables, some of which are difficult to determine when addressing practical geotechnical problems. Furthermore, the assumption of a bimodal pore size distribution does not apply to all expansive materials, e.g. clay shales have a rather monomodal pore size distribution as has been shown for Callovo-Oxfordian clay shale by Mohajerani et al. [25] and Opalinus clay shale by Seiphoori et al. [38].

Until now, little efforts have been made to describe the behaviour of expansive geomaterials with constitutive models outside of elasto-plastic frameworks. A hypoplastic model for unsaturated soils was introduced by Mašín and Khalili [23], however it does not allow simulations of expansive geomaterials. Adopting some concepts from existing models, this paper presents a novel 1D constitutive model in the framework of hypoplasticity to describe the most essential features of the behaviour of expansive soils. The model’s development takes a phenomenological approach and aims to facilitate the material calibration process. Rate dependency, creep, anhydritic swelling, anisotropy or cementation are not considered. The model is formulated in terms of net stress (excess of total stress over air pressure) and effective degree of saturation. The preloading state defines a boundary for the reversible material response (analogously to a yield surface) which is assumed to evolve with the deformation and the changes in saturation. The primary consolidation and the evolution of swelling over time are out of the scope of this paper since they are related to the transport of water and, therefore, scale dependent. Hence, and contrary to other approaches [18, 21], they should be considered at the finite element level and not at the material level [27]. One novelty of the model lies in the linking of the material behavior during wetting (development of swelling strain or stress) with the preloading state instead of the widely used correlation of the maximum swelling stress/strain with the dry density, cf. [24, 37, 43, 45].

Deviating from the BBM/BExM, the proposed model uses the degree of saturation instead of the suction, which greatly simplifies many of the model’s evolution equations. Although the degree of saturation also determines the current state, the constitutive model handles it as a given variable because its evolution is governed by the mass balance at the finite element (and not at the material point) level. This allows any hydraulic constitutive relation between suction and degree of saturation to be linked. In the model, the strain rate is divided into two parts: one is related to changes in the degree of saturation of the material while the other one is used for the evolution of net stress. This decomposition allows to predict both swelling strains and swelling stresses, depending on the mechanical and hydraulic boundary conditions. The saturation driven strain can lead to irreversible strain accumulation even for stresses that are much smaller than the preloading stress. For constant volume conditions, the strain decomposition produces an increase of stress (swelling pressure). Adopting the concept of overstress by Olszak and Perzyna [32] to quantify the proximity of the current stress to the preloading stress, the model can distinguish between loading and unloading using a single equation. On this basis, the proposed constitutive model can predict both, swelling strains and swelling stresses, loading/unloading as well as combinations thereof for different degrees of saturation with a single set of only seven material parameters.

The paper is structured as follows: First, the constitutive model is introduced in Sect. 2, with a common approach to simulate loading and unloading/reloading paths on oedometric tests. The constitutive equations are stepwise extended to include the influence of saturation on the first loading, the reduction of stiffness with wetting, and the saturation driven swelling strain rate to describe unconfined and confined swelling paths. The evolution equations for the state variables that track the loading history and the parameters of the proposed model are introduced thereafter. An detailed discussion of the model with focus on the main mechanisms is presented in Sect. 3. The determination of the material parameters and their significance is discussed in detail in Sect. 4. To evaluate the performance of the model, laboratory tests on three different materials were simulated and their results are contrasted in Sect. 5. Finally, a conclusion is drawn in Sect. 6.

2 Constitutive model

2.1 Oedometric compression: loading and unloading

Similar to the approach by Niemunis et al. [28], the model starts with the common description of an oedometric loading and unloading/reloading process consisting of two equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \ln \dfrac{1+e_0}{1+e} = \lambda \ln \dfrac{\sigma }{\sigma _0} &{} \quad \text { or}\quad \dot{\sigma }= \dfrac{\sigma }{\lambda } \dot{\epsilon }\quad \mathrm{for~loading}, \\ \ln \dfrac{1+e_0}{1+e} = \kappa \ln \dfrac{\sigma }{\sigma _0} &{} \quad \text { or}\quad \dot{\sigma }= \dfrac{\sigma }{\kappa } \dot{\epsilon }\quad \mathrm{for~unloading/reloading,} \end{array} \right. \end{aligned}$$
(1)

where \(\lambda\) and \(\kappa\) are the first loading index and the swelling index, respectively. Note that although Eq. (1) is given in a 1D formulation, under oedometric conditions \(\sigma\) corresponds to the vertical (axial) stress and not the mean effective stress. This definition is used consistently in the following. In this paper, we adopt the logarithmic strain \(\epsilon = \ln \dfrac{1+e_0}{1+e}\) and the geotechnical conventions, where compressive stress and strain are positive. The values \((\sigma _0,e_0)\) represent an arbitrary point from which the deformation is to be measured. In Eq. (1) both points \((\sigma _0,e_0)\) and \((\sigma ,e)\) must lie on the same (loading or unloading) branch. When using the rate form of Eq. (1) for loading, the first (virgin) compression line is defined as the curve in the \(\ln (1+e)-\ln \sigma -\)space with slope \(\lambda\) passing through a fixed reference point \((\sigma _d,e_d)\). We denote this line as the B-line, see Fig. 1.

Following the concept of overstress by Olszak and Perzyna [32], we consider the response of the material to be reversible for stresses within a certain bounding stress \(\sigma _B(e)\). The bounding stress is the stress corresponding to the current void ratio e on the B-line, see Fig. 1.

Fig. 1
figure 1

Idealized loading and unloading/reloading paths, B-line with reference point \((\sigma _d,e_d)\), and definition of the bounding stress \(\sigma _B\) corresponding to the current void ratio e

Full size image

Loading beyond that bounding stress results in anelastic flow. The proximity of the current net stress \(\sigma\) to the bounding stress \(\sigma _B\) is expressed by the so called overconsolidation ratio \(\mathrm{OCR}=\sigma _B/\sigma\). States \((\sigma ,e)\) on the left hand side of the B-line (\(\mathrm{OCR}>1\)) in Fig. 1 are called overconsolidated whereas those on the B-line (\(\mathrm{OCR}=1\)) are called normal consolidated. Using the \(\mathrm{OCR}\), Eq. (1) can be approximated by a single hypoplastic equation

$$\begin{aligned} \dot{\sigma } = \dfrac{\sigma }{\kappa } \left( \dot{\epsilon }- Y \mathrm{OCR}^{-m} \vert \dot{\epsilon }\vert \right) \quad \text { with}\quad Y = \dfrac{\lambda -\kappa }{\lambda }, \quad \mathrm{OCR}=\sigma _B/\sigma . \end{aligned}$$
(2)

The factor \(Y \mathrm{OCR}^{-m}\), with \(m>1\), allows to simulate both elastic unloading/reloading and anelastic loading without the need of switching between equations in Eq. (1):

  • For overconsolidated (elastic) states \(\mathrm{OCR}> 1\), the factor \(Y \mathrm{OCR}^{-m}\) in Eq. (2) becomes negligible, and the expression \(\dot{\sigma }= \dfrac{\sigma }{\kappa } \dot{\epsilon }\) from Eq. (1) for unloading/reloading is recovered.

  • For normal consolidated states \(\mathrm{OCR}\approx 1\) and \(\dot{\epsilon }>1\), Eq. (2) simplifies to \(\dot{\sigma }= \dfrac{\sigma }{\kappa }\left( 1-\dfrac{\lambda -\kappa }{\lambda }\right) \dot{\epsilon }\), which is identical to the expression \(\dot{\sigma }= \dfrac{\sigma }{\lambda } \dot{\epsilon }\) for loading in Eq. (1).

The material constant m in Eq. (2) enforces the change from elastic to anelastic material behavior: the higher m, the sharper the transition from elastic to anelastic behavior. From the authors’ experience, \(m=6\) is an applicable choice for most materials. Notice that states with \(\mathrm{OCR}<1\) (beyond the bounding stress \(\sigma _B\)) are also allowed by Eq. (2).

2.2 Oedometric compression: influence of saturation

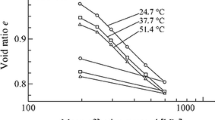
Several experimental campaigns [22, 26, 30] show that after oedometric compression up to high stresses (exceeding the preconsolidation stress) under constant suction, samples with different degrees of saturation approach a unique compression line: the so called Normal Compression Curve (NCC), see Fig. 2. Even nearly dry samples seem to approach the NCC at very high stresses. Therefore, the NCC can be thought as an attractor: a line reached upon compression regardless of the initial state and the degree of saturation. The concept of a NCC is incorporated into the proposed constitutive model through a unique function \(\sigma _e(e)\) that returns the stress \(\sigma _e\) on the NCC for a given void ratio e.

Fig. 2
figure 2

Idealized oedometric compression paths at constant suction for different initial degrees of saturation \(S_1<S_2<S_3\). After compression up to stresses exceeding the preconsolidation stress, all samples approach the Normal Compression Curve NCC

Full size image

This unique function \(\sigma _e(e)\) can be described by the Butterfield’s [7] Eq. \(\ln \dfrac{1+e_0}{1+e} = \Lambda \ln \dfrac{\sigma _e}{\sigma _0}\) as commonly done for compression lines of clayey materials. Therein, three material constants are required: \(\sigma _0,e_0\) and the slope \(\Lambda\). To prevent negative or excessively large void ratios at high and low stresses, respectively, a 1D formulation of Bauer’s [5] equation is used in the present work to describe the NCC:

$$\begin{aligned} \sigma _e(e) = h_s \left[ -\ln (e/e_N)\right] ^{1/n}. \end{aligned}$$
(3)

Compared with the Butterfield’s equation, the main advantage of Eq. (3) is that it remains valid over a wider stress range \(0\le \sigma _e < \infty\), see Fig. 10. In addition, the flexibility of the Bauer’s formula (Eq. (3)) permits a better approximation the experiments requiring the same number of material constants than the Butterfield’s one: the stress at the inflection point \(h_s\) (in kPa), the void ratio at zero stress \(e_N\), and the exponent n.

Notice that the higher the degree of saturation, the sooner the NCC is reached upon compression, see Fig. 2. For fully saturated samples \(S=1\), the first compression line from Eq. (2) and the NCC should become almost identical. Experiments indicate that samples with lower degrees of saturation reach the NCC line at higher pressures [22, 26, 30]. To incorporate this behaviour into the constitutive model, the compression of a sample with a low degree of saturation is considered, see Fig. 3. It is assumed that at the beginning of the compression (from point 0 to 1), the sample behaves elastically (reloading along a \(\kappa -\)slope) until the B-line is reached. Along the B-line, the sample follows the first loading path with a slope \(\lambda (e)\). However, in order to reach the NCC upon further compression, the B-line must be shifted towards the NCC. To achieve this, the reference point \((\sigma _d,e_d)\), which fixes the position of the B-line, must move towards the NCC during compression (from point 1 to 2). Hence, the reference point \((\sigma _d,e_d)\) becomes a state variable that evolves with the loading history. The evolution of \(\sigma _d\) and \(e_d\) will be discussed in Sect. 2.6.

Fig. 3
figure 3

Compression of a sample with low degree of saturation: shift of the B-line from state 1 to 2 during compression at high stresses to approximate NCC

Full size image

It is further assumed that the path followed during first compression along the B-line is affine to the NCC. This means that for a given void ratio e, the slope \(\lambda =-\dfrac{\sigma }{1+e}\dfrac{\mathrm{d}e}{\mathrm{d}\sigma }\) for the first compression (i.e. the B-line) is identical to the slope \(\lambda (e)_{NCC}\) of the NCC. By computing the derivative \(\dfrac{\mathrm{d}e}{\mathrm{d}\sigma _e}\) from Eq. (3), we obtain the slope \(\lambda\) as

$$\begin{aligned} \lambda = \lambda (e) = \lambda _{NCC}(e) = n \left( \sigma _e/h_s\right) ^n \dfrac{e}{1+e} \quad \text { with}\quad \lambda > \kappa . \end{aligned}$$
(4)

Notice that, in contrast to the BBM [1] or other elasto-plastic formulations, e.g. by Bosch et al. [6], the slope \(\lambda (e)\) does not depend on the suction (or on the degree of saturation). The apparent dependency of \(\lambda\) on the suction is accounted for as the slope resulting from the transition from \(\kappa\) to \(\lambda\) with a shifting B-line in this model.

2.3 Unloading/reloading for partial saturation

Experiments further show a pronounced reduction of the elastic stiffness with increasing degree of saturation [26, 29, 30]. To take this into account, the dependency of \(\kappa (S)\) on the degree of saturation S is included in the model by assuming a simple linear interpolation between dry and saturated conditions:

$$\begin{aligned} \kappa (S) = \kappa _d + S \left( \kappa _w -\kappa _d\right) . \end{aligned}$$
(5)

Therein, \(\kappa _d\) denotes the swelling index at dry and \(\kappa _w\) at fully saturated conditions, respectively. Figure 4 shows the loading and unloading behavior for two samples with different degrees of saturation \(S_1 < S_2\),

Fig. 4
figure 4

Swelling indexes \(\kappa (S_1)\) and \(\kappa (S_2)\) for samples with degrees of saturation \(S_1\) and \(S_2\), respectively. The lower the degree of saturation, the higher the elastic stiffness. For \(S_1<S_2\), \(\kappa (S_1)< \kappa (S_2)\) holds

Full size image

Equation (5) bears the problem that \(\kappa _d\) is a theoretical value (unloading stiffness at degree of saturation \(S=0\)) which is difficult to measure in the laboratory. Considering that a nearly dry sample under atmospheric conditions has a residual water content, Eq. (5) can be reformulated in analogy to the concept of the effective degree of saturation as follows:

$$\begin{aligned} \kappa (S^e) = \kappa _\mathrm{{ref}} + S^e \left( \kappa _w -\kappa _\mathrm{{ref}}\right) \end{aligned}$$
(6)

Therein, \(\kappa _\mathrm{{ref}}\) denotes the unloading stiffness measured in the laboratory in a reference degree of saturation \(S_\mathrm{{ref}}\). \(S^e=(S-S^r)/(1-S^r)\) is the effective degree of saturation and \(S^r\) the residual degree of saturation. For the determination of \(\kappa _\mathrm{{ref}} =\kappa (S_\mathrm{{ref}})\), it is strongly recommended to select the driest possible state of the material \(S_\mathrm{{ref}}=S^r\), or, in other words, a state as close as possible to \(S^e=0\). The illustration of the saturation dependent unloading stiffness \(\kappa (S)\) in Fig. 4 also applies to the interpolation with the effective degree of saturation \(\kappa (S^e)\).

Notice that the saturation dependent swelling index of Eq. (6) differs from the constant elastic stiffness of the original formulations of BBM/BExM [1, 12]. However, more recent formulations also consider the swelling index as a function of suction (hence of degree of saturation) [8, 36, 42].

2.4 Unconfined swelling

The extensions introduced in the following account for deformations caused by changes in the degree of saturation at constant net stresses. The relation between void ratio e and water content w in partial saturated samples during drying-wetting tests has been widely studied [11, 14, 40]. After a few drying-wetting cycles at constant net stress, the samples followed a nearly identical path in the \(e-w-\)space, see Fig. 5. Starting at very low water contents \(w \le w_s\) (where \(w_s\) is the shrinkage limit) the samples swelled upon wetting (\(\dot{S}>0\)) until a given void ratio \(e_w\) was reached at full saturation (\(S=1\)). After a subsequent drying process, the void ratio reduced up to \(e_s\) (the void ratio at the shrinkage limit). Thus, the void ratios \(e_w\) and \(e_s\) can be seen as limit values for the void ratio during wetting and drying processes, respectively. Experiments performed at different stress levels show that the limits \(e_w\) and \(e_s\) are both functions of the net stress and the loading history as presented in Fig. 6 and Sect. 2.6.

Fig. 5
figure 5

Idealized evolution of the void ratio upon drying and wetting at constant net stress after Estabragh et al. [11]

Full size image

To include these observation into the constitutive model, the total strain rate \(\dot{\epsilon }\) is decomposed into a portion \(\dot{\epsilon }^w\) and a portion \(\dot{\epsilon }^h\): \(\dot{\epsilon }= \dot{\epsilon }^h + \dot{\epsilon }^w\). The strain rate portion \(\dot{\epsilon }^w\) is related the changes in the degree of saturation (the saturation driven strain rate). The remaining strain rate portion \(\dot{\epsilon }^h\) is used to describe the evolution of the net stress, so that Eq. (2) is rewritten as:

$$\begin{aligned} \dot{\sigma }= \dfrac{\sigma }{\kappa } \left( \dot{\epsilon }^h - Y \mathrm{OCR}^{-m} \vert \dot{\epsilon }^h\vert \right) \quad \text { with}\quad \dot{\epsilon }^h = \dot{\epsilon }- \dot{\epsilon }^w. \end{aligned}$$
(7)

Notice that for unconfined swelling \(\dot{\epsilon }^w \ne 0\), the portion \(\dot{\epsilon }^h\) must be zero to satisfy the condition of constant net stress \(\dot{\sigma }=0\) in Eq. (7). Thus, the relationship between the deformation changes and the change in the degree of saturation \(\dot{S}\) is obtained from the above mentioned observations. As for Eq. (6), the effective degree of saturation \(S^e\) is used rather than the (total) degree of saturation S. This choice reflects the difficulty attached to the evaluation of swelling processes on nearly dry samples under atmospheric conditions. By choosing \(S^e\), only swelling/shrinking processes that ranges from this (reference) state to full saturation are considered in the model. During wetting \(\dot{S}^e>0\), the volume of the sample increases \(\dot{\epsilon }^w<0\) until the void ratio reaches the limiting value \(e \rightarrow e_w\) at full saturation, i.e. \(\dot{\epsilon }^w \sim (e-e_w) \dot{S}^e\). During drying \(\dot{S}^e<0\), the volume of the sample reduces \(\dot{\epsilon }^w>0\) until the limiting void ratio \(e \rightarrow e_s\) is reached at nearly dry conditions, i.e. \(\dot{\epsilon }^w \sim (e_s-e)\dot{S}^e\). These two processes can be described by a single evolution equation:

$$\begin{aligned} \dot{\epsilon }^w = -b\dfrac{ e}{\left( 1+e\right) } \left[ \left( e_w-e\right) \left( S^e\right) ^2 \left\langle \dot{S}^e\right\rangle + \left( e_s-e\right) \left( 1-S^e\right) ^2 \left\langle -\dot{S}^e\right\rangle \right] \end{aligned}$$
(8)

where b is a material constant that controls the shape of the \(e-w-\)pathFootnote 1. The Macaulay brackets are defined as \(\left\langle \sqcup \right\rangle =(\sqcup + \vert \sqcup \vert )/2\). The factors \(\left( S^e\right) ^2\) and \(\left( 1-S^e\right) ^2\) decelerate the evolution of \(\dot{\epsilon }^w\) upon changes in the effective degree of saturation at nearly dry and fully saturated states, respectively, as observed in Fig. 5.

Notice that the maximum strain reached at the end of a wetting process depends on the net stress. To illustrate this observation, consider the set of idealized swelling experiments in Fig. 6. A sample is statically compacted under \(\sigma _d\) and reaches the void ratio \(e_d\) (point 0). After unloading (from 0 to 1), the saturation is increased and the sample swells under constant net stress (from 1 to 2). At point 2, the void ratio reaches its limit value \(e_w\) and the saturation driven strain rate vanishes according to Eq. (8). If the wetting process were initiated at a higher stress (e.g. path 0-1-3), the void ratio would increase under constant net stress and would reach the point 4 at \(e=e_w\). The final swelling strain along the path 0-1-3-4 (at a higher stress) is smaller than the one along the path 0-1-2 (at a lower stress). Even smaller swelling strains would be obtained at higher stresses, e.g. path 0-1-5-6.

Since at the end of all these paths the limiting void ratio \(e_w\) is reached, a relation \(e_w(\sigma )\) for samples prepared at the same preloading (\(\sigma _d,e_d\)) can be constructed as the curve connecting the end points 2, 4, 6, \(\cdots\). This curve, which is a reinterpretation of the commonly reported relation of \(\epsilon _{\max } \sim \rho _d\) [43, 45], can then be used to predict the maximum swelling strain \(\epsilon _{\max }\) under constant stress \(\sigma\) for a sample prepared at given preloading \(\sigma _d\). Note that this hypothetical connection line shows an affinity to the NCC.

Fig. 6
figure 6

Idealization of different unconfined swelling tests for samples wetted under different loads

Full size image

2.5 Confined swelling

In the proposed model, the maximum swelling pressure \(\sigma _{\max }\) is obtained as a confined swelling process: during wetting, the saturation driven strain increases \(\dot{\epsilon }^w \ne 0\) until the asymptotic value \(e=e_w\) is reached, while the total strain is constrained by the constant volume condition \(\dot{\epsilon }=\dot{\epsilon }^w + \dot{\epsilon }^h=0\). The remaining strain portion \(\dot{\epsilon }^h = - \dot{\epsilon }^w\) induces the changes of the net stress according to Eq. (7).

Due to its practical importance, predictions of the maximum swelling pressure \(\sigma _{\max }\) have been widely studied over the last decades. Those studies usually include experiments on dry samples subjected to full saturation under constant volume conditions.

The maximum swelling pressure \(\sigma _{\max }\) thus determined is often linked to the dry density \(\rho _d\) using exponential relationships \(\sigma _{\max }\sim \exp \left( \rho _d\right)\), whereby \(\rho _d\) is evaluated the beginning of the wetting process [24, 37, 43, 45]. However, a more evident relation can be found between \(\sigma _{\max }\) and the preloading stress \(\sigma _d\), i.e. the maximum stress at which the dry sample was subject before wetting.

Fig. 7
figure 7

Idealization of confined swelling tests of samples prepared at different preconsolidation pressures

Full size image

To illustrate this relationship, consider a set of idealized constrained swelling tests shown in Fig. 7. Similar to the procedure described in Fig. 6, a nearly dry sample is statically compacted under a vertical net stress \(\sigma _d\) reaching the void ratio \(e_d\) (point a). After unloading (from a to 1), the saturation increases while the volume is kept unchanged. Since the tendency of the sample to swell is restricted (constant volume conditions), the measured stress increases (from point 1 to 2). The final value of the stress (at point 2) is the maximum swelling pressure \(\sigma _{\max }\) that corresponds to the preloading \(\sigma _d\) (or the density given by \(e_d\)). If a second nearly dry sample is preloaded up to a lower stress (point b), then unloaded (from b to 3), and finally subjected to a wetting process (from 3 to 4), the maximum swelling pressure (at point 4) would be smaller than the one reached along the path a-1-2. Therefore, the maximum swelling pressure is directly related to the preloading stress. Analogously to the previous Section 2.4, a curve connecting the end points of the swelling process 2, 4, 6, 8 can be constructed. This curve is also affine to NCC. This relationship can be found in several experimental campaigns. For example, Fig. 8 presents the preloading stress \(\sigma _d\) and its corresponding maximum swelling stress \(\sigma _{\max }\) for different materials [4, 17, 43].

Fig. 8
figure 8

Maximum swelling \(\sigma _{\max }\) and preloading pressures \(\sigma _d\) for different materials [4, 17, 43]

Full size image

It can be seen that for a given material, the maximum swelling stress \(\sigma _{\max }(e)\) at a given void ratio e is always smaller than the corresponding preloading stress \(\sigma _d(e)\). In addition, by connecting all preloading stresses \(\sigma _d\) of a single material, we obtain a line that is nearly parallel to the line connecting the corresponding maximum stresses \(\sigma _{\max }\). Since the preloading is carried out by increasing the vertical stress (oedometric loading), the former line can be interpreted as the B-line (see Fig. 7). On the other hand, the second line connects the states at the end of wetting processes (where the void ratio reaches the limiting value \(e=e_w\) at \(S=1\)). The final values for each confined swelling test can be related to as a respective third line, which is introduced as the w-line. Note, that in contrast to NCC, the w-line is not unique. It differs slightly for each test, since the magnitude of the saturation driven strain \(\epsilon _w\), which causes the development of swelling pressure, depends on the initial void ratio. However, the slope of each individual w-line is very similar and is affine to the connecting line, which in turn is affine to the B-line.

This simplification suggests that the w-line can be used not only to predict the maximum swelling pressure \(\sigma _{\max }\), but also the maximum swelling strain \(\epsilon _{\max }\), where the same affinity of the line connecting the final states \(e_w\) and the B-line was observed, see Sect. 2.4).

Swelling under confined and unconfined conditions is idealized in the proposed model by using three characteristic lines, see Fig. 9. A nearly dry sample is compressed (from point 0 to 1) under the stress \(\sigma _d\), then unloaded (from 1 to 3), and finally subjected to a wetting process. The w-line (\(e=e_w\)) can be reached either upon free (from 3 to 4a, left) or constrained (from 3 to 4b, right) swelling.

Fig. 9
figure 9

Idealization of swelling processes: at the end stage of wetting, the w-line can be reached either by keeping the stress (left) or the volume (right) constant

Full size image

2.6 Characteristic curves

In the previous sections, three characteristic curves in the \(e-\ln \sigma -\)space have been introduced:

  • the B-line: the first (or) virgin compression line \(\sigma _B(e{, sv})\),

  • the NCC: an attractor \(\sigma _e(e)\) reached after long compression regardless of the initial state of the sample, and

  • the w-line: a state reached by the sample at the end of a full saturation process \(\sigma _w(e{, sv})\).

Note that the B-line and the w-line are state sv dependent, i.e. they evolve with the change of deformation (change in void ratio) and saturation. These lines constitute the core of the proposed material model, see Fig. 10. For the complete description of the model, however, the relative position of those lines in \(e-\ln \sigma -\)space is required. Since the NCC (Eq. (3)) is an attractor, its position is given by the material constants \(e_N, h_s\) and n and remains constant during any loading process. In contrast to the NCC, the B-line and the w-line evolve with the loading history. Based on the experiments already referred to in Sect. 2.4 and 5, we assume a) that the B-line lies always on the right hand side of the w-line and b) that the NCC is located between the B-line and the w-line as shown in Fig. 10. That means, that for any given void ratio e

$$\begin{aligned} \sigma _w(e) \le \sigma _e(e) \le \sigma _B(e) \end{aligned}$$
(9)

holds. The bounding stress \(\sigma _B(e)\) is the stress corresponding to the current void ratio e on the B-line. The B-line tracks the material’s loading history and is affine to the NCC (Eq. (3)).

Thus, the B-line

$$\begin{aligned} \sigma _B(e) = R \cdot \sigma _e(e) = R \cdot h_s \left[ -\ln \left( e/e_N\right) \right] ^{1/n} \end{aligned}$$
(10)

has the same constants \(e_N,h_s\) and n as the NCC, but is shifted to the right of the NCC by a factor R. The factor R is found from the condition that the B-line (Eq. (10)) passes through (\(\sigma _d, e_d\)):

$$\begin{aligned} R = \dfrac{\sigma _d}{h_s}\left[ -\ln \left( e_d/e_{N}\right) \right] ^{-1/n} =\dfrac{\sigma _B}{\sigma _e}. \end{aligned}$$
(11)

Therefore, the preloading state (\(\sigma _d, e_d\)) controls the position of the B-line on which the bounding stress \(\sigma _B\) is computed. The evolution of the preloading (\(\sigma _d, e_d\)) is given in Sect. 2.6.

Fig. 10
figure 10

Three characteristic lines of the model and their relative position described by the equivalent stress \(\sigma _e\) on the Normal Compression Curve NCC, the bounding stress \(\sigma _B\) on the B-line and stress reached for full saturation process \(\sigma _w\) for any void ratio e

Full size image

We assume that the w-line is also affine to the NCC, i.e. it has the same constants, but it is shifted to the left by the same factor R in Eq. (11)

$$\begin{aligned} \sigma _w(e) = \sigma _e(e)/R, \end{aligned}$$
(12)

thus,

$$\begin{aligned} R=\dfrac{\sigma _B}{\sigma _e} = \dfrac{\sigma _e}{\sigma _w}. \end{aligned}$$
(13)

For a given stress \(\sigma\), we compute the limit void ratio \(e_w(\sigma )\) from the w-line as:

$$\begin{aligned} e_w = e_{N} \exp \left[ -\left( \dfrac{\sigma R}{h_s }\right) ^n\right] . \end{aligned}$$
(14)

Following Eq. (10) and (14), for a given void ratio e, the slope \(\lambda\) of all three lines (NCC, w-line and B-line) is identical.

Therefore, for \(R=1\), the w-line and the B-line coincide with the NCC.

In addition to \(e_w\), the saturation driven strain rate further requires the limit void ratio \(e_s\) at the shrinkage limit \(w_s\). For \(e_s\) we propose:

$$\begin{aligned} e_s =\left\{ \begin{array}{ll} \left( 1+e_d\right) \left( \sigma _d/\sigma \right) ^{\kappa _{\text {ref}}} -1 &{} \mathrm{for} ~\sigma <\sigma _d,\\ e_d &{} \mathrm{for} ~ \sigma \ge \sigma _d. \end{array}\right. \end{aligned}$$
(15)

2.7 Evolution equations for the state variables

In addition to the net stress, the proposed constitutive model introduces three variables \((e,\sigma _d,e_d)\) to describe the current state. This section provides their corresponding evolution equations. Although the degree of saturation also determines the current state, the constitutive model handles it as a given variable because its evolution is governed by the mass balance at the finite element (and not at the material point) level.

The evolution of the void ratio is given by

$$\begin{aligned} \dot{e} = - (1+e)\dot{\epsilon }, \end{aligned}$$
(16)

where changes of the void ratio are directly related to the total strain rate.

The preloading stress \(\sigma _d\) changes with the deformation and with the saturation. After long monotonic compression, \(\sigma _d\) increases and \(e_d\) decreases. They follow a path similar to first loading. On the other hand, experiments by Nitsch et al. [29] and Nowamooz and Masrouri [30] suggest that wetting processes reduce the preloading stress \(\sigma _d\). In this case R reduces forcing both, the B-line and the w-line to move closer to the NCC. Therefore, we propose the following equation for the evolution of \(\sigma _d\):

$$\begin{aligned} \dot{\sigma }_d = \dot{\sigma }_{d +} + \dot{\sigma }_{d -}, \end{aligned}$$
(17)

where

$$\begin{aligned} \dot{\sigma }_{d +} = \dfrac{ \sigma _d }{\lambda (e_d)} \left( \dfrac{\sigma _d}{\sigma }\right) ^{-m} \dot{\epsilon }^h \end{aligned}$$
(18)

is the buildup term due to loading beyond the preloading state and

$$\begin{aligned} \dot{\sigma }_{d -} = \dfrac{ \sigma _e(e_d)-\sigma _d }{\lambda (e_d)} \left[ -\dot{\epsilon }^w \cdot \dfrac{S^{2}}{c\left( e_w-e_s\right) } + S \cdot \dot{\epsilon }^h \right] \end{aligned}$$
(19)

is the degradation term related to changes of the degree of saturation and loading under constant saturation. Notice the usage of the total degree of saturation S (instead of \(S^e\)) to capture the observation that even samples with very low degree of saturation \(S^e\approx 0\) tend to approximate the NCC upon compression [30]. Only in the ideal case of a perfectly dry sample (with \(S=0\)), the compression line will not approach the NCC. Finally, for the void ratio \(e_d\) corresponding to the preloading we propose:

$$\begin{aligned} \dot{e}_d = -(1 + e) \left( \dfrac{\sigma _d}{\sigma }\right) ^{-m} \dot{\epsilon }^h \end{aligned}$$
(20)

In Eq. (20), \(e_d\) remains nearly constant upon unloading because \(\left( \sigma _d/\sigma \right) ^{-m}\) becomes negligible. For loading beyond the preloading state, the factor \(\left( \sigma _d/\sigma \right) ^{-m}\) approaches 1 and \(e_d\) evolves in the same way as e. In this case Eq. (20) becomes nearly identical to Eq. (16), if the degree of saturation remains constant during that loading process.

2.8 Parameters of the model

The proposed constitutive model requires seven parameters, see Table 1, which can be determined from standard laboratory tests. Note that the exponent m for \(\mathrm{OCR}\) is not considered as a model parameter, but is considered as a constant for all materials in the scope of this work. From the authors’ experience, \(m=6\) produces an adequate transition from elastic to anelastic behavior.

The parameter calibration is explained in further detail in Sect. 4.

Table 1 Parameters for the constitutive model
Full size table

In addition to the material parameters, the initial state of the material described in Table 2 must be defined for every simulation.

Table 2 Initial conditions
Full size table

3 Discussion of the model

In this section, the features of the proposed model are examined for different hydro-mechanical loading paths. All these loading paths are simulated with a single (arbitrary) set of material parameters. Most of the simulations include the preparation of the sample in the laboratory, which usually consists of two steps. First, the sample is statically loaded up to a certain stress \(\sigma _d\) at which the prescribed dry density, i.e. void ratio \(e_d\), is reached. This state (\(\sigma _d , e_d\)) is denoted as the preloading of the sample (reference state at nearly dry \(S=S^r\) conditions) and its evolution upon hydro-mechanical loading is tracked by the constitutive model. Before the actual test or simulation is run, the sample is unloaded to a stress \(\sigma < \sigma _d\). Since the sample is nearly dry, we assume that the void ratio after unloading corresponds to the void ratio at the shrinkage limit.

3.1 Oedometric compression under constant saturation

The response of the model (right) to loading and unloading paths at constant saturation for different initial degrees of saturation (left) are shown in Fig. 11. The path A-B-A* represents loading and unloading for the driest case possible (\(S^e=0\)). The preloading state (\(\sigma _{d,0} , e_{d,0}\)), which lays on the B-line, marks the end of the elastic reloading. The slope of the subsequent loading line is affine to the slope \(\lambda (e)\) of the NCC. With increasing degree of saturation, the NCC is reached sooner upon compression. This is achieved by the reduction of the preloading stress \(\sigma _d\) with the deformation (see Eq. (19)). For the simulation in the fully saturated state (I-J-I*), the compression path almost coincides with the NCC. Furthermore, the reduction of elastic stiffness according to Eq. (6) for both, reloading \(\sigma \le \sigma _d\) and unloading, can be clearly shown.

Fig. 11
figure 11

Oedometric loading and unloading for different degrees of saturation

Full size image

3.2 Saturation induced deformation

Figure 12 presents the response of the model to full saturation at constant-stress conditions. The compression curve and loading sequence for a test in the nearly dry state \(S=S^{r}\) (A-B-A*) is shown as well to illustrate the loading history. Starting at \((\sigma _{d,0} , e_{d,0})\), the stress is reduced to points A, D, F and H. Then, the degree of saturation is increased while keeping the stress constant. The deformation reached in each simulation at the fully saturated state is determined by the position of the w-line. Hence, the points C, E, G and I coincide with the void ratio \(e_w\) according to Eq. (14). The saturation induced deformation decreases with the stress, which is achieved by the affinity of the w-line to the NCC.

Fig. 12
figure 12

Saturation induced deformation at different stresses: stress and wetting paths (left) and response of the model (right)

Full size image

3.3 Swelling pressure

Figure 13 presents response of the model to wetting at volume-constant conditions for different initial densities. After unloading from \((\sigma _{d,0} , e_{d,0})\) to A (nearly dry state \(S=S^{r}\)), the degree of saturation was increased until \(S=1\). As reaction to the constant-volume constraint, the stress increases up to C. The states D, F, and H were reached by preparing the samples at lower preloading stresses (higher void ratios). The magnitude of the maximum swelling pressure at points C, E, G and I in the fully saturated state is determined by the position of the w-line.

Fig. 13
figure 13

Wetting induced swelling pressure (S=1) at different initial void ratios due to increments of degree of saturation: stress and wetting paths (left) and response of the model (right)

Full size image

3.4 Collapse upon Wetting

Similar to the BBM [1], a transition point from swelling to collapse behavior exits in the proposed constitutive model. Collapse occurs when the stress at which wetting takes place is larger than the stress on the w-line for the current void ratio, i.e. \(\sigma > \sigma _w(e)\). For this condition, the sign of the saturation driven strain rate in Eq. (8) becomes positive, because \(e>e_w\). The response of the model for wetting induced collapse is shown in Fig. 14. The compression curve and loading sequence for a test in the nearly dry state \(S=S^{r}\) (A-B-A*) is also shown. After a partial unloading from \((\sigma _{d,0} , e_{d,0})\), the degree of saturation was increased until \(S=1\) while the stress was kept constant. The deformation increases until the void ratio reaches its limit value \(e=e_w\) (according to Eq. (14)) at point C on the w-line.

Fig. 14
figure 14

Wetting induced collapse (S=1) due to increments of degree of saturation: stress and wetting paths (left) and response of the model (right)

Full size image

4 Determination of the material parameters and their significance

As described in Sect. 2.8, the proposed model requires seven parameters. The parameters of the model can be directly determined from the results of common laboratory tests apart from the watering parameter b and the yielding parameter c, whose significance will therefore be discussed in more detail. In the following, all laboratory tests refer to tests under oedometric conditions.

Note that together with the proposed constitutive model, the simulation of laboratory test require an additional hydraulic model which is not part of this work. Thus, the residual degree of saturation \(S^r\) and the van-Genuchten parameters \(\alpha\) and n need to be specified as shown in the simulations of Sect. 5. A detailed method for the determination of the model parameters and the recommended laboratory tests are presented below.

The values of the parameters and typical ranges will be presented for three different materials in the following Sect. 5.

4.1 Parameters \(e_N, h_s\), and n of the normal compression curve (NCC)

The NCC is the core of the model. Its three parameters can be best obtained simultaneously by fitting the Bauer equation (Eq. (3)) to the loading path of an oedometer test preceded by unconfined swelling up to full saturation or two the respective parts of the loading paths of two separate tests. However, the parameters can be individually adjusted to match specific laboratory tests. For example, the void ratio \(e_N\) at zero net stress can be estimated from an unconfined axial swelling strain test conducted at a very low stress level. Compression tests up to very large stresses can be used to estimate the stress at the inflection point \(h_s\) of the NCC. Also the exponent n can be adjusted from such tests. Since for a given void ratio e the maximum swelling pressure \(\sigma _{\text {max}}\) should always be smaller than the equivalent stress \(\sigma _e(e)\), the plausibility of the position of the NCC can be validated by swelling pressure tests.

4.2 Swelling indexes \(\kappa _{\text {ref}}\) and \(\kappa _w\)

To compute the elastic stiffness \(\sigma /\kappa\) of the model (see Eq. (7)), the saturation dependent swelling index \(\kappa =\kappa (S)\) is interpolated from the constants \(\kappa _{\text {ref}}\) and \(\kappa _w\), see Eq. (6). The swelling index \(\kappa _{\text {ref}}\) can be directly obtained from unloading paths of an oedometer test at the driest possible state. The swelling index \(\kappa _w\) can be calibrated by means of an oedometer test on a full saturated sample or from the unloading path of a multi-step swelling test under oedometric conditions, e.g. following the Huder-Amberg-method [16].

4.3 Parameter b for the Evolution of the Saturation Driven Strain

The parameter b controls the evolution of the strain upon changes in the degree of saturation, see Eq. (8). The parameter b can be found from a back-calculation of an unconfined axial swelling strain test. In the \(\epsilon -S-\)space, unconfined swelling results in an around its inflection point point-symmetrical sigmoid-shaped path (similar to Fig. 5). For small values of b, the inflection point of this path occurs at high degrees of saturation. If b is too small, the limit void ratio \(e_w\) may not be reached at full saturation and the saturation driven strain may be underestimated. For large values of b the evolution of the saturation strain flattens out prematurely and may also be underestimated. Since the limit void ratio \(e_w\) in Eq. (8) depends on the preloading–and therefore on the parameter c–, both b and c should be simultaneously optimised. For a first estimation of b, a value of \(c=1.0\) can be chosen.

4.3.1 Significance of b

The influence of different values for b on the evolution of the horizontal distance \(R=\sigma _B/\sigma _e\) between B-line/w-line and NCC, hence the evolution of the bounding stress \(\sigma _B\), and on the deformation upon wetting during an unconfined axial swelling strain test (\(S=1\)) are shown in Fig. 15. Note that the parameter for yielding is chosen arbitrarily as \(c=2.6\) in all three calculations. No unique trend can be observed with a variation of b, since not only the curvature of the sigmoid-function, but also the final value is influenced by the parameter b. With increasing b the inflection point of the \(e-w\)-curve is shifted to a lower water content, therefore an pronounced plateau can be observed, and the deformation does not reach its final value (\(b=50\), lightest curve in Fig. 15, right). In contrast, with a small value for b the inflection point may not yet be reached and the \(e-w\)-curve does not flatten (\(b=5\), darkest curve in Fig. 15, right). Both extreme values are not able to reproduce the deformation upon wetting correctly and underestimate the deformation due to wetting, see Fig. 15, left and right. The same observation can be made for the reduction of bounding stress upon wetting, see Fig. 15, center. For the studied material, the medium value \(b=17\) produces a well shaped sigmoid-function for the evolution of deformation with watering and thus for the evolution of \(R=\sigma _B/\sigma _e\) as well.

Fig. 15
figure 15

Influence of wetting parameter b during volumetric deformation (S=1): deformation (left), horizontal distance \(R=\sigma _B/\sigma _e\) between B-line/w-line and NCC (center) and void ratio vs. water content (right)

Full size image

4.4 Parameter c associated with yielding

The constant c, which controls the evolution of the preloading pressure \(\sigma _d\) with the saturation and the deformation (see Eq. (19)), should be determined as the last parameter, but optimised together with b. The parameter c strongly impacts the prediction of stress/strain at fully and partially saturated conditions. For a preliminary determination, at least one confined and one unconfined swelling test (ideally followed by oedometric loading) are required. Having a first estimation of b, the parameter c must then be chosen in such a way, that the magnitude of the deformation upon wetting in the partially saturated state as well as the slope of the subsequent oedometric compression path (see Fig. 2) are simulated correctly. Further improvements require a gradual and simultaneous adjustment of b and c.

4.4.1 Significance of c

A clear influence of the parameter c for yielding on the evolution of \(R=\sigma _B/\sigma _e\) and on the deformation upon wetting can be seen in Fig. 16 during an unconfined axial swelling strain test. Note that the value of \(b=17\) was chosen in all three calculations, i.e. the medium dark curves correspond to each other in Fig. 15 and 16. An additional oedometric compression is added to the calculations to clearly evaluate the influence on the preloading pressure, hence the transition from elastic to unelastic material behavior. For the sake of clarity, the compression paths are only shown in Fig. 16, left (dashed lines). With an reduction of R, the B-line is shifted closer to the NCC and thus also the w-line at the same time.

For \(c=1.0\) the evolution of the bounding stress \(\sigma _B\) and preloading stress \(\sigma _d\) are most pronounced and their reduction takes place very fast. With increasing c the reduction of R is slowed down (Fig. 16, center) and a smaller deformation takes place.

Fig. 16
figure 16

Influence of yielding parameter c during volumetric deformation (S=1): deformation (left), horizontal distance \(R=\sigma _B/\sigma _e\) between B-line/w-line and NCC (center) and void ratio vs. water content (right)

Full size image

The influence of c becomes clear during the whole wetting process. As a consequence not only the fully saturated material behavior is strongly dependent on the magnitude of c, but also the partially saturated behavior. Without slowing the reduction of R down, hence \(c=1.0\) the evolution of R is already complete for partially saturated conditions (\(c=1.0\), darkest curve in Fig. 16). As a consequence, a fully and partially saturated test do not distinguish in the transition point from elastic to anelastic behavior, nor in the magnitude of the deformation. With an increase of c the reduction of R becomes so slow, that the differences for partial saturation are not significant enough and both, the transition point from elastic to anelastic behavior, and the magnitude of deformation upon wetting, do not differ enough overall (\(c=7.0\), lightest curve in Fig. 16). In both cases, the material behavior which is commonly observed during unconfined swelling and oedometric loading of partially saturated samples cannot be reproduced. For the studied material, the medium value \(c=2.6\) produces a well shaped \(R-S\)-curve (see Fig. 16), center and is also suited to predict partially saturated behavior.

5 Simulation of laboratory tests

To evaluate its performance, a set of laboratory tests on three different expansive materials is simulated using the proposed model. The experiments include the most representative hydro-mechanical loading paths. Hence, the simulations focus, among others, on the prediction of the maximum swelling strain and stress upon full saturation, the reduction of stiffness with increasing degree of saturation, and the overall mechanical material response to subsequent oedometric loading/unloading paths.

For each material, a single set of material parameters was used to simulate all the experiments. Since the suction was controlled in some of the experiments, a simple soil water retention curve SWRC after Van Genuchten [41] was used to relate the suction with the degree of saturation (which was required by the constitutive model).

5.1 Tests on reconstituted opalinus clay shale

The experimental campaign by Nitsch et al. [29] focussed mainly on the swelling behavior of reconstituted Opalinus clay shale (with 5% smectite and 32% illite content) and its influence on the mechanical behaviour during monotonic loading and unloading. Starting from nearly dry states, samples with similar void ratios were fully saturated and then subjected to oedometric loading and unloading paths. The saturation occurred under different conditions: (a) constant-volume (swelling pressure test, OPA-0-34); (b) constant-volume (swelling pressure test, OPA-0-07) followed by unloading; and (c) constant-stress (unconfined axial swelling strain test, OPA-0-24). For comparison, another sample was loaded at dry conditions (without the saturation stage, OPA-0-33).

Fig. 17
figure 17

Simulation of oedometric compression tests preceded by different swelling phases after [29]

Full size image

Figure 17 shows the simulations (right) of the experiments (left) on reconstituted Opalinus clay shale. The material constants and the initial conditions used in the simulations are listed in Tables 3 and 6, respectively. The model is able to predict the mechanical response in the dry state and after different wetting paths with subsequent oedometric loading and unloading. The experiments support the hypothesis of a unique NCC after long monotonic compression, see Sect. 2.2. The similar slope \(\lambda (e)\) of the NCC and the loading branch of the test on nearly dry material (OPA-0-33), which corresponds to the B-line, can be clearly identified. The pronounced increase of the unloading/reloading slope from the reference \(\kappa _{\text {ref}}\) state to the saturated \(\kappa _w\) conditions can be clearly observed in the experiments, see Sect. 2.3. The results show that the model is able to reproduce both the maximum swelling pressure and the maximum swelling strain with a single set of material parameters.

Table 3 Initial conditions for the simulations on Opalinus clay shale from Nitsch et al. [29]
Full size table

5.2 Tests on partially saturated bentonite-silt mixtures

In an extensive experimental campaign, Nowamooz and Masrouri [30, 31] reported suction-controlled wetting tests followed by oedometric compression on a Silt-Bentonite-Mixture with 62 % montmorillonite. Figure 19 compares the experiments (left) of with the simulations (right) performed with the proposed model. The material constants and the initial conditions for the simulations are listed in Tables 4 and 6, respectively. Starting from a similar initial stress and void ratio, the samples were subjected to different increments of saturation while keeping the net stress constant. The sample M1 reached full saturation while samples M4 and M5 reached lower degrees of saturation: \(S=0.79\) and \(S=0.54\), respectively. The swelling stage was followed by oedometric compression up to 1 MPa and finally by oedometric unloading.

Since the degree of saturation is a driving variable for the simulations, the suction-controlled conditions of the experiments had to be transformed into saturation-controlled ones. This was achieved by using a simple soil water retention curve SWRC as a one-to-one suction-saturation relationship. The SWRC resulted by fitting the experimental data, i.e. suction measurements for six different water contents, to the van Genuchten Eq. (21) with constants \(\alpha =0.361, n=2.026, S^{\text {r}}=0.261\):

$$\begin{aligned} S = S^{r} + (1-S^{r}) \,\left( \dfrac{1}{1+(\alpha \cdot \,s)^n}\right) ^{ 1-\frac{1}{n}}. \end{aligned}$$
(21)

The experimental data and van Genuchten fit is shown in Fig. 18.

Fig. 18
figure 18

Soil water retention curve (SWRC): experimental data from Nowamooz and Masrouri [30] and van Genuchten fit

Full size image
Table 4 Initial conditions for tests on a Bentonite-Silt-Mixture from Nowamooz and Masrouri [30]
Full size table
Fig. 19
figure 19

Simulation of swelling strain and oedometric compression test on partially and fully saturated samples after Nowamooz and Masrouri [30]

Full size image

The simulations show that the NCC was reached after a long monotonic loading path for all tests. Both the stiffness of the loading paths and preconsolidation stress are well reproduced by the model. The simulations further show the reduction of elastic stiffness with an increasing degree of saturation.

The magnitude of the strain during wetting is not optimally reproduced by the model for all tests. This can be attributed to uncertainties in the data supporting the SWRC and to the assumption of a simple hydraulic model. However, the model is able to qualitatively reproduce the increasing deformation with increasing degree of saturation. In summary, the model can satisfactorily simulate the main features of partially saturated unconfined swelling and the subsequent oedometric compression with a single set of material parameters.

5.3 Tests on partially saturated Sand-Bentonite mixtures

Lang [20] conducted a large number of experiments on Sand-Bentonite-mixtures with \(30-35 \%\) montmorillonite content using different stress and saturation paths.

To evaluate the performance of the proposed model, swelling strain and swelling pressure tests with subsequent oedometric loading have been simulated.

Lang also investigated the dependency of the soil water retention curves on the net stress. Among all the SWRCs, two extreme cases were fitted to the van Genuchten Eq. (21): one for unconfined (zero stress) (black, \(\alpha =2.976, n=1.269\)) and other for confined (increasing stress) (grey, \(\alpha =0.401, n=1.482\)) conditions, as shown in Fig. 20. The residual degree of saturation was \(S^r=0.26\). The material constants and the initial conditions for the simulations are listed in Tables 5 and 6, respectively.

Fig. 20
figure 20

Soil water retention curve: experimental data from [20] and van Genuchten Fit for unconfined (black) and confined (grey) conditions

Full size image

Figure 21 compares the experiments (left) with the simulations (right) performed with the proposed model for unconfined swelling with subsequent oedometric loading and unloading. The van Genuchten fit for unconfined conditions was used for these calculations. Prior to the oedometric loading, the samples reached different degrees of saturation upon constant stress conditions: BS-SCR-1 (\(S=1.0\)), BS-SCR-2 (\(S=0.64\)), BS-SCR-3 (\(S=0.55\)), and BS-SCR-4 (\(S=S^r=0.26\)).

Similar to the previous Sections 5.1 and 5.2, the magnitude of deformation, the stiffness of the loading and unloading/reloading paths, and the magnitude of the preconsolidation stress are well reproduced by the model. With increasing degree of saturation, the NCC is approached more rapidly and the reduction of the unloading stiffness is more pronounced.

Fig. 21
figure 21

Simulation of swelling strain and oedometric compression test on partially and fully saturated samples after Lang [20]: (a) Experiments and (b) NCC and Simulation

Full size image

Figure 22 compares the results of swelling pressure tests for different saturation degrees (left) with their simulations using the SWRC for confined conditions (right). In the experiments (left), each of the reached swelling pressures corresponds to a final value of suction. For the simulation however, suction was transformed to saturation through the SWRC for confined conditions (right). To illustrate the influence of the chosen SWRC on the model’s performance, Fig. 22 (center) presents the simulation results using the SWRC for unconfined conditions.

Fig. 22
figure 22

Simulation of swelling pressure on partially and fully saturated samples after Lang [20]: Experiments (left) and simulations using unconfined SWRC (center) and confined SWRC (right)

Full size image

As it can be observed, the swelling pressure in the fully saturated state is well predicted, but both simulations show significant deficits for the prediction of swelling pressure in the partially saturated states. With the unconfined SWRC (Fig. 22, center) the swelling pressure for small degrees of saturation is underestimated (BS-WCV-7), but well predicted for higher degrees of saturation (BS-WCV-5) and full saturation (BS-WCV-1). In contrast, with the confined SWRC (Fig. 22, right), the prediction is better for lower degrees for saturation. This shows that the quality of the hydraulic model needs to be as good as the quality of the constitutive model in order to achieve good predictions of swelling pressure tests under partially saturated conditions.

Table 5 Initial conditions for tests on a Bentonite-Sand-Mixture from Lang [20]
Full size table

5.4 Remarks on model parameters

As Table 6 shows, a typical range can be given for the parameters based on the validation of the constitutive model on three materials. The exponent for \(\mathrm{OCR}\) was chosen as \(m=6\) for all tests.

Table 6 Model parameters for three experimental campaigns and typical range. The respective content of high-swellable clay minerals is given in brackets
Full size table

The typical range of some of the model parameters, e.g. the void ratio \(e_N\) at zero stress of the Bauer Eq. (3), can be associated with the range of content of high-swellable clay minerals from the presented materials. Other model parameters seem to be almost independent of the type of expansive material, e.g. the curvature parameter n of the Bauer-Eq. (3).

In the past efforts have been made by e.g. [19, 35, 44] amongst others to compute the swelling pressure depending on the montmorillonite or bentonite content of a material. Various approaches have proven to be suitable. Since the swelling pressure development is only one of the responses to the swelling mechanism in the proposed model, that is for confined boundary conditions, it is assumed that the entire response of a material subjected to hydro-mechanical loading can be related to the amount of expansive clay minerals in the material. Further investigations are required to support this thesis.

6 Conclusions

  • The proposed model is able to reproduce essential features of the behaviour of partially saturated expansive soils under oedometric conditions. Among others, processes like swelling, wetting/drying at constant volume, monotonic loading, and reversible unloading/reloading for samples at different degrees of saturation can be simulated with a single set of material constants. Also the volumetric collapse, i.e. the reduction of the void ratio upon wetting, can be captured by the model.

  • Oedometric tests with varied hydro-mechanical loading paths on three different expansive materials could be satisfactorily simulated by the model.

  • Whereas the maximum swelling strain and the maximum swelling pressure can be predicted with a simple soil water retention curve, a more sophisticated approach to the hydraulic model is required to simulate the swelling pressure at partially saturated conditions due to the dependency of the SWRC on the stress and void ratio.

  • The basic ideas of the model – that is, a saturation driven strain rate, the dependence of stiffness on the degree of saturation, and state variables tracking the loading history – can be extended to formulate three dimensional constitutive models. The promising results of the 1D version of the model motivate the extension to a 3D formulation, which is in the scope of future work.