1 Introduction

Internal erosion is a significant threat to levees and dams [9, 13, 16, 33], but time scales of the failure process are hard to quantify [12]. Different types of internal erosion can be distinguished: concentrated leak erosion, suffusion, contact erosion, and backward erosion piping. Backward erosion piping (BEP) can be defined as the failure process by which seepage under a structure erodes the granular foundation that is covered by a cohesive roof, forming a hydraulic shortcut. For many levees, backward erosion piping is the most common form of internal erosion because of the cohesive deposits which form a roof above sandy aquifers.

1.1 Piping process description

The BEP failure process starts with high external water levels that cause excess water pressure at the landward toe of the structure. When a cohesive blanket is present at the landward side, erosion can occur through either pre-existing defects in the blanket or cracks caused by uplift and rupture. If the vertical pressure gradient over the exit through the confining layer is sufficiently high to initiate vertical transport of sand, a cavity forms below the exit hole and the sand settles around the exit hole as a sand boil. At some point, a small pipe starts to develop from the cavity in the upstream direction. When the head difference (H) over the levee is sufficiently high and prolonged, the erosion continues in the upstream (backward) direction until a hydraulic shortcut forms, which likely results in a levee breach. However, if the head difference is too low or drops too quickly, an equilibrium occurs with a partially developed pipe.

The head drop at which equilibrium occurs (Heq) varies with pipe length (l) [21, 46]. The maximum H for which an equilibrium exists in stationary conditions is defined as the critical head difference Hc, and lc is the corresponding pipe length. This point (Hc,lc) marks the transition from the regressive phase (l < lc) to the progressive phase (l > lc). Exceeding this head difference Hc long enough ultimately leads to a levee breach.

Most previous BEP research focused on this critical head difference Hc and the influence of aquifer geometry and sand properties on this critical condition, for example [4, 21, 46, 52]. Such a stationary approach, which neglects the development over time, may be sufficient in many cases such as rivers with relatively long floods or dams with permanent pools. However, when the flood duration is short compared to the time scale of backward erosion, a dike may survive a short duration flood, whereas it would fail under a long duration flood [21]. These insights are important for levee safety assessments and for emergency response.

This raises the question of how to predict the temporal development of the backward erosion process. The twentieth century studies of Miesel, Müller-Kirchenbauer and Hanses [21, 29, 31] report very limited data on the development over time. More recently, several researchers studied pipe progression rates (dl/dt) experimentally [3, 35, 36, 38, 41, 51]. Robbins et al. [38] used cylindrical flumes and correlated progression rates to seepage velocity and void ratio. Allan [3] studied progression rates under overloading (H > Hc) in a rectangular setup with hole-type exit (seepage length L = 1.3 m). Vandenboer et al. [51] also studied the effect of overloading, but in a small-scale (L = 0.3 m) rectangular flume with hole-type exit. Pol et al. [35] derived progression rates from various available BEP experiments, and correlated these to hydraulic conductivity and the global horizontal hydraulic gradient. Robbins et al. [41] analyzed progression rates in small-scale flumes with a slope-type exit, for a wide range of grain sizes. Finally, Pol et al. [36] report pipe progression rates in a large-scale experiment. These studies [3, 35, 38, 41, 51] show that the progression rate is related to head difference, grain size and degree of compaction. Measured progression rates vary several orders of magnitude between different setups (e.g., slope or hole), sand types and degree of overloading.

A challenge in interpreting these results is that most experiments were performed on much smaller scales than typical levee dimensions (seepage length and aquifer depth in the order of 10−100 m). Since the progression rate appears to be a function of the applied and critical head, which do not scale linearly with seepage length, extrapolation to field conditions introduces a large uncertainty in predicted progression rates [35]. Scaling requires relating the progression rate to local, scale-independent conditions. Only Robbins et al. [38] and Pol et al. [36] evaluated local hydraulic gradients at the pipe tip, which are considered scale independent erosion criteria. The other studies only present global hydraulic gradients.

1.2 Piping process in non-equilibrium conditions

BEP consists of two distinct types of erosion [21]: lengthening of the pipe by detachment of grains from the soil skeleton at the pipe tip (primary erosion) and enlargement of the pipe cross section (secondary erosion). The primary erosion mechanism can be considered as successive slope failures which occur if the forces exerted on the grains by the seepage flow exceed the resistance [22, 44]. Particles slide in the pipe, may rest temporarily on the bed, and are gradually transported by the flow. When detached grains rest temporarily on the bed or roll through the pipe, the shallower pipe results in a temporarily higher flow velocity, higher pipe gradient, and therefore a lower tip gradient (Fig. 1). That delays or stops the pipe lengthening. The tip gradient will increase due to the removal of grains in the pipe and the next slope failure occurs when the tip gradient has recovered to the critical value [37]. This intermittent pipe lengthening has been observed for example by Hanses [21]. The description above is based on observations when the pipe is close to equilibrium. In case of high progression rates, there will be continuously a layer of moving grains because the critical gradient at the pipe tip has been exceeded by such an amount that the influence of the sediment load in the pipe is not sufficient to reduce the pipe tip gradient below the critical value. In the case of internally unstable soils, the tip failures may also be delayed by erosion of the finer fraction from the coarser soil matrix [23]. In case of very fine dense sand, the rate of slope failures may be limited by dilatancy effects. Soil matrix expansion up to the critical porosity requires an inflow of water. The lower the permeability, the more time is needed to supply this water. Therefore it can pose a limit on the rate of primary erosion, similar to breaching flow slides described by Van Rhee [57]. At the same time, the pipe downstream deepens by secondary erosion if the bed shear stress exceeds its critical value [52]. Deepening reduces the gradient in the pipe and hence increases the tip gradient, so the two types of erosion are coupled.

Fig. 1
figure 1

Conceptual description of primary and secondary erosion near the pipe tip. The lower panel indicates the head profile and tip gradients (i) during stage a−c

Full size image

Given these two erosion processes, the time scale of erosion can be considered as the combination of (1) time needed for erosion of grains in the pipe until the local tip gradient recovers to the critical value, (2) time needed for erosion of a finer fraction at the tip, and (3) time needed for dilation of soil matrix at the tip. For the sands considered in this paper, we assume that the second and third component can be neglected.

1.3 Modeling of pipe progression rates

Several methods have been proposed to model the development of the pipe length over time for engineering purposes, which are summarized here. Kézdi [24] hypothesized that the progression rate of BEP is proportional to the pore flow velocity at the pipe tip. However, his model of pipe progression neglects pipe resistance, seepage concentration at the pipe tip, and includes no critical pore velocity. Furthermore, there is hardly any experimental data to test this hypothesis. Some empirical relations between erosion rate and seepage gradient were developed in the context of streambank erosion of cohesive soils due to seepage [8, 14]. Robbins et al. [41] determined such a relation for BEP experiments based on modeled seepage gradients and measured progression rates, and included this in a quasi-stationary BEP model. Additionally, several numerical models have been developed to predict BEP by coupling seepage, pipe flow and sediment transport relations [43, 59]. However, the pipe length development as predicted by these models has not been validated on different types of BEP experiments, as experiments with suitable measurements are very limited.

1.4 Objective

The goal of this study is to better understand and model the development of piping erosion over time. To achieve this, we measured local, scale-independent, conditions that explain the temporal development of piping (i.e., the progression rate). We modified a commonly used BEP laboratory setup to measure pore pressures and pipe pressures during the piping process with a high spatial and temporal resolution. The experimental program included different sand types with varying degree of compaction to explore the effects of grain size and compaction. Part of the experimental method and a small part of the results were presented in Pol et al. [37]. The paper is structured as follows: chapter 2 describes the experimental method, chapter 3 the primary experimental results, chapter 4 an analysis of local flow conditions, pipe development and sediment transport, and chapters 5 and 6 contain the discussion and conclusions, respectively.

2 Experiments

2.1 Modification of box-type setup

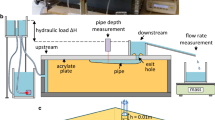
Previous research into BEP progression rates has either used a rectangular box-type setup [3, 41, 51] or a cylinder-type setup [38]. The box-type setup poses less restrictions on flow from the sides and results in flow concentration toward the exit. On the other hand, a cylinder forces the pipe to grow right below a row of sensors to measure pipe pressures. To combine the advantages of both types, we modified the box-type setup used by [52] and [51] so that pipe pressures can be measured.

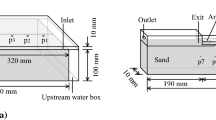
The sample dimensions are 0.48 × 0.30 × 0.1 m (Fig. 2). The box has a 10 mm thick acrylate cover with a 6 mm diameter exit hole. The seepage length L equals 0.352 m, between upstream filter and the exit. The modification is twofold. First, two permeable barriers of filter fabric (0.05 mm aperture) were placed longitudinally and 35 mm apart to prevent sideward pipe growth but allow flow to pass. Second, silicon strips (0.3 mm high, 3 mm wide, 10 mm long) were placed diagonally with 20 mm spacing between the rows, and sand was sprinkled over them while the silicon dried (grey strips in Fig. 2). These two steps restrict the pipe path to the middle 35 mm of the box, without significantly influencing the flow. Hereby, the pipe can meander slightly, while also being close to the sensors and not significantly influencing the piping process. At the interface with the guides, the porosity may be slightly higher as the grains do not interlock. However, as will be demonstrated in Sect. 3.2, this does not have a significant effect on the results, as the pipe tip generally propagates at some distance from the guides. Finally, 20 mm spaced pressure ports were added in the center axis of the box and connected to pressure sensors at the side of the box. Influence of the ports on progression is expected to be negligible, given their limited volume and not extruding into the sand.

Fig. 2
figure 2

Drawing of experimental setup

Full size image

2.2 Materials and measurement techniques

The experiments include three fine, uniform sands with characteristics as shown in Table 1. The FPH sand was also used in Pol et al. [36]; the Baskarp B25 sand was used in Akrami et al. [2] and Rosenbrand et al. [42]. Grain sizes were determined by dry sieving. Porosity nmin is based on the method in ASTM4253 (dry method, vibrating needle instead of vibrating table) and nmax on ASTM4254 (funnel method). The porosity nsb and slope angle θsb of the sand boil per sand type were determined by measuring its height, diameter, and dry mass at the end of each test. The water temperature was between 20 and 22 °C.

Table 1 Sand characteristics
Full size table

Water levels at the upstream and downstream sides were measured using riser tubes at least every 5 min, up to every minute during progression. The flow rate was measured at the same frequency using a digital scale. Pore pressures were measured by differential pressure transducers (Sensortechnics RPOP001D6A), through the ports P1−P19 (Fig. 2), at a sampling frequency of 10 Hz.

Three cameras recorded the erosion development. The main camera above the setup provides a top view of the sand sample, every 10 s. In some tests, we recorded short close-up videos of the erosion process using a second camera, which was placed temporarily on top of the cover. The last camera recorded the volume of the eroded sand, every minute. Pipe length and sand boil diameter were estimated visually at least every five minutes, up to every minute during progression (Fig. 3).

Fig. 3
figure 3

Top view of the setup at the end of experiment B25_245

Full size image

Pipe depth in equilibrium conditions was measured using a laser device (DSE ODS 120) mounted on a movable frame to create transects perpendicular to the pipe. Pipe depth measurements during pipe progression were not feasible as the laser device would limit observation of the pipe by blocking the view from top and moving particles would affect the depth measurement.

Pipe flow velocities in equilibrium conditions were extracted from videos of dye tracer injections. A red dye was injected under low pressure through one of the pressure ports (usually P14 or P15) for approximately 2 s. The propagation velocity of the dye in the x-direction is obtained by tracking the change in color intensity relative to a video frame before injection [18]. Usually, we injected 5−7 times in the same equilibrium conditions, from which we take the median propagation velocity. We assume that this represents the maximum flow velocity over the velocity profile in a cross section (umax).

2.3 Test procedure

The test procedure as described in [37] consists of sample preparation, loading, and measurement cycles. First, the sample is prepared with the box in the vertical position by sprinkling dry sand in de-aired water, and the sample is compacted by tapping the box with a hammer. Then, the box is closed and placed in the horizontal position, and the head at both sides of the sample is leveled. The loading procedure is as follows: keep the head difference constant if there is still erosion after 5 min, or increase it otherwise. The head difference is increased by reducing the downstream head, and the upstream head is kept constant. When the pipe reached the upstream filter, the downstream head was raised (suddenly) to stop erosion. Then, the head difference was increased in small steps of 2 mm until grains started moving somewhere in the pipe. If the movement continued, the head difference was decreased by 2 mm. This procedure was iterated until the bed was just in equilibrium. In those conditions, the head drop was kept constant and the pipe depth, local hydraulic gradients in the pipe, and local maximum flow velocity umax were measured to determine the critical bed shear stress. During the test, measurements of pipe length, sand boil radius, flow rate and total head drop were taken every five minutes, up to every minute during progression. After the test, the sand boil was collected, dried and weighed.

2.4 Test program

The test program consists of two phases as shown in Table 2. First, tests 217−222 are reference tests without guides to verify that the changes in experimental setup do not influence the critical head difference and average progression rate. Note that tests 218 and 219 are not representative as the pipe initially developed toward the side of the box, affecting the critical head. Tests 223−231 were not included in Table 2 since these involved iterative improvements of the guides to obtain stable results. Phase 2 consists of tests 232−250 with the adapted setup and varying sand type, degree of compaction and hydraulic loading. Densely packed samples have a relative density (Dr) of 0.7−0.8 and loose samples of 0.5−0.55. The standard loading scenario L1 is to gradually increase the head difference to the critical head difference (Hc) and then keep it constant. L3 and L4 are overloading scenarios, which means that after a stable pipe developed with pipe length l ≈ 0.14 m (Table 2), the head is suddenly increased to 1.2·Hc (L3) and 1.1·Hc (L4), respectively, and then kept constant. Note that the effective head drop over the sample (Hcorr) is not always constant after Hc is reached, due to filter and exit losses changing with flow rate. Correction for filter and exit losses is described in Sect. 3.2. Furthermore, the hydraulic conductivity k is estimated from flow rate and pressure gradient near the upstream filter, so it may be less reliable for tests 217−222 (marked with #). The results in Table 2 are discussed in Sect. 3.2.

Table 2 Overview of experiments and primary results
Full size table

3 Experimental results

This section reports the experimental observations and the basic measurements of hydraulic head and pipe geometry. Analyses of progression rates, shear stresses and sediment transport require more interpretation and are therefore described separately in Sect. 4.

3.1 General observations on the erosion process

This section describes the observed phases of the BEP process and (visual) observations of the erosion process at the grain scale. Like in other hole-type experiments [29, 51, 52], each test showed several phases for an increasing head drop: fluidization of sand in the exit hole, formation of a circular void (lens) around the exit hole, pipe growth toward an equilibrium (regressive) and progressive pipe growth until the pipe forms a hydraulic shortcut. Figure 4 indicates these phases in a plot of the head at each transducer. Before the erosion phases, the heads respond almost instantaneously to an increasing head drop. During erosion, the heads decrease also gradually under a constant head drop due to the pipe lengthening. It was also observed that after a head increase, the location in the pipe where grains started eroding was not always the same. Visual observations during the head increase indicate that erosion sometimes starts in the bed, sometimes at the tip. This suggests that both the bed and the tip are close to critical conditions, at least in the regressive phase.

Fig. 4
figure 4

Head development in sensor P1−P15 and erosion phases in test B25_245

Full size image

At a few instances during the test program, the erosion process at the pipe tip was visualized using close-up videos. Grain detachment at the tip generally occurred in cycles. Sometimes, first a small displacement of particles in the zone upstream of the tip was observed, which increased the porosity locally. Sometimes, there was rearrangement of a few small particles in the sand upstream of the tip without the other grains moving. Quickly after the small displacement, a group of grains detached and moved into the pipe. Part of the grains washed away directly, while another part settled close to the tip. These settled grains were transported gradually until the cycle repeated. Between the group detachments, also individual particles detach. At higher progression rates, it was more difficult to distinguish separate cycles and the erosion process is more continuous. There is much variation between and within tests regarding the occurrence and duration of these steps in the erosion cycle, but the process generally followed this cycle.

One test (B25_245) includes a close-up video of the tip during a transition from equilibrium to erosion and simultaneously the pipe tip grows closely under the pressure sensors, which allows to observe the effect of particle detachment on the pressure gradients at the tip and in the pipe. Based on this example, Pol et al. [37] show that the pipe resistance induced by the detached particles reduces the tip gradient temporarily below the critical tip gradient and temporarily stops the tip erosion. These observations indicate that the transport in the pipe affects the progression rate.

3.2 Critical head, pipe length and hydraulic gradients

The main results of the experiments are given in Table 2. The measured critical head drop Hc is the sum of the head drop over the sample Hc,corr, the upstream filter loss, and the exit losses. The filter loss was estimated by a linear regression of the head profile through sensors P14−P15. The exit loss is estimated from regression on sensors P2−P5, but due to nonlinearities in the head profile around the tip this is only reliable when the tip has passed P5 (x > 0.25 m, l > 0.115 m). Therefore, for l > 0.115 m, the exit loss from regression was related to the flow rate Q for each test. Ultimately, the estimated exit loss throughout the test is based on this relation between exit loss and measured flow rate. At the critical pipe length, the average estimated filter and exit losses were 6.1 and 5.6 mm, respectively. The critical pipe length lc = xtip,c−xexit is the pipe length when the head reaches Hc. The average progression rate after the critical head has been reached vc,avg = (L−lc)/(tend−tc) is based on visual observations of the pipe tip position. Hydraulic gradients between transducer pairs were derived from the pressure measurements, mostly having a 0.02 m spacing (Fig. 5). Critical tip gradients ic,tip are defined as the maximum gradient of the transducer pairs passed during the regressive phase (so pipe is close to equilibrium). These values are not available for all tests, as the pipe tip sometimes passed besides all pressure ports in the regressive phase. If multiple values were obtained for one test, Table 2 gives the maximum.

Fig. 5
figure 5

Example of the head profile close to critical conditions in test B25_245. □ = downstream head. x = head at filter. Estimates based on regression are indicated by the grey dot and cross

Full size image

Modification of the setup (guides and pressure ports) did not lead to significant differences between the control group of dense B25 sand (tests 217 and 220−222, see Table 2) and modified group (tests 232, 236, 243), in terms of critical head Hc,corr (6.3−6.8 cm before, 5.9−6.2 cm after), critical length lc (10−19.5 cm before, 15.6−18.6 cm after) and progression rate vc,avg (0.05−0.09 mm/s before, 0.05−0.10 mm/s after). The slightly lower Hc (9%) after modification may be the result of a locally lower Dr and hence higher conductivity at the guides. In case of the coarse FS35 sand, however, the pipe width may have been limited by the guide distance of 35 mm (see Sect. 2.1), resulting in slightly deeper pipes compared to a situation without guides.

Both the net head drop over the sample Hc,corr (Table 2) and the local critical tip gradient ic,tip have a positive relation with Dr for both the B25 and FS35 sands (Fig. 6), which confirms findings by [38]. The critical pipe length lc varied between 30 and 60% of the seepage length. Given the large variability in lc, it is not possible to infer significant effects of grain size or compaction.

Fig. 6
figure 6

Critical head drop (a) and local critical tip gradient (b) as function of relative density Dr

Full size image

3.3 Pipe length development

Kezdi [24] expected acceleration of the pipe development because of the increasing upstream secant (average) gradient with increasing pipe length. Figure 7 shows the pipe length development between the critical length l = lc and when the upstream filter is reached (l = L). Pipe length and time are normalized. The normalized pipe length becomes ln = (l − lc)/(L − lc) and the normalized time tn = (t − tc)/(tend − tc), in which tc is the time when l = lc and tend is the time when l = L. On average, there is some acceleration in normal loading tests, which are closer to equilibrium. However, there is hardly acceleration in the B25 overloading tests as indicated by the nearly linear curve (note that absolute progression rates are higher).

Fig. 7
figure 7

Normalized pipe length development in normal loading and overloading tests, average of tests per sand type

Full size image

This confirms experiments by Vandenboer et al. [51] using the same setup, and another hole-type experiment by Miesel [30]. However, slope-type experiments by Robbins et al. [41] showed very rapid progression and did not accelerate. Slope-type tests are initiation-dominated [52] and therefore overloaded more severely under a constant head. Apparently, the progression rate does not increase with pipe length in those overloading conditions, despite the increasing upstream secant gradient. That indicates that the progression rate is limited by the transport of sediment down the pipe rather than the limited supply of water to the pipe tip in severely overloaded conditions. The observation of acceleration shows that the progression rate (load effect) is not constant for a constant load. Here it is noted that the upstream filter resistance increased slightly with pipe length in several tests, resulting in a decreasing head drop over the sample. Without that resistance, the acceleration is expected to be even more pronounced.

3.4 Pipe geometry after test

The pipe geometry was analyzed to estimate the shear stress acting on the pipe bottom during equilibrium in a fully formed pipe. When a pipe had fully developed to the upstream filter and the head drop was lowered to bring the grains in equilibrium (see Sect. 2.3), the pipe geometry was measured at several transects between x = 0.22 m and x = 0.46 m (approx. 2 cm spacing) using a laser scanner. From these cross sections, longitudinal profiles of the average pipe depth (aavg), maximum pipe depth (amax), area (A), hydraulic radius (R) and pipe width (wavg = A/aavg) were determined for the situation that the pipe reached the upstream filter. Note that several tests showed some erosion between the pipe reaching the filter and the laser measurement, as shown by the photos and sand boil dimensions. Based on the sand boil dimensions at these two moments in B25 and FS35 tests 232−250 and an assumed total pipe width of 25 mm (B25) or 30 mm (FS35), this resulted in an average depth increase of 0.1 mm.

When the pipes progressed, the channels were often migrating sideward, especially in the downstream parts of the finer sands B25 and FPH. This results in inactive channels without sediment transport and presumably a low flow rate. As we assume that the main flow conveying channel is representative for the pipe flow conditions such as shear stress, using the entire channel would lead to an incorrect bed shear stress τ (as aavg is underestimated). This channel migration is not the result of the setup modification as it also occurs in [50], though it is expected to occur less due to the application of the guides, see Fig. 2. The definition of the boundaries of the main channel is based on visual interpretation of the depth profile (Fig. 8). If one channel is clearly larger than the other, the largest is selected as main channel. If both are equally large or there is only one, the main channel equals the entire channel. Figure 9 shows pipe geometry based on the entire channel and the main channel. The main channel approach yields higher aavg, lower wavg and more consistent geometries across the three sands. In Sect. 4.1 (Fig. 10) we show that the main channel approach yields more consistent shear stresses. Therefore, the main channel geometry is a better representation of the pipe flow than the entire cross section and we use it to estimate pipe flow conditions.

Fig. 8
figure 8

Example of cross section at x = 0.22 m at the end of test B25_245

Full size image
Fig. 9
figure 9

Pipe geometry during equilibrium with fully developed pipe in tests 232−250, excluding B25_244. Based on entire channel (left) and main channel (right). Error bars indicate ± one standard deviation. x = 0.48 is the upstream boundary

Full size image
Fig. 10
figure 10

Critical Shields number during equilibrium with fully developed pipe in tests 232−250, average value per sand type, plotted with empirical relations [6, 52] and experiments in laminar flow in classical flumes [19, 25, 28, 34, 55, 58, 60, 61, 65] and piping cylinders [55]

Full size image

Figure 9 shows the resulting depth profile (aavg) per sand type. The solid line indicates the average of tests 232−250, the error bars indicate ± one standard deviation. The pipe depth scales with the permeability as \(a\sim \sqrt[3]{\kappa }\)[50]. Scaling with d50 gives reasonable results too for these sands; which one scales better can only be assessed with a wider range of grain size and uniformity. The depth profile can be approximated with a power function as:

$$a_{{{\text{avg}}}} = 6.0 \cdot \sqrt[3]{{\kappa (x_{{tip}} - x)}} \, [{\text{m}}]$$
(1)

The profiles of amax and R (not shown in Fig. 9) have a similar form with coefficients 10 and 2.8, respectively. The shape of the depth profile will depend on the spatial distribution of seepage toward the pipe, so on aquifer geometry. As this relation is purely empirical, it is only to be used to analyze the current experiments. Three B25 tests (230, 236 and 245) include depth measurements when the pipe was partially developed (l < L). From the depth data (not shown here), it follows that the partially developed depth profile is similar to Eq. 1. Therefore, we assume that Eq. 1 also holds during progression. Figure 9b indicates that there was no significant difference in equilibrium depth profiles between the average of all tests and the ones with overloading (L3 and L4). Therefore, we assume that overloading does not lead to significant differences in depth.

The average pipe width wavg is rather constant along the pipe (Fig. 9d) and in the order of 60 times d50 for B25 and FPH sands. This results in a main channel wavg/aavg ratio of 10 at the downstream side to 25 near the pipe tip. Furthermore, based on the photos taken from top, we found the tip width to be approximately 30 times d50, confirming [53, 63]. However, the tip width increases with the degree of overloading, up to 45·d50 at 1.2·Hc. The pipe width in FS35 sand is lower than in B25 and FPH sand, with wavg = 40·d50. This may be caused by the limited space (35 mm) between the filter fabric guides. This restriction may have caused narrower and deeper cross sections, which could explain the underestimated FS35 depth using Eq. 1 (Fig. 9).

4 Pipe progression analysis

This section analyzes the pipe progression rates and its relationship with tip seepage velocity and pipe shear stress. First, the bed shear stress in equilibrium conditions with a fully developed pipe is computed with different approaches and compared to existing data of critical bed shear stress. This information is subsequently used to determine the bed shear stress during pipe progression. The tip seepage velocity is calculated from the measured tip gradient itip, conductivity k and porosity n, and both parameters are related to the pipe progression rate. Finally, the sediment transport is compared to sediment transport relations from classical, laminar flume experiments conducted for studies of sediment transport in open channels.

4.1 Critical bed shear stress measurements during equilibrium

The critical bed shear stress for incipient motion is an important parameter to predict piping and was determined from measurements at the end of each test, for the situation of a fully developed pipe. The pipe geometry is based on the main channel (see Sect. 3.4). The local hydraulic gradients between transducer pairs are only calculated for those pairs below which the pipe progressed. The maximum flow velocity in the pipe was measured by injection of a dye in one of the pressure ports close to the filter (P14 or P15).

Bed shear stress can be calculated based on either pressure gradient and pipe depth, pressure gradient and flow velocity or flow velocity and pipe depth. First, we present the three equations to calculate shear stress. Later, we show the resulting shear stresses for the piping experiments. In the equations below, the subscript of τ indicates on which quantities it is based, for example τai is based on pipe depth and hydraulic gradient. First, from a balance of forces it follows that the average shear stress along the wetted perimeter is the product of hydraulic radius R = a/2 and local pressure gradient in the pipe dp/dx, which gives for parallel plates [46]:

$$\tau_{ai} = R\frac{{{\text{d}}p}}{{{\text{d}}x}} = \rho_{w} g\frac{a}{2}i$$
(2)

Alternatively, one can use the relation between depth-averaged flow velocity \(U\), pressure gradient and pipe depth from the Poiseuille equation for laminar flow between parallel plates [46]:

$$\frac{{{\text{d}}p}}{{{\text{d}}x}}a^{3} w = 12Uwa\mu$$
(3)

In which \(U = 2/3u_{\max }\) [48]. Substitution of a in the shear stress Eqs. (2) by (3) gives:

$$\tau_{ui} = \sqrt {3\mu U\frac{{{\text{d}}p}}{{{\text{d}}x}}}$$
(4)

Alternatively, substitution of dp/dx in the shear stress Eqs. (2) by (3) gives:

$$\tau_{ua} = \frac{6\mu U}{a}$$
(5)

Note that the Reynolds number (Re = 4RU/v) during equilibrium at the end of the tests was in the order of 40 for FPH sand, 80 for B25 sand and 280 for FS35 sand, which confirms that the flow was laminar (Re < 2100). As the main channel w/a ratio lies in the range of 10 to 25, the assumption of parallel plates is a reasonable approximation [48, 52].

These three expressions (Eqs. 2, 4 and 5) for the shear stress are equivalent under the assumption of laminar flow between parallel plates but require different input. During equilibrium conditions, all three inputs (pipe depth aavg, local gradient between transducer pairs i, and flow velocity umax) were measured along the pipe to be able to compare Eqs. 2, 4 and 5. Finally, the measured shear stress τ(x) is averaged over the length of the pipe. In the analysis we assume that water density ρw = 1000 kg·m−3, and dynamic viscosity μ = 1 mPa·s (20 degrees C). Figure 10 shows the resulting critical bed shear stress from Eqs. 2, 4 and 5 during equilibrium (average of all tests with equal d50), plotted as critical Shields number \({\Theta }_{{\text{c}}} = \frac{{\tau_{{\text{c}}} }}{{(\rho_{s} - \rho_{{\text{w}}} ) g d}}\) against dimensionless particle diameter \(D_{*} = \left( { \frac{\Delta g}{{\upsilon^{2} }} } \right)^{1/3} d_{50}\). Results of Eqs. 2 and 5 are plotted for both the average depth aavg of the main channel and of the entire channel. With the entire channel, Eqs. 2, 4 and 5 yield different results, especially in case of the finer sands. With the main channel, the results from Eqs. 2, 4 and 5 are much closer, supporting the assumption of parallel plates and the use of the main channel depth. The main channel results are in good agreement with classical flume experiments on a plane bed [19, 25, 28, 34, 58, 60, 61, 65], piping experiments in cylinders [55] and predictions of critical shear stress by [6, 52]. In terms of \(\tau_{{\text{c}}}\), the main channel results are in the range of 0.314−0.360 Pa for FPH, 0.368−0.385 Pa for B25, and 0.417−0.564 Pa for FS35. So, the observed critical shear stresses as calculated using Eqs. 2, 4 and 5 are in line with other experiments, and therefore these equations are also applied to calculate shear stress during progression (Sect. 4.2).

4.2 Drivers of the progression rate

The progression rate v = dl/dt is a practical engineering metric for the temporal development of the piping process. This section correlates the observed progression rate during the progressive erosion phase to two variables: (1) seepage velocities upstream of the pipe tip following Kézdi [24], and (2) bed shear stresses in the pipe.

The seepage velocity just upstream of the pipe tip is derived from measured tip gradients:

$$u_{p} = \frac{{k \cdot i_{{{\text{tip}}}} }}{n}$$
(6)

In which \(i_{{{\text{tip}}}}\) is the local hydraulic gradient measured over a distance of 2 cm (transducer spacing) upstream of the pipe tip, and k and n are the initial hydraulic conductivity and porosity. While Kézdi [24] neglects head loss in the pipe and assumed that \(i_{{{\text{tip}}}}\) equals the average upstream gradient, this section applies the same concept, except for using measured local gradients. In contrast, [41] used back-calculated tip gradients from a FEM model.

The bed shear stress is calculated with Eq. 2 during the progressive erosion phase, since no flow velocity measurements during progression are available:

$$\tau (x,t) = 0.5\rho_{{\text{w}}} ga(x,t)i(x,t)$$
(7)

The pipe gradient i is calculated as the hydraulic gradient between the transducers downstream of the pipe tip. Shear stress is calculated both based on the average of all transducer pairs downstream of the tip (\(\tau_{{\text{bed,average,all}}}\)) and based on the average of the transducer pairs where the pipe passed right under both ports (\(\tau_{{\text{bed,average,passed}}}\)). The first may include more scatter from transducers pairs which are partly above and partly besides the pipe but contain more datapoints to be included in the averaging.

Due to a lack of depth measurements during progression, we assume that the depth profile has the same shape as during equilibrium at the end of the tests (Eq. 1):

$$a(x,t) = 6.0 \cdot \sqrt[3]{{\kappa (x_{{{\text{tip}}}} (t) - x)}} \, - 0.0001\left[ {\text{m}} \right]$$
(8)

The depth of 0.0001 m is subtracted to account for the residual erosion after reaching the upstream filter (see Sect. 3.4). We believe this provides a reasonable estimate of the depth profile as it is similar to some depth measurements made for partially developed pipes in three B25 tests (see Sect. 3.4). Furthermore, Eq. 8 was verified for test B25_247 (at l = 0.14 m) using the Poiseuille relation (Eq. 3) and measured gradient near the exit (i = 0.153 between transducers P2−P4), flow rate (\(Q = {\text{Uwa}}\) = 1.12 mL/s), and pipe width (w = 0.01 m). Equation 3 yields a calculated depth of a = 0.96 mm, whereas Eq. 8 yields a = 1.1 mm.

We calculated seepage velocity (Eq. 6) and pipe shear stress (Eq. 7) for each time that the tip passed a pressure port in the progressive phase (l > lc). However, we omit seepage velocity and tip gradient data if the pipe tip passed besides that transducer, as this data are unreliable. And we omit shear stress data if no value is measured for either \(\tau_{{\text{bed,average,passed}}}\) or \(\tau_{{\text{bed,average,all}}}\). This results in 75 datapoints from test 232−250 for seepage velocity and 103 datapoints from test 233−250 for shear stresses, which are from different sand types and degrees of overloading and measured at different pipe lengths. Note that using an equal number of datapoints for all parameters in Fig. 11 would not affect the trends in Fig. 11, but the lesser datapoints would make the analysis in Table 3 unreliable. Finally, the corresponding progression rate at these passing moments is calculated using a moving average (over 3 datapoints; usually 3 min) of the visually observed tip position.

Fig. 11
figure 11

Relation between progression rate and seepage velocity, bed shear stress, tip gradient, conductivity, and compaction. Color indicates loading type; marker indicates sand type

Full size image
Table 3 Estimated critical bed shear stress [Pa] during progression
Full size table

Figure 11 shows the relations between progression rate and several parameters related to seepage velocity and pipe shear stress. Values of ρp indicate Pearson correlations. Figure 11a shows that the progression rate is proportional to the tip seepage velocity up for tests with normal loading (L1) on different sand types. However, the overloading tests (L3 and L4) on B25 sand show higher progression rates which cannot be explained by the seepage velocity as the seepage velocity hardly changes under overloading. Figure 11a−c show how the effect of up is composed of k and itip and that the hydraulic conductivity explains most of the variation in progression rate observed in normal loading tests, not the tip gradient. Furthermore, the measured local tip gradient itip does not seem to increase with the degree of overloading, although there is substantial variability in these measurements. This can be caused by a higher porosity at the tip, or by higher resistance in the pipe (due to high sediment load). Furthermore, it is likely that the tip gradient cannot exceed its critical value much, as the tip material will collapse (see Fig. 1). Figure 11e−f shows that the bed shear stress is a better predictor, see also Sect. 4.3 for more discussion. Compared to the seepage velocity it predicts the overloading tests reasonably well and explains part of the variation within groups (e.g., group FS35,L1). \(\tau_{{\text{bed,average,all}}}\) gives an even stronger relation (Fig. 11f), probably due to the averaging of noise caused by some pressure ports being besides the pipe and that generally a larger part of the pipe is included in the averaging due to less strict criteria. Finally, the data show no relation between Dr and progression rate in normal loading tests (Fig. 11d).

4.3 Critical bed shear stress during pipe development

Section 4.1 shows measured critical bed shear stresses \({\tau }_{\mathrm{c}}\) during equilibrium at the end of the tests. However, \({\tau }_{\mathrm{c}}\) during progression can also be estimated from the plots in Fig. 11f, as the point where the progression rate reaches 0. We fitted a linear regression line through the same data as in Fig. 11e and f, of which the intercept is a proxy of the critical bed shear stress during progression. The same procedure was followed for the shear stress at the first transducer pair downstream of the tip and for the average shear stress between the five transducers (P2−P6) closest to the exit. Table 3 shows the obtained results, including the values with fully developed pipes at the end of the tests. It appears that the estimated \({\tau }_{\mathrm{c}}\) during progression is lower than during equilibrium in fully developed pipes. The estimated \({\tau }_{\mathrm{c}}\) near the exit is similar to the average \({\tau }_{\mathrm{c}}\) in the pipe, but the estimated \({\tau }_{\mathrm{c}}\) near the pipe tip is clearly lower.

There is a general consensus that upward seepage reduces both the occurring shear stress due to a change in velocity profile as well as the critical shear stress [7, 15, 26]. Regarding the impact on sediment transport rates, these studies show diverging results. Upward seepage effects were omitted from the Sellmeijer model [47] as they expected that this would not affect the eroding grains on top of the bed. As upward seepage is most severe at the pipe tip, this effect could explain the lower critical shear stress near the tip in Table 3. The critical bed shear stress under upward seepage is equal to \(\tau_{{\text{c}}} = \tau_{{{\text{c}},0}} \left( {1 - \frac{{i_{{\text{u}}} }}{{i_{{\text{f}}} }}} \right)\) where τc,0 is the critical bed shear stress without seepage, iu is the upward hydraulic gradient in the bed, and if is the critical gradient for fluidization [7]. Finite element simulations of test B25_245 (for l = 0.185 m) [39] show that the upward seepage gradient below the pipe varies from approximately 0.35 at the tip to 0.2 at a distance of 3 cm from the tip. The fluidization gradient is \(i_{{\text{f}}} = (1 - n)\left( {\rho_{s} /\rho_{{\text{w}}} - 1} \right)\) [49], which equals 1 for B25 sand with n = 0.4. The resulting 20−35% reduction in \(\tau_{{\text{c}}}\) partly explains the lower experimentally obtained critical shear stress ‘during progression’ as compared to ‘during equilibrium’ (Table 3). These findings indicate that upward seepage may have a significant effect on \(\tau_{{\text{c}}}\) in BEP. Upward seepage affects the acting shear stress \(\tau\) through a change in the near-bed velocity profile [7]. A full quantification of these effects for the case of laminar flow in rectangular ducts is beyond the scope of this research and needs to be verified with modeling or future experiments with more detailed information on pipe depth, pipe velocity profile, and upward seepage gradients in case of partially developed pipes. Omitting the upward seepage effect from BEP models may be acceptable if the effect on the acting shear stress \(\tau\) balances the effect on the critical shear stress \(\tau_{{\text{c}}}\).

4.4 Sediment transport

The dependence on the bed shear stress raises the question whether the piping erosion rate can be predicted using sediment transport equations. Sediment transport (bed load) in turbulent flow is typically related to the bed shear stress through:

$${\text{q}}_{*E} = \alpha_{1} \left( {{\Theta } - {\Theta }_{{\text{c}}} } \right)^{{\alpha_{2} }}$$
(9)

in which the Einstein number \(q_{*E} = \frac{{q_{{\text{v}}} }}{{d\sqrt {\Delta gd} }}\), \(q_{{\text{v}}}\) a volumetric sediment flux per unit width, \(\Theta\) the Shields number \(\Theta = \frac{{\tau }}{{(\rho_{s} - \rho_{w} ) g d}}\), critical Shields number \(\Theta_{{\text{c}}} = f \left( {{\text{Re}}_{*} } \right)\), and the coefficients for turbulent flow are \(\alpha_{1} \approx 4, \alpha_{2} \approx 1.5\) [62]. Similar equations exist for laminar flow [5, 6, 27, 32, 64]. The sediment transport rate in laminar flow scales better by a viscous scaling rather than the inertial scaling of the Einstein number [5, 32]:

$$q_{*v} = \frac{{q_{{\text{v}}} }}{{(\rho_{s} - \rho_{{\text{w}}} )gd^{3} /\upsilon }}$$
(10)

Although our experiments were not specifically designed for this purpose, we complemented the available experimental data on sediment transport rates in laminar flow [1, 5, 10, 11, 20, 27, 45] with estimated sediment transport rates from the piping experiments in this paper. Table 4 summarizes the materials and flow conditions in the classical flume experiments. The sediment transport rate \(q_{{\text{v}}}\) (volume per unit width) in the piping experiments is estimated from the growth rate of the sand boil radius (Fig. 3) and an average main channel width near the exit of 40*d50 (Fig. 10). Assuming a cone-shaped sand boil with equal inner and outer slopes, its sediment volume is given by:

$$V = (1 - n_{{{\text{sb}}}} )\frac{\pi }{4} \cdot \tan \theta_{{{\text{sb}}}} \left[ {r_{{\text{b}}}^{3} + r_{{\text{e}}}^{3} - r_{{\text{e}}} r_{{\text{b}}}^{2} r_{{\text{b}}} r_{{\text{e}}}^{3} } \right]$$
(11)
Table 4 Characteristics of classical flume experiments on sediment transport in laminar flow
Full size table

In which nsb the porosity in the sand boil, θsb the slope angle, rb the radius of the sand boil (observed during the tests), and re the exit hole radius (0.003 m). Values of nsb and θsb given in Table 1 are based on sand boil dimensions and dry sand mass measured at the end of tests 224−250. The Shields number \({\Theta }\) at the downstream end of the pipe is based on Eq. 7 using the average pipe gradient over the 5 transducers near the exit (P2−P6) and pipe depth aavg at the exit (x = 0.125 m) from Eq. 8, which increases with pipe length. The critical Shields numbers \({\Theta }_{{\text{c}}}\) at the downstream end of the pipe are calculated as 0.0736 (FPH), 0.0705 (B25) and 0.0615 (FS35) from τexit in Table 3, so from extrapolating the shear stress to v = 0. Note that this estimate of \({\Theta }_{{\text{c}}}\) during progression is relatively low compared to the value at the end of the tests (Fig. 10), which is possibly due to upward seepage during the piping experiments.

Figure 12 shows the sediment transport rate \(q_{*v}\) as function of \({\Theta }\left( {{\Theta } - {\Theta }_{{\text{c}}} } \right)\), for both the classical flume experiments and the piping experiments. The experimental data mostly follows the same trend. Only the data of Charru et al. [5] is below the range of other data, and Grass and Ayoub [20] shows a higher exponent. The transport rate in the piping experiments is approximately a factor 5 below the average trend, but falls within the experimental range, and shows a similar trend with increasing Shields number. As can be expected, the scatter in the piping experiments is larger than in classical flume experiments because there is intermittent erosion, no wide uniform bed and flow profile, and no depth profile measurements during progression.

Fig. 12
figure 12

Sediment transport rate as function of Θ(Θ − Θc) in classical flume experiments from literature and the piping experiments in this paper

Full size image

Least square fitting of the flume data alone results in the following empirical relation with R2 = 0.90 and a median absolute percentage error (|qpredict − qexp|/qexp) of 0.373, drawn in Fig. 12:

$${\text{q}}_{*v} = 0.39 {\Theta }\left( {{\Theta } - {\Theta }_{{\text{c}}} } \right)$$
(12)

Figure 13 shows the ability of Eq. 12 and the models by Yalin [64], Charru et al. [5], Cheng [6] and Ouriemi et al. [32] to predict the classical flume experiments from the literature [1, 5, 10, 11, 20, 27, 45]. Cheng [6] and Ouriemi et al. [32] fit well to the higher transport rates, but overestimate the transport for flow conditions close to critical. Yalin [64] generally performs well but shows some underestimation closer to critical. The empirical model by Charru is about one order of magnitude below the average trend of the flume data, which is in line with findings of Wewer et al. [59] that Charru underestimates the pipe progression. However, it is a lower bound for the piping data. The simple empirical regression from Eq. 12 performs well over a wide range of measurements but underestimates the highest transport rates. As in the piping experiments \(q_{*v}\) < 10−2, Eq. 12 is a suitable empirical model.

Fig. 13
figure 13

Experimental data in classical flume experiments (see Fig. 12) as predicted by several sediment transport equations including Eq. 12

Full size image

So far, the analysis focused on the relation between transport rate and shear stress in the classical flume experiments and piping experiments. The measured transport rate can also be used for an additional cross-check on the assumptions on the pipe geometry during progression. For a progressing pipe, the sediment mass balance states that the increase in pipe volume per unit time (dl(1 − n)·Aexit) is equal to the total sediment transport at the downstream end of that pipe (Qv·dt). Assuming a rectangular cross section (Aexit = wexit·aexit), this relates the progression rate dl/dt to the sediment transport rate as:

$$v_{{{\text{predict}},{\text{V}}}} = \frac{{{\text{d}}l}}{{{\text{d}}t}} = \frac{{{\text{q}}_{v} }}{{\left( {1 - n} \right)a_{{{\text{exit}}}} }}$$
(13)

Combining Eqs. 12 and 13 results in a progression rate as function of the measured shear stress near the exit:

$$v_{{{\text{predict}},{\Theta }}} = \frac{{(\rho_{s} - \rho_{{\text{w}}} )gd^{3} }}{\upsilon } \cdot \frac{{0.39 {\Theta }_{{{\text{exit}}}} \left( {{\Theta }_{{{\text{exit}}}} - {\Theta }_{{\text{exit,c}}} } \right)}}{{\left( {1 - n} \right)a_{{{\text{exit}}}} }}$$
(14)

For the same data as in Fig. 10 and using aexit from Eq. 8 and assuming wexit = 40·d50, Eqs. 13 and 14 were evaluated and compared to the measured progression rate. Figure 14a shows that \(v_{{{\text{predict}},{\text{V}}}}\) yields a correct magnitude of dl/dt, providing a cross-check that reasonable assumptions were made regarding aexit and wexit. Figure 14b shows that Eq. 14 results in an over-prediction of the progression rate by a factor 5, which agrees with the difference between piping tests and classical flume experiments in Fig. 12. Therefore, we recommend using a coefficient of 0.08 instead of 0.39 in Eq. 12 when modeling BEP using sediment transport relations, until more is known about the applicability of these sediment transport relations for BEP.

Fig. 14
figure 14

Measured progression rate in piping experiments and predictions using Eqs. 13 and 14

Full size image

5 Discussion

This discussion section compares the results to previous experiments, reflects on the experimental setup and finally discusses the erosion process and some implications for modeling the temporal development of BEP.

5.1 Comparison with other experiments

First, we compare our results with previous BEP experiments. No experiments with progression rates on these specific sands and with the same setup have been reported, but there are several experiments with a similar setup and sand of a similar size. The critical head of B25 is similar to tests on M32 sand (d50 = 0.251 mm) by Vandenboer [50], but is lower than small-scale scale tests on Itterbeck 125−250 sand (d50 = 0.219 mm) by Van Beek et al. [53] due to lower permeability. We find a slightly larger pipe depth at the end of the tests compared to Vandenboer [50], but this can be explained by differences in test procedure, as Vandenboer stopped the experiment immediately when reaching the filter, whereas we brought the pipe in equilibrium conditions.

In terms of progression rates, the closest comparison can be made between the tests on FPH sand and tests on M34 sand (d50 = 0.155 mm) by Vandenboer et al. [51], which were both conducted in small-scale setups with hole-type exit. For loading conditions of H/Hc = 1 (like L1), Vandenboer reports an average progression rate of 7.3·10−5 m/s which is comparable to our rate of 4.7·10−5 m/s for FPH sand. Comparing with small-scale slope exit experiments by Van Beek [35, 54] and Robbins et al. [41], we find almost one order of magnitude lower progression rates. As explained in Sect. 3.3, this is likely due to fact that slope setups are generally initiation-dominated and therefore are more severely overloaded when the pipe length increases. This indicates that a model with local parameters can be more accurate compared to one using average gradients and average progression rates. Robbins et al. [41] proposed a relation with the local tip gradient:

$$v_{{{\text{predict}}}} = 0.15 \cdot \left( {\frac{{d_{50} }}{{1.27 \cdot 10^{ - 3} }}} \right)^{ - 0.84} \cdot \left( {\frac{e}{0.647}} \right)^{ - 3.1} \cdot \frac{{k \cdot {i}_{{{\text{tip}}}} }}{n}$$
(15)

In which e = n/(1 − n) is the void ratio. Figure 15 shows that Eq. 15 cannot predict our measurements accurately for both normal loading and overloading based on measured gradients.

Fig. 15
figure 15

Measured progression rate in piping experiments and prediction using Eq. 15 [41]

Full size image

5.2 Reflection on the analysis and experimental setup

In this section, we discuss several assumptions in our analysis which may influence the results.

First, this research focuses on the internal erosion mechanism of backward erosion piping, which can occur when there is a supporting cohesive roof above the cohesionless soil. In this case, erosion takes place predominantly in the sand, resulting in relatively wide pipes which can be approximated by flow in wide rectangular ducts. In case of other forms of internal erosion, such as concentrated leak erosion, the erodible surface is all around, resulting in circular pipes. Findings in this paper cannot be applied directly to other forms of internal erosion. Due to the assumption of laminar flow, the sediment transport equations may also not apply to the process of pipe widening (enlargement) after a hydraulic shortcut formed, which likely results in turbulent pipe flow.

Second, the critical local tip gradient (Fig. 5b) can serve as a local criterion for pipe progression. Like a cylindrical setup [38], our adapted setup is very suitable to measure these criteria. However, it is important to note that its value depends on the sensor spacing, and when applied in numerical modeling this should match with the grid size for instance.

Third, as we have no frequent pipe depth measurements during progression, we assume that the shape of the equilibrium depth profile at the end of the tests also applies to partially developed pipes. This assumption affects the computed bed shear stresses. Yet, we expect this provides a reasonable estimate of the depth profile as it matches depth measurements made for partially developed pipes in three B25 tests 230, 236 and 245.

Fourth, based on a preliminary analysis we found a difference between the critical bed shear stress in equilibrium conditions at the end of the tests and during progression. Furthermore, during progression, the estimated critical shear stress near the pipe tip is lower than near the exit. A possible explanation for this finding is the effect of upward seepage on the grain stability, which is absent the end of the tests. Upward seepage also affects the pipe flow velocity profile, and thus the relation between pipe flow rate and bed shear stress. For modeling purposes, it is important to apply a critical shear stress that is consistent with the applied pipe flow equations. It is recommended to investigate whether computations with and without upward seepage give a significant difference in critical pipe gradient.

Finally, we find that the sediment transport rate in our experiments is approximately a factor five below what is expected based on most classical flume experiments, although still above Charru’s data [5]. The reason for the lower transport rate in piping tests is not clear, as there are several possible explanations. First, the ratio of the flow depth to the particle diameter (aavg/d50) is relatively low, which may restrict the transport. Second, the intermittent erosion in BEP may result in a lower transport rate as the change in sand boil size is measured over a longer interval (typically 5 min). Furthermore, values of Θ and Θc during progression depend on the assumed depth profile, but this cannot explain a factor 5. Finally, the grains may be transported over a smaller width than 40*d50, concentrated in the channel center, which would increase \(q_{*v}\), but also cannot explain a factor 5. Given the uncertainties in the determination of \({\Theta }\), \({\Theta }_{{\text{c}}}\) and \(q_{*v}\) during progression, we recommend testing whether this difference can be confirmed by BEP experiments with more detailed measurements of sediment transport rate and both acting and critical shear stress.

The adapted setup allows to force the pipe development in the vicinity of the pore pressure sensors, and thus allows to measure local pipe gradients and flow velocities. This in turn, allows to determine local hydraulic gradients and bed shear stresses during equilibrium and pipe development. We see some further improvements of the setup to obtain better measurements. First, additional pressure sensors to measure the exit head loss and vertical gradients below the pipe. Pressure ports using wider slots instead of small holes would allow for a more accurate measurement of tip gradients, as it reduces the scatter from the pipe passing at some distance from the center line. Second, to reduce uncertainties in the pipe depth development during progression, more geometry measurements should be taken during the regressive and progressive erosion phase. This will yield more reliable estimates of acting and critical shear stress during pipe development.

5.3 Erosion process

Pipe lengthening occurs if the stability criterion at the pipe tip (e.g., local gradient) is exceeded [21]. On the other hand this often requires pipe deepening which is governed by the critical bed shear stress in the pipe [46]. As conceptualized in the introduction, the time scale of the BEP erosion process (time between successive tip failures) can be dominated by gradual removal of finer material from the soil matrix at the tip, by gradual soil matrix expansion due to limited inflow (dilatancy), or by the sediment transport capacity of the pipe. In these uniform sands and in near-critical conditions, our experiments show no gradual removal of fines from the tip, as assumed by Fujisawa et al. [17] amongst others, but instead a stable soil matrix at the tip between successive tip failures. If the process would be driven by gradual removal of fines or by dilatancy, one would expect a strong relation between progression rate and tip gradient, which was not found in both normal and overloading conditions. It was also observed in near-critical conditions that grain detachment leads to a temporary increase in pipe gradient and corresponding decrease in tip gradient, indicating that the time between tip failures depends on the time needed for clearing the pipe. This importance of the sediment transport capacity is supported by the strong correlation between progression rate and bed shear stress in our experiments, in both normal and overloading conditions. We expect that in practice the pipe sediment transport capacity dominates the BEP time scale, because most river levees susceptible to piping are built on uniform sand and are only moderately overloaded in terms of critical head. Removal of finer particles may be important for graded material, and dilatancy may start to play a role in case of very strong overloading of dense sand.

5.4 Implications for modeling

The results indicate that the progression rate is more complex than just a function of the seepage velocity or gradient at the tip. During overloading, for example, the progression rate increases much more than is expected based on the seepage velocity only. Because the sediment transport rate in the piping experiments shows a similar relation with the bed shear stress as in classical flume experiments in laminar flow, we propose to use a transport relation like Eq. 12 for BEP modeling, similar to the recent work by Wewer et al. [59]. However, as progression occurs on exceedance of a critical condition at the pipe tip [40], such a condition would further improve the model. Therefore we propose to implement a sediment balance (Exner), a transport relation like Eq. 12 and a critical tip gradient in a 3-dimensional BEP model [56]. Such a coupled model may still need calibration on experiments like the ones presented here. Finally, we note that values assumed for \({\Theta }_{{\text{c}}}\) must be consistent with the modeling of \({\Theta }\), in terms of whether is accounted for effects of vertical seepage on the velocity profile and the bed shear stress.

6 Conclusions

To better understand the processes determining the temporal development of backward erosion piping, we performed a series of small-scale experiments. Our experimental setup guides the eroding pipe along a densely spaced row of pressure transducers, which allows local pressure measurements right in the pipe during equilibrium and progression. This is an advantage compared to most previous experiments [3, 41, 51]. Pipe geometry and flow velocity measurements allow for calculating bed shear stresses. The guiding of the pipe did not significantly influence the progression rate. We used three fine uniform sands (0.185 < d50 < 0.422 mm), compacted to a relative density between approximately 50% and 80%. In addition to the regular loading up to the critical head, some experiments were overloaded at 10−20% above the critical head.

The results confirm the positive relation between progression rate and grain size or permeability [3, 35, 38], as well as the distinct effect of even a small degree of overloading [51]. The finding that the progression rate depends on the loading introduces an important problem. For a given head drop H, the loading effect which drives progression (e.g., tip gradient or bed shear stress) depends on both the scale of the problem (i.e., seepage length) and the length of the pipe. Therefore, the progression rate will be time- and scale-dependent. Kézdi [24] and Robbins et al. [41] proposed to relate the progression rate to the local hydraulic gradient or seepage velocity at the pipe tip, which is modeled as function of time and scale. However, the current experiments indicate that the sediment transport in the pipe is a stronger predictor than the seepage velocity at the tip. First, the tip gradient does not increase significantly with the degree of overloading. Second, groups of detached sediment create extra pipe flow resistance and temporarily reduce the tip gradient, and thus control the time scale of tip erosion. Third, the estimated bed shear stress during pipe progression correlates well (ρ = 0.84) with the progression rate, compared to ρ = 0.33 for seepage velocity. Especially the overloading situations are predicted better by bed shear stress than by seepage velocity. This suggests that the sediment transport capacity is a main, limiting factor in BEP progression rates of uniform sands.

The critical bed shear stress has been determined for the first time in a rectangular piping setup. The values after the tests (complete pipe) are in good agreement with piping tests in a cylindrical setup [55] and classical flume tests in laminar flows. However, the estimated critical shear stress for a partially developed pipe are much lower and seem to decrease in the vicinity of the pipe tip. This reduction can be partly explained by the effect of strong upward seepage [63]. Seepage is known to decrease both the exerted and critical shear stress in turbulent flows [7], but this has not been fully quantified for laminar pipe flow, and requires further study.

The relation between sediment transport rate and Shields number in the BEP experiments follows a similar trend as in classical, laminar flume experiments [e.g., 20]. We fitted an empirical relation (Eq. 12) to describe the sediment transport as function of the Shields number. Since there is a large scatter in the data from both the piping experiments and flume experiments at low transport rates, this should be studied further with more accurate measurements. If these relations indeed apply to backward erosion piping, time-dependent pipe progression can be modeled by coupling a BEP model [56] with sediment transport relations (Eq. 12) and a sediment mass balance [59] and a local critical tip gradient as primary erosion criterion [40]. Such a model would contribute to more accurate assessments of the risk of piping failure in case of a limited duration of the hydraulic load, and therefore support more efficient designs of flood defenses.