Displacement based seismic assessment of base restrained retaining walls

Abstract

The present work deals with assessment of earthquake-induced displacement of the base restrained retaining walls (RW’s). A detailed and rigorous finite element (FE) investigation has been carried out following the shaking table experiments on a scaled-down RW model. The FE simulations were performed by conducting several nonlinear time history analyses on a two-dimensional (2D) plane strain FE model of a prototype RW. The hardening and softening of backfill have been simulated by calibrating the Mohr Coulomb material model against the triaxial test results. Role of different backfill into the seismic performance of base restrained RW has also been investigated. It was observed that the cohesionless backfill has a slight influence on the earthquake induced displacement of base restrained RW’s. Amplification of horizontal acceleration in backfill has been observed with no direct correlation with the applied earthquake excitation. The understanding and findings based on shaking table experiment and FE simulations have been used for development of an analytical model for estimation of earthquake induced displacement of base restrained RW. The validity of proposed analytical model has also been examined against the shaking table experiment and FE simulation results.

Introduction

Retaining walls (RW’s) are the key element of modern infrastructure system and used for a wide range of applications. Satisfactory performance of RW’s during an earthquake should be ensured for a safe and reliable infrastructure system. Seismic performance of earth retaining structures during past earthquakes has been studied by several researchers. During the Northridge earthquake (1994, 0.94g maximum recorded peak ground acceleration, PGA), significant damage to earth retaining structures near to the epicentre has been observed along with excessive sliding and rotation of conventional RW’s [30, 46]. Similar to the Northridge earthquake, the conventional free-standing RW showed excessive sliding and rotation during the Kobe earthquake (1994, 0.8g maximum recorded PGA). However, the reinforced concrete RW's founded on piled foundation showed limited damage [20, 21, 51]. Earthquake loading generates inertial forces in backfill and RW and due to the backfill inertial forces an additional lateral thrust starts acting from the backfill to the RW, which is also known as the dynamic earth pressure [34, 38]. Several researchers studied the force based seismic assessment of RW’s by conducting experiment, analytical and numerical investigations. Okabe [38] and Mononobe and Matsuo [34] performed analytical and shaking table investigations for understanding the earthquake induced backfill pressure on RW and modified the existing Coulomb earth pressure theory for estimating the linearly varying backfill pressure along the RW height. Bolton and Steedman [7] performed centrifuge experiments on scaled down RW and observed that the earthquake induced permanent displacement of RW is significantly affected by the RW inertia. Ortiz et al. [40] performed centrifuge experiments on flexible RW and observed nonlinear distribution of backfill pressure behind the RW. Several researchers performed shaking table investigations on scaled down RW models for understanding the dynamic backfill pressure on RW and its various failure modes [13, 17, 19, 24, 28]. Mikola and Sitar [32] performed centrifuge experiments and numerical investigations on different RW's and reported that the MO method can adequately estimate the backfill pressure on RW. Matuo and O’hara [31] performed analytical investigations for estimation of earthquake induced lateral pressure on quay walls by considering the seismic pressure from backfill and water; they observed that the lateral force on quay wall profoundly depends on wall height and lateral seismic coefficient. Veletsos and Younan [54] performed analytical investigations on flexible and rigid RW and observed that the flexibility of the base retrained RW could significantly affect the backfill pressure. Li and Aguilar [26] studied the seismic performance of rigid RW by performing a detailed analytical investigation, they related the point of application of dynamic thrust with the shear wave velocity (V_SH) in backfill and foundation soil. Santhoshkumar & Ghosh [47] studied the passive response of hunchbacked RW using a pseudo-dynamic approach and observed a larger failure domain size with increasing base excitation. Cakir [8] investigated the seismic displacement of base restrained RW by calibrating a two-degree (2D) of freedom model with finite element (FE) analyses results. They observed that the foundation soil could significantly affect the seismic performance of rigid RW. Estimation of earthquake induced displacement of RW is an important aspect of modern performance based seismic design [56]. Richard and Elem [44] modified the Newmark sliding block model [37] for estimation of the earthquake induced displacement of gravity RW. Several researchers performed numerical investigations for understanding the earthquake response of RW’s. Taiebat et al. [49] performed numerical analyses on basement walls and observed a nonlinear dynamic soil pressure along the basement wall height; they also observed that the traditional MO method provides conservative seismic force values. Osouli & Zamiran [41] performed FE investigations for understanding the effects of backfill cohesion on earthquake response of cantilever RW and observed that the point of application of backfill thrust slightly influenced by the cohesive nature of backfill. Bakr [4, 5] performed numerical investigations for understanding the earthquake induced displacement of sliding RW and observed that the Newmark sliding block approach overestimates the earthquake induced displacement of sliding RW. Aghamolaei et al. [2] performed a detailed numerical investigation for understanding the earthquake induced displacement of free standing RW considering near fault ground excitations and observed high RW displacements for PGA > 0.4g.

It was observed from the extensive literature review that many studies were focused on the earthquake induced backfill pressure on RW. However, a detailed experimental and numerical investigation on base restrained RW's considering displacement as primary focus of study is not addressed in the literature. Moreover, a simplified approach for estimation of seismic displacement of base restrained RW's is also not present in the literature. Therefore, a rigorous and detailed experimental, numerical and analytical investigation has been carried out to establish a displacement based seismic assessment method for base restrained earth retaining structures.

Shaking table experiment at the University of Melbourne

Construction of scaled down RW model

To understand the earthquake response of base restrained RW, a detailed and rigorous shaking table investigation was performed on a scaled down base restrained RW model at The University of Melbourne. Aluminium plate of 0.4 m length, 0.4 m width and 4 mm thickness has been used to retain the backfill. Similar kind of experimental set-up has also been adopted by various researchers to study seismic behaviour of RW [13, 19]. It should be noted herein that the scaling effects in backfill such as particle size, particle-to-particle interaction and surface irregularities could affect the seismic response of scaled down RW. However, studies suggested that the backfill particle interactions does not have high influence on the earthquake response of scaled down RW model [35, 36, 50]. It was assumed that the scaled down RW is a true replica of a prototype RW. A scaled down factor (λ) of 10 has been considered for similitude analyses [33]. Table 1 shows the details of different scaling laws considered for scaled down modelling of base restrained aluminium RW. Figure 1 shows the layout of experimental set-up for shaking table experiment. Wooden container has been fabricated to retain the backfill. The wooden container was 1.75 m long and 0.4 m wide and has a height of 0.5 m. Aluminium plate has been fixed at the front side of container. Several layers of high density foam have been placed at back side of container for minimizing the reflection of stress waves [57]. Sandpaper has been applied at the base of wooden container to initiate friction between backfill and container base.

Table 1 Scaling laws used for scaled down modelling of base restrained RW

Fig. 1

Details of scaled down RW model and instrumentation set-up at the University of Melbourne

Backfill construction and instrumentation

Crushed rock has been used as backfill material due to the easiness in backfill construction and characterization. Several geotechnical testings have been performed on crushed rocks in order to obtain their engineering properties. Table 2 shows different engineering properties obtained from various geotechnical testings on crushed rock. Scaled down backfill with a total height of 0.4 m has been constructed in four layers. The height of backfill in every layer was kept as 100 mm. The mass of backfill required for each layer has been calculated using the maximum dry density of crushed rock (1790 kg/m³). In order to compact and level the backfill, a series of low frequency sinusoidal motions have been applied to the scaled down RW model while keeping the aluminium RW completely restrained. The displacement response of RW has been captured using the high precision intelligent laser optical transduces. To capture the acceleration response of aluminium RW and backfill, several accelerometers have been attached to the RW and inserted inside the backfill. Low sampling frequency has been used for capturing the acceleration and displacement of scaled down RW model. Figure 2 shows the fabricated scaled down RW model at The University of Melbourne along with the instrumentation set up.

Table 2 Details of geotechnical testings on crushed rocks (used for the backfill construction)

Fig. 2

Fabricated scaled down RW (base restrained) model, placed on the shaking table at The University of Melbourne, particle size distribution curve for backfill [53]

Earthquake response of scaled down RW model

The shaking table experiment has been performed by applying different pulses to the scaled down RW model. A series of pluck tests have been performed for understanding the free vibration response of scaled down RW model. Several high-velocity quarter cycle sine pulses have been applied at the base of scaled down RW model using the shaking table. The fundamental vibration modes were then obtained by performing frequency domain analyses on free vibration part of acceleration time history captured by the accelerometers placed inside the backfill. Figure 3 shows the fundamental vibration modes observed after frequency domain analyses of the pluck test result, and pulse used to excite the scaled down model is also shown in the inset of Fig. 3. Dominance of first vibration mode on the seismic response of scaled down RW has been observed from the results of frequency domain analyses. Active state displacement of RW (away from the backfill) along with the separation of RW and backfill has also been observed during all pluck tests.

Fig. 3

Fundamental vibration modes observed during pluck test

The scaled down RW model was also excited using different strings of pulses for understanding its displacement and acceleration response along with the estimation of shear wave velocity in backfill [53]. The frequency of applied excitation has been chosen as 3 Hz [57]. Figure 4 shows the relative displacement at RW top for two different pulses. Active state (away from the backfill) relative displacement of RW has been observed when excited using different strings of pulses. Both pulses used for shaking table experiment are also shown in the inset of Fig. 4. It was observed from the shaking table experiments that the high backfill inertial forces which were predominately dominated by the 1^st vibration mode are accountable for active state displacement of base restrained RW. Residual displacement of RW has also been observed at the end of shaking table experiment for both pulses. Figure 5 shows the horizontal acceleration captured at backfill base and top. Significant amplification of horizontal acceleration at backfill top is observed from Fig. 5, which is responsible for higher inertial forces at backfill top; this results in higher active and residual displacement of RW.

Fig. 4

Relative displacement at RW top (relative to RW base) observed during shaking table experiment and FE simulations (Tiwari and Lam, [53])

Fig. 5

Amplification of horizontal acceleration and estimation of shear wave velocity in backfill

The shear wave velocity of backfill has also been estimated using the acceleration time history captured by accelerometers placed at backfill base and top. Figure 5 also shows the estimation of shear wave velocity of backfill using captured acceleration time history. The average shear wave velocity for scaled down backfill has been estimated as 31 m/sec (for 0.4 m height backfill) which represents a shear wave velocity of 98 m/sec in prototype backfill of 4 m height. The dimensional relationship for shear wave velocity is given by Eq. 1, where ${\lambda }_{\mathrm{V}}$ represents dimensionless ratio of shear wave velocity in prototype (${V}_{\mathrm{P}}$) and scaled-down model (${V}_{\mathrm{S}}$), respectively. The dimensionless ratios for constrained modulus and backfill densities are denoted as ${\lambda }_{\mathrm{E}}$ and ${\lambda }_{\uprho },$ respectively. Anderson [3], Yazdandoust [57] and Wang et al. [55] also reported low values of ${V}_{\mathrm{P}}$ for prototype backfills.

$$\lambda_{{\text{V}}} = \frac{{V_{{\text{P}}} }}{{V_{{\text{S}}} }} = \sqrt {\frac{{\lambda_{{\text{E}}} }}{{\lambda_{{\uprho }} }}} = \sqrt {\lambda_{{\text{l}}} }$$

(1)

It should be noted herein that the primary objective of the shaking table experiment on scaled down RW was to understand the earthquake response of scaled down base restrained RW along with the characterization of backfill. Various engineering properties of backfill based on several geotechnical testings are presented in Table 2. The observations and learnings from shaking table experiments are used for the development of an accurate and realistic FE model of prototype base restrained RW.

Layout of finite element study of seismic actions on base restrained RW

Earthquake response of base restrained RW has been studied by conducting a detailed and rigorous FE investigation on two-dimensional (2D) plane strain models of prototype RW. Effects of different backfills on the seismic performance of the base restrained RW have also been investigated. Three different types of backfills have been considered for the parametric investigations. Figure 6 shows the detailed layout of parametric investigations along with the details of different backfills used in the FE study. Several nonlinear dynamic time history analyses have been carried out on the FE RW models for understanding their seismic performance. The primary objective of performing nonlinear dynamic time history FE investigations was to assess the earthquake induced displacement of RW. Therefore, the input base excitations (accelerograms) have been selected with increasing peak ground acceleration (PGA) [2]. In the present study, five synthetic [23] and five historical [42] accelerograms were considered with a PGA range from 0.093g to 0.85g. The results of FE analyses have been analysed to study the displacement response behaviour of the base restrained RW, distribution of the backfill pressure up the RW height and amplification of horizontal acceleration.

Fig. 6

Layout of the parametric investigation on the base restrained RC RW

Development of the FE model of base restrained reinforced concrete RW

Geometric modelling, surface interaction, boundary conditions and solution scheme

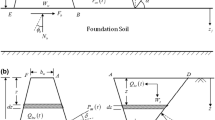
The FE model of base restrained reinforced concrete (RC) RW has been developed using the FE software Abaqus [1]. Figure 7a shows the geometrical details of the base restrained RW model. Plane strain conditions have been assumed for the development of 2D RC RW model. In order to simplify the boundary value problem, it was assumed that the RW and backfill are resting over a firm rock outcrop. The RW, backfill and base rock have been modelled using the 2D solid sections, and the steel reinforcement has been modelled using the wire element option available in Abaqus. Figure 7b shows the reinforcement details of the base restrained RW. The 25 mm diameter steel bar has been used as the primary rebar (backfill side) with 250 mm c/c spacing. The 16 mm diameter steel bar has been used as secondary rebar with 250 mm c/c spacing. The base of the RW has also been reinforced using the 16 mm diameter rebars with 250 mm c/c spacing. The rebar frame has been embedded inside the RW using the embedded region option available in Abaqus. The base slab of the RW has been restrained with the rock by modelling fixity between the base slab of the RW and the top surface of the base rock. Frictional contact has been modelled between (i) the backfill and the base rock, (ii) the RW stem and the backfill and (iii) the RW heel slab and the backfill. A friction coefficient of $\frac{2}{3}\mathrm{tan\phi }$ has been specified for modelling the frictional surface interaction, where $\phi$ is the angle of internal friction of the backfill. In order to prevent the mesh penetration and formulate pressure overclosure relation between different frictional contact surfaces, a hard contact has been modelled in the normal direction for all the contact surfaces.

Fig. 7

Geometrical details and two-dimension plane strain FE model of base restrained RW

The boundaries of the FE model have been modelled using the acceleration and displacement controlled boundary option available in Abaqus. The base of the FE model has been modelled as pinned support type which was free to translate in “x” direction (lateral direction) and restrained in “y” direction (vertical direction). The sign conventions used in the FE investigation are shown in Fig. 7. The spring and dashpot system has also been adopted to model the vertical (viscous) boundaries of the FE model as shown in Fig. 7c. The viscous boundaries have proven effective for reducing the boundary effects and the computational time [8, 22]. Details of domain size analyses and viscous boundaries are presented in Sect. 4.3 of the present manuscript.

Geostatic stresses have also been defined for the backfill and the base rock domain. The prime objective to define the geostatic stresses was to ensure equilibrium of forces and accuracy of the FE results. Gravitational loading has also been applied to the entire FE model. The earthquake loading has been applied at the base of the FE model using “x” direction acceleration.

The nonlinear dynamic time history FE analyses have been carried out in the dynamic explicit module of Abaqus. The dynamic explicit solution scheme of the FE software Abaqus is popular for the large deformation numerical analysis [1]. The dynamic explicit analyses of Abaqus use an explicit central difference integration rule and adopt several small time increments for solving the boundary value problems. Low sampling frequency has been kept for capturing the FE analyses results in order to reduce the data noise.

Constitutive modelling of the materials

Constitutive modelling of the backfill

To understand the role of backfill into the seismic performance of the base restrained RW, a detailed parametric investigation has been carried out for three different backfill types. The dune sand [11], Fontainebleau sand [12] and crushed rocks (present study) have been considered as backfill material for the parametric FE investigations. The constitutive behaviour of soils observed during the consolidated drained (CD) triaxial test is shown in Fig. 8.

Fig. 8

Constitutive behaviour of different soils considered as backfill, calibration of the MC model with the CD triaxial test results

The Mohr Coulomb (MC) material model has been used for modelling the constitutive behaviour of backfill. Several studies used the MC material model for simulating the pre and post yield behaviour of backfill [2, 48]. It should be noted herein that the post yield behaviour of soil could also be simulated by providing an extension to the MC material model [43, 48]. Therefore, in the present study the MC model has been calibrated using the available triaxial test results of all three backfills considered for the FE investigations. Details of the MC material model and calibrations with the triaxial test data have been presented by Song [48]. The triaxial test results obtained from the calibrated MC material model (hardening and softening) have been compared with the laboratory triaxial test results of different backfills. The details of MC material modelling, calibrations of post yield response of backfill with triaxial test data and modelling of Rayleigh damping of backfill have been presented by the authors in a separate investigation [53]. Figure 8 shows the comparison of constitutive behaviour of different backfills observed during the triaxial testings and simulated using the calibrated MC model. Figure 9 shows the particle size distribution curve for the crushed rock used in the backfill construction.

Fig. 9

Particle size distribution curve for crushed rock

Constitutive modelling of the concrete

The concrete has been modelled using the concrete damaged plasticity (CDP) model which is built into the FE software Abaqus. The CDP model is popular in modelling the constitutive behaviour of concrete [27, 52]. The CDP model simulates the constitutive behaviour of concrete in compression and tension using the following formulation:

$${\upsigma }_{{\text{t}}} = \left( {1 - d_{{\text{t}}} } \right)E_{0}^{{{\text{el}}}} :\left( {{\upvarepsilon } - {\upvarepsilon }_{{\text{t}}}^{{{\text{pl}}}} } \right)$$

(2)

$${\upsigma }_{{\text{c}}} = \left( {1 - d_{{\text{c}}} } \right)E_{0}^{{{\text{el}}}} :\left( {{\upvarepsilon } - {\upvarepsilon }_{{\text{c}}}^{{{\text{pl}}}} } \right)$$

(3)

where, ${\upsigma }_{\mathrm{t}}$ and ${\upsigma }_{\mathrm{c}}$ represent the stress vectors for the compressive and tensile stresses, respectively. The ${\upvarepsilon }_{\mathrm{t}}^{\mathrm{pl}}$ and ${\upvarepsilon }_{\mathrm{c}}^{\mathrm{pl}}$ represent the equivalent plastic strains in tension and compression, respectively. The initial undamaged elastic modulus $\left({E}_{0}^{\mathrm{el}}\right)$ has been calculated from the stress–strain response of uniaxial compressive strength test of concrete (as shown in Fig. 10a). Damage variables ${d}_{\mathrm{t}}$ and ${d}_{\mathrm{c}}$ are functions of the plastic strains [1].

Fig. 10

Response of the plain concrete in uniaxial compression and constitutive behaviour of steel

The yield function of the CDP model is initially developed by Lubliner et al. [29] and later modified by Lee and Fenves [25]. Details of the CDP yield function could be found in the Abaqus/Explicit User’s Manual [1]. The CDP model follows a non-associative flow rule. The plastic potential function is controlled by the dilation angle (at the deviatoric stress plane) and the eccentricity.

Table 3 shows the engineering properties considered for modelling the concrete using the CDP model. The stress–strain response of concrete with a characteristic strength (f_cu) of 40 MPa has been generated using the procedure suggested by Carreira and Chu [9] and shown in Fig. 10b. It was assumed that the inelastic behaviour of the concrete (in compression) starts when the stresses in the concrete reaches to 0.4 f_cu.

Table 3 The engineering properties used to model concrete and steel

The tensile behaviour of the concrete against the uniaxial tension has been modelled using the fracture energy approach. The tensile failure of concrete has been simulated by a linear softening model. Equations 4 and 5 were used to calculate the tensile strength of concrete (f_t) and the fracture energy (G_f) respectively.

The f_t and G_f have been calculated for the maximum compressive strength of concrete (f_cu) and the maximum aggregate size (d_a), [1, 27].

$$f_{{\text{t}}} = 1.4\left( {\frac{{f_{{{\text{cu}}}} - 8}}{10}} \right)^{\frac{2}{3}}$$

(4)

$$G_{{\text{f}}} = \left( {0.0469d_{a}^{2} - 0.5d_{a} + 26} \right)\left( {\frac{{f_{{{\text{cu}}}} }}{10}} \right)^{0.7}$$

(5)

Constitutive modelling of the reinforcement steel

The bilinear stress–strain response of the steel has been used to simulate the constitutive behaviour of steel. The details of steel are shown in Table 3. Figure 10c shows the stress–strain response of the steel considered in the present study [14]. The von Mises plasticity model has been used to model the plastic behaviour of steel. In the von Mises plasticity model, an isotropic hardening of the material has been defined with the help of the uniaxial yield stress and equivalent plastic strain. It should be noted herein that the size of the yield surface in the isotropic hardening changes uniformly in all directions [1].

Effect of the soil domain size on the seismic behaviour of the base restrained RW

Boundary effects may significantly affect the results of the FE simulations [5, 28]. Therefore, a detailed parametric investigation has been performed for different backfill domain lengths behind the plain concrete RW for estimating an optimum backfill domain length. Three RW models with 25 m, 50 m and 100 m backfill domain length have been considered for the domain size study. The crushed rock has been used as the backfill type for all three RW models. The MC model (Sect. 4.2.1) has been used to model the backfill. The Northridge accelerogram (090 CDMG Station 24278) has been used as the input base excitation for the nonlinear time history FE analyses for backfill domain size study.

Figure 11a shows the relative displacement time history at the top of the RW; observed from different backfill domain lengths. Higher active state displacement of the RW's with 25 m and 50 m long backfill domains was observed than the RW with 100 m long backfill domain which is due to the higher reflection of stress waves from the boundaries of 25 m and 50 m long backfill domain, respectively. However, the computational time for the RW with 100 m long backfill domain was significantly higher than the 50 m and 25 m long backfill domains. Therefore, for reducing the boundary effects and minimizing the computational time the vertical boundaries of the FE model have been modelled using the viscous boundaries (spring and dashpot system) as shown in Fig. 7.

Fig. 11

Domain size and mesh sensitivity analyses for backfill

A typical spring and dashpot system available in the FE software Abaqus is shown in the inset of Fig. 11a [1]. The stiffness and damping for the spring and dashpot system have been estimated for 80 m long backfill domain. The vertical spacing between the consecutive spring and dashpot sets has been kept as 200 mm. It was assumed that the external side of each spring and dashpot set is connected to the high stiffness rock located at the left and right hand sides of the FE model. The Northridge accelerogram (090 CDMG Station 24278) has been used as the input base excitation for the nonlinear time history FE analyses with spring and dashpot boundaries.

Figure 11a also shows the relative displacement at the top of the RW (with spring and dashpot boundaries). It was observed that the RW with the spring and dashpot boundaries shows lesser displacement than other considered backfill domain lengths. Moreover, the relative displacement of the RW with spring and dashpot boundaries was close to the relative displacement of RW with 100 m long backfill domain length. Apart from this, the computational time for the RW with spring and dashpot boundaries was significantly lesser than the computational time for the RW with 50 m and 100 m long backfill domains.

Mesh sensitivity analysis for the base restrained RW

The mesh sensitivity analyses have been carried out to study the effects of mesh sizes on the seismic response of the base restrained RW. Plane strain elements with reduced integration and hourglass control (CPE4R) have been used to model the FE model except the steel reinforcement. The steel reinforcement (rebar) has been meshed using beam element (B31). Several researchers have studied the effects of the mesh size on the structural response and observed that the FE analyses results are sensitive to mesh size. Moreover, an optimum mesh size could provide accurate FE results with lesser computational time [8, 22].

It was observed during the shaking table experiments on scaled down RW model and the FE investigations performed by Tiwari and Lam [53] that the backfill near the RW stem and the heel slab highly influence seismic response of the base restrained RW. Therefore, the mesh sensitivity analyses have been performed for different mesh sizes at the RW and the backfill contact locations.

The mesh sensitivity analyses were performed by varying the mesh sizes of the backfill near the RW stem and heel. A medium dense mesh was used for the RW and the base rock for minimizing the shear locking effects. Four different backfill mesh sizes (15 mm, 25 mm, 50 mm and 200 mm) have been used for the mesh sensitivity analyses. The FE model (with spring and dashpot boundaries) used for the domain size study (Sect. 2.3) has been used for the mesh sensitivity analyses.

Figure 11b shows the relative displacement at the top of the RW observed form different backfill mesh sizes. A minor difference has been observed between the results from different backfill mesh sizes. Based on the mesh sensitivity analyses, 25 mm mesh size of the backfill has been selected for the detailed FE investigations.

Validation of FE modelling approach

The capability of present FE modelling approach has been verified against the shaking table experiment results performed by the authors. A 2D plane strain FE model of the scaled down RW has been developed using the FE modelling approached defined in Sects. 4.1–4.4. The aluminium RW has been modelled using the elastic material properties, and the backfill has been modelled using the MC material model. The post-yield behaviour of the scaled down backfill has also been simulated for 7 kPa confinement pressure. Tables 2 and 3 show properties of different materials considered for the FE modelling of the scaled down RW. The earthquake response of scaled down RW model has been evaluated for two different base excitations as shown in the inset of Fig. 4. The nonlinear time history analyses have been performed in the dynamic explicit scheme of the FE software Abaqus. It should be noted herein that the captured displacement time history of the shaking table base during the shaking table experiment has been used as input base excitation for the FE models. Figure 4 also shows the comparison of relative displacement at the RW top observed during the shaking table experiment and obtained from the FE simulations. A good agreement has been observed between the shaking table experiment and the FE simulation results. The authors have also performed numerical investigations for evaluating the capabilities of the scaled down RW models for replication of seismic response of prototype RW's. Good agreement has been observed between the seismic response of scaled down and prototype RW’s (Tiwari and Lam; [53]). Therefore, it can be concluded that the present FE modelling approach can effectively replicate the seismic response of base restrained RW’s.

Results of parametric investigation on the base restrained RC RW

Displacement demand of the base restrained RW with different backfill types

A detailed and rigorous FE investigation has been performed for understanding the seismic response of the base restrained RW. As mentioned in Sect. 3 the influence of different cohesionless backfills on the seismic response of the base restrained RW has been studied by performing nonlinear time history FE analyses on base restrained RW. Figure 12 shows the time histories of relative displacement at the top of the RW for different backfill types when subjected to different base excitations. Higher relative displacement at the top of the RW can be seen with increasing peak ground acceleration (PGA). Permanent deformation of the RW has also been observed for all cases.

Fig. 12

Relative displacement at the top of the RW when subjected to different accelerograms, dune sand as the backfill

It was also observed from the FE analyses results that due to the high inertial forces from the backfill, relative displacement of the RW occurs only in the “x” direction (i.e. in the direction away from the backfill—active state). Similar active displacement of the base restrained RW was observed during the shaking table experiments (Fig. 4). It can be seen from Fig. 12a to c that the RW with crushed rock backfill shows slightly higher displacement when excited using synthetic accelerograms. Due to the higher amplifications of horizontal accelerations in crushed rock backfill, it applies high inertial forces to the RW which results in higher seismic displacement of RW with crushed rock backfill. However, when excited using historical accelerograms, the RW with different backfills shows almost similar displacement which might be due to the longer duration of historical accelerograms.

Figure 13 shows the comparison of maximum residual displacement at the top of the RW when subjected to synthetic and historical accelerograms. When subjected to the synthetic accelerogram (Fig. 13a) with RSA < 1.43g, the RW shows almost similar relative displacement for all three backfill types. For RSA > 1.43g (synthetic accelerogram), the RW with crushed rock backfill show slightly higher displacement than other two backfill types.

Fig. 13

Summary of the maximum relative displacement at the top of the RW for different backfill type, against different base excitations

Dynamic backfill pressure on the base restrained RW with different backfill types

A comparison of dynamic backfill pressure along the RW height for different backfill types is shown in Fig. 14. The time histories of dynamic backfill pressure at the RW top, middle and base were used for finding the time corresponds to the maximum dynamic backfill pressure (t_p-max). The backfill pressure at t_p-max then was used to plot the dynamic soil pressure along the RW height.

Fig. 14

Comparison of maximum backfill pressure up the RW height for different backfill type

Nonlinear distribution of the dynamic soil pressure along the RW height was observed for all backfills. In some cases, higher stress concentrations were observed near the RW base (3.55 m from the top) which could be due to the higher mesh contact forces near the RW base. It can be observed from Fig. 14 that the Fontainebleau sand shows slightly higher backfill pressure along the RW height. However, no correlation was observed between the timing of PGA and the maximum dynamic backfill pressure.

Figure 15 shows the residual backfill pressure at the end of the FE analysis. Nonlinear residual backfill pressure has been observed for all backfills. Fontainebleau sand showed higher residual backfill pressure especially when subjected to historical ground excitations. The residual backfill pressure is higher than the active state soil pressure for all backfill types which is due to the formation of the active failure plane behind the RW as small amount of RW deformation could lead to the generation of active failure wedge behind the RW [10]. Figure 15 also shows the permanent deformation of RW along its height observed at the end of the FE analyses. Nonlinear displacement pattern of the RW stem has been observed, for PGA ≤ 0.2g. The plastic strains have been observed at the RW stem base when PGA $>$ 0.2g, due to which a linear displacement up the stem wall height was observed for PGA $>$ 0.2g.

Fig. 15

Comparison of residual backfill pressure and permanent displacement up the RW height for different backfill type

It was observed that the RW with Fontainebleau sand backfill shows slightly higher permanent deformation in some cases which is due to the higher residual backfill pressure from Fontainebleau sand. Figure 16 shows the plastic strains in the backfill at the end of the FE analyses when analysed against a synthetic accelerogram with PGA = 0.66g. Small variation of plastic strains has been observed for all three backfills. However, the Fontainebleau sand shows slightly higher plastic strains than other backfill types which is due to higher relative deformation of the RW with Fontainebleau sand as backfill. It should be noted herein that the constitutive behaviour of Fontainebleau sand shows significant reduction in shear strength once it reaches to the critical state (Fig. 8c). However, in the case of dune sand and crushed rock higher shear strength was observed after post-yield stage (Fig. 8a and b).

Fig. 16

Comparison of plastic strain (PE) in backfill at the end of analysis when subjected to M(6.9)-R(10 km) earthquake, PGA = 0.66g

Therefore, it can be concluded that the displacement demand of base restrained RW is highly depends on applied PGA. However, the type of cohesionless backfill does not have a high influence on the displacement demand of base retrained RW. Moreover, the post-yield strength behaviour of cohesionless soil can influence the seismic displacement of base restrained retaining wall.

Amplification of the horizontal acceleration

Amplification of horizontal acceleration in all three backfill types was also studied with the help of captured horizontal acceleration at the backfill base, middle and top. Figure 17 shows the bar charts of amplification factor (AF) estimated at the backfill base, middle and top for all three backfills considered for the FE investigation. The response spectrum method used to obtain the AF in backfill is also presented at the bottom left of Fig. 17. For all the three backfills no co-relation has been observed between the peak response spectral acceleration (RSA) and obtained AF. However, slight increment in average AF was observed with increasing angle of internal friction of backfill. Therefore, it can be concluded that the strength properties of backfill have high influence on amplification of stress wave and severity of earthquake shaking can be misleading in estimating the AF in backfills.

Fig. 17

Amplification factor (horizontal acceleration) for base restrained RW, when subjected to different backfill type and base excitations

Simplified analytical model to estimate the earthquake induced displacement of the base restrained RW

Earthquake induced displacement of the base restrained RW can be estimated by performing FE analysis on the RW models. However, performing FE analyses on the prototype RW models requires experience in the FE simulations along with expertise in constitutive modelling of materials. Therefore, a force based displacement check model has been suggested for estimating the maximum earthquake induced elastic displacement (${\updelta }_{\mathrm{max}}$) of the base restrained RW with cohesionless backfill. Figure 18 shows the base restrained RW model considered for the development of analytical formulations. The height and thickness of RW are “H” and “t_w”, respectively. Figure 18 shows the seismic body force (W1_AE) on the RW stem and the dynamic soil force per unit width of the RW (W2_AE) (assuming triangular distribution) along the RW height. The formulations used to estimate the maximum RW displacement are also shown in Fig. 18.

Fig. 18

Steps to estimate the maximum elastic seismic displacement of the base restrained RW

It should be noted herein that the base restrained RW supports a uniform and horizontal cohesionless backfill behind it. The interface angle ($\updelta$) between the RW and the backfill has been considered as $\phi /2$. The seismic pressure behind the RW stem has been estimated using the MO equation [34]. The MO equation provides the pseudo-static pressure on the RW stem, which increases linearly along the RW depth. The pseudo-static lateral pressure coefficient (K_AE) has been estimated for 100% K_h (EN 1998-5). The seismic force (P_AE) along the RW height was estimated using Eq. 6.

$$P_{{{\text{AE}}}} = AF_{{\text{H}}} K_{{{\text{AE}}}} {\upgamma }_{{{\text{Backfill}}}} H$$

(6)

where AF_H is the amplification of the horizontal acceleration in the backfill.

The maximum displacement due to the RW inertia forces (${\updelta 1}_{max}$) has been calculated using the following formulation:

$${\updelta }1_{{{\text{max}}}} = \left( {\frac{{W1_{{{\text{AE}}}} H^{4} }}{8EI}} \right)$$

(7)

where W1_AE = body force at unit height of RW = (${{AF}_{\mathrm{H}}\times {k}_{\mathrm{h}}\times W}_{\mathrm{Wall}})$.

E = Young’s modulus of the RW, I = moment of Inertia of the RW, ${\upgamma }_{\mathrm{Backfill}}$ = unit weight of the backfill, ${k}_{\mathrm{h}}$ = horizontal seismic coefficient, ${W}_{\mathrm{wall}}$ = weight of the RW.

The maximum displacement due to the seismic active pressure of backfill (${\updelta 2}_{\mathrm{max}}$) has been calculated using the following formulation:

$${\updelta }2_{max} = \left( {\frac{{W2_{{{\text{AE}}}} H^{4} }}{30EI}} \right)$$

(8)

where, W2_AE = P_AE = Seismic force per unit width of the RW.

Once ${\updelta 1}_{\mathrm{max}}$ and ${\updelta 2}_{\mathrm{max}}$ are calculated the maximum displacement at the top of the RW can be calculated by submission of the ${\updelta 1}_{\mathrm{max}}$ and ${\updelta 2}_{\mathrm{max}}$. Figure 18 also shows the detailed process for estimation of the earthquake induced elastic displacement of the base restrained RW with cohesionless backfill.

Validation of the analytical model results with the shaking table experiment results

The validity of the proposed hand calculations has been examined by comparing the maximum RW displacements obtained from the hand calculations with the shaking table experiment results. It should be noted herein that the maximum acceleration obtained at the shaking table base has been used as PGA (K_h) for the analytical model.

During the shaking table experiments, a gap formulation has been observed between the aluminium RW and the backfill due to which the backfill pressure behind the RW has dropped [6, 16, 39]. However, in the analytical model, the lateral coefficient for the seismic active earth pressure (K_AE) has been estimated for 100% PGA or maximum possible PGA [15]. Because of this, the amplification of the horizontal acceleration for the scaled down RW model is neglected (AF_H = 1); considering the amplification of the horizontal acceleration in the backfill with K_AE (100% PGA) will overestimate the seismic pressure on the scaled down RW model. It should be noted herein that from the shaking table experiment and the FE simulations the dominance of the first vibration mode on the seismic response of the base restrained RW has been observed. Therefore, the analytical model has been proposed for estimation of the maximum elastic displacement of the base restrained RW.

Table 4 shows the comparison of the maximum displacement at the top of the RW obtained from the proposed analytical model and observed during the shaking table experiment. Details of the base excitations and recorded PGA at the shaking table base are also shown in Table 4. Details of scaling factors ($\uplambda$) used for scaling accelerograms during the shaking table experiment have also presented in Table 4. Figure 19 shows the comparison of maximum elastic displacements recorded during the shaking table experiment and estimated from the proposed analytical model which demonstrates a good agreement.

Table 4 Comparison of the maximum seismic displacement of the scaled down RW, obtained from the proposed hand calculations and shaking table experiments

Fig. 19

Comparison of the maximum elastic displacement of the base restrained RW, obtained from the hand calculations and shaking table experiments

Validation of the analytical model results with the FE simulation results

The validity of the proposed analytical model was also examined for estimation of the maximum elastic displacement of the prototype RW’s (base restrained). A detailed parametric FE investigation has been performed for flexible and rigid RW’s with different cohesionless backfills. Table 5 shows the geometrical and material properties of the prototype base restrained RW’s considered for the validation studies. Steps shown in Fig. 18 were used for estimating the ${\updelta }_{\mathrm{max}}$ for the prototype RW.

Table 5 Geometrical and material details of the prototype base restrained RW

The details of the FE modelling of seismic actions on the base restrained RW are discussed in Sect. 4. The nonlinear time history FE analyses have been carried out for different synthetic base excitations (PGA range from 0.093g to 0.74g).

In order to estimate the maximum displacement of the base restrained RW using proposed analytical model, a range of AF_H has been considered based on the type of RW and backfill. During the shaking table experiment on scaled down flexible RW (${\lambda }_{\mathrm{l}}=10\, \&\, H=0.4 m$), an AF_H of around 2 was observed (Fig. 5) for crushed rock backfill. Therefore, for flexible RW 1 (H = 3.625 m, t_w = 0.15 m, crushed rock backfill), an AF_H = 2 has been considered. It was observed by various researchers that the amplification in horizontal acceleration reduces with decreasing friction angle of backfill [6, 18]. Therefore, AF_H = 1.5 and 1.25 has been considered for the RW with Fontainebleau sand ($\phi ={39}^{0}$) and dune sand ($\phi ={34}^{0}$) backfill, respectively.

The amplification of horizontal acceleration in soil layers resting over the bed rock decreases with increasing height of the soil layer as the deformation of soil layers of greater heights also plays an important role into the energy dissipation [45]. Therefore, in the case of flexible RW 2 (H = 9 m, t_w = 0.5 m), AF_H = 1.5, 1.35 and 1.00 has been considered for crushed rock ($\phi ={44}^{0}$), Fontainebleau sand ($\phi ={39}^{0}$) and dune sand ($\phi ={34}^{0}$) backfill, respectively. In the case of stiff RW (H = 3.625 m, t_w = 0.65 m) higher accelerations at RW stem (increasing towards the RW top) has been observed due to high stiffness and less movement. Similar observations were reported by Mikola and Sitar [32] during the centrifuge testing of non-displacing basement walls. Therefore, AF_H = 5, 4.5 and 4.0 has been considered for the RW with crushed rock ($\phi ={44}^{0}$), Fontainebleau sand ($\phi ={39}^{0}$) and Dune sand ($\phi ={34}^{0}$) backfill, respectively.

Figure 20 shows the comparison of ${\updelta }_{\mathrm{max}}$ (${\Delta }_{\mathrm{R at RW Top}}$) of the base restrained RW's; obtained from the FE simulations and estimated using the proposed hand calculations. Good agreement has been observed between the hand calculations and the FE analysis results.

Fig. 20

Comparison of the maximum elastic displacement of the base restrained RW, obtained from the hand calculations and FE simulations

Conclusion

A detailed investigation has been undertaken for gaining insights into the seismic response behaviour of a base restrained retaining wall (RW) with granular backfill. The investigation involved conducting shaking table experiments on the scaled down model of the RW and the backfill. Dominance by the first vibration mode of the scaled down soil-structure system was observed. The amplified inertial forces from the backfill (as observed in the experiments) resulted in active state displacement behaviour of the base restrained RW. Residual displacement of the RW was also observed.

Rigorous nonlinear time history analyses of the finite element (FE) model were also undertaken on the 2D plane strain reinforced concrete (RC) RW models based on the use of synthetic, and historically recorded, accelerograms as input into the analyses. The FE simulations also revealed active state residual displacement of the RC RW, consistent with experimental observations. Amplification of the horizontal acceleration (which was observed for all backfill types) was found to be not in correlation with the applied peak ground acceleration (PGA). Changing the type of backfill was found to have only a slight influence on the seismic displacement demand. The critical state constitutive behaviour of the backfill had more influence. Nonlinear dynamic soil pressure, and residual pressure, has been recorded up the height of the RW for all backfill types.

A simplified analytical model has been developed for estimation of the earthquake induced maximum displacement demand of the base restrained RW with cohesionless backfill. The analytical model has been verified by comparison of results obtained from the model with results from shaking table experiments, and from FE simulations, demonstrating good agreement.