Theoretical solution for drained cylindrical cavity expansion in clays with fabric anisotropy and structure

Abstract

This paper presents a novel, exact, semi-analytical solution for the quasi-static drained expansion of a cylindrical cavity in soft soils with fabric anisotropy and structure. The assumed constitutive model is the S-CLAY1S model, which is a Cam clay-type model that considers fabric anisotropy that evolves with plastic strains, structure and gradual degradation of bonding (destructuration) due to plastic straining. The solution involves the numerical integration of a system of eight first-order ordinary differential equations, three of them corresponding to the effective stresses in cylindrical coordinates, other three corresponding to the components of the fabric tensor and one corresponding to the amount of bonding and another corresponding to the specific volume. The solution is validated against finite element analyses. When destructuration is considered, the solution provides slightly lower values of the effective radial and mean stresses near the cavity wall. Besides, the specific volume is further reduced due to loss of bonding. Parametric analyses and discussion of the influence of soil overconsolidation, expansion of the cavity and initial amount of bonding are presented.

1 Introduction

Cavity expansion theory has been applied widely in geotechnical problems (e.g. [24, 25, 38]). Analytical solutions cover both cylindrical and spherical cavities, expansion from a null or finite initial radius, undrained or drained conditions and different types of material constitutive models (e.g. [43]). Chen and Abousleiman [7] developed a rigorous semi-analytical solution for the undrained expansion of a cylindrical finite cavity in a modified Cam clay (MCC) material. The solution is rigorous because it is developed without any approximation imposed on the mean and deviatoric stresses and it is semi-analytical because it requires the numerical integration of a system of three first-order ordinary differential equations, corresponding to the effective stresses in cylindrical coordinates. Vrakas [39] has later presented a more general solution for the undrained cylindrical cavity expansion, considering any type of two-invariant model belonging to the critical state (Cam clay) family, using large strain formulation also in the elastic zone and reducing the numerical procedure to a single nonlinear equation.

Chen and Abousleiman [8] extended their previous solution [7] to drained conditions. The extension is non-trivial because the volumetric strain is no longer null and must be considered as an additional variable in combination with the effective stresses. The distinctive feature of Chen and Abousleiman [8] is the ingenious introduction of an auxiliary variable that is the ratio of the particle displacement in the radial direction to its present radial position (ξ = u_r/r). Thus, the solution for drained conditions requires adding a partial differential equation for the specific volume ($\upsilon$) and using the auxiliary variable (ξ) instead of the radial coordinate (r).

Chen and Abousleiman [7, 8] solutions have opened the path for semi-analytical solutions for anisotropic critical state plasticity models, and it is a subject currently undergoing intense study [5, 6, 9, 10, 18,19,20,21,22, 34, 44]. These anisotropic solutions add three partial differential equations to the system, corresponding to the fabric tensor. All these anisotropic models assume isotropic elasticity for simplicity. Models that consider anisotropic elasticity (e.g. [4, 29] are beyond the scope here. Table 1 summarizes the main features of the solutions that follow the Chen and Abousleiman [7, 8] approach for the cylindrical cavity expansion problem and are directly related to the proposed solution here. Sivasithamparam and Castro [34] showed that the rotational hardening law must be considered to obtain realistic results, and Chen et al. [10] discussed the benefits of using a rotational hardening law that predicts a unique critical state as done by Sivasithamparam and Castro [34], using the SCLAY1 [40] model for the cylindrical cavity expansion problem.

Table 1 Summary of semi-analytical cavity expansion solutions directly related to the proposed solution

The authors [35] have recently developed a theoretical solution that considers fabric anisotropy and structure using the S-CLAY1S constitutive model [16] for undrained conditions. Using a constitutive model that considers soil structure and gradual degradation of bonding (destructuration) allows reproducing the strength loss in sensitive clays (e.g. immediately after pile driving) [35]. This paper presents the corresponding solution for drained conditions using the auxiliary variable proposed by Chen and Abousleiman [8]. Although solutions for cavity expansion in isotropic strain-softening soils (e.g. [24]) and interpretation of pressuremeter tests in sensitive soils (e.g. [17, 30, 31]) using a post-failure strain softening had been presented, the authors’ solutions are the first ones for anisotropic, structure (inter-particle bonding) and destructuration behaviour of plastic nature of clays. It is worth noting that neglecting soil structure leads to inaccurate predictions of clay responses under external loading (e.g. [3, 13, 15, 27, 28]).

In this way, this paper presents a novel, exact and semi-analytical cylindrical cavity expansion solution for drained conditions and for natural clays, which exhibit fabric anisotropy and structure. The solution is developed using the S-CLAY1S constitutive model [16], which considers fabric anisotropy that evolves with plastic strains, structure and gradual degradation of bonding (destructuration) due to plastic straining. In cavity expansion problems, real situations are commonly close to the undrained case for clays, but depending on the rate of loading and the soil permeability, the behaviour may be partially drained (e.g. [15]). For these cases, the proposed drained solution sets the other limit values.

The assumptions and mathematical derivation of the semi-analytical solution are presented in Sect. 2. A system of eight first-order ordinary differential equations that require numerical integration is obtained. Details of the mathematical formulation are included as separate appendixes for simplicity and clarity. Validation of the semi-analytical solution against finite element analyses, results and parametric analyses are portrayed in Sect. 3. The solution allows to obtain the increase in the cavity pressure with the radial expansion of the cavity and variations of stresses, specific volume, fabric anisotropy and amount of bonding around the cavity (Sect. 3). Besides, the stress paths at the cavity wall are also presented in Sect. 3. Finally, the main conclusions are summarized in Sect. 4.

2 Mathematical formulation and semi-analytical solution

2.1 Assumptions and basic equations

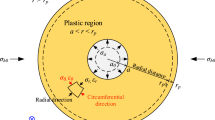
The following assumptions are made to simplify the study of the quasi-static expansion of a cylindrical cavity of initial radius a₀ under drained conditions:

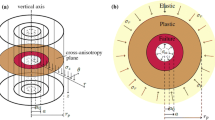
• 1. The axis of the cylindrical cavity is assumed as the vertical axis, and the initial stress state is homogeneous and consists of a horizontal effective stress and a vertical effective stress ($\sigma_{{\text{H}}}^{\prime } ,\sigma_{{\text{V}}}^{\prime }$).

• 2. The soil has an initial uniform void ratio (${e}_{0}={\upsilon }_{0}-1$).

• 3. The pore water pressure is always equal to its initial hydrostatic value (u₀); consequently, its value is irrelevant for the solution. For the sake of simplicity, its value is assumed as 0 here, and effective and total stresses are the same ($\sigma_{{\text{H}}} = \sigma_{{\text{H}}}^{\prime } ,\sigma_{{\text{V}}} = \sigma_{{\text{V}}}^{\prime }$).

• 4. The initial horizontal stress on the cavity is also σ_H, and it increases up to σ_a, upon expanding the cavity to a final radius a (Fig. 1).

• 5. Soil behaviour is reproduced using the S-CLAY1S constitutive model [16], which assumes isotropic elasticity.

• 6. The symmetry axis of the initial soil plastic cross-anisotropy (transversely isotropic material) is the vertical one. This ensures that the cavity keeps as a cylinder and does not change to an elliptic shape (e.g. [45]).

• 7. The problem has axial symmetry; thus, shear stresses vanish and, due to the infinite extent of the soil, plane strain conditions hold.

• 8. Cylindrical coordinates (r,θ,z) are used throughout the paper because they are principal directions for this problem. Principal effective stresses are radial ${\sigma }_{r}^{^{\prime}}$, tangential ${\sigma }_{\theta }^{^{\prime}}$ and vertical ${\sigma }_{z}^{^{\prime}}$.

• 9. Large strain deformation is considered in the plastic region using natural (or logarithmic) strains, but small-strain deformation is used in the elastic region.

Fig. 1

Geometry of cylindrical cavity expansion: a cylindrical cavity; b horizontal cross section

The last simplifying assumption has a negligible influence on the results because in the elastic region, the strains are much smaller than those in the plastic annulus. For example, Vrakas [39] presented a solution that considers large strains also in the elastic zone, and the differences are insignificant.

The equilibrium equation in the radial direction for cylindrical coordinates, which are principal directions, using effective stresses may be written as

$$\frac{{\partial \sigma_{r}^{\prime } }}{\partial r} + \frac{{\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } }}{r} = 0$$

(1)

where r is the current radial position of a soil particle. As per assumption 3 above, total and effective stresses are the same.

Under drained conditions, the Eulerian equation for a soil particle at a specific moment with the aid of the auxiliary independent variable $\xi$ proposed by Chen and Abousleiman [8] can be converted to the Lagrangian form as

$$\xi =\frac{{u}_{\mathrm{r}}}{r}=\frac{r-{r}_{0}}{r}$$

(2)

2.2 Constitutive model: S-CLAY1S

The S-CLAY1S model, developed by Karstunen et al. [16], is an extension of the S-CLAY1 model [40] incorporating the influence of bonding and destructuration. Anisotropic plastic behaviour is included in the model through an inclined yield surface and a rotational component of hardening to represent the development or erasure of fabric anisotropy during plastic straining. Soil structure is modelled using intrinsic and natural yield surfaces [14]. To make the paper self-contained, the two yield surfaces (intrinsic and natural) and the three hardening laws of the S-CLAY1S model are summarized in the following.

For the simplified conditions of a triaxial stress space and for an initial cross-anisotropy fabric with the main axis being the vertical one (e.g. a vertically cut sample), the yield function can be expressed as [40]

$${f}_{y}={\left(q-\alpha {p}^{^{\prime}}\right)}^{2}-\left({M}^{2}-{\alpha }^{2}\right)\left({p}_{m}^{^{\prime}}-{p}^{^{\prime}}\right)p$$

(3)

where q is the deviatoric stress, $p^{\prime }$ is the mean effective stress, M is the critical state value of the stress ratio (where $\eta = q/p^{\prime }$) and $p_{m}^{\prime }$ and α define the size and inclination of the natural yield curve, respectively (Fig. 2).

Fig. 2

The S-CLAY1S natural and intrinsic yield surfaces in triaxial stress space and visualization of invariant $\overline{q }$

The intrinsic yield surface is of smaller size but same orientation as the yield curve of the natural soil (Fig. 2). The size of the intrinsic yield surface is defined by the state variable ${p}_{mi}^{^{\prime}}$ which is linked to the size of the natural yield surface by

$${p}_{m}^{^{\prime}}=\left(1+\chi \right){p}_{mi}^{^{\prime}}$$

(4)

where $\chi$ defines the amount of bonding.

The first hardening law is analogous to that of the MCC and describes the change of size of the yield curve, which is assumed to be related solely to plastic volumetric strains (as in MCC)

$$\mathrm{d}{p}_{mi}^{^{\prime}}=\frac{\upsilon {p}_{mi}^{^{\prime}}}{{\lambda }_{i}-\kappa }\mathrm{d}{\varepsilon }_{v}^{p}$$

(5)

where $\upsilon$ is the specific volume, λ_i is the slope of the intrinsic post-yield compression curve in the $\upsilon$ − ln $p^{\prime }$ plane and $\kappa$ is the slope of the swelling line in the compression plane.

The second hardening law (rotational hardening) describes the change of inclination of the yield curve produced by plastic straining, both volumetric and shear strains.

$$\mathrm{d}\alpha =\omega \left[\left(\frac{3\eta }{4}-\alpha \right)\langle \mathrm{d}{\varepsilon }_{v}^{p}\rangle +{\omega }_{d}\left(\frac{\eta }{3}-\alpha \right)\left|\mathrm{d}{\varepsilon }_{d}^{p}\right|\right]$$

(6)

where ω is a material constant that controls the absolute effectiveness of plastic strains in rotating the yield surface towards the target value. Similarly, ω_d controls the relative effectiveness of shear and volumetric strains.

The third hardening law (destructuration) [16] describes the degradation of bonding with plastic straining by both volumetric and shear strains.

$$\mathrm{d}\chi =-\xi \chi \left(\left|\mathrm{d}{\varepsilon }_{v}^{p}\right|+{\xi }_{\mathrm{d}}\left|\mathrm{d}{\varepsilon }_{d}^{p}\right|\right)$$

(7)

where $\xi$ and ${\xi }_{\mathrm{d}}$ are two additional model constants controlling the rate of degradation (in an analogous manner to ω and ω_d in Eq. 6). Full details of the hardening laws and determination of the model constants may be found in [16, 40].

2.3 Invariants

The natural yield surface of the model (Fig. 2) can be expressed in generalized form as

$$f_{y} = \frac{3}{2}\left( {{\varvec{\sigma}}_{{\varvec{d}}}^{\prime } - {\varvec{\alpha}}_{d} p^{\prime } } \right)^{T} \left( {{\varvec{\sigma}}_{{\varvec{d}}}^{\prime } - {\varvec{\alpha}}_{d} p^{\prime } } \right) - \left( {M^{2} - {\varvec{\alpha}}_{d}^{T} {\varvec{\alpha}}_{d} } \right)\left( {p_{m}^{\prime } - p^{\prime } } \right)p^{\prime }$$

(8)

where

$${\varvec{\sigma}}_{{\varvec{d}}}^{\prime } = \left[ {\begin{array}{*{20}l} {\sigma_{r}^{\prime } - p^{\prime } } & {\sigma_{\theta }^{\prime } - p^{\prime } } & {\sigma_{z}^{\prime } - p^{\prime } } \\ \end{array} } \right]^{T}$$

(9)

and

$${\boldsymbol{\alpha }}_{{\varvec{d}}}={\left[\begin{array}{lll}{\alpha }_{r}-1& {\alpha }_{\theta }-1& {\alpha }_{z}-1\end{array}\right]}^{T}$$

(10)

$$p^{\prime } = \frac{{\left( {\sigma_{r}^{\prime } + \sigma_{\theta }^{\prime } + \sigma_{z}^{\prime } } \right)}}{3}{.}$$

(11)

Sivasithamparam and Castro [34] proposed a new invariant for the S-CLAY1 model ($\overline{q }$), which simplifies the development of mathematical solutions for cylindrical cavity expansion in plastic anisotropic soils. The same invariant was also used for S-CLAY1S [35]

$$\overline{q }=\sqrt{\frac{3}{2}Q}$$

(12)

where

$$Q = \left( {{\varvec{\sigma}}_{{\varvec{d}}}^{\prime } - {\varvec{\alpha}}_{d} p^{\prime } } \right)^{T} \left( {{\varvec{\sigma}}_{{\varvec{d}}}^{\prime } - {\varvec{\alpha}}_{d} p^{\prime } } \right) = s_{r}^{2} + s_{\theta }^{2} + s_{z}^{2}$$

(13)

and ${s}_{i}$ are the following deviatoric stresses

$$s_{i} = \sigma_{i}^{\prime d} - \alpha_{i}^{d} p^{\prime } = \sigma_{i}^{\prime } - \left( {\alpha_{i}^{d} + 1} \right)p^{\prime } \quad {\text{for}}\,\,\,i = r,\theta ,z$$

(14)

and ${\alpha }_{i}^{d}$ are deviatoric components of the fabric tensor.

Using this invariant ($\overline{q }$), the natural yield surface of the S-CLAY1S model has a similar form as that of isotropic Cam clay models

$$f_{y} = \overline{q}^{2} - \left( {M^{2} - \alpha^{2} } \right)\left( {p_{m}^{\prime } - p^{\prime } } \right)p^{\prime } .$$

(15)

2.4 Elastoplastic stiffness matrix

The increments of elastic strains in $r$, $\theta$ and $z$ directions may be obtained using the isotropic linear elastic stress–strain relationship as

$$\left\{ {\begin{array}{*{20}l} {{\text{d}}\varepsilon_{r}^{e} } \\ {{\text{d}}\varepsilon_{\theta }^{e} } \\ {{\text{d}}\varepsilon_{z}^{e} } \\ \end{array} } \right\} = \frac{1}{E}\left[ {\begin{array}{*{20}l} 1 & { - \nu { }} & { - \nu } \\ { - \nu } & 1 & { - \nu } \\ { - \nu } & { - \nu } & 1 \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}l} {{\text{d}}\sigma_{r}^{\prime } } \\ {{\text{d}}\sigma_{\theta }^{\prime } } \\ {{\text{d}}\sigma_{z}^{\prime } } \\ \end{array} } \right\}$$

(16)

where Young's modulus $E$ is defined in terms of shear modulus $G$ and Poisson's ratio $\nu$ as

$$E = G\left( {1 + \nu } \right).$$

(17)

$G$ is calculated in the S-CLAY1S model using the current stress state as

$$G = \frac{{3\left( {1 - 2\nu } \right)\upsilon }}{{2\left( {1 + \nu } \right)\kappa }}p^{\prime }$$

(18)

The components of plastic strain increments $\mathrm{d}{{\varvec{\varepsilon}}}^{p}$ in $r$, $\theta$ and $z$ directions are calculated using the plastic multiplier $\Lambda$ for the S-CLAY1S model, which considers an associated flow rule.

$$\left\{ {\begin{array}{*{20}l} {{\text{d}}\varepsilon_{r}^{p} } \\ {{\text{d}}\varepsilon_{\theta }^{p} } \\ {{\text{d}}\varepsilon_{z}^{p} } \\ \end{array} } \right\} = {\Lambda } \cdot \left\{ {\begin{array}{*{20}l} {\frac{{\partial f_{y} }}{{\partial \sigma_{r}^{\prime } }}} \\ {\frac{{\partial f_{y} }}{{\partial \sigma_{\theta }^{\prime } }}} \\ {\frac{{\partial f_{y} }}{{\partial \sigma_{z}^{\prime } }}} \\ \end{array} } \right\}$$

(19)

The plastic multiplier can be written in a matrix form as

$$\Lambda = {\mathcal{H}}\left[ {\begin{array}{*{20}l} {\frac{{\partial f_{y} }}{{\partial \sigma_{r}^{\prime } }}} & {\frac{{\partial f_{y} }}{{\partial \sigma_{\theta }^{\prime } }}} & {\frac{{\partial f_{y} }}{{\partial \sigma_{z}^{\prime } }}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\text{d}}\sigma_{r}^{\prime } } \\ {{\text{d}}\sigma_{\theta }^{\prime } } \\ {{\text{d}}\sigma_{z}^{\prime } } \\ \end{array} } \right\}$$

(20)

where

$$\mathcal{H}=-\frac{1}{{\mathcal{H}}_{0}+{\mathcal{H}}_{\alpha }+{\mathcal{H}}_{\chi }}$$

(21)

$${\mathcal{H}}_{0}=\frac{{\partial f}_{y}}{\partial {p}_{mi}^{^{\prime}}}\frac{\partial {p}_{mi}^{^{\prime}}}{\partial {\varepsilon }_{v}^{p}}\frac{{\partial f}_{y}}{\partial {p}^{^{\prime}}}$$

(22)

$${\mathcal{H}}_{\alpha } = \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\alpha}}^{d} }}} \right\}^{T} \left[ {\left\{ {\frac{{\partial {\varvec{\alpha}}^{d} }}{{\partial \varepsilon_{v}^{p} }}} \right\} \cdot \left\langle {\frac{{\partial f_{y} }}{{\partial p^{\prime } }}} \right\rangle + \left\{ {\frac{{\partial {\varvec{\alpha}}^{d} }}{{\partial \varepsilon_{d}^{p} }}} \right\} \cdot \sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\}} } \right]$$

(23)

$${\mathcal{H}}_{\chi } = \frac{{\partial f_{y} }}{\partial \chi }\left[ {\frac{\partial \chi }{{\partial \varepsilon_{v}^{p} }}\left| {\frac{{\partial f_{y} }}{{\partial p^{\prime } }}} \right| + \frac{\partial \chi }{{\partial \varepsilon_{d}^{p} }}\sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\}} } \right]$$

(24)

All required derivatives and the derivation of the plastic multiplier are presented in Appendixes 1 and 2, respectively.

Using decomposition of the strain vector ($\mathrm{d}{\varvec{\varepsilon}}=\mathrm{d}{{\varvec{\varepsilon}}}^{e}+\mathrm{d}{{\varvec{\varepsilon}}}^{p}$) and Eqs. (16–24), the elastoplastic constitutive equations in the form of compliance and stiffness matrixes can be derived as

$$\left\{\begin{array}{c}\mathrm{d}{\varepsilon }_{r}\\ \mathrm{d}{\varepsilon }_{\theta }\\ \mathrm{d}{\varepsilon }_{z}\end{array}\right\}=\left[\begin{array}{lll}\frac{1}{E}+\mathcal{H}{n}_{r}^{2}& -\frac{\nu }{E}+\mathcal{H}{n}_{r}{n}_{\theta }& -\frac{\nu }{E}+\mathcal{H}{n}_{r}{n}_{z}\\ -\frac{\nu }{E}+\mathcal{H}{n}_{\theta }{n}_{r}& \frac{1}{E}+\mathcal{H}{n}_{\theta }^{2}& -\frac{\nu }{E}+\mathcal{H}{n}_{\theta }{n}_{z}\\ -\frac{\nu }{E}+\mathcal{H}{n}_{z}{n}_{r}& -\frac{\nu }{E}+\mathcal{H}{n}_{z}{n}_{\theta }& \frac{1}{E}+\mathcal{H}{n}_{z}^{2}\end{array}\right]\cdot \left\{\begin{array}{c}\mathrm{d}{\sigma }_{r}^{^{\prime}}\\ \mathrm{d}{\sigma }_{\theta }^{^{\prime}}\\ \mathrm{d}{\sigma }_{z}^{^{\prime}}\end{array}\right\}$$

(25)

$$\left\{\begin{array}{c}\mathrm{d}{\sigma }_{r}^{^{\prime}}\\ \mathrm{d}{\sigma }_{\theta }^{^{\prime}}\\ \mathrm{d}{\sigma }_{z}^{^{\prime}}\end{array}\right\}=\frac{1}{\Gamma }\left[\begin{array}{lll}{c}_{11}& {c}_{12}& {c}_{13}\\ {c}_{21}& {c}_{22}& {c}_{23}\\ {c}_{31}& {c}_{32}& {c}_{33}\end{array}\right]\cdot \left\{\begin{array}{c}\mathrm{d}{\varepsilon }_{r}\\ \mathrm{d}{\varepsilon }_{\theta }\\ \mathrm{d}{\varepsilon }_{z}\end{array}\right\}$$

(26)

All terms in Eq. (26) are defined in Appendix 3.

2.5 Rotational hardening rule

As derived by Sivasithamparam and Castro [34], the changes in the fabric components (${\mathrm{d}\alpha }_{r}^{d}$, $\mathrm{d}{\alpha }_{\theta }^{d}$ and $\mathrm{d}{\alpha }_{z}^{d}$) with the radial direction are

$$\frac{{{\text{d}}\alpha_{i}^{d} }}{{{\text{d}}r}} = \Phi_{i} {\mathcal{H}}\left( {n_{r} \frac{{{\text{d}}\sigma_{r}^{^{\prime}} }}{{{\text{d}}r}} + n_{\theta } \frac{{{\text{d}}\sigma_{\theta }^{^{\prime}} }}{{{\text{d}}r}} + n_{z} \frac{{{\text{d}}\sigma_{z}^{^{\prime}} }}{{{\text{d}}r}}} \right)\quad {\text{for}}\,\,i = r,\theta ,z$$

(27)

where

$$\Phi_{i} = \omega \left( {\left( {\frac{{3\left( {\sigma_{i}^{^{\prime}} - p^{\prime } } \right)}}{{4p^{\prime } }} - \alpha_{i}^{d} } \right)\left\langle {\frac{{\partial f_{y} }}{{\partial p^{\prime}}}} \right\rangle + \omega_{d} \left( {\frac{{\left( {\sigma_{i}^{^{\prime}} - p^{\prime } } \right)}}{{3p^{\prime } }} - \alpha_{i}^{d} } \right)\sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{^{\prime}d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{^{\prime}d} }}} \right\}} } \right)\quad {\text{for}}\,\,i = r,\theta ,z$$

(28)

2.6 Bonding and destructuration

The degradation of bonding with plastic straining is given by the destructuration hardening law (Eq. 7). In three dimensions, the plastic strain increments $\mathrm{d}{\varepsilon }_{v}^{p}$ and $\mathrm{d}{\varepsilon }_{d}^{p}$ are defined as

$$\mathrm{d}{\varepsilon }_{v}^{p}=\Lambda \frac{{\partial f}_{y}}{\partial {p}^{^{\prime}}}$$

(29)

$${\text{d}}\varepsilon_{d}^{p} = {\Lambda }\sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\}}$$

(30)

Degradation of bonding along the radial direction can be obtained by substituting Eqs. (29–30) with Eq. (20) (plastic multiplier) into Eq. (7).

$$\frac{\mathrm{d}\chi }{\mathrm{d}r}=\Omega \mathcal{H}\left({n}_{r}\frac{\mathrm{d}{\sigma }_{r}^{^{\prime}}}{\mathrm{d}r}+{n}_{\theta }\frac{\mathrm{d}{\sigma }_{\theta }^{^{\prime}}}{\mathrm{d}r}+{n}_{z}\frac{\mathrm{d}{\sigma }_{z}^{^{\prime}}}{\mathrm{d}r}\right)$$

(31)

where

$${\Omega } = \chi \xi \left( {\left\langle {\frac{{\partial f_{y} }}{{\partial p^{\prime}}}} \right\rangle + \xi_{d} \sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\}} } \right)$$

(32)

2.7 Hardening rule of the intrinsic yield surface

The changes in size of the intrinsic yield surface are provided by the hardening law (Eq. 5) and can be obtained as

$$\mathrm{d}{p}_{mi}^{^{\prime}}=\Lambda \frac{\upsilon }{{\lambda }_{i}-\kappa }{p}_{mi}^{^{\prime}}\frac{{\partial f}_{y}}{\partial {p}^{^{\prime}}}$$

(33)

2.8 Solution procedure

The radial and tangential strain increments may be defined in natural strain form as

$${\text{d}}\varepsilon_{r} = - \frac{{\partial \left( {{\text{d}}r} \right)}}{\partial r}\quad {\text{and}}\quad {\text{d}}\varepsilon_{\theta } = - \frac{{{\text{d}}r}}{r}$$

(34)

where $r$ and $\mathrm{d}r$ are position of a material particle in the radial direction and change in the position of that particle, respectively.

For cylindrical cavity and plane strain conditions, the vertical strain is zero, i.e. $\mathrm{d}{\varepsilon }_{z}=0$, and the volumetric strain

$$\mathrm{d}{\varepsilon }_{v}=\mathrm{d}{\varepsilon }_{r}+\mathrm{d}{\varepsilon }_{\theta }$$

(35)

The auxiliary independent variable $\xi$ defined in Eq. (2) can be written in differential form as

$$\frac{\mathrm{d}r}{r}=\frac{\mathrm{d}\xi }{1-\xi }$$

(36)

By substituting Eqs. (34, 36) and $\mathrm{d}{\varepsilon }_{v}=\frac{\mathrm{d}\upsilon }{\upsilon }$ into Eq. (35)

$$\mathrm{d}{\varepsilon }_{r}=-\frac{\mathrm{d}\upsilon }{\upsilon }+\frac{\mathrm{d}\xi }{1-\xi }$$

(37)

By substituting Eq. (34, 36) into (26, 27, 31), applying plane strain conditions, i.e. $\mathrm{d}{\varepsilon }_{z}=0$, and following the approach used by Chen and Abousleiman [8], the change of specific volume can be obtained from Eqs. (2, 34, 37), and the following eight partial differential equations in terms of the auxiliary variable $\xi$ are found (three corresponding to stress increments, one to specific volume change, three to rotation of the yield surface and one to destructuration)

$$\begin{aligned} \frac{{{\text{d}}\sigma_{r}^{\prime } }}{{{\text{d}}\xi }} & = - \frac{{\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } }}{{1 - \xi - \frac{{\upsilon_{0} }}{{\upsilon \left( {1 - \xi } \right)}}}} \\ \frac{{{\text{d}}\sigma_{\theta }^{\prime } }}{{{\text{d}}\xi }} & = - \frac{{c_{12} }}{{c_{11} }}\left[ {\frac{{\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } }}{{1 - \xi - \frac{{\upsilon_{0} }}{{\upsilon \left( {1 - \xi } \right)}}}} + \frac{{c_{11} - c_{12} }}{{\Gamma \left( {1 - \xi } \right)}}} \right] - \frac{{\left( {c_{22} - c_{12} } \right)}}{{\Gamma \left( {1 - \xi } \right)}} \\ \frac{{{\text{d}}\sigma_{z}^{\prime } }}{{{\text{d}}\xi }} & = - \frac{{c_{31} }}{{c_{11} }}\left[ {\frac{{\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } }}{{1 - \xi - \frac{{\upsilon_{0} }}{{\upsilon \left( {1 - \xi } \right)}}}} + \frac{{c_{11} - c_{12} }}{{\Gamma \left( {1 - \xi } \right)}}} \right] - \frac{{\left( {c_{32} - c_{31} } \right)}}{{\Gamma \left( {1 - \xi } \right)}} \\ \frac{{{\text{d}}\upsilon }}{{{\text{d}}\xi }} & = \frac{\Gamma \upsilon }{{c_{11} }}\left[ {\frac{{\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } }}{{1 - \xi - \frac{{\upsilon_{0} }}{{\upsilon \left( {1 - \xi } \right)}}}} + \frac{{c_{11} - c_{12} }}{{\Gamma \left( {1 - \xi } \right)}}} \right] \\ \frac{{{\text{d}}\alpha_{r}^{d} }}{{{\text{d}}\xi }} & = \Phi_{r} {\mathcal{H}}\left( {n_{r} \frac{{{\text{d}}\sigma_{r}^{\prime } }}{{{\text{d}}\xi }} + n_{\theta } \frac{{{\text{d}}\sigma_{\theta }^{\prime } }}{{{\text{d}}\xi }} + n_{z} \frac{{{\text{d}}\sigma_{z}^{\prime } }}{{{\text{d}}\xi }}} \right) \\ \frac{{{\text{d}}\alpha_{\theta }^{d} }}{{{\text{d}}\xi }} & = \Phi_{\theta } {\mathcal{H}}\left( {n_{r} \frac{{{\text{d}}\sigma_{r}^{\prime } }}{{{\text{d}}\xi }} + n_{\theta } \frac{{{\text{d}}\sigma_{\theta }^{\prime } }}{{{\text{d}}\xi }} + n_{z} \frac{{{\text{d}}\sigma_{z}^{\prime } }}{{{\text{d}}\xi }}} \right) \\ \frac{{{\text{d}}\alpha_{z}^{d} }}{{{\text{d}}\xi }} & = \Phi_{z} {\mathcal{H}}\left( {n_{r} \frac{{{\text{d}}\sigma_{r}^{\prime } }}{{{\text{d}}\xi }} + n_{\theta } \frac{{{\text{d}}\sigma_{\theta }^{\prime } }}{{{\text{d}}\xi }} + n_{z} \frac{{{\text{d}}\sigma_{z}^{\prime } }}{{{\text{d}}\xi }}} \right) \\ \frac{{{\text{d}}\chi}}{{{\text{d}}\xi }} & =\Omega {\mathcal{H}}\left( {n_{r} \frac{{{\text{d}}\sigma_{r}^{\prime } }}{{{\text{d}}\xi }} + n_{\theta } \frac{{{\text{d}}\sigma_{\theta }^{\prime } }}{{{\text{d}}\xi }} + n_{z} \frac{{{\text{d}}\sigma_{z}^{\prime } }}{{{\text{d}}\xi }}} \right) \\ \end{aligned}$$

(38)

The system of eight first-order ordinary differential equations (Eq. 38) governs the expansion of the cylindrical cavity in the plastic region. Boundary conditions for the elastic/plastic boundary and the elastic solution (Appendix 4) are required for the complete mathematical formulation of the problem. The corresponding stress state at the elastic/plastic boundary is the same as that for the undrained case of the S-CLAY1S model [35] because the natural yield surface is the same (Fig. 2) and the volumetric strains are null in the elastic region (Appendix 4). Thus, the specific volume and the stresses at the elastic/plastic interface are

$$\begin{aligned} \upsilon_{p} & = \upsilon_{0}\end{aligned}$$

(39)

$$\begin{aligned} \sigma_{z,p }^{\prime } & = \frac{3}{{1 + 2K_{0} }}p_{0}^{\prime } \\ \sigma_{r,p }^{\prime } & = \sigma_{r0 }^{\prime } + \sqrt {\frac{1}{3}\left( {q^{2} - \left( {\sigma_{z0 }^{\prime } - K_{0} \sigma_{z0 }^{\prime } } \right)^{2} } \right)} \\ \sigma_{\theta ,p}^{\prime } & = \sigma_{\theta 0}^{\prime } - \sqrt {\frac{1}{3}\left( {q^{2} - \left( {\sigma_{z0 }^{\prime } - K_{0} \sigma_{z0 }^{\prime } } \right)^{2} } \right)} \\ \end{aligned}$$

(40)

where

$$\sigma_{r0 }^{\prime } = \sigma_{\theta 0 }^{\prime } = \frac{{3K_{0} }}{{1 + 2K_{0} }}p_{0}^{\prime } \quad {\text{and}}\quad \sigma_{z0 }^{\prime } = \frac{3}{{1 + 2K_{0} }}p_{0}^{\prime }$$

(41)

and

$$q=\sqrt{{q}_{0}^{2}+\left({\overline{q} }^{2}-{\left({q}_{0}-\alpha {p}_{0}^{^{\prime}}\right)}^{2}\right)}$$

(42)

$${q}_{0}= \sqrt{\frac{3}{2}\left({\left({\sigma }_{r0 }^{^{\prime}}-{p}_{0}^{^{\prime}}\right)}^{2}+{\left({\sigma }_{\theta 0 }^{^{\prime}}-{p}_{0}^{^{\prime}}\right)}^{2}+{\left({\sigma }_{z0 }^{^{\prime}}-{p}_{0}^{^{\prime}}\right)}^{2}\right)}$$

(43)

$$\overline{q }=\sqrt{\left({M}^{2}-{\alpha }_{0}^{2}\right)\left({p}_{m}^{^{\prime}}-{p}_{0}^{^{\prime}}\right){p}^{^{\prime}}}$$

(44)

Equations (39,40) and the initial values of the amount of bonding and the fabric tensor (anisotropic components) are the initial conditions for solving the differential equations in Eq. (38). The position of the elastic/plastic interface using the auxiliary variable, ${\xi }_{p}$, is

$${\xi }_{p}={\left(\frac{{u}_{\mathrm{r}}}{r}\right)}_{r={r}_{p}}=\frac{{\sigma }_{r,p }^{^{\prime}}-{\sigma }_{r0 }^{^{\prime}}}{2{G}_{0}}$$

(45)

As presented by Chen and Abousleiman [8], a relationship between $\xi$ and $r$ can be written in the form of the specific volume

$$\frac{\mathrm{d}r}{r}=\frac{{\upsilon }_{\xi }\left(1-\xi \right)}{{{\upsilon }_{\xi }\left(1-\xi \right)}^{2}-{\upsilon }_{0}}\mathrm{d}\xi$$

(46)

Integrating the above equation, the material position, $r$, can be expressed as

$$\frac{r}{a}=\mathrm{exp}\left({\int }_{{\xi }_{a}}^{\xi }\frac{{\upsilon }_{\xi }\left(1-\xi \right)}{{{\upsilon }_{\xi }\left(1-\xi \right)}^{2}-{\upsilon }_{0}}\mathrm{d}\xi \right)$$

(47)

where ${\xi }_{a}$ is the value of the auxiliary variable at the cavity wall and is ${\xi }_{a}=1-(\frac{a}{{a}_{0}})$.

Substituting Eq. (45) into (47), the position of the elastic/plastic boundary may be obtained

$$\frac{{r}_{p}}{a}=\mathrm{exp}\left({\int }_{{\xi }_{a}}^{{\xi }_{p}}\frac{{\upsilon }_{\xi }\left(1-\xi \right)}{{{\upsilon }_{\xi }\left(1-\xi \right)}^{2}-{\upsilon }_{0}}\mathrm{d}\xi \right)$$

(48)

The system of equations (Eq. 38), imposing the boundary conditions at the elastic/plastic interface can be solved numerically; here, the standard differential solver ‘lsode’ available in GNU Octave v4.0 was used. Figure 3 summarizes the solution procedure.

Fig. 3

Solution procedure for solving ordinary differential equations of cylindrical cavity expansion in GNU Octave

3 Results and discussion

3.1 Validation

Validation of the proposed semi-analytical solution has been performed by comparison of its results with finite element simulations using the commercial code Plaxis 2D 2019 [2]. The S-CLAY1S model has been implemented as a user-defined soil model in Plaxis, using an automatic substepping in combination with a modified Newton–Raphson integration scheme [32, 33].

The geometrical model (Fig. 4) is based on that used by González et al. [15] for plane strain cylindrical cavity expansion. The boundary condition at the outer boundary is a fixed radial stress (equal to the initial value) and free radial displacements. Sensitivity analyses of mesh refinement and load step size were performed to confirm their small influence.

Fig. 4

Finite element model for cylindrical cavity expansion

To account for large displacements, the numerical code uses an updated Lagrangian formulation [23] and adopts the co-rotational rate of Kirchhoff stress (also known as Hill stress rate). The details of the implementation can be found in Van Langen [37].

For the sake of comparison with previous studies, Boston blue clay (BBC) is considered and its modified Cam clay (MCC) parameters are taken from Chen and Abousleiman [7] and additional anisotropic parameters from [34] (S-CLAY1) (see Table 2). Additional parameters for intrinsic compressibility, bonding and destructuration are those used in Sivasithamparam and Castro [35], which were based on information available in the literature. These parameters are just for illustrative purposes, without aiming to reach a detailed calibration of the parameters using experimental tests.

Table 2 Soil properties, Boston blue clay

BBC is a moderately sensitive marine clay and, for example, Whittle et al. [41] use a value of S_t = 4.5. For the S-CLAY1S model, that implies χ₀ = 3.5 (Table 2). For parametric analyses, four times this value (χ₀ = 14) and a null value (χ₀ = 0) have also been used.

The overconsolidation ratio (OCR) of BBC varies with depth. To provide a broad representation of different depths, several OCR values are considered, namely 1, 1.5, 3 and 5. Their corresponding initial state parameters are shown in Table 3 and are the same as in Sivasithamparam and Castro [34, 35] for the sake of comparison.

Table 3 Soil state parameters, Boston blue clay

The results of the finite element simulations perfectly match those of the proposed semi-analytical solution as may be observed in Fig. 5 for the void ratio and stresses around the cavity as an example. In this paper, the stresses are normalized by the initial vertical stress, either effective or total stress since they are the same. The finite element analyses are slightly less computationally demanding and in slightly better agreement with the semi-analytical solution than for the undrained case [35] because the soil is not incompressible.

Fig. 5

Validation of the theoretical solution against finite element analyses

3.2 Internal cavity pressure

To expand the cavity, an internal pressure (radial stress), σ_a, must be applied. Its value must monotonically increase to continue with the expansion of the cavity. When the cavity has been notably expanded (around a/a₀ > 2), σ_a approaches an asymptotic limit value, sometimes called pressuremeter limit pressure.

Figure 6 shows its variation with the normalized cavity radius for different OCR and χ₀ values. As expected, the radial stress increases with the OCR and decreases with the initial amount of bonding (χ₀). As happens for undrained conditions [35], mechanical overconsolidation and initial bonding have similar effects on the load–displacement curve (Fig. 6), but the influence of the initial bonding is limited beyond values around χ₀ > 3.5. For drained conditions, the radial stress is larger and increases more gradually than for undrained conditions. For example, for a/a₀ = 2, the radial stress is around 90% the limit pressure for drained conditions, while it is around 97% for undrained conditions [35].

Fig. 6

Radial stress at cavity wall during cavity expansion: a influence of overconsolidation; b influence of initial bonding

3.3 Stresses around the cavity

Figure 7 shows the stresses and the specific volume around the cavity when the cavity radius is twice the initial one (a/a₀ = 2). For the sake of comparison, results for the case without destructuration (S-CLAY1, i.e. λ = 0.15 and χ₀ = 0) are also included in Fig. 7. The extension of the plastic annulus depends on the OCR. For normally consolidated conditions, all the material points yield just when the cavity expansion begins, but plastic strains are negligible beyond r > 10a.

Fig. 7

Influence of destructuration on specific volume and stress distributions around the cavity: a OCR = 1; b OCR = 1.5; c OCR = 5

It is worth noting that the extensions of the plastic annuli are slightly different for the cases with and without destructuration. Their values are the same using the auxiliary variable (Eq. 45), but when that value is converted to the radial coordinate (Eq. 48), they are slightly different because the soil compressibilities, i.e. the specific volume variations, are different.

Near the cavity, the vertical stress is usually the intermediate one and it is equal to the average of the other two (plane strain conditions):

$$\sigma_{z}^{\prime } = \, (\sigma_{r}^{\prime } + \sigma_{\theta }^{\prime } )/{2}$$

(49)

When destructuration is considered, critical state (CS) is not usually reached for common expansions of the cavity (e.g. a/a₀ = 2) and common rates of destructuration (e.g. ξ = 9 and ξ_d = 0.2), because very large strains are necessary for a complete loss of structure (fully remoulded state).

Normalized effective mean stresses for different OCR values are plotted in Fig. 8. The increase in the effective mean stress may be correlated with the improvement of the soil, e.g. its stiffening. The area of increase in the effective mean stress is limited to 3–4 cavity radii. This area of influence is similar to that of the undrained case [35] and to that measured by some authors (e.g. [1, 26]).

Fig. 8

Increase in effective mean pressure around the cavity

3.4 Specific volume

As well-known, volumetric strains are null in the elastic region (e.g. [43]), but in the plastic region, the soil compresses and the initial void ratio or specific volume decreases (Fig. 7). The loss of bonding near the cavity increases the soil compressibility, and therefore, the specific volume is lower near the cavity when destructuration is considered (S-CLAY1S).

Figure 9 shows the decrease of the specific volume at the cavity wall as the cavity expands for different OCRs and χ₀. When the soil is overconsolidated, the specific volume does not nearly change at the beginning of the cavity expansion, but later, the specific volume reduction is similar to the normally consolidated case. The loss of bonding causes an important reduction of the specific volume from the beginning. The specific volume tends to a final asymptotic value that correspond to CS conditions.

Fig. 9

Specific volume at cavity wall during cavity expansion: a influence of overconsolidation; b influence of initial bonding

The decrease of the specific volume of a point at the cavity wall during cavity expansion is represented in a $p^{\prime } - \upsilon$ plane (Fig. 10) for different OCR values, namely 1, 1.5 and 5, and for the cases with and without destructuration, i.e. S-CLAY1S (λ_i = 0.12 and χ₀ = 3.5) and S-CLAY1 (λ = 0.15 and χ₀ = 0), respectively. The lines represent the path from the beginning of the expansion (initial specific volume υ₀) (a/a₀ = 1) until a cavity expansion large enough to reach the critical state line (CSL), namely a/a₀ = 10. It is worth noting that the initial specific volumes for the cases using the S-CLAY1S model are the same ones as those when the S-CLAY1 model is used and those in Sivasithamparam and Castro [35] for the sake of comparison. Consequently, slightly different void ratios of the CSL for different OCRs were obtained when using the S-CLAY1S model. Destructuration causes a further reduction of the specific volume and a slightly lower mean effective stress at CS.

Fig. 10

Specific volume variations with effective mean pressure at cavity wall until a/a₀ = 10

3.5 Stress paths

For a better understanding of the problem, it is useful to observe the effective stress paths (ESP) followed by a point at the cavity wall during cavity expansion. Figures 11 and 12 show the stress paths for different OCR values in $p^{\prime } - q$ stress plane and deviatoric stress plane (π-plane), respectively. The stress paths illustrate the stress state of a point at the cavity wall from the beginning of the expansion (initial K₀ state) (a/a₀ = 1) until a final cavity expansion of a/a₀ = 10. In Fig. 11, the point corresponding to a/a₀ = 2 is also indicated with an open square symbol for the sake of comparison.

Fig. 11

$p^{\prime }$-q stress paths at cavity wall until a/a₀ = 10: a OCR = 1; b OCR = 1.5; c OCR = 5

Fig. 12

Stress paths at cavity wall in π-plane until a/a₀ = 10: a OCR = 1; b OCR = 1.5; c OCR = 5

In the $p^{\prime } - q$ stress plane, if the soil is overconsolidated, the stress paths goes up vertically until reaching the yield surface. It is worth noting that the initial yield surface (YS₀) plotted in Fig. 11 corresponds to the triaxial plane, while yielding is here reached for a different value of the Lode’s angle (Fig. 12) [10]. Later, the stress path progressively approaches the CSL. The yield surface rotates towards plain state condition and increases due to the increase in the mean effective pressure caused by the drained expansion of the cavity (Figs. 11 and 12).

The initial amount of bonding (χ₀) does not notably change the followed stress paths (Fig. 13), but higher values of χ₀ cause larger destructurations (Eq. 7), and consequently, lower final stresses.

Fig. 13

Influence of initial bonding on stress paths (until a/a₀ = 10). a $p^{\prime }$–q plane; b π-plane

Figure 12 also shows the path followed by the α·$p^{\prime }$ vector, which depicts the centre of the anisotropic yield surface. It shows how the yield surface rotates from triaxial compression conditions towards plane strain conditions. Destructuration causes a reduction of effective stresses ($p^{\prime }$), but the influence of destructuration on the evolution of fabric anisotropy (α) is minor, as it will be presented in the next section.

3.6 Fabric anisotropy

The evolution of fabric anisotropy is quite similar for the cases with and without destructuration, i.e. for the S-CLAY1S and S-CLAY1 models, respectively (Fig. 14). The anisotropic hardening law (Eq. 6) is the same for both models, and the differences are mainly caused by the differences in the specific volume.

Fig. 14

Changes in fabric anisotropy: a OCR = 1; b OCR = 1.5; c OCR = 5

At the cavity wall, the fabric tensor approaches a constant value that may be analytically obtained as $\left[ {\begin{array}{*{20}l} {\alpha_{r} } & {\alpha_{\theta } } & {\alpha_{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {1 + \sqrt 3 M/9} & {1 - \sqrt 3 M/9} & 1 \\ \end{array} } \right]$ ($\alpha =M/3$), which corresponds to critical state and plane strain conditions (refer to Sivasithamparam and Castro [34] for further details). Please note that this value is the same for both drained and undrained conditions and for the S-CLAY1 and S-CLAY1S models. When destructuration is considered, large strains are necessary to reach CS (i.e., full loss of bonding). For example, in Fig. 14 ($a/{a}_{0}=2$), $\alpha$ is close to $M/3$, but not exactly $M/3$ yet.

3.7 Structure and amount of bonding

Cavity expansion usually generates plastic strains, which in turn cause a loss of bonding of the structured clay (Fig. 15) as per the assumed destructuration hardening law (Eq. 7). The loss of bonding (destructuration) is proportional to the current bonding parameter (Eq. 7). Consequently, the loss of bonding may be normalized by the initial amount of bonding in Fig. 15.

Fig. 15

Loss of bonding caused by cavity expansion

It may be observed in Fig. 15 that the loss of bonding at the cavity wall is nearly independent of OCR, and only the extension of the plastic zone and, consequently, the extension of the zone where the amount of bonding decreases is influenced by OCR. Figure 15 corresponds to the case with $a/{a}_{0}=2$, but larger radial expansions of the cavity generate larger soil distortions and larger destructuration of the soil, both in terms of extension and amount of destructuration. For example, for $a/{a}_{0}=10$, full loss of bonding is reached at the cavity wall (Fig. 9).

4 Conclusions

A novel, exact and semi-analytical cylindrical cavity expansion solution for natural clays has been rigorously developed using the S-CLAY1S constitutive model, which is a Cam clay type of model that considers fabric anisotropy that evolves with plastic strains, structure and gradual degradation of bonding (destructuration) due to plastic straining. The solution involves the numerical integration of a system of eight first-order ordinary differential equations, three of them corresponding to the effective stresses in cylindrical coordinates, other three corresponding to the components of the fabric tensor and one corresponding to the amount of bonding and another for the specific volume.

The semi-analytical solution has been developed using the auxiliary variable introduced by Chen and Abouisleiman 8, and the solution has been validated against finite element analyses, using Boston blue clay as the reference natural clay.

When destructuration is considered, i.e. using the S-CLAY1S model, the solution provides lower values of the effective radial and mean stresses near the cavity wall than those obtained when destructuration is not considered (S-CLAY1). Besides, the specific volume is further reduced due to loss of bonding.

Evolution of fabric anisotropy is similar with both S-CLAY1 and S-CLAY1S soil models. The slight differences are caused by the different soil compressibilities. The initial vertical cross-anisotropy caused by the soil deposition changes towards a radial anisotropy after cavity expansion. Analytical values are provided for the fabric anisotropy at the cavity wall for large cavity expansions, i.e. at CS. Those analytical values are the same for drained and undrained conditions and for both S-CLAY1 and S-CLAY1S soil models.

For common values, the soil near the cavity does not reach CS, i.e. full remoulding and a constant stress state. The loss of bonding extends along the plastic annulus surrounding the cavity (larger for larger OCR and imposed radial displacements), being the largest at the cavity wall and progressively decreasing until a null loss of bonding in the elastic zone.

Appendices

Appendix 1: Derivatives

The partial derivatives used in the analytical solution are

$$\frac{{\partial f_{y} }}{{\partial \sigma_{i}^{^{\prime}} }} = \frac{{p^{\prime } \left( {M^{2} - \alpha^{2} - \overline{\eta }^{2} } \right)}}{3} + \left( {3s_{i} - s_{r} \alpha_{r}^{d} - s_{\theta } \alpha_{\theta }^{d} - s_{z} \alpha_{z}^{d} } \right)\quad {\text{for}}\,\, i = r,\theta ,z$$

where

$$\begin{aligned} \overline{\eta } & = \frac{{\overline{q}}}{{p^{\prime } }} \\ \overline{q} & = \sqrt {\frac{3}{2}Q} \\ \end{aligned}$$

and

$$\begin{aligned} \frac{{\partial f_{y} }}{{\partial p_{mi}^{^{\prime}} }} & = - p^{\prime } \left( {M^{2} - \alpha^{2} } \right)\left( {1 + \chi } \right) \\ \frac{{\partial p_{mi}^{\prime } }}{{\partial \varepsilon_{v}^{p} }} & = \frac{{\upsilon p^{\prime } }}{{\left( {\lambda_{i} - \kappa } \right)\left( {1 + \chi } \right)\left( {M^{2} - \alpha^{2} } \right)}}\left( {M^{2} - \alpha^{2} + \overline{\eta }^{2} { }} \right) \\ \frac{{\partial f_{y} }}{{\partial p^{\prime}}} & = p^{\prime } \left( {M^{2} - \alpha^{2} - \overline{\eta }^{2} } \right) - 3\left( {s_{r} \alpha_{r}^{d} + s_{\theta } \alpha_{\theta }^{d} + s_{z} \alpha_{z}^{d} } \right) \\ \frac{{\partial f_{y} }}{{\partial \alpha_{i}^{d} }} & = - 3s_{i} p^{\prime } + 3\alpha_{i}^{d} \frac{{\overline{q}^{2} }}{{M^{2} - \alpha^{2} }} \quad {\text{for}}\quad i = r,\theta ,z \\ \frac{{\partial f_{y} }}{{\partial \sigma_{i}^{^{\prime}d} }} & = 3s_{i} \quad {\text{for}}\quad i = r,\theta ,z \\ \frac{{\partial \alpha_{i}^{d} }}{{\partial \varepsilon_{v}^{p} }} & = \omega \left( {\frac{{3\left( {\sigma_{i}^{^{\prime}} - p^{\prime } } \right)}}{{4p^{\prime } }} - \alpha_{i}^{d} } \right)\quad {\text{for}}\quad i = r,\theta ,z \\ \frac{{\partial \alpha_{i}^{d} }}{{\partial \varepsilon_{d}^{p} }} & = \omega \omega_{d} \left( {\frac{{\left( {\sigma_{i}^{\prime } - p^{\prime } } \right)}}{{3p^{\prime } }} - \alpha_{i}^{d} } \right)\quad {\text{for}}\quad i = r,\theta ,z \\ & \sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{\prime d} }}} \right\} = } 2\overline{q} \\ \frac{{\partial f_{y} }}{{\partial {\varvec{\chi}}}} & = - \frac{{p^{\prime 2} }}{{\left( {1 + \chi } \right)}}\left[ {M^{2} - \alpha^{2} + \overline{\eta }^{2} } \right] \\ \frac{\partial \chi }{{\partial \varepsilon_{v}^{p} }} & = - \xi \chi \\ \frac{\partial \chi }{{\partial \varepsilon_{d}^{p} }} & = - \xi \xi_{d} \chi \\ \end{aligned}$$

Appendix 2: Derivation of the plastic multiplier

The consistency condition ($\dot{f}_{y} = 0$) is developed as:

$$\dot{f}_{y} = \frac{{\partial f_{y} }}{{\partial \sigma_{i}^{\prime } }}{\text{d}}\sigma_{i}^{\prime } + \frac{{\partial f_{y} }}{{\partial p_{mi}^{\prime } }}{\text{d}}p_{mi}^{\prime } + \frac{{\partial f_{y} }}{{\partial {\varvec{\alpha}}_{{\varvec{d}}} }}{\text{d}}{\varvec{\alpha}}_{{\varvec{d}}} + \frac{{\partial f_{y} }}{{\partial {\chi }}}{\text{d}\chi } = 0\quad {\text{for}}\,\,i = r,\theta ,z$$

and in terms of plastic strains, it is:

$$\begin{aligned} \dot{f}_{y} & = \frac{{\partial f_{y} }}{{\partial \sigma_{i}^{^{\prime}} }}{\text{d}}\sigma_{i}^{^{\prime}} + \frac{{\partial f_{y} }}{{\partial p_{m}^{^{\prime}} }}\frac{{\partial p_{m}^{^{\prime}} }}{{\partial \varepsilon_{v}^{p} }}{\text{d}}\varepsilon_{v}^{p} + \frac{{\partial f_{y} }}{{\partial {\varvec{\alpha}}_{{\varvec{d}}} }}\frac{{\partial {\varvec{\alpha}}_{d} }}{{\partial \varepsilon_{v}^{p} }}{\text{d}}\varepsilon_{v}^{p} + \frac{{\partial f_{y} }}{{\partial {\varvec{\alpha}}_{{\varvec{d}}} }}\frac{{\partial {\varvec{\alpha}}_{d} }}{{\partial \varepsilon_{d}^{p} }}\left| {{\text{d}}\varepsilon_{d}^{p} } \right| \\ & \quad + \frac{{\partial f_{y} }}{\partial \chi }\frac{\partial \chi }{{\partial \varepsilon_{v}^{p} }}{\text{d}}\varepsilon_{v}^{p} + \frac{{\partial f_{y} }}{\partial \chi }\frac{\partial \chi }{{\partial \varepsilon_{d}^{p} }}\left| {{\text{d}}\varepsilon_{d}^{p} } \right| = 0\quad {\text{for}}\,\,\,i = r,\theta ,z \\ \end{aligned}$$

Thus, the plastic multiplier is

$$\Lambda = - \frac{{\frac{{\partial f_{y} }}{{\partial \sigma_{i}^{^{\prime}} }}{\text{d}}\sigma_{i}^{^{\prime}} }}{{\frac{{\partial f_{y} }}{{\partial p_{mi}^{^{\prime}} }}\frac{{\partial p_{mi}^{^{\prime}} }}{{\partial \varepsilon_{v}^{p} }}\frac{{\partial f_{y} }}{{\partial p^{\prime}}} + \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\alpha}}_{d} }}} \right\}^{T} \left[ {\left\{ {\frac{{\partial {\varvec{\alpha}}_{d} }}{{\partial \varepsilon_{v}^{p} }}} \right\} \cdot \frac{{\partial f_{y} }}{\partial p^{\prime}} + \left\{ {\frac{{\partial {\varvec{\alpha}}_{d} }}{{\partial \varepsilon_{d}^{p} }}} \right\} \cdot \sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}_{d}^{^{\prime}} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}_{d}^{^{\prime}} }}} \right\}} } \right] + \frac{{\partial f_{y} }}{\partial \chi }\left[ {\frac{\partial \chi }{{\partial \varepsilon_{v}^{p} }}\left| {\frac{{\partial f_{y} }}{{\partial p^{\prime}}}} \right| + \frac{\partial \chi }{{\partial \varepsilon_{d}^{p} }}\sqrt {\frac{2}{3}\left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{^{\prime}d} }}} \right\} \cdot \left\{ {\frac{{\partial f_{y} }}{{\partial {\varvec{\sigma}}^{^{\prime}d} }}} \right\}} } \right]}}$$

Appendix 3: Elastoplastic solution

$$\begin{aligned} c_{11} & = \frac{1}{{E^{2} }}\left( {1 - \nu^{2} + E{\mathcal{H}}n_{\theta }^{2} + 2E\nu {\mathcal{H}}n_{\theta } n_{z} + E{\mathcal{H}}n_{z}^{2} } \right) \\ c_{12} & = c_{21} = \frac{1}{{E^{2} }}\left[ { - E{\mathcal{H}}\left( {n_{\theta } + \nu n_{z} } \right) + \nu \left( {1 + \nu - E{\mathcal{H}}n_{\theta } n_{z} + E{\mathcal{H}}n_{z}^{2} } \right)} \right] \\ c_{13} & = c_{31} = \frac{1}{{E^{2} }}\left[ { - E{\mathcal{H}}n_{r} \left( {\nu n_{\theta } + n_{z} } \right) + \nu \left( {1 + \nu - E{\mathcal{H}}n_{\theta }^{2} + E{\mathcal{H}}n_{\theta } n_{z} } \right)} \right] \\ c_{22} & = \frac{1}{{E^{2} }}\left( {1 - \nu^{2} + E{\mathcal{H}}n_{r}^{2} + 2E\nu {\mathcal{H}}n_{r} n_{z} + E{\mathcal{H}}n_{z}^{2} } \right) \\ c_{23} & = c_{32} = \frac{1}{{E^{2} }}\left[ {\nu + \nu^{2} + E{\mathcal{H}}\nu n_{r}^{2} - E{\mathcal{H}}n_{\theta } n_{z} - E{\mathcal{H}}\nu n_{r} \left( {n_{\theta } + n_{z} } \right)} \right] \\ c_{33} & = \frac{1}{{E^{2} }}\left( {1 - \nu^{2} + E{\mathcal{H}}n_{r}^{2} + 2E\nu {\mathcal{H}}n_{r} n_{\theta } + E{\mathcal{H}}n_{\theta }^{2} } \right) \\ \Gamma & = - \frac{1 + \nu }{{E^{3} }}\left[ {\begin{array}{*{20}l} {\left( { - 1 + \nu + 2\nu^{2} } \right) + EH\left( { - 1 + \nu } \right)n_{r}^{2} + EH\left( { - 1 + \nu } \right)n_{\theta }^{2} } \\ { - 2EH\nu n_{\theta } n_{z} - EHn_{z}^{2} + EH\nu n_{z}^{2} - 2EH\nu n_{r} \left( {n_{\theta } + n_{z} } \right)} \\ \end{array} } \right] \\ \end{aligned}$$

where

$$n_{i} = \frac{{\partial f_{y} }}{{\partial \sigma_{i}^{\prime } }}\quad {\text{for}}\,\,i = r,\theta ,z$$

Appendix 4: Elastic solution

The solution for the elastic stresses ($\sigma_{r}^{\prime }$, $\sigma_{\theta }^{\prime }$, $\sigma_{z}^{\prime }$) (total and effective stresses are the same here) and the radial displacement (${u}_{\mathrm{r}}$) may be found, for example, in Yu [43]

$$\sigma_{r}^{\prime } = \sigma_{H}^{\prime } + \left( {\sigma_{r,p}^{\prime } - \sigma_{H}^{\prime } } \right)\left( {\frac{{r_{p} }}{r}} \right)^{2}$$

(50)

$$\sigma_{\theta }^{\prime } = \sigma_{H}^{\prime } + \left( {\sigma_{r,p}^{\prime } - \sigma_{H}^{\prime } } \right)\left( {\frac{{r_{p} }}{r}} \right)^{2}$$

(51)

$$\sigma_{z}^{\prime } = \sigma_{V}^{\prime }$$

(52)

$$u_{r} = \frac{{\sigma_{r,p}^{\prime } - \sigma_{H}^{\prime } }}{{2G_{0} }}\frac{{r_{p}^{2} }}{r}$$

(53)

where $\sigma_{r,p}^{\prime }$ is the radial stress at the elastic/plastic boundary (Eq. 40) and $\sigma_{H}^{\prime }$ and $\sigma_{V}^{\prime }$ are the horizontal and vertical stresses, respectively.