Comparative 3D DEM simulations of sand–structure interfaces with similarly shaped clumps versus spheres with contact moments

Abstract

Three-dimensional simulations of a monotonic quasi-static interface behaviour between initially dense cohesionless sand and a rigid wall of different roughness during tests in a parallelly guided direct shear test under constant normal stress are presented. Numerical modelling was carried out by the discrete element method (DEM) using clumps in the form of convex non-symmetric irregularly shaped grains. The clumps had an aspect ratio of 1.5. A regular grid of triangular grooves (asperities) along the wall with a different height at the same distance was assumed. The numerical results with clumps were directly compared under the same conditions with our earlier DEM simulations using pure spheres with contact moments with respect to the peak and residual interface friction angle, width of the interface shear zone, ratio between grain slips and grain rotations, distribution of contact forces and stresses. The difference between the behaviour of clumps and pure spheres with contact moments proved to be noticeable in the post-peak regime due to a different particle shape. The rolling resistance model with pure spheres was proved to be limited for capturing particle shape effects. Three different boundary conditions along the interface were proposed for micropolar continua, considering grain rotations and grain slips, wall grain moments and wall grain forces, and normalized interface roughness. The numerical results in this paper offer a better understanding of the interface behaviour of granular bodies in DEM and FEM simulations.

1 Introduction

The safety of engineering systems adjacent to soils in static and dynamic conditions is strongly affected by the strength of soil–structure interfaces. The behaviour of interfaces is characterized by the formation of shear zones with a certain thickness in the soil adjacent to structures, i.e. thin zones of intense shearing with both pronounced grain rotations and volume changes [52, 58]. The thickness of wall shear zones determines the forces transferred from soils to structures. To properly describe the width of shear zones in finite element simulations, continuum models must be enriched by a characteristic length of micro-structure [56,57,58,59] by means of, e.g., micropolar, second-gradient, non-local or viscous terms (e.g. [2, 40, 54, 68]). Micropolar models are, in particular, physically realistic for cohesionless soils since they include grain rotations that are visible in experiments [52]. In those models, the characteristic length of micro-structure directly corresponds to a mean grain radius/diameter (e.g. [56,57,58,59]). In the case of enriched continua including, e.g. second-gradient, non-local or viscous terms, the characteristic length is determined with an inverse identification process of experimental  data [2], [54]. Up to now, there do not exist consistent micropolar continuum boundary conditions for walls of different roughness [10, 11, 20, 58, 60]. There are some elasto-plastic and hypoplastic models in the classical continuum for describing granular soil–structure interface behaviour (e.g. [37, 45, 49, 51]). However, Coulomb’s friction law is usually used in problems of the soil–structure interface, based on the assumption of a constant ratio between the shear and normal stresses on the interface. This assumption is incorrect since: (1) the mobilized friction angle can change significantly during shearing along rough or very rough walls in contact [52, 58] and (2) the mobilized wall friction angle is not a state constant since it depends on boundary conditions, contact pressure level, initial stress state and specimen size [52, 58]. Therefore, the laboratory wall friction angles obtained from different tests (in particular, their peak values) cannot always be directly transferred to other boundary value problems [52].

The interface behaviour between granular materials and structures has been investigated using various testing devices and methods (see the overview in [15]), mainly with the aid of interface direct shear apparatuses (e.g. [5,6,7,8,9, 17, 19, 42,43,44, 48, 50, 52, 58, 70, 72]). The experimental results showed a pronounced effect of the interface roughness, grain size, grain angularity, grain hardness, pressure level, normal stiffness, initial density, specimen size and shear velocity on the peak wall friction angle and wall shear zone thickness. The shear zone thickness was found to raise with increasing interface roughness [5,6,7,8,9, 17, 19, 42,43,44, 48, 50, 70, 72], initial unit weight [6, 52], grain size [52], specimen size [52, 58], grain angularity [6] and to reduce with increasing grain hardness [6] and normal stiffness [6]. As to the pressure effect, the shear zone thickness increased [52] or decreased [6] with growing pressure. The mobilized wall friction angle at the peak grew with increasing interface roughness [5,6,7,8,9, 17, 19, 42,43,44, 48, 50, 70, 72], grain size [52], grain angularity [6] and initial unit weight [6, 52], and decreased with growing pressure [6, 52], normal stiffness [6] and specimen size [52, 58]. Moreover, large void fluctuations, grain mixing and grain segregation were observed in a shear zone during interface experiments in the Couette apparatus [32]; the shear zone thickness and the mobilized interface friction angle at the peak increased with raising shear strain rate.

The maximum interface strength was achieved, e.g. for an asperity distance to mean grain diameter ratio between 1.0 and 3.0, and an asperity height to mean grain diameter ratio greater than 0.9 [9]. An asperity angle of 50° or greater yielded the maximum efficiency for any given asperity spacing or height [9]. The maximum interface friction angle was found to be larger than the internal friction angle of soils due to the passive resistance caused by surface asperities [21, 22, 52]. It varied in a bi-linear fashion as a function of the normalized roughness [19, 42, 50]. The critical normalized roughness was mainly about 0.40–0.50 and above this value, the maximum interface friction angle insignificantly increased. The literature overview on the interface behaviour between cohesionless sand and rigid wall of different roughness with respect to numerical solutions within continuum mechanics and discrete mechanics was given in [15]. There exist many DEM studies of sand–structure interfaces under 2D (e.g. [13, 14, 16, 22, 64, 65, 74]) and 3D conditions [12, 15, 24, 69, 73]. In those studies, disks with contact moments were used in 2D simulations [13, 14, 16, 22, 64, 65, 74] or spheres with contact moments were used in 3D simulations [12, 15, 24, 69]. The clumps were either assumed in 2D [22] or 3D simulations [73]. Zhou et al. [73] performed comprehensive 3D simulations of the soil–structure interface behaviour with different interface roughness, particle sphericity and initial fabric, using three types of clustered particles. The shear strength of the interface was found to grow as the interface roughness and particle orientation increased and particle sphericity reduced. However, the DEM studies directly comparing the behaviour of spheres including contact moments with clumps in the soil–structure interface problems under the same conditions are missing. Those comparative studies with a different particle shape are needed since the majority of DEM simulations are carried out using disks/spheres with contact moments to strongly shorten the computation time. This approach is physically less realistic than the approach with clumps. A comprehensive comparison between the rolling resistance and particle shape effects was carried out with DEM for triaxial compression tests only, without taking shear localization into account [31, 71]. It was shown that the rolling resistance model was limited in its ability to capture particle shape effects [71]. The existing DEM simulations also exhibited a bi-linear relationship between the interface resistance and normalized interface roughness [15, 24, 69, 73]. The critical normalized roughness was found to be in 3D studies about 0.40–0.75 [15, 24, 69, 73].

In our earlier paper [15], the monotonic quasi-static interface behaviour between cohesionless sand and a rigid wall of different surface topography using a direct shear box under conditions of constant normal stress was comprehensively analysed using 3D DEM (the particle-based open-source code YADE). To approximately simulate the irregularity of sand particles’ shape of ‘Karlsruhe’ sand, spheres with contact moments were used. The artificial wall surface topography was created by regularly arranged triangular grooves (asperities) in the form of a standard saw-tooth surface. Some calculation results were compared with our corresponding monotonic quasi-static sand–structure interface tests on cohesionless ‘Karlsruhe’ sand in a parallelly guided direct shear box, performed at Karlsruhe University [52, 58]. They were also compared with reported experimental results for similar interface roughness in the literature. The calculations were carried out with the different interface roughness, expressed by the varying height, spacing and inclination of wall grooves, initial void ratio of sand and vertical pressure. The effect of the groove distance was found to be small up to a certain value and the effect of the groove height and groove inclination was significant on the peak interface friction angle and the thickness of the shear zone. In addition, three wall boundary conditions for 2D micropolar continua were proposed: (1) the ratio between the micropolar rotation and slip, (2) the ratio between the interface shear stress and interface couple moment and (3) the ratio between the tangential interface force and tangential wall moment.

In the current paper, the 3D interface behaviour was investigated under the same conditions, using both the same direct shear box and granular material. However, instead of pure spheres with contact moments [15], we assumed irregular grains of the same shape composed of sphere clumps that more realistically reproduced the real grain shape. The aspect ratio of grains was 1.5. In the present calculations, the initial void ratio and vertical pressure were also the same. The artificial wall surface topography was again created by regularly arranged triangular grooves (asperities) at the same spacing [15]. The attention was focused on differences in the sand–structure interface behaviour, described by two different DEM approaches, with respect to the evolution and magnitude of the mobilized wall friction angle, wall shear zone, interface displacements, interface rotations, stresses, interface forces/moments and contact forces in the granular assembly for the interface of the different roughness. The goal was to find if a rolling resistance model with spheres is able to capture particle shape effects. In addition, interface boundary conditions of different roughness were assumed for clumps within micropolar continuum by considering grain rotations, slips, moments and forces. They were directly connected with the normalized interface roughness, using simple relationships. As compared to [15], the ratio between the slip and the total imposed displacement along the interface was proposed instead of the ratio between the horizontal shear stress multiplied by the mean grain diameter and the horizontal couple stress. The ratios between interface grain rotations and interface grain slips and between interface grain forces and interface grain moments were not measured in experiments yet. The particle slip was separately measured in experiments by DeJong et al. [6].

The paper includes the following novel points: (1) comprehensive 3D analyses of the interface behaviour with the real mean grain diameter of the sand using irregularly shaped grains by taking into account the effect of different interface roughness, (2) a detailed comparison of the interface behaviour between grain clumps of the same shape and pure spheres with contact moments under the same conditions to show the particle shape effect on the shear resistance and shear localization (such a comparison was not performed for sand–structure interface problems yet) and (3) a proposal of simplified interface boundary conditions of different roughness for micropolar continua by considering grain rotations, slips, moments and forces related to the normalized interface roughness. The findings presented in this paper can help to better understand both: (1) the sand–structure interface mechanism when using two different DEM approaches and (2) the boundary conditions along the interface of different roughness for micropolar continua to simulate large soil–structure systems with the finite element method.

The paper is arranged as follows. In Sect. 2, the proposed numerical DEM framework was presented in detail. The model calibration is shown in Sect. 3. Results of the effect of the interface roughness on friction angle and shear localization with key findings are described in Sect. 4. Section 5 discusses interface boundary conditions in the frame of the micropolar (Cosserat) continuum. The main results were summarized and some conclusions are stated in Sect. 6.

2 3D DEM model

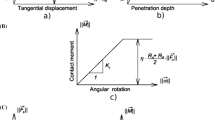
DEM is a very efficient and powerful numerical tool for modelling granular assemblies. The 3D spherical discrete element model YADE developed at the University of Grenoble [27, 28, 47] was employed to simulate the interface behaviour. To simulate the irregularity of the particles’ shape of ‘Karlsruhe’ sand, clumps composed of spheres were used [30]. YADE takes advantage of the so-called soft-particle approach, i.e. the model allows for particle deformation which is modelled as an overlap of particles (interpreted as a local contact deformation). The mechanical response of the contact model when using clumps is presented in Fig. 1. The DEM model for spheres with contact moments was presented in [15]. Below, the basic equations of the DEM model for clustered particles are summarized [27, 28, 47]:

$$\vec{F}_{{\text{n}}} = K_{{\text{n}}} U\vec{N}$$

(1)

$$\vec{F}_{{\text{s}}} = \vec{F}_{{\text{s,prev}}} + \Delta \vec{F}_{{\text{s}}} \quad {\text{with}}\quad \Delta \vec{F}_{{\text{s}}} = K_{{\text{s}}} \Delta \vec{X}_{{\text{s}}} ,$$

(2)

$$K_{{\text{n}}} = E_{{\text{c}}} \frac{{2R_{{\text{A}}} R_{{\text{B}}} }}{{R_{{\text{A}}} + R_{{\text{B}}} }}\quad {\text{and}}\quad K_{{\text{s}}} = \upsilon_{{\text{c}}} E_{{\text{c}}} \frac{{2R_{{\text{A}}} R_{{\text{B}}} }}{{R_{{\text{A}}} + R_{{\text{B}}} }},$$

(3)

$$\left|\left|\vec{F}_{{\text{s}}}\right|\right| - \left|\left|\vec{F}_{{\text{n}}}\right|\right| \times \tan \mu \le 0,$$

(4)

$$\vec{F}_{{{\text{damp}}}}^{k} = \vec{F}^{k} - \alpha_{{\text{d}}} \cdot {\text{sgn}} \left( {\vec{\nu }^{k} } \right)\left| {\vec{F}^{k} } \right|,$$

(5)

Fig. 1

Mechanical response of linear contact DEM model: a tangential contact model and b normal contact model [27, 28, 47]

where $\vec{F}_{{\text{n}}}$ the normal contact force, U the overlap between discrete elements, $\vec{F}_{{\text{s}}}$ the tangential contact force, $\vec{F}_{{\text{s,prev}}}$ the tangential contact force from the previous iteration, $\vec{N}$ the unit normal vector at each contact point, $\vec{X}_{{\text{s}}}$ the relative tangential displacement of the sphere centre, K_n the normal contact stiffness, K_s the tangential contact stiffness, μ the Coulomb inter-particle friction angle, R the element radius, R_A and R_B the contacting grain radii, E_c the elastic modulus of the grain contact, ν_c the Poisson’s ratio of the grain contact, $\vec{F}_{{{\text{damp}}}}^{k}$ the damped contact force, $\vec{F}^{k}$ the kth components of the residual contact force vector, $\vec{\nu }^{k}$ are the kth components of the translational velocities of grains and α_d the positive numerical damping coefficient smaller than 1 [4] (sgn(·) returns the sign of the kth component of the translational and rotational velocity). No forces are transmitted when grains are separated.

The three main local material parameters are necessary for our DEM simulations: E_c (modulus of elasticity of the grain contact), ν_c (Poisson’s ratio of the grain contact), μ (inter-particle friction angle). In addition, a particle radius R, particle mass density ρ and numerical damping parameter α_d are required. The DEM material parameters: E_c, ν_c and μ were calibrated using the corresponding homogeneous axisymmetric triaxial laboratory test results on ‘Karlsruhe’ sand with the different initial void ratio and lateral pressure [31] that were compared with the corresponding experiments [26, 66]. The procedure for determining the material parameters in DEM was described in detail by Kozicki et al. [30, 31]. Note that the representative elastic contact moduli E_c and ν_c are different from the elastic moduli of grains. The effect of damping (if α_d ≤ 0.10) is negligible in quasi-static calculations [30, 31].

All DEM calculations on the interface behaviour were performed with convex non-symmetric irregularly shaped grains of a diameter d_clump, composed of 4 spheres of different diameters (d_sphere = 0.50–0.60 × d_clump) (Fig. 2). Each granular assembly was prepared by putting clumps of a random diameter according to the grain distribution curve. The aspect index (the ratio between the maximum and minimum clump diameter) was 1.50, the convexity index ‘1’ (the ratio between the smallest sphere volume encompassing the cluster and the cluster volume) was 2.07 and the convexity index ‘2’ (the ratio between the smallest convex volume encompassing the cluster and the cluster volume) was 1.16.

Fig. 2

Non-symmetric convex clump with diameter of 0.5 mm in coordinate space XYZ composed of 4 spheres used in DEM simulations (grid size is equal to 0.1 mm)

3 Model calibration based on triaxial compression

To find the material parameters in DEM (E_c, ν_c and μ), a series of numerical homogeneous quasi-static triaxial compression tests with rigid smooth walls on cohesionless sand were initially performed [30]. The DEM results were compared with corresponding comprehensive experimental triaxial compression results with ‘Karlsruhe’ sand for the different initial void ratios and lateral pressures [26, 66] (Fig. 3). The triaxial compression test is the most homogeneous laboratory test in soil mechanics and hence is frequently used for soil calibration. The index properties of ‘Karlsruhe’ sand are: the mean grain diameter d₅₀ = 0.50 mm, grain size between 0.08 and 1.8 mm, uniformity coefficient U_c = 2, maximum specific weight γ_d^max = 17.4 kN/m³, minimum void ratio e_min = 0.53, minimum specific weight γ_d^min = 14.6 kN/m³ and maximum void ratio e_max = 0.84. The sand grains were classified as sub-rounded/sub-angular. The material parameters could not be calibrated with our interface shear tests [58] since we did not have full knowledge of the wall surface whose roughness was very non-uniform and random.

Fig. 3

Triaxial compression test on initially very dense sand (initial void ratio e_o = 0.53) using clumps: a DEM model set-up and b calculated vertical normal stress σ₁ and c calculated volumetric strain ε_v versus vertical normal strain ε₁ from DEM compared to laboratory experiments [26] for different initial lateral pressure: σ_c = 50 kPa, σ_c = 200 kPa and σ_c = 500 kPa

For DEM simulations, a cubical specimen of size 10 × 10 × 10 cm³ (composed of about 8000 grain clumps as in [15]) (Fig. 3a). The grain diameter of sand linearly varied between 2.5 and 7.5 mm and its mean grain diameter was d₅₀ = 5 mm (10 times larger than the real one d₅₀ = 0.5 mm). The mass density was 2600 kg/m³. The DEM simulations were carried out for initially very dense sand (initial void ratio e_o = e_min = 0.53) with three different lateral pressures σ_c = 50 kPa, 200 kPa and 500 kPa (Fig. 3b, c) assuming the material parameters listed in Table 1. A satisfactory agreement was obtained, in particular, for the stress–strain curves (Fig. 3b). This agreement with laboratory tests was slightly worse than for pure spheres with contact moments [15] since the DEM model for spheres had a higher number of material parameters [15] (five against three). When using clustered particles, a better agreement with experiments is solely possible with more realistic grain shapes, obtained with the aid of, e.g. 3D micro-CT images [25, 41]. The effect of E_c and μ on the sand behaviour is presented for σ_c = 200 MPa in Fig. 4. The lower the parameter E_c, the lower are the global elastic modulus E, maximum internal fiction angle ϕ_max and volumetric strain ε_v and the higher is the vertical normal strain ε₁ corresponding to ϕ_max. The reduction of E_c by factor 3 diminishes E by 60%, ϕ_max by 3% and ε_v by 10%, and increases ε₁ corresponding to ϕ_max by 50%. The lower the parameter μ, the lower are the maximum internal fiction angle ϕ_max and volumetric strain ε_v. The reduction of μ by 20% diminishes ϕ_max by 10% and ε_v by 20%. The residual internal fiction angle ϕ_res is not affected by E_c and μ. The vertical normal strain ε₁ corresponding to ϕ_max is 5–7% (Fig. 4A).

Table 1 Material parameters assumed in all DEM simulations

Fig. 4

Triaxial compression test on initially very dense sand (initial void ratio e_o = 0.53, lateral pressure σ_c = 200 kPa) using clumps: effect of elastic modulus of contact E_c and inter-particle friction angle μ on calculated vertical normal stress σ₁ (A) and calculated volumetric strain ε_v (B) versus vertical normal strain ε₁ (a) E_c = 300 MPa and μ = 26°, (b) E_c = 100 MPa and μ = 26° and (c) E_c = 300 MPa and μ = 21°

A simple linear elastic normal contact was chosen to capture on average various contact possibilities present in real sands [39] and to reduce the computation time [67]. We performed comparative simulations for spheres with contact moments between a linear and nonlinear contact model [36] following Hertz [18] and Mindlin and Deresiewicz [35], based on a plane compression test without shear localization. The comparative analyses were carried out only with respect to macroscopic quantities (measured in real laboratory tests) due to the lack of experimental data on microscopic quantities (Fig. 5). The results of triaxial compression indicated some negligible differences between the two contact models for spheres and contact moments. Both the global maximum mobilized internal friction angle and dilatancy angle for initially dense sand were almost the same using both approaches, and the global macroscopic elastic parameters (elastic modulus and Poisson’s ratio) differed about by 10% only. For initially dense sand and confining pressure σ_c = 200 kPa, the global macroscopic elastic parameters were E = 80 MPa and ν = 0.25 using spheres with contact moments and a linear contact model, and E = 70 MPa and ν = 0.22 using spheres with contact moments and a nonlinear contact model. The global maximum mobilized internal friction angle φ_max and dilatancy angle were φ_max = 42° and ψ = 30° (spheres with contact moments and a linear contact model), and φ_max = 42.1° and ψ = 30° (spheres with contact moments and a nonlinear contact model) (Fig. 5). Although a nonlinear contact model is more realistic (in particular for small loads) [39], a linear elastic contact law provides similar DEM results with the significantly reduced computation time [67] and therefore was used in current simulations. The elastic constants of the grain contact in our DEM model do not correspond to the elastic constants of the spheres’ material in the Hertz law (the parameter K_n in Eq. 3 is several times larger than the mean normal stiffness of the spherical grain material) [1].

Fig. 5

Mobilized internal friction ϕ and volumetric strain ε_v versus ε₁ for initially dense sand (e_o = 0.53) with different lateral pressure σ_c from DEM (spheres with contact moments, E_c = 300 MPa, ν_c = 0.3, μ = 18°, β = 0.7 and η = 0.4) compared to experiments [66] during homogeneous triaxial compression test (σ_c = 50–500 kPa, d₅₀ = 5 mm) with: A linear contact model and B nonlinear contact model (calculations: a) σ_c = 50 kPa, c) σ_c = 200 kPa, e) σ_c = 500 kPa), (experiments: b) σ_c = 50 kPa, d) σ_c = 200 kPa, f) σ_c = 500 kPa) (β—dimensionless rolling stiffness coefficient, η-dimensionless limit rolling coefficient)

4 DEM simulations of monotonic direct interface shearing tests

4.1 DEM model

The 3D granular specimen included 80 000 grain clumps (Fig. 6). The specimen length (l = 100 mm) and the height (h = 20 mm) (Fig. 6A) were the same as in the experiment [52, 58]. The width of the granular specimen with clumps was D = 5 mm (10 × d₅₀) in all DEM simulations instead of D = 100 mm as in the experiment, based on preliminary simulations of a direct interface shearing test using pure spheres with contact moments [15]. The reduction of the specimen width from D = 100 mm down to D = 5 mm did not affect the results [15] but strongly diminished the computation time. The gap equal to the maximum grain diameter was left between the bottom and vertical walls (see the zoom in Fig. 6A) as in the experiment [52, 58] to prevent locking of particles at the bottom corners during shearing. The sand leakage during shearing had a minor effect on void ratio and volumetric strain (< 0.5%). The maximum number of clumps beyond the box after the test was solely 350. The comparative calculations without a gap indicated similar results; however, the evolution of the interface friction angle showed more fluctuations caused by grain interlocking at ends. The grain diameter of sand linearly varied between 0.25 mm (d_min = 0.25 mm) and 0.75 mm (d_max = 0.75 mm). The mean grain diameter of d₅₀ = 0.5 mm was as in the experiment [52]. The sand was horizontally sheared along the bottom wall under a constant velocity of the shear box du_x/dt = 0.5 mm/s (from the left to the right, u_x—the positive horizontal displacement) (Fig. 6). The horizontal velocity of the shear box was small enough to consider the test as quasi-static (the inertial number I was kept below 10e⁻⁴)  [34]. The rigid bottom wall was fixed. The top and side rigid walls were movable and smooth. The frictional coefficient along those walls was tanφ_w = tanμ = tan18° = 0.32.

Fig. 6

Direct sand–structure interface test in DEM using clumps of Fig. 2: A geometry of three-dimensional DEM model and B rigid bottom wall sections with different normalized interface roughness parameter R_n = h_g/d₅₀: a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (h_g-groove height, s_g-groove distance, α_g-groove inclination and d₅₀-mean grain diameter, u_x-horizontal displacement, T-horizontal force)

In DEM simulations, the interface roughness was simulated in a various way [12, 23, 64]. As in [15], a regular saw-tooth surface with varied asperity height and the same distance was chosen. The regularly arranged triangular grooves (asperities) had the same distance but a different inclination. The interface roughness was characterized by the normalized interface roughness parameter R_n = h_g/d₅₀, where h_g is the groove height and d₅₀ denotes the mean grain diameter [58, 61, 69]. The parameter R_n was 2.0, 1.0, 0.75, 0.50, 0.25, 0.10 and 0.01 (Fig. 6B). The groove distance s_g was always the same (s_g = 2 × d₅₀). The groove inclination to the bottom α_g diminished with decreasing R_n (e.g. α_g = 45° for R_n = 1.0) (Fig. 6B). The constant uniform vertical pressure σ_n was applied to the top area of the shear box. The interface friction angle between particles and grooves/walls was assumed to be φ_w = 18°. The comparative calculations with particle clumps versus pure spheres with contact moments [15] were limited in the current paper to initially dense sand with e₀ = 0.55 and one vertical pressure of σ_n = 100 kPa (as in [15]). The effect of the different vertical pressure σ_n and initial void ratio e₀ on the sand behaviour was investigated for spheres with contact moments in [15]. For clumps, a similar effect is expected. The same initial void ratio was assumed in both approaches since the calculations concerned the same sand. We did not have problems generating numerically this initial void ratio for clumps due to an overlap of particles. The relative initial density of the granular material should be controlled if different sands are compared with each other [38]. The relative density was controlled in DEM simulations of the interface shear behaviour for different sands by, e.g. Zhou et al. [73]. The interface friction angle φ was calculated as φ = arctan(T/N) (T—the sum of horizontal forces acting on the top and lateral walls and N—the sum of vertical forces acting on the top wall). The calculation time for clumps was larger by factor 4 as compared to that for spheres with contact moments.

4.2 Effect of interface roughness on mobilized friction angle

The normalized interface roughness parameter R_n varied between R_n = 0.01 and R_n = 2.0 for e₀ = 0.55 and σ_n = 100 kPa (Fig. 7) as in DEM analyses with pure spheres including contact moments [15]. The values of the peak interface friction angle φ_w,max, residual interface friction angle φ_w,res and volumetric strain ε_v are given in Table 2 as compared to pure spheres with contact moments [15]. The relationship between the computed values of φ_w,max and φ_w,res and R_n and grain shape is shown in Fig. 8.

Fig. 7

Mobilized interface friction angle φ_w (A) and volumetric strain ε_v versus horizontal displacement u_x (B) for clumps of Fig. 2 from DEM for different normalized interface roughness parameter R_n (initial void ratio e₀ = 0.55 and vertical pressure σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01

Table 2 Calculated values of peak wall friction angle φ_w,max, residual wall friction angle φ_w,res and residual volumetric strain ε_v for different normalized interface roughness parameter R_n using clumps of Fig. 2 (values for pure spheres with contact moments [15] are given in parentheses)

Fig. 8

Relationship between peak interface friction angle φ_w,max and residual interface friction angle φ_w,res and normalized interface roughness parameter R_n from DEM for: a) clumps and b) pure spheres with contact moments [15] (black colour indicates φ_w,max and red colour indicates φ_w,res) (color figure online)

4.2.1 Evolution of mobilized interface friction angle and volumetric strain

The evolution shape of the curves φ_w = f(u_x) and ε_v = f(u_x) (Fig. 7) for the initially dense sand are similar as for pure spheres with contact moments [15]. The peak φ_w,max and the residual interface friction angle φ_w,res continuously grew with increasing roughness parameter. The peak values of φ_w,max were very similar for both clumps and pure spheres (Table 2); however, the residual values of φ_w,res and residual volumetric strains were slightly lower for clumps with the normalized interface roughness parameter R_n ≥ 0.25 (e.g. they were lower by 3° for R_n ≥ 0.5 and by 6° for R_n = 0.25).

The clear critical surface roughness R_n(crit) concerning the peak interface friction angle φ_w,max was not reached with clumps in contrast to pure spheres with contact moments wherein the clear critical surface roughness was obtained for R_n(crit) = 0.50–0.75, beyond which their effect became negligible (Table 2). The relationship between the values of φ_w,max and R_n was more parabolic for clumps in opposite to a bi-linear one for pure spheres although the changes of the peak interface friction angle were small for clumps above the value of R_n ≥ 0.75 (Fig. 8). The relationship between the values of φ_w,res and R_n was, however, bi-linear for both clumps and pure spheres [15]. The value of φ_w,max = 18º for R_n = 0.01 was obviously equal to the assumed interface friction angle between particles and grooves. The slightly lower values of R_n(crit) were obtained in the experiments by Hu and Pu [19, 24] (R_n(crit) = 0.40) and DEM calculations by Jing et al. [23, 73], Zhou et al. [69, 73] (R_n(crit) = 0.375–0.50) and Zhang and Evans [69] (R_n(crit) = 0.40). A similar value of R_n(crit) was obtained in the laboratory tests by Su et al. [50] (it was between 0.5 and 1.0). The volumetric strain of sand also changed with increasing R_n (Fig. 7B); its greatest value at the residual state was lower by 20% than for pure spheres with contact moments [15].

Figure 9 shows the effect of different frictional angles between sand particles and lateral walls of the shear box (10° and 26°) on the DEM results. The effect was insignificant on the residual friction angle at the interface and volume changes of the granulate. The difference between the maximum interface friction angles was 5% only.

Fig. 9

Mobilized friction angle φ_w at interface (A) and volumetric strain ε_v versus horizontal displacement u_x (B) for clumps of Fig. 2 (initial void ratio e₀ = 0.55, vertical pressure σ_n = 100 kPa, normalized roughness parameter R_n = 1.0) from DEM with different frictional angles between sand particles and side walls: a) 10°_, b) 18° and c) 26°

As in [15], the DEM results were also compared with our interface experiments [52, 58]. In experiments, the interface roughness was classified as smooth (0 < R_n ≤ 0.1 × d₅₀), rough (0.1 × d₅₀ < R_n < 0.5 × d₅₀) and very rough (R_n ≥ d₅₀). The rough interface was obtained in a corrosion chamber, and a very rough interface was obtained with the aid of random glueing of particles of ‘Karlsruhe’ sand with the mean diameter equal to and higher than 0.5 mm to the wall. Thus, the experimental interface roughness was different. The DEM calculation results were compared with the experiments in Fig. 10. A satisfactory agreement with the experimental results was obtained with respect to the shape of curves φ_w = f(u_x) and ε_v = f(u_x) and peak interface friction angles φ_w,max. However, the calculated residual interface friction angles φ_w,res were much smaller than the experimental values for the rough and very rough interface. The calculated displacements corresponding to φ_w,max were also smaller (by factor 3) for the rough and very rough interface than in the experiment. Thus, the numerical initial sand response was too stiff. The calculated volumetric strain ε_v was also too large by factor 1.5 as compared to the experiments for the rough and very rough wall. Those discrepancies were caused by the fact that the experimental interface roughness and particle shapes were not faithfully reproduced in DEM simulations. A drop/growth of the parameter μ causes a decrease/increase of the parameters φ_w,max and ε_v, whereas the value of φ_w,res remains the same (Fig. 4A). A decrease of E_c improves the initial material response, volumetric strain and the location of φ_w,max but worsens φ_w,max (Fig. 4) as compared to the experiments (Fig. 10) without affecting again the value of φ_w,res. Hence, the parameter μ must be higher. On the other hand, a small value of E_c is not realistic with respect to triaxial compression laboratory tests (Fig. 4). To increase φ_w,res for better fitting with the experiments (Fig. 10), the grain shape with a higher aspect ratio should be used [30]. Note that the experimental results in the initial shear phase may be affected by some test inaccuracies that contribute to a weaker sand response at the beginning of deformation. The measured horizontal displacement u_x corresponding to φ_w,max for very rough walls was about 1.5 mm (Fig. 10). The sand strain corresponding to this displacement, approximately calculated as ε_x = u_x/t_s=1.5 mm/6 mm = 0.25 (t_s the thickness of the shear zone at the interface, Fig. 13), is much too high by comparing it with triaxial laboratory test results (Fig. 3).

Fig. 10

DEM results of mobilized interface friction angle φ_w (a) and volumetric strain ε_v (b) at interface versus horizontal displacement u_x (continuous lines) for initially dense specimen (e_o = 0.55) under vertical pressure of σ_n = 100 kPa compared to experimental results [52, 58] (dashed lines) for different normalized interface roughness parameter R_n: R_n = 1.0 (very rough surface), R_n = 0.25 (rough wall) and R_n = 0.01 (smooth wall)

4.2.2 Distribution of particle rotation, particle displacement and void ratio

The effect of the normalized interface roughness parameter R_n on the sphere rotations ω in the entire sand specimen is shown at the residual state (u_x = 7 mm) in Fig. 11. The values of rotations ω were calculated from a cubic averaging cell of the size 5d₅₀ × 5d₅₀ × 5d₅₀ being moved by d₅₀. In the averaging cell, the centres of spheres were considered independently of their diameter (clockwise rotation is positive). Figure 12 presents the zoom on single sphere rotations in the granular segment at the front side (mid-length). In Fig. 13, the relationship between the shear zone thickness t_s and normalized interface roughness parameter R_n is demonstrated as compared to pure spheres with contact moments [15]. Figure 14 shows the distribution of sphere horizontal displacements u_x, sphere rotations ω and void ratio e across the normalized specimen height h/d₅₀ at the specimen mid-region at the residual state. The values of u_x, ω and e were calculated from the averaging cell of the size 5d₅₀ × 5d₅₀ × 1d₅₀ (length × width × height) being moved by d₅₀. The relationship between the horizontal interface slip and total prescribed horizontal displacement and normalized interface roughness parameter R_n is presented in Fig. 15. Figure 16 demonstrates the evolution of the ratio between the interface grain rotation and interface grain slip A = (ωd₅₀)/u during interface shearing at the box mid-length. The distribution of the residual ratio between the grain rotation multiplied by the mean grain diameter ωd₅₀ and the sphere slip u (ωd₅₀)/u across the specimen height at the specimen mid-point for the different parameter R_n is shown in Fig. 17. The ratio A at the residual state is shown in Table 3.

Fig. 11

Distribution of grain rotations ω with attached scale in [rad] at residual state for u_x = 7 mm for clumps of Fig. 2 from DEM with different normalized interface roughness parameter R_n (e_o = 0.55 and σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (e_o = 0.55 and σ_n = 100 kPa) (positive sign—clockwise rotation, negative sign—anti-clockwise rotation)

Fig. 12

Zoom on distribution of grain rotations across granular segment at front side in residual state (u_x = 7.0 mm) for clumps of Fig. 2 from DEM with different normalized interface roughness parameter R_n (e_o = 0.55 and σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (red colour—clockwise rotations, blue colour—anti-clockwise rotations, white colour—no rotation) (color figure online)

Fig. 13

Relationship between shear zone thickness t_s and normalized interface roughness parameter R_n at residual state from DEM (e_o = 0.55 and σ_n = 100 kPa) for: a) clumps of Fig. 2 and b) pure spheres with contact moments [15]

Fig. 14

Distribution of horizontal grain displacement u_x (A), grain rotation ω (B) and void ratio e (C) across normalized specimen height h/d₅₀ at the specimen mid-point at residual state for u_x = 7.0 mm for clumps of Fig. 2 from DEM with different normalized interface roughness parameter R_n (e_o = 0.55 and σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (e_o = 0.55 and σ_n = 100 kPa)

Fig. 15

Relationship between horizontal slip u/u_x along grooves and normalized interface roughness parameter R_n at residual state from DEM (e_o = 0.55 and σ_n = 100 kPa) for: a) clumps and b) pure spheres with contact moments [15]

Fig. 16

Evolution of wall rotation/slip ratio A = ωd₅₀/u_x versus horizontal displacement u_x for different normalized interface roughness parameter R_n using clumps of Fig. 2: a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (initial void ratio e_o = 0.55 and vertical pressure σ_n = 100 kPa)

Fig. 17

Distribution of ratio A = ωd₅₀/u across normalized specimen height h/d₅₀ at specimen mid-point at residual state for u_x = 7.0 mm A clumps of Fig. 2 and B pure spheres with contact moments [15]) with different normalized interface roughness parameter R_n: a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01 (e_o = 0.55 and σ_n = 100 kPa)

Table 3 Ratio between wall grain rotation and wall grain slip A = ωd₅₀/u for clumps of Fig. 2 and pure spheres with contact moments at residual state [15]

The particle rotations and increasing void ratio are the best indicators for shear localization [15, 52, 56,57,58,59]. Based on particle rotations (Fig. 11), it can be seen that during interface shearing with the different normalized interface roughness parameter R_n, an almost horizontal dilatant shear zone was created at the interface (R_n > 0.01). The grain rotations had nearly always the same positive sign (clock-wise rotation) (Fig. 11). More grains rotated in the opposite direction (Fig. 12) as compared to pure spheres with contact moments [15]. The thickness of the shear zone was estimated, based on an inflection point in the distribution of sphere rotations ω where the rotation was ω ≤ 5% of the maximum particle rotation ω_max in the wall shear zone (Fig. 14B). The thickness of the shear zone t_s at the interface increased in an approximate parabolic way (Fig. 13a). It was equal to t_s = 12 × d₅₀ (R_n = 2.0), t_s = 11.0 × d₅₀ (R_n = 1.0), t_s = 10 × d₅₀ (R_n = 0.75), t_s = 8 × d₅₀ (R_n = 0.50), t_s = 6 × d₅₀ (R_n = 0.25), t_s = 3 × d₅₀ (R_n = 0.10) and t_s = 1 × d₅₀ (R_n = 0.01) (Fig. 11) (for pure spheres, it changed in a bi-linear one, Fig. 13b). The calculated maximum thickness was in agreement with the maximum experimental value of 9 × d₅₀ [6]. The thickness was lower than for spheres [15] by 15–40% for R_n ≥ 0.50 (Fig. 13) due to higher grain rotations at the wall (Fig. 14B). Similarly, as for pure spheres with contact moments [15], the largest grain rotation was located slightly above the interface (h/d₅₀ = 3–5) for R_n > 0.5, and for R_n ≤ 0.5 it was directly located at the interface (Fig. 14B) where it diminished with the reduction of R_n. For R_n > 0.5, the sphere rotations approached zero at the bottom wall (equal to the situation with particles trapped in asperities). Above the shear zone, all spheres were almost motionless (Figs. 11 and 14B). The maximum residual grain rotation for R_n ≥ 0.75 was equal to about 60°, whereas for pure spheres with contact moments, it was about 45° [15].

Both the maximum horizontal displacement (Fig. 14A) and void ratio (Fig. 14C) increased in the shear zone at the interface with growing R_n. The distribution of the horizontal displacement and void ratio across the specimen height was similar as in interface shear laboratory tests using the particle image velocimetry PIV [5,6,7]. The maximum void ratio in the dilatant wall shear zone at the residual state changed between e = 0.55 (R_n = 0.01) and e = 0.86 (R_n = 2.0). The horizontal slip u along the wall obviously decreased with increasing R_n, and was about 0% (R_n = 2.0), 7% (R_n = 1.0), 14% (R_n = 0.75), 35% (R_n = 0.50), 70% (R_n = 0.25), 95% (R_n = 0.10) and 99% (R_n = 0.01) of the total prescribed horizontal displacement of u_x = 7 mm (Fig. 15a). The ratio B = u/u_x was similar (R_n ≤ 0.25) or slightly higher (R_n > 0.25) than for pure spheres with contact moments (Fig. 15b). The evolution of ratio B was hyperbolic in the range 0 ≤ R_n ≤ 2.0 and almost linear in the range 0 ≤ R_n ≤ 1.0 as in interface shear laboratory tests using the particle image velocimetry PIV [6].

The ratio between the interface grain rotation multiplied by the mean grain particle and interface grain slip A = ωd₅₀/u was almost the same during shearing (Fig. 16). The ratio A = ωd₅₀/u at the residual state systematically reduced with decreasing R_n (Table 3) (Fig. 17): A = 0.75 (R_n = 2.0), A = 0.65 (R_n = 1.0), A = 0.40 (R_n = 0.75), A = 0.20 (R_n = 0.50), A = 0.10 (R_n = 0.25), A = 0.02 (R_n = 0.10) and A = 0.01 (R_n = 0.01). This ratio ωd₅₀/u was approximately equal to 0.5R_n [(A = ωd₅₀)/u ≅ 0.5R_n] in contrast to pure spheres with contact moments, where [A = (ωd₅₀)/u ≅ R_n] for R_n ≤ 0.75 [15]. It was caused by greater grain rotations of clumps than of pure spheres with contact moments. Thus, the ratio A also depends on the grain shape.

4.2.3 Distribution of contact forces

Figure 18 demonstrates the 3D distribution of the normal contact forces in the entire granular specimen at the residual state (front view) for the different normalized interface roughness R_n.

Fig. 18

Distribution of contact normal forces in granular specimen at residual state for u_x = 7.0 mm from DEM with different normalized interface roughness parameter (e_o = 0.55 and σ_n = 100 kPa): A R_n = 1.0, B R_n = 0.50 and C R_n = 0.01 a) clumps of Fig. 2 and b) pure spheres with contact moments [15] (red colour corresponds to normal contact forces higher than mean value, maximum value of forces is 0.50 N) (color figure online)

The normal contact forces were higher at the left side wall where a passive state developed in contrast to an active state at the right lateral wall. The non-uniformity of contact forces increased with growing normalized interface roughness R_n. It was pronounced during shearing at the very rough and rough interface (R_n ≥ 0.50). It was higher for pure spheres with contact moments (Fig. 18) [15].

Figure 19 presents a polar distribution of contact forces in the x–y plane (mean amplitude and orientation to the horizontal) [24, 46] at the beginning of the test after a contracting process (settlement) and at the residual state for clumps. Initially, the vertical mean contact forces (with the orientation to the horizontal of 90°) dominated due to vertical pressure σ_n imposed on the specimen. As a sand–structure interface process proceeded, the direction of mean contact forces changed from a vertical to a diagonal as in other DEM results in [15, 24, 46]. Depending on the normalized interface roughness, the orientation of the mean contact forces to the horizontal at the residual state varied from 135° (R_n = 0.01) up to 140° (R_n = 0.25–2.0) for clumps and from 125° (R_n = 0.01) up to 160° (R_n = 0.75–2.0) for pure spheres with contact moments [15]. For rough and very rough surfaces, the final maximum diagonal contact forces were twice higher than the maximum initial vertical contact forces. The similar visible differences between clumps and spheres with contact moments regarding induced anisotropy of contact normal forces were also indicated in [71] for a triaxial compression test. They grew with an increase in the aspect ratio of clumps.

Fig. 19

Polar mean contact force distribution in granular specimen at beginning of test (black line) and at residual state (red line) for clumps of Fig. 2 from DEM with different normalized roughness parameter (e_o = 0.55 and σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 0.50, c) R_n = 0.10

The number of all grain contacts, expressed by the coordination number c in initially dense sand (R_n = 1.0 and σ_n = 100 kPa), is shown in Fig. 20 for clumps (Fig. 20a) and pure spheres with contact moments (Fig. 20b) [15]. The coordination number is an important measure to quantify the internal structure of granular materials.

Fig. 20

Evolution of coordination number c in initially dense sand (e₀ = 0.55) from DEM simulations (R_n = 1.0 and σ_n = 100 kPa) for: a) clumps of Fig. 2 and b) pure spheres with contact moments [15]

The coordination number c was higher (by 55–70%) in clumps than in pure spheres with contact moments (Fig. 20). The maximum value of c was c = 9.0 (clumps) and c = 5.25 (pure spheres) and the residual one was c = 7.2 (clumps) and c = 4.6 (pure spheres). The coordination number diminished with shear due to material dilatancy, reaching an asymptote at the residual state (Fig. 7B).

4.2.4 Distribution of stresses and couple stresses

The stresses of a single sphere were calculated as [33]

$$\sigma_{ij} = \frac{1}{{V^{p} }}\mathop \sum \limits_{c = 1}^{N} x_{i}^{c} f_{j}^{c} ,$$

(6)

where N is the number of the contact points, $x_{i}^{c}$ the ith component of branch vector jointing from the centre of mass of the particle to the contact point ‘c’, $f_{j}^{c}$ the jth component of the total force at the contact point ‘c’ and V^p the cell volume. The values of σ_ij were again calculated from an averaging cell of the size 5d₅₀ × 5d₅₀ × 1d₅₀ being moved by d₅₀.

Figures 21 and 22 show the distribution of the normal stresses σ_ii and shear stresses σ_ij across the normalized specimen height h/d₅₀ at the specimen mid-point at residual state for the horizontal displacement u_x = 7.0 mm for the different normalized interface roughness parameter R_n (σ₁₁ horizontal normal stress, σ₂₂ vertical normal stress, σ₁₂ horizontal shear stress, σ₂₁ vertical shear stress).

Fig. 21

Distribution of horizontal σ₁₂ (A) and vertical shear stress σ₂₁ (B) across normalized height h/d₅₀ for clumps at residual state at specimen mid-point with different normalized interface roughness parameter R_n (e_o = 0.55 and σ_n = 100 kPa): a) R_n = 2.0, b) R_n = 1.0, c) R_n = 0.75, d) R_n = 0.50, e) R_n = 0.25, f) R_n = 0.10 and g) R_n = 0.01

Fig. 22

Distribution of stress components (e_o = 0.55 and σ_n = 100 kPa) for clumps: horizontal normal stress σ₁₁ (a), vertical normal stress σ₂₂ (b), horizontal shear stress σ₁₂ (c) and vertical shear stress σ₂₁ (d) across normalized specimen height h/d₅₀ at residual state at specimen mid-point with different normalized interface roughness parameter R_n: A R_n = 1.0, B R_n = 0.50 and C R_n = 0.01

The stress distribution shapes were similar to those for pure spheres with contact moments [15]. The interface shear stresses σ₁₂ and σ₂₁ grew with increasing interface roughness and were slightly non-symmetric at the interface (σ₁₂≠ σ₁₂) (Fig. 21). The non-symmetry was higher by 5–10% than for pure spheres [15]. The distribution of the vertical normal stress σ₂₂ was almost the same across the specimen height in contrast to the horizontal normal stress σ₁₁ and shear stresses σ₁₂ and σ₂₁. The calculated stress distributions are in agreement with FEM results within micropolar continuum [52, 55, 60] and with other DEM results [29].

4.2.5 Distribution of grain forces at interface

First, the interface grain forces n and t and interface grain moments m along the grooves (Fig. 23) were calculated at the specimen mid-region at the residual state for u_x = 7.0 mm with the different normalized interface roughness parameter R_n. The moments were evaluated by multiplying the tangential and normal contact forces by their distance from the gravity centres r_t and r_n of clumps (Fig. 23). The values were computed from the area 5d₅₀ × 5d₅₀. Next, the forces and moments were transformed into a global system. Figure 24 presents the normal interface force n′ in the global vertical direction, tangential interface force t′ in the global horizontal direction, tangential interface moment m′ in the global horizontal direction and ratio between the tangential interface force and tangential interface moment ratio C = (t′ × d₅₀)/m′ in the global horizontal direction at the groove height in the granular segment.

Fig. 23

Normal and tangential interface forces n and t acting on inclined wall grooves (‘O’ clump centre, ‘C’ wall contact point, r_t and r_n lever arms of contact forces against point ‘O’)

Fig. 24

Relationships for clumps between normal interface force n′ in vertical direction (a), tangential interface force t′ in horizontal direction (b) (A), tangential interface moment m′ in horizontal direction (B) and ratio between tangential interface force and interface wall moment C = t′ × d₅₀/m′ in horizontal direction versus normalized interface roughness parameter R_n at grooves’ height (C) at residual state (e_o = 0.55 and σ_n = 100 kPa)

The distribution of the vertical normal wall force n′ was obviously constant due to the constant vertical pressure (Fig. 24Aa). The relationship between the horizontal tangential interface force t′ and normalized roughness parameter R_n was also bi-linear (Fig. 24Ab) as in the case of the residual interface friction angles φ_w.res in Fig. 8. The horizontal tangential interface moment m′ grew almost parabolically with increasing interface roughness 0 ≤ R_n ≤ 2.0 or linearly with increasing interface roughness 0 ≤ R_n ≤ 1.0 (Fig. 24B). The evolution of the ratio between the horizontal tangential interface force multiplied by the mean grain diameter force and horizontal tangential interface moment, C = (t′ × d₅₀)/m′, was similar to this for pure spheres with contact moments [15]. It changed in a hyperbolic way between 1.0 (R_n = 2) and 40 (R_n = 0.01) and between 1.0 (R_n = 2) and 8.0 (R_n = 0.10) (Fig. 24C). In the case of pure spheres with contact moments, it varied also in a hyperbolic way between 4.5 (R_n = 2) and 40 (R_n = 0.01) and between 4.5 (R_n = 2) and 7.0 (R_n = 0.10) [15].

5 Micropolar boundary conditions

Modelling of shear zones within continuum mechanics using FEM can be only performed with constitutive models enriched by a characteristic length of  micro-structure [52, 56, 57, 59]. Moreover, the constitutive models have to take the salient behaviour of granular materials into account by considering major influential factors such as the initial density, pressure sensitivity and mean grain diameter of soils [55]. The boundary conditions at interfaces with consideration of a characteristic length of microstructure were investigated following different enriched approaches, e.g. within micropolar elasto-plasticity [20, 52, 58], strain gradient elasto-plasticity [63] and micropolar hypoplasticity [53]. Some micropolar boundary conditions were proposed in [10, 11, 20, 60] for describing the interface roughness. In [60], the 2D boundary conditions along the horizontal rigid interface included two ratios connected to the normalized interface roughness (a ratio of the micropolar rotation multiplied by the mean grain diameter and the horizontal displacement and a ratio between the horizontal shear stress multiplied by the mean grain diameter and the horizontal couple stress). In [10, 11, 20], as a boundary condition in 2D analyses, the ratio between the slip and the total imposed displacement at the interface was assumed instead of the ratio between the horizontal shear stress multiplied by the mean grain diameter and the horizontal couple stress.

Based on present DEM simulation results, the following three boundary conditions at the interface, based on the ratios A = (ωd₅₀)/u (Fig. 17, Table 3), B = u/u_x (Fig. 15) and C = (t′ × d₅₀)/m′ (Fig. 24C) may be used in 2D conditions. Those ratios slightly depend on the particle shape. For the case of R_n ≥ 0.75, where all grain rotations ω tend to zero at the interface, the boundary condition can be simplified as ω = 0, u = 0 and v = 0 (no rotations and displacements) as in the experiment [52, 58].

The calculated ratios A (Fig. 17, Table 3), B (Fig. 15) and C (Fig. 24C) for clumps of Fig. 2 may be approximated yet in the range 0 ≤ R_n < 0.75 as

$$A = (\omega \times d_{50} )/u \cong 0.5R_{{\text{n}}} ,$$

(7)

$$B = u/u_{x} = 1 - R_{{\text{n}}} ,$$

(8)

$$C = \left( {t^{\prime } \times d_{50} } \right)/m^{\prime } = 1/R_{{\text{n}}} .$$

(9)

All ratios depend on a simple way on R_n only. The proposed boundary conditions may be prescribed in nodes of FE meshes along the interface in micropolar simulations (the particle rotation ω may be replaced by the micropolar (Cosserat) rotation ω^c [29, 58, 60]). The boundary conditions will be also checked in DEM interface simulations by assuming different grain shapes, grain size distributions and mean grain sizes.

6 Conclusions

Comprehensive DEM simulations of the sand–structure interface behaviour with varying interface roughness were performed for cohesionless sand that was simulated by non-symmetric convex granular clumps of the same shape (aspect ratio equal to 1.5). The results were confronted with similar simulation outcomes performed for pure spheres with contact moments [15] to show the effect of the particle shape on the interface resistance and shear localization. Interface boundary conditions within micropolar continua were proposed. The following major conclusions can be summarized from our simulations:

• As compared to spheres with contact moments, clumps provided in general due to a different particle shape the higher residual interface resistance, coordination numbers, particle rotations and slips, and the lower thickness of the shear zone at the interface, volume changes, orientation range of mean contact forces to the horizontal, ratios between the particle rotation multiplied by the mean grain diameter and slip along at the interface and ratios between the horizontal tangential interface force multiplied by the mean grain diameter force and horizontal tangential interface moment. The peak interface resistance solely was similar. The rolling resistance model was proved to be limited to capture particle shape effects.

• The normalized interface roughness had a huge influence on the mobilized interface friction angle and thickness of the interface shear zone. The interface resistance increased with increasing interface roughness. The peak and the residual interface friction angle grew with the raising normalized roughness parameter. The relationship between the peak/residual interface friction angle and normalized interface roughness was parabolic/bi-linear. The residual interface friction angle was by 3°–7° lower than for pure spheres with contact moments (R_n ≥ 0.25).

• The sand–structure interface resistance was strictly combined with the thickness of the shear zone at the interface wherein pronounced grain rotations occurred. The thickness of the shear zone at the interface increased with the growing normalized interface roughness parameter in a bi-linear way as the residual interface friction angle. The thickness of the interface shear zone expanded in a parabolic way from 1 × d₅₀ up to 12 × d₅₀ for R_n = 0.01–2.0. It was smaller by 15–40% than for pure spheres with contact moments (R_n ≥ 0.25).

• The coordination number was higher by 55–70% than for pure spheres with contact moments.

• For the very rough interface (R_n ≥ 0.75), the largest sphere rotation was located slightly above the interface (h/d₅₀ = 3–5) and for R_n ≤ 0.5 it was directly located at the interface where it diminished with the reduction of R_n. For R_n ≥ 0.75, the sphere rotations were approaching zero at the interface (the spheres were trapped in asperities). The largest rotation at the interface was higher by 30% than for pure spheres with contact moments (R_n ≥ 0.25).

• The ratio between the horizontal slip and total horizontal displacement along the interface decreased with increasing interface roughness. This ratio was similar (R_n ≤ 0.25) or slightly higher (R_n > 0.25) than for pure spheres with contact moments. The evolution was hyperbolic in the range 0 ≤ R_n ≤ 2.0 and almost linear in the range 0 ≤ R_n ≤ 1.0.

• The ratio between the interface grain rotation multiplied by the mean grain diameter and interface grain slip was almost the same during shearing at the interface. It systematically reduced with decreasing normalized interface roughness parameter. It was twice smaller as for pure spheres with contact moments.

• The evolution of the ratio between the horizontal tangential force and horizontal tangential moment at the interface changed in a hyperbolic way between 1.0 (R_n = 2) and 40 (R_n = 0.01) and between 1.0 (R_n = 2) and 8.0 (R_n = 0.10). The evolution shape was similar to this for pure spheres with contact moments.

• The non-uniformity of contact forces in granular specimens at the interface increased with the growing normalized interface roughness. It was lower than for pure spheres with contact moments. The orientation of mean contact forces to the horizontal at the residual state also grew with the increasing normalized interface roughness (from 135° up to 140°). This orientation range was lower than for pure spheres with contact moments (125°–160°).

• Three different relationships were proposed to describe the interface boundary conditions in micropolar continua. They included the ratio between the micropolar rotation multiplied by the mean grain diameter and slip along the interface, the ratio of the slip at the interface and total imposed horizontal displacement and the ratio between the horizontal tangential force multiplied by the mean grain diameter and horizontal tangential moment along the interface. All those ratios slightly depended on the particle shape. They were approximately related to the normalized interface roughness parameter only.