Large deformation dynamic analysis of progressive failure in layered clayey slopes under seismic loading using the particle finite element method

Abstract

This paper presents the failure analysis of layered clayey slopes with emphasis on the combined effect of the clay’s weakening behavior and the seismic loading using the particle finite element method (PFEM). Diverse failure mechanisms have been disclosed via the PFEM modelling when the strain-weakening behavior of clay is concerned. In contrast to a single layered slope exhibiting either a shallow or a deep failure mode, a layered slope may undergo both failure modes with a time interval in between. Seismic loadings also enlarge the scale of slope failure in clays with weakening behavior. The failure of a real layered slope (i.e. the 1988 Saint-Adelphe landslide, Canada) triggered by the Saguenay earthquake is also studied in this paper. The simulation results reveal that the choice of the strain-softening value controls the slip surface of the landslide and the amplification effect is important in the triggering of the landslide.

1 Introduction

Stability analysis of slopes in earthquakes has long been recognized as a challenging problem in geotechnical engineering. The simplest way to estimate the slope stability in earthquakes might be the limit-equilibrium method in which the seismic loading is introduced as a permanent body force. Known as pseudo-static analysis, this approach provides a factor of safety (FOS) to indicate if the slope is stable or not [34]. Despite its wide application in practice, the choice of seismic coefficient is empirical. Alternatively, a so-called permanent-displacement analysis method [26] can be adopted to compute the deformation of slopes during an earthquake. Notwithstanding its simplicity, the model can fairly predict the deformation of the slope if the geometry, soil properties and earthquake motions are reasonably predefined [39]. With the continuing development of numerical techniques, particularly the finite element method (FEM), sophisticated soil constitutive models capturing pronounced feature of soil behaviors can be applied in the simulations to predict the evolution of slopes subjected to seismic loadings [13].

Among soil features, the weakening feature of clays plays as a significant role in slope failure. As indicated in [5, 37, 48], if the weakening is not considered in the simulation an unstable slope may reach a new state of equilibrium after experiencing just a very limited movement, which does not agree with observations in many practical cases. Additionally, the failure surfaces obtained from analysis with and without the weakening behavior might also differ [36].

Despite numerous contributions to slope stability in earthquakes, most efforts were devoted to investigating the failure process [13] which is, to a large extent, owing to the limitation of the traditional FEM. Indeed, a large magnitude of change in geometry usually occurs in the post-failure process of a slope for which the traditional FEM cannot handle because of the severe mesh distortions and free-surface evolutions. More recent development of numerical techniques for large deformation analysis in geotechnics provides the possibility of simulating both the failure and post-failure stages. Representative numerical approaches of this capability include, but are not limited to, the Arbitrary Lagrangian–Eulerian (ALE) technique [8], the Coupled Eulerian–Lagrangian (CEL) method [12, 30], the Material Point Method (MPM) [32], the Particle Finite Element Method (PFEM) [27, 46, 48], and the Smooth Particle Hydrodynamics (SPH) [9, 23, 28, 38, 44, 45]. Recently, the CEL method has been adopted to investigate the large deformation behavior of clayey slopes under seismic loading with the weakening of clays being concerned [12].

In this paper, we focus on investigating the slope failure in layered clay of strain softening subjected to seismic loading. Owing to the low permeability of clays, the effects of the dissipation of pore water pressure are limited and thus the total stress analysis is performed which is in line with the studies for landslides in clays in [7, 12]. For comparison purpose, a two-layer slopes with and without strain softening are studied using static analysis to determine the corresponding FOS. Dynamic analysis of these slopes with the reduced strength is also carried out using the PFEM to predict the complete failure and post-failure evolutions. Additionally, the failure modes of the two-layer slope subjected to seismic loadings are studied and compared to the results from the strength reduction method. Finally, a case study of a landslide occurred in 1988 Saguenay earthquake is carried out.

The objectives of this study are four-fold which are: (i) presenting the failure pattern captured by static and dynamic analyses; (ii) investigating the role of strain-weakening in failure patterns; (iii) studying the effects of seismic loading acting on slope failures; and (iv) reconstructing a real clayey landslide controlled by seismic-weakening effects.

2 Particle finite element method based on mathematical programming

In the finite element analysis, computational domains are discretized using meshes in which shape functions are adopted for the interpolation of physical variables. Meshes of high quality are important to the accuracy and convergence of the finite element analysis. However, when modelling large deformation geotechnical problems using the traditional FEM, a large change of geometry inevitably leads to mesh distortions and severe free-surface evolutions. To circumvent these issues, a Lagrangian approach called the particle finite element method (PFEM) was proposed which treats mesh nodes as free particles that may separate from the domain they originally belong to [27]. To date, the PFEM or its variants [42, 48] have been applied to analyze a variety of large deformation problems in geotechnics such as free-surface flows [18], fluid–structure interaction [11], granular flows [6, 46], ground excavation [3], penetration problems [25], etc. Owing to its capability in treating arbitrarily large deformations, the PFEM has also been used for studying landslides with focuses on their final run-out distance [4, 31, 47]. Both failure and post-failure analyses can be conducted in the framework of the PFEM when using appropriate soil constitutive models. Applications of the PFEM to failure and post-failure analyses of homogeneous conceptual slope model can be found in [37, 48]. Its possibility for modelling more complicated cases, such as practical landslides in clays of high sensitivity [43, 49] and submarine landslides [50], has also been explored.

2.1 Governing equations

In this section, the equations governing the rate-independent elastoplastic plane-strain problem for slope instability analysis are presented. These equations include the momentum equilibrium equations, the strain–displacement relation, the constitutive equations and the boundary conditions, which are

(a) Momentum equilibrium equations

$$\nabla^{T}\varvec{\sigma}+ \varvec{b} = \rho \dot{\varvec{v}}$$

(1)

(b) Strain–displacement relation

$$\varvec{\varepsilon}= \nabla {\mathbf{u}}$$

(2)

(c) Boundary conditions

$$\varvec{N\sigma } = \varvec{t}$$

(3a)

$$\varvec{u} = \varvec{u}^{\text{p}}$$

(3b)

(d) Constitutive equations

$$\begin{aligned} & \Delta\varvec{\varepsilon}= \Delta\varvec{\varepsilon}^{\text{e}} + \Delta\varvec{\varepsilon}^{\text{p}} \\ & \Delta\varvec{\varepsilon}^{\text{e}} = {\mathbb{C}}\Delta\varvec{\sigma},\Delta\varvec{\varepsilon}^{\text{p}} = \Delta \lambda \nabla F\left(\varvec{\sigma}\right) \\ & \lambda \ge 0,\Delta \lambda F = 0 \\ \end{aligned}$$

(4a)

Tresca yield criterion:

$$F(\varvec{\sigma}) = \sqrt {\left( {\sigma_{xx} - \sigma_{yy} } \right)^{2} + 4\sigma_{xy}^{2} } - 2c \le 0$$

(4b)

where $\varvec{\sigma}$ is the stress; b is the body force; $\rho$ is the density; v is the velocity; $\varvec{\varepsilon}$ is the strain consisting of the elastic component $\varvec{\varepsilon}^{\text{e}}$ and the plastic component $\varvec{\varepsilon}^{\text{p}}$; u is the displacement; $\varvec{N} = \left( {n_{x} , 0, 0, n_{y} ; 0, n_{y} , 0, n_{x} } \right)$ is the outward unit vector of the boundary; t is the prescribed traction; $\varvec{u}^{\text{p}}$ is the prescribed displacement; $F(\varvec{\sigma})$ is the yield function; ${\mathbb{C}}$ is the elastic compliance matrix; $\lambda$ is the plastic multiplier; $\nabla$ is the nabla operator; and $\Delta$ represents increment; c is the undrained cohesion.

2.2 Discretization and mathematical programming problem

The θ-method is introduced for the time integration of Eq. (1) that is:

$$\nabla^{T} \left[ {\theta_{1}\varvec{\sigma}_{n + 1} + \left( {1 - \theta_{1} } \right)\varvec{\sigma}_{n} } \right] + \varvec{b} = \rho \frac{{\varvec{v}_{n + 1} - \varvec{v}_{n} }}{\Delta t}$$

(5a)

$$\theta_{2} \varvec{v}_{n + 1} + \left( {1 - \theta_{2} } \right)\varvec{v}_{n} = \frac{{\varvec{u}_{n + 1} - \varvec{u}_{n} }}{\Delta t}$$

(5b)

where θ₁ and θ₂ are coefficients and subscripts n and n + 1 represent the known and unknown states, respectively. Substituting Eq. (5b) into (5a) leads to:

$$\nabla^{T}\varvec{\sigma}_{n + 1} + \frac{{\left( {1 - \theta_{1} } \right)}}{{\theta_{1} }}\nabla^{T}\varvec{\sigma}_{n} + \tilde{\varvec{b}} =\varvec{\gamma}_{n + 1}$$

(6a)

in which

$$\tilde{\rho } = \frac{\rho }{{\theta_{1} \theta_{2} }}, \tilde{\varvec{b}} = \frac{1}{{\theta_{1} }}\varvec{b} + \tilde{\rho }\frac{{\varvec{v}_{n} }}{\Delta t},\varvec{\gamma}_{n + 1} = \tilde{\rho }\frac{{\Delta \varvec{u}}}{{\Delta t^{2} }}$$

(6b)

The boundary condition in (3a) is discretized in the same manner which is

$$\varvec{N\sigma }_{n + 1} + \frac{{1 - \theta_{1} }}{{\theta_{1} }}\varvec{N\sigma }_{n} = \tilde{\varvec{t}}\quad {\text{with}}\quad \tilde{\varvec{t}} = \frac{1}{{\theta_{1} }}\varvec{t}$$

(7)

Both θ₁ and θ₂ are set to be 1 in our simulation implying the Backward Euler scheme.

The mixed triangular element (see Fig. 1) is utilized for the space discretization of the stress σ, the displacement u and the inertial force $\varvec{\gamma}$:

$$\varvec{\sigma}\approx \varvec{N}_{\sigma } \hat{\varvec{\sigma }}; \varvec{u} \approx \varvec{N}_{u} \hat{\varvec{u}};\varvec{\gamma}\approx \varvec{N}_{\gamma } \hat{\varvec{\gamma }}$$

(8)

in which $\varvec{N}_{\sigma }$, $\varvec{N}_{u}$ and $\varvec{N}_{\gamma }$ are the matrices consisting of the corresponding shape functions. The displacement and stress fields are interpolated using quadratic and linear shape functions, respectively. Hence the proposed mixed element dose not suffer from volumetric locking when modelling incompressible materials which has been demonstrated in [50].

Fig. 1

The mixed isotropic triangular element utilized in the simulation [17]

According to [46], after discretized using the approximation in (8) the governing equations can be reformulated as an equivalent mathematical programming problem:

$$_{{\left( {\hat{\varvec{\sigma }},\hat{\varvec{\gamma }}} \right)_{n + 1} }}^{\hbox{max} } - \frac{1}{2}\Delta \hat{\varvec{\sigma }}^{T} \varvec{C}\Delta \hat{\varvec{\sigma }} - \frac{1}{2}\Delta t^{2} \hat{\varvec{\gamma }}_{n + 1}^{T} \varvec{D}\hat{\varvec{\gamma }}_{n + 1}$$

(9a)

$${\text{subject to }}\quad F\left( {\hat{\varvec{\sigma }}_{n + 1} } \right) \le 0$$

(9b)

$$\varvec{B}^{T} \hat{\varvec{\sigma }}_{n + 1} + \varvec{A}^{T} \hat{\varvec{\gamma }}_{n + 1} = \tilde{\varvec{f}}$$

(9c)

where

$$\varvec{B} = \mathop \smallint \limits_{V}^{ } \varvec{N}_{\sigma }^{T} \varvec{B}_{u} dV,\varvec{B}_{u} = \nabla \varvec{N}_{u}$$

(10a)

$$\varvec{C} = \mathop \smallint \limits_{V}^{ } \varvec{N}_{\sigma }^{T} {\mathbb{C}}\varvec{N}_{\sigma } dV$$

(10b)

$$\varvec{D} = \mathop \smallint \limits_{V}^{ } \varvec{N}_{\gamma }^{T} \tilde{\rho }^{ - 1} \varvec{N}_{\gamma } dV$$

(10c)

$$\varvec{A} = \mathop \smallint \limits_{V}^{ } \varvec{N}_{\gamma }^{T} \varvec{N}_{u} dV$$

(10d)

$$\tilde{\varvec{f}} = \mathop \smallint \limits_{V}^{\varvec{ }} \varvec{N}_{u}^{T} \tilde{\varvec{b}}dV + \mathop \smallint \limits_{S}^{\varvec{ }} \varvec{N}_{u}^{T} \tilde{\varvec{t}}dS - \frac{{\left( {1 - \theta_{1} } \right)}}{{\theta_{1} }}\varvec{B}^{T} \hat{\varvec{\sigma }}_{n}$$

(10e)

The above maximization problem is submitted to available optimization engines for solutions following [37]. Such a solution strategy is called the finite element method in mathematical programming. A typical advantage of this solution strategy as indicated in [16] is the natural treatment of some typical failure criteria with singularity. For example, the Mohr–Coulomb yield function for plane-strain problems can be casted as a standard cone and dealt with straightforward in second-order cone programming [16]. The general 3D Mohr–Coulomb yield function can also be handled without difficulties by solving the problem in semidefinite programming following [24]. This is in contrast to the treatment of such yield criteria in the traditional Newton–Raphson based FEM in which a special treatment at the singular point of the yield function is required.

2.3 Particle finite element technique

The PFEM used in this study is the one developed in [46] in which the operations of re-meshing and variable mapping have to be performed due to the history-dependency of the concerned geomaterials. In a given time interval $\left[ {t_{n} ,t_{n + 1} } \right]$, the basic steps of the PFEM are summarized as follows (see also Fig. 2):

Fig. 2

Basic steps of the particle finite element method

• 1. Update the coordinates of mesh nodes using the solved incremental displacement and obtain a cloud of particles, $C_{n + 1}$ (Fig. 2a, b);

• 2. Apply the α-shape method to recognize the new computational domain $\varOmega_{n + 1}$ based on the position of particles $C_{n + 1}$ (Fig. 2c);

• 3. Use Delaunay triangulation to discretize $\varOmega_{n + 1}$ and obtain a new mesh $M_{n + 1}$ (Fig. 2d);

• 4. Map the history variables from the old mesh $M_{n}$ to the new mesh $M_{n + 1}$ using the Unique Element Method;

• 5. Conduct the incremental finite element analysis on the new mesh $M_{n + 1}$ and loop the above process for all time steps.

Although the governing equations applied in the presented PFEM is based on infinitesimal strain theory, numerous studies have shown the possibility of using a series of incremental analyses based on the infinitesimal strain theory for analyzing problems with large deformations. A typical example is the sequential limit analysis that has been used successfully for modelling truss systems, metal materials and pipe-soil interactions with large changes in geometry [15, 20, 41]. This idea has also been adopted in the development of the so-called Remeshing and Interpolation Technique with Small Strain (RITSS) with successes in various large deformation geotechnical problems [35]. The PFEM technique used in this study has also been applied to numerous challenging large deformation problems such as the breakage of a water dam, the granular column collapse, the underwater granular flow and induced waves [50] for which good agreements between the simulation results and the lab testing data are obtained.

3 Conceptual model

A two-layer slope in purely cohesive soils is a simplified conceptual model for widely found natural clayey slopes [12]. Previous studies on layered clayey slopes were carried out with major focuses on their stability [10, 29] where influences of control parameters such as geometries, soil properties, strength ratios on its stability condition and failure mechanisms are investigated. In this paper, the PFEM is adopted to investigate the slope failures in layered clay with special attentions paid on the effects of the ratio of material strengths and the material weakening on the failure mechanism and evolution process of layered clayey slopes subjected to seismic loadings (Fig. 3).

Fig. 3

An undrained slope model discretized using 10,013 triangular elements with geometry being H = 18 m, D = 2H and tan β = 0.5 and material parameters being elastic modulus E = 100 MPa, Poisson’s ratio υ = 0.3, density ρ = 2000 kg/m³ and c₁ = 60 kPa that are in line with those in [10]. In lateral boundaries only vertical displacements are allowed and the bottom is fully fixed

3.1 Static stability analysis (Static analysis)

Firstly, the static stability analysis is performed through the static module of the code, in which the shear strength reduction method and binary algorithm are implemented to approach the critical state [37]. By means of the static finite element analysis, the transition from a deep failure pattern to a shallow failure pattern is obtained from our simulations by increasing the strength ratio of the two layers (c₂/c₁). Figure 4 shows the corresponding failure mechanism for each case where the factor of safety (FOS) are also illustrated.

Fig. 4

Identified slip surfaces through normalized equivalent plastic strain (normalized with respect to the maximum value and values greater than 1% are plotted) for five cases: a c₂/c₁ = 1; b c₂/c₁ = 1.2; c c₂/c₁ = 1.4; d c₂/c₁ = 1.6; e c₂/c₁ = 2

For the homogeneous case shown in Fig. 4a, a clear deep rotational slip surface is generated which is similar to the slip surface in case of c₂/c₁ = 1.2 in Fig. 4b. With the increase of c₂/c₁, the plastic strain accumulates at the interface between two layers, leading to an incomplete potential shallow slip surface in Fig. 4c. When c₂/c₁ is further increased to 1.6 and 2, the shallow failure pattern dominates and the FOS tends to be independent of the strength of the lower clay layer. According to these observations, it can be concluded that in a two-layer undrained clayey slope two distinct potential slip surfaces, controlled by the strength ratio, may form during the initiation stage which coincides with the findings in [10].

3.2 Large deformation analysis (PFEM analysis)

Although numerous efforts have been devoted to investigating the failure of two-layer clayey slopes, they are limited to the small-deformation analysis under quasi-static conditions. For slopes in clay with strain-softening behavior or subjected to seismic loading, the failure mechanism is more complicated and the slip surface obtained from static analysis cannot reflect the entire scenario. For example, a series of slope failure may occur in slopes in sensitive clay leading to unexpected retrogression distance as shown in [21], which cannot be captured in small-deformation static analysis.

In this part, the PFEM is adopted for large-deformation dynamic failure analysis of the two-layer clayey slope. To trigger the failure, the shear strength is reduced by a Reduction Factor (RF) such that the reduced cohesion is c’ = c/RF. Cases for clay with and without strain-softening are considered in this part and the adaptive time step is used to ensure that the maximum incremental displacement is smaller than the edge length of the element.

3.2.1 Without strain-softening

Figure 5 illustrates the failure patterns for the two-layer slope in clay without strain softening. The run-out distance of the slope failure is relatively small at critical state (Fig. 5a, c). Although the increase of RF contributes to its mobility (Fig. 5 (b, d)), the magnitude of displacement is still very limited. For the case c₂/c₁ = 1.4, the deep failure pattern is observed and the slide moves along the deep slip surface identified by the static analysis (Fig. 5 (e, f)). For c₂/c₁ = 1.6, the shallow slip surface obtained from the dynamic analysis agrees with that from the static analysis. However, a deep movement is also observed (Fig. 5c). From Fig. 5g, it can be seen that the deep slip surface is not fully developed. However, this deep movement causes a deep failure mode when RF increases as shown in Fig. 5d, h.

Fig. 5

Final slope profiles with the distributions of displacement and the normalized equivalent plastic strain: a–d displacement; e–h equivalent plastic strain normalized with respect to the maximum value. Black and red dash lines are the identified deep and shallow slip surfaces through static analysis, respectively

With strain-softening

It is known that the degradation from peak to residual strength induces the progressive failure in sensitive clays, and contributes to the high mobility of large landslides [21]. This progressive failure has been successfully captured through large deformation analysis with the inclusion of a strain-softening model [7]. In this part, numerical simulations are carried out to investigate the influence of the strain-softening on the failure of the two-layer slope. To this end, a strain-softening model where the cohesion drops with the increase of the accumulated deviatoric plastic strain in a linear form [36] shown in Fig. 6 is implemented and applied to both clay layers in the PFEM framework.

Fig. 6

Variation of cohesion c with deviatoric plastic strain k. Subscripts p and r represent peak and residual states respectively. $k = \smallint \dot{k}dt$. $\dot{k} = \sqrt {0.5\dot{e}_{ij}^{p} \dot{e}_{ij}^{p} }$ and $\dot{e}_{ij}^{p}$ is the rate of deviatoric plastic strain tensor given by $\dot{e}_{ij}^{p} = \dot{\varepsilon }_{ij}^{p} - \frac{1}{3}\dot{\varepsilon }_{kk}^{p} \delta_{ij}$, in which $\delta_{ij}$ is Kronecker’s delta and $\dot{\varepsilon }_{ij}^{p}$ is the rate of the plastic strain tensor (k_p = 0.1, k_r = 1 and c_p/c_r = 5 in this section)

Case 1

c₂/c₁ = 1.4

Figure 7 shows the failure mode of the two-layer slope with c₂/c₁ = 1.4. When clay sensitivity is considered, the slope first fails in a mode of deep rotation which is similar to that from static analysis without considering strain-softening behavior. Afterward, a small retrogressive failure occurs when the clay involved in the first failure propagates forward. It is clear, although the static analysis captures the first deep rotational failure mechanism, it cannot predict this sequential retrogressive failure pattern.

Fig. 7

Contours at four time instants for c₂/c₁ = 1.4 and RF = FOS with the strain-softening model: a–d velocity; e–h equivalent plastic strain. Dash lines are the identified deep slip surfaces through static analysis

Case 2

c₂/c₁ = 1.6

The failure depicted in Fig. 8 is in a shallow pattern which is in contrast to the deep rotational failure observed for c₂/c₁ = 1.4 (Fig. 7). Nevertheless, in this case the initial failure is also followed by a retrogressive failure as in the case of c₂/c₁ = 1.4. Notably, an incomplete deep slip surface is generated (Fig. 8a), which however, does not evolve into a global failure as shown in Fig. 8c–d.

Fig. 8

Contours at four time instants for c₂/c₁ = 1.6 and RF = FOS with the strain-softening model: a—d velocity; e–h equivalent plastic strain. Dash lines are the identified shallow slip surfaces through static analysis

Increasing RF from FOS to 1.15 FOS, the incomplete deep failure shown in Figs. 8a and 9a evolves into a deep failure mode. It is clear that the shallow slide moves faster than the deep one in Fig. 9b, c and they further merge and move as a whole as displayed in Fig. 9d.

Fig. 9

Contours at four time instants for c₂/c₁ = 1.6 and RF = 1.15 FOS with the strain-softening model: a–d velocity; e–h equivalent plastic strain. Black and red dash lines are the identified slip surfaces for deep and shallow failure modes through static analysis, respectively

Compared with the cases without the strain-softening behavior, a progressive failure with higher mobility is observed for all cases with the strain-softening behavior leading to complex failure modes. Obviously, the classical static analysis fails in capturing these failures, though it can predict the first failure. Apart from the retrogressive behavior in softening clays, the dynamic analysis also shows that a mixture of shallow and deep failure mechanisms may co-exist in a clayey slope, which is also indicated in [10].

4 Seismic loading

The direct action on a slope by an earthquake consists of the stresses caused by the seismic ground motion. It has been acknowledged that the dynamic response of a slope to seismic motion is controlled by various factors that can amplify and de-amplify signals, including the excitation signal, local topography, material property, and discontinuities [40]. The accurate wave propagation modelling requires high quality mesh, efficient artificial boundary conditions, smaller time step and suitable wave in-put methods. For the landside modelling composed of pre-&post-failure processes, it is hard to implement the true wave propagation due to the existence of discontinuities. A practical way is to treat the seismic loading as an inertial force to the slope. More specifically, body forces are added by two terms b_x and b_y, in which b_x = ρa_x, b_y = ρa_y, and a_x and a_y are prescribed accelerations in horizontal and vertical directions for two-dimensional cases. To investigate the two-layer slope subjected to seismic loadings, the seismic signal of the 1940 El Centro earthquake obtained from COSMOS virtual data center [2] shown in Fig. 10 is used. A hyperbolic distribution of seismic coefficient is introduced to consider the amplification from the base to the ground [14]:

$$a_{h} = a\left( {1 + 2\left( {h/{\text{D}}} \right)^{2} } \right)$$

(11)

where a_h is the coefficient at height h measured from base, a is the prescribed acceleration, and D is the total height of the model.

Fig. 10

1940 EI Centro seismic signal (data from COSMOS [2])

The EI Centro signal is treated as horizontal body force in this section and boundary condition is set the same as that in Sect. 3. The used time step is Δt = 0.02 s in line with the time interval of the used EI Centro signal.

Case 1

c₂/c₁ = 1.05

Because the slope is unstable when c₂ = c₁ = 60 kPa, the case with a small strength ratio c₂/c₁ = 1.05 (FOS = 1.01) is adopted here. Subjected to the seismic loading, the failure is still in a deep mode (Fig. 11), however the slip surface does not coincide with the one predicted by the static analysis. Failure occurs first at the bottom of the slope (Fig. 11a) and then propagates towards the ground (Fig. 11b) forming a global failure eventually (Fig. 11c). Due to the complexity in seismic loading and strain-softening behavior, the progressive failure in seismic clayey slope is more complex, leading to the formation of several blocks. The deposit shown in Fig. 11c is not the final profile of the landslide. The sequential failure process after t = 8.0 s is similar to that discussed in [49]. For instance, the newly formed back scarp resulting from the previous collapse may fail as well with the disturbed geomaterials migrating forward until a stable back scarp is formed which is termed as the retrogressive landslide.

Fig. 11

Failure surfaces depicted by the equivalent plastic strain at three instants for c₂/c₁ = 1.05. Black dash lines are the deep failure surfaces predicted by static analysis

Case 2

c₂/c₁ = 1.4

The progressive failure for c₂/c₁ = 1.4 shown in Fig. 12 is similar to the one depicted in Fig. 11. From Fig. 12b, the deep failure is also larger than the predicted one by static analysis. The global failure appears at t = 9 s in this case, which is later than in the case of c₂/c₁ = 1.05 (t = 8 s). Afterward, several new blocks form near the global deep failure, as shown in Fig. 12c.

Fig. 12

Failure surfaces depicted by equivalent plastic strain at three instants for c₂/c₁ = 1.4. Black dash lines are the deep failure surfaces predicted by static analysis

Case 3

c₂/c₁ = 1.6

As for the case c₂/c₁ = 1.6, a mixture of shallow and deep failure mechanisms is observed when subjected to seismic loading (Fig. 13). It is notable that an apparent time delay between the first shallow failure (Fig. 13a) and the subsequent deep failure (Fig. 13c) is observed in the simulation. The shallow failure is first observed, coinciding with the predicted critical failure mode by static analysis. After more than 10 s, the deep movement (as shown in Fig. 5c, d, Figs. 8a and 9a) forms a large deep failure, due to the impact of the seismic loading and the softening. This indicates that a huge landslide may take place after a series of shallow failures for a slope of large strength ratios in an earthquake event. The combination of seismic loadings and strain-softening leads to a considerable change in the scale and evolution of the slope failure.

Fig. 13

Failure surfaces depicted by the equivalent plastic strain at three instants for c₂/c₁ = 1.6. Red dash lines are the shallow failure surfaces predicted by static analysis

5 Case study: 1988 Saint-Adelphe landslide

Based on the numerical investigations on the conceptual slope model, it has been found that weakening effects play a critical role in both the failure patterns and scales. With additional seismic loadings, the failure initiates from the vulnerable section and propagates to the ground, leading to global slip surfaces. In this section, the Saint-Adelphe landslide, Canada, occurred on November 25th, 1988, after the Saguenay earthquake with magnitude of 5.9, is studied using the present modelling technique. It was speculated that the landslide was caused by an undrained failure with the strength loss in the cohesive soils involved in the slide [33]. Geotechnical tests and numerical studies indicated that the implementation of strain-weakening model may result in a reasonable back analysis of the progressive failure of the slope [1].

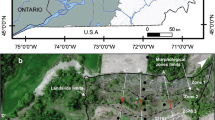
In this study the analysis is performed on the A–A section of the slope as shown in Fig. 14, which is the same section analyzed in [1]. Differing from numerical analyses in [1], the strain-weakening behavior is considered here in conjunction with dynamic analysis to highlight the role of weakening effects under seismic loadings.

Fig. 14

A-A section of the Saint-Adelphe landslide: upper from [1]; lower is the discretized finite elements with colorful polygons representing the layers. This is the central part of the model adopted in numerical simulation, which is 300 m long

The whole model is composed of 6554 elements (the length of the model is 300 m, that is the lateral extension of Fig. 14), and the boundary condition is in line with the one in Sect. 4. The cohesion of clay decreases from 50 kPa at the top of stiff layer to 18 kPa at the top of soft clay layer, and then gradually increases with the depth by 3 kPa/m in the soft clay layer. The cohesion of silty sand layer is set as 100 kPa. Other material parameters are: density is 1700 kg/m³, elastic modulus is 20 MPa, and Poisson’s ratio is 0.487 [1].

The EI Centro seismic waveform is used to represent inertial effects since the ground motion near the position of the landslide was not monitored during the 1988 Saguenay earthquake. The amplitude of the EI Centro signal in Fig. 10 is re-scaled by a factor of A_p = 1/3 to fit the estimated peak acceleration 0.1 g in [1]. The seismic loading is excited as horizontal and vertical body force terms (vertical is set as half of horizontal force), distributed as Eq. (11). Numerical simulations are conducted to study the response of the slope under 50 s excitation and the time step is set as 0.02 s.

(1) Degradation of cohesion: Δc_p

To account for the strain-softening behavior the cohesion is degraded with plastic shear strain ($\varepsilon_{xy}^{p}$) in soft clay layer which is computed at each time step

$$c_{\text{r}} = c_{\text{p}} - \varepsilon_{xy}^{p} \Delta c_{\text{p}}$$

(12)

where c_p and c_r are peak and residual values of the cohesion, respectively.

According to experimental tests the measured value of Δc_p is 0.5 kPa/%, while the value from back-analysis is usually shown more brittle than that from the shear tests [1, 22]. Three values of Δc_p (Δc_p = 0.6 kPa/%, 0.8 kPa/%, and 1 kPa/%) are adopted here to investigate the influence of Δc_p on the slip surface.

From Fig. 15, it appears that the case with Δc_p = 1 kPa/% provides a reasonable slip surface compared to the observed data. As can be seen in Fig. 15a, for Δc_p = 0.6 kPa/% a small magnitude of the plastic strain accumulates near the toe of the slope, while no clear slip surface is generated. The slip surface becomes clearer with the increase of Δc_p. Other predicted slip surfaces are from [1], where static drained analysis, dynamic undrained analysis, and post-seismic analysis with strain-softening model (Δc_p = 0.8 kPa/%) were performed. The slip surface from our simulation agrees well with the observed one as shown in Fig. 15c, suggesting that both the seismic loading and the strain-weakening contribute to the initiation of the landslide.

Fig. 15

Contour of equivalent plastic strain from dynamic analysis compared with the observed slip surface and numerical results from [1] for three cases: Δc_p = 0.6, 0.8 and 1 kPa/%

(2) Amplitude of signal: A_p = 1

Another simulation is conducted to investigate the slip surface with a larger amplitude, since the slip surface in Fig. 15a is incomplete. The factor of amplitude A_p is set as 1 here, instead of 1/3 as in the previous simulations. As shown in Fig. 16, the increase of amplitude causes a larger plastic zone. It is notable that the slip surface still cannot be observed for Δc_p = 0.6 kPa/ indicating that the failure of the landslide is significantly controlled by weakening effects.

Fig. 16

Contour of the equivalent plastic strain from dynamic analysis compared with the observed slip surface and numerical results from [1] for two cases: Δc_p = 0.6 and 1 kPa/%

(3) Back analysis for run-out distance (A_p = 1/3)

The generation of slip surface is properly captured with the assumption that the value of Δc_p is slightly higher than the experimental value. The slip surface forms from the accumulated plastic strain at toe to the crest and finally leads to the failure of landslide with 1 m runout distance (Fig. 17a), which is smaller than the reported value (8–10 m) [19]. Increasing the value of Δc_p to 2 kPa/%, the runout distance reaches to 3 m, which indicates that the mobility of the failed mass is controlled by strain-softening behavior. It can be inferred that the real material during seismic shaking might be even weaker, or additional factors after earthquake activate its mobility.

Fig. 17

Final profile of landslide with displacement distribution for Δc_p = 1 kPa/% and Δc_p = 2 kPa/%

(4) Amplification effects

The distribution of acceleration in Eq. (11) was proposed in [14] to improve the performance of the pseudo-static approach applied to seismic stability analysis of slopes, and it is used here to include the amplification effects in the simulations. An investigation is conducted to present the failure mechanism without this hyperbolic distribution (acceleration is uniformly distributed and A_p = 1/3).

As can be seen in Fig. 18, two large values of Δc_p are used and a small scale local failure has been captured with maximum displacement being 0.1 and 4 m, respectively. The failure is different from the observed one, and this indicates that the amplification of the acceleration is important to the failure mechanism in this landslide.

Fig. 18

Final profiles of the landslide with displacement distribution for Δc_p = 2 and 4 kPa/%

6 Conclusion

Failures of clayey slopes are usually complicated and are significantly controlled by the change of strength. As a representative model, the study of layered clayey slopes has attracted great attention from researchers, but most studies were conducted under the assumption of limited deformation. A particle finite element code is used in this paper to investigate the inertial-weakening effects on the failure mechanisms of clayey slopes where large deformations are expected to occur. The conclusions drawn from this study are as follows:

(i) The failure of a two-layer clayey slope can transit from a deep to a shallow mode as predicted by static analysis and the failure pattern is sensitive to the strength ratio of the two layers.

(ii) According to the dynamic analysis without strain-softening, the slide mainly moves along the slip surface identified by static analysis. For the case that is predicted as a shallow failure in static analysis, a sliding movement along deep slip surface is also observed. This indicates that a complete deep failure may form during dynamic evolution of the slope.

(iii) The inclusion of strain-softening behavior leads to the progressive failure in clays and retrogressive failure is observed in all cases. The mass involved in the first failure in all cases moves along the identified slip surface from the static analysis. A mixture mechanism of shallow and deep failure patterns is observed for the case c₂/c₁ = 1.6, when material is reduced by a value larger than the FOS.

(iv) With additional seismic loadings, it is found that the first failure is nearly in line with the one provided by the static analysis. The combination of seismic loadings and strain softening enlarges the scale of failure and causes the formation of more sliding blocks. A time delay between the shallow failure and the deep failure has been observed indicating that a huge catastrophic landslide in a deep failure pattern may occur after a shallow failure in earthquakes.

(v) A case study on the 1988 Saint-Adelphe landslide shows that the choice of strain-softening parameter affects the slip surface, though the same rotational mechanism is found. The amplification is important when generating the seismic loadings and the inclusion of a simplified hyperbolic form of acceleration distribution provides a more reasonable failure surface.

(vi) The transition from failure to post-failure in real landslides is complex, and current numerical simulations are incapable to well describe it. More efforts including field surveys and experimental tests should be conducted to understand the physical process. For the studied 1988 Saint-Adelphe landslide, the displacement and post-failure behavior are not well described though slip surface is well reproduced.

The present study on the simplified layered clayey slopes shows that the use of the classical static analysis is not able to predict failure types well. The dynamic analysis using the PFEM is more suitable for assessing the evolution of slope failure when the clay has strain softening behavior in an earthquake. Nevertheless, it should also be stressed that more efforts are required for reasonable considerations of the seismic wave propagation and the soil behaviors.