Modeling of the effects of weakness planes in rock masses on the stability of tunnels using an equivalent continuum and damage model

Abstract

This paper proposes an equivalent continuum model to describe the mechanical behavior of transversely isotropic rocks. In this model, the transverse isotropy of deformation and strength was achieved based on the Mohr–Coulomb and maximum tensile-stress criteria, and the damage was captured by adopting a statistical damage evolution rule. The application of the model is verified through numerical simulation of conventional triaxial tests. The model is then used to reveal the non-uniform mechanical response of the surrounding rock and the secondary lining for a tunnel situated in a weak layered rock mass. The results show that: (1) The proposed model can capture the transverse isotropy in deformation and strength of rocks, and the proposed damage formulation can represent the deterioration and degree of failure of rocks; (2) The fracturing pattern, failure strength and stress–strain curves obtained from the proposed model agree well with test results for three typical rocks with different directional variations in strength; (3) The damage distribution based on the proposed model can identify the failure of layered rock mass; and (4) The damage zones of the surrounding rock and the loads on the secondary lining after tunnel excavation show distinctly asymmetric behavior, that is, the damaged zones are concentrated in the tunnel direction normal to the weak planes, and the positive bending moment and larger axial force are parallel and vertical to the weak planes, respectively.

Appendices

Appendix I: Formulation of stiffness matrix in the global coordinate

The stiffness matrix in the global coordinate $[C]$ is expressed as

$$[C] = [Q][C^{{\prime}} ][Q]^{T}$$

(I.1)

where $[Q]$ is the transformation matrix defined as follows:

$$\begin{aligned}&[Q] \\=& \left[ {\begin{array}{*{20}c} {l_{1}^{2} } & {m_{1}^{2} } & {n_{1}^{2} } & {2m_{1} n_{1} } & {2n_{1} l_{1} } & {2l_{1} m_{1} } \\ {l_{2}^{2} } & {m_{2}^{2} } & {n_{2}^{2} } & {2m_{2} n_{2} } & {2n_{2} l_{2} } & {2l_{2} m_{2} } \\ {l_{3}^{2} } & {m_{3}^{2} } & {n_{3}^{2} } & {2m_{3} n_{3} } & {2n_{3} l_{3} } & {2l_{3} m_{3} } \\ {l_{2} l_{3} } & {m_{2} m_{3} } & {n_{2} n_{3} } & {m_{2} n_{3} + m_{3} n_{2} } & {n_{2} l_{3} + n_{3} l_{2} } & {l_{2} m_{3} + l_{3} m_{2} } \\ {l_{3} l_{1} } & {m_{3} m_{1} } & {n_{3} n_{1} } & {m_{3} n_{1} + m_{1} n_{3} } & {n_{3} l_{1} + n_{1} l_{3} } & {l_{3} m_{1} + l_{1} m_{3} } \\ {l_{1} l_{2} } & {m_{1} m_{2} } & {n_{1} n_{2} } & {m_{1} n_{2} + m_{2} n_{1} } & {n_{1} l_{2} + n_{2} l_{1} } & {l_{1} m_{2} + l_{2} m_{1} } \\ \end{array} } \right] \end{aligned}$$

(I.2)

where l_i, m_i and n_i (i = 1,2,3) are the directional cosines of axis x^’, y^’ and z^’, respectively. The matrix of directional cosines [R] is

$$[R] = \left[ {\begin{array}{*{20}c} {l_{1} } & {m_{1} } & {n_{1} } \\ {l_{2} } & {m_{2} } & {n_{2} } \\ {l_{3} } & {m_{3} } & {n_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin \alpha \cos \beta } & {\cos \alpha \cos \beta } & { - \sin \beta } \\ { - \cos \alpha } & {\sin \alpha } & 0 \\ {\sin \alpha \sin \beta } & {\cos \alpha \sin \beta } & {\cos \beta } \\ \end{array} } \right]$$

(I.3)

where α and β are the dip direction and dip angle of weak planes, respectively.

Thus, final form of the stiffness matrix [C] is:

$$[C] = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & {C_{14} } & {C_{15} } & {C_{16} } \\ {C_{21} } & {C_{22} } & {C_{23} } & {C_{24} } & {C_{25} } & {C_{26} } \\ {C_{31} } & {C_{32} } & {C_{33} } & {C_{34} } & {C_{35} } & {C_{36} } \\ {C_{41} } & {C_{42} } & {C_{43} } & {C_{44} } & {C_{45} } & {C_{46} } \\ {C_{51} } & {C_{52} } & {C_{53} } & {C_{54} } & {C_{55} } & {C_{56} } \\ {C_{61} } & {C_{62} } & {C_{63} } & {C_{64} } & {C_{65} } & {C_{66} } \\ \end{array} } \right]$$

(I.4)

where the elements of matrix [C] can be calculated based on Eqs. 4, I.2 and I.3.

Appendix II: implementation of the proposed constitutive model in FLAC 3D

The three-dimensional explicit finite difference implementation of the proposed model are outlined in this Appendix.

• 1. Deformations of the rock matrix

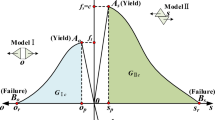
The function h(σ₁, σ₃) = 0, which is represented by the diagonal between the strength envelopes of f^s = 0 and f^t = 0 in the principal stress plane (Fig. 

Fig. 18

Determination of yielding type: a definition of h and domains used in determining yield type of the rock matrix; b definition of h_j and the domains used in determining yield type of the weak planes (after Itasca [26])

18a), is defined to determine the model of yielding of rock matrix:

$$h = \sigma_{3} - D\sigma_{t} + \alpha^{p} (\sigma_{1} - \sigma^{p} )$$

(II.1)

where

$$\alpha^{p} = \sqrt {1 + N_{\varphi d}^{2} } + N_{\varphi d}$$

(II.2)

$$\sigma^{p} = D\sigma_{{\text{t}}} N_{\varphi d} - 2Dc\sqrt {N_{\varphi d} }$$

(II.3)

$$N_{\varphi d} = \left( {{1} + {\sin}\left( {D\varphi } \right)} \right)/\left( {{1} - {\sin}\left( {D\varphi } \right)} \right)$$

(II.4)

If the stress state falls within domain 1, then shear failure occurs, and the new stress is revised using the flow rule derived from g^s. If the stress falls within domain 2, then tensile failure occurs, and the new stress is re-calculated adopting the flow rule derived from g^t.

For shear failure, partial differentiation of Eq. 8 with damage yields

$$\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{x} }} = 1,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{y} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{z} }} = - N_{\psi } ,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{xy} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{yz} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{xz} }} = 0$$

(II.5)

Thus, the expressions of the new stress are

$$\sigma_{x}^{N} = \hat{\sigma }_{x}^{I} - \lambda^{*} (C_{11} - C_{13} N_{\psi } )\quad \sigma_{y}^{N} = \hat{\sigma }_{y}^{I} - \lambda^{*} (C_{21} - C_{23} N_{\psi } )$$

$$\sigma_{z}^{N} = \hat{\sigma }_{z}^{I} - \lambda^{*} (C_{31} - C_{33} N_{\psi } )\quad \sigma_{yz}^{N} = \hat{\sigma }_{yz}^{I} - \lambda^{*} (C_{41} - C_{43} N_{\psi } )$$

(II.6)

$$\sigma_{xz}^{N} = \hat{\sigma }_{xz}^{I} - \lambda^{*} (C_{51} - C_{53} N_{\psi } )\quad \sigma_{xy}^{N} = \hat{\sigma }_{xy}^{I} - \lambda^{*} (C_{61} - C_{63} N_{\psi } )$$

where

$$\lambda^{*} = \frac{{f^{{\text{s}}} = \sigma_{1} - \sigma_{3} N_{\varphi d} + 2Dc\sqrt {N_{\varphi d} } }}{{(C_{11} - C_{13} )N_{\psi } - (C_{31} - C_{33} N_{\psi } )N_{\varphi d} }}$$

(II.7)

For tensile failure, partial differentiation of Eq. 9 with damage gives

$$\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{x} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{y} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \sigma_{z} }} = - 1,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{xy} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{yz} }} = 0,\frac{{\partial {\text{g}}^{{\text{s}}} }}{{\partial \tau_{xz} }} = 0$$

(II.8)

Thus, the expressions of the new stress are

$$\sigma_{x}^{N} = \hat{\sigma }_{x}^{I} - \lambda^{*} C_{13} \quad \sigma_{y}^{N} = \hat{\sigma }_{y}^{I} - \lambda^{*} C_{23}$$

$$\sigma_{z}^{N} = \hat{\sigma }_{z}^{I} - \lambda^{*} C_{33} \quad \sigma_{yz}^{N} = \hat{\sigma }_{yz}^{I} - \lambda^{*} C_{43}$$

(II.9)

$$\sigma_{xz}^{N} = \hat{\sigma }_{xz}^{I} - \lambda^{*} C_{53} \quad \sigma_{xy}^{N} = \hat{\sigma }_{xy}^{I} - \lambda^{*} C_{63}$$

where

$$\lambda^{*} = \frac{{\sigma_{td} - \sigma_{t3} }}{{(C_{11} - C_{13} )N_{\psi } - (C_{31} - C_{33} N_{\psi } )N_{\varphi d} }}$$

(II.10)

• 2. Deformations of the weak planes

The function h_j(σ₁, σ₃) = 0, which is represented by the diagonal between the strength envelope of f_j^s = 0 and f_j^t = 0 in the principal stress plane (Fig. 18b), is defined:

$$h_{{\text{j}}} = \tau - \tau_{{\text{j}}}^{{\text{p}}} - \alpha_{{\text{j}}}^{{\text{p}}} (\sigma_{{\text{n}}} - \sigma_{{\text{j}}}^{{\text{t}}} )$$

(II.11)

where

$$\tau_{{\text{j}}}^{{\text{p}}} = Dc_{{\text{j}}} - \tan (D\varphi_{{\text{j}}} )D\sigma_{{\text{j}}}^{{\text{t}}}$$

(II.12)

$$\alpha_{{\text{j}}}^{{\text{p}}} = \sqrt {1 + \tan (D\varphi_{{\text{j}}}^{{}} )^{2} } - \tan (D\varphi_{{\text{j}}} )$$

(II.13)

If the stress falls within domain 1, then shear failure occurs, and the new stress is revised using the flow rule derived from g_j^s. If the stress falls within domain 2, then tensile failure occurs, and the new stress is re-calculated adopting the flow rule derived from g_j^t.

For shear failure, partial differentiation of Eq. 12 yields

$$\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{s}}} }}{{\partial \sigma_{{x^{{\prime}} }} }} = 0,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{s}}} }}{{\partial \sigma_{{y^{{\prime}} }} }} = 0,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{s}}} }}{{\partial \sigma_{{z^{{\prime}} }} }} = \tan \psi_{j} ,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{s}}} }}{\partial \tau } = 1$$

(II.14)

Thus, the expressions of the new stress are

$$\left\{ \begin{gathered} \sigma_{{x^{{\prime}} }}^{N} = \sigma_{{x^{{\prime}} }}^{I} - \lambda^{s} C_{13} \tan \psi_{{\text{j}}} \hfill \\ \sigma_{{y^{{\prime}} }}^{N} = \sigma_{{y^{{\prime}} }}^{I} - \lambda^{s} C_{13} \tan \psi_{{\text{j}}} \hfill \\ \sigma_{{z^{{\prime}} }}^{N} = \sigma_{{z^{{\prime}} }}^{I} - \lambda^{s} C_{33} \tan \psi_{{\text{j}}} \hfill \\ \tau^{N} = \tau^{I} - 2\lambda^{s} C_{44} \hfill \\ \end{gathered} \right..$$

(II.15)

where

$$\lambda^{{\text{s}}} { = }\frac{{\tau - \sigma_{{\text{n}}} \tan (D\varphi_{{\text{j}}} ) - Dc_{{\text{j}}} }}{{2C_{44} + C_{33} \tan \psi_{j} \tan (D\varphi_{j} )}}$$

(II.16)

For tensile failure, partial differentiation of Eq. 13 gives

$$\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{t}}} }}{{\partial \sigma_{{x^{{\prime}} }} }} = 0,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{t}}} }}{{\partial \sigma_{{y^{{\prime}} }} }} = 0,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{t}}} }}{{\partial \sigma_{{z^{{\prime}} }} }} = 1,\frac{{\partial {\text{g}}_{{\text{j}}}^{{\text{t}}} }}{\partial \tau } = 0$$

(II.17)

Thus, the expressions of the new and updated stresses are

$$\left\{ \begin{gathered} \sigma_{{x^{{\prime}} }}^{N} = \sigma_{{x^{{\prime}} }}^{I} - \lambda^{t} C_{13} \hfill \\ \sigma_{{y^{{\prime}} }}^{N} = \sigma_{{y^{{\prime}} }}^{I} - \lambda^{t} C_{13} \hfill \\ \sigma_{{z^{{\prime}} }}^{N} = \sigma_{{z^{{\prime}} }}^{I} - \lambda^{t} C_{33} \hfill \\ \end{gathered} \right.$$

(II.18)

where

$$\lambda^{t} = \frac{{\sigma_{{\text{n}}} - D\sigma_{{\text{j}}}^{{\text{t}}} }}{{C_{33} }}$$

(II.19)

The flowchart of the implementation of the proposed model is shown in Fig. 

Fig. 19

Flowchart of the implementation of the proposed model

19. The main steps are as follows:

• 1. Assume that the rock behaves elastically, and the trial stresses in global coordinate are initially obtained.

• 2. Judge the yielding state of the rock matrix element based on the M-C criterion and modify its stress and strain if it yields. In addition, the plastic parameters of the element will be updated based on the damage evolutional law.

• 3. Convert the stress tensor from the global coordinate to the local coordinate and judge the yielding state of the weak plane element based on the M-C criterion and modify its stress and strain if it yields. In addition, the plastic parameters of the element will be updated based on the damage evolutional law.

• 4. Steps 1–3 are repeated until convergence of calculation is reached.