On the effects of pore water pressure buildup and dissipation on the seismic performance of a propped r.c. diaphragm wall in sand

Abstract

The study concerns the analysis of a retaining structure composed by a couple of r.c. diaphragm walls propped at the crest in loose and medium-dense, variably saturated sand under seismic conditions. Fully coupled dynamic equilibrium conditions and pore water flow in the porous soil have been taken into account, in order to assess the effects that the development and subsequent dissipation of excess pore water pressures can have on the performance of such structures under seismic conditions. To this end, a series of simulations in which the saturated soil permeability is varied of about two orders of magnitude has been carried out, in order to consider different evolution rates for the dynamic consolidation process. The von Wolffersdorff hypoplastic model and the van Genuchten water retention equation have been used to describe the mechanical and hydraulic behavior of the sand. The results obtained in a large series of finite element simulations show a significant dependence of the seismic performance of the structure evaluated in terms of permanent rotations and structural loads, in view of the modern performance-based design criteria on the excess pore pressures buildup during the seismic shaking and on its dissipation with time. For the particular seismic input considered, neither fully drained nor fully undrained conditions can be considered applicable in most of the cases considered. In such conditions, the quantitative assessment of wall and soil displacements, pore water pressures and effective stress distributions within the soil requires necessarily the solution of a fully coupled, nonlinear dynamic consolidation problem.

1 Introduction

The seismic behavior of diaphragm walls supported retaining structures has recently attracted significant interest in the geotechnical scientific community and among practicing geotechnical engineers, in view of their importance in the development of underground transportation infrastructures, notably in urban environments.

In particular, much attention has been paid on the use of performance-based concepts to assess the safety of the structure against earthquake loading. In this approach, the attention is focused on the evaluation of the deformation response of the soil–structure system under a given seismic load, rather than on the assessment of system stability based on conventional safety factors typically determined by means of a limit equilibrium evaluation of earth pressures and structural loads.

Simplified methods for the prediction of seismically induced permanent displacements of rigid and flexible retaining structures have been based on modifications of the classical Newmark method [37]. Examples of applications for retaining structures in dry coarse-grained soils are provided in refs. [5, 6, 9,10,11, 15, 43], among others.

However, the current state of development of: (i) computer hardware; (ii) advanced numerical tools for the solution of nonlinear coupled dynamic hydromechanical (consolidation) problems; and (iii) advanced inelastic constitutive equations capable of reproducing the main aspects of cyclic/dynamic behavior of soils, suggests that a possible alternative approach to this problem could be the direct FE solution of the full dynamic problem, considering both the retaining structure and the surrounding soils as (inelastic and possibly multiphase) continuous media, subjected to an earthquake excitation at the bedrock.

Several examples of application of this analysis strategy for the assessment of the seismic performance of flexible retaining structures in terms of wall and soil displacements can be found in the scientific literature. In most cases, the soil is treated either as fully drained (e.g., in presence of dry sands only) as in refs. [8, 11, 30, 34] or fully undrained (e.g., in presence of saturated clays) as in Ref. [7]. Fully coupled dynamic consolidation analysis has been carried out by Madabushi and Zeng [31] for gravity walls; by Alyami et al. [1], Iai and coworkers et al. [23,24,25] and Tashiro [48], who considered different types of quay walls with the main objective of modeling the occurrence of dynamic liquefaction; by Morigi et al.  [35] and Wang et al.  [49], who analyzed excavations supported by cantilevered or anchored diaphragm walls in saturated sands.

The aim of this paper is to provide a contribution towards the better understanding of the role played by excess pore pressure buildup and dissipation on the seismic performance of propped r.c. diaphragm walls in variably saturated sands, exploring: (i) the effects of the ratio between the characteristic time of the imposed seismic loading (i.e., the predominant period of the input accelerogram) and the characteristic time of the excess pore pressure dissipation within the soil mass, mainly controlled by soil permeability; and (ii) the effect of soil relative density, which controls the contractant/dilatant behavior of the soil upon shear deformation and may have an important effect on excess pore pressure buildup.

To this end, an extensive series of coupled nonlinear dynamic consolidation FE analyses have been performed, describing the soil as a hypoplastic material, using an advanced version of von Wolffersdorff constitutive model [54], extended to cyclic/dynamic loading conditions by means of the intergranular strain concept [39, 50]. In the simulations, the soil has been assumed either as looser than critical or denser than critical by considering two different initial void ratio profiles. For both soil densities, the saturated permeability has been varied within a relatively large range, to investigate situations which could be considered neither fully drained nor fully undrained and to explore the role of pore pressure dissipation rate on the overall response of the retaining structure.

The paper is organized as follows: Sect. 2 illustrates the problem considered, i.e., an ideal but realistic deep excavation in a variably saturated sand. Sects. 3 and 4 provide the details of the governing equations for the dynamic soil–structure interaction problem and of the constitutive equations for the porous medium, including: (i) the inelastic model chosen for the solid skeleton; (ii) the soil–water retention model linking suction and degree of saturation; and, (iii) the hydraulic properties of the soil. The details of the FE model adopted and of the complete simulation program are given in Sect. 5. The main results obtained in the simulations are illustrated in Sect. 6, focusing on the earthquake loading stage only. Finally, Sect. 7 summarizes the main conclusions of the paper and provides some directions for the prosecution of the research activity.

1.1 Notation

In the following, soil mechanics sign convention (compression positive) is used throughout, except when otherwise stated. The pore water pressure $u_w$ is assumed positive in compression. Direct notation is used, with vector and tensor quantities written in boldface letters. A special boldface sans–serif font is used for fourth-order tensors, as, for example, in $\varvec{{\mathsf {D}}}$. The scalar product between two vectors or two second-order tensors is denoted by the dot operator “$\cdot$”, as in $c = \varvec{a}\cdot \varvec{b} = a_ib_i$ or $C = \varvec{A}\cdot \varvec{B} = A_{ij}B_{ij}$. The dyadic (tensor) product between two vectors or two second-order tensors is denoted by the operator “$\otimes$”, as in $\varvec{C} = \varvec{a}\otimes \varvec{b}$, with $C_{ij} = a_ib_j$ and $\varvec{{\mathsf {C}}}= \varvec{A}\otimes \varvec{B}$, with ${\mathsf {C}}_{ijkl} = A_{ij}B_{kl}$. The tensors $\varvec{1}$, with $1_{ij} = \delta _{ij}$, and $\varvec{{\mathsf {I}}}$, with ${\mathsf {I}}_{ijkl} = (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})/2$, denote the second-order and the fourth-order identity tensors, respectively. The operator $\text {tr}(\cdot )$ evaluates the trace of a second-order tensor, as in $\text {tr}\varvec{a} = \varvec{a}\cdot \varvec{1}=a_{kk}$. For the representation of the effective stress tensor $\varvec{\sigma }$, the following invariant quantities will be used whenever necessary:

$$\begin{aligned} p = \frac{1}{3}\varvec{\sigma }\cdot \varvec{1} \quad q = \sqrt{\frac{3}{2}\varvec{s}\cdot \varvec{s}} \quad \theta = \frac{1}{3}\sin ^{-1}\left\{ \frac{9}{2}\,\frac{\text {tr}\left( \varvec{s}^3\right) }{q^3}\right\} \end{aligned}$$

with $\varvec{s} = {\text {dev}}(\varvec{\sigma })$.

2 Problem setting

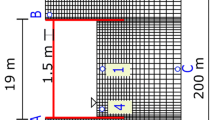
The problem considered in this study consists of a deep excavation, with height H = 8.0 m and half-width B = 9.0 m, supported by a pair of r.c. diaphragm walls propped at the crest, at a depth a = 0.5 m from the ground surface, see Fig. 1. In order to guarantee an adequate level of safety under static conditions according to the current Italian building code [33], the walls embedment depth d has been set to 6.0 m.

The excavated soil is a single homogeneous layer of either loose or medium-dense sand, 25 m thick, underlain by a rigid, impervious bedrock. In the initial conditions, the pore water is assumed to be in a hydrostatic state, with a piezometric surface located at a depth of 8.0 m below the ground surface (i.e., at the bottom of the excavation). The upper part of the soil layer is nonsaturated, with the degree of saturation $S_r$ provided as a function of pore water suction s by the van Genuchten [17] soil–water retention curve, see Sect. 4.

Fig. 1

Problem geometry (values in m)

The natural accelerogram recorded during the 1997 Umbria–Marche earthquake in Assisi (NS component) [45] has been chosen as the seismic input at the bottom of the soil layer, see Fig. 2. The accelerogram has been scaled to 0.2 g by applying a small correction factor to the recorded data. Baseline correction has been performed to correct for the spurious effects of data sampling. Some representative ground motion characteristics (peak acceleration $a_{\max }$; fundamental period T; predominant frequency f; Arias intensity $I_A$; duration $t_d$) of the Assisi earthquake are summarized in Table 1.

Fig. 2

Acceleration time history and Fourier spectrum of the seismic input considered

Table 1 Synthetic properties of the seismic input considered

3 Balance equations

Under the assumptions of: (i) linearized kinematics (“small strains”); (ii) incompressible solid grains; (iii) negligible relative acceleration of the liquid phase with respect to the solid skeleton; and (iv) unsaturated soil with pore gas phase at constant atmospheric pressure ($u_g = 0$), the balance equations governing the dynamic soil–structure interaction problem in the case at hand are given by (see, e.g., Ref. [55], Sect. 2.3):

$$\begin{aligned}&\nabla \cdot \varvec{\tau } - \rho \varvec{b} + \rho \ddot{\varvec{u}} = \varvec{0} \end{aligned}$$

(1)

$$\begin{aligned}&\nabla \cdot \varvec{v} - S_r\text {tr}\left( \dot{\varvec{\epsilon }}\right) + \frac{1}{Q}\dot{u}_w = 0 \end{aligned}$$

(2)

where $\varvec{\tau }$ is the total stress tensor; $S_r$ is the degree of saturation of the soil; $\rho = (1-n)\rho _s + S_rn\rho _w$ is the mass per unit volume of the soil, where n is the soil porosity and $\rho _s$ and $\rho _w$ are the solid grains and pore water densities, respectively; $\varvec{b}$ is the body force density per unit mass; $\ddot{\varvec{u}}$ is the solid skeleton acceleration; $\varvec{v}$ is Darcy’s seepage velocity; $\text {tr}(\dot{\varvec{\epsilon }})$ is the volumetric strain rate; $u_w$ is the pore water pressure; and

$$\begin{aligned} \frac{1}{Q} = n\frac{\partial S_r}{\partial u_w} + \frac{nS_r}{K_w} \end{aligned}$$

is a storage coefficient depending on the changes of the degree of saturation of the solid skeleton with changing pore water pressure and on the bulk compressibility of the pore water which, assuming a barotropic behavior, is given by $1/K_w = (1/\rho _w)d\rho _w/du_w$.

In the particular case of saturated soil ($S_r = 1$), Eqs. (1) and (2) are still valid, with the storage coefficient now depending only on pore water compressibility, i.e., $1/Q = n/K_w$.

4 Constitutive models adopted

4.1 Soil solid skeleton

The hypoplastic constitutive model proposed by von Wolffersdorff (HPvW, [54]) for saturated coarse-grained soils has been used in this work as a reasonable compromise between the competing needs of capturing qualitatively and quantitatively all the salient features of the mechanical response of the material, e.g., non-linearity, irreversibility, dependence on pressure (barotropy), density (pyknotropy) and loading history, and possessing a relatively simple mathematical structure, in which the material properties are defined in terms of a small number of constants which can be easy determined with conventional experimental techniques [19].

To deal with the unsaturated soil above the phreatic surface, the “single effective stress” approach of Bishop has been used, adopting the averaged skeleton stress of eq. (3) (Sect. 4.2) in place of the classical effective stress. For sand hypoplasticity, the single effective stress approach has been advocated for the first time by Gudehus [18] and explored further by Niemunis [38]. In our study, this approach can be considered justified in view of the relatively low compressibility of the sand considered and of the limited amount of suction which can be developed with the hydraulic properties assigned in Sect. 4.2, see Fig. 3.

In order to improve the model response at small strain levels and in cyclic/dynamic loading conditions, the version of the HPvW model adopted is equipped with a tensorial internal variable—the so-called Intergranular Strain $\varvec{\delta }$ [39]—which stores the memory of the previous deformation history. The original formulation of Niemunis & Herle has been modified as suggested by Wegener [50] and Wegener & Herle [51] in order to eliminate ratcheting effects in small amplitude cycles. The full set of constitutive equations for the HPvW model is provided in Appendix A.

The capabilities of HPvW model in reproducing the cyclic/dynamic behavior of sands as observed in laboratory have been assessed over the past decade by several authors, in its extension to either the intergranular strain (IS) concept [20,21,22, 42, 50, 51] or in the more recent version of Intergranular Strain Anisotropy (ISA) approach [16, 41, 53]. An extensive comparison between the observed response of sands in undrained cyclic loading conditions and the corresponding model predictions, performed by Wegener and Herle [50, 51], has shown the excellent predictive capabilities of the HPvW model in reproducing the salient features of the soil response of main interest for the present work (shear stiffness degradation with increasing shear strain amplitude, excess pore pressure buildup, cyclic mobility under large number of cycles). Based on the results of an extensive experimental campaign, Wichtmann et al.  [53] have demonstrated that the predictive capabilities of the HPvW model, equipped with either IS or ISA extensions, are comparable or superior to that of an advanced kinematic hardening elastoplastic model (SANISAND [12]).

The HPvW model is fully characterized by 10 material constants, collected in the following 5 groups:

• (a) Critical state friction angle, $\phi _c$;

• (b) Granular hardness, $h_s$;

• (c) Maximum, minimum and critical void ratios at zero mean effective stress, $e_{i0}$, $e_{d0}$, $e_{c0}$;

• (d) Pyknotropy and barotropy constants, n, $\alpha$ and $\beta$;

• (e) Intergranular strain constants, R, $\beta _r$, $m_R$, $m_T$, $\chi$, $\vartheta$.

The constants $\phi _c$, $e_{i0}$, $e_{d0}$ and $e_{c0}$ can be determined from the results of simple, standard classification tests on reconstituted samples. According to Herle & Gudehus [19], the critical friction angle $\phi _c$ can be estimated as the angle of repose of the material in a very loose state. Indicating with $e_{\min }$ and $e_{\max }$, the “conventional” void ratios in the densest and loosest states, measured according to ASTM standards [2, 3], Herle & Gudehus suggest that the constant $e_{d0}$ can be set approximately equal to $e_{\min }$. In addition, they report values of the ratio $e_{c0}/e_{\max }$ ranging between 0.96 and 1.0 and assume that the ratio $e_{i0}/e_{\max }$ can be approximately set equal to 1.2. The determination of the granular hardness, of the barotropy and pyknotropy constants, as well as of all the other constants of the standard model (except the intergranular strain constants) is discussed in detail in Ref. [19]. The calibration of the intergranular strain constants with particular reference to the application to dynamic loading conditions is addressed by Wegener [50].

In the present work, the soil layer has been assumed to have the properties of Toyoura sand. The corresponding material constants for the HPvW model have been calibrated in Ref. [50] and are summarized in Table 2. The table provides also the saturated and dry mass densities adopted for the soil.

Table 2 Constants of HPvW model for Toyoura sand (from [50])

In the HPvW model with intergranular strains, the state of the material is given by the effective stress $\varvec{\sigma }$, the void ratio e and the intergranular strain $\varvec{\delta }$, the evolution of which depends on the recent strain history. The definition of the initial values for these state variables is discussed in Sect. 5.2.

4.2 Effective stress and soil–water retention model

In the initial static equilibrium conditions, due to the water retention characteristics of the coarse-grained soil considered, the upper part of the sand layer, above the piezometric surface, is in unsaturated conditions. The degree of saturation $S_r$ decreases rapidly with decreasing depth z from ground surface, passing from $S_r = 1$ at z = 8.0 m to $S_r = S_{r,\text {res}}$, as z goes to zero, see Fig. 5.

When the soil is in a unsaturated state, the definition of effective stress needs to be modified and an additional hydraulic constitutive equation has to be provided to quantify the soil water retention properties. In this work, the effective stress for unsaturated states is assumed to be given by:

$$\begin{aligned} \varvec{\sigma }= \varvec{\tau }-\{(1-S_r)u_g+S_ru_w\}\varvec{1} = \varvec{\tau } - S_r u_w\varvec{1} \end{aligned}$$

(3)

also known as average skeleton stress. The definition in eq. (3) has been introduced by Schrefler [46] and has been used, among others, in refs. [4, 13, 26, 47]. For saturated states ($S_r$ = 1), the average skeleton stress reduces to the classical Terzaghi effective stress.

The soil–water retention curve proposed by van Genuchten [17] has been used to link the degree of saturation $S_r$ to suction $s = u_g - u_w = -u_w \ge 0$:

$$\begin{aligned} S_{re}(s) = \Big \{ 1+\left( g_a\,\frac{s}{\rho _w g}\right) ^{g_n} \Big \}^{ \frac{1-g_n}{g_n}} \end{aligned}$$

(4)

where $S_{re}$ is the effective degree of saturation, defined as:

$$\begin{aligned} S_{re} = \frac{S_r - S_{r,\text {res}}}{1 - S_{r,\text {res}}} \end{aligned}$$

(5)

g is the gravity acceleration, $S_{r,\text {res}}$ is the residual degree of saturation of the soil at very high suction levels and $g_a$ and $g_n$ are model constants. The quantity $1/g_a$ is an approximation of the soil air-entry piezometric head (height of the capillary fringe) while the constant $g_n$ controls the rate at which $S_{r}$ decreases with increasing suction. A set of van Genuchten constants typical of a poorly graded silty sand—see Ref. [29]—has been adopted for the soil layer. The corresponding retention curve is shown in Fig. 3, together with the corresponding van Genuchten constants.

Fig. 3

van Genuchten soil water retention curve adopted for the sand layer. Model constants are provided in the figure inset

4.3 Soil hydraulic conductivity

Darcy’s law provides the constitutive equation governing the water flow in the soil. Neglecting the contribution of water inertia forces, it can be written as:

$$\begin{aligned} \varvec{v} = -k_{\text {rel}}(S_{re})\frac{1}{\mu _w}\varvec{\kappa }_s\nabla \left( \rho _w g\zeta + u_w\right) \end{aligned}$$

(6)

where $\zeta$ is the elevation head, $\mu _w$ is the viscosity of the pore water, $\varvec{\kappa }_s$ is the intrinsic hydraulic conductivity of the saturated soil, related to Darcy’s permeability $\varvec{k}_s$ by the relation:

$$\begin{aligned} \varvec{k}_s = \frac{\rho _w g}{\mu _w}\,\varvec{\kappa }_s \end{aligned}$$

and $k_{\text {rel}} \le 1$ is the relative permeability accounting for the effects of partial saturation. In the present work, the saturated permeability of the soil is assumed isotropic, and thus,

$$\begin{aligned} \varvec{\kappa }_s = \kappa _s\,\varvec{1} \qquad \varvec{k}_s = k_s\,\varvec{1} \end{aligned}$$

The van Genuchten–Mualem expression—obtained by combining Eq. (5) with the capillary model of Mualem [36]—has been used for the relative permeability function:

$$\begin{aligned} k_{rel}(S_{re})= (S_{re})^{g_l} \left[ 1- \left( 1 - {S_{re}}^{\frac{g_n}{g_n-1}} \right) ^\frac{g_n-1}{g_n} \right] ^2 \end{aligned}$$

(7)

where $g_l > -2g_n/(g_n - 1)$ is an additional model constant accounting for pore tortuosity and pore connectivity. The complete set of hydraulic properties adopted for the soil is shown in Fig. 3. As the objective of the work is to investigate the effects of seismically induced excess pore pressure buildup and dissipation on the performance of the retaining structure, the saturated permeability $k_s$ has been varied in the range 3.0E−4 m/s (quasi-undrained conditions) to 3.5E−2 m/s (almost drained conditions).

4.4 Structural elements

The r.c. diaphragm walls considered in this study have a length L = 14.0 m and a thickness t = 1.0 m. The walls are supported by a r.c. strut 18 m long, with thickness s = 1.0 m, hinged at the top of the two diaphragm walls. Both the walls and the supporting strut are assumed as linear elastic. The geometry of the sections and the material constants adopted for the reinforced concrete are provided in Table 3.

Table 3 Geometry and material constants adopted for the r.c. structural elements

5 Finite element model and simulation program

The numerical simulations of the seismic response of the retaining structure have been carried out using the commercial FE code Tochnog Professional [44]. The standard model library of the code includes the HPvW model as well as the van Genuchten water retention model and the van Genuchten–Mualem relative permeability functions. To integrate the coupled balance of mass and momentum equations in time, the code uses the backward Euler algorithm, after reducing the second-order dynamic equations of motion into a system of first-order ODEs. An adaptive time-stepping scheme has been adopted with $\Delta t_{\max }$ = 0.01 s and $\Delta t_{\min }$ = 10$^{-5}$ s in all the simulations.

5.1 FE discretization

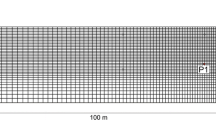
The 2-d, plane strain FE discretization adopted in the numerical simulations is shown in Fig. 4, where only one half of the numerical model is represented for clarity. A few points considered in the post-processing of the results are also indicated in the figure.

Fig. 4

Finite element discretization and boundary conditions adopted (only half model is shown): a boundary conditions for quasi-static stages; b boundary conditions for seismic stage

The soil is discretized with 3866 Q4P4 bi-linear 4-noded elements, with 2 displacement and 1 pore pressure dofs per node. Particular care has been placed in the selection of the maximum element size to avoid filtering of high frequencies [27], taking into account the characteristics of the seismic input considered. In addition, a relatively large distance has been adopted between the retaining structures and the fictitious vertical boundaries of the domain, in order to minimize the effects of eventual spurious reflections. As the continuum elements adopted do not satisfy the LBB condition—see, e.g., White & Borja [52]—a realistic compressibility for the pore water ($C_w$ = 1.0E−5 kPa$^{-1}$) has been adopted to avoid spurious instabilities close to the incompressible limit (soil fully saturated with low permeability).

The two diaphragm walls have been modeled with 112 Q4 bi-linear 4-noded elements, with 2 displacement dofs per node, while 4 linear, two-noded beam elements have been used to model the strut. Perfect hinges have been placed at the connections between the walls and the strut to avoid moment transfer. The use of continuum one-phase elements in place of beam elements for the walls guarantees the perfect impermeability of the walls and the independence of the pore pressure fields on the excavated and retained faces. The structural elements of the walls and the struts are characterized by rectangular cross sections with the dimensions and material properties given in Table 3.

A thin layer of continuous elements has been employed on both sides of the two walls to simulate the interface behavior, see [14]. For the case at hand, where the r.c. walls are cast in place within the soil and a condition of full adhesion at the soil–wall contact appears reasonable, the continuous interface elements have been assigned the same properties of the surrounding soil, see Table 2.

5.2 Initial and boundary conditions

A suitable approximation for the initial geostatic conditions for the soil profile has been obtained analytically by assuming that:

• (i) The soil is fully saturated below the piezometric surface (located at depth $z_w$ = 8.0 m) and completely dry above it;

• (ii) The pore water pressure is hydrostatic below the piezometric surface and zero above it;

• (iii) The coefficient of earth pressure at rest can be estimated using the Jaky expression: $K_0 = 1- \sin \phi _c$, which provides $K_0$ = 0.5 for $\phi _c$ = 30$^\circ$;

• (iv) The initial “relative density” $\mathcal {E}_0$ of the soil, defined in terms of the characteristic void ratio functions of the HPvW model:

  $$\begin{aligned} \mathcal {E}_0 = \frac{e_i - e_0}{e_i - e_d} \in [0,1], \end{aligned}$$

  (8)

  is uniform on the entire layer.

Assumptions (i)–(iii) provide the following (approximate) distributions of pore water pressures, total and effective stresses with depth z from the ground surface:

$$\begin{aligned} \tau _z = {\left\{ \begin{array}{ll} \rho _d g z &{} z \le z_w \\ \rho _d g z_w + \rho g(z-z_w) &{} \text {otherwise} \end{array}\right. }\\[3pt] u_w = {\left\{ \begin{array}{ll} 0 &{} z \le z_w \\ \rho _w g (z-z_w) &{} \text {otherwise} \end{array}\right. }\\[3pt] \begin{aligned} \sigma _z &= \tau _z - u_w & \sigma _x &= \sigma _y = K_0\sigma _z& \tau _x &= \tau _y = K_0\sigma _z + u_w \end{aligned}\end{aligned}$$

see Fig. 5a. The correct geostatic stress state compatible with the effective soil suction and degree of saturation profiles provided by the hydraulic constitutive model (Fig. 5c) is recovered in a preliminary geostatic step carried out at the beginning of the simulation. In all the simulations performed, the deformations and displacements accumulated during this stage have been checked to be negligible.

Assumption (iv) provides a depth-dependent initial void ratio profile due to the increase in mean effective stress with depth:

$$\begin{aligned} e_0(p) = e_i(p) - \mathcal {E}_0\left\{ e_i(p)-e_d(p)\right\} \end{aligned}$$

where the functions $e_i(p)$ and $e_d(p)$ are provided by Eq. (25) of Appendix A. In this work, two different values of the initial relative density $\mathcal {E}_0$ have been considered, namely 0.15 and 0.30. The corresponding void ratio profiles are shown in Fig. 5b. It is worth noting that with the material constants provided in Table 2, the relative density $\mathcal {E}_c$ corresponding to the critical state void ratios is constant with depth and equal to 0.245. Therefore, at all depths, the deposit with $\mathcal {E}_0$ = 0.15 is largely looser than critical and thus can be classified as a loose sand, while the deposit with $\mathcal {E}_0$ = 0.30 is denser than critical and therefore can be classified as a medium-dense sand. In terms of conventional relative density, the two soil profiles have an average value of $D_r$ of about 18% and 35%, respectively.

Fig. 5

Initial geostatic conditions: a approximate total vertical stress, effective vertical stress and pore water pressure; b void ratio profiles for loose and medium-dense sand; c degree of saturation

As for the boundary conditions, for the static simulation stages performed to simulate the excavation process and initialize various fields before the seismic loading stage, fixed horizontal displacements have been assumed at the lateral boundaries and fixed horizontal and vertical displacements have been imposed at the base of the model, see Fig. 4a. The transient dynamic analysis for the simulation of the seismic event has been performed imposing the chosen acceleration time histories at the base of the model, while periodic boundary conditions have been imposed on the lateral boundaries to keep the spurious reflections to a minimum, see Fig. 4b.

5.3 Simulations program

The full program of numerical simulations carried out in this work is detailed in Table 4. The first group of simulations (r01–r05) have been performed considering the soil layer as loose, while a medium-dense initial state is considered in the second group (r06–r10).

Table 4 Program of FE simulations

As anticipated in Introduction, the aim of the present work is to investigate the effect of excess pore water pressure buildup and dissipation on the seismic performance of the retaining structure, as the ratio between the characteristic time of the transient consolidation process and the fundamental period of the seismic excitation is varied in a relatively wide range. To this end, five different values of the saturated permeability $k_s$ have been considered for each group of simulations, ranging to very high to relatively low for coarse-grained soils. All the FE simulations have been performed in the following stages:

• 1. Approximate initialization of the state variable fields as detailed in Sect. 5.2 and execution of a geostatic step to recover the final equilibrium conditions;

• 2. First excavation stage in one step of 0.5 m;

• 3. Activation of the strut elements;

• 4. Second excavation stage, in 15 steps of 0.5 m, up to the final excavation depth H = 8.0 m;

• 5. Activation of the periodic boundary conditions on the lateral boundaries and application of the horizontal acceleration history at the bottom of the soil layer.

The geostatic and excavation stages 1, 2, 3 and 4 have been modeled assuming quasi-static, drained conditions. These stages are required to produce the initial equilibrium state for the soil–wall system before the earthquake loading. Note that the stress and strain state in the soil, as well as the loads in the structural elements at the beginning of the seismic loading stage, is slightly different for the simulations r01–r05 (loose soil) and r06–r10 (medium-dense soil), as the behavior of the HPvW model is affected by the initial density through the pyknotropy function. During the seismic stage 5, fully coupled hydromechanical conditions (dynamic consolidation) have been enforced by activating the relevant degrees of freedom for the balance of mass equation.

6 Results of the simulations: earthquake loading

6.1 Ground accelerations

Figures  6 and 7 show the time histories of the horizontal accelerations at points F (bedrock), G (ground surface, free field) and A (top of right wall), see Fig. 4, for the simulations with the largest (r01, r06) and smallest (r05, r10) permeability, respectively. In each plot, the solutions obtained for the loose sand case are compared with the corresponding solution for the medium-dense sand case.

Fig. 6

Time histories of the horizontal acceleration, $k_s$ = 3.5E−2 m/s. a Bedrock; b ground surface, free field; c top of right wall

Fig. 7

Time histories of the horizontal acceleration, $k_s$ = 3.0E−4 m/s. a Bedrock; b ground surface, free field; c top of right wall

By comparing the acceleration histories at the bedrock and in free-field conditions for any given $k_s$ considered, a non-negligible attenuation in peak horizontal acceleration can be observed, with PGA reducing from about 2 m/s$^2$ to 1.5 m/s$^2$. On the contrary, no significant changes are observed in the peak horizontal acceleration between the bedrock and the top of the wall, where the accelerations are higher than in free-field conditions due to geometric effects. Regardless of the saturated permeability, the initial relative density of the sand has almost no effect on the acceleration records at all the points considered. Very small differences are also observed in ground accelerations by passing from a very high permeability (simulations r01 and r06) to a relatively low permeability (simulations r05 and r10).

The acceleration response spectra at 5% damping, evaluated at the same locations for both loose and medium-dense sand cases, are shown in Fig. 8 for the largest permeability (simulations r01 and r06) and in Fig. 9 for the smallest permeability (simulations r05 and r10). The examination of the response spectra provides a picture of the different frequency content of the seismic signals at the bedrock, in free-field conditions and at the top of the wall. Important amplification effects are observed close to the excavation for period T in the range 0.4 to 2 s, while smaller differences are observed between the bedrock and the free field. Neither soil density nor saturated permeability appears to play a significant role.

Fig. 8

Acceleration response spectra at different locations for loose and medium-dense sand cases, $k_s$ = 3.5E−2 m/s

Fig. 9

Acceleration response spectra at different locations for loose and medium-dense sand cases, $k_s$ = 3.0E−4 m/s

6.2 Pore water pressures and effective stress

6.2.1 Loose sand

A general view of the evolution in space and time of pore water pressures during the seismic event is provided, for the case of loose sand, by the contour maps of the modified hydraulic head $h^* := \rho _w gh$, shown in Fig. 10, for different time stations and 3 values of the saturated permeability (high, $k_s$ = 3.5E−2 m/s; medium, $k_s$ = 8.0E−3 m/s; low, $k_s$ = 3.0E−4 m/s). The choice of representing this particular quantity is motivated by the fact that:

$$\begin{aligned} h^* -h^*_0 = \rho _wg\left( \zeta + \frac{u_w}{\rho _wg} - \zeta _0 - \frac{u_{w0}}{\rho _wg}\right) = \Delta u_w \end{aligned}$$

where $\zeta = \zeta _0$ is the elevation head at the point where $h^*$ is computed. Therefore, the regions where large variations in $u_w$ occur are easy to identify in the contour plots as those zones where $h^*$ is largely different from its initial value $h^*_0$. For the assumed initial pore water pressure field, $h^*_0$ = 167 kPa (see Sect. 5.2).

Fig. 10

Loose sand case: contour maps of $h^{*}$ at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

From the examination of Fig. 10, it can be noted that when the saturated permeability is high (left column), the excess pore pressures within the soil mass are very small. Noticeable changes are only observable during the earthquake (at t = 7 s, close to the peak acceleration at the base) below the excavation level, in the zone of soil confined by the two walls. These excess pore pressures are quickly dissipated well before the end of the seismic event.

As the permeability decreases (central and right columns in the figure), larger positive excess pore pressures are observed below the bottom of the excavation at the beginning of the earthquake event. For the medium permeability case, excess pore pressure dissipation is still occurring during the event, so that the peak values of $\Delta u_w$ occur well before the end of the shaking. On the contrary, for the low permeability case, the characteristic time for excess pore pressure dissipation is large enough, compared to the duration of the seismic event, that in the zone of soil beneath the excavation level the peak values of $\Delta u_w$ are obtained at the end of the simulations.

A more detailed picture of the time evolution of $u_w$ at two characteristic points located close to the right wall—i.e., point D on the active side and point C on the passive side, see Fig. 4—is provided in Fig. 11, showing the time histories of $\Delta u_w$ for all the five simulations of the loose soil case. In the active zone (Fig. 11a), all the simulations except r05, the one with the smallest permeability, provide $\Delta u_w$ values which increase during the earthquake reaching their peaks (10 to 20 kPa) at t in the range between 7 and 9 s. Subsequently, $\Delta u_w$ dissipates at different rates, depending on saturated permeability. The opposite behavior is manifested by the results of simulation r05, with the lowest saturated permeability, where $u_w$ first decreases significantly, and then increases again reaching a maximum value of about 20 kPa. This behavior is probably due to the different kinematics of the walls in this particular case, see Sect. 6.4.

In the passive zone (Fig. 11b), positive excess pore pressures buildup during the earthquake, reaching a peak (around t = 7-8 s) of about 30 kPa in all the simulations except r01, the case with the largest permeability, where excess pore pressure dissipation is faster. In the remaining simulations, the excess pore pressure reduces after the peak with a rate that depends on permeability: the larger the permeability, the faster the dissipation. In the latter two cases (r04 and r05), the dissipation is so slow that the pore pressure at the end of the earthquake is almost equal to the peak one.

Fig. 11

Loose sand case: time histories of $\Delta u_w$ for different values of $k_s$. a Active side; b passive side

It is interesting to explore how the changes in pore water pressures reported before affect the effective stress field, and if dynamic liquefaction, defined by the condition:

$$\begin{aligned} p(\varvec{x},t) = \frac{1}{3}\varvec{\tau }\cdot \varvec{1}-u_w = p_\tau -u_w = 0 \qquad (S_r = 1) \end{aligned}$$

(9)

, occurs in any zone of the soil surrounding the excavation during the earthquake excitation. To this end, the stress paths at the same two points C (passive side) and D (active side) are provided in Fig. 12 for the cases of high permeability (simulation r01), medium permeability (simulation r03) and low permeability (simulation r05). In the figure, each stress path is represented by its projection in the q:p plane (effective stress paths) or in the q:$p_\tau$ plane (total stress paths, $p_\tau$ being the mean total stress), and in the deviatoric plane, adopting (q, $\theta$) as polar coordinates. In the q:p plane, the two critical state lines corresponding to the axisymmetric compression ($\sigma _1 > \sigma _2 = \sigma _3$, $\theta = \pi /6$) and extension ($\sigma _1 = \sigma _2 > \sigma _3$, $\theta = -\pi /6$) conditions are also plotted for reference. The slopes of the two lines—$M_c$ for axisymmetric compression and $M_e$ for axisymmetric extension—are related to the friction angle at critical state $\phi _c$ by the relations:

$$\begin{aligned} M_c = \frac{6\sin \phi _c}{3-\sin \phi _c} \qquad M_e = \frac{6\sin \phi _c}{3+\sin \phi _c} \end{aligned}$$

In the HPvW model, the critical state locus in stress space is a cone whose equation is provided by the following Matsuoka–Nakai function:

$$\begin{aligned} f(p,q,\theta ) = q - M(\theta )p = 0 \quad \Leftrightarrow \quad q = M(\theta )p \end{aligned}$$

(10)

where

$$\begin{aligned} M(\theta ) = \frac{3\sin \phi _c}{\sqrt{4-\cos ^2\phi _c}}\, \frac{1}{\cos \left\{ \frac{1}{3}\cos ^{-1}\left[ \xi \cos (3\theta )\right] \right\} } \end{aligned}$$

(11)

and

$$\begin{aligned} \xi = \frac{\sin \phi _c(8+\cos ^2\phi _c)}{\left( 4-\cos ^2\phi _c\right) ^{3/2}} \end{aligned}$$

see [40]. According to eqs. (10) and (11), for any value of the Lode angle $\theta$ in the range $(-\pi /6,\pi /6)$, the projection of the critical state locus in the q:p plane is a line with a constant slope M varying continuously between $M_e$ and $M_c$. It is worth recalling that in hypoplasticity, and in the HPvW model in particular, the critical state locus is not a bounding surface separating admissible from impossible stress states, but rather an attractor towards which all the stress paths converge when the material deforms at large deviatoric strains under constant effective stress and void ratio, see, for example, Ref. [32].

Fig. 12

Loose sand case: effective and total stress paths at two selected points. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s). Left plots refer to point C (passive side); right plots refer to point D (active side)

Looking at the different stress paths in Fig. 12, it is immediately apparent that the effective stress state at point C, on the passive side of the wall, is undergoing a strong reduction in both isotropic and deviatoric components, which takes place from the beginning of the seismic event. In particular, the strong reduction in p is due to the buildup of excess pore water pressure $\Delta u_w$, see Fig. 11b, which is significant even for the case with the highest permeability. In this case, with the rapid dissipation of $\Delta u_w$, the effective mean stress increases again towards the end of the seismic stage, see Fig. 12a. On the contrary, a liquefaction condition is observed at the same point for the cases with medium and low permeabilities, see Fig. 12b and c. At point D, on the active side of the wall, the effective stress paths show a tendency towards the increase in the stress ratio at the beginning of the seismic loading stage. This tendency is inverted in the final stage of the simulation with the medium permeability (Fig. 12b), possibly due to the dissipation of the positive excess pore pressures at this stage, see Fig. 11a. In general, the effective stress paths on the active side remain quite far from the origin of the stress space and no liquefaction is observed in the three cases considered.

The observations made at the two individual points considered motivate the interest in assessing the position and extension of those volumes of the soil which might have been affected by liquefaction during the shaking. To this end, we have plotted in Fig. 13 the contour maps of the maximum compressive principal stress $\sigma _1$ at different time stations for simulations r01 (high permeability, Fig. 13a), r03 (medium permeability, Fig. 13b) and r05 (low permeability, Fig. 13c). The cohesionless nature of the soil considered guarantees that eq. (9) is satisfied if $\sigma _{1}$ = 0.

Due to the increase in pore water pressures, in the soil around the excavation a generalized reduction in $\sigma _1$ is observed during the earthquake in all the 3 cases considered, notably in the volume of soil enclosed within the two walls, below the excavation level. This reduction is stronger and more widely spread as the permeability decreases. In particular, for the case of large permeability, the zone of soil where $\sigma _1$ reduces to zero is confined to a shallow layer of soil beneath the excavation, and this zone is only visible during the early stage of the earthquake, when ground accelerations reach their peak values. Immediately after, the very fast dissipation of excess pore pressures brings the state of effective stress back to the compressive range. Thus, liquefaction only occurs in a relatively confined region and only for a limited amount of time.

Fig. 13

Loose sand case: contour maps of $\sigma _1$ at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

It is worth noting that, even for the large permeability value adopted ($k_s$ = 3.5E−2 m/s), the response of the soil around the retaining structure to the seismic loading is not fully drained. Modeling this problem in drained conditions would result in a underestimation of the mean effective stress reduction in the passive zone, and, consequently, in an overestimation of soil stiffness and shear strength.

On the contrary, in the other two cases considered (medium and low permeability), the liquefied zone within the two walls is much larger, affecting the entire embedded length of the walls, and also more persistent in time, as the dissipation of excess pore pressures is much slower than in the previous case. Based on these observations, it is possible to anticipate that simulations r03 and r05 predict much larger wall permanent displacements and rotations than in simulation r01.

6.2.2 Medium-dense sand

As in the loose sand case, a general view of the evolution in space and time of pore water pressures during the seismic event is provided by the contour maps at different time stations of the modified hydraulic head $h^*$. Such contours, obtained for the medium-dense soil case from simulations r06 (high permeability), r08 (medium permeability) and r10 (low permeability), are shown in Fig. 14.

Fig. 14

Medium-dense sand case: contour maps of $h^{*}$ at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

The general pattern of excess pore pressure development with time and with reducing permeability is very close to the one previously observed for the case of loose sand, albeit with slightly smaller maximum $h^*$ values. In particular, it is worth noting that in the two simulations with medium (r08, Fig. 14b) and low (r10, Fig. 14c) permeability, large positive excess pore pressures of the order of 50-80 kPa are predicted in the soil region enclosed between the two walls. This is somewhat unexpected, as a potentially dilatant behavior upon shear—accompanied by a decrease in $u_w$—would have been expected from a soil with an initial density higher than critical.

Similar observations can be made with reference to the time evolutions of $u_w$ at two characteristic points D, on the active side of the right wall, and C, on the passive side of the right wall, shown in Fig. 15, which are only marginally different to those of the loose soil case.

Fig. 15

Medium-dense sand case: time histories of $\Delta u_w$ for different values of $k_s$. a Active side; b passive side

The effective and total stress paths at points C and D are provided in Fig. 16, again considering the cases of high permeability (simulation r06), medium permeability (simulation r08) and low permeability (simulation r10). Looking at the plots in Fig. 16, the similarity between the present case and the loose sand case is apparent. On the passive side, the stress paths move steadily towards the origin of the stress space and, while liquefaction is actually observed only in the low permeability case, the final values of mean effective stress are quite low even for the high permeability case. This is consistent with the previous observations made on the time evolution of excess pore water pressures at point C reported in Fig. 15b. At point D, on the active side of the wall, the effective stress paths remain quite far from the origin of the stress space and no liquefaction is observed in the three cases considered.

Fig. 16

Medium-dense sand case: effective and total stress paths at two selected points. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s). Left plots refer to point C (passive side); right plots refer to point D (active side)

One of the most relevant consequences of the relative lack of sensitivity of the excess pore pressure field $\Delta u_w(\varvec{x},t)$ on the initial density of the soil is that even for the medium-dense soil case, persistent liquefaction phenomena can occur in the passive zone of soil between the two walls if soil permeability is sufficiently low, as shown by the contour maps of $\sigma _1$ at different time stations reported in Fig. 17.

Fig. 17

Medium-dense sand case: contour maps of $\sigma _1$ at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

Again, this observation is quite unexpected for a soil which—based on his initial relative density—could be considered as non-liquefiable. Typically, the distinction between liquefiable and non-liquefiable soils is based on the observation of pore pressure buildup in free-field conditions (one-dimensional shear wave propagation from the bedrock to the ground surface), where soil dilatancy or contractancy plays a major role. However, the stress and strain fields around the excavation are quite far from free-field conditions, due to the excavation geometry and the interaction of the soil with the retaining structure. Therefore, it is most likely that, in this case, the evolution of total mean stress with time may have played an important role in the observed changes of $u_w$ in space and time, in addition to shear-induced dilatancy/contractancy of the soil.

6.3 Soil deformations

A picture of the volumetric and shear deformations occurring in the soil around the excavation during the seismic event can be obtained by looking at the contour maps of void ratio e—linked to volumetric strain by the kinematic relation $\Delta \epsilon _v = -\Delta e/(1+e_0)$—and of shear strain $\gamma _{xy}$ at different time stations, provided in the following for the two cases of loose and medium-dense sand. To assess the effect of excess pore water dissipation on the deformation pattern, the 3 cases of high, medium and low permeability have been compared, as in Sect. 6.2.

6.3.1 Loose sand

Figure 18 shows the contour maps of void ratio at different time stations and 3 different values of the saturated permeability (high, medium and low). For the case of high permeability (Fig. 18a), significant reductions in void ratio—i.e., compressive volumetric strains—are observed below the excavation level starting from t = 12 s, when excess pore water pressures in the passive zone are almost completely dissipated (see Figs. 10a and 11b). From this point on, the deformation occurs under almost drained conditions and the soil is free to compact under the cyclic loading induced by the seismic shaking, experiencing a maximum volumetric strain increment $\Delta \epsilon _v\simeq 6$ %.

Fig. 18

Loose sand case: contour maps of void ratio e at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0E−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

As soil permeability decreases, the dissipation of excess pore pressures is much slower, and therefore, the changes of void ratio much more contained, except towards the end of the earthquake and close to the draining boundaries in the medium permeability case (Fig. 18b). For the low permeability case (Fig. 18c), the deformation of the soil occurs almost at constant volume, close to ideally undrained conditions.

Figure 19 shows the contour maps of shear strain $\gamma _{xy}$ at different time stations and the same values of the saturated permeability. In producing the contour maps of a quantity which spans over several orders of magnitude, the upper and lower limits in the color scale have been kept to relatively low values (from − 2 to + 2% in the high and medium permeability cases, to − 8 to + 8% in the low permeability case) to highlight the spatial distribution of $\gamma _{xy}$ in the low to medium strain range. For the case of high permeability (Fig. 19a), in which the soil deforms in almost drained conditions after the first 10 seconds of shaking, shear strains remain relatively small and tend to concentrate into two pairs of localized zones. On the active sides, they localize into two shear zones originating from their tips of the walls and propagating upwards, consistently with the expected kinematics of the walls, which are forced to rotate at their tops by the presence of the strut. On the passive side, the shear strains concentrate close to the soil–wall interface, due to the tendency of the soil to move upwards—in the deepest part of the passive zone, due to the wall rotations—or downwards—close to the bottom of the excavation, due to soil compaction.

Fig. 19

Loose sand case: contour maps of shear strain $\gamma _{xy}$ at different time stations. a High permeability ($k_s$ = 3.5E−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

When the permeability decreases (Fig. 19b and c), the shear deformation patterns in the active sides behind the walls remain qualitatively the same, although the magnitude of $\gamma _{xy}$ is much larger and the shear zones are wider, as a consequence of the larger wall rotations. The situation is much different in the passive zone, where the development of large excess pore pressures leads to a significant reduction in the mean effective stress level up to liquefaction towards the end of the shaking and thus to a significant reduction in soil stiffness. In such conditions, large deformations occur in the passive zone. These are almost purely deviatoric, due to the slow dissipation of $\Delta u_w$, see Fig. 18b, c. Shear strains now are not only localized at the soil–wall interface, but also diffused in the entire volume of soil below the excavation level.

6.3.2 Medium-dense sand

For the medium-dense sand case, the evolution in space and time of void ratio e and shear strains $\gamma _{xy}$ during the seismic event is given in Figs. 20 and 21, respectively. As time progresses, the general pattern of void ratio changes $\Delta e$ is very close to the one previously observed for the loose sand case, when soil permeability is high (Figs. 20a) or low (Figs. 20c), with almost drained behavior for the former case and almost undrained behavior for the latter. The largest volumetric strain experienced by the soil below the excavation level is now about 5% and, as expected, slightly lower than in the loose soil case. Things are somewhat different for the medium permeability soil, as the dissipation of excess pore pressures in the passive zone is faster than for the loose soil case, see Figs. 14b and 15b. Appreciable soil compaction now occurs in the passive zone towards the end of the seismic event.

Fig. 20

Medium-dense sand case: contour maps of void ratio e at different time stations. a high permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0E−4 m/s)

The contour maps of Fig. 21 indicate that the distribution of shear strain $\gamma _{xy}$ in the soil mass evolves with time in a very similar pattern as in the loose soil case for all the permeability values. However, the magnitudes of $\gamma _{xy}$ are now much smaller, particularly for the low permeability value.

Fig. 21

Medium-dense sand case: contour maps of shear strain $\gamma _{xy}$ at different time stations. a High permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

6.4 Soil and wall displacements

6.4.1 Loose sand

The contour maps of horizontal displacements computed for the cases of low, medium and high permeability in the loose sand case—taken either at the end of the earthquake (t = 28.44 s) or at the time station in which the displacement field in the passive zone becomes inaccurate due to the occurrence of liquefaction and of large wall rotations (t = 25 s for r03 and t = 12 s for r05)—are shown in Fig. 22.

Fig. 22

Loose sand case: contour maps of $u_x$ at the end of the earthquake or at failure. a High permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

As expected, given the previous observations on the time and space evolution of pore pressure and effective stress fields, large differences are observed in permanent soil and wall displacements as permeability decreases. The horizontal displacements close to the walls (Fig.22) range from a few centimeters in the high permeability simulation to several decimeters in the medium and low permeability simulations.

In general, the walls display a tendency to rotate rigidly around the strut. The larger the rotation, the smaller are the displacements due to wall bending. It is also worth noting that the displacement field is not necessarily symmetric about the excavation axis, as rightward or leftward movements may prevail depending on the accumulated inelastic strains. Therefore, the rigid body rotation of the wall around the strut can be considered a more significant global indicator of the seismic wall performance than the maximum displacement at the wall tip or at the excavation level.

A more detailed description of the kinematics of the retaining structure is given in Fig. 23 which, for all the simulations performed for the loose sand case, provides the time histories of the right wall rotation $\Theta$, defined as:

$$\begin{aligned} \Theta := \frac{u_{x,B}-u_{x,A}}{L} \end{aligned}$$

(12)

where $u_{x,A}$ and $u_{x,B}$ are the horizontal displacements of the points A (top of the wall) and B (bottom of the wall), see Fig. 4, while $L = H + d$ (= 14 m) is the total wall length. According to the definition of Eq. (12), $\Theta$ is positive for counterclockwise rotations and negative for clockwise rotations, which is the case of the right wall.

Fig. 23

Loose sand case: time histories of right wall rotation $\Theta$ (positive counterclockwise)

In all the simulations, $\Theta$ increases monotonically with time—except for small oscillations—until the maximum value is reached at the end of the earthquake. The value of $\Theta _{\max }$ increases significantly as the permeability decreases. In the figure, the horizontal dashed line represents the rotation at which the relative displacement $\Delta u_x := \left| {u_{x,B}-u_{x,A}}\right|$ between the top and the bottom of the wall is equal to 100 mm. This limit marks the difference between the cases in which wall movements can be considered relatively “small” and those where they are “large.” The data in the figure highlight clearly the importance of pore pressure buildup and of the soil ability to dissipate it rapidly on the performance of the retaining structure.

It is interesting to note that the evolution of wall rotations in time occurs relatively smoothly in the first 3 cases, in the time interval between 5 and 10 s, which corresponds to the most significant part of the input accelerogram. On the contrary, in the last two cases, the rotation experiences a sudden jump at $t \simeq$ 7 s. This is the result of the onset of soil liquefaction below the excavation level, with the rapid decrease in the soil support on the passive side of the wall.

Figure 24 shows the contour maps of vertical displacements computed for the cases of low, medium and high permeability in the loose sand case—taken either at the end of the earthquake or at the time station in which the displacement field in the passive zone becomes inaccurate due to the occurrence of liquefaction and of large wall rotations.

Fig. 24

Loose sand case: contour maps of $u_y$ at the end of the earthquake or at failure. a High permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

The larger effects are observed at the bottom of the excavation and in the active region of soil behind the walls. Again, the maximum displacements range from a few centimeters in the high permeability simulation to several decimeters in the medium and low permeability simulations. In all cases, the soil behind the walls experiences settlements in a well-defined wedge-shaped region, with a settlement through at the ground surface which extends for about twice the excavation height from the wall. The amount of surface settlements is of the same order of the horizontal wall displacements.

The soil at the bottom of excavation accumulates permanent settlements in the simulations with high and medium permeability, while a significant bottom heave is predicted for the low permeability case. This is due to the fact that in simulations r01 and r03 the contractant behavior of the soil, activated as soon as the excess pore pressure dissipate, prevails over the upward movements induced by the compression of the soil between the two rotating walls, whose movements are still relatively small in these two cases. On the contrary, in simulation r05 the deformation of the soil below the excavation occurs in almost undrained conditions, so the soil between the walls is forced to displace upwards by the very large rotations of the walls.

The details of the time evolution of vertical displacements at the bottom of the excavation—at point E, on the excavation centerline (Fig. 4)—are provided, for all the simulations of the loose sand case, in Fig. 25.

Fig. 25

Loose sand case: time histories of vertical displacement $u_y$ at the center of the final excavation surface (positive upwards)

The interplay between the soil compaction occurring as a consequence of excess pore pressure dissipation and the upward movement induced under almost undrained conditions by wall movements is clearly visible in the time histories of vertical displacements as permeability decreases. In simulation r01 (with the highest $k_s$), the dissipation of excess pore pressures is very fast while the rotation of the walls is minimal; the cyclic compaction of the soil, occurring mainly in the time interval between 5 and 10 s (with the largest accelerations), gives rise to significant settlements of the ground surface. On the contrary, in simulation r05 (with the lowest $k_s$), the response of the soil below the excavation level is almost undrained, thus isochoric, while the occurrence of soil liquefaction during the same time interval gives rise to very large wall rotations, accompanied by significant soil heave. In the intermediate cases, as permeability decreased, the excess pore water pressure dissipation becomes slower and an initial tendency towards heave is contrasted, in the last part of the earthquake event, by a subsequent time-dependent settlement.

6.4.2 Medium-dense sand

For the medium-dense sand case, the results obtained in terms of displacements are reported as in the previous section, with: the contour maps of horizontal displacements—taken either at the end of the earthquake (t = 28.44 s) or at the time station in which the displacement field in the passive zone becomes inaccurate (t = 12 s for r10)—given in Fig. 26; the time histories of the right wall rotation $\Theta$ shown in Fig. 27; the contour maps of vertical displacements, taken at the same time stations as for the horizontal displacements, shown in Fig. 28; and finally, the time evolution of vertical displacements at point E, at the bottom of the excavation, given in Fig. 29.

Fig. 26

Medium-dense sand case: contour maps of $u_x$ at the end of the earthquake or at failure. a High permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

Fig. 27

Medium-dense sand case: time histories of right wall rotation $\Theta$ (positive counterclockwise)

Overall, as the soil saturated permeability decreases, the patterns of soil and wall displacements around the excavation are qualitatively similar to the ones previously observed for the loose soil case. In particular, wall rotations are relatively small when the dissipation of excess pore pressures is fast, and very large when the pore pressure buildup with no or small dissipation induces a liquefaction process in the soil below the excavation level (simulation r10); vertical ground displacements at the bottom of the excavations change from negative (settlement) for high $k_s$ values to positive (heave) as $k_s$ decreases.

Fig. 28

Medium-dense sand case: contour maps of $u_y$ at the end of the earthquake or at failure. a High permeability ($k_s$ = 3.5e−2 m/s); b medium permeability ($k_s$ = 8.0e−3 m/s); c low permeability ($k_s$ = 3.0e−4 m/s)

Fig. 29

Medium-dense sand case: time histories of vertical displacement $u_y$ at the center of the final excavation surface (positive upwards)

The major difference observed in passing from loose to medium-dense soil is in the quantitative values of the predicted displacements, which are significantly smaller for the medium-dense sand case. In particular, only the last two simulations r09 (with $k_s$ = 4.0E−3 m/s) and r10 (with $k_s$ = 3.0E−4 m/S) show final wall rotations which appear larger than an acceptable threshold, yet they are about one half of the final rotations observed in the corresponding simulations r04 and r05 in loose sand. Moreover, the time history of $\Theta$ in these two cases does not show any abrupt increase with time.

The same considerations apply to the predicted bottom heave. When the effects of soil compaction are predominant, the higher density of the soil gives rise to smaller vertical settlements; when isochoric deformations prevail, the accumulated bottom heave is smaller than in the loose sand case due to the smaller wall rotations.

6.5 Seismic performance of the retaining structure

As relevant indicators of the seismic performance of the retaining structures, we have considered two specific features of their predicted seismic behavior: the final residual bending moments in the walls and the residual wall rotations (limited to the right wall only).

Figure 30 provides the final distributions of the absolute values of the bending moment, |M|, on the left and right walls, respectively, for both the loose sand case (Fig. 30a) and the medium-dense sand case (Fig. 30b). The plots in the figure report also the moment distributions computed at the end of the excavation stage (dashed lines) for reference.

Fig. 30

Post-seismic bending moment distributions (absolute values) on the left and right walls. a Loose sand case; b medium-dense sand case

In all the cases examined, regardless of soil saturated permeability or initial density, the post-seismic bending moments are much larger than the initial ones, at the end of the excavation, with only minor differences in the peak values (around 750 kNm/m, achieved at large $k_s$ values) between medium-dense and loose soils. This is due to the increased bending deformations induced on the two walls by the irreversible strains and permanent displacements accumulated during the earthquake event. As the saturated permeability decreases, and wall rotations increase, the rigid body rotation of the wall becomes predominant over its bending deformation mode. Therefore, the permanent bending moments tend to reduce with decreasing $k_s$, reaching a minimum for simulations r05 and r10 where wall failure due to soil liquefaction on the passive side is occurring. When the soil is initially loose, such an effect is also visible in simulations r04 and r03, with larger saturated permeabilities. This is not the case when the soil is initially medium dense, where only minor differences are observed in the moment distributions predicted in simulations r06–r09.

The effects of soil permeability and initial density on permanent wall rotations are summarized in Fig. 31, where the computed values of $\Theta$ at the end of the earthquake are plotted as a function of $k_s$. The figure also reports the specific values of wall rotations corresponding to relative displacements $\Delta u_x$ between top and bottom of the wall equal to 100, 150 and 200 mm, respectively. These values can be considered as possible acceptability limits for the seismic performance of the structure in terms of displacements.

Fig. 31

Post-seismic right wall rotations vs. soil saturated permeability (wall rotations positive counterclockwise)

As expected, $\Theta$ values monotonically decrease (in absolute value) with increasing $k_s$, with smaller permanent rotations for medium-dense sand as compared to loose sand. According to the performance limits indicated in the figure, an acceptable performance is predicted only for permeability values in the order of 1.0E−2 m/s. As the permeability decreases to 4.0E−3 m/s (about one order of magnitude), the seismic performance of the structure in all the cases considered degrades significantly, with an almost twofold increase in $\Theta$. For such high values of $k_s$, it would be tempting to consider the soil as fully drained. However, this would lead to a significant underestimation of the permanent rotation.

7 Concluding remarks

In this study, the effects of the hydrodynamical coupling between the solid skeleton and the pore fluids on seismic performance of an excavation supported by a propped diaphragm wall in a variably saturated sand layer have been explored by means of a series of dynamic nonlinear FE simulations, performed with an advanced hypoplastic model [54], extended to cyclic/dynamic loading conditions by means of the intergranular strain concept.

In particular, the effects of the initial relative density and of the saturated permeability of the soil have been considered. The first quantity controls the tendency of the soil to contract or dilate upon shear, and therefore the nature of excess pore pressure which may develop in the soil upon undrained or partially drained conditions. For a given seismic input and problem geometry, the second quantity controls the ratio between the characteristic time of the imposed seismic loading (i.e., the predominant period of the input accelerogram) and the characteristic time of the excess pore pressure dissipation within the soil mass.

The main results of the extensive FE simulation program presented in the previous sections can be summarized as follows. As far as horizontal accelerations at ground surface in free-field conditions and at the diaphragm wall crest are concerned, the effects of soil initial density and saturated permeability are almost negligible. This could be explained by the fact that: (i) the accelerations at both points are largely affected by the soil deformations in the upper unsaturated portion of the sand layer where, due to the low value of the degree of saturation, the response of the soil is largely unaffected by the permeability of the soil in saturated conditions, and (ii) the presence of the strut limits the possible horizontal deformations of the soil close to the top of the wall.

Things change dramatically when the response of the soil in terms of excess pore pressures buildup is considered. A strong influence of $k_s$ on $\Delta u_w$ is observed in the passive zone of soil below the excavation level. In the loose soil case, the cyclic accumulation of positive excess pore pressure in this zone generates a temporary liquefaction condition even in the simulation with the highest permeability. When soil permeability is very high, the subsequent hydrodynamic dissipation of these excess pore pressure brings the soil back to a non-liquefied condition towards the end of the earthquake event. When the soil permeability is relatively low, the soil confined between the two walls remains in a liquefied state up to the end of the earthquake event.

For the medium-dense soil case, the general pattern of excess pore pressure development with reducing permeability is quite similar to the one observed in the loose sand case, albeit with some slight quantitative changes in the computed values of $\Delta u_w$. In particular, persistent liquefaction of the passive zone of soil beneath the excavation level is predicted for the smaller values of soil permeability. This result is quite unexpected for a soil which—based on his high initial value of ${\mathcal {E}}$ (with $\mathcal {E}_0 > {\mathcal {E}}_c$)—could be considered as non-liquefiable. A possible explanation for this observation is to be found in the role played by the seismic-induced total stress changes in the passive region, which may give rise to changes in pore water pressure of the same order or larger than those induced by soil dilatancy upon shear.

Not surprisingly, when the seismic performance of the retaining structure is of concern, a similar dramatic effect is played by soil permeability, both in the loose and medium-dense soil cases. Taking as a reliable quantitative indicator of such performance the permanent rotation accumulated by one of the walls at the end of the earthquake event, it is clearly apparent from the results of Fig. 31 that the performance of the retaining structure deteriorates quickly passing from $k_s$ values larger than 1.0E−2 m/s to values smaller than 4.0E−3 m/s. Depending on the choice of an acceptable practical threshold for wall rotations, 3 of the 5 loose sand simulations and 2 of the 5 medium-dense sand simulations might lead to consider the structure as “unstable.”

It is important to note that the transition between “stable” and “unstable” behavior occurs in a relatively narrow range of permeabilities (about one order of magnitude). It is therefore quite important, during the site investigation, to obtain direct measurements of this property with a sufficient level of accuracy. It is also worth noting that all the $k_s$ values considered are relatively large: it is not infrequent that some natural sand deposit is characterized by a $k_s$ of the order of 1.0E−5 m/s [28], and the highest saturated permeability adopted can be considered a sort of upper bound for $k_s$ in sands. Therefore, at least for the upper range of $k_s$ values considered, it would be tempting to assume the soil as fully drained. The results of this study show that—for the specific seismic input considered—this assumption would lead to an unsafe assessment of the seismic performance of the structure.

For the particular seismic input considered, neither fully drained nor fully undrained conditions (except perhaps simulations r05 and r10 with the lowest saturated permeability) can be considered applicable. The quantitative assessment of wall and soil displacements, pore water pressures and effective stress distributions within the soil require necessarily the solution of a fully coupled, nonlinear dynamic consolidation problem.

It is quite possible that, by considering seismic inputs with different amplitudes and frequency contents, the impact of pore water pressure buildup and dissipation on the predicted response of the soil–structure system could be different. The influence of the characteristics of the seismic input on pore water pressure buildup and dissipation, as well as the impact of wall bending strength on the kinematics of the failure mechanism, is currently under investigation and will be discussed in forthcoming papers.

Appendix A: hypoplastic HPvW model

The general format of the hypoplastic constitutive equations for the von Wolffersdorff model [54] with intergranular strains read:

$$\begin{aligned} \dot{\varvec{\sigma }}\,=\, & {} \varvec{\mathsf {D}}\left( \varvec{\sigma },e,\varvec{\delta }\right) \dot{\varvec{\epsilon }} \end{aligned}$$

(13)

$$\begin{aligned} \dot{\varvec{\delta }}\,=\, & {} \varvec{\mathsf {H}}\left( \varvec{\delta }\right) \dot{\varvec{\epsilon }} \end{aligned}$$

(14)

where $\varvec{\mathsf {D}}$ and $\varvec{\mathsf {H}}$ are the tangent stiffness and hardening tensors, given by:

$$\begin{aligned}&\varvec{\mathsf {D}}= \left\{ \rho ^\chi +(1-\rho )^\chi \right\} \varvec{\mathsf {L}}+\varvec{\mathsf {A}} \end{aligned}$$

(15)

$$\begin{aligned}&\varvec{\mathsf {A}}= {\left\{ \begin{array}{ll} \rho ^\chi (1-m_T)(\varvec{\mathsf {L}}\varvec{\eta }_{\delta })\otimes \varvec{\eta }_{\delta }+\rho ^\vartheta \varvec{N}\otimes \varvec{\eta }_{\delta }&{} \text {for}~\varvec{\eta }_{\delta }\cdot \dot{\varvec{\epsilon }}>0\\ \rho ^\chi (m_R-m_T)(\varvec{\mathsf {L}}\varvec{\eta }_{\delta })\otimes \varvec{\eta }_{\delta }&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(16)

$$\begin{aligned}&\varvec{\mathsf {H}}= {\left\{ \begin{array}{ll} \varvec{\mathsf {I}}-\rho ^{\beta_r}\varvec{\eta }_{\delta }\otimes \varvec{\eta }_{\delta }&{} \text {for}~\varvec{\eta }_{\delta }\cdot \dot{\varvec{\epsilon }}>0\\ \varvec{\mathsf {I}}&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(17)

In Eqs. (15)–(17), the quantities $\varvec{\eta }_{\delta }:= \varvec{\delta }/\left\| {\varvec{\delta }}\right\|$ and $\rho := \left\| {\varvec{\delta }}\right\| /R$, with R a material constant, denote the direction of the intergranular strain tensor and its scaled norm, respectively. The constitutive functions $\varvec{\mathsf {L}}$ and $\varvec{N}$ are defined as follows:

$$\begin{aligned}&\varvec{\mathsf {L}}=f_bf_e\frac{1}{\text {tr}(\varvec{\eta }_{\sigma }^2)}\left[ F^2\varvec{\mathsf {I}}+a^{2}\varvec{\eta }_{\sigma }\otimes \varvec{\eta }_{\sigma }\right] \end{aligned}$$

(18)

$$\begin{aligned}&\varvec{N}=f_bf_ef_d\frac{1}{\text {tr}(\varvec{\eta }_{\sigma }^2)}aF\big [\varvec{\eta }_{\sigma }+\text {dev}(\varvec{\eta }_{\sigma })\big ] \end{aligned}$$

(19)

in which $\varvec{\eta }_{\sigma }:= \varvec{\sigma }/(3p)$; the functions F and a are provided by:

$$\begin{aligned}&F=\sqrt{\frac{1}{8}\tan ^{2}\psi +\frac{2-\tan ^{2}\psi }{2+\sqrt{2}\tan \psi \cos (3\theta ^*)}}-\frac{1}{2\sqrt{2}}\tan \psi \end{aligned}$$

(20)

$$\begin{aligned}&a = \frac{\sqrt{3}\left( 3-\sin \phi _c\right) }{2\sqrt{2}\sin \phi _c} \end{aligned}$$

(21)

with:

$$\begin{aligned} \tan \psi &= \sqrt{3}\left\| {\text {dev}(\varvec{\eta }_{\sigma })}\right\| & \cos (3\theta ^*) &= -\sqrt{6}\;\frac{\text {tr}[\text {dev}(\varvec{\eta }_{\sigma })^3]}{\left\| {\text {dev}(\varvec{\eta }_{\sigma })}\right\| ^{3}} = \cos \left( 3\theta +\frac{\pi }{2}\right) \end{aligned}$$

providing the stress ratio and the cosine of three times the Lode angle, respectively, while

$$\begin{aligned}&f_e=\left( \frac{e_c}{e}\right) ^\beta \end{aligned}$$

(22)

$$\begin{aligned}&f_d=\left( \frac{e-e_d}{e_c-e_d}\right) ^\alpha \end{aligned}$$

(23)

$$\begin{aligned}&f_b=\frac{\displaystyle \frac{h_s}{n}\left( \frac{1+e_i}{e_i}\right) \left( \frac{e_{i0}}{e_{c0}}\right) ^\beta \left( -\frac{3p}{h_s}\right) ^{1-n}}{\displaystyle 3+a^2-\sqrt{3}\, a\left( \frac{e_{i0}-e_{d0}}{e_{c0}-e_{d0}}\right) ^\alpha } \end{aligned}$$

(24)

are the pyknotropy and barotropy functions, respectively. The characteristic values (loosest, critical and densest) of the void ratio are given by:

$$\begin{aligned} \frac{e_i}{e_{i0}} = \frac{e_c}{e_{c0}} = \frac{e_d}{e_{d0}} = \exp \left\{ -\left( \frac{3\left| {p}\right| }{h_s}\right) ^n\right\} \end{aligned}$$

(25)

as a function of the mean effective stress p.

The model is fully characterized by 14 material constants, 8 for the standard model ($\phi _c$, $h_s$, $e_{i0}$, $e_{c0}$, $e_{d0}$, n, $\alpha$, $\beta$) and 6 for the intergranular strain extension (R, $\beta _r$, $m_R$, $m_T$, $\chi$, $\vartheta$).