Cyclic and creep combination effects on the long-term undrained behavior of overconsolidated clay

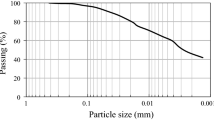
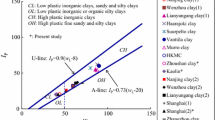
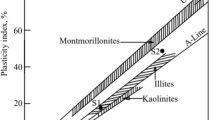
Abstract

Soft soil subjected to cyclic loading typically exhibits an increase in excess pore pressure under undrained condition which brings the soil to an overconsolidated state. Then, under a subsequent large number of cycles (e.g. more than one million) which also takes time, the creep at overconsolidated state influences the cyclic effect and thus results in a complicated long-term undrained behavior. This paper aims to clarify this long-term undrained behavior of overconsolidated clay. The reconstituted samples are prepared from natural samples retrieved in the north of France. First, the shear strength characteristics along monotonic triaxial stress paths are identified. Then load control cyclic tests on overconsolidated specimens are conducted in fully saturated and undrained conditions. Small cyclic deviatoric stresses are applied in order to investigate more particularly the behavior under a very large number of cycles, during which an unusual pore pressure evolution is observed. To explain this, undrained triaxial creep tests are performed on reconstituted specimens with different values of OCRs under some specified stress states. The evolutions of axial strain, excess pore pressure, stress ratio, stress path, plastic strain rates and stress dilatancy during undrained creep are discussed. The additional undrained creep tests also show that two processes are simultaneously acting in a competitive manner: increase in the pore pressure due to the cyclic loading and decrease in the pore pressure because of creep.

Appendix: Determination of plastic strain rates

The undrained triaxial condition implies null volumetric strain $\left( {{\text{d}}\varepsilon_{\text{a}} + 2{\text{d}}\varepsilon_{\text{r}} = 0} \right)$. Thus, during undrained creep the incremental deviatoric strain can be obtained:

$$ {\text{d}}\varepsilon_{\text{d}} = \frac{2}{3}({\text{d}}\varepsilon_{\text{a}} - {\text{d}}\varepsilon_{\text{r}} ) = {\text{d}}\varepsilon_{\text{a}} $$

(A1)

Because of the null change of the deviatoric stress during undrained creep test, the elastic deviatoric strain increment is null. Therefore, Eq. (A1) can be used for the incremental plastic deviatoric strain.

The null volumetric strain condition also implies the relationship “dε ^p_ν  = − dε ^p_ν ” between plastic and elastic volumetric strains. Thus, the increment of plastic volumetric strain can be obtained by the change of mean effective stress due to the generation of excess pore pressure (dp′ =− du), as follows:

$$ {\text{d}}\varepsilon_{\text{v}}^{\text{p}} = \frac{du}{K} $$

(A2)

with the bulk modulus $K = \left( {1 + e_{0} } \right)p^{{\prime }} /\kappa$ and $p^{{\prime }} = p_{0} + \Delta q/3 - \Delta u$.