Deterioration of an infrastructure cutting subjected to climate change

Abstract

Observations show that many soils in linear geotechnical infrastructure including embankments and cuttings undergo seasonal volume changes, and different studies confirm that this is due to cycles in climatic and hydrological conditions. These cycles can give rise to progressive failure of the soil mass, which in turn may lead to deterioration of performance and ultimately slope failure. It is expected that the magnitude of the seasonal cycles of pore pressure will be increased by more extreme and more frequent events of wet and dry periods predicted by future climate scenarios. In this paper, numerical modelling has been undertaken to simulate a continuous time series pore water pressure within a representative cutting in London Clay. The approach uses synthetic control and future climate scenarios from a weather generator to investigate the potential impacts of climate change on cutting stability. Surface pore water pressures are obtained by a hydrological model, which are then applied to a coupled fluid-mechanical model. These models are able to capture the significant soil–vegetation–atmospheric interaction processes allowing the induced unsaturated hydro-mechanical response to be investigated. The chosen hydraulic conductivity variables in the model are shown to affect the total magnitude of pore pressure fluctuation and hence the rate of progressive failure. The results demonstrate for the first time that higher total magnitude of annual variation in pore pressures caused by future climate scenarios can have a significant effect on deformations in cuttings. This in turn leads to increased rates of deterioration and reduces time to failure.

Introduction

There is now agreement within the scientific community that the climate is changing and those changes have been quantified for a number of scenarios within the UK [36, 38]. Engineers must assess how that change will affect infrastructure in order to prepare to minimise disruption [41] and financial risk [18]. Natural slopes and infrastructure cuttings constructed within a clay material are susceptible to seasonal changes in pore water pressures during infiltration. These changes have been continuously monitored by a number of authors [14, 34, 56, 61, 67, 69]. These changes in pore pressures over time can be correlated with variable meteorological conditions [62, 63]. In turn, understanding the effect of these meteorological conditions and vegetation-driven processes such as suction generation, shrink-swell and desiccation cracking along with the potential implications of climate variability on stability are identified as being important [22, 30, 41, 46, 48, 66, 75]. As such a number of researchers have undertaken numerical modelling studies to investigate soil–atmosphere interactions and effects of meteorological boundary conditions on natural and engineering slopes [24]. An initial numerical approach to address soil–atmosphere interaction relied on the application of this representative climate boundary in the form of a suction to a slope surface [43, 53]. The above methodology was able to demonstrate non recoverable plastic deformation of the modelled slope that led to failure. However using this technique the effect of hydraulic conductivity was not accounted for. Following this, the hydrological model was improved upon in the work of Nyambayo et al. [51] so that variations in the hydraulic conductivity resulted in variation in the modelled pore water pressures, demonstrating that hydraulic conductivity can affect the mechanical response of an embankment. More recently, Rouainia et al. [57] undertook modelling work making use of daily meteorological data allowing the modelling of the gradual transition between seasonal pore pressure conditions. The effect of changing vegetation on stability during the lifecycle of slopes has been investigated, demonstrating that vegetation contributes to increased stability due to rooting reinforcement and the generation of large suctions, however this in turn can negatively impact serviceability [8, 32, 49, 70]. These modelled results are supported by field observations [10]. Emphasis has been placed on understanding the effect of antecedent weather conditions including rainfall and temperature on slope hydrology, serviceability and stability [4, 33, 68].

The primary meteorological related mechanism, which affects slopes, are the changes in effective stress as a result of infiltration and extraction of water [66]. This in turn, affects the stability of the slope [68]. Changes in pore pressures are often seasonal and cyclic and can lead to volumetric changes with swelling during saturation and shrinking under drying [72]. Successive cycles may cause non-recoverable deformations which in turn may lead to strain softening and ultimately failure of the slope [45, 65]. Strain magnitudes can be seen to be directly related to the magnitude of pore pressure variation. Therefore, to estimate seasonal deformation it is necessary to model the flow of water into, out of and through a slope [24], whereby infiltration into the slope surface will occur during precipitation events and extraction of water will occur due to evapotranspiration [3, 19]. A significant control on the infiltration and removal of water from the soil is the effective hydraulic conductivity, which determines the rate at which water can infiltrate into the soil and move upwards through the soil column to ultimately be extracted at the surface [10, 21]. Evapotranspiration rates are therefore dependent on the degree of saturation of the soil column, reducing from the potential rate as the degree of saturation decreases and reaching zero at soil suctions equal to the permanent wilting point of the vegetation [15]. In cases where the rate of precipitation exceeds the infiltration rate of the soil or where the phreatic level rises to the surface, run-off or ponding will occur. Run off can be estimated by a number of analytical or empirical methods. These methods commonly rely on physical parameters to describe slope gradient, length (and therefore energy) and soil/water frictional properties [7].

This paper further develops the methodology described by Rouainia et al. [57], and for the first time, uses it to simulate a continuous time series pore water pressure within a representative cutting. The approach adopted is to employ synthetic control and future climatic data from the UKCP09 weather generator. The effects of the synthetic climate on pore water pressure cycles and subsequent changes in effective stress are then modelled in order to investigate the rate of deterioration due to progressive failure and how this process is likely to be exacerbated in the future.

Modelling strategy

The focus of the work presented here has been concentrated on climate impact analysis. A hydrological model, SHETRAN [1, 27], capable of simulating a wide range of processes affecting slope pore water pressures (including hourly meteorological inputs, the capability to model infiltration, evapo-transpiration and overland flow) was used to derive daily near surface pore water pressures, which were used as the surface boundary condition in the fully coupled hydro-mechanical finite difference code FLAC Two-Phase Flow [37], leading to (un)saturated flow and pore pressure changes causing mechanical deformation. Flow model verification and validation of the pore pressure transfer method are detailed within Davies et al. [16] and use in modelling a natural slope failure is summarised in Davies et al. [17]. In summary this method enables the simulation of temporal deformations of a slope as a response to weather and, over long time periods, climate.

Hydrological model

In SHETRAN the subsurface is modelled as a porous, heterogeneous medium with variable saturation [26]. Vegetation behaviour in SHETRAN is simulated using a modified version of the Rutter et al. [58] model for rainfall interception. This controls canopy water storage, evaporation from the stored water on the canopy, as well as precipitation throughfall and stemflow and is described in Abbot et al. [1]. A root water uptake model is also included where user specified root density and depth along with a relationship between pore water suction and transpiration, controls vegetation root water uptake behaviour.

SHETRAN uses the extended Richard’s equation to describe variably saturated flow. This is given in its pressure form for two dimensions in terms of saturated conductivity, $(k_{x}^{\mathrm{w}}, k_{z}^{\mathrm{w}})$, relative conductivity, $k_{\mathrm{r}}$, pressure potential, $\psi$, and the volumetric flow rate for flow out of the medium $q_{\mathrm{t}}$ (actual transpiration) as follows: [1, 54]:

$$\begin{aligned} \eta \frac{\partial \psi }{\partial t}=\frac{\partial }{\partial x}\left[ k_{x}^{\mathrm{w}}k_{\mathrm{r}}\frac{\partial \psi }{\partial x}\right] +\frac{\partial }{\partial z}\left[ k_{z}^{w}k_{\mathrm{r}}\frac{\partial \psi }{\partial z}\right] +\frac{\partial (k_{\mathrm{r}}k_{z}^{\mathrm{w}})}{\partial z}-{q_{\mathrm{t}}} \end{aligned}$$

(1)

where $\eta$ is the storage coefficient defined using specific storage, $S_{\mathrm{s}}$, porosity (assumed to be the same as saturated volumetric water content), $\theta _{\mathrm{s}}$, volumetric water content, $\theta$ and the pressure potential as:

$$\begin{aligned} \eta = \frac{\theta S_{\mathrm{s}}}{\theta _{\mathrm{s}}}+\frac{\mathrm{d}\theta }{\mathrm{d}\psi } \end{aligned}$$

(2)

$S_{\mathrm{s}}$ is a function of the compressibility of the soil and is derived as follows [74]:

$$\begin{aligned} S_{\mathrm{s}} = \rho _{\mathrm{w}}g\left( \frac{1}{K}+\theta _{\mathrm{s}}\frac{1}{K_{\mathrm{w}}}\right) \end{aligned}$$

(3)

where $\rho _{\mathrm{w}}$ is the fluid density, g is gravatational acceleration, K is the bulk modulus of the soil and $K_{\mathrm{w}}$ is the fluid bulk modulus (2.2 GPa). The surface boundary flux due to surface evaporation ($q_{\mathrm{e}}$) and rainfall reaching the ground surface ($q_{\mathrm{p}}$) where no surface ponding has occurred is given by the following:

$$\begin{aligned} k_{\mathrm{r}}k^{\mathrm{w}}_{z}\left( \frac{\partial \psi }{\partial z}+1\right) =q_{\mathrm{p}}-q_{\mathrm{e}} \end{aligned}$$

(4)

Whenever ponding has occurred, the surface boundary flux switches to a head condition based on the depth of the ponded water.

Mechanical model

In the SHETRAN model used in this work, potential evapotranspiration (PET) is converted into actual evapotranspiration (AET) based on the magnitude of soil suction. To disaggregate potential transpiration (PT) from potential evaporation (PE), assumptions must be made about the ground vegetation cover. As such PT is a function of the area of ground surface covered by vegetation in plan view, known as the plant leaf area index ($p_1$). The proportion of PET assigned to transpiration is equal to $p_1$ and that to PE is equal to the area of bare ground ($1-p_1$). PT is distributed across the defined rooting depth ($d_{\mathrm{r}}$), with proportions allocated to differing depths within the rooting zone, equal to the proportion of the total root mass ($n_{\mathrm{r}}$) at depth $d_{\mathrm{r}}$. PT is in turn scaled to actual transpiration ($q_{\mathrm{t}}$) by SHETRAN as a function of soil suction for each defined section of the root zone (see Table 2) and PE is scaled to actual evaporation ($q_{\mathrm{e}}$) based on the suction at the soil surface. This is based on the approach of Feddes et al. [28]:

$$\begin{aligned} q_{\mathrm{t}}(d_{\mathrm{r}})=\alpha _{\mathrm{r}}p_1PT \end{aligned}$$

(5)

where $\alpha _{\mathrm{r}}$ varies as a function of the matric suction as per Fig. 1. From this, four specific values of matric suction can be identified. $\psi _{\mathrm{m}}^\mathrm{a}$ which is the anaerobiosis suction, below this suction root water uptake does not occur ($\alpha _{\mathrm{r}}$ = 0), at suctions greater than this value, $\alpha _{\mathrm{r}}$ increases, reaching a maximum at $\psi _{\mathrm{m}}^{1}$. This represents the lower limit of the readily available water (RAW) range, the upper limit being at $\psi _{\mathrm{m}}^{2}$. Within this range $\alpha _{\mathrm{r}}$ = 1 and evapotranspiration occurs at the potential rate. Above this suction value ($\psi _{\mathrm{m}}^{2}$), plant stress begins to occur where with increasing suction, $\alpha _{\mathrm{r}}$ begins to fall, reaching zero at the permanent wilting point ($\psi _{\mathrm{m}}^{\mathrm{w}}$). $\psi _{\mathrm{m}}^\mathrm{a}$ to $\psi _{\mathrm{m}}^{\mathrm{w}}$ represents the totally available water (TAW) range. "Appendix 1" gives the vegetation model and parameters used for the canopy model used in SHETRAN. For further information see Abbot et al. [1].

Fig. 1

Limiting function on root water uptake due to matric suction. See Table 1

Fluid flow in FLAC is a function of the pore water, $p_{\mathrm{w}}$ and pore air, $p_{\mathrm{g}}$, pressures. These are related to the matric suction, $p_{\mathrm{m}}$, whereby $p_{\mathrm{m}}=p_{\mathrm{g}}-p_{\mathrm{w}}$. To describe the soil water retention curve (SWRC) which is the relationship between $p_{\mathrm{m}}$ and the effective saturation, $\theta _{\mathrm{e}}$, SHETRAN and FLAC use the closed form version of the van Genuchten equation [27, 71]:

$$\begin{aligned} p_{\mathrm{c}}(S_{\mathrm{w}})= \frac{\rho _{\mathrm{w}}g}{\alpha }\left[ \theta _{\mathrm{e}}^{-1/m}-1\right] ^{1-m} \end{aligned}$$

(6)

The coefficients $\alpha$ and m were derived here by curve fitting. In turn, $\theta _{\mathrm{e}}$ can be related to $\theta$ or the degree of water saturation, $S_{\mathrm{w}}$, as follows:

$$\begin{aligned} \theta _{\mathrm{e}} =\frac{\theta -\theta _{\mathrm{r}}}{\theta _{\mathrm{s}}-\theta _{\mathrm{r}}}=\frac{S_{\mathrm{w}}-S_{\mathrm{r}}}{1-S_{\mathrm{r}}} \end{aligned}$$

(7)

where $\theta _{\mathrm{r}}$ and $S_{\mathrm{r}}$ are the residual volumetric moisture content and residual water saturation, respectively. In FLAC, the flow velocities for the wetting ($q_\mathrm{i}^{\mathrm{w}}$) and non-wetting ($q_\mathrm{i}^{\mathrm{g}}$) fluid are calculated as follows [37]:

$$\begin{aligned} q_\mathrm{i}^{\mathrm{w}}&= -\frac{k_{\mathrm{r}}^{\mathrm{w}}}{g\rho _{\mathrm{w}}}\frac{\partial }{\partial x_\mathrm{j}}(p_{\mathrm{w}}-\rho _{\mathrm{w}}g_\mathrm{k}x_\mathrm{k}) \end{aligned}$$

(8)

$$\begin{aligned} q_\mathrm{i}^{\mathrm{g}}&= -\frac{k_{\mathrm{r}}^{\mathrm{g}}}{g\rho _{\mathrm{w}}}\frac{\partial }{\partial x_\mathrm{j}}(p_{\mathrm{g}}-\rho _{\mathrm{g}}g_\mathrm{k}x_\mathrm{k}) \end{aligned}$$

(9)

where $\mu _{\mathrm{w}}/\mu _{\mathrm{g}}$ are the fluid and gas viscosities defining the viscosity ratio and $\rho _{\mathrm{w}}$ and $\rho _{\mathrm{g}}$ are fluid and gas densities. In FLAC and SHETRAN, the unsaturated hydraulic conductivity of the soil to the fluid, $k^{\mathrm{w}}_{\mathrm{r}}$, and the gas phases, $k^{\mathrm{g}}_{\mathrm{r}}$, at a given effective saturation, $\theta _{\mathrm{e}}$, are derived using the van Genuchten-Maulem equation [71]:

$$\begin{aligned} k_{\mathrm{r}}^{\mathrm{w}}&= k^{\mathrm{w}}(\theta _{\mathrm{e}})^{0.5}\left[ 1-\left( 1-\theta _{\mathrm{e}}^{\frac{1}{m}}\right) ^m\right] ^2 \end{aligned}$$

(10)

$$\begin{aligned} k_{\mathrm{r}}^{\mathrm{g}}&= k^{\mathrm{w}}\frac{\mu _{\mathrm{w}}}{\mu _{\mathrm{g}}}(1-\theta _{\mathrm{e}})^{0.5}\left[ 1-\theta _{\mathrm{e}}^{\frac{1}{m}}\right] ^{2m} \end{aligned}$$

(11)

The surface non-wetting pore pressure was fixed at atmospheric in the modelling undertaken here, however wetting and non-wetting pressures were free to develop within the model and in turn influence the capillary pressure and hence effective stress (see the mechanical model section for more information).

Recent field work undertaken at Newbury to measure in-situ hydraulic conductivity [21] has demonstrated that the near surface values (<1m depth) are significantly higher than at greater depths. This region has been incorporated into the model as a zone of elevated hydraulic conductivity (1.0$\times$10$^{-8}$ m/s) in the uppermost elements. Below this region, a mean effective stress ($p'$) dependent relation was used to define the saturated hydraulic conductivity ($k^{w}$) distribution with depth within the model taking the following form [73]:

$$\begin{aligned} k^{\mathrm{w}}=k_\mathrm{ref}\times \exp ^{\mathrm{ap}'} \end{aligned}$$

(12)

where $k_\mathrm{ref}$ is the reference hydraulic conductivity at zero mean effective stress and a is a parameter describing the change in conductivity with $p'$ ($a=-0.003$ [44]).

In this work SHETRAN has been used to model the meteorologically driven seasonal fluctuations in pore water pressure and FLAC Two-Phase Flow has been used to create the fully coupled hydro-mechanical models. The primary mechanism of deterioration examined in this work is progressive failure attributed to strain softening of the soil mass. Previous numerical modelling studies of slope stability in London Clay adopted the use of a strain softening Mohr–Coulomb constitutive model with effective stress dependent elastic parameters to model the mechanical response and potential progressive failure of infrastructure slopes and cuttings [25, 43, 51, 53, 55, 57]. A similar constitutive model is adopted in this work (see Fig. 2).

In FLAC the linear momentum balance and mass balance equations are discretised in space and time at each node of the finite deference mesh and solved simultaneously using explicit algorithms. At each time step, grid point quantities such as velocity, displacement, pore pressures and saturation are evaluated based on previous values. The Updated Lagrangian approach is adopted, whereby the grid point co-ordinates are changed as deformation progresses and the constitutive law is then invoked to update the effective stress based on the strain increment and the previous stress state. This cycle occurs within a single time step, $\Delta t$, the size of which is calculated by the code as a function of the minimum element size, $L_{\mathrm{e}}$, and the compressive wave velocity, $V_{\mathrm{p}}$:

$$\begin{aligned} \Delta t=\frac{L_{\mathrm{e}}}{V_{\mathrm{p}}} \end{aligned}$$

(13)

where $V_{\mathrm{p}}$ is a function of the density, $\rho$, and the bulk, K, and shear, G, moduli of the material. During cycling, in the event of plasticity, the stress state is returned to the strain softening Mohr–Coulomb yield surface. For partially saturated materials, the plasticity models in FLAC Two-Phase Flow use a Bishop’s effective stress, $\varvec{\sigma }'$, formulation with the following form:

$$\begin{aligned} \varvec{\sigma '}=\varvec{\sigma }-(S_{\mathrm{w}}p_{\mathrm{w}}+S_{\mathrm{g}}p_{\mathrm{g}})\varvec{I} \end{aligned}$$

(14)

where $\varvec{\sigma }$ is total stress, $S_{\mathrm{g}}$ is the degree of saturation of the air phase ($S_{\mathrm{g}}=1-S_{\mathrm{w}}$) and $\varvec{I}$ is the identity vector. It has been recognised that the phenomenon of wetting-induced collapse is not well captured by the Bishop’s effective stress. However, it is generally accepted in the literature that the increase of shear strength with suction can be determined by this form of unsaturated effective stress and is also valid for high degree of saturations when the air phase is discontinuous, such as the conditions in this work. The selection of an unsaturated effective stress has been the subject of considerable debate [29, 40, 50].

To derive the stiffness of the London Clay used in the model, a constant value of Poisson’s ratio is adopted and the Young’s modulus, E, of the London Clay used in the model was dependent on $p'$ based on the following relation [55]:

$$\begin{aligned} E=25\times (p'+100)\geqslant 4000\,\text {kPa} \end{aligned}$$

(15)

To describe the strength of the material the Mohr–Coulomb strain-softening constitutive model was utilised where a post failure reduction in strength occurs at user specified plastic shear strain increments ($\Delta \varepsilon ^{ps}$).

$$\begin{aligned} \Delta \varepsilon ^{ps}&= \frac{1}{6}\left[ (2\Delta \varepsilon _{1}^{\mathrm{ps}}-\Delta \varepsilon _{3}^{\mathrm{ps}})^2+(\Delta \varepsilon _{1}^{\mathrm{ps}}+\Delta \varepsilon _{3}^{\mathrm{ps}})^2\right. \nonumber \\&\quad\left. +(2\Delta \varepsilon _{3}^{\mathrm{ps}}-\Delta \varepsilon _{1}^{\mathrm{ps}})^2 \right] ^\frac{1}{2} \end{aligned}$$

(16)

in which $\Delta \varepsilon _{j}^{\mathrm{ps}},\,(j=1,3)$ are the principal plastic shear strain increments. To quantify the degree of softening, the residual factor, $R_\mathrm{f}$, for the failure surface is calculated as follows [60]:

$$\begin{aligned} R_\mathrm{f}=\frac{\tau _{\mathrm{p}}-\tau }{\tau _{\mathrm{p}}-\tau _{\mathrm{r}}} \end{aligned}$$

(17)

where $\tau$ is the current shear strength available on the slip surface, $\tau _{\mathrm{p}}$ and $\tau _{\mathrm{r}}$ are the peak and residual shear strengths, respectively.

Fig. 2

Conceptual strain softening behaviour adopted for London Clay

Climate scenarios

In this work the UK Climate Projections 2009 (UKCP09) weather generator [42] was used to produce rainfall and PET time series data representative of control and future climates which were applied to the SHETRAN slope model as boundary conditions. UKCP09 makes use of a period between 1961–1995 to derive baseline weather statistics in order to calibrate the weather for a control climate period [39].

The UKCP09 methodology makes use of a stochastic rainfall generator to produce rainfall time series that match the observed rainfall statistics as closely as possible, from which the other weather parameters (temperature, humidity, sunshine duration and solar radiation) are generated based on statistical correlations between the individual parameters and rainfall. These time series represent statistically plausible synthetic weather data for use as a baseline control climate period. The control climate synthetic weather datasets along with climate change factors from the future climate projections are used to create a future climate scenario by scaling the rainfall events and altering their annual distribution and in turn altering the dependent weather parameters. From these, PET is calculated by the weather generator using the Food and Agriculture Organization (FAO) modified version of the Penman–Monteith equation to derive reference evapotranspiration [3]. For a full description of this process the readers are referred to Jones et al. [39] and Ekström et al. [23].

For this paper, two time series outputs were generated both representing the weather for a 5 km grid containing the Newbury cutting. The first output represented a 100 year long baseline control climate, the second represented 100 years of progressively more extreme future climate from 2000 to 2100. It should be noted that the weather generator synthesises future climate data between 2020 and 2090. Therefore, the initial 20 years of weather data from 2000 to 2020 have been obtained by upscaling the control climate based on the average rainfall and PET, which have been interpolated between the average for the control period and 2020. The final decade has the same climate change properties as 2080–2090, since there was no data available to attempt to extrapolate change factors outside of the dataset. A 5 year period of the control climate weather data is also used to condition the SHETRAN model used for validation before applying the site monitored data. To assess the potential impacts of climate change on a slope, two separate climate scenarios were considered. The first scenario represented a climate control period intended as a baseline for comparison with the second, which represented a potential future climate scenario, showing progressive changes from 2000 through to the 2090s.

To put the climate scenarios used for this work into context with the broader UKCP09 projections, the cumulative sum of monthly surface water balance (SWB) derived from the difference between rainfall and PET (SWB = Precipitation—PET) are compared to the same data for one hundred differing control and future climate UKCP09 scenarios (see Fig. 3). Positive values represent net flow into the slope surface and negative values a net loss. From this plot the influence of the increased rates of PET predicted by a future climate on the SWB when compared to the control climate become apparent, whereby the control climate models all show a continued trend of net water addition to the surface (SWB: Max = 31,161 mm, Mean = 22,047 mm, Min = 15,024 mm), whereas the future climate models indicate greater variability and that the increased rates of PET in many cases lead to dryer conditions than the control data (as is the case for the modelled future climate), and in extremis even a potential net loss of water due to PET exceeding rainfall (SWB: Max = 27,794 mm, Mean = 13,398 mm, Min = $-1180$ mm). When considering the modelled data, the selected control climate yields a cumulative water balance of 21,183 mm versus 13,222 mm for the future climate. As such the future climate model will be significantly drier than that of the control climate.

Fig. 3

Cumulative surface water balance for a control climate scenarios and b future climate scenarios

Model validation

In order to validate the hydrological model’s ability to capture meteorologically driven pore pressure changes in a slope, a model of Newbury Cutting was created in SHETRAN. Monitored weather data from Newbury were applied as a boundary condition and the resultant modelled pore pressure time series was compared to the site monitored data.

Previous work has used the replication of undrained triaxial test data to validate the mechanical response of a strain softening model for London Clay [55]. This approach is adopted here to validate the ability of FLAC to capture the single element undrained behaviour. The softening parameters are then applied to a numerical model of cut slope excavation resulting in dissipation of excavation induced pore pressures which in turn cause strain softening. The time to failure of this model is compared to the published results [55].

Hydrological model validation

In order to have increased confidence in the hydrological model for the representative cutting, data from a real slope was required. It was decided to make use of the Newbury cutting due to the prior publication of data [61, 62]. However it should be noted that the aim of this work was to develop a model representative of transport infrastructure cut slopes in high plasticity clays in general and not to undertake a specific back analysis of Newbury. Where possible the model is informed first by laboratory and field data from Newbury, second by previously published data from the site, and then where gaps in the data set existed these were in turn filled by published field and laboratory data, or from modelling exercises performed from similar sites.

The slope is an east facing 8 m high and 28 m long cutting on the A34 in Southern England. The profile of the slope can be seen in Fig. 4. The cutting was constructed in 1997 and has been extensively monitored by Smethurst et al. [61, 62]. The pore-water pressure monitoring instruments from which the validation data were derived, were installed in four boreholes spaced 6 m apart (labelled A–D in Fig. 4). The cutting was made in London Clay, which is approximately 20 m thick in the area of interest. The cutting material consisted of predominately stiff grey clay with several thin layers of silty clay and flint bands. Vegetation on the slope comprised rough grass and herbs with some small shrubs less than 0.5 m in height [61]. A canopy of trees was set back behind the crest of the slope.

Fig. 4

Newbury slope geometry

Seasonal pore pressure changes within the Newbury cutting were monitored by Smethurst et al. [61, 62]. This included on site monitoring of weather data and near surface suction measurements using tensiometers. The precipitation and PET from this weather data were used as inputs for a SHETRAN hydrological model of the site. The results of this modelling were compared to the tensiometer data in order to demonstrate that the model is capable of replicating seasonal pore pressures cycles as observed in the field.

Initial conditions for the hydrological validation model

An initial pore pressure distribution was applied to the model in order to replicate post construction conditions. This was followed by 6 years of synthetic control climate weather data from the UKCP09 weather generator, which was applied to condition the model for the period from 1997 to 2003, prior to the application of the site monitored precipitation and PET. The synthetic weather data generation is described in Sect. 3. This weather data covered the period ranging from Jan. 2003 to the end of 2008.

The London Clay at the site is described as a van Genuchten-Maulem material with parameters derived from the drying portion of the soil water retention curve (SWRC) [61] in conjunction with published SWRC parameters for London Clay [9, 13]. The SWRC and resultant hydraulic conductivity functions (HCF) are summarised in Fig. 5 and the corresponding input parameters are shown in Table 1. The hydraulic conductivity was assumed to be depth dependent (derived from the mean effective stress [44]).

Fig. 5

Soil water retention curve for London Clay adopted in this work after [61, 62]

Table 1 London Clay hydrological parameters [9, 61]

Figure 6 depicts the hydraulic conductivity profiles used in the modelling undertaken herein. The figure incorporates published hydraulic conductivity profiles used in previous modelling [44, 55] along with field monitoring data [20, 31] which helped to constrain the range of investigated hydraulic conductivities. The slope surface was modelled as having a grass cover, using a root water uptake plant limiting function based on that published by Feddes et al. [28] and described in Sect. 2. The canopy interception model is described in "Appendix 1" and the vegetation parameters applied in the model are summarised in Table 2.

Fig. 6

Hydraulic conductivity distributions for London Clay

Table 2 Vegetation parameters—for more detail see "Appendix 1"

The modelled pore water pressures and site monitored tensiometer data at 0.3 m depth corresponding to instrument groups A and C [61, 62] can be seen in Fig. 7. It can be observed that the timing of annual cycles of suction generation and dissipation in the SHETRAN model and the recorded data are in reasonable agreement, however, the magnitude of the cycles is underestimated in the model. The model also seems to be more effective at replicating the extreme wet years in 2007 and 2008 than the extreme dry summers of 2003 and 2004. This could be explained by the absence of hysteresis behaviour in the SWRC adopted in the analysis.

Fig. 7

Modelled and monitored pore pressure data at Newbury a group A and b group C [9, 61]

Mechanical model validation

The dissipation of construction generated pore pressures along with the adopted strain softening parameters will have a significant effect on the response and time to failure of a modelled cut slope. As such it was necessary to validate the FLAC model to ensure it was capable of replicating this behaviour. The validation consists of a modelled undrained triaxial test compared to published laboratory and model data as well as replicating a previously published cut-slope model.

The mechanical parameters used for the validation of the Mohr–Coulomb strain softening model are summarised in Table 3. The model adopts the same stiffness, strength and softening parameters as those used in [55]. Dilation angle has been set to zero due to the likely thickness of sheared zones and the resultant excessive generation of pore pressures due to volume change that would occur if a non-zero value were used. This is thought reasonable in the absence of site specific data and reflects previous work [25, 53, 55, 70].

Table 3 Material properties

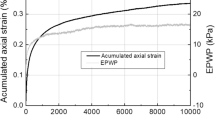
Figure 8 shows the stress–strain and pore pressure responses during the undrained triaxial test. It can be seen that the model simulation of the stress–strain behaviour is in good agreement with the experimental data and with that published in [55]. However, the pore pressure generated during shearing is slightly underestimated.

Fig. 8

Validation of strain softening model based on undrained triaxial test data from Brown London Clay. a stress:strain response and b pore pressure response [59]

In addition, a representative slope scale example was selected in which data on failure mechanism, shear surface progression, and time to failure were available [55]. The model selected was the 10m high, 3:1 slope which using the published shear strength parameters, initial and boundary stress and hydraulic conductivity distribution failed after approximately 14.5 years due to partial dissipation of excess pore suctions at the slope toe [55]. The FLAC model was initialised with a hydrostatic pore water pressure distribution with a phreatic line situated 1 m below the upper model boundary, representative of a UK winter condition [52, 73] as used in [55]. The base and side boundaries were set to be impermeable to air and water flow. To replicate the behaviour of the published model slope, the wetting saturation was fixed at 1 throughout the grid for the cutting excavation and pore pressure dissipation phases. The hydraulic conductivity distribution applied was that adopted in [55] (see the associated profile in Fig. 6). In-situ stresses were initialised assuming a coefficient of earth pressure at rest, $K_0$ equal to 1.5.

The strength and stiffness values adopted for the initial comparison are reported in Table 3. Laboratory and field data indicate that at large strains there is a further reduction in shear strength with a total loss of cohesion [6, 11, 47]. As such, capturing this behaviour is important in problems where large plastic strains are anticipated and so an additional segment was added to the softening curve. The revised strength and strain softening properties adopted for the London Clay are also summarised in Table 3 and the conceptual softening model adopted is summarised in Fig. 2.

Excavation of the cutting was undertaken to match that of the validation example and once excavation was complete a suction of 10 kPa was applied to the model surface. During model stepping, histories of horizontal displacement at the mid slope surface were recorded. The model was allowed to step until failure occurred. Once this was completed, the exercise was repeated for the revised strength properties simulating a total loss of cohesion and further reduction of friction angle at large strains (summarised in Table 3).

The mid slope displacements for the two models are recorded in Fig. 9. The plot indicates that using the parameters originally adopted by Potts et al. [55] the model fails after approximately 15.25 years, however the deformation rate starts to increase after approximately 13.5 years. It should be noted that the model with a residual cohesion of zero at large strain fails after 14 years due to the greater loss of strength and additional shedding of stress onto neighbouring soil elements on the failure surface leading to more rapid failure. This phenomena is discussed in detail in Leroueil [45].

Fig. 9

Horizontal mid-slope displacement of a 1:3 10m high cut slope in London Clay from start of excavation through to failure

This validation procedure demonstrates that SHETRAN is able to replicate the timing of seasonal pore pressure cycles at the near surface effectively, however, their total magnitude is underestimated in very dry years. This validation, in combination with prior work [5] gives confidence that the hydrological model can predict meteorologically driven pore pressure changes. The mechanical modelling demonstrated that FLAC was able to describe the softening behaviour seen for London Clay in an undrained triaxial test, however, pore pressure generation was underestimated. The slope scale modelling showed that FLAC can be used to accurately estimate the time to failure of a cut slope model and that the use of large strain residual strength parameters can have an influence on the modelled time to failure.

Application of the control and future scenarios to the cut slope model

In this section the modelled stability of cut slopes representative of Newbury (as described in Sect. 4) which are subject to varying climates are summarised. The model grid used for this work can be seen in Fig. 10 and makes use of $0.8\,\hbox {m}^{2}$ elements.

Fig. 10

FLAC grid used for the coupled hydro-mechanical modelling of Newbury to undertake the climate study

Initial conditions, cutting construction and climate boundary conditions

London Clay has undergone extensive overconsolidation which has been shown to influence the stand up time of cut slopes in stiff clays (see for example [25, 55]). A value of $K_{0} = 1.5$ was selected for application to the models in this work based on field observations [35]. Further to this, it was deemed to be relatively conservative as a low value of $K_{0}$ will result in lower values of mean effective stress. In turn this leads to decreased stiffness and strength, which when combined with an increased rate of pore pressure dissipation due to the resultant elevated hydraulic conductivity at a given depth within the models, will lead to accelerated failure. The initial pore water pressure distribution was hydrostatic with a phreatic surface 1 m below the upper model boundary, representative of a UK winter condition [52, 73] as used in [55]. The construction of the cutting was simulated in 10 equal stages of 0.8 m height. The model was stepped for a period of ten days after each excavation phase leading to a 100 day excavation period.

The pore water and pore air pressures were free to vary during cutting excavation. The climate boundary is applied to the FLAC model in the form of surface pore water pressures extracted from each of the surface zones of the SHETRAN model as a daily time series along with a pore air pressure of zero. The resultant FLAC surface fluid saturation is calculated from the pore pressure. This was repeated for each day within the fully coupled FLAC model until the total prescribed model run time of 100 years was reached or failure was detected.

Modelling scenarios

For the initial climate impact assessment, the control and future climate scenarios were applied to the Newbury cut slope model using a hydraulic conductivity profile with $k_\mathrm{ref} = 2.5\times 10^{-9}$ m/s and $a=-0.003$ (see Eq. 12 and Fig. 6). These baseline models best demonstrate the effect of a control versus future climate on time to failure of a representative cutting in London Clay. To determine the impact of the differing hydraulic conductivity distributions on stability, the base line simulations in FLAC were repeated using the hydraulic conductivity distributions summarised in Fig. 6 and Table 3.

Pore water pressures

In order to interpret the pore pressure behaviour it is useful to have an understanding of the net surface flow which is a function of rainfall and PET. Figure 11 shows the surface water balances and pore pressure variations in the mid-slope (see Point 1 and 2 in Fig. 10) for both the control and future climate simulations. The assumption of stationarity for the control climate means that there is no change in average rates of PET over time and hence no increase in typical near surface summer suctions when compared to the pore pressures generated within the future climate model. Post excavation excess pore pressure dissipation is evident from 2000 to 2020 at 5.6 m below surface, with this process being largely complete at shallow depth by 2007.

Fig. 11

a Control climate surface water balance, b control climate mid-slope pore pressures, c future climate surface water balance, d future climate mid-slope pore pressures for hydraulic conductivity profile 3

In a number of cases where the total summer suction is low ($<-$ 20 kPa pore water pressure) the summer near surface suctions are entirely dissipated by wet events. This is a combination of relatively high summer rainfall dissipating the suctions, a resultant elevated near surface relative hydraulic conductivity making the model react more rapidly to following wetting events and lower than average rates of PET during these summers. The future climate pore water pressures display a more complex trend due to the changing climate over time. Broadly, this can be split into two periods. An initial period from 2000 to 2030 where behaviour is similar to that of the control data, and then from 2030 onwards where the climate becomes progressively warmer with resultant increases in PET and hence progressively larger suctions. Also of note is the wet period from 2027 to 2030 where net water balance is wholly positive leading to low summer suctions.

In the period before 2030, Fig. 11d shows that at 5.6 m depth post construction pore pressure dissipation is largely complete by 2020 for the future climate model. This matches the behaviour seen in the control climate model (Fig. 11b) and is a function of the small difference between the control climate and the initial 20 year period of the future climate.

Post 2030 there is a clear increase in summer suctions through time due to the increasing summer drying seen in the surface water balance. Post 2050, the pore water pressures at depth are starting to be suppressed by the elevated suctions and no longer return to their typical winter value ($\approx$ 50 kPa). From Fig. 10 it can be seen that the near surface annual suction cycles become progressively larger over time in the future climate model when compared to the same location in the control climate simulation.

The elevated suctions of the future climate model surface pore pressures are down to several mechanisms, which include:

• High temperatures leading to increased rates of evapotranspiration

• Increased evapotranspiration draws water out of the slope leading to lower saturation at the near surface

• Lower saturation leads to reduced relative hydraulic conductivity which reduces water movement within the slope and leads to the development of larger suctions but reduces the ability of surface recharge due to rainfall to allow their dissipation

• Increased rainfall rate and a lower relative hydraulic conductivity leads to increased run-off and reduced infiltration

This will have a number of implications; increased pore pressures during winter cause a reduction in effective stress and volume increase. Conversely, suction during the summer months results in increased effective stress and volume reduction. Plastic strains are induced by this cyclic movement which can, over several cycles, lead to strain softening at the toe which progresses through the slope. This seasonal down slope ratcheting with softening has been described by Leroueil [45] and Take and Bolton [65].

Mechanical response

The rate of lateral displacement for the two scenarios is initially very similar with both slopes under going approximately 0.2 m of modelled displacement by 2030 (see Fig. 12a and b). A significant portion ($\approx 80\%$) of this displacement occurs in the first five years after construction, which coincides with construction induced displacements and initial rapid dissipation of excavation induced pore pressures (see Fig. 12c and d). The residual factor remains at zero for both the control and future climate models for the first two years before an initial increase occurs (see Fig. 12e and f). This is due to the initiation of softening at 5% plastic shear strain affecting the toe of the slope. As pore pressure equilibrium occurs, the rate of softening and deformation reduce, coinciding with the halt of the rapid dissipation of pore pressures seen in Fig. 11. A continuation of dissipation of excess pore pressure at a reduced rate through to 2030 causes further deformation in both the control and future climate models, with slightly larger increase in residual factor and larger displacements in the future climate model which are attributed to the larger total magnitude of seasonal pore pressure cycles.

Fig. 12

Mid-slope horizontal displacement: a control climate; b future climate. Mid-slope pore pressure: c control climate; d future climate. Residual factor for (potential) slip surface: e control climate; f future climate. All simulations use hydraulic conductivity profile 3 ($k_\mathrm{ref} 2.5\times 10^{-9}\,\hbox {m/s}$)

Post 2030, both the control and future climate experience a succession of relatively dry summers (2031–2036), which cause a spike in near surface suctions and a suppression of pore pressures at depth, which correspond with an increase in the residual factor and an increase in the rate of deformation. During this period the models start to diverge in terms of mid slope displacement and deterioration of shear strength (evidenced by the differing rates of increase in residual factor).

Post 2050, the two models have diverged even further with the future climate experiencing approximately 0.35 m of displacement (vs. 0.25 m for the control climate) and the residual factor has increased to a value of 20% on the failure surface (vs. 10% for the control climate model). This appears to be a function of the differing magnitude of pore pressure cycles with the control climate slope undergoing cycles from 8 kPa to a max. negative pore water pressure of of approx. $-25$ kPa versus $-60$ to $-80$ kPa for the future climate model.

The effect of hydraulic conductivity on cut slope stability

The effect of hydraulic conductivity when modelling the stability of embankments has been investigated in the past by Nyambayo et al. [51] and Rouainia et al. [57]. They found that increased hydraulic conductivity led to increased deformations and an accelerated rate of failure in a diagnostic embankment. That trend also appears to be true for the modelled cutting in this work, however there is also a change in timing and mechanism with decreases in hydraulic conductivity for the future climate models (see Fig. 13). At hydraulic conductivity values greater than $2\times 10^{-10}$ m/s there is an increase in time to failure as hydraulic conductivity decreases for all modelled hydraulic conductivity distributions subjected to both control and future climates. This trend continues at lower hydraulic conductivity values for the control climate slope models. Time to failure varies from 50 years for the highest hydraulic conductivity slopes ($1\times 10^{-8}$ m/s), to greater than 100 years for control climate models with hydraulic conductivities greater than $2.5\times 10^{-9}$ m/s. For future climate models, the time to failure increases from 44 years ($1\times 10^{-8}$ m/s) through to 96 years ($5\times 10^{-10}$ m/s). For future climate models with hydraulic conductivities less than $5\times 10^{-10}$ m/s there is a change to a shallower failure mechanism and a resultant decrease in time to failure of approximately 87 years versus greater than 100 years for the control climate models. It seems clear that this increased stability with decreasing hydraulic conductivity is in part a function of the slower dissipation of post construction pore pressures as seen in Fig. 13.

Fig. 13

Mid-Slope horizontal displacement and pore pressures for varying hydraulic conductivity distributions (see chart labels) and climate scenarios

Typical failure mechanisms can be seen in Fig. 14. For the higher hydraulic conductivity models it can be seen from Fig. 14a and b that the failure mechanisms are rotational and deep seated. This is due to the elevated hydraulic conductivity allowing the construction induced negative pore pressure to dissipate more rapidly. Furthermore, the size of the seasonal pore pressure cycles at depth are larger than those obtained with lower hydraulic conductivities (see Fig. 13) , causing accelerated deterioration. The low hydraulic conductivity models subject to a future climate show suppressed pore pressures at 5.6 m depth (approx. 50% of their equilibrium value) from 2030 to 2060 but a steadily increasing surface deformation, this is interpreted as the development of the near surface residual zone which in these models appears to increase in depth with time. The near surface deformation begins to accelerate post 2070 coinciding with a pore pressure increase at depth. Ultimately, this leads to a shallow rotational failure. The pore pressure increase, coincident with this event, is thought to be due to the deformation as a result of the climate driven softening and is a function of the hydromechanical coupling of the model. This near surface deterioration along with the shallow failure can be seen in Fig. 14c and d, where significant softening at the near surface has occurred which is absent from the future climate models with increased hydraulic conductivity (Fig. 14a and b). This near surface deterioration would likely coincide with desiccation cracking, which would further reduce strength and increase near surface hydraulic conductivity. This behaviour is not captured in this model as further field and laboratory work would be required to derive the necessary parameters for London Clay to implement one and then validate it.

Fig. 14

Displacement vectors at failure for slopes with varying hydraulic conductivity distributions

Conclusion

In this work, a methodology has been described for modelling the progressive failure of a cut slope due to fluctuations in pore water pressure as driven by meteorological boundary conditions. This methodology was applied to a model of a cut slope in stiff, high plasticity clay representative of the Newbury cutting. The work demonstrated that capturing the reduction of shear strength parameters to residual values at large strains ($\approx$100%) has implications for time to failure. The annual total magnitude of fluctuation of pore pressure was found to be significant in controlling the rate of progressive failure. In the control climate models, average annual variation is lower than for the future climate, in which the higher total magnitude of annual variation in pore pressures causes elevated rates of softening compared to the control climate scenario at the near surface. This leads to a more rapid deterioration in strength, and ultimately contributes to future climate slopes failing more rapidly than those subject to the control climate.

In both the control and future climate slopes, the value of saturated hydraulic conductivity plays a key role in controlling time to failure, whereby the lower the hydraulic conductivity of the material, the longer the stand up time of the cut slope. In this instance, this is primarily related to the decreasing rate of dissipation of construction-induced suctions within the slope. All control and future climate models with elevated hydraulic conductivity undergo deep seated rotational failure mechansism following a period of pore pressure equilibration coupled with climate cycling. This differs from the future climate models with lower hydraulic conductivity ($< 5\times 10^{-10}\,\hbox {m/s}$) where failure takes the form of a shallower rotational slip, which is preceded by significant near surface deterioration. This would potentially have implications for serviceability.

The reduction in strength due to pore pressure equilibration along with seasonal cycling is essentially a deterioration process which this modelling approach captures. However, it is worthwhile mentioning that the larger magnitudes of pore pressure cycling at the near surface in lower hydraulic conductivity materials are in turn likely to cause increased desiccation behaviour. It is suggested that this phenomenon needs to be investigated further in order to allow the development and validation of improved constitutive and numerical tools.

Appendix 1

Root water uptake ($\alpha _{\mathrm{r}}$) is simulated by scaling the PET as a function of soil suction with linear interpolation between the specified points with root water uptake falling to zero at the plant permanent wilting point (1500 kPa) based on the model of [28]. The proportion of water removed at varying root depths is controlled by $n_{\mathrm{r}}$ with the water extraction distributed at user specified proportions of AET and rooting depths. The values of the parameters adopted in this work are summarised in Table 2.

The uptake of water by roots from the soil leading to transpiration losses and the infiltration and evaporation from the ground surface were described in Sect. 2, however the net rainfall ($q_{\mathrm{p}}$) in Eq. 4 is a function of a vegetation canopy model based on that of Rutter et al. [58] described in more detail here.

The model calculates net rainfall reaching the ground which is a function of canopy rainfall interception, rain through fall (i.e. that proportion of rain not intercepted by any part of the canopy), canopy water storage, canopy evaporation and canopy drainage.

The amount of rainfall intercepted by the canopy is the proportion of ground in plan view covered by vegetation, known as the plant leaf area index ($p_1$). The area of bare ground (and hence the proportion of the rainfall assumed to fall though the canopy) is therefore $1-p_1$. The vegetation canopy is assumed to have a storage capacity S (this can be thought of as a depth of water that can be stored on the canopy). S also limits the maximum water that can be stored by the vegetation canopy before drainage losses occur (equal to a water depth on the canopy of 1.5 mm). The total available area for this storage is known as the canopy leaf area index ($p_2$) and is defined as the ratio of total leaf area to the area of ground covered by vegetation. $p_2$ may be greater than unity as depending on the vegetation type, leaves may overlie one another.

A proportion of this stored water will be lost by evaporation from the leaf surface, E, and some by drainage from the canopy, Q. The rate of these losses is controlled by the ratio of actual stored water, $C_{\mathrm{s}}$, to the storage capacity, S. As $C_{\mathrm{s}}$ is seen to equal or exceed S, evaporation will occur from the canopy at the potential rate (this causes root water uptake to drop to zero). If $C_{\mathrm{s}}$ drops below S, then the rate of evaporation from stored water on the canopy is scaled according to the ratio of $C_{\mathrm{s}}$ to S (and root water uptake may restart depending on soil suction and PET).

The rate of change of canopy storage due to drainage, $\delta C_{\mathrm{s}}=\delta t$, is assumed to be zero while $C_{\mathrm{s}}$ is less than S, drainage only begins to occur once $C_{\mathrm{s}}$ equals or exceeds S at a rate controlled by the equation shown in Fig. 15 where Q is the canopy drainage, $C_{\mathrm{b}}$ is the fractional rate of change of drainage with respect to storage (5.1 1/mm) and $C_\mathrm{k}$ is the leaf drainage rate when $S = C_{\mathrm{s}}$ ($1.4\times 10^{-5}\,\hbox {mm/s}$).

FLAC requires assumptions to be made about the wetting and non wetting fluids in order to derive hydraulic conductivity based on their relative viscosities. Fluid viscosity ($\mu _{\mathrm{w}}$) is a function of fluid temperature and can be calculated for the wetting fluid (assumed to be water in this work) using the following [2]:

$$\begin{aligned} \mu _{\mathrm{w}}&= a10^{b/(T_{\mathrm{w}}+c)} \end{aligned}$$

(18)

in which a ($2.414\times 10^{-5}$), b (247.8) and c (133.15) are constants and $T_{\mathrm{w}}$ is the fluid temperature ($12\,^\circ\, \hbox {C}$).

The non-wetting fluid is assumed to be air and the non-wetting fluid viscosity ($\mu _{\mathrm{g}}$) is estimated using Sutherland’s equation [64] which is dependent on temperature as follows:

$$\begin{aligned} \mu _{\mathrm{g}}&= \mu _{0}\left( \frac{T_\mathrm{g0}+C_{\mathrm{s}}}{T_{\mathrm{g}}+C_{\mathrm{s}}}\right) \left( \frac{T_{\mathrm{g}}}{T_\mathrm{g0}}\right) ^{\frac{3}{2}} \end{aligned}$$

(19)

where $\mu _{0}$ is the reference viscosity ($1.72\times 10^{-5}\,\hbox {Pa s}$) at the reference temperature $T_\mathrm{g0}$ ($273.15\,^\circ \hbox {K}$), $T_{\mathrm{g}}$ is the non-wetting fluid temperature ($285.15\,^\circ \hbox {K}$) and $C_{\mathrm{s}}$ is Sutherland’s constant (110.4).

The temperature was assumed to be $12\,^\circ \hbox {C}$ based on the work by Busby [12], which indicates that seasonal temperature fluctuations are attenuated at depths of around 5m and these values approximate the annual average, which at the nearest measurement point to Newbury (Reading) is equal to $12\,^\circ \hbox {C}$. This yields a value for $\mu _{\mathrm{g}}$ and $\mu _{\mathrm{w}}$ of $1.78\times 10^{-5}$ Pa-s and $1.23\times 10^{-3}$ Pa-s, respectively. In turn the viscosity ratio ($\mu _{\mathrm{w}}/\mu _{\mathrm{g}}$) is equal to 69.15.

Fig. 15

Conceptual model of interception loss implemented in SHETRAN based on the Rutter model