Abstract
The self-boring pressuremeter (SBP) test was designed to measure in situ engineering properties of the ground with a relatively small amount of disturbance. The properties that may be inferred from the test depend on the mechanical model used for its interpretation and on the significance given to other previously available information. In this paper, numerical modelling using the advanced kinematic hardening structure model (KHSM) for natural soils has been performed to investigate the influence of the initial structure and the degradation of structure on the SBP cavity pore pressures and expansion curves within London Clay. The validation of the KHSM against well-known analytical solutions and the calibration procedure used to identify the material parameters are presented. The numerical analyses reveal that the simulations of the SBP tests using the KHSM model provide a very close match of the expansion curves to the experimental data, but underestimate the pore pressures at the initial stage of the SBP expansion test. A parametric study has been carried out to determine the effects induced by the parameters of the destructuration model along with the disturbance experienced during the SBP installation, which is difficult to estimate in situ. Two disturbance scenarios were considered where the initial structure was assumed to vary linearly across an area close to the wall of the cavity. These simulations indicate that accounting for installation disturbance leads to a substantial improvement in pore pressure predictions for the SBP.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The mechanical response of soils in terms of stiffness and strength is dependent on the stress state and stress history prior to testing. However, clays cannot be described only by current stress and overconsolidation ratio (OCR); the description should also include structure. For soils in general, structure has been defined as the combined effect of soil fabric and the bonding between particles [38]. Compared with clays reconstituted in the laboratory, natural clays generally exhibit extra strength and are able to exist at a higher void ratio than the equivalent reconstituted soils at a given stress [8, 34]. These characteristics have significant engineering implications.
The effects of structure in laboratory observations have been well captured by numerous constitutive models. Just within the elastoplastic framework, [5, 31, 47, 61] explicitly account for structure and damage to structure. Some of these models have been implemented in finite element (FE) codes and are available for use in boundary value problems. For instance, the kinematic hardening structure model (KHSM) proposed by Rouainia and Muir Wood [47] has been implemented in a finite element procedure and subsequently used, amongst other applications, to analyse short-term displacements around a tunnel excavation in London Clay [20] and a deep excavation in Boston Blue Clay [49], as well as to investigate the failure height of a full-scale embankment on a soft clay [43]. It was shown that the initial structure strongly affected some important simulation outcomes such as tunnel lining loads and embankment failure height. The relevance of the initial structure has been confirmed by other researchers using analogous formulations [59].
Despite this, the uptake of models incorporating structure in geotechnical practice has been limited. A significant obstacle for practical application of advanced models is difficult calibration and/or initialisation [52]. Indeed, available procedures for quantification of structure and related parameters involve relatively elaborate laboratory tests on high-quality samples. In many circumstances, this is not feasible and alternative procedures, preferably based on in situ tests, would be beneficial. Within the framework of classical critical state soil mechanics, Mayne [37] has advocated the use of in situ testing in the initialisation of state variables, such as OCR. The role of laboratory testing should be to provide model parameters, preferably those not very sensitive to sampling-induced disturbance. This idea was extended by González et al. [21] to elastoplastic models incorporating structure. They argued that reference or reconstituted properties of soils featuring in such models should be obtained from laboratory test data, while structure and other initial state variables should be retrieved from in situ test results. They also identified the self-boring pressuremeter (SBP) as the most suitable in situ test for that purpose because it can be analysed using relatively simple models and introduces little disturbance in the soil [1].
Pressuremeters have been classically analysed using a cylindrical cavity expansion analogy. This reduces the problem to one spatial dimension and allows analytical solutions even for relatively complex constitutive models [14, 16, 54]. One-dimensional numerical analysis is possible and efficient even for highly advanced constitutive models or coupled analysis [30, 39, 51]. This contrasts with the more involved numerical procedures that are required to simulate other in situ tests, such as the cone penetration test (CPT) [40, 41]. The SBP was also conceived as an instrument that will cause minimal disturbance in the soil during installation [4, 6, 11]. However, later research has shown that the insertion of a SBP into the ground is not always perfect [2, 17, 33, 35, 46, 53]. Installation defects such as overdrilling, underdrilling and partial pushing may all take place as the instrument is advanced into the soil.
In this work, the potential use of the SBP as a tool for structure quantification in clay is further explored. To this end, the KHSM is used to analyse a series of SBP tests performed as part of an actual site investigation. The material investigated is London Clay, for which much previous work is available on its geotechnical characteristics and likely stress history. We take advantage of the ample experience with kinematic hardening models and, in particular, a previous calibration of the KHSM [20, 22] to focus on structure, structure-related parameters and possible damage to structure during installation. In the following, we describe the case study and the numerical model employed for the analysis of the SBP tests, before the obtained results are presented and conclusions are drawn.
2 Case study
2.1 London Clay
London Clay is characterised as a very stiff and heavily overconsolidated fissured clay and was deposited in marine conditions approximately 30 million years ago during the Eocene period. The London Clay Formation comprises a sequence of marine silty clays, clayey and sandy silts, and subordinate sands [25]. A combination of biostratigraphy and lithological variation suggested a division of the London Clay Formation into five principal units, named A to E in a bottom-up succession [32]. In the majority of the London area, only the lower part of the sequence is preserved, i.e. units C and below. This subdivision of the London Clay is useful for geotechnical purposes because it helps in the comparison and correlation of data across different sites. The presence and effects of structure of London Clay were examined in detail during the geotechnical investigations motivated by the construction of Heathrow Airport Terminal 5. Gasparre et al. [19] tested samples of natural London Clay along with reconstituted samples. The existence of structure was apparent; for instance, they observed that the state boundary line was significantly higher for the natural clay than for the reconstituted samples. As summarised by Hight et al. [26], the structure of London Clay affected its peak shear strength, compression behaviour and permeability. A further useful distinction highlighted in the research was between structure and nature for London Clay units. The nature of the clay would influence its intrinsic behaviour, whereas structure would separate the mechanical response of different lithological units. There is an extensive literature discussing constitutive models for London Clay. Although other approaches have proved useful in the past [29], there is a growing trend towards formulations based on elastoplastic kinematic hardening approaches [3, 5, 23, 24, 57].
2.2 Test location
The Denmark Place site is located in central London, to the south-east of the junction of Charring Cross Road and Andrew Borde Street. The geological map indicated that the site was underlain by Quaternary River Terrace deposits followed by the London Clay Formation then the Lambeth Group and the Thanet Sand formation, which in turn overlie the White Chalk Subgroup at depth. The existing topography and history of development of the site indicated that in addition to these natural strata, made ground may be present on the site. This profile was confirmed by boreholes. Ground conditions at the site were fairly uniform, with the groundwater table encountered at a depth of 5.6 m below ground level. The site investigation comprised of a number of laboratory tests (identification, state and UU and CIU triaxial tests) on soil specimens retrieved with a driven U100 sampler. That sampling method is known to cause disturbance [10] imposing strains [13] that would significantly modify soil structure. In situ testing comprised of SPT and self-boring pressuremeter (SBP) tests. The SBP tests were performed by Cambridge Insitu Ltd, using a SBP of the Cambridge design [28]. Average values of the liquid limit and plasticity index of London Clay at the Denmark Place site were 67% and 40%, respectively. The bulk unit weight was calculated as 20 kN/m\(^3\). These values are in line with previous measurements on other sites [25].
Denmark Place is in close proximity (\(\approx\) 500 m) to the Royal Opera House, a site for which detailed profiles have been presented by Hight et al. [25] amongst others. SPT measurements taken at both sites indicate a quite similar soil profile (Fig. 1a). SPT profiles, however, are not useful for delineating the different units of London Clay, a purpose for which water content profiles are far better [58]. The water content profiles at Denmark Place and the Royal Opera House are compared in Fig. 1b, c, respectively. Taking then as a cue the lithology boundaries identified at the Royal Opera House, a tentative London Clay unit division has been indicated on the Denmark Place profile.
Soil profile and identification of lithological units in London Clay: a SPT values, b water content at Denmark Place site and c water content at Royal Opera House [25]
3 Model description
3.1 Finite element model
The fundamental assumption that the pressuremeter test can be simulated as the expansion of an infinitely long cylindrical cavity has been reported by Collins and Yu [14]. This essentially reduces the problem to one dimension as any movement of the membrane will occur in the radial plane. The SBPs used on the site had characteristics (membrane length-to-diameter ratio above 6; cavity strain deduced from displacement sensors at the central plane) that made the cylindrical cavity approximation reasonable. Although this study could have been addressed using a dedicated one-dimensional FE model such as [50], an axisymmetric 2D model (Fig. 2) was used instead, as the KHSM was already implemented in a general stress space finite element code [45]. The two-dimensional axisymmetric idealised geometry of the self-boring pressuremeter was constructed with approximately 110 15-node triangular elements in order to avoid mesh-dependent results [56]. To avoid the influence of the external boundaries, the geometry was extended 30 times the initial cavity radius \(a_0\) [21, 53, 62]. Simulation took place assuming fully undrained conditions.
3.2 Constitutive model
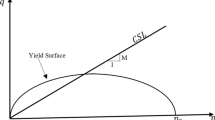
The KHSM model [47] is an elastoplastic kinematic hardening model. The model contains three surfaces. The smaller (bubble) surface is the yield surface containing the elastic domain of the soil and moves around within the larger structure surface. The structure surface reduces to a reference bounding surface for structureless soils. The degree of structure, r, describes the relative sizes of the structure and reference surfaces. The reduction in r takes place through an exponential damage law:
where \(r_0\) denotes the initial structure, k is a parameter that describes the rate of destructuration process with strain, and \(\lambda ^*\) and \(\kappa ^*\) are the slope of the normal compression line and the slope of the swelling line, respectively. The increment of the destructuration strain \(\delta {\varepsilon _d}\) will be assumed to have the following form:
where A is a non-dimensional scaling parameter and \(\delta {\varepsilon }_q^p\) and \(\delta {\varepsilon }_v^p\) are the increments of plastic shear strain and plastic volumetric strain, respectively. For more details on the formulation and implementation of the KHSM, see [47, 63].
The nonlinear elastic behaviour is assumed to be described by the following equation proposed by Viggiani and Atkinson [60]:
where \(A_G\), n and m are dimensionless stiffness parameters which were estimated using the plasticity index of London Clay, \(p_r\) is a reference pressure which is usually taken equal to 1 kPa and \(R_0 =2p_c/p_0\) is the overconsolidation ratio with \(p_c\) being the intrinsic preconsolidation pressure (the mean effective stress that defines the size of the reference surface).
3.3 Model validation
The numerical model was validated against the well-known analytical results obtained by Collins and Yu [14], which presented cavity expansion solutions for a soil obeying the modified Cam Clay model (see Table 1). When the initial structure is null (\(r_0\)=1), the KHSM model reduces to modified Cam Clay through an appropriate choice of parameters (e.g. R=1). Four cavity expansion tests were simulated under an isotropic initial state (\(\sigma '_r\)=\(\sigma '_y\) =\(\sigma '_z\)=170.8 kPa) with varying degrees of isotropic overconsolidation (OCR=1, 4, 15, 30 and 50). Cavity wall was expanded to double the size of the initial cavity (\(a/a_0\)=2). The values of the excess pore pressures at the cavity wall were then recorded and normalised by the theoretical triaxial compression undrained shear strength of the soils, \(S_u\), given by Muir Wood [42]:
Figure 3 shows that the magnitude of the predicted excess pore pressures is in good agreement with the analytical results.
Normalised excess pore water pressures for various OCR: Comparison of KHSM predictions and analytical results [14]
3.4 Model calibration
The nonlinear elastic model has three material parameters: \(A_g\), n and m [60]. The values of these (\(A_g\)=590, n = 0.87, m = 0.28) were all assigned using the empirical correlations with plasticity index proposed by the original authors. From the site investigation results, an average plasticity index \(I_p\) = 40% was selected for this purpose.
Using reconstituted samples, Gasparre and Coop [18] determined some intrinsic parameters common for the different LC units. These parameters are reproduced here in Table 2. Some fundamental soil properties are more reliable than others. In the absence of test data from the Denmark Place site, the material parameters of London Clay which describe the intrinsic properties of the soil such as \(\lambda ^*\), \(\kappa ^*\) and M were fixed from the start and were set to 0.097, 0.003 and 0.87, respectively. These parameters were derived for a kinematic hardening model (M3-SKH) by Grammatikopoulou et al. [24]. Also associated with the intrinsic properties of a soil are the basic kinematic hardening parameters: bubble size, R, and the plastic modulus parameters, B and \(\psi\). These were calibrated for London Clay by González et al. [20], for the analysis of a tunnel excavation, and were assumed, respectively, as \(R=0.016\), \(B=4.0\) and \(\psi =6.0\).
The plastic parameters related to structure in KHSM are k and A (see Eqs. 1 and 2). For A, a value of 0.75 was adopted. This value implies that the contribution of the plastic volumetric strains in the destructuration process is 3 times higher than the contribution of the plastic deviatoric strains. This assumption was in accordance with observations by Callisto and Rampello [9] who stated that the plastic volumetric strains contribute to structure degradation is 2 to 3.5 times more than the plastic deviatoric strains.
The parameter k, which controls the rate at which destructuring occurs with strain, will have a significant effect on the soil stress–strain response. González et al. [20] obtained values of between 0.5 and 1.25, by matching the triaxial response of intact T5 London Clay samples. However, that calibration was poorly constrained, because the effect of k is mostly seen on post-peak responses, which for the London Clay specimens were strongly affected by pervasive shear localisation. On the other hand, simulations for softer natural clays, where the post-peak response is better defined, typically require destructuration rate values almost one order of magnitude higher [43, 47]. No significant effect of the value of k was observed in the St James’ tunnel case study [20] due to the small strain level dominant in that problem. For pressuremeter tests to attain much larger strains, the same assumption could not be made. As such, it was tentatively decided to initially assign relatively large values to this parameter to ensure the model was capable of capturing this behaviour, fine-tuning them as necessary to reproduce the observed SBP response.
3.5 Model initialisation
The KHSM model requires initialisation of five variables: initial stress state, intrinsic preconsolidation pressure of the soil, \(p_{c0}\), initial position of the bubble centre, the magnitude of the initial structure, \(r_0\), and structure-induced initial anisotropy, \(\eta _0\). A stress history simulation of the site was performed to initialise stress and intrinsic preconsolidation pressure. Stress history simulations aim to represent the geological processes of deposition and erosion [44]. The amount of eroded material varies throughout both the London and Hampshire Basins [15]. At St James’ Park, similar work with other kinematic hardening models [24] had assumed about 180 m of erosion. Given the proximity of Denmark Place to St James’ Park, the same value was assumed here. The stress history simulation results at Denmark Place were compared with the estimate of stress given by the SBP tests. The initial horizontal stress and pore water pressure at each depth were read from the SBP curve at liftoff. Vertical stress at the corresponding depth was computed from the unit weight of London Clay. Figure 4 illustrates the comparison of the predicted \(K_0\) profile from the stress history simulation and the measurements from the Denmark Place site. The overall values are well within the range expected for London Clay [55]. It is clear that the profile deduced from the stress history simulation lies between the values estimated from the SBP tests. Despite this, the SBP values show a significant variability, which may be taken as a first indication of imperfect installation. Figure 4 also includes values of \(K_0\) at Heathrow T5, derived from suction measurements on thin-wall samples using a suction probe on-site soon after sampling [25]. The direct comparison between measurements at T5 and Denmark Place is feasible, since the elevation of the top of the London Clay for both sites is very similar. It is clear that the suction-derived measurements are also in agreement with the simulation trend, showing less variability than the SBP values.
\(K_0\) profile from KHSM measurements at Denmark Place and T5 [25]
It should be noted that the stress history simulation was carried out using the KHSM with the initial structure \(r_0\) set equal to 1. This is necessary since any measure of the initial structure will degrade in the presence of mechanical loading. Although the development of structure may be modelled as a geochemical process, there is very little information about the specific process that caused London Clay structure. The initial location of the centre of the bubble was chosen to coincide with the initial stress state. Although it is also possible to initialise this variable using the stress history simulation, experimental work from Clayton and Heymann [12] indicated that creep erases the stress history effects that are associated with the most recent loading. The initial degree of structure, \(r_0\), was selected using the results that were obtained analysing the detailed experimental campaign carried out for Heathrow Terminal T5. As described by González et al. [20], estimates of structure were obtained using observed yield points and swelling indices from oedometer tests as well as matching peak strengths of undrained triaxial tests (Fig. 5). The values from Heathrow T5 were applied with success in the tunnel analysis of St James using a matching criterion based on the different horizons of London Clay. The same strategy was used here for the simulation of SBP tests. An initial estimate of \(r_0\) was made and later adjusted to better fit the SBP curves. Finally, a small amount of structure-induced initial anisotropy (\(\eta _0\) = 0.1) was introduced, after the inspection of the triaxial bounding surface for London Clay reported by Gasparre [19]. As expected, for the strongly overconsolidated London Clay, this initial plastic anisotropy is far smaller than values applied to model normally consolidated clays [49].
4 Simulation of SBP tests at Denmark Place
A series of simulations assuming fully undrained conditions have been carried out to predict the SBP test curves conducted in London Clay at three different depths. The values of the soil parameters used in the simulations are listed in Table 2.
4.1 Self-boring pressuremeter test 102T2
The first finite element analysis simulates the SBP test 102T2 conducted at depth 14 m below ground level. Figure 6a shows the comparison between the model predictions and the experimental results. It is apparent that the general trend is well captured in terms of cavity strain–cavity pressure response during the expansion and contraction stages of the test. The pore water pressure–cavity strain response agrees reasonably well with those measured, as shown in Fig. 6b. There is a noticeable overestimation of the predicted pore water pressures towards the end the expansion phase of the test; however, the model is able to adequately replicate the general trend during the contraction phase.
Figure 7 shows the structure distribution at the end of the analysis for the SBP test 102T2. It is clear that complete destructuration, with \(r=1.0\), takes place in the soil elements adjacent to the cavity face. A gradual decrease in destructuration was then predicted until the initial degree of structure corresponding to \(r=2.1\) is maintained away from the cavity wall.
4.2 Self-boring pressuremeter test 102T3
Typical results of the SBP test 102T3 from the depth 20 m are shown in Fig. 8. Note that the values of \(r_0\) and k have been slightly changed for the clay from depth 20 m, as noted in Table 2. Figure 8a shows that the effect of the destructuration process has introduced a steepening of the predicted cavity pressure–cavity strain relationship in the initial stages of the expansion and contraction of the pressuremeter test, but the general trend is well captured. The predicted pore water pressures are slightly lower than those observed up to the end of the loading stage, as shown in Fig. 8b. Thereafter the KHSM predicts a comparable reduction in pore water pressures to that induced in the soil during the unloading stage.
4.3 Self-boring pressuremeter test 102T4
Figure 9a shows a comparison of the observed cavity strain–cavity pressure and the predicted results from a finite element analysis of the SBP test 102T4, from depth 26 m. Note that the initial degree of structure, \(r_0\), has been increased for the clay from depth 26 m (as noted in Table 2). Again, it can be seen that the KHSM model predicted a cavity expansion pressure very close to the observed data from the onset of loading and unloading. Marginally stiffer responses were observed with the numerical prediction at the beginning of loading and unloading stages. As in the previous tests, the rise of cavity pore pressure during loading is significantly underpredicted (Fig. 9b). Possible reasons for this underprediction are explored in the next section.
5 Discussion
Overall, the SBP simulations are remarkably successful in matching the magnitude of the cavity expansion pressure during the loading and unloading stages for all the simulated SBP tests. The pore pressure match is also generally good, although two aspects appear unsatisfactory: the apparent lack of pore pressure response to small unloading loops and the relatively slow initial rise in pore pressure during virgin loading.
The first issue is related to limitations of the elastic model used in this work [60]. The model is nonlinear but isotropic and has no coupling between shear and volumetric responses. Cylindrical cavity expansion in isotropic elastic materials has been shown to be purely deviatoric [36], and no pore pressure changes are expected. This is observed in the intermediate loading/unloading cycles, where the response is predominately elastic, and as a result, there is little change in pore pressure. When unloading continues and plastic response dominates, the pore pressure response is well predicted, as evident during the final unloading stage. The incorporation of a more rigorous anisotropic elastic model [7, 27, 48] is likely to improve the prediction, but was beyond the scope of this study.
The slow rise of pore pressure during virgin loading is, on the other hand, taking place during plastic loading. As noted above, the larger uncertainties during calibration and initialisation were associated with the destructuration rate, k, and the initial degree of structure, \(r_0\). The final values of \(r_0\) adjusted in the simulations were very close to those suggested by the Heathrow T5 test results (see Fig. 5). The final values for k were about twice those applied in the St James’ tunnel simulation. There were valid reasons for the choices made, but parameter optimisation in advanced models is challenging and perhaps other optimal solutions exist. In addition, it was likely that a certain amount of disturbance to the clay structure at the cavity wall may have occurred during SBP installation into the ground.
To explore these assumptions, a parametric study was carried out to identify the effects of the destructuration parameters \(r_0\) and k and the extent of installation disturbance on the pore water pressures at the initial stage of the SBP expansion. In the following, we illustrate the results obtained for the case of SBP test 102T4; similar results were obtained for the other two tests. It should be noted that all properties not explicitly changed in the parametric study remain as described in Table 2.
The reference value of the initial \(r_0\) in this case was 3. Results from two more simulations in which this value is either halved or doubled are presented in Fig. 10a, b. This change has a direct and dramatic effect on the both the limit values of cavity pressure and the final value of pore water pressure. A larger value of \(r_0\) leads to a stiffer, stronger response that clearly overestimates recorded test responses. The opposite behaviour is observed when the initial degree of structure is halved. It is also apparent that the initial steep cavity pore pressure rise observed in the test is not greatly affected by changing the initial structure.
Changing the value of k influences the rate at which destructuration occurs with plastic strain. The initial guess of k for this level was 3. Results from two more simulations in which this value is either halved or doubled are presented in Fig. 11. A high value of k leads to very rapid loss of structure, so that a softer response in the cavity pressure is obtained, whereas this response is much stiffer with a smaller value of k (Fig. 12a). The variation of k does not appear to have a notable influence on the loading part of the pore pressure curve (Fig. 12b), but does have a significant influence on the response during the unloading phase.
Figure 12 depicts the distribution of structure at the end of the simulations for the three cases analysed (k, 2k and 0.5k). For the base case, the test results in complete clay destructuration up to a distance of 2 radius from the cavity wall, while at 6 radius from the wall the material remains intact. When the rate of destructuration is doubled, the same destructuration profile is essentially translated deeper into the clay. On the contrary, when the destructuration parameter is halved, the destructuration process is incomplete even at the cavity wall.
Finally, a series of simulations were conducted to investigate the effects induced by possible drilling disturbance. It is considered that the extent of the installation disturbance is limited, and may be described by a linear variation of structure close to the cavity wall. Accordingly, the distributions of the initial structure for the two adopted scenarios are given in Fig. 13. Distribution 1 consists of a reduced initial degree of structure \(r_0\) to 1.4 from the intact calibrated value of \(r_0=3.0\). Distribution 2 similarly considers the effect of a level of damage to the initial structure in the area close to the cavity wall, with a reduced value of \(r_0\) of 2. In both scenarios, the installation disturbance extends for a distance of \(a/a_0=0.5\) beyond the cavity wall where the clay returns to an undisturbed state. This distance was based on a study carried out by Liu [35] in which the strain path method was to investigate the magnitude of SBP installation disturbance.
Figure 14 shows the comparison between the experimental data and the results of the model for the two disturbance scenarios (Distributions 1 and 2). For both, installation disturbance has surprisingly little effect on the cavity pressure–cavity strain response, as shown in Fig. 14a. However, it is apparent that reducing the value of the initial structure in the area close to the cavity wall has a significant effect on the predicted pore water pressures, as shown in Fig. 14b. The model simulations are in good agreement with the experimental data in terms of pore pressure response in the initial stage of the expansion of the SBP test. However, the most significant improvement is observed for Distribution 2, i.e. the less damaging, which can be seen after around 2% of cavity strain, where the model is remarkably successful in matching the general shape of the pore pressure response. This is compared with an overestimation of the pore pressure by approximately 20% for Distribution 1 at the end of the loading stage. A similar behaviour was also observed for the self-boring pressuremeter tests 102T2 and 102T3 in terms of improved pore pressure responses when the installation disturbance is included using Distribution 2.
6 Conclusion
Extending the use of advanced soil models such as the KHSM requires clear pathways to calibration and initialisation. This work set out to explore the possibility of using an in situ test, such as the SBP, to back-analyse structure and structure-related parameters and dispense, at least partly, with the onerous task of recovering and testing high-quality undisturbed soil samples.
The calibration of advanced soil models benefits from a multifaceted approach in which correlations, data on reconstituted samples, tests on intact clay and ancillary stress history simulations all play a part. It is feasible to calibrate the initial structure, \(r_0\), from back-analysis of the pressuremeter response since the obtained loading curves are highly sensitive to this input value. This, however, requires all the remaining elastic and plastic parameters to be identified beforehand. The values of structure back-analysed for London Clay units in locations as distant as Heathrow and Denmark Place are very close. This suggests that this important property may show less spatial variation across the formation than may have been expected. The same applies to the destructuration rate although this parameter appears more sensitive to the responses observed upon final unloading.
It was shown that pore pressure prediction was greatly improved by accounting for disturbance to the clay structure during installation. The simulations appear to provide a good indication of the damage caused to the clay structure during the installation process. The presence of a certain amount of installation-induced disturbance on structure seems almost inevitable, even for tightly controlled tests such as the SBP. This disturbance may leave clear signals on the SBP results, but it is likely to complicate the back-analysis. More research is needed to clarify how the extent of this disturbance may be either controlled or easily measured.
References
Arroyo M, González N, Butlanska J, Gens A, Dalton C (2008) SBPM testing in Bothkennar clay: structure effects. In: 3rd international conference on site characterization (ISC’3). Taylor & Francis, Taipei, pp 456–462
Aubeny C, Whittle A, Ladd C (2000) Effects of disturbance on undrained strengths interpreted from pressuremeter tests. J Geotech Eng: ASCE 126(12):1133–1144
Avgerinos V, Potts DM, Standing JR (2016) The use of kinematic hardening models for predicting tunnelling-induced ground movements in London Clay. Géotechnique 66(2):106–120
Baguelin F, Jezequel J, Lemee E, Mehause A (1972) Expansion of cylindrical probe in cohesive soils. J Soil Mech Found Div: ASCE 98(11):1129–1142
Baudet B, Stallebrass S (2004) A constitutive model for structured clays. Géotechnique 54(4):269–278
Benoit J, Clough GW (1986) Self-boring pressuremeter tests in soft clays. J Geotech Eng: ASCE 116(1):60–78
Borja RI, Tamagnini C, Amorosi A (1997) Coupling plasticity and energy-conserving elasticity models for clays. J Geotech Geoenviron Eng 123(10):948–957
Burland JB (1990) On the compressibility and shear strength of natural clays. Géotechnique 40(3):329–378
Callisto L, Rampello G (2004) An interpretation of structural degradation for three natural clays. Can Geotech J 41:392–407
Chandler RJ, Harwood AH, Skinner PJ (1992) Sample disturbance in London clay. Géotechnique 42(4):577–585
Clarke BG (1995) Pressuremeters in geotechnical design. Blackie Academic and Professional, London
Clayton CRI, Heymann G (2001) Stiffness of geomaterials at very small strains. Gótechnique 51(3):245–255
Clayton CRI, Siddique A (1999) Tube sampling disturbance—forgotten truths and new perspectives. P I Civ Eng Civ En 137(3):127–135
Collins IF, Yu HS (1996) Undrained cavity expansions in critical state soils. Int J Numer Anal Meth 20(7):489–516
De Freitas MH, Mannion WG (2007) A biostratigraphy for the London Clay in London. In: Proceedings of conference on stiff sedimentary clays—genesis and engineering behaviourur, pp 91–99
Fahey M, Carter JP (1993) A finite element study of the pressuremeter test in sand using a nonlinear elastic plastic model. Can Geotech J 30(2):348–362
Fahey M, Randolph MF (1984) Effect of disturbance on parameters derived from self-boring pressuremeter tests in sand. Géotechnique 34(1):81–97
Gasparre A, Coop MR (2008) Quantification of the effects of structure on the compression of a stiff clay. Can Geotech J 45(9):1324–1334
Gasparre A, Nishimura S, Minh NA, Coop MR, Jardine RJ (2007) The stiffness of natural London clay. Géotechnique 57(1):33–47
González N, Rouainia M, Arroyo M, Gens A (1012) Analysis of tunnel excavation in London Clay incorporating soil structure. Géotechnique 62(12):1095–1109
González N, Arroyo M, Gens A (2009) Identification of bonded clay parameters in SBPM tests: a numerical study. Soils Found 29(3):329–340
González N, Gens A, Arroyo M, Rouainia M (2011) Modelling the behaviour of structured London Clay. In: International symposium on deformation characteristics of geomaterials, September 1 3, 2010. Seoul, Korea, pp 1052–1059
Grammatikopoulou A, Zdravkovic L, Potts DM (2006) General formulation of two kinematic hardening constitutive models with a smooth elastoplastic transition. Int J Geomech 6(5):291–302
Grammatikopoulou A, Zdravkovic L, Potts DM (2008) The Influence of previous stress history and stress path direction on the surface settlement trough induced by tunnelling. Géotechnique 58(4):267–281
Hight DW, McMillan F, Powell JJM, Jardine RJ, Allenou CP (2003) Some characteristics of London Clay. In: Proceedings conference on characterisation and engineering, National University Singapore, Balkema vol 2, pp 851–907
Hight DW, Gasparre A, Nishimura S, Minh NA, Jardine RJ, Coop MR (2007) Characteristics of the London clay from the terminal 5 site at Heathrow Airport. Géotechnique 57(1):3–18
Houlsby GT, Amorosi A, Rojas E (2005) Elastic moduli of soils dependent on pressure: a hyperelastic formulation. Gótechnique 55(5):383–392
Hughes JMO, Wroth CP, Windle D (1977) Pressuremeter tests in sands. Géotechnique 27(4):455–477
Jardine RJ, Standing JR, Kovacevic N (2005) Lessons learned from full scale observations and the practical application of advanced testing and modeling. In: Proceedings of the 3rd international symposium on deformation characteristics of geomaterials, Lyon, France, vol 2, pp 201–245
Jin YF, Yin ZY, Zhou WH, Horpibulsuk S (2019) Identifying parameters of advanced soil models using an enhanced transitional Markov chain Monte Carlo method. Acta Geotech 14:1925–1947
Kavvadas M, Amorosi A (2000) A constitutive model for structured clays. Géotechnique 50(3):263–273
King C (1981) The stratigraphy of the London Basin and associated deposits. Tertiary Research Special Paper, vol 6, Backhuys, Rotterdam
Law KT, Eden WJ (1985) Effects of soil disturbance in pressuremeter tests. In: Proceedings of conference on updating subsurface sampling of soils and in-situ testing. Santa Barbara, Calif, pp 291–303
Leroueil S, Vaughan PR (1990) The General and congruent effects of structure in natural and weak rocks. Géotechnique 40(3):467–488
Liu L (2011) Disturbance analysis of the self-boring pressuremeter tests, PhD University of Cambridge
Mair RJ, Wood DM (1987) Pressuremeter testing. Methods and interpretation, 1st edn. Butterworth-Heinemann
Mayne PW (2001) Stress-strain-strength-flow parameters from enhanced in-situ tests. In: Proceedings of internatioinal conference on in situ measurement of soil properties and case histories, Bali, pp 27–47
Mitchell JK, Soga K (2005) Fundamentals of soil behaviour. Wiley, New York
Mo PQ, Yu HS (2017) Undrained cavity expansion analysis with a unified state parameter model for clay and sand. Géotechnique 67(6):503–515
Monforte L, Arroyo M, Carbonell JM, Gens A (2017) Numerical simulation of undrained insertion problems in geotechnical engineering with the Particle Finite Element Method (PFEM). Comput Geotech 82:144–156
Monforte L, Arroyo M, Carbonell JM, Gens A (2018) Coupled effective stress analysis of insertion problems in geotechnics with the particle finite element method. Comput Geotech 101:114–129
Muir Wood D (1990) Soil behaviour and critical state soil mechanics. Cambridge University Press, Cambridge
Panayides S, Rouainia M, Muir Wood D (2012) Influence of degradation of structure on the behaviour of a full-scale embankment. Can Geotech J 49:1–13
Pantelidou H, Simpson B (2007) London clay behaviour across central London. Géotechnique 57(1):101–112
Plaxis 2D. Delft, Netherlands: Plaxis bv; (2016)
Prapaharan S, Chameau J-L, Altschaeffl AG, Holtz RD (1990) Effect of disturbance on pressuremeter results in clay. J Geotech Eng : ASCE 116(1):35–53
Rouainia M, Muir Wood D (2000) Constitutive model for natural clays with loss of structure. Géotechnique 50(2):153–164
Rouainia M, Muir Wood D (2006) Computational aspects in finite strain plasticity analysis. Mech Res Commun 33(123):133
Rouainia M, Elia G, Panayides S, Scott P (2017) Nonlinear finite-element prediction of the performance of a deep excavation in Boston Blue Clay. J Geotech Geoenviron Eng 143(5):04017005
Rui Y, Yin M (2018) Interpretation of pressuremeter test by finite-element method. P I Civil Eng-Geotech 171(2):121–132
Russell AR, Khalili N (2002) Drained cavity expansion in sands exhibiting particle crushing. Int J Numer Anal Met 26(4):323–340
Schweiger HF (2013) Issues of parameter identification for numerical analysis with advanced constitutive models. In: Proceeding of the 15th european conference on soil mechanics and geotechnical engineering. Athen, Greece, pp 131–138
Silvestri V (2011) Disturbance effects in pressuremeter tests in clay. Can Geotech J 41(4):738–759
Sivasithamparam N, Castro J (2018) Undrained expansion of a cylindrical cavity in clays with fabric anisotropy: theoretical solution. Acta Geotech 13:729–746
Skempton AW, La Rochelle P (1965) The Bradwell slip: a short-term failure in London Clay. Geotechnique 15(3):221–241
Sloan SW, Randolph MF (1982) Numerical prediction of collapse loads using finite element methods. Int J Numer Anal Meth 6:47–76
Smith P, Jardine R, Hight D (1992) The yielding of Bothkennar clay. Géotechnique 42(2):257–274
Standing JR, Burland JB (2006) Unexpected tunnelling volume losses in the Westminster area, London. Géotechnique 56:11–26
Taechakumthorn C, Rowe RK (2012) Performance of a reinforced embankment on a sensitive Champlain clay deposit. Can Geotech J 49(8):917–927
Viggiani G, Atkinson JH (1995) Stiffness of fine-grained soil at very small strains. Géotechnique 45(2):249–265
Wheeler SJ, Näätänen A, Karstunen M, Lojander M (2003) An anisotropic elasto-plastic model for soft clays. Can Geotech J 40(2):403–418
Zentar R, Hicher PY, Moulin G (2001) Identification of soil parameters by inverse analysis. Comput Geotech 28:129–144
Zhao J, Sheng D, Rouainia M, Sloan SW (2005) Explicit stress integration of complex soil models. Int J Numer Anal Meth 29(12):1209–1229
Acknowledgements
The first author would like to acknowledge funding provided by the Engineering and Physical Sciences Research Council (EPSRC) GR/S84897/01. The authors are grateful to Cambridge Insitu Ltd for making available the pressuremeter data on London Clay.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rouainia, M., Panayides, S., Arroyo, M. et al. A pressuremeter-based evaluation of structure in London Clay using a kinematic hardening constitutive model. Acta Geotech. 15, 2089–2101 (2020). https://doi.org/10.1007/s11440-020-00940-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-020-00940-w