1 Introduction

Subsurface rocks are often heterogeneous, characterised by discontinuities which could be naturally occurring or artificially induced by anthropogenic activities. The heterogeneity is more obvious when the subsurface environment is viewed as a geographical expansive system consisting of features that differ in morphology and material constitution. The extensive nature of subsurface systems often implies the existence of compositional as well as structural non-uniformity or discontinuities as a result of prehistoric geological activities. This may occur due to natural phenomena such as tectonic movements due to changes in stress systems, creating folds and/or faults, or it may occur as a result of geological deposits that give rise to formations with peculiar litho-stratification or arrangement of facies. Also, non-uniformity could occur due to anthropogenic events. Examples of such activities include drilling for exploitation of oil and gas resources, mining for coal and other solid minerals, waste disposal and extraction of geothermal energy. All these have, to varying degrees, altered the subsurface stress regimes and in some cases caused irrecoverable deformations and/or fractures.

Discontinuities can be generally classified according to their origin. Differences in mechanical and environmental processes within geological systems have led to the creation of four major categories of discontinuities. These are described in Aydan and Kawamoto [5] as tension discontinuities, shear discontinuities, discontinuities caused by periodic sedimentation and discontinuities caused by metamorphism. As the appellations suggest, tension and shear discontinuities are created by excessive generation tensile and shear stress, respectively. The main types of discontinuities include faults, shear zones, fractures, joints, bedding planes, planes of foliation (schistosity) and planes of cleavage [12, 83, 97]. Their formation and characteristics is a function of the petrologic history and rock group amongst other factors. They affect the formation performance; for instance, the enhancement in permeability of the chalk reservoir of Ekofisk oil field in the North Sea, south of Norway, is attributed to existing fractures [32].

Some studies have been conducted to understand the effect of discontinuities on some aspects of fracture behaviour [4, 15, 16, 22, 25, 27, 37, 66, 72, 81, 82, 85, 90, 92, 98, 99]. The influence of important variables such as the net pressure at the fracture or faults, differential stress, angle of inclination of natural fracture and rock frictional coefficient is considered in Chuprakov et al. [25]. In Blair et al. [15], an alternative technique for monitoring fracture growth using tracking wires was applied to observe the interaction of fractures at interfaces using pressure history records, while in Casas et al. [22], fracture behaviour at interfaces with different physical and material properties was observed to determine the effect of interface properties on the extent and pattern of fracture growth.

The influence of certain features related to stratification has also been examined [4, 27, 66, 82]. Some of the features considered include distinctions in material properties of rock layers, variation in in situ stresses between layers, pressure gradients as well as differences in interface properties considered with respect to its significance to fracture propagation patterns and, more importantly, containment. According to Athavale and Miskimins [4], fracture pattern (morphology) in specimens with layers of different material properties is complex and non-planar with diversions at the interfaces. This phenomenon was attributed to dissimilarities in material properties of the contributing layers and properties of the interface. On the other hand, planar bi-winged fractures developed in specimens with homogeneous structures and properties. The performance of fractures at interfaces, as depicted by Daneshy [27], asserts the relevance of bond strength between layers, with interfaces with stronger bonds being more able to contain fractures. With respect to the containment of mode 1 fracturing and ignoring contributions from interfaces, Simonson et al. [82] investigated the effect of differences in material properties between layers, differences in in situ stress and hydrostatic pressure gradients. Similar work was carried out by Hanson et al. [37], Settari [81] and van Eekelen [90] that also included the effects of fluid viscosity, rheology, fracture toughness and temperature. Hanson et al. [37] also studied the fracturing behaviour at unbounded interfaces as a function of interface friction and observed that an intersection is more likely to occur in areas of lower friction. Furthermore, the significance of external loading on stress concentration, stress distribution and fracture containment has been explored by Philipp et al. [66].

Joints are features which often influence the rock mass behaviour. In this context, they are referred to as extensive discontinuities that may or may not separate two dissimilar rock sections and include natural occurring pre-existing faults, extensive pre-existing fractures and bedding planes that typically occur between layers with different material properties. The characteristics of joints are complex, and previous investigations have been carried out to assess certain aspects of their behaviour. Their existence in the rock mass affects the overall rock behaviour which is also dependent on the characteristic of the joint and where more than two joints are involved, on the network. The influence of joints on rock behaviour is also attributed to the following [46]: their lower strength in comparison with the surrounding rock materials, where they are embedded, the occurrence of anisotropic regions due to their presence and the establishment of a ‘scale effect’. The accuracy of the evaluation of rock behaviour is highly dependent on the ability to account for scale effects. Most of the standards in use are derived from direct observations, which are then used to develop rock mass classification systems (RMC). Examples of such empirical derivations are included in Barton et al. [11], Bieniawski [14], Hoek [38], Palmstrom [63, 64], Hoek and Brown [39] and Barton [9]. In Ivars et al. [46], a numerical methodology, referred to as synthetic rock mass (SRM) approach, for characterising the mechanical behaviour of jointed rocks is developed.

The existence of joints within a rock mass alters the behaviour of the rock. The mechanical properties and the performance of the rock are affected [21, 50] especially when assessed at large scales. Joint properties, geometry and distribution play a principal role especially if they occur in significant numbers or are situated in critical locations. The contributions of joints can be further ascertained if some of the phenomena that govern joint behaviour are understood. Joint behaviours are complicated, and until date, majority of the models developed to predict their behaviour are based on many assumptions.

Previous studies include Ladany and Archambault [51], Barton [8], Barton and Choubey [10], Bandis et al. [6], Park and Song [65] and Lee et al. [53]; some of these have examined the dilatancy, the occurrence and influence of asperities and contact of joint planes (surfaces), as factors determining the shear behaviour of joints. Grasselli and Egger [34] proposed a model to study the frictional behaviour of joints subjected to shear at constant normal loading conditions. Other constitutive models for joints have been developed by Wang et al. [91], Ohnishi et al. [62], Plesha [70], Amadei and Saeb [1] and Plesha [69], and a constitutive model for rock masses consisting of densely distributed joints is presented in Cai and Horii [21]. The behaviour of joints subjected to certain external conditions has also been considered by Kulatilake et al. [50], in which the dependence of rock strength and mode of failure on joint geometry is presented by investigating the impact of some joint geometry parameters such as joint orientation, density and size distribution. The fracture tensor parameter which incorporates variables including joint density, orientation and distribution was used as a measure for observing the effect of joint geometry. It was shown that the uniaxial compressive strength decreases, albeit nonlinearly with increasing magnitude of components of the fracture tensor. Occurrences of any of the three modes of fracture (mode I, mode II and mode III) were also shown to be related to the joint configuration.

The definition of joints in the above context precludes induced fractures which could occur due to anthropogenic underground activities or small-scale naturally occurring tectonic movements/seismic events. Fractures intentionally caused via the process of hydraulic fracturing are also termed as artificial fractures. Whether they are induced deliberately or they occur due to natural geological events, the understanding of the fracturing process including the interaction of induced fractures with discontinuities including pre-existing joints and/or fractures is crucial for effective and sustainable management of the subsurface environment. Other forms of discontinuities occur due to layering, often observed in stratified formations. In layered systems, the spacing of fractures increases with layer thickness [40, 47, 48, 52, 61, 84, 93]. Also, Mode I fractures grow perpendicularly to the boundaries of the layer and are more likely to do so in stiffer and more brittle layers [76]. Schopfer et al. [76] depicts the inhibiting nature of interfacial slips and the restriction of fracture spacing as a measure of fracture system maturity in layered rocks exhibiting such interfacial characteristics. Fracture spacing decreases with increasing normal stress (vertical confining stress); however, it increases with tensile strength [76].

For bonded joint systems, the bond strength (tensile and shear) and cohesion are important properties. In addition to other factors, the joint strength is governed by the presence of asperities and infills that may form an adhesive bond between the planes and the stiffness of the contacting planes. Some aspects of joint infills have been investigated [44, 88, 96]. Infills reduce the friction and shear strength of joints, and their thickness and properties may govern the entire joint behaviour if present in significant quantities [44].

Previous investigations into the role of some fracture properties on its behaviour are often based on continuum formulations in which the host rock and fluid are individually treated as continuous, with each material having spatially identical characteristics. Discontinuities are then permitted to occur in form of fractures or faults with peculiar features that distinguish it from the host rock material. The difficulty of such techniques is such that only isolated fractures can be realistically represented without compromising accuracy; moreover, it is often computationally demanding. The process is even more challenging where fracturing mechanisms are to be embedded during the coupling procedure necessary for multiphase flow interactions; this is despite improvements provided, for instance, in XFEM (extended finite element method) models [58], PUFEM (partition-of-unity finite element method) models [56, 57, 73] and fully coupled cohesive fracture discrete models [77–80].

In discrete element method (DEM), particle behaviour, interparticle exchanges and multiphase interactions can be modelled microscopically enabling a more accurate and dynamic representation of the mechanics of particle movement, fluid flow and fracturing processes. This technique has been implemented using Particle Flow Code (PFC2D), a DEM-based program which builds models as an assembly of distinct and arbitrarily shaped particles that displace independently and interact at contacts or interparticle interfaces.

At the pore scale, other numerical schemes for simulating localised deformation and microfracturing include FEM techniques. The assumed enhanced strain (AES) FEM being an improvement on the extended FEM (XFEM) [18] can be used in resolving strong discontinuities at the element level. In comparison with XFEM, AES is better at capturing strain singularity at crack tips. Microfracturing is modelled by applying the ‘strong discontinuity approach’ [87], where abrupt changes in the displacement field occur at the element level. AES can be used to predict the micromechanical behaviour of microfracturing while restricting the process to the pore scale—i.e. without propagating to larger scales [87]. Also, because AES is based on a piecewise constant interpolation of displacement that changes at the interface between elements, it is more able, in comparison with XFEM, to account for greater slips or softer responses due to steep gradients. Generally, in implementing AES, microfractures are inserted into finite elements as displacement jumps or strong discontinuities. The propagation of these fractures is not tracked. Rather, fracture growth is shown as a cluster of discontinuous microfractures formed in adjoining finite elements soften by the strong discontinuity in the direction of the displacement jump [86, 87].

Other FEM-based techniques that are applied in simulating crack propagation are illustrated in Haghighat and Pietruszczak [36] and Li and Konietzky [54]. In Haghighat and Pietruszczak [36], a FEM procedure involving a constitutive relation with embedded discontinuity (CLED) [67, 68] is coupled with the level set method for modelling the propagation of discrete cracks and shear bands in cohesive-frictional materials. Results from this approach are shown to be in agreement with XFEM. The crack propagation scheme developed by Konietzky et al. [49] was modified in Li and Konietzky [54] to produce other schemes used for improved lifetime predictions of crack propagation in brittle rocks. A fundamental part of their work was the enforcement of the propagation of the initial crack to continue in the direction of its original orientation, and the linearisation of the curved crack shape. Macrocracks were considered to be formed by a coalescence of microcracks controlled by the material microstructural characteristics.

In FEM techniques, microfractures are embedded as a function of the strength of the finite element, which must be softened. The placement of in situ microfractures is an important feature of enhanced FEM (e.g. XFEM and AES FEM) techniques as it enables a better imitation of the initial condition of a rock mass which naturally consist of discontinuities. Microfracturing is affected by material heterogeneity caused by, for instance, the direction of fracture growth relative to the bedding plane, the presence of pockets of incongruent materials (e.g. organic materials) and voids within the material [13]. The algorithm in DEM is normally constituted to generate a homogenous assemble of regular-shaped (spherical) or irregular-shaped (clumps) particles. Nevertheless, recent improvements in DEM have allowed the creation of the SRM (e.g. [26, 60]) via the inclusion of pre-existing fractures as an integral part of the initial rock condition. It is also relatively easier to evaluate the susceptibility of micromechanisms (e.g. bond breakage and the alteration of the fabric tensor and coordination number of parallel bonds) to changes in conditions such as the heterogeneity of particle size distribution, confining pressure, and stress orientation, distribution and density [29].

The DEM is a microscale-based numerical approach formulated on the premise of the elemental state of solid materials at the microlevel. In comparison with FEM, it captures the following phenomena more dynamically: the initiation and propagation of the fracturing process, fluid pressure propagation, and the coupling between fluid flow/pressure and the deformation and fracturing of the solid matrix. This allows an improved appraisal of geomechanical processes at the microscale.

The DEM has been used here to establish a correlative relationship between propagation of hydraulic fractures and the proximity of joints. To this end, several issues are considered including the extent and pattern of fracture growth, potentials for fracture interaction, joint features and the characteristic of the rock mass. Special emphasis has been placed on the joint strength and deformation in terms of the shearing resistance. In this work, the smooth joint contact model is specially adopted to simulate the behaviour of interfaces.

The peculiarity of the numerical approach in this study lies in the combination of the fluid flow scheme and hydromechanical coupling illustrated in Eshiet and Sheng [30] with a smooth joint model (SJM) that has been specifically calibrated to represent an unbonded rock joint as described in Barton [7, 8] and Barton and Choubey [10]. The SJM in this study is formulated to resemble a shear joint formed as a result of tectonic movements. This kind of joint is often planar and remarkably different from non-planar tension joints which have appreciable roughness. Tensile joints with negligible surface undulations may be regarded as planar and similar to shear joints.

This study

  • demonstrates the capability of incorporating the fluid flow scheme consisting of interconnecting reservoir (domains)—where flow is calculated by the modified Poiseuille equation—within an intact rock model comprising isolated unbonded joints represented by the SJM,

  • derives key equations for the prediction of fracture proliferation as a function of joint frictional resistance, and

  • highlights some of the governing elements that determine the ability of rock joints in controlling approaching fractures.

2 Smooth joint contact model and fluid flow algorithm

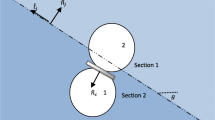
Full descriptions of the smooth joint contact model are provided in Itasca Consulting Group [45], and a summary of some of the key features is presented here. The smooth joint model is specifically formulated to simulate interfaces at discontinuities and replaces the initial contact models installed during the building of the SRM. It can only occur at contacts between particles. Joints are made up of two contacting planes which are parallel to each other. Each of these planes consists of particles that lie on either side of the joint (Fig. 1). A unit normal vector defined by the dip angle and dip orientation is used to define the joint plane orientation, \(\hat{n}_{\it{j}}\), which may be different from the unit normal vector defining the contact position of the two contacting particles, \(\hat{n}_{\text{c}}\). The unit normal vector defining the joint plane is given as

$$\hat{n}_{\text{j}} = \left[ {\sin \,(\theta ), \cos \,(\theta )} \right]$$
(1)

where θ is the dip angle. Other joint properties such as stiffness and bonded system properties (bond tensile strength, bonded system cohesion and bonded system friction angle) are assigned based on the properties of the contact and contacting particles. The smooth joint consists of a collection of smooth joint contacts created by contacting pair of particles. The dot product unit normal vector of the joint, \(\hat{n}_{\text{j}}\), and the contact unit normal vector, \(\hat{n}_{\text{c}}\), are used to identify contacts that make up the joint. Within the affected region, the smooth joint model replaces the existing contact model and/or parallel bond, and the properties may either be inherited from the contact and contacting particles or be explicitly assigned. This excludes the dip angle and direction which must be assigned explicitly as a joint property.

Fig. 1
figure 1

Orientation of joint and smooth joint contact [45]

Full size image

Where the smooth joint is bonded, the joint only breaks when the bond normal and shear strengths are exceeded. The presence of a contact bond invalidates the slip behaviour (as would occur in granular materials), and when a bond breaks in tension, it nullifies the shear strength. Similarly, bond breakage in shear nullifies the bond tensile strength. All joints are unfilled and remain in tight contact; as such they are modelled as unbonded but frictional. The aperture (space between opposite planes) may open under sufficient pressure.

Details of the fluid flow model are presented in Eshiet and Sheng [30]. In summary, it comprises a network of interconnecting domains used to represent voids between particles. These domains are linked by pipes that denote particle contacts. The pipes are modelled as parallel-plate channels with fluid flow calculated by a modified Poiseuille equation given as

$$Q_{\text{p}} = \frac{{wa^{3} }}{12\mu }\frac{\Delta P}{{L_{\text{p}} }}$$
(2)

where w is the width of the channel, a is the aperture between contacting particles, ∆P is the pressure difference between a pair of connecting domains, μ is the fluid dynamic viscosity, and L p is the channel length. Further definitions of a and L p are given in Eshiet and Sheng [30]. Hydromechanical coupling is implemented through the fluid pressure via Eq. 3

$$\Delta P = \frac{{K_{\text{f}} }}{{V_{\text{d}} }}\left( {\sum Q\Delta t - \Delta V_{\text{d}} } \right)$$
(3)

where K f is the bulk modulus of the fluid, V d is the apparent volume of the domain, Q is the inflow from surrounding channels, and ∆t is the time step. The rock and joint permeabilities are governed by the aperture, a, and the fluid pressure influences the rock strength and deformation.

3 Tests and calibration

3.1 Determination/calibration of rock properties

Details of the generation and calibration of a typical rock model are described in Eshiet et al. [31]. Several input microparameters were used to build the DEM assembly prior to the coupling process. It is essential for the behaviour of the synthetic material to match the physical behaviour of real materials. One way of doing this is to ensure that the properties defining the deformability and strength characteristics at the macroscale are matched. To achieve this, values of selected microparameters that have direct or indirect effect on the macrobehaviour are assigned and several numerical material tests (similar to laboratory tests) are carried out. Macroparameters characterising material deformability include the Young’s modulus (E) and Poisson’s ratio (\(\upsilon\)), while the material strength is characterised by compressive strength, \(\hat{q}\) (confined and unconfined) and tensile strength (T). According to the literature [59, 95], there are approximate relationships that correlate microproperties with macroproperties. Young’s modulus is influenced by the particle–particle contact modulus and the particle stiffness ratio, Poisson’s ratio is influenced by the particle stiffness ratio, and the compressive and tensile strength is influenced by the normal and shear bond strength. Even though the inclusion of scaling relations may invalidate the effect of particle size, the possible effects of other microproperties are not ignored.

Scaling laws provide relationships between macroproperties and microproperties of synthetic specimens. These relationships are correlative, implying that with given values of microproperties, the corresponding macroproperties can be estimated. According to the scaling relations derived by Yang et al. [95], the effect of particle size is trivial when juxtaposed with other microparameters. Thus, in applying these scaling equations, the effect of particle size may be ignored contrary to other microparameters such as particle stiffness ratio, bond normal strength, bond shear strength and the ratio of bond normal strength to shear strength.

The intact rock model representative of reservoir sandstone was built by generating a bonded particle assembly where interparticle interactions are represented using a contact bond model (Table 1). The contact bond characterises the behaviour of minute cementitious materials existing between interfaces between particles.

Table 1 Microproperties of rock sample
Full size table

For this investigation, the behaviour of reservoir sandstone is simulated. In order to match the characteristics of the rock type (sandstone), two sets of virtual tests were performed: biaxial tests consisting of unconfined and confined compression tests and shear tests, to determine and calibrate the actual rock behaviour and joint properties, respectively. To determine the actual compressive strengths, unconfined compression tests were conducted. The confined compression tests were performed at confining pressures of 1, 2, 3 and 4 MPa; these tests were necessary to establish the trend in compressive strength for varying confining pressures, which becomes useful (if the specimen is assumed to behave as a Mohr–Coulomb material) when defining the secant slope of strength envelopes used to determine the corresponding friction angle and cohesion. During biaxial tests, values of the differential stress \(\left( {\sigma_{\text{D}} = \sigma_{y} - \sigma_{x} } \right)\) are plotted against the axial strain, e y . The compressive strength (\(\hat{q}\)) is taken as the peak value of this plot. The material generation and model calibration were carried out assuming plain strain conditions where \(\upsilon\) and E, defined in plane stress, are replaced by \(\upsilon^{*}\) and \(E^{*}\), respectively. These are given in Eq. 4. Using test results, \(E^{*}\) and \(\upsilon^{*}\) are obtained as [89]

$$\upsilon^{*} = \upsilon /\left( {1 + \upsilon } \right)$$
(4a)
$$\upsilon = - \Delta e_{x} /\Delta e_{y}$$
(4b)
$$E^{*} = E/\left( {1 - \upsilon^{2} } \right)$$
(4c)
$$E = \Delta \sigma_{y} /\Delta e_{y}$$
(4d)

where \(\upsilon\) and E are the plane stress Poisson’s ratio and Young’s modulus, respectively. The plane strain condition presupposes an infinitesimal value for the out-of-plane strain, e z . Simulations were carried out to replicate properties of generic rocks (e.g. sandstone). The deciding stress–strain curve that established the unconfined compressive strength of the synthetic rock material, which matches the real rock, is illustrated in Fig. 2. The trend line for the stress–strain curve of the synthetic material (Fig. 2a) follows a path similar to that for an idealised rock in compression [43] (Fig. 2b), while, most importantly, the peak uniaxial compressive strength matches the real sandstone of interest. Values of the mechanical properties of the actual rock are given in Table 2. The tensile strength (Brazilian strength) was determined from Brazilian tests on the synthetic rock material.

Fig. 2
figure 2

a Stress–strain curve for compressive strength. b Complete typical stress–strain curve for rock showing (i) stiffness and strength and (ii) differences with respect to brittleness and ductility [43]

Full size image
Table 2 Mechanical properties
Full size table

3.2 Determination/calibration of joint properties

Direct shear tests were carried out mainly to determine joint properties such as the cohesive strength, frictional resistance, joint wall compressive strength (JCS) and joint roughness coefficient (JRC). The shear strength can be derived from known values of cohesive strengths and frictional resistance.

The behaviour of a jointed rock mass is to a great extent influenced by the joint characteristics. The shear strength of joints therefore plays an important role. One of the major influences of the shear strength is the cohesive strength and angle of internal friction. The angle of friction is also affected by the dilatancy which, in the case of joints, is controlled by the joint roughness. The joint roughness coefficient is a measure of its smoothness [8, 20] and could be used for the assessment of non-planer joints [7]. The effective normal stress across the joint also contributes to its shear strength. The relationship between these parameters is encompassed in the Mohr–Coulomb expression for shear strength, given as

$$\tau_{\text{p}} = c + \sigma_{\text{n}} \tan \phi$$
(5)

where τ p is the peak shear strength, c is the cohesive strength, σ n is the normal stress, and ϕ is the angle of internal friction (friction angle). Where the shear strength is reduced to a residual value, τ r, the cohesive strength is removed, and there is a decrease in the friction angle to a residual value, ϕ r. Equation 5 becomes

$$\tau_{\text{r}} = \sigma_{\text{n}} \tan \phi_{\text{r}}$$
(6)

The generalised peak shear envelope for the rock joint is [8]

$$\tau = \sigma_{\text{n}} \tan \left( {{\text{JRC}}\,\log_{10} \left( {\frac{\text{JCS}}{{\sigma_{\text{n}} }}} \right) + \phi_{\text{r}} } \right)$$
(7)

where JRC is the joint roughness coefficient, JCS is the joint compressive strength, and ϕ r is the residual friction angle. For smooth planar or nearly planar joints, JRC = 0. Equation 7 is reduced to Eq. 6.

The Mohr–Coulomb expression can therefore be used to determine the shearing properties of rock discontinuities. In order to ascertain as well as calibrate the joint properties, a joint with specified values of properties was created in samples of the rock mass and direct shear tests conducted under varying effective normal stress conditions (ranging between 1e6 and 5e6 MPa). For the first series of tests, the microproperty representing the joint friction angle was varied with each successive test, but the joint cohesive strength was held constant at zero. The values of the microscopic properties of the synthetic rock sample and assigned joint properties are given in Tables 1 and 2.

Using samples with dimensions of height 0.3 m and width 0.6 m, a single planar longitudinal joint was created along the centre of the intact sample (Fig. 3). The joints were made to be smooth and as such have negligible joint roughness coefficients (JRC ≈ 0). Barton and Choubey [10] provide standard curves that state values of JRC corresponding to the roughness of joints. A value of JRC ranging between 0 and 2 is suggested for smooth planar joints. Particles bordering the two planar surfaces of the joint that meet the criterion for selection for the smooth joint contact were identified, and a zero bond strength was allocated to those contacts (Fig. 3a) dividing the two joint surfaces.

Fig. 3
figure 3

Joint configuration and position of contacts. a Collection of smooth joint contacts that form the joint. b Alignment of the smooth joint contacts with the joint geometry

Full size image

The layout of the shear tests is shown in Fig. 4. Vertical stresses representing effective normal stresses were applied via the horizontal walls. A servo mechanism was used to control the velocities of the horizontal walls so as to maintain a constant confining stress. The bottom right wall was fixed in the horizontal direction, but particles in contact with it were allowed to slide vertically. Similarly, particles were able to slide laterally along the top and bottom horizontal walls. To apply a steady load, a constant horizontal velocity was applied to the top left vertical wall in the left–right direction. The horizontal velocity was set to 0.003 m/s to guarantee quasi-static equilibrium during the test. Stable solutions during calculations can only be achieved if the time steps do not exceed a critical value. The critical time step is dependent on the mass and stiffness of the discrete bodies (contact and particles) and is usually infinitesimal. Calculations in PFC are based on Newton’s second law and the time step set to very small values (e.g. 10−7 s) especially for quasi-static analysis. A mechanical time step of approximately 10−7 s was used for the tests implying a loading rate sufficiently slow to ensure quasi-static equilibrium. Therefore, though the velocity of the loading wall is apparently high, the actual cumulative motion of the wall is small. Higher loading rates of 0.3 and 0.1 m/s have been successfully applied in Park and Song [65] and Cho et al. [24], respectively.

Fig. 4
figure 4

Configuration of shear test and boundary conditions. a Schematic of test configuration showing boundary conditions. b Alignment of walls with respect to the synthetic sample

Full size image

Following the movement of the particles at the joint, new contacts that were not previously defined with the smooth joint contact model are redefined as such with the joint properties, provided they satisfy a predefined criterion. This criterion is set in terms of the proximity of the new contacts to the joint location as measured by its coordinates and dip.

For a specified value of joint friction coefficient, several tests were conducted and values of shear stresses and shear displacements were recorded for each round. Each test was therefore carried out under set values of normal stress and joint friction coefficient. Figure 5 depicts the shearing behaviour of different frictional joints under different normal loading conditions. The shear stress reaches a peak strength value before gradually reducing to a residual strength. Whereas, a shear envelope based on the residual strengths may be derived, the peak strength values were used instead as they encompass the actual strength characteristics of the joints under prevailing conditions. The rate at which the joint reaches its peak strength is much higher than the reduction to its residual strength. This is observed from the steepness of the slope at the left-hand side of the curves (Fig. 5). It implies that it takes a much longer time for a joint to reach its residual strength after yielding. Shear strength increases with frictional resistance as well as effective stresses normal to the joint plane.

Fig. 5
figure 5

Shear behaviour under different normal stress conditions. a Comparison of shear behaviours of a joint with a friction coefficient of 0.2. b Comparison of shear behaviours of a joint with a friction coefficient of 0.5

Full size image

Residual stresses were achieved naturally for all vertical (normal) loading conditions. The horizontal velocity of the upper left wall which acts as a loading platen was set to a very small value (0.003 m/s) to ensure stability and quasi-static equilibrium. Where the loading rate is relatively high, as shown in Cho et al. [24] and Park and Song [65], the corresponding time steps are set to very small values to reduce dynamic effects. Also, due to the near-uniform lateral orientation and the small undulation of the assembly of smooth joint contacts, the level of stress fluctuation during sliding is further reduced.

To complete the calibration of the joint friction property, failure envelopes were constructed for various assigned friction coefficients, using peak shear strength values and effective stresses normal to the joint plane as shown in Fig. 6. Figure 6a indicates the limit of the shear strength when a friction coefficient of 0.2 is specified as an input parameter value during joint creation. The equation describing the curve in terms of the peak shear stress and effective normal stress is

$$\tau = 0.0045 + 0.1993\sigma_{\text{n}}$$
(8a)

From Eq. 8, the cohesive strength (C) is 0.0045 MPa, which is negligible (C ≈ 0). The friction coefficient (ϕ) is 0.1993 (≈0.2), and the corresponding friction angle is 11.27°

$$\phi = \tan^{ - 1} \left( {0.1993} \right) = 11.27^{\circ }$$
(8b)

Likewise, when a friction coefficient of 0.5 is set as an input parameter value to define the joint characteristics, the shear envelope derived is describe by

$$\tau = 0.0261 + 0.4729\sigma_{\text{n}}$$
(9a)

The cohesive strength (C) is 0.0261 MPa, which is also relatively negligible. The friction coefficient (ϕ) is 0.4729 (≈0.5), and the corresponding friction angle is given as

$$\phi = \tan^{ - 1} \left( {0.4729} \right) = 25.31^{\circ }$$
(9b)

There are some distinctions in the shear curve for joints with different friction coefficients; however, for joints with identical characteristics, there is a broad similarity in the trend of the shear path when subjected to different normal loading conditions. Joints with a friction coefficient of 0.2 exhibit a very steep shear stiffness and attain the peak shear stress early. The shapes of the shear path for varying vertical loading are analogous, albeit with increasing magnitudes of shear corresponding to a raise in normal stress. For joints with a friction coefficient of 0.5, the shear stiffness is flatter and the time lapse before the peak shear stress is extended. Shear stiffness slightly increases with normal stress. Also, as with the joints with a friction coefficient of 0.2, the shapes of the shear curve are akin for the different normal loads even though the shear strength increases with normal stress.

Fig. 6
figure 6

Joint failure envelope for an assigned friction coefficient of 0.5. a Friction coefficient—0.2. b Friction coefficient—0.5

Full size image

The shear envelope determined from Fig. 6b for a joint friction coefficient of 0.5 is described by Eq. 9a. From this equation, the friction coefficient is 0.473 (≈0.5). The disparity in peak strength of about 5% falls within an acceptable confidence interval and is attributed to computational approximations such as round-off errors. This does not have a significant impact on the result.

Joint roughness contributes to the shear strength; nonetheless, in this case, the joints are planar with negligible roughness and dilatancy. For this type of joint, the shear strength is, hence, ideally expected to be the product of the friction coefficient and the normal stress.

From Eqs. 8 to 9, the derived joint strength properties match the values of the input macroparameters (e.g. friction angle and cohesive strength). Shear tests using other values of inputted friction coefficient and cohesive strength also show matching results. Table 3 shows a comparison of some of the results.

Table 3 Comparison between inputted and derived joint properties
Full size table

The contact force distribution for joints with friction coefficients of 0.2 and 0.5 is shown in Figs. 7 and 8, respectively. Localised concentration of contact forces occurs at the joint surface, and the distribution of such spots along the joint increases with the normal stress. This is attributed to the increase in contact area between the two planes of each joint as the stress acting normally to it increases. Higher concentrations of contact forces also exist at the top left and bottom right sections of the rock mass, mainly because of the pressure/loading on the top left wall as well as the lateral restrictive support of the bottom right wall. Relatively, the concentration and distribution of contact forces increase with the normal stress as localisation is more distinct at lower normal stresses. The contact force chains is categorised into tensile and compressive forces, and the compressive forces are further classified as normal or shear depending on the mode of action with respect to contacting particles. At higher normal stresses, there are greater concentrations of tensile contact forces at the bottom left and top right sections, indicating greater magnitude of tensile stresses in the same sections (Figs. 9, 10). This is more pronounced for joints with lower friction angles (Fig. 9). Under the same conditions, compressive and shear contact forces are predominant at the bottom right and top left sections, although it is more evenly spread at the bottom half when the joint friction coefficient is lower (Fig. 9b). As expected, compressive and shear contact forces are predominant along the joint planes due to sliding and the effect of the normal stress. The pattern of contact forces is caused by the impact of the servo walls, the loading platen (top left wall) and the fixed wall (bottom right wall) that exert high compressive stresses, thereby limiting the occurrence of tensile stresses at close proximity. The effect is absent at the free sections. Figure 11 shows the microtensile and shear cracks, mostly initiated near the joint planes. The prevalence of microcracks increases with normal stress and joint frictional resistance.

Fig. 7
figure 7

Contact force distribution at various normal stress conditions (friction coefficient = 0.2) (tensile: red, compressive: black, joint unit normal vector: blue). a Contact force distribution (normal stress, 1 MPa). b Contact force distribution (normal stress, 5 MPa) (colour figure online)

Full size image
Fig. 8
figure 8

Contact force distribution at various normal stress conditions (friction coefficient = 0.5) (tensile: red, compressive: black). a Contact force distribution (normal stress, 1 MPa). b Contact force distribution (normal stress, 5 MPa) (colour figure online)

Full size image
Fig. 9
figure 9

Pattern of tensile, compressive and shear force chains (normal stress, 5 MPa; friction coefficient, 0.2). a Tensile contact forces, b compressive contact forces, c shear contact forces

Full size image
Fig. 10
figure 10

Pattern of tensile, compressive and shear contact force chains (normal stress, 5 MPa; friction coefficient, 0.5). a tensile contact forces, b compressive contact forces, c shear contact forces

Full size image
Fig. 11
figure 11

Microcrack distribution at different conditions (tensile: red, shear: blue). a Microcrack distribution (normal stress, 4 MPa; friction coefficient, 0.2), b microcrack distribution (normal stress, 3 MPa; friction coefficient, 0.5) (colour figure online)

Full size image

The joint and smooth joint contacts have distinct but interdependent properties. The friction and dilatancy angles are joint macroscopic properties. Because we are not investigating the effect of the latter, it was made negligible implying no dilation during the series of shear tests conducted. Nonetheless, even where dilatancy angles are specified, the dilation of joints is restrained at higher normal stresses [7, 65].

Although similar patterns exist when the normal stress is significantly lowered (Figs. 12, 13), there is a fairly even distribution of compressive and shear contact forces for joints with lower friction coefficients (Fig. 13b, c) because of the additional effect of a lower sliding resistance.

Fig. 12
figure 12

Pattern of tensile, compressive and shear contact force chains (normal stress, 1 MPa; friction coefficient, 0.5). a Tensile contact forces, b compressive contact forces, c shear contact forces

Full size image
Fig. 13
figure 13

Pattern of tensile, compressive and shear contact force chains (normal stress, 1 MPa; friction coefficient, 0.2). a Tensile contact forces, b compressive contact forces, c shear contact forces

Full size image

4 Simulation methodology

4.1 Features of the model domain

Rock masses comprise discontinuities which contribute to its mechanical and physical behaviour. As previously mentioned, the primary types of discontinuities consist of faults, shear zones, fractures, joints, bedding planes, planes of foliation and planes of cleavage. Joints have distinctive features. They are created when a rock in tension splits after being stretched beyond its limit and is many times smaller in comparison with faults. Joints do not completely separate rocks, and, unlike faults, their extent of displacement is often trivial, or in some instances, there are no movements.

Joints are, in essence, extensional fracture, made up of planes of separation without prior shear displacement. They are ubiquitous in occurrence and usually exist in a collection of distinct structured patterns know as a joint set which is an assembly of joints with analogous orientation and features. An agglomeration of joint sets is termed a joint system.

This is the first of a series of investigation being conducted to ascertain the influencing behaviour of joints on fluid flow, fluid pressure propagation and crack development. A joint set with characteristic morphology is being modelled. At this instance, the joint set consists of two matching, planar and parallel lateral joints separated by a distance of 0.3 m. This is representative of bedding-parallel joints commonly found to be narrowly spaced in thinner beds than within thick beds [17, 61, 71]. The key properties defining a joint set are joint friction, dilatancy, roughness, cohesion, tortuosity, density and network. The frictional resistance is the main focus of this study. Both joints are planar, non-dilatant and non-undulating.

Samples of synthetic rock materials with properties similar to that tested (e.g. using biaxial and direct shear tests) were adopted. The synthetic rock material is a representative of sandstone. Whereas the microproperties and mechanical properties are given in Tables 1 and 2, the sample’s dimensions are enlarged such that the width is 2 m and the height 1.2 m (Fig. 14). Also the rock domain is deliberately jointed within by placing joints at designed locations. The tests presented in this paper were conducted on a rock mass consisting of two parallel through joints inserted at locations of equal distance (0.15 m) from the centre of the domain. Both joints are lateral spanning in the XY direction in 2D (Fig. 14). It is expected that in a 3D domain, the joints will cut across the out-of-plane direction (Z plane).

Fig. 14
figure 14

Layout of rock mass including two parallel lateral joints

Full size image

4.2 Boundary conditions and loading

Top and bottom vertical stresses, representing an overburden effect, are applied in addition to lateral confining stresses. The combination of these generates in situ stress conditions. The maximum principal stress (\(\sigma_{1}^{\prime }\)) and minimum principal stresses \(\sigma_{3}^{\prime }\) act in the vertical and horizontal directions, respectively, where \(\sigma_{\text{v}}\) = 2.5 MPa and \(\sigma_{\text{H}}\) = 2.0 MPa, similar to geomechanical conditions at around a 120-m depth. The model is a 2D representation assuming plane strain conditions. This implies negligible strain in the out-of-plane direction. The deformation parameters are modified to account for this, where E and \(\upsilon\) are replaced in accordance with Eq. 4. \(E^{*}\) and \(\upsilon^{*}\) are the respective Young’s modulus and Poisson’s ratio in plane strain. This modifies the in-plane strains (i.e. normal strains in the x and y directions, along with shear strains), which are thus redefined as [19]

$$\varepsilon_{xx} = \frac{1}{{E^{*} }}\left( {\sigma_{xx} - \upsilon^{*} \sigma_{yy} } \right)$$
(10a)
$$\varepsilon_{yy} = \frac{1}{{E^{*} }}\left( {\sigma_{yy} - \upsilon^{*} \sigma_{xx} } \right)$$
(10b)
$$\gamma_{xy} = \frac{1}{G}\sigma_{xy} = \frac{{2\left( {1 + \upsilon^{*} } \right)}}{{E^{*} }}\sigma_{xy}$$
(10c)

Servo-controlled vertical and lateral walls are used to generate in situ stresses in the main model domain. The boundary stresses denoting the total overburden and confining stress conditions are used to control the initial and evolving stresses within the rock at a specific depth. This is different from the effective stress conditions applied in Sect. 3 for the test and model calibration. Within the domain, gravity is ignored because of the relatively short segment (1.2 m) being considered.

Fluid is introduced at the centre of the rock mass (Fig. 15) at a final injection pressure of 35 MPa, maintained for the entire duration of the simulation. The loading is intended to cause a perturbation of fluid pressure as a result of the flow of fluid from a remote and singular location (e.g. an injection well).

Fig. 15
figure 15

Fluid injected at the centre of the rock mass in between two parallel joints

Full size image

The given pressure denotes a given peak level occurring as a result of uncontrolled build-up at the vicinity of injection. The maximum allowable pressure in reservoirs has been shown to attain magnitudes commensurate to 40 MPa, over protracted periods [30, 33]. Likewise, reservoir pressure build-up reaching 33 and 25 MPa is demonstrated in Xu et al. [94] and Rutqvist et al. [74], respectively. At excessively high pressures, rock failure manifests in forms such as extensive deformations, sliding, reactivation of pre-existing faults and fracturing. Formation rock failure is dependent on several factors including material properties, in situ stresses and well-operating conditions [30]. The main fluid properties are presented in Table 4.

Table 4 Fluid properties
Full size table

The actual well is not modelled, but the outlet of the injection tubing/perforation which is significantly smaller than the main well bore. An injection well consists of three main pipe sections: the steel casing or surface pipe, the injection casing and the injection tubing. They are progressively smaller in diameter in the order mentioned. For a class 1 injection well, the surface casing is between 0.165 and 0.381 m in outside diameter, the injection casing is between 0.114 and 0.254 m in outside diameter, and the injection tubing is between 0.064 and 0.178 m in diameter [35]. The outlet of an injection tubing with a diameter of 0.1 m is represented here.

4.3 Incorporated fluid flow scheme

Fluid injection and flow is modelled following a procedure described in Eshiet and Sheng [30]. The formulation entails a full coupling between the deformable fluid and assembly of particles. Fluid flow is allowed to occur through parallel-plate channels placed at contacts. The aperture of these channels increases during bond breakage and particle separation, enabling a corresponding acceleration in flow. There is a network of reservoirs associated with the size and number of neighbouring flow channels. The pressure developed within these reservoirs is borne by contiguous particles and is regularly updated. The injected fluid is CO2.

5 Results and discussion

The key properties controlling joint behaviour include the shearing resistance, dilatancy, surface roughness and joint wall compressive strength. The direct impact of these properties on the overall joint performance and the corresponding role of the affected joints in association with subsurface events are of interest. Joint shearing resistance is described by its friction angle (or friction coefficient) which contributes to the shear strength and is in fact considered a measure of the joint shear strength. Variations in the joint friction angle will therefore affect its responses to natural and induced phenomena as well as alter the way in which the joint impacts on surrounding activities. The first series of analyses involves an assessment of the extent of the dependence of subsurface events on the frictional behaviour of joints within proximity of such occurrences. A typical case of a subsurface activity is the perturbation caused by fluid pressure (hydrostatic or via fluid flow) and the resulting onset and proliferation of fractures. Propagation and interconnectivity of fractures is an important phenomenon that has numerous advantageous and disadvantageous influences depending on the desired effect. As a product of fluid pressure perturbation, the pattern and intensity of fractures as a function of changes in the joint frictional resistance were evaluated. The friction coefficient was varied according to the following values: 0.0, 0.2, 0.5, 0.7 and 1.0, which correspond to friction angles of 0.0°, 11.3°, 26.6°, 35.0° and 45.0°, respectively. Some of the results are shown in Figs. 16, 17 and 18.

Fig. 16
figure 16

Fracture development and interaction at different joint frictional resistance (joint unit normal vector: blue). a Friction coefficient: 0.0, b friction coefficient: 0.2, c friction coefficient: 0.5, d friction coefficient: 0.7, e friction coefficient: 1.0 (colour figure online)

Full size image
Fig. 17
figure 17

Population of tensile and shear cracks at various joint frictional resistance. a Friction coefficient: 0.0, b friction coefficient: 0.2, c friction coefficient: 0.5, d friction coefficient: 0.7, e friction coefficient: 1.0

Full size image
Fig. 18
figure 18

Effect of joint frictional resistance on fracture development. a Total crack development, b tensile crack development, c shear crack development

Full size image

5.1 Joint frictional behaviour and variances in fracture processes

The fracturing behaviour of a jointed rock mass is influenced by the frictional resistance of joints, especially those that are within proximity of the fluid pressure perturbations. Numerical experiments were conducted using twin lateral joints of identical properties, enclosing a point source of fluid injection. Though the joints were planar and non-dilatant, the shearing strength (frictional resistance) was varied for each case within the limit of 0.0°–45° denoting a lower limit of non-dilatant frictionless joints and an upper limit of non-dilatant but highly frictional joints. The containment and patterns of fracturing are shown in Fig. 16. Due to the presence of non-frictional joints, fractures propagate mostly in the north–south (N–S) and west–east (W–E) directions (Fig. 16a). This pattern, although less conspicuous, is also observed at low joint frictional resistance (Fig. 16b) but changes at medium to high joint frictional resistance (Fig. 16c–e). Between the friction angle of 27° and 45°, the fracturing pattern becomes progressively diagonal. At a joint friction angle of 27°, fracturing is constricted laterally, but vertical propagation still occurs. The pattern of fracturing almost entirely becomes diagonal when the friction angle is increased to 45°. Fractures are more likely to be restrained by joints with low frictional resistance (e.g. Fig. 16b); however, for non-frictional joints, isolated zones of crack occur both within the enclosure (between the joints) and at the outer upper and lower regions. This is attributed to non-restrictions to sliding such that the joints are unlimitedly allowed to slide in response to fluid pressure perturbations. Shearing or lateral movements of the joint planes against each other inhibit the progression of fractures beyond their point of contact with the joint. Lateral displacements of fractures are not necessarily caused by slippage; it could be a result of changes in friction along the joint [2]. Fracturing is therefore mostly contained if the joint frictional resistance is very low but not necessarily non-existent. In this test, a friction angle of 11° tends to prevent a significant vertical progression of fractures without the associated pressure perturbations that initiate cracks at point locations.

The presence of in situ and confining stresses also impacts on the direction and orientation of fracturing events. Although the initiation of a fracture may happen when the fluid pressure is greater than the minimum principal stress, its growth is mainly in the direction of the maximum principal stress. This phenomenon is valid where the effects of other factors are not prominent.

Following the onset of fracture, it generally propagates in the direction of the maximum principal stress and perpendicularly to the minimum principal stress. This established concept is shown in Hubbert and Willis [41], Hubbert and Willis [42] and the many other more recent literature on fracture mechanisms [23, 28, 30, 55, 75]. At the subsurface, fractures tend to propagate vertically in tectonically relaxed regions with normal fault regimes, where the maximum stress is generated by the overburden pressure. In tectonically active regions [strike-slip fault and thrust (reverse) fault regimes] which are prevalently compressed, the horizontal stress component is greater and so lateral fractures are formed. These are ideal behaviours of fractures as they could be influenced by several factors such as well inclination, orientation and distance of existing faults, stratification. The theory of the arrangement of principal stresses in the subsurface is described in Anderson [3].

The extent of the material (rock) heterogeneity, the boundary conditions and the presence of discontinuities and their characteristics generally influence the fracturing process. Where the effect of the joint characteristics reduces, the boundary conditions and any induced state become more dominant, thereby controlling the fracturing behaviour. Assuming the effect of other factors is minimised, and the pattern of fracturing is controlled by the magnitude and direction of the principal stresses. In such situations, diagonal fractures tend to occur as the difference between the maximum and minimum principal stresses decreases. If the magnitudes of the principal stresses are the same, the inclination of fracturing should theoretically occur at 45° to both principal stress directions.

As the frictional resistance of the joints increases, its contribution to the fracturing process and its ability to contain propagating fracture diminishes, thereby allowing the impact of other factors/features to be increasingly greater. In Fig. 16e, where the joints have a friction angle of 45°, the fracturing process is unhindered.

One of the key advantages of the particle-based DEM model is that microcracks are modelled as individual bond breakages and hence can be quantified. This feature offers an additional way of appraising the fracturing process in relation to joint frictional resistances by assessing the extent and rate of proliferation of cracks. The trend of development of the various modes of cracks at different joint frictional resistances is shown in Figs. 17, 18. For both rock masses with non-frictional joints (Fig. 17a) and rock masses with frictional joints (Fig. 17b–e), there is a dominance of shear cracks when compared to the population of tensile cracks. The disparity between the population of the two modes of cracks increases with time, but a threshold is observed for a joint friction angle of 27° where the difference between the numbers of the two modes of cracks is at the minimum. Above and below these value, the deviation between the numbers of tensile and shear cracks increases; the highest deviations occur when the joints are frictionless. Whereas the rate of creation of tensile cracks could be approximately described using a logarithmic expression, the rate of creation of shear cracks may be described by either a logarithmic or a polynomial expression, where the crack population is dependent on the elapsed time, t. Some equations that approximately describe the rate of development of tensile and shear cracks within the rock mass for different joint friction angles are presented in Table 5. For a rock mass with a joint friction angle of 35°, Eq. 11 estimates the rate of generation of tensile and shear cracks. Similarly, Eqs. 12–13 calculate the rate of generation of tensile and shear cracks for joint friction angles of 27° and 11° (denoting a low frictional joint), respectively. Where the joints are frictionless, Eq. 14 expresses the rate of generation in tensile and shear cracks, in which N tc and N sc are the number of tensile cracks and shear cracks, respectively.

Table 5 Rate of proliferation of fractures
Full size table

For frictionless and low frictional joints, polynomial expressions may therefore be used to estimate the population of shear cracks; however, where the friction angle is higher (i.e. ≥27°), logarithmic relationships are more suitable.

The joint frictional resistance affects crack generation as illustrated in Fig. 18. The rate of fracture development and the population of total cracks created decrease with increasing frictional resistance. This trend reverses beyond a critical value of friction angle (friction coefficient), which implies that above this value, there is a progressive increase in the rate of fracture growth and the population of total cracks as the friction angle is further increased.

The critical friction angle for this case has been identified as 27° (friction coefficient = 0.5) (Fig. 19). As the friction coefficient decreases below the critical value, the rate of fracture development and the number of total cracks increase accordingly. Likewise, an increase beyond the critical value increases the rate of fracture development and the number of total cracks. If x denotes an arbitrary value of friction coefficient and x c denotes the critical friction coefficient, an expression for this is given as

$$x_{2} < x_{\text{c}} < x_{1}$$
(15a)

For a critical friction coefficient of 0.5, Eq. 15a is rewritten as

$$x_{2} < 0.5 < x_{1}$$
(15b)

where x 1 and x 2 represent any friction coefficient less and greater than the critical value, respectively. For the same amount of deviation above the critical value, the increase in intensity of fracturing is greater when the friction coefficient is below the critical friction coefficient. For instance, a joint friction coefficient of 0.2 would result in a higher number of cracks in comparison with a joint friction coefficient of 0.8. The deviation from the critical value for both cases is −0.3 and +0.3, respectively.

Fig. 19
figure 19

Relationship between joint frictional resistance and fracture development. a Amount of additional shear cracks above the maximum number of tensile cracks, b comparison between tensile and shear fracture development

Full size image

The increase in the intensity of fracturing should not be confused with the propagation of fractures across the joint planes and the coalescence of the cracks generated. After the joints are encountered by fractures, joints with low friction angles tend to restrict further fracture growths which are perpendicular or crossing the joint plane, and the ability to contain further fracturing diminishes as the frictional resistance of the joint increases (Fig. 16). Coalescence of cracks is another feature influenced by the frictional resistance of the joints, especially those within the vicinity of the source of fluid pressure. Cracks tend to coalesce to form well-defined fractures with fewer isolated zones of cracks occurring at higher joint frictional resistances; the higher the frictional resistance, the greater the coherence of cracks. Similar trends are noticed for both tensile- and shear-induced cracks (Fig. 18a–c), even though a greater number of shear cracks are generally created irrespective of the frictional status of the joints.

The ratio of shear cracks to tensile cracks indicates a disparity that increases as the proportion of shear cracks rises with time. The curves depicting shear crack development are generally steeper than curves describing tensile crack development. As such, the proportion of shear cracks increases with time due to the greater rate of creation of shear cracks in comparison with increments in tensile cracks. The severity of crack generation is influenced by the joint frictional resistance (Fig. 19a), which also has an analogous impact on the amount of additional shear cracks occurring in excess of the total tensile cracks (Fig. 19b). The additional shear cracks are determined as the difference between the maximum number of shear cracks and the maximum number of tensile cracks.

An almost linear relationship exists between the number of shear and tensile cracks, which allows for an estimation of the other parameter if the quantity of one parameter is known (Fig. 20). For instance, at a given time lapse the extent of tensile fracturing may be estimated if the intensity of shear fracturing is specified. Note that each marker in Fig. 20 denotes the corresponding population of tensile and shear cracks with time. A line of best fit for the curves in Fig. 20 gives the following linear equations:

$$N_{\text{sc}} = 2.04N_{\text{tc}} + 0.36$$
(16a)
$$N_{\text{sc}} = 1.93N_{\text{tc}} + 0.19$$
(16b)

Equation 16a is applicable to the range of joint frictional resistance 0.5–1.0 (Fig. 20b) and provides a rough estimate of the extent of a particular mode of fracturing given that the other mode of fracturing has been quantified. For a joint frictional resistance of 0.2, a similar expression can be established. Equation 16b fits the relationship depicted in Fig. 20c to a linear line. Reviewing Eqs. 16a and 16b shows that the rate of initiation of shear cracks is about twice the rate of initiation of tensile cracks.

Fig. 20
figure 20

Relationship between shear and tensile cracks. a Friction coefficients between 0.0 and 1.0, b friction coefficients between 0.5 and 1.0, c friction coefficient: 0.2

Full size image

The impact of joint frictional resistance on the intensity of fracturing may also be illustrated by relating the total number of tensile cracks generated to the total number of shear cracks at the end of a specified period and for individual joint frictional resistances. This is exemplified in Fig. 21 for an elapsed time of 1.43 × 102 s The linear line fitted to the curve gives the following relationship:

$$N_{\text{sc}} = 2.12N_{\text{tc}} - 0.4$$
(17)

Equation 17 is not generalised as it is mostly applicable at the later stages of fracture development; however, the trend which depicts a proportional increase in the number of shear and tensile cracks as the joint frictional resistance changes is a general characteristic that can be adopted for predictions of fracture intensity. As demonstrated in Fig. 21, the critical joint frictional coefficient is 0.5. Above and below this value, the amount of tensile and shear fracturing increases.

Fig. 21
figure 21

Effect of frictional resistance on crack development (friction coefficient in red)

Full size image

6 Conclusion

Subsurface formations are often characterised by discontinuities, which may be naturally occurring or artificially caused by human interference. The behaviour of bonded discontinuities is directly influenced by the type of fill, and as a function of the type of formation and fill, it could range from highly impermeable to highly permeable. In unbonded discontinuities devoid of cementitious substances, the mechanical and physical properties dominate its behaviour. Amongst these, the compressive strength (JCS), shear strength and dilatancy of the interface are some of the main factors governing its performance. Their influence is especially apparent in shallow formations where the effects of the overburden pressure and in situ stresses are relegated. Therefore, it is important to assess the effects of the properties of discontinuities on hydraulic fracturing in underground rock formations.

In this paper, the dependency of geomechanical processes on the frictional characteristics of rock joints was assessed during fluid pressure perturbations by a particle–fluid coupled modelling method. Many interesting and important behaviours of unbonded discontinuities were observed from the modelling results, particularly from those quantitative microcracks results that are very difficult to achieve by other numerical methods. The fracturing behaviour of a jointed rock mass is influenced by the joint shear resistance. There is a greater tendency for the propagation of fractures to be restrained by joints of low frictional resistance. One of the major contributing factors is the shearing or lateral movements of joint planes against each other, which obstructs the growth of fractures moving across the joints. Lateral displacements of discontinuities are caused by slippage and/or changes and variations in friction at sections of the joint surface. Although fractures can be contained by joints of low frictional resistance, the uninhibited sliding of non-frictional joints may cause reinitiated and proliferation of fractures at other locations. Generally, the extent of rock heterogeneity, the network of discontinuities and their characteristics influence the fracturing process. The severity of fracturing reduces appreciably as the joint frictional resistance increases; an increase in the frictional resistance of rock joints reduces its ability to suppress fracture growth but permits an increase in the influence of other factors/features such as in situ stresses and overburden conditions.

Crack initiation along joint planes is preponderantly induced by shear failure, but the propagation of the resulting fractures is mainly caused by tensile failure of the rock material. The intensity of shear-induced fractures is considerably greater than that of tensile-induced fractures, and the predominance of shear fractures is attributed to the sliding of the joint planes.