Abstract
The granular column collapse is a well-established experiment which consists of having a vertical column of granular material on a flat surface and letting it collapse by gravity. Despite its simplicity in execution, the numerical modelling of a column collapse remains challenging. So far, much attention has been dedicated in assessing the ability of various numerical methods in modelling the large deformation and little to the role of the constitutive model on both the triggering mechanism and the flow behaviour. Furthermore, the influence of the initial density, and its associated dilatancy and strength characteristics, have never been included in the analyses. Most past numerical investigations had relied on simple constitutive relations which do not consider the softening behaviours. The aim of this study is to illustrate the influence of the constitutive model on the on-set of failure, the flow behaviour and the deposition profile using the material point method. Three constitutive models were used to simulate the collapse of two granular columns with different geometries and for two densities. The results of the simulations showed that the constitutive model had a twofold influence on the collapse behaviour. It defined the volume of the mobilised mass which spread along the flat surface and controlled the dissipation of its energy. The initial density was found to enhance the failure angle and flow behaviours and was more significant for small columns than for larger ones. The analysis of the potential energy of the mobilised mass explained the existence of two collapse regimes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
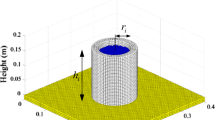
The collapse of a granular column is a well-established experiment which consists in releasing a column of granular material by removing its lateral support on to a flat surface. The column then fails and some of its mass crumbles and flows on to the flat surface before it is deposited. The instability within the material is solely driven by the self-weight of the column. Figure 1 shows a schematic description of the experiment. Among the extensive data available in the literature, the work of Lajeunesse et al. [18, 19] and Lube et al. [21–23] provide the most complete set of data. Both groups of researchers independently investigated the collapse of granular columns. Lajeunesse et al. [18, 19] investigated the behaviour of columns of different sizes made out of glass beads and described them in terms of final deposition profiles. Lube et al. [21–23] investigated the behaviour of different material (e.g. silt, sand, rice, sugar and couscous) and described them in terms of flow behaviour. Nonetheless, the conclusions of both groups were consistent with each other. Two types of collapse were identified and characterised by their initial aspect ratio (Eq. 1). The first type (Regime 1) concerned columns with small aspect ratios and the inertia effect was limited. A small volume of mass was mobilised and slid in a single flow motion. Two sub-categories were proposed by Lajeunesse et al. [18] depending upon whether the deposition was truncated (Regime 1a) or totally consumed by the collapse (Regime 1b). The second type (Regime 2) concerned taller columns in which the inertia effect dominated the collapse behaviour and resulted in complex multi-flow behaviours. The deposition profile took the shape of a ‘Mexican hat’. Balmorth and Kerswell [2] pointed out that there was a gradual transition from the ‘slow avalanches of shallow columns’ (Regime 1) to ‘violent cascading collapses of tall columns’ (Regime 2).
where a is the aspect ratio, \(h_0\) the initial height and \(r_0\) the initial radius.
Lajeunesse et al. [18, 19] and Lube et al. [21–23] showed that the final deposition (e.g. run-out distance and final height) was mainly controlled by the initial aspect ratio of the column. However, Balmforth and Kerswell [2] carried out a series of column collapses for three different materials (glass beads, grit and polystyrene balls) and showed that there was some dependency on the material and on the width of the channel. Furthermore, Daerr and Douady [10] noticed an influence of the initial density of the granular material for a small aspect ratio column. In summary, the collapsing behaviour of a granular column and its final deposition profile are largely controlled by the initial aspect ratio. However, the influence of the mechanical properties of the material and its initial state on the run-out distance are unknown even though these are important in the initiation of instabilities from the point of view of classical soil mechanics.
2 Simulating the column collapse
Despite the apparent simplicity of the experiment, the description and prediction of the collapse remains challenging from an experimental, numerical and theoretical point of view [29]. Many attempts to model the column collapse have already been undertaken both with particle and continuum based methods.
Staron and Hinch [36] presented discrete element (DEM) simulations which showed good agreement with the experimental results in terms of run-out distance. However, they commented on the absence of physical explanation on the power law relationship between the initial aspect ratio and the run-out distance. Furthermore, the influence of the material properties and the initial state on the collapse behaviour were not investigated. Zenit [44] also presented DEM simulations using soft particles and observed differences between the simulations and the experimental results which were attributed to the estimation of the angle of repose. Both Staron and Hinch [36] and Zenit [44] focused on the final deposition profiles with little insight on the collapse mechanism. Lacaze et al. [17] carried out DEM simulations with good agreement with the experimental results, both in terms of flow behaviour and run-out distance. However, the authors commented on the necessity of investigating the influence of multi-sized particles. Girolami et al. [13] used spheres rather than discs in their DEM simulation which gave better prediction of the experiments. Utili et al. [40] used multi-sized particles which and gave better results when using an angle of repose closer to experimental values. They commented on the influence of the shape of the grains on the angle repose and discussed the dilatancy characteristics of the granular material but did not consider it in the simulations. Kumar [16] carried out DEM simulations to investigate the role of the initial grain properties and showed that it had had a significant influence on the flow kinematics and the internal flow structure.
DEM is well suited for micro-mechanical analyses but suffers from its computational cost when applied to large scale problems. For this reason, many researchers have favoured continuum methods such as the adaptive Lagrangian–Eulerian finite element method (ALE FEM). Crosta et al. [9] presented a series of simulation using ALE FEM with a Mohr–Coulomb model. The results were in line with the experimental results. However, the authors commented on the computational cost of the method. The smoothed particle hydrodynamics (SPH) method is computationally cheaper when modelling large deformation problems. Chen and Qiu [7] as well as Liang and He [20] carried out simulations using SPH with, respectively, a Drucker–Prager and a rate dependent Mohr–Coulomb failure criteria. Despite good agreement with the experimental data in terms of run-out distances and final heights, both models are simple failure criteria which do not take the density or softening behaviours into account. It is known that softening behaviours play a key role in slope instabilities and that simple models cannot capture the complexity of the mechanical behaviour [28]. Furthermore, SPH suffers from difficulties in applying boundary conditions due to the absence of a computational mesh.
An alternative to SPH is the material point method (MPM) which was developed from the particle-in-cell method (PIC) by Sulsky et al. [37, 38]. MPM is an Eulerian–Lagrangian method designed for large deformation problems. It differs from PIC in that it is formulated in the weak form. This implies that history-dependent constitutive models can be formulated within the material points in the same way as for the finite element method (FEM). MPM can be seen as an ALE FEM in which all computational variables, including mass, are stored in every single material point. Its application to geotechnical engineering has been discussed and demonstrated by Solowski and Sloan [35]. Its ability to tackle fluid-like behaviours of granular material has been demonstrated by Wieckowski [42]. Andersen [1] showed that MPM was able to model the column collapse using a simple Mohr–Coulomb model. Bandara [3] simulated the column collapse with both SPH and MPM and obtained the same results. However, the SPH simulation required a large number of particles to obtain an accurate run-out distance making it computationally more expensive. Solowski and Sloan [34, 35] compared MPM simulations with the experimental data of Lube et al. [23] and showed that the Mohr–Coulomb model did not dissipate sufficient energy. Hence, the run-out distances were largely overestimated and numerical damping had to be applied in order to match the experimental results. Kumar [16] carried out simulations of the column collapse with both MPM and DEM and showed that MPM with a Mohr–Coulomb model suffered from insufficient dissipation of energy in comparison with DEM. It was attributed to the absence of inter-particle collisions which dissipates some energy. He also compared the standard MPM formulation [37, 38] with the generalised interpolation material point method (GIMP) [4] and found no apparent improvement for column collapse simulations.
So far, all the discussions focused on the method itself with little investigation on what role the constitutive model played in the prediction. Mast et al. [24] carried out column collapse simulations using a Drucker–Prager model and a hardening–softening Matsuoka–Nakai model and showed that the choice of the constitutive model impacted the final deposition profile in terms of final height and run-out distance. Furthermore, they showed that an enhancement of the peak strength resulted in larger final heights and shorter run-out distances. Following this path, this paper investigates the role of the constitutive model in the column collapse.
2.1 The material point method
The concept of MPM is to discretise the continuum body into a finite number of Lagrangian point masses called material points. They are sometimes referred to as ‘particles’ but, unlike the name suggests, they do not represent individual soil grains but a piece of continuum solid. Figure 2 shows a schematic description of the discretisation of the continuum body into material points. Each material point carries a constant mass, which is conserved throughout the entire simulation, as well as all the information required for the computation. The material points move in a background grid which is used to solve the governing equation and purely chosen for computational reasons. For each computational cycle, the information in the material points is mapped to the nodes of the grid which is then used to solve the governing equation. The velocity fields are then obtained for each node of the grid and mapped back to each material point. The velocity of each material point is updated and used to calculate its new position. Figure 3 illustrates the computational cycle. As for FEM, the choice of size of the grid can influence the results but does not carry any permanent information which is the reason why MPM is sometimes referred to as a meshless method. The use of a background grid reduces the computational costs with regard to other meshless methods such as SPH. It also facilitates the definition of the boundary conditions as they can be defined with the grid. Inter-material-point penetration is avoided as the material points move in a single valued velocity field; the velocities of the material points are interpolated from the nodal velocities. Its proximity to FEM allows it inherit many of its developments such as the constitutive models.
2.2 Constitutive modelling for large deformation
MPM is used for large deformation simulations in which some regions of the continuum body undergoes large deformations and others small deformations. Therefore, the constitutive model must be able to handle both cases. Many MPM simulations presented in the literature used simple failure criteria such as Mohr–Coulomb (e.g. [1, 3, 16, 34, 35]). The model parameters were chosen as being close to the critical state values (\(\varphi ^{\prime } \approx \varphi ^{\prime }_{\mathrm{cs}}\) and \(\psi \approx 0\)) favouring the large strained areas and neglecting their mechanical behaviour at small strains. The necessity of using more advanced models has already been highlighted in the literature. For instance, Yerro et al. [43] suggested using a Mohr–Coulomb Strain Softening model to simulate progressive landslides and Mast et al. [24] suggested a hardening and softening Matsuoka–Nakai model to simulate column collapses. The aim of this paper is to discuss the role of the constitutive model in simulation of column collapses and to capture the necessary feature of the constitutive model for large deformation modelling.
2.2.1 Critical state constitutive models
The critical state theory [31] suggests that any soil sheared sufficiently will achieve an ultimate and unique state called the critical state. At this point, the soil will be continuously deformed without any changes in volume or stresses (Eq. 2). The critical state is uniquely defined in a (p, q, e) space by the critical state locus (CSL) at which point the dilatancy D is nil (Eq. 4) and the stress ratio \(\eta\) constant (Eq. 3).
where \(p^{\prime }\) is the mean effective stress, q is the deviatoric stress, \(\varepsilon _v\) and \(\varepsilon _d\) are, respectively, the volumetric and deviatoric strains.
where \(\eta ^{\prime } = q/p^{\prime }\) is the effective stress ratio, M the critical state stress ratio, \(D = d\varepsilon _v / d\varepsilon _d\) the dilatancy rate and \(e_c\) the critical state void ratio.
In this study, it is assumed that the granular material, which has failed and flows, will reach the critical state. However, different soil models will reach this state differently. The critical state can be achieved by classical failure criteria such as Mohr–Coulomb by carefully choosing the model parameters (i.e. critical state friction angle with zero dilation angle). In other cases, the critical state is systematically reached and independently from the choice of the model parameters. These models are referred to as critical state models set within the critical state framework [33]. The two conditions (Eqs. 3, 4) can be simultaneously fulfilled such as in Cam-Clay [30] or independently fulfilled such as in Nor-Sand [14].
2.2.2 Mohr–Coulomb
Mohr–Coulomb predicts the failure of soil upon shearing by considering two parameters—the cohesion c and the friction angle \(\varphi ^{\prime }\). A yield function can be formulated from it (Eq. 5). It is often implemented with a non-associative flow rule and a potential function given in Eq. 6. It introduces a third parameter—the dilatancy angle \(\psi\). Granular materials are cohesionless (\(c^{\prime } = 0\)) which reduces the number of plastic parameters to two—the friction angle \(\varphi ^{\prime }\) and the dilatancy angle \(\psi\). In this study, the Mohr–Coulomb model was implemented as an elastic–plastic model in which the hardening phase is purely elastic and defined by Young’s modulus E and the Poisson ratio.
where F is the yield function, \(c^{\prime }\) the effective cohesion, \(\varphi ^{\prime }\) the effective friction angle, \(\theta\) the Lode angle, P the potential function and \(a_{pp}\) the distance to the apex.
When using a simple Mohr–Coulomb model, a choice has to be made between favouring the small strain behaviour (peak strength) or the large strain behaviour (critical state strength). Figure 4 shows twice the same simulations—(a) using peak state parameters with a high friction angle and a positive dilatancy angle and (b) using critical state parameters with the critical state friction angle and a nil dilatancy angle. The results of the peak state case shows a steep failure surface defining the boundary between the static cone, mapped in blue, and the mobilised mass, mapped in red. It also shows an increase in volume of the mobilised mass which will dilate to infinity. This should not be the case as the material has exhibited more than a 100 % deviatoric strain and must be at critical state. The results of the critical state case show a low failure angle. The static cone, mapped in blue, is smaller than for the peak state case and the mobilised mass, mapped in red, is initially smaller larger than for the peak state case.
2.2.3 Mohr–Coulomb Strain Softening
A natural extension of the elastic-plastic Mohr–Coulomb model to include a variation in the model parameters is the Mohr–Coulomb Strain Softening model. It allows the friction angle, cohesion and dilatancy angle to decrease with accumulated plastic deviatoric strain \(E_d^p\) to a residual value. Different formulations of the model exist and in the present case, an exponential softening rule was chosen (Eqs. 7–9).
where \(\beta\) is the shape coefficient which controls the rate of softening and the subscripts res, peak and max correspond to the residual state, peak state and maximum value.
The reduction in strength and dilatancy allows the model to soften. Following the critical state theory (Eqs. 3, 4), the residual values must be those of the critical state; the residual dilatancy angle must be nil (\(\psi _{\mathrm{res}} = \psi _{\mathrm{cs}} = 0\)) and the residual friction angle must be the critical state friction angle (\(\varphi ^{\prime }_{\mathrm{res}} = \varphi ^{\prime }_{\mathrm{cs}}\)).
The accumulated plastic deviatoric strain \(E_d^p\) is a material point variable stored in the material point and specific to it. It tracks the history of shearing and dictates how it should soften independently of the stress state and density of the soil. Mohr–Coulomb Strain Softening possesses some deficiencies. The peak strength is modelled as a yielding point, and therefore, the hardening phase is a purely elastic behaviour. Furthermore, the peak strength occurs at the end of the contraction phase and before any dilatancy take place. The model ignores the fact that the peak strength of a granular material is determined by its dilatancy characteristics. Taylor [39], followed by Rowe [32] among others, showed that the peak strength was the sum of the critical state strength and the maximum dilatancy rate and is known as the stress-dilatancy theory. The maximum dilatancy rate is density and pressure dependent [5, 6]. Therefore, the dependency on the density is implicitly embedded in the model parameters of Mohr–Coulomb (friction and dilatancy angle in this case).
2.2.4 Nor-Sand
The necessity to include the density as a model variable encouraged Jefferies [14] to develop a new constitutive model called Nor-Sand. It is a simple elasto-plastic model for sand which allows plastic deformation to take place prior to the peak state. It was developed from the critical state theory and based on Nova’s stress-dilatancy rule [27]. The yield function (Eq. 10) was derived by means of normality in the same way Roscoe and Schofield [30] derived the yield function for original Cam-Clay and is thus associative. However, Nor-Sand shapes the yield surface according to the dilatancy characteristics as shown in Fig. 5. It also sizes the yield surface with the image pressure \(p_i\) which is the pressure at the summit of the yield surface and is always located on the critical state line. It is equivalent to Cam-Clay’s preconsolidation pressure.
where M the critical state stress ratio, N the dilatancy parameter and \(p_i\) is the image pressure.
Nor-Sand decouples the concept of over-consolidation from density which allows normally consolidated but dense sand to dilate and models the peak strength as a consequence of dilatancy. Furthermore, it includes the density as a model variable through a state index called the state parameter \({\varPsi }\) [5] and shown in Eq. 11. To avoid confusion, the dilatancy angle is noted small \(\psi\) and the state parameter capital \({\varPsi }\). The inclusion of density as a model variable through the state parameter implies that a single set of model parameters is required for a given material. There is no need to use different model parameters for different initial densities as for Mohr–Coulomb Strain Softening. The state parameter captures the dilatancy behaviour of the soil which is nil at critical state. Further information on Nor-Sand can be found in the appendix.
The critical state line was derived from the relative dilatancy index \(I_R\) (Eq. 19) [6] which is nil at critical state due to nil dilatancy condition (\(D = 0 \rightarrow I_R = 0\)). In doing so, a nonlinear critical state locus can be formulated (Eq. 12) and was suggested by Mitchell and Soga [25]. The critical state void ratio \(e_c\) is a function of the minimum void ratio \(e_{\mathrm{min}}\) , the maximum void ratio \(e_{\mathrm{max}}\), the mean effective stress \(p^{\prime }\) and the crushing pressure Q which is the pressure at which individual soil particles are broken apart [6].
2.2.5 Calibration of the constitutive models
The calibration of the model parameters was based on previous work done on a Japanese silica sand called Chiba sand [12]. Drained triaxial compression tests were simulated using the MPM code with an initial mean stress of \(p^{\prime }_0\) = 20 kPa and for two densities (loose \(e_0 = 0.8\) and dense \(e_0 = 0.6\)). The stress–strain curves were first generated with Nor-Sand and then calibrated for Mohr–Coulomb and Mohr–Coulomb Strain Softening. Figure 6 shows the calibration of the three models. The model parameters for the Mohr–Coulomb model (critical state values) are given in Table 1. The model parameters for the Mohr–Coulomb Strain Softening for both loose and dense sand in Table 2 and those for Nor-Sand in Table 3.
2.3 Definition of geometry and mesh
Two geometries were chosen to investigate the behaviour of the column collapse with an initial aspect ratio of 1.0 (Column 1) and 2.0 (Column 2) as shown in Fig. 7. These two initial aspect ratios are respectively in the upper limit of Regime 1 and lower limit of Regime 2 according to the experimental data [18, 19, 21–23]. The columns rested on a thin layer called the base layer which provided the friction necessary for the deposition. It is modelled as a stiff elastic body. According to the experimental data, the friction of the base layer plays a small role in the column collapse [18] and was confirmed numerically when some realistic friction angles were applied [3]. The opening of the gate was not modelled as such in the simulation. It was assumed that it was instantaneous and had no affect on the collapse mechanism. However, this may lead to some differences between the experimental and numerical observations, which was not investigated in this study.
The MPM code used for this study was provided by the MPM Research Community (http://mpm-dredge.eu). The domain was meshed with unstructured tetrahedral elements and is used to initialise the material points. It implied that fine meshes with smaller cells initialised more material points with smaller masses than with coarser meshes. The unstructured nature of the mesh implied that the mass of a material point can differ from one point to another as the cells have different volumes. However, for the present simulations, the mesh was very regular and extreme differences in cell sizes were avoided. The number of material points initialised in each cell can be changed. A mesh sensitivity analysis was carried out prior to the analysis in order to understand and minimise its influence. Three mesh sizes were investigated for which the number of material points per cell ranged from 4 to 10. Table 4 summarises the different cases.
The results of the mesh sensitivity analysis are shown in Fig. 8 in which the mesh is visible. The colour mapping represents the deviatoric strain—0 % blue and 100 % red. The results show that the failure surface, which is the interface between the blue and the red material points, was influenced by the mesh size. It is concave for the coarse meshes and convex for the fine meshes. It will be shown later that the convex shape is related to a process called avalanching which is mesh-dependent. Increasing the number of material points in a coarse mesh did not significantly improve the results as was also observed by Kumar [16]. However, a refinement of the mesh, which indirectly initialised more material points, improved the results significantly.
3 Simulation results for Column 1
The results of the simulations for Column 1 are presented in Fig. 9. Two snapshots are shown for each constitutive model and density. The first snapshot is at \(T = 0.3\) s. It shows the primary failure surface and the formation of the sliding wedge. The second snapshot is at \(T = 2.5\) s and shows the final deposition profile. The colour mapping corresponds to the deviatoric strain— 0 % blue and 100 % red. Therefore, the static cone is mapped in blue and the mobilised mass in red.
The Mohr–Coulomb simulations were carried out using the critical state parameters (\(\varphi ^{\prime }_{\mathrm{cs}} = 33^\circ\), \(\psi = 0^\circ\)). The development of the primary failure surface is fast and defines the boundary between the static cone with small strains and the mobilised mass which takes the form of a sliding wedge. During the collapse, the mobilised mass slides as a rigid body along the failure surface and crumbles upon contact with the base. The friction between the mobilised mass and the static regions dissipates energy and slows down the mobilised mass until it is static. Figure 9a shows the collapse at \(T = 0.3\) s in which the sliding wedge has started to crumble upon contact with the base. The mobilised mass is mapped in light blue and red. The static cone in dark blue. The failure surface is located at the interface of both regions and is planar. Material points in contact with the base layer are slowed down by friction until they are eventually immobilised. The other material points carry on flowing (\(T = 0.6\) s). Those in contact with the immobilised mass are in turn slowed down and successive static layers are built from the base layer to the surface of the flow. During that phase, the static cone, which is mapped in blue, is gradually eroded by an avalanching process (\(T = 0.8-1.0\) s). However, this process is influenced by the size of the grid as previously shown in Fig. 8. The avalanching process changes the shape of the failure surface which goes from a straight line to concave. This avalanching process is consistent with experimental observations [21–23]. Finally, the collapse gets to a hold (\(T = 0.8-2.5\) s). Figure 9b shows the final deposition profile. The static cone is mapped in blue and has decreased in size during the avalanching process. The mobilised mass, which is static, is mapped in red. The results show that the deposition slope has smaller angle than the friction angle due to the inertia of the mobilised mass. The normalised run-out distance (Eq. 13) is 1.75 and is larger than the empirical prediction of 1.20 [21]. A popular approach to minimise this run-out distance is to apply some numerical damping as suggested by Solowski and Sloan [34]. Numerical damping aims to mitigate numerical oscillations by reducing the out-of-balance force and is hence reducing the dynamic effects. The use of numerical damping to reduce the run-out distance is rather a modification of the dynamic problem than a proper energy dissipating mechanism.
where \(r^*\) is the normalised run-out distance, \(r_0\) the initial radius and \(r_f\) the final radius.
The simulations with the Mohr–Coulomb Strain Softening model were carried out for two initial densities (loose and dense) with two different sets of model parameters (loose: \(\varphi ^{\prime }_{\mathrm{peak}} = 39^\circ\), \(\psi _{\mathrm{peak}} = 6^\circ\), dense: \(\varphi ^{\prime }_{\mathrm{peak}} = 50^\circ\), \(\psi _{\mathrm{peak}} = 25^\circ\)). The results for the loose case show a fast developing failure surface which defines the static cone and the mobilised mass. The angle of the failure surface is steeper than for the Mohr–Coulomb simulation with critical state parameters and is due to the higher peak strength. Consequently, the initially mobilised mass is smaller and the static cone larger. During the collapse, the mobilised mass slides as a rigid body along the failure surface and crumbles upon contact with the base. Figure 9c shows the collapse at \(T = 0.3\) s in which the sliding wedge has started to crumble upon contact with the base. The flow is then progressively slowed down by frictional contact with static layers (\(T = 0.6-0.8\) s). The avalanching process then gradually takes place, eroding the summit of the column (\(T = 0.8-2.5\) s). The deposition profile (\(T = 2.5\)), as shown in Fig. 9d, has a similar shape than for the critical state Mohr–Coulomb but with a shorter run-out distance (\(r^* = 1.5\)). This is due to the smaller mobilised mass and additional dissipation of energy, albeit limited as the mobilised mass has mostly the critical state friction angle. The collapse behaviour of the loose sand with a Mohr–Coulomb Strain Softening model is very similar to the one observed with Mohr–Coulomb. The results for the dense case still show a fast development of the primary failure surface. However, the failure angle is significantly larger and the mobilised mass smaller than for the previous cases as shown in Fig. 9e. It is due to a high peak friction angle. Then, the mobilised mass slides down and crumbles upon contact with the base layer (\(T = 0.4\) s). Static layers are then built bottom-up by frictional contact with the base layer (\(T = 0.6\) s). The high peak friction angle dissipates more energy than for the previous cases, and the run-out distance is shorter (\(r^* = 1.20\)). It is within the range of the experimental predictions but with a steeper deposition slope. However, there is evidence that the experiments were conducted with loose to medium-dense sand rather than dense.
The simulations with Nor-Sand were carried out for two initial densities (loose and dense) but with a unique set of model parameters as Nor-Sand includes the void ratio as a model variable. The results for the loose case show that the development of the primary failure surface is slower than for the Mohr–Coulomb cases. A sensitivity analysis showed that this lag time is caused by the plastic hardening. The position and angle of the failure surface evolves with the plastic hardening. Figure 9g shows the collapse at \(T = 0.3\) s and in which the ‘hardened’ failure surface is shown. The mobilised mass formed a wedge which slide along the failure and crumbled upon contact with the base (\(T = 0.5\) s). It then flowed as a single mass. The material in contact with the failure surface and the base, albeit not exclusively, was slowed down by frictional contact. Successive static layers were gradually build from the base to the surface (\(T = 0.7 - 0.9\) s). No avalanching was observed during the collapse of the column with loose sand. The deposition profile (\(T = 2.5\) s) is a truncated cone with a slope corresponding to the critical state friction angle. The run-out distance is within the range of the experimental prediction (\(r^* = 1.2\)) and is shorter than with the Mohr–Coulomb cases but is in the range of the experimental predictions. It is due to additional dissipation of energy during the hardening phase and the dissipation of energy within the mobilised mass. This point will be further developed in the discussion section.
The results for the dense case with Nor-Sand show a steep failure surface. The speed of the development of the failure surface is influenced by the hardening rate and the failure slope by the peak strength as for the Mohr–Coulomb case. Figure 9i shows the collapse at \(T = 0.3\) s. It can be seen that the failed mass, mapped in red, is smaller than for the loose case. The dilative nature of dense sand causes the sand to expand and explains the way the lateral free surface has underwent high shearing. As the material hardens, the slope of the failure surface increases. Therefore, the mobilised and flowing mass is reduced. Once this reduced mobilised has reached the base and stabilised, an intensive avalanching phase starts (\(T = 0.5\) s) in which the static cone continuously shreds (\(T = 0.7 - 0.9\) s). This process is slow and was still continuing at \(T = 2.5\) s as shown in Fig. 9j. However, the shredded material affected the upper part of the column but did not affect the short run-out distance (\(r^* = 0.75\)). It has been shown by Darve et al. [11] that the avalanching process is strongly related to a diffuse mode of failure and that localised mode (typically by shear band formation) and diffuse mode (typically by avalanches) can coexist spatially and/or appear successively temporally in boundary value problems involving granular media.
4 Simulation results for Column 2
The results of the simulations for Column 2 are presented in Fig. 9. As for Column 1, two snapshots are shown for each simulation, respectively, for constitutive model and density. The first snapshot is at \(T = 0.3\) s which shows the primary failure surface and the formation of the sliding wedge. The second snapshot is at \(T = 2.5\) s which shows the final deposition profile. The colour mapping corresponds to the deviatoric strain—0 % blue and 100 % red. Therefore, the contrast in colour shows the static cone and the mobilised mass.
The Mohr–Coulomb simulations were carried out using the critical state parameters (\(\varphi ^{\prime }_{\mathrm{cs}} = 33^\circ\), \(\psi = 0^\circ\)). The development of the primary failure surface is fast and defines the static cone with small strains and the mobilised mass which takes the form of a sliding wedge. During the collapse, the mobilised mass slides as a rigid body along the primary failure surface and crumbles upon contact with the base. Figure 10a shows the collapse at \(T = 0.3\) s in which the sliding wedge has started to crumble upon contact with the base. Unlike Column 1, the primary failure surface is not straight but concave. The wedge slides and rotates along the concave failure surface as a rigid body (\(T = 0.3\) s) but, unlike Column 1, a secondary failure surface is observed. However, the size of the primary failure surfaces for Column 1 and Column 2, on which energy is dissipated by frictional contact, are similar. Unlike for Column 1, The mobilised mass is also more significant than the static cone. The friction between the mobilised mass and the static regions dissipates energy and slows down the mobilised until its is static. The toe of the wedge rapidly loses momentum due to the frictional contact with the base. The momentum of the mobilised mass is significant due to its mass and flows on (\(T = 0.6\)). During this phase, the flow exhibits multiple smaller flows due to multiple shear zone. The mobilised mass then flows gradually before losing momentum (\(T = 0.8\) s). The stabilisation of the mobilised mass is built bottom-up by successive layers (\(T = 0.8 - 2.5\) s) and is shown in Fig. 10b. The final run-out distance is significantly larger than the experimental prediction (\(r^* = 4.0\)).
The simulations with the Mohr–Coulomb Strain Softening model were carried out for two initial densities (loose and dense) with two different sets of model parameters (loose: \(\varphi ^{\prime }_{\mathrm{peak}} = 39^\circ\), \(\psi _{\mathrm{peak}} = 6^\circ\), dense: \(\varphi ^{\prime }_{\mathrm{peak}} = 50^\circ\), \(\psi _{\mathrm{peak}} = 25^\circ\)). The results for the loose case show a fast developing failure surface. As for the Mohr–Coulomb case with critical state parameters, the failure surface is concave and has a similar shape. Figure 10c shows the collapse at \(T = 0.3\) s in which the sliding wedge has started to crumble upon contact with the base. The primary and secondary failure surfaces have similar shapes as for the Mohr–Coulomb simulation. The flow is then progressively slow down by frictional contact with static layers (\(T = 0.6 -0.8\) s). As previously noticed for the Mohr–Coulomb case, the multiple flow surface appear in the flowing mass. The avalanching process then gradually takes place eroding the summit of the column (\(T = 0.8 - 2.5\) s). The deposition profile (\(T = 2.5\)), as shown in Fig. 10d, has a shape similar to that of the critical state Mohr–Coulomb. The deposition profile is very similar to the Mohr–Coulomb one. The run-out distance is the same (\(r^{*} = 4.0\)) and is much larger than the experimental prediction. The results for the dense case show a fast development of the primary failure surface. However, the failure angle is larger and is planar. Figure 9e shows the results at \(T = 0.3\) s. The newly-formed wedge slides down until the toe reaches the base layer and crumbles (\(T = 0.6\) s). Successive layers of stabilised mass build up from the base to the surface (\(T = 0.8\)), while an avalanching process starts at the summit of the static cone. These two processes continue until the mobilised mass is stabilised (\(T = 2.5\) s). The deposition profile has a run-out distance similar to the ones observed for the other two Mohr–Coulomb cases (\(r^* = 4.0\)). This can be explained by the large inertia of the mobilised mass.
The simulations with Nor-Sand were carried out for two initial densities (loose and dense) but with a unique set of model parameters as Nor-Sand includes the void ratio as a model variable. The results for the loose case show that the development of the primary failure surface is slower than for the Mohr–Coulomb cases, albeit not as significantly slower as for Column 1. Figure 10g shows the collapse at \(T = 0.3\) s. Unlike for the Mohr–Coulomb cases, the mobilised mass is subjected to a planar primary failure surface and a multitude of minor secondary ones which divide the mobilised mass into blocks. The blocks then slide while being distorted (\(T = 0.5\) s) and finally crumble upon contact with the base layer (\(T = 0.7\) s). The material then flows on the horizontal surface building the successive static layers (\(T = 0.9\) s). Figure 10f shows the final deposition profile which has an angle of repose close to the critical state angle. The run-out distance (\(r^* = 2.3\)) is shorter than for the Mohr–Coulomb cases and is caused by additional energy dissipation of plastic deformation modelled by Nor-Sand. The run-out distance is within the range of the experimental predictions [21].
The results for the dense case with Nor-Sand show a fast developing and steep failure surface, albeit slower than for the loose case. Figure 10i shows the collapse at \(T = 0.3\) s. The high density of the material causes it to dilate and harden. As the material hardens, the slope of the failure surface increases. Therefore, the mobilised and flowing mass is reduced. Once this reduced mobilised has reached the base and stabilised, an intensive avalanching phase starts (\(T = 0.5\) s) in which the static cone continuously shreds off layers of material (\(T = 0.7 - 0.9\) s). This process is slow and was still continuing at \(T = 2.5\) s as shown in Fig. 10j. The shredding affected mainly the summit of the static cone. The material then free falls or flows on the upper part of the deposited mass. It stabilises on it before reaching the toe of the flow. Therefore, the final run-out distance (\(r^* = 2.2\)) is the one at \(T = 2.5\) s. Unlike for Column 1, the run-out distance of the dense case for Column 2 is comparable to the loose case and within the range of the experimental results [21]. This difference comes from comparable mobilised masses as is explained later in the paper.
5 Tracking individual material points
Four material points were tracked for each simulation. The initial position of these four material points are shown in Fig. 7. Three material points were located at mid-width of the column and the fourth in the top corner next to the free surface. Figures 11 and 12 show their flow paths, displacements and velocities for both columns and, respectively, for Mohr–Coulomb Strain Softening and Nor-Sand. The time increment for each marker is 0.1 s. The analysis of these four points illustrates differences in the collapse behaviour. Note that the flow paths, displacements and velocities are for specific material points and are local quantities. Therefore, the flow distance of a specific material points does not necessarily reflect the run-out distance of the entire column collapse. The run-out distance is the maximum travel distance of all material points.
Figure 11a shows the flow paths for the simulations of Column 1 with the Mohr–Coulomb Strain Softening model and for both densities. The results show that only the two upper material points were mobilised and flowed with a concave path. The material point located in the top corner next to the free surface (MP 774) had the same flow path both in time and in space for both the loose and the dense case. The material point located at mid-distance and a the top of the column (MP 290) had a similar path for the loose and the dense case, but it travelled a shorter distance for the dense case. The two other material point (MP 5633 and 1521) were not mobilised in the collapse.
Figure 11b shows the flow path for simulations of Column 2 with the Mohr–Coulomb Strain Softening model. The results that three out of the four material points were mobilised for the loose case, whereas only two were for the dense case. Their flow paths are concave as they also were for Column 1. The flow paths of the two material points located at the top of the column (MP 6530 and 5520) show the same concave flow paths.
Figure 11c, d show the development of displacements over time of the four material points respectively for Column 1 and Column 2. It shows when the material points were mobilised and immobilised. Two differences appear between the loose and the dense case with a Mohr–Coulomb Strain Softening model. The first difference is whether a material point is mobilised by the primary failure surface or not. It can be seen that MP 290 and MP 5748, respectively for Column 1 and for Column 2, are only mobilised for the loose case. The second difference is whether an avalanching process takes place or not. It can be seen that MP 290 in Column 1 is mobilised by the primary failure surface for the loose case but by the avalanching process for the dense case. Furthermore, it is mobilised later in case of avalanching.
Figure 11e, f show the development of the velocities of the four material points for simulations with the Mohr–Coulomb Strain Softening model. The aforementioned differences between the loose and the dense cases are also observed. It can be seen that the velocities of the material points located at the top corner (MP 774 and 6350) exhibit velocities higher than the other material points—2.75 m/s for Column 1 and 3.5 m/s for Column 2. It can also be seen that the avalanching process took place in Column 1 after the stabilisation of initially mobilised mass; material point MP 290 in Column 1 was mobilised at T = 0.8 s and was stabilised at T = 2.5 s. Note that a material point which was mobilised by the primary failure in both columns and for both densities exhibited the exact same flow path, displacement and velocity. The only difference between the loose and the dense case is whether a material point is mobilised or not.
Figure 12a shows the flow paths for Column 2 with Nor-Sand. The results show that two material points (MP 774 and 290) were mobilised for the loose case as for the Mohr–Coulomb Strain Softening simulation, whereas only one of the four material point (MP 290) was mobilised for the dense case. The flow paths with Nor-Sand were more complex than for the Mohr–Coulomb Strain Softening cases and were due to rapid changes in density which were directly taken into account by Nor-Sand. The flow path of the loose sand with Nor-Sand resembled the flow path of the loose sand with Mohr–Coulomb Strain Softening. However, the flow path of the dense case with Nor-Sand is different as it predicts an intensive avalanching process.
Figure 12b shows the flow paths for Column 2 with Nor-Sand and for both densities. The results show that two out of the four material points (MP 6350 and 5522) were mobilised. Unlike Mohr–Coulomb Strain Softening, Nor-Sand predicted different flow paths for loose and dense cases. The loose case with Nor-Sand resembles the loose case with Mohr–Coulomb Strain Softening, albeit the primary failure surface was steeper.
Figure 12c, d show the development of the displacements over time for both Column 1 and Column 2 with Nor-Sand. Differences between the loose and the dense case can be seen for Column 1 in terms of mobilisation of material points and their stabilisation. It can be seen that the material point located in the top corner (MP 774) travelled further and was immobilised later for the loose case than for the dense case. These differences are limited for Column 2.
Figure 12e, f show the development of the velocities for simulations with Nor-Sand. The results show some fluctuation in the evolution of the velocities. This is due to the inclusion of density in the constitutive model. As the material flowed, local variation in density appeared and hence difference mechanical responses were predicted by Nor-Sand. The maximum velocities obtained with Nor-Sand were slightly higher than the those obtained with Mohr–Coulomb Strain Softening—2.75 m/s for Column 1 and 4 m/s for Column 2. Furthermore, a lag time of the onset of the failure is observed between the loose and the dense case of Column 2. This difference is not observed for Column 1.
6 Discussion
The collapse behaviour of a granular column can be analysed by considering the energy balance of the mobilised mass (Eq. 14). The mass of the mobilised part is governed by the constitutive equation which defines the initial failure surface and influences the amount of potential energy initially in the system. This potential energy is then converted into kinetic energy, controlling the velocity of the flow, and is dissipated, which is also controlled by the constitutive model. Therefore, the influence of the constitutive model is twofold.
The amount of potential energy of the mobilised part can be calculated at the initial state as illustrated in Fig. 13 and by assuming the initial failure angle to be equal to the friction angle. Two cases must be distinguished—the small and large aspect ratios cases. The equations of the potential energy of the mobilised part are given in Eqs. 15 and 16.
• for small aspect ratios:
• for large aspect ratios:
where \(E_{\mathrm{pot}}^{\mathrm{mob}}\) the potential energy of the mobilised mass, \(m_{\mathrm{mob}}\) the mass of the mobilised part, \(m_{\mathrm{tot}}\) the mass of the column and \(m_{\mathrm{stat}}\) the mass of the static cone, g gravity, \(h_{\mathrm{mob}}^\mathrm{CG}\) the position of the centre of gravity of the mobilised part, \(h_{\mathrm{tot}}^\mathrm{CG}\) the centre of gravity of the column, \(h_{\mathrm{stat}}^\mathrm{CG}\) the centre of gravity of the static part, \(h_0\) and \(r_0\) respectively, the initial height and radius of the column, \(\varphi ^{\prime }\) the friction angle, n the porosity and \(\rho _s\) the specific gravity of the soil.
The friction angle defining the initial failure angle can be estimated by considering the strength and dilatancy characteristics of the material [6]. The friction angle is the consequence of the critical state friction angle and the dilatancy angle (Eq. 17). The dilatancy angle can be estimated by a state index such as the relative dilatancy index \(I_R\) (Eqs. 18, 19) which includes the effect of density though the relative density index \(I_D\) (Eq. 20) and the pressure through the relative crushing index \(I_c\) (Eq. 21) [6].
where \(\varphi ^{\prime }\) is the friction angle, \(\varphi ^{\prime }_{\mathrm{cs}}\) the critical state friction angle, \(\psi\) the dilatancy angle, \(\alpha\) the relative dilatancy coefficient with \(\alpha = 5\) for plane strain conditions, Q the crushing pressure, \(p^{\prime }\) the pressure, \(R = 1\) a fitting parameter, e the void ratio, \(e_{\mathrm{min}}\) and \(e_{\mathrm{max}}\) respectively, the minimum and maximum void ratio and p the mean effective stress.
The potential energy of the mobilised mass was calculated for a 10 cm wide column for which the height was increased (\(r_0\) = 1 m and \(h_0 = a \times r_0\)). The material properties were taken from Fern et al. [12] and are typical of silica sand (\(\rho _s\) = 2700 kg/m\(^3\), \(\varphi ^{\prime }_{\mathrm{cs}}\) = 33\(^ \circ\), Q = 10 MPa, \(e_{\mathrm{min}}\) = 0.500, \(e_{\mathrm{max}}\) = 0.946). The pressure can be estimated by considering the self-weight of the mobilised mass through an iterative process as the volume of the mobilised mass depends on the friction angle. However, the pressure is known to be low and has a limited influence of the potential energy of the mobilised mass and was assumed to be 1 kPa. The consequence is a higher dilatancy angle, albeit limited. Figure 14 shows the potential energy of the mobilised mass for relative densities ranging from 10 to 90 %. The figure shows that the increase in the initial potential energy of the mobilised mass is bi-linear in a log–log plane commonly used in the literature (i.e. [19]). The transition between small and large columns changes with density and occurs in the region of a = 1.0 and is consistent with the experimental observations [19, 21, 41]. The figure also shows that the influence of the initial density on the relative amount of potential energy in the system is significant for small aspect ratio but not for large one.
The simulations with Mohr–Coulomb predicted similar run-out distances for loose and dense sands and for both Column 1 and Column 2. In contrast, the simulations with Nor-Sand predicted different run-out distances for loose and dense sand for Column 1 and similar run-out distances for Column 2. This difference in predictions can be explained by considering the energy dissipation mechanism. Mohr–Coulomb predicted a sliding rigid wedge for both loose and dense sand which dissipates energy by frictional contact along the primary failure surface and the base. The rigid wedge exhibit limited distortion and hence dissipated little energy. Furthermore, the hardening phase is modelled as elastic and dissipated no energy. Nor-Sand predicted a sliding soft wedge in which intense shearing took place. Therefore, energy was dissipated along the primary failure surface, the base and inside the wedge. Furthermore, it allows plastic deformation to take place during the hardening phase and thus energy was dissipated. The differences between Mohr–Coulomb and Nor-Sand are largely due to their historical development. The Mohr–Coulomb evolved from Coulomb’s frictional law applied to a shear band on which a block is sliding [8] to a failure criteria [26] and then converted to a constitutive model by including an elastic hardening phase. The Mohr-softening Strain Softening is an adaptation of Mohr–Coulomb to accommodate variation in the model parameters in order to satisfy the critical state theory [31] and mimic the mechanical behaviour of soil. Nor-Sand [14] was developed directly from the critical state theory to model the stress–strain relationship of sand. Its energy dissipation law is based on stress-dilatancy theory and allows energy to be dissipated when distorted and this from the very beginning of the shearing process.
7 Conclusion
The results from this study show that the constitutive model plays a key role in the collapse behaviour of granular material. It influences the behaviour at small and large strains by defining the mobilised mass and controlling the energy dissipation mechanism. The influencing factors of a column collapse can be summarised as follows and according to their impact.
-
1.
The initial geometry controls the size of the column and the amount of energy available in the system.
-
2.
The constitutive model defines the failure surface which splits the column into the static cone and the mobilised mass. The total potential energy of the column is split accordingly. The static cone undergoes very small deformations and most of its potential energy is conserved as such. The mobilised part undergoes very large deformation and most of its potential energy is converted into kinetic energy and dissipated by the constitutive model. Therefore, the influence of the constitutive model is twofold.
-
3.
The initial density influences the constitutive models by an enhancement of its mechanical behaviour. It can be captured by an enhancement of the model parameters such as in Mohr–Coulomb or directly through its inclusion as a model variable such as in Nor-Sand. It influences the dilatancy characteristics and consequently the failure angle. The enhancement of the angle of failure by density influences, in turn, the volume of the mobilised mass, its potential energy and, in some cases, the dissipation of that energy. The analysis of the initial potential energy showed that the influence of density is more significant for small columns than for larger ones. It also explains the existence of two families of collapse regimes as suggested by Lajeunesse et al. [18, 19] and Lube et al. [21–23].
The dissipation of the energy is a key part in predicting the collapse behaviour and the run-out distance. The dissipation is controlled by the constitutive model in which the hardening and the softening play an important role. Additionally, modelling assumptions such as the elasto-plastic hardening phase (see [14] for more information) allow to dissipate energy at an earlier stage than for a failure criterion. The enhancement of mechanical behaviour by density influences the hardening and softening phases and subsequently the dissipation of energy. This behaviour is modelled by Nor-Sand. This additional plastic dissipation gives less run-out distances when Nor-Sand model is used and the evaluated run-out distance appears to match well to the experimental data when compared to the prediction made by Mohr Coulomb models.
References
Andersen S (2009) Material-point analysis of large-strain problems : modelling of landslides. Ph.D. thesis, Aalborg University
Balmforth NJ, Kerswell RR (2005) Granular collapse in two dimensions. J Fluid Mech 538:399–428. doi:10.1017/S0022112005005537
Bandara S (2013) Material point method to simulate large deformation problems in fluid-saturated granular medium. Ph.D. thesis, University of Cambridge
Bardenhagen SG, Kober EM (2004) The generalized interpolation material point method. Comput Model Eng Sci 5(6):477–495
Been K, Jefferies M (1985) State parameter for sands. Géotechnique 35(2):99–112
Bolton M (1986) The strength and dilatancy of sands. Géotechnique 36(1):65–78
Chen W, Qiu T (2012) Numerical simulations for large deformation of granular materials using smoothed particle hydrodynamics method. Int J Geomech 12(April):127–135. doi:10.1061/(ASCE)GM.1943-5622.0000149
Coulomb C (1776) Essai sur une application des règles de maximis & minimis à quelques problèmes de statique relatif à l’architecture. De l’Imprimerie Royale
Crosta GB, Imposimato S, Roddeman D (2009) Numerical modeling of 2-D granular step collapse on erodible and nonerodible surface. J Geophys Res Solid Earth 114:1–19. doi:10.1029/2008JF001186
Daerr A, Douady S (1999) Sensitivity of granular surface flows to preparation. Europhys Lett 47(August):324–330
Darve F, Servant G, Laouafa F, Khoa H (2004) Failure in geomaterials: continuous and discrete analyses. Comput Methods Appl Mech Eng 193(27–29):3057–3085. doi:10.1016/j.cma.2003.11.011
Fern J, Sakanoue T, Soga K (2015) Modelling the shear strength and dilatancy of dry sand in triaxial compression tests. In: Soga K, Kumar K, Biscontin G, Kuo M (eds) Geomechanics from micro to macro. Taylor & Francis, London, pp 673–678
Girolami L, Hergault V, Vinay G, Wachs A (2012) A three-dimensional discrete-grain model for the simulation of dam-break rectangular collapses: comparison between numerical results and experiments. Granul Matter 14:381–392. doi:10.1007/s10035-012-0342-3
Jefferies M (1993) Nor-Sand: a simple critical state model for sand. Géotechnique 43(1):91–103
Jefferies M, Been K (2006) Soil liquefaction: a critical state approach. Taylor & Francis, London
Kumar K (2014) Multi-scale multiphase modelling of granular flows. Ph.D. thesis, University of Cambridge
Lacaze L, Phillips JC, Kerswell RR (2008) Planar collapse of a granular column: experiments and discrete element simulations. Phys Fluids 20(6):063,302. doi:10.1063/1.2929375
Lajeunesse E, Mangeney-Castelnau A, Vilotte JP (2004) Spreading of a granular mass on a horizontal plane. Phys Fluids 16(7):2371–2381. doi:10.1063/1.1736611
Lajeunesse E, Monnier JB, Homsy GM (2005) Granular slumping on a horizontal surface. Phys Fluids 17(10):103,302. doi:10.1063/1.2087687
Liang D, He XZ (2014) A comparison of conventional and shear-rate dependent Mohr–Coulomb models for simulating landslides. J Mt Sci 11(6):1478–1490. doi:10.1007/s11629-014-3041-1
Lube G, Huppert H, Sparks R, Freundt A (2005) Collapses of two-dimensional granular columns. Phys Rev E 72(4):1–10. doi:10.1103/PhysRevE.72.041301
Lube G, Huppert H, Sparks R, Hallworth M (2004) Axisymmetric collapses of granular columns. J Fluid Mech 508:175–199. doi:10.1017/S0022112004009036
Lube G, Huppert H, Sparks RSJ, Freundt A (2007) Static and flowing regions in granular collapses down channels. Phys Fluids 19(4):043301. doi:10.1063/1.2712431
Mast C, Arduino P, Mackenzie-Helnwein P, Miller GR (2014) Simulating granular column collapse using the material point method. Acta Geotech. doi:10.1007/s11440-014-0309-0
Mitchell J, Soga K (2005) Fundamentals of soil behavior, 3rd edn. Wiley, Hoboken
Mohr CO (1928) Welche Umstaad Bedingen des Elastizitaetsgrenzen und den Bruch eines material? Abhandlingen aus dem Gebiete der Technischen Mechanik, 3rd edn. Ernst und Sohn, Berlin
Nova R (1982) A constitutive model for soil under monotonic and cyclic loading. In: Pande GN, Zienkiewicz C (eds) Soil mechanics—transient and cyclic loading. Wiley, Chichester, pp 343–373
Potts D, Zdravkovic L (2001) Finite element analysis in geotechnical engineering—application. Thomas Telford Ltd, London
Pouliquen O (1999) Scaling laws in granular flows down rough inclined planes. Phys Fluids 11(3):542–548
Roscoe KH, Schofield A (1963) Mechanical behaviour of an idealised wet clay. In: 2nd European conference on soil mechanics and foundation engineering. Wiesbaden, pp 47–54
Roscoe KH, Schofield A, Wroth CP (1958) On the yielding of soils. Géotechnique 8(1):22–53. doi:10.1680/geot.1958.8.1.22
Rowe PW (1962) The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. In: Proceedings of the Royal Society A: mathematical, physical and engineering sciences, vol 269. The Royal Society, pp 500–527
Schofield A, Wroth P (1968) Critical state soil mechanics, 2nd edn. McGraw-Hill, London
Solowski WT, Sloan SW (2013) Modelling of sand column collapse with material point method. In: Pande GN, Pietruszczak S (eds) Computational geomechanics 2013, vol 553, pp 698–705. http://ogma.newcastle.edu.au/vital/access/manager/Repository/uon:17186
Solowski WT, Sloan SW (2015) Evaluation of material point method for use in geotechnics. Int J Numer Anal Meth Geomech 39(7):685–701. doi:10.1002/nag.2321
Staron L, Hinch EJ (2005) Study of the collapse of granular columns using two-dimensional discrete-grain simulation. J Fluid Mech 545(–1):1. doi:10.1017/S0022112005006415
Sulsky DL, Chen Z, Schreyer H (1994) A particle method for history-dependent materials. Comput Methods Appl Mech Eng 118:179–196
Sulsky DL, Zhou SJ, Schreyer H (1995) Application of a particle-in-cell method to solid mechanics. Comput Phys Commun 87:236–252
Taylor D (1948) Fundamentals of soil mechanics. Wiley, New York
Utili S, Zhao T, Houlsby G (2015) 3D DEM investigation of granular column collapse: evaluation of debris motion and its destructive power. Eng Geol 186:3–16
Warnett JM (2014) Stationary and rotational axisymmetric granular column collapse. Jason Warnett School of Engineering. Ph.D. thesis, University of Warwick
Wieckowski Z (2004) The material point method in large strain engineering problems. Comput Methods Appl Mech Eng 193(39–41):4417–4438. doi:10.1016/j.cma.2004.01.035
Yerro A, Alonso E, Pinyol N (2015) The material point method for unsaturated soils. Géotechnique 65(3):201–217. doi:10.1680/geot.14.P.163
Zenit R (2005) Computer simulations of the collapse of a granular column. Phys Fluids 17(3):031,703. doi:10.1063/1.1862240
Acknowledgments
This project has received funding from the European Unions Seventh Framework Programme for research, technological development and demonstration under Grant Agreement No. PIAP-GA-2012-324522 and the Swiss National Science Foundation under Grant Agreement P1SKP2 158621.
Author information
Authors and Affiliations
Corresponding author
Appendix: Additional information on Nor-Sand
Appendix: Additional information on Nor-Sand
Nor-Sand uses the tangent elastic modulus. In the current implementation, the elastic shear modulus G is defined as a function of the mean effective stress p (Eq. 22). The bulk modulus K is derived from it by assuming a constant value of the Poisson ratio \(\nu\) (23).
where A is the shear modulus constant, b the shear modulus exponent and \(\nu\) the Poisson ratio.
Nor-Sand assumes that the hardening and softening (Eq. 24) are proportional to the difference between the current image state, defined by the image pressure \(p_i\), and the projection of the peak image state, defined by the maximum image pressure \(p_{i,{\mathrm{max}}}\) (Eq. 25).
where H is the hardening modulus and \(p_{i,{\mathrm{max}}}\) the maximum image pressure, M the critical state stress ratio and \(M_{\mathrm{tc}}\) the critical state stress ratio in triaxial compression conditions.
The maximum image pressure is estimated by considering the dilatancy characteristics of the sand. The minimum dilatancy rate at image condition needs to be estimated. This can be done by using a state index such as the state parameter (Eq. 26).
where \(\hbox{d}\varepsilon _v^p\) and \(\hbox{d}\varepsilon _d^p\) respectively the plastic volumetric and deviatoric strain increments, \(\chi\) the dilatancy coefficient and \({\varPsi }_i = e - e_c (p_i)\) the image state parameter.
The proportionality between the hardening/softening rate \(({\hbox {d}p_i} / {\hbox {d}\varepsilon _d^p})\) and the difference between the current and maximum image pressure \(( p_i - p_{i,{\mathrm{max}}} )\) is controlled by a modulus called the hardening modulus H. It controls the brittleness of the sand. The hardening modulus has no physical meaning and is obtained experimentally. Jefferies and Been [15] provide an extensive list of values for different types of sand and suggest values between 50 and 1000 for compression cases. They also suggest formulating it as a function of the state parameters (Eq. 27). It implies that dense sands will have higher values of the hardening modulus and will be more brittle than loose ones. It has been acknowledged throughout time that the value of the hardening modulus is stress state dependent. It is reflected by a number of hardening laws available in the literature.
where \(H_{\mathrm{min}}\) is the minimum value of the hardening modulus and \(\delta _h\) the hardening coefficient.
The version of Nor-Sand presented in this paper has nine model: three elastic parameters (A, b, \(\nu\)), three critical state parameters (\(e_{\mathrm{min}}\), \(e_{\mathrm{max}}\), M), two dilatancy parameters (N, \(\chi\)) and two hardening/softening parameters (\(H_{\mathrm{min}}\), \(\delta _H\)) which are the only two parameters which have to be numerically calibrated. All other parameters can be derived from element tests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fern, E.J., Soga, K. The role of constitutive models in MPM simulations of granular column collapses. Acta Geotech. 11, 659–678 (2016). https://doi.org/10.1007/s11440-016-0436-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-016-0436-x