Abstract
New experimental insight into the spalling behavior of concrete in fire conditions is presented in this paper. Spalling was recorded by a high-speed camera. The slow-motion sequences allow us to determine the size, shape, and velocity of the spalled-off pieces. With this information at hand, the released energy associated with every spalling event is computed and compared to the energies associated with pore-pressure and thermal-stress spalling. This comparison provides new insight into the impact of the various thermal, mechanical, and hydral processes controlling concrete spalling.




















Similar content being viewed by others
Notes
The four screen shots in Fig. 6 corresponding to 80 ≤ t ≤ 200 ms show three pieces in free fall. The visible path in the slow-motion sequence is L = 13 cm. Assuming zero velocity after detaching from the bottom surface of the specimen, the time span for a piece to move 13 cm in consequence of gravity acceleration (g = 9.81 m/s2) is given by
$$ t =\sqrt{{\frac{2 L}{g}}} = \sqrt{{\frac{2 \cdot 0.13} {9.81}}} = 0.16\,\hbox{s}. $$(1)The time span between the first and the last of the respective screen shots in Fig. 6 is 0.12 s which—considering that the pieces are already in the downward motion at t = 80 ms—corresponds well to the situation of free fall.
The previously built-up vapor pressure in consequence of vaporization of water was considered to be released abruptly when the spalled-off piece is detaching. Hereby, a certain initial volume, related to an initial crack width prior to dislocation of the spalled-off piece, was assigned to this vapor pressure.
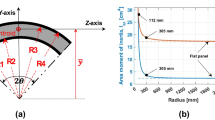
dmax is set to the location where (p0−p)/p0 < tol at t = tmax (see Fig. 11), where tmax [s] is the time instant at which p = patm and a p = 0.
Since the considered increase of the initial pore volume causes an increase of t max, max[v th p ] is determined in an iterative manner.
Adiabatic and isothermal conditions represent the two limiting cases regarding expansion of vapor. Parameter studies showed that the assumption of adiabatic expansion results in a considerable temperature drop, resulting in very low and even negative temperatures. Therefore, isothermal conditions were assumed.
Obviously, the energy released during expansion of vapor is independent of the thickness of the spalled-off piece. The rather moderate dependence of E thkin is caused by the influencing region d max increasing for larger values of d.
In addition to friction, crushing of the beam at the supports is mentioned in [18]. This effect is eliminated by determining the net displacement of the beam (mid-span deflection minus vertical displacement of the beam above the supports).
The depicted empirical relation is obtained in [28] from compressive-strength data. It is assumed that this relation holds for the increase of G F in consequence of aging.
References
Anderberg Y (1997) Spalling phenomena in HPC and OC. In: Phan LT, Carino NJ, Duthinh D, Garboczi E (eds) Proceedings of the International Workshop on Fire Performance of High-Strength Concrete, NIST, Gaithersburg, Maryland, pp 69–73
Anderberg Y, Thelandersson S (1976) Stress and deformation characteristics of concrete at high temperatures: 2. Experimental investigation and material behaviour model, Tech. Rep. 54, Lund Institute of Technology, Lund
Baierl CW (2008) Betonplatten für den Gleiskörper von Eisenbahntunnel—Brandversuche [Concrete slabs for the railroad embankment of tunnels—Fire experiments] (in German). Master’s thesis, Vienna University of Technology, Vienna, Austria
Bamonte PF, Felicetti R (2007) On the tensile behavior of thermally-damaged concrete. In: Carpinteri A, Gambarova P, Ferro G, Plizzari G (eds) Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Taylor & Francis, London, UK, pp 1715–1722
Bažant ZP (1997) Analysis of pore pressure, thermal stress and fracture in rapidly heated concrete. In: Phan LT, Carino NJ, Duthinh D, Garboczi E (eds) Proceedings of the International Workshop on Fire Performance of High-Strength Concrete, NIST, Gaithersburg, Maryland, pp 155–164
Bažant ZP (2005) Concrete creep at high temperature and its interaction with fracture: recent progress. In: Pijaudier-Cabot G, Gérard B, Acker P (eds) Proceedings of the 7th International Conference on Creep, Shrinkage and Durability of Concrete and Concrete Structures, Hermes Science, London, pp 449–460
Bažant ZP, Prat P (1988) Effect of temperature and humidity on fracture energy of concrete. ACI Mater J 85:262–271
Brux G (1997) Brand im Eurotunnel, Ursachen, Schäden und Sanierung [Fire in the channel tunnel, causes, damage, and repair measures] (in German). Tunnel 16(6):31
Burghardt MD, Harbach JA (1993) Enigneering thermodynamics, 4th edn. Harper Collins College, New York
CEB (1991) Fire design of concrete structures. Bulletin d’Information 208, CEB, Lausanne, Switzerland
Consolazio GR, McVay MC, Rish JW III (1997) Measurement and prediction of pore pressure in cement mortar subjected to elevated temperature. In: Phan LT, Carino NJ, Duthinh D, Garboczi E (eds) Proceedings of the International Workshop on Fire Performance of High-Strength Concrete, NIST, Gaithersburg, Maryland, pp 125–148
Diamond S (2000) Mercury porosimetry: an inappropriate method for the measurement of pore size distributions in cement-based materials, Cement Concrete Res 30:1517–1525
Diamond S, Leeman M (1995) Pore size distribution in hardened cement paste by SEM image analysis. In: Diamond S, Mindess S, Glasser F, Roberts L, Skalny J, Wakely L (eds) Microstructure of Cement-based systems / Bonding and Interfaces in Cementitious Materials, vol 370. Materials Research Society, Pittsburgh, pp 217–226
Elices M, Guinea GV, Planas J (1992) Measurement of the fracture energy using three-point bend tests: Part 3—Influence of cutting the P−δ tail. Mater Struct 25(6):327–334
Elices M, Guinea GV, Planas J (1997) On the measurement of concrete fracture energy using three-point bend tests. Mater Struct 30:375
Felicetti R, Gambarova PG (1998) On the residual tensile properties of high performance siliceous concrete exposed to high temperature. In: Special Volume in honor of Z. P. Bažant’s 60th Anniversary, Hermes, Prague, pp 167–186
Gawin D, Pesavento F, Schrefler BA (2006) Towards prediction of the thermal spalling risk through a multi-phase porous media model of concrete. Comput Methods Appl Mech Eng 195:5707–5729
Guinea GV, Planas J, Elices M (1992) Measurement of the fracture energy using three-point bend tests: Part 1—Influence of experimental procedures. Mater Struct 25(4):212–218
Guo XH, Gilbert RI (2000) The effect of specimen size on the fracture energy and softening function of concrete. Mater Struct 33:309–316
Haack A (2002) Generelle Überlegungen zur Sicherheit in Verkehrstunneln [General considerations concerning safety in tunnels] (in German). Tech. rep., Studiengesellschaft für unterirdische Verkehrsanlagen e.V. (STUVA), Köln
Hertz KD (2003) Limits of spalling of fire-exposed concrete. Fire Saf J 38:103–116
Kalifa P, Menneteau F-D, Quenard D (2000) Spalling and pore pressure in HPC at high temperatures. Cement Concrete Res 30:1915–1927
Khoury G (2006) Tunnel concretes under fire: Part 1—explosive spalling. Concrete (London) 40(10):62–64
Khoury G, Majorana CE (2003) Spalling. In: Khoury G, Majorana CE (eds) Effect of heat on concrete. International Centre for Mechanical Science, Udine, pp 1–11
Khoury GA, Grainger BN, Sullivan PJE (1985) Strain of concrete during first heating to 600°C. Mag Concrete Res 37(133):195–215
Khoury GA, Grainger BN, Sullivan PJE (1985) Transient thermal strain of concrete: literature review, conditions within specimen and behaviour of individual constituents. Mag Concrete Res 37(132):131–144
Meyer-Ottens C (1972) Zur Frage der Abplatzungen an Betonbauteilen aus Normalbeton bei Brandbeanspruchung [Spalling of normal–strength concrete structures under fire loading] (in German). Ph.D. thesis, Braunschweig University of Technology, Braunschweig, Germany
Neville A (1981) Properties of concrete, 3rd edn. Pitman, London
Nielsen CV, Bićanić N (2004) Residual fracture energy of high-performance and normal concrete subject to high temperatures. Mater Struct 36:515–521
ÖNORM B4710-1, Beton—Teil 1: Festlegung, Herstellung, Verwendung und Konformitätsnachweis [Concrete—Part 1: Specification, production, use and verification of conformity] (in German). Österreichisches Normungsinstitut (2004)
ÖNORM EN1992-1-2, Eurocode 2—Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken—Teil 1-2: Allgemeine Regeln—Tragwerksbemessung für den Brandfall [Eurocode 2—Design of concrete structures—Part 1-2: General rules—Structural fire design] (in German). European Committee for Standardization (CEN) (2007)
Petersson PE (1981) Crack growth and development of fracture zones in plain concrete and similar materials, Tech. Rep. TVBM-1006, Division of Building Materials, University of Lund, Lund, Sweden
Pichler C, Lackner R, Mang HA (2007) A multiscale micromechanics model for the autogenous-shrinkage deformation of early-age cement-based materials. Eng Fract Mech 74:34–58
Planas J, Elices M, Guinea GV (1992) Measurement of the fracture energy using three-point bend tests: Part 2—Influence of bulk energy dissipation. Mater Struct 25(5):305–312
prEN1991-1-2, Eurocode 1—Actions on structures—Part 1-2: General actions—Actions on structures exposed to fire, European Committee for Standardization (CEN) (2002)
RILEM TC 50-FMC (1985) Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams. Mater Struct 18(4):285–290
Schneider U (1979) Ein Beitrag zur Frage des Kriechens und der Relaxation von Beton unter hohen Temperaturen [Contribution to creep and relaxation of concrete under high temperatures] (in German). Habilitation thesis, TU Braunschweig, Braunschweig, Germany
Schneider U (1988) Concrete at high temperature—a general review, Fire Saf J 13:55–68
Schneider U, Horvath J (2002) Abplatzverhalten an Tunnelinnenschalenbeton [Spalling of concrete for tunnel linings] (in German). Beton Stahlbetonbau 97(4):185–190
Sinkovits G (2008) Betonplatten für den Gleiskörper von Eisenbahntunnel—Betontechnologische Untersuchungen [Concrete slabs for the railroad embankment of tunnels—Material tests] (in German). Master’s thesis, Vienna University of Technology, Vienna, Austria
Ulm F-J, Coussy O, Bažant ZP (1999) The “Chunnel" fire I: chemoplastic softening in rapidly heated concrete. J Eng Mech (ASCE) 125(3):272–282
Zeiml M, Lackner R, Pesavento F, Schrefler BA (2008) Thermo-hydro-chemical couplings considered in safety assessment of shallow tunnels subjected to fire load. Fire Saf J 43(2):83–95
Zhang B, Bićanić N (2001) Fracture energy of high performance concrete at temperatures up to 450°C. In: de Borst R, Mazars J, Pijaudier-Cabot J, van Mier JGM (eds) Proceedings of the 4th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Balkema, Cachan, pp 461–468
Acknowledgments
The authors wish to thank Ulrich Schneider, Heinrich Bruckner, Johannes Kirnbauer, Günter Sinkovits, and Michael Baierl from Vienna University of Technology, Vienna, Austria, for the fruitful cooperation and assistance within the described fire experiments and they wish to thank Karl Ponweiser and Andreas Werner from Vienna University of Technology, Vienna, Austria, for valuable discussions on the spalling kinetics. Moreover, they are grateful to Roberto Felicetti from Milan University of Technology, Milan, Italy, for helpful discussions on the fracture energy of concrete. This research was conducted with financial support by the Austrian Science Fund (FWF) via project P16517-N07 “Transport processes in concrete at high temperatures”.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Determination of pressurized pore volume V 0
For determination of the pore volume right before spalling, V 0 [m3]—containing water vapor at pressure p 0 [Pa]—the ratio between pore volume V p [m3] and total concrete volume (i.e., the porosity ϕ [–]) is assumed to be equal to the area ratio of an arbitrary plane section cut through the porous medium, giving
with A p [m2] as the cumulative area of the pore sections cut by this plane. In addition, the following is assumed:
-
1.
Pores cut by an arbitrary plane section have different diameters, with the distribution of these diameters following the pore-size distribution obtained from, e.g., mercury-intrusion porosimetry (MIP) and/or image analysis. According to [12, 13, 33], a combination of the two mentioned techniques is appropriate for identification of the pore structure of concrete. For the underlying evaluation, the real pore-size distribution is approximated by a straight line in the log (D)-V p -diagram (see Fig. 21a).
-
2.
Assuming spherical pores, an arbitrary section through concrete does not cut all pores at mid section but rather cuts them in a distributed manner (see Figs. 9, 22). Hence, pores of equal diameter contribute differently to the total area A p . This is taken into account by evenly distributing the location of the intersecting plane over the sphere diameter (see Fig. 22).
Illustration of a approximation of the pore-size distribution by [−k log (D/D max)] [33] and b division of employed pore-size distribution into sub-pore ranges
Based on Assumption (1), the employed pore-size distribution is divided into a finite number of sub-pore ranges (see Fig. 21b) and the number of pores corresponding to the i-th sub-pore range, N i [–], is determined from A p,i [m2] and D i [m]. Subsequently, the corresponding sub-pore volume, V 0,i [m3], and the total corresponding pore volume right before spalling, V 0 [m3], are determined as
Appendix 2: Experimental determination of specific fracture energy of concrete by three-point bending tests
The fracture energy of concrete can be determined by (i) direct tension or (ii) bending tests (see Fig. 23). Regarding the latter, the fracture energy may be determined according to [36]. Hereby, (i) weight-compensated tests (where the self weight of the beam is eliminated by a counter-weight system) and (ii) tests without weight compensation are distinguished. In case of no self-weight compensation, the fracture energy G F [J/m2] is given by (see Fig. 23)
with A lig [m2] as the area of the ligament (with A lig = b(h−a), where b [m] is the beam width, h [m] is the beam height, and a [m] is the notch height). In Eq. (16),
is the external work W 0 [J] (area under the experimentally obtained load-deflection curve) and
is the work performed by the mass of the beam between the supports, m 1 [kg], and the mass of the part of the loading device not attached to the machine, m 2 [kg] (following the beam until failure), g = 9.81 m/s is the gravity acceleration, and δ0 [m] is the mid-span beam deflection at failure. According to [19, 32], W 3 can be neglected.
Three-point bending test: a test setup and b load-deflection curve in case of no weight compensation [19]
According to [14, 15, 18, 34], the so-obtained fracture energy changes with sample size which is attributed to the following characteristics of the experimental setup:
-
1.
At the supports, friction Footnote 7 between support and beam leads to an overestimation of the fracture energy by 2–5% [18].
-
2.
Dissipation of energy in the bulk material results in an overestimation of the fracture energy by 5–10% due to damage at central support and 1–2% due to damage in regions of high tensile stresses, respectively [34].
-
3.
W2 is determined by assuming rigid-body motion of the two parts of the beam [14, 15], giving
$$M = b \int\limits_0^{z_c} \sigma\left[w(z)\right] z dz = {\frac{b} {\theta^2}} \int\limits_0^{w(z_c)} \sigma\left(w\right) w dw = {\frac{\zeta b} {\theta^2}}, $$(19)where θ [rad] is the opening angle and z was substituted by w/θ (see Fig. 23a). Inserting
$$ M = \left[ P_{\rm exp} + \left( {\frac{m_1} {2}} + m_2 \right) g \right] {\frac{l}{4}} = {\frac{P l}{4}} \quad \hbox{and} \quad \theta = {\frac{4 \delta}{l}} $$(20)into Eq. (19) leads to [14, 15]
$$ {\frac{M}{b}} = {\frac{1}{\theta^2}} \zeta \quad \hbox{and} \quad P = {\frac{\zeta b l}{4 \delta^2}}, $$(21)allowing extrapolation of the experimental P−δ curve as indicated in Fig. 23b. Hereby, the unknown parameter ζ [N] (introduced in Eq. (19)) is obtained from linear regression of the experimental results (see Fig. 24).
Determination of parameter ζ from linear regression of the part of the bending experiment close to failure of the beam, i.e., for large values of θ [14]
Accordingly, the fracture energy G F , determined from application of Eqs. (16) and (21) to the results of the three-point bending experiments, was reduced by 10%, accounting for the aforementioned dissipative processes. Moreover, aging of concrete was considered by the empirical relation Footnote 8 [7, 28]
Concerning the temperature dependence of the fracture energy, contradictory experimental results are reported in the open literature:
-
In [7], the fracture energy of concrete was determined at elevated temperatures up to 200°C, showing a decrease of G F with temperature.
-
In [29, 43], the residual fracture energy continuously increased up to a temperature of 300–400°C and decreased thereafter. The fracture energy obtained on hot concrete specimens, on the other hand, showed a decreasing behavior up to a temperature of 150°C followed by a continuous increase. It is, however, stated in [29, 43] that transient effects at temperatures up to 150°C may have altered the experimental results for G F at the respective temperatures.
-
In [4, 16], no clear trend for the residual fracture energy was obtained and it was therefore concluded that G F may be assumed to be independent of temperature.
Considering these contradictory conclusions regarding the temperature-dependence of the fracture energy of concrete, G F was assumed to be temperature-independent, with a mean value for the fracture energy obtained from 46 experiments given by G F = 90 J/m2 (see Table 2).
Rights and permissions
About this article
Cite this article
Zeiml, M., Lackner, R. & Mang, H.A. Experimental insight into spalling behavior of concrete tunnel linings under fire loading. Acta Geotech. 3, 295–308 (2008). https://doi.org/10.1007/s11440-008-0069-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-008-0069-9