Abstract
An irreducibly simple climate-sensitivity model is designed to empower even non-specialists to research the question how much global warming we may cause. In 1990, the First Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) expressed “substantial confidence” that near-term global warming would occur twice as fast as subsequent observation. Given rising CO2 concentration, few models predicted no warming since 2001. Between the pre-final and published drafts of the Fifth Assessment Report, IPCC cut its near-term warming projection substantially, substituting “expert assessment” for models’ near-term predictions. Yet its long-range predictions remain unaltered. The model indicates that IPCC’s reduction of the feedback sum from 1.9 to 1.5 W m−2 K−1 mandates a reduction from 3.2 to 2.2 K in its central climate-sensitivity estimate; that, since feedbacks are likely to be net-negative, a better estimate is 1.0 K; that there is no unrealized global warming in the pipeline; that global warming this century will be <1 K; and that combustion of all recoverable fossil fuels will cause <2.2 K global warming to equilibrium. Resolving the discrepancies between the methodology adopted by IPCC in its Fourth and Fifth Assessment Reports that are highlighted in the present paper is vital. Once those discrepancies are taken into account, the impact of anthropogenic global warming over the next century, and even as far as equilibrium many millennia hence, may be no more than one-third to one-half of IPCC’s current projections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
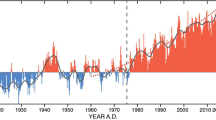
Are global-warming predictions reliable? In the 25 years of IPCC’s First to Fifth Assessment Reports [1–5], the atmosphere has warmed at half the rate predicted in FAR (Fig. 1); yet, Professor Ross Garnaut [6] has written, “The outsider to climate science has no rational choice but to accept that, on a balance of probabilities, the mainstream science is right in pointing to high risks from unmitigated climate change.” However, as Sir Fred Hoyle put it, “Understanding the Earth’s greenhouse effect does not require complex computer models in order to calculate useful numbers for debating the issue. ···To raise a delicate point, it really is not very sensible to make approximations ···and then to perform a highly complicated computer calculation, while claiming the arithmetical accuracy of the computer as the standard for the whole investigation” [7].
The present paper describes an irreducibly simple but robustly calibrated climate-sensitivity model that fairly represents the key determinants of climate sensitivity, flexibly encompasses all reasonably foreseeable outcomes, and reliably determines how much global warming we may cause both in the short term and in the long term. The model investigates and identifies possible reasons for the widening discrepancy between prediction and observation.
Simplification need not lead to error. It can expose anomalies in more complex models that have caused them to run hot. The simple climate model outlined here is not intended as a substitute for the general-circulation models. Its purpose is to investigate discrepancies between IPCC’s Fourth (AR4) and Fifth (AR5) Assessment Reports and to reach a clearer understanding of how the general-circulation models arrive at their predictions, and, in particular, of how the balance between forcings and feedbacks affects climate-sensitivity estimates. Is the mainstream science settled? Or is there more debate [8] than Professor Garnaut suggests? The simple model provides a benchmark against which to measure the soundness of the more complex models’ predictions.
2 Empirical evidence of models running hot
How reliable are the general-circulation models the authority of whose output Professor Garnaut invites us to accept without question? In 1990, FAR predicted with “substantial confidence” that, in the 35 years 1991–2025, global temperature would rise by 1.0 [0.7, 1.5] K, equivalent to 2.8 [1.9, 4.2] K century−1. Yet 25 years after that prediction the outturn, expressed as the trend on the mean of the two satellite monthly global mean surface temperature anomaly datasets [9, 10], is 0.34 °C, equivalent to 1.4 °C century−1—half the central estimate in FAR and beneath the lower bound of the then-projected warming interval (Fig. 1). Global temperature would have to rise over the coming decade at a rate almost twice as high as the greatest supra-decadal rate observed since the global instrumental record began in 1850 to attain even the lower bound of the predictions in FAR, and would have to rise at more than thrice the previous record rate—i.e., at 0.67 K over the decade—to correspond with the central prediction.
Since 1990, IPCC has all but halved its estimates both of anthropogenic forcing since 1750 and of near-term warming. Though the pre-final draft of AR5 had followed models in projecting warming at 0.5 [0.3, 0.7] K over 30 years, equivalent to 2.3 [1.3, 3.3] °C century−1, approximating the projections on the four RCP scenarios, the final draft cut the near-term projection to 1.7 [1.0, 2.3] °C century−1, little more than half the 1990 interval and only marginally overlapping it (Fig. 2).
Near-term global warming projection intervals from FAR (red arrows) and AR5 (expert assessment: green arrows), overlaid on the CMIP5 model projections based on the four RCP scenarios from AR5, which zeroed the models’ projections to observed temperature (black curve) in 1990. Based on AR5 [5]
Empirically based reports of validation failure in complex general-circulation models abound in the journals [14–29]. Most recently, Zhang et al. [30] reported that some 93.4 % of altocumulus clouds observed by collocated CALIPSO and CloudSat satellites cannot be resolved by climate models with a grid resolution >1° (110 km). Studies of paleo-vegetation and pollens in China during the mid-Holocene climate optimum 6,000 years ago find January (i.e., winter minimum) temperatures to have been 6–8 K warmer than present. Yet, Jiang et al. [31] showed that all 36 models in the Paleoclimate Modeling Intercomparison Project backcast winter temperatures for the mid-Holocene cooler than the present. Also, all but one model incorrectly simulated annual-mean mid-Holocene temperatures in China as cooler than the present [31]. Suggestions that current models accurately simulate the mid-Holocene climate optimum rely on comparisons between projected and observed summer warming only, overlooking models’ failure to represent winter temperatures correctly, perhaps through undue sensitivity to CO2-driven warming.
3 An irreducibly simple climate-sensitivity model
An irreducibly simple climate-sensitivity model is now described. It is intended to enable even non-specialists to study why the models are running hot and to obtain reasonable estimates of future anthropogenic temperature change. The model is calibrated against the climate-sensitivity interval projected by the CMIP3 suite of models and against global warming since 1850. Its utility is demonstrated by its application to the principal outputs of the CMIP5 models and to other questions related to climate sensitivity.
The simple model, encapsulated in Eq. (1), determines the temperature response ΔT t to anthropogenic radiative forcings and consequent temperature feedbacks over any given period of years t:
where \( q_{t} \) is the fraction of total anthropogenic forcing represented by CO2 over t years, and its reciprocal allows for non-CO2 forcings as well as the CO2 forcing; ΔF t is the radiative forcing in response to a change in atmospheric CO2 concentration over t years, which is the product of a constant k and the proportionate change (C t / C 0) in CO2 concentration over the period [3, 32]; r t is the transience fraction, which is the fraction of equilibrium sensitivity expected to be attained over t years; and λ ∞ is the equilibrium climate-sensitivity parameter, which is the product of the Planck sensitivity parameter λ 0 [4] and the open-loop or system gain G, which is itself the reciprocal of 1 minus the closed-loop gain g, which is in turn the product of λ 0 and the sum f t of all temperature feedbacks acting over the period.
This simple equation represents, in an elementary but revealing fashion, the essential determinants of the temperature response to any anthropogenic radiative perturbation of the climate and permits even the non-specialist to generate respectable approximate estimates of temperature response over time. It is not, of course, intended to replace the far more complex general-circulation models; rather, it is intended to illuminate them.
4 Parameters of the simple model
The parameters of the simple model are now described.
4.1 The CO2 fraction q t
The principal direct anthropogenic radiative forcing is CO2. Other influential greenhouse gases are CH4, N2O, and tropospheric O3. In AR4, it was estimated that CO2 would contribute some 70 % of total net anthropogenic forcing from 2001 to 2100, so that q 100 = 0.7. Likewise, AR5, on the RCP 8.5 business-as-usual radiative-forcing scenario, projects that CO2 concentration by 2100 will be 936 ppmv, but that the influence of other greenhouse gases will raise that value to 1,313 ppmv CO2 equivalent (CO2e), again implying a CO2 fraction q 100 = 0.7. Note that the discrepancy between ratios of forcings and of CO2 concentrations is small over the relevant intervals.
However, AR5 concludes at p. 165 that CO2 contributed 80 % of greenhouse-gas forcing from 2005 to 2011: “Based on updated in situ observations, this assessment concludes that these trends resulted in a 7.5 % increase in RF from GHGs from 2005 to 2011, with carbon dioxide (CO2) contributing 80 %.” Furthermore, models have greatly exaggerated the growth of atmospheric CH4 concentration. It is reasonable to suppose that CO2 will represent not <83 % of total anthropogenic forcings over the twenty-first century: i.e., q t ≥ 0.83. To retain compatibility with IPCC’s practice of expressing the CO2 fraction q t as a percentage of total anthropogenic forcing, the convention has been retained here. Accordingly, the total anthropogenic forcing may be derived by taking the reciprocal of the CO2 fraction; thus, q t ≥ 0.83 ⇒ q −1 t ≤ 1.2. The CO2 radiative forcing (ΔF t ) is essentially being scaled by this factor, as a measure of weighting the CO2.
4.2 The CO2 radiative forcing ΔF t
The CO2 radiative forcing is the product of a coefficient k and the proportionate change in CO2 concentration [4]; thus, where C 0 is the unperturbed concentration,
The value of the coefficient k was reduced by 15 %, from 6.3 in SAR to 5.35 in TAR. Thus, for instance, if CO2 concentration doubles, ΔF t will be 5.35 ln 2 = 3.708 W m−2. IPCC now expresses “very high confidence” [5] in the greenhouse-gas radiative forcings including that from CO2, which, applying Eq. (2) to pre-industrial and 2011 forcings of approximately 280 and 394 ppmv, respectively, is 1.82 W m−2, the value given in AR5. Therefore, the value of k is here taken as constant. However, its current value 5.35 was obtained by intercomparison between three models [32]. It has not been convincingly derived empirically.
4.3 The Planck climate-sensitivity parameter λ 0
To determine climate sensitivity where feedbacks are absent or net-zero, a direct forcing is multiplied by the Planck or instantaneous sensitivity parameter λ 0, denominated in Kelvin per Watt per square meter. Where feedbacks are absent or net-zero, the equilibrium-sensitivity parameter λ ∞ is equal to λ 0. At the characteristic-emission altitude (CEA), at about the 300-mb pressure altitude, where incoming and outgoing radiative fluxes are by definition equal, Eq. (3) gives incoming and hence, by definition, outgoing radiative flux F E :
where F E is the product of the ratio πr 2/4πr 2 of the surface area of the disk the Earth presents to the Sun to that of the rotating sphere; total solar irradiance S = 1,368 W m−2; and 1 – α, where α = 0.3 is the Earth’s albedo. Then, since
mean CEA effective temperature T E is given by Eq. (5),
where emissivity ε = 1 and the Stefan–Boltzmann constant σ = 5.67 × 10−8 W m−2 K−4.
The CEA is ~5 km above ground level. Since mean surface temperature is 288 K and the mean tropospheric lapse rate is about 6.5 K km−1, Earth’s effective radiating temperature T E = 288 − 5(6.5) = 255 K, in agreement with Eq. (5). Accordingly, a first approximation of the zero-feedback sensitivity parameter λ 0 is ΔT E /ΔF E , thus
However, [33], cited in AR4, pointed out that “[i]ntermodel differences in λ 0 arise from different spatial patterns of warming; models with greater high-latitude warming, where the temperature is colder, have smaller values of λ 0.”
Accordingly [33], followed by AR4, gave λ 0 = 3.2−1 = 0.3125 K W−1 m2 to allow for variation with latitude (note, however, that AR4 expresses λ 0 in W m−2 K−1). Other values of λ 0 in the literature are 0.29–0.30 [34–37]. Though the value of λ 0 may vary somewhat over time, IPCC’s value 0.3125 K W−1 m2 may safely be taken as constant at sub-millennial timescales.
4.4 The temperature-feedback sum f t
The temperature change driven by a direct forcing may itself engender temperature feedbacks—additional forcings whose magnitude is dependent upon that of the temperature change that triggered them. The direct forcing may be amplified by positive feedbacks or attenuated by negative feedbacks. Feedbacks are thus denominated in W m−2 K−1 of directly caused temperature change. The feedback sum f t = ∑ i f i , the sum of all temperature feedbacks acting on the climate over some period t, is the prime determinant of climate sensitivity in that, in IPCC’s understanding, it doubles or triples a direct forcing. Yet its value is far from settled. Indeed, uncertainty as to the magnitude of f t is the greatest of the many uncertainties in the determination of climate sensitivity. As Fig. 3 shows, IPCC’s interval 1.9 [1.5, 2.4] W m−2 K−1 in AR4 [cf. 33] was sharply cut to 1.5 [1.0, 2.2] W m−2 K−1 in AR5. Yet, the climate-sensitivity interval [2.0, 4.5] K in the CMIP3 model ensemble [4] was slightly increased to [2.1, 4.7] K in CMIP5 [5]. The user may adopt any chosen value for the feedback sum.
Individual climate-relevant temperature feedbacks and their estimated values. Central estimates in AR4 are marked with leftward-pointing blue arrows; in AR5 with rightward-pointing red arrows. The feedback sum f (right-hand column) falls on 1.5 [1.0, 2.2] W m–2 K–1 for AR5, compared with 1.9 [1.5, 2.4] W m–2 K–1 for AR4. The Planck value shown as a “feedback” is not a true feedback, but a part of the climatic reference system. Diagram adapted from [5]
4.5 The closed-loop gain g t and the open-loop or system gain G t
The effect of temperature feedbacks is to augment or diminish the instantaneous temperature response ΔT 0 to a direct forcing. The closed-loop gain g t is the product of the instantaneous or Planck climate-sensitivity parameter λ 0 and the feedback sum f t . The open-loop or system gain factor G t is equal to (1 − g t ) −1. Both g t and G t are unitless. The equilibrium temperature response ΔT ∞ is the product of the instantaneous temperature response ΔT 0 and the system gain factor G t .
4.6 The equilibrium climate-sensitivity parameter λ ∞
The equilibrium-sensitivity parameter λ ∞, in K W−1 m2, is the product of the Planck parameter λ 0 = 3.2−1 K W−1 m2 and the system gain factor G t . Climate sensitivity ΔT ∞ is the product of λ ∞ and a given forcing ΔF ∞.
4.7 Derivation of G ∞ , g ∞ , and f ∞ from ΔT ∞ /ΔF ∞
To find the system gain G ∞ , the loop gain g ∞ and the feedback sum f ∞ , implicit in any given equilibrium-response projection ΔT ∞ , first divide ΔT ∞ by ΔF ∞ to obtain λ ∞. Then, G ∞ , g ∞ , f ∞ are all functions of λ ∞ and λ 0, thus:
Table 1 shows the given feedback sums f ∞ in AR4, AR5, with the implicit central estimates of g ∞, G ∞, and λ ∞ .
4.8 The transience fraction r t
Not all temperature feedbacks operate instantaneously. Instead, feedbacks act over varying timescales from decades to millennia. Some, such as water vapor or sea ice, are short-acting, and are thought to bring about approximately half of the equilibrium warming in response to a given forcing over a century. Thus, though approximately half of the equilibrium temperature response to be expected from a given forcing will typically manifest itself within 100 years of the forcing (Fig. 4), the equilibrium temperature response may not be attained for several millennia [38, 39]. In Eq. (1), the delay in the action of feedbacks and hence in surface temperature response to a given forcing is accounted for by the transience fraction r t . For instance, it has been suggested in recent years that the long and unpredicted hiatus in global warming may be caused by uptake of heat in the benthic strata of the global ocean (for a fuller discussion of the cause of the hiatus, see the supplementary matter). The construction of an appropriate response curve via variations over time in the value of the transience fraction r t allows delays of this kind in the emergence of global warming to be modeled at the user’s will.
The time evolution of the probability distribution of future climate states, generated by a simple climate model forced by a step-function climate forcing ΔF ∞ = 4 W m–2 at t = 0. The climate model··· considers a range of different feedback strengths and has a reference sensitivity ΔT 0 = 1.2 K. The black curve shows the time evolution of the state with the mean sensitivity, flanked by the 95 % confidence interval (blue region). Right panel: equilibrium [i.e. t = ∞] probability distribution. Higher-sensitivity climates have a larger response time and take longer to equilibrate. Note the switch to a log time axis after 500 years. The equilibrium sensitivity interval ΔT ∞ on 3.5 [2.0, 12.7] K shown in the graph corresponds to a loop gain g ∞ = 0.7 [0.4, 0.9] and a feedback-sum f ∞ = 2.1 [1.3, 2.9] W m–2 K–1. Adapted from [38]
In [38], a simple climate model was used, comprising an advective–diffusive ocean and an atmosphere with a Planck sensitivity ΔT 0 = 1.2 K, the product of the direct radiative forcing 5.35 ln 2 = 3.708 W m−2 in response to a CO2 doubling and the zero-feedback climate-sensitivity parameter λ 0 = 3.2−1 K W−1 m2. The climate object thus defined was forced with a 4 W m−2 pulse at t = 0, and the evolutionary curve of climate sensitivity (Fig. 4) was determined. Equilibrium sensitivity was found to be 3.5 K, of which 1.95 K is shown as occurring after 50 years, implying r 50 = 0.56. For comparison, AR4 gave 3.26 K as its central estimate of equilibrium climate sensitivity to a doubling of CO2 concentration, implying λ ∞ = 3.26/(5.35 ln 2) = 0.88 K W−1 m2. The mean of projected concentrations on the six SRES emissions scenarios in AR4, obtained by enlarging the graphs and overlaying a precise grid on them and reading off and averaging the annual values, is 713 ppmv in 2100 compared with 368 ppmv in 2000.
The central estimate of twenty-first-century warming in AR4 was 2.8 K, of which 0.6 K was committed warming already in the pipeline. Of the remaining 2.2 K, some 70 %, or 1.54 K, was CO2 driven. AR4’s implicit centennial sensitivity parameter λ 100 was thus 1.54 K / [5.35 ln(713 / 368) W m−2], or 0.44 K W−1 m2, which is half of the implicit equilibrium-sensitivity parameter λ ∞ = 0.88 K W−1 m2. In AR4, the implicit centennial transience fraction r 100 is thus 0.50, close to the 0.56 found in [38]. Table 2 gives approximate values of r t corresponding to f ∞ ≤ 0 and f ∞ = 0.5, 1.3, 2.1, and 2.9. Where f t ≤ 0.3, for all t, r t may safely be taken as unity: at sufficiently small f t , there is little difference between instantaneous and equilibrium response. For f ∞ on 2.1 [1.3, 2.9], r t is simply the fraction of equilibrium sensitivity attained in year t, as shown in Fig. 4.
It is not possible to provide a similar table for values of f ∞ given in AR4 or AR5, since IPCC provides no evolutionary curve similar to that in Fig. 4. Nevertheless, Table 2, derived from [38], allows approximate values of r t to be estimated.
5 How does the model represent different conditions?
The simple model has only five tunable parameters: the CO2 fraction q t , dependent on projected CO2 concentration change; the CO2 radiative forcing ΔF t ; the transience fraction r t ; the Planck sensitivity parameter λ 0, on which the instantaneous temperature response ΔT 0 and the system gain G t are separately dependent; and the feedback sum f t , of which the equilibrium-sensitivity parameter λ ∞ is a function.
These five parameters permit representation of any combination of anthropogenic forcings; of expected warming at any stage from inception to equilibrium after perturbation by forcings of any magnitude or sign; and of any combination of feedbacks, positive or negative, linear or nonlinear. The model makes explicit the relative contributions of forcings and feedbacks to projected anthropogenic global warming. Feedbacks, mentioned >1,000 times in AR5, are the greatest source of uncertainty in predicting anthropogenic temperature change.
6 Calibration against climate-sensitivity projections in AR4
To establish that the model generates climate sensitivities sufficiently close to IPCC’s values, its output is compared to the equilibrium Charney climate-sensitivity interval 3.26 [2.0, 4.5] K in response to a CO2 doubling (AR4). Here, the equilibrium value of the transience fraction r ∞ in (1) is unity by definition;, since CO2 alone is the focus of equilibrium-sensitivity studies, q −1 t is likewise unity. Thus, ΔT ∞ becomes simply the product of λ ∞ and ΔF t (Table 3).
The chief reason why the central estimate in AR4 is 14 % greater than the model’s central estimate is that IPCC’s central estimate is close to the mean of the upper and lower bounds, while the model’s central estimate is closer to the lower than to the upper bound because it is derived from AR4’s central estimate of the feedback sum. This asymmetry is inherent in Eq. (1), but is not reflected in AR4’s central estimate. The sensitivity interval 2.9 [2.2, 4.6] K found by the simple model is accordingly close enough to the interval 3.26 [2.0, 4.5] K in AR4, Box 10.2, to calibrate the model.
7 Calibration against observed temperature change since 1850
The HadCRUT global surface temperature dataset [12] shows global warming of 0.8 K from January 1850 to April 2014. CO2 concentration in 1850 was ~285 ppmv against 393 ppmv in 2011, so that ΔF t = 5.35 ln(393 / 285) = 1.72 W m−2. Total radiative forcing from 1750 to 2011 was 2.29 W m−2 (AR5). Taking forcing from 1750 to 1850 as approximately 0.1 W m−2, forcing from 1850 to 2011 was about 2.19 W m−2, so that q −1 t = 2.19 / 1.72 = 1.27. Using these inputs, warming since 1850 is determined by the model and compared with observation in Table 4.
Assuming that all global warming since 1850 was anthropogenic, the model fairly reproduces the change in global temperature since then, suggesting that the 0.6 K committed but unrealized warming mentioned in AR4, AR5 is non-existent. If some global warming was natural, then a fortiori the likelihood of committed but unrealized warming is small.
8 Application of the model to global-warming projections in AR5
8.1 The climate-sensitivity interval
In FAR, the implicit central estimate of λ ∞ was 0.769 K W−1 m2, giving an equilibrium climate sensitivity 2.9 K in response to a CO2 doubling. The CMIP3 model ensemble in AR4, p. 798, box 10.2 gave as its central estimate an equilibrium sensitivity of 3.26 K, implying that λ ∞ = 0.879 K W−1 m2 and consequently that f = 2.063 W m−2 K−1, somewhat above the 1.9 W m−2 K−1 given in [32].
In AR5, however, the reduction in the central estimate of f to 1.5 W m−2 K−1 cut IPCC’s implicit central estimate of λ ∞ to 0.588 K W−1 m2, halving the feedback component λ ∞ − λ 0 in λ ∞ from 0.566 to 0.275 K W−1 m2. IPCC, by reducing the feedback sum enough to halve the contribution of feedbacks to equilibrium sensitivity in AR5, had in effect cut its central estimate of climate sensitivity by one-third, from 3.3 to 2.2 K. Yet, for the first time, the panel decided that no central estimate of climate sensitivity would be published. The Summary for Policymakers in AR5 says
No best estimate for equilibrium climate sensitivity can now be given because of a lack of agreement on values across assessed lines of evidence and studies.
The simple model indicates that, as a result of the fall in the interval of estimates of f from 1.9 [1.5, 2.4] W m−2 K−1 in AR4 to 1.5 [1.0, 2.2] W m−2 K−1 in AR5, the Charney-sensitivity interval in response to a CO2 doubling should have been reduced from 3.26 [2.0. 4.5] K to 2.2 [1.7, 2.7] K. Yet, the CMIP5 climate-sensitivity interval given in AR5 is 3.2 [2.1, 4.7] K (AR5).
The central estimate is near half as high again as it would have been if the method in AR4 had been followed (Table 5). The simple model suggests that the CMIP5 Charney-sensitivity estimates published in AR5 are unduly high and that the central estimate has apparently been overstated by almost half.
8.2 Projected warming in the RCP forcing scenarios
In AR5, IPCC introduces four new forcing scenarios, based on net anthropogenic forcings of 2.6, 4.5, 6.0, and 8.5 W m−2 over 1750–2100, of which approximately 2.3 W m−2 is shown as having occurred by 2011. There has also been global warming of approximately 0.9 K since 1750.
In Table 6, IPCC’s projected intervals of warming from 1750–2100 on each of the four scenarios in AR5 are compared with the output of the model. On all four scenarios, IPCC’s projected values for twenty-first-century warming are greatly in excess of the simple model’s projections. One reason for the discrepancy is that IPCC bases its projections not on the period 2014–2100 but on the difference between the means of two 20-year intervals 1986–2005 and 2081–2100, separated by 95 years. IPCC’s method thus takes no account of the absence of global warming in the past two decades.
8.3 An observationally based estimate of global warming to 2100
The simple model may be deployed to obtain observationally based best estimates of global warming to 2100, for instance, by adopting realistic values of the CO2 forcing ΔF t , the feedback sum f, the CO2 fraction q t , and the transience fraction r t .
8.3.1 The CO2 forcing ΔF t
RCP 8.5 is the “business-as-usual” scenario in AR5. However, the assumptions underlying it are unrealistic (see Discussion). In the more realistic RCP 6.0 scenario, atmospheric CO2 concentration, currently 400 ppmv, is projected to reach 670 ppmv by 2100, so that ΔF t from 2015 to 2100 will be 5.35 ln(670/400), or 2.760 W m−2.
8.3.2 The feedback sum f
A plausible upper bound to f may be found by recalling that absolute surface temperature has varied by only 1 % or 3 K either side of the 810,000-year mean [40, 41]. This robust thermostasis [42, 43], notwithstanding Milankovich and other forcings, suggests the absence of strongly net-positive temperature feedbacks acting on the climate.
In Fig. 5, a regime of temperature stability is represented by g ∞ ≤ +0.1, the maximum value allowed by process engineers designing electronic circuits intended not to oscillate under any operating conditions. Thus, assuming g ∞ ≥ 0.5, values of f ∞ fall on [−1.6, +0.3], giving λ ∞ on [0.21, 0.35]. Where f ∞ is thus at most barely net-positive, the corresponding equilibrium-sensitivity interval is well constrained, falling on [0.8, 1.3] K. Of course, other assumptions might be made; however, in a near-perfectly thermostatic system, net-negative feedback is plausible, indicating that the climate—far from amplifying any temperature changes caused by a direct forcing—dampens them instead. Indeed, this damping should be expected, since temperature change is not merely a bare output, as voltage change is in an electronic circuit: temperature change is also the instrument of self-equilibration in the system, since radiative balance following a forcing is restored by the prevalence of a higher temperature. Also, in electronic circuits, the singularity at g ∞ = +1, where the voltage transits from the positive to the negative rail, has a physical meaning: in the climate, it has none. A damping term absent in the models is thus required in Eq. (7) and may be represented in Eq. (1) by a reduction of λ ∞ .
8.3.3 The CO2 fraction q t
IPCC’s implicit value for q t falls on [0.71, 0.89], the higher values corresponding to the lower projected total anthropogenic forcings. A reasonable interval for q t corresponding to low values of f t is thus [0.8, 0.9], so that q −1 t falls on [1.10, 1.25]. For comparison, on RCP 6.0 in AR5, the implicit value for q −1 t is 1.194 (Table 6).
8.3.4 The transience fraction r t
Where f t ≤ 0.3, little error will arise if, for all t, r t is taken as unity: For at sufficiently small f t , there is little difference between instantaneous and equilibrium response.
8.3.5 Projected global warming from 2014 to 2100
From the values of f t , q −1 t , and r t thus determined, the model projects global warming to 2100 (Table 7). On the assumptions that ΔF t = 2.760, r t = 1, f falls on [−1.6, +0.32] W m−2 K−1, and q −1 falls on [1.10, 1.25], model-projected warming ΔT t falls on 0.8 [0.6, 1.2] K. The narrow response interval is a consequence of the temperature stability where g t falls on [−0.5, +0.1] (Fig. 5). This stability is consistent with the observed near-thermostasis over the past 810,000 years [40], with which IPCC’s implicit loop-gain interval g t on [+0.23, +0.74] seems inconsistent. For comparison, the projection in AR5 on RCP 6.0 is 2.2 [1.4, 3.1] K and on RCP 8.5 is 3.7 [2.6, 4.8] K.
8.4 How much post-1850 global warming was anthropogenic?
Assuming 285 ppmv CO2 in 1850 and 400 ppmv in 2014, and applying the observationally derived values of f t , holding r t at unity, and taking q −1 t = 2.29/1.813 = 1.263 to allow for the greater fraction of past warming attributable to CH4, the simple model determines the approximate fraction of the 0.8 K observed global warming since 1850 that was anthropogenic as 78 % [62 %, 104 %].
If it is assumed that g t < +0.1, warming is already at equilibrium, since r t → 1 for the implicit values f t ≤ +0.3 W m−2 K−1, on this scenario there is probably no committed but unrealized global warming. If AR4 is correct in its estimate that 0.6 K warming is in the pipeline, then <0.2 K anthropogenic warming has occurred since 1850, indicating that warming realized since then is substantially natural.
8.5 An observationally based estimate of Charney sensitivity
With the observationally derived values of f, the model provides a new estimate of the Charney sensitivity (Table 7). If temperature feedbacks are at most weakly net-positive, with loop gain g on [−0.5, +0.1] as Fig. 5 and 810,000 years of thermostasis suggest, Charney sensitivity may fall on 1.0 [0.8, 1.3] K. The model’s central estimate is one-third of the 3.2 K central estimate from the CMIP5 model ensemble in AR5, or of the 3.26 K central estimate from the CMIP3 model ensemble in AR4.
For comparison, in [44], g is found to fall on [−1.5, +0.7], so that, assuming the forcing at CO2 doubling is 4 W m−2, a little above the 3.71 W m−2 that IPCC currently regards as canonical, the equilibrium Charney sensitivity ΔT 2× falls on [0.5, 4.2] K. The model’s climate-sensitivity interval is better constrained than the CMIP models’ intervals because across a broad interval of weakly positive to net-negative feedbacks there is little change in the temperature response.
8.5.1 Charney sensitivity: summary of results
Table 8 summarizes the Charney climate-sensitivity intervals in IPCC’s five successive Assessment Reports FAR, SAR, TAR, AR4, and AR5 as amended in the light of the simple model’s results and as found by the model itself.
As Table 8 shows, correcting the output of the CMIP5 models to determine the central estimate of temperature response from the central estimate of the feedback sum and to determine the entire sensitivity interval from the revised feedback-sum interval given in AR5 reduces the sensitivity interval from 3.2 [2.1, 4.7] K to 2.2 [1.7, 3.9] K, bringing the CMIP5 feedback-sum interval into line with IPCC’s interval.
If, however, the loop gain g is indeed below the process engineers’ limit for stability, namely +0.1, compatible with the results in [21, 23], then the simple model’s output giving a climate-sensitivity interval 1.0 [0.8, 1.3] K may be preferable.
9 How skillful is the model?
Remarkably, though the model is very simple, its output proves to be broadly consistent with observation, while the now-realized projections of the general-circulation models have proven to be relentlessly exaggerated. If, for instance, the observed temperature trend of recent decades were extrapolated several decades into the future, the model’s output would coincident with the observations thus extrapolated (Fig. 6).
10 Discussion
The irreducibly simple model presented here aims specifically to study climate sensitivity. Though it is capable of representing in a rough and ready fashion all the forcings and feedbacks discussed in AR5, the question arises whether extreme simplicity renders such models altogether valueless in contrast to the more complex general-circulation models.
Recently, it was explained in [45] that although the complex models cover many physical, chemical and biological processes in their representation of the Earth’s climate system, the added complexity has naturally led to great difficulty in identifying the chains of causality in the climate object—what the authors call “the processes most responsible for a certain effect.”
Two recent examples of the substantial uncertainty in representing climate by complex models indicate that greater complexity does not necessarily entail improved performance, despite myriad improvements and intense scrutiny.
The first example: It was recently reported [46] that increased spatial resolution had led to improvements in simulations of sea-level pressure, surface temperatures, etc., in GISS’ latest model, E2, but that simultaneously, “some degradations are seen in precipitation and cloud metrics.” Increased spatial resolution in a model, therefore, does not automatically lead to improvement.
The second example: The IPSL-CM5A modeling group’s recent study [47] of the skill of horizontal and vertical atmospheric grid configuration in representing the observed climate reported that, when the number of atmospheric layers was increased from 19 to 39 to improve stratospheric resolution, a substantial global energy imbalance requiring retuning of model parameters resulted, but that, paradoxically, these significant impacts of the model’s grid resolution had not led to any significant changes in projected climate sensitivity.
It is not necessarily true, therefore, that improvements in the resolution of a model will refine the determination of climate sensitivity. By the same token, a reduction in complexity—even an irreducible reduction—does not necessarily entail a reduction in the reliability with which climate sensitivity is determined.
On the other hand, it would be inappropriate to claim that the simple model is preferable to the complex general-circulation models. Its purpose is more limited than theirs, being narrowly focused on determining the transient and equilibrium responses of global temperature to specified radiative forcings and feedbacks in a simplified fashion. The simple model is not a replacement for the general-circulation models, but it is capable of illuminating their performance. It also puts climate-sensitivity modeling within the reach of those who have no access to or familiarity with the general-circulation models. In effect, this paper is the user manual for the simple model, bringing it within the reach of all who have a working knowledge of elementary mathematics and physics.
Irreducible simplicity is the chief innovation embodied in the simple model. While it is rooted in the mainstream mathematics and physics of climate sensitivity and is capable of reflecting no less wide a range of scenarios than the general-circulation models, it allows a rapid but not unreliable determination of climate sensitivity by anyone even at undergraduate level, providing insights not only into the relevant physics but also into the extent to which the more complex models are adequately reflecting the physics.
The complex general-circulation models have been running hot for a quarter of a century. The simple model confirms the hot running and exposes several of the reasons for it.
Firstly, application of the simple model reveals that the central climate-sensitivity estimate in the CMIP5 ensemble is somewhat too high because IPCC has taken its mid-range climate-sensitivity estimate as the mean of its upper- and lower-bound estimates rather than determining it from the mean feedback sum f ∞ . By contrast, in [38] the central climate-sensitivity estimate was perhaps more correctly derived from the central feedback-sum estimate f ∞ = 2.1 W m−2 K−1, the exact mean of the lower and upper bounds f ∞ on [1.3, 2.9] W m−2 K−1. Accordingly, in [38] the central climate-sensitivity estimate 3.5 K is significantly closer to the lower-bound estimate 2.0 K than to the upper-bound estimate 12.7 K. The rapidly increasing slope of climate sensitivity against loop gain g ∞ as the value of g ∞ approaches unity (the singularity in the Bode feedback-amplification equation [48]), is the reason for this asymmetry (Fig. 5), and is also the reason for the extremely high-sensitivity estimates sometimes presented in the journals. Implicitly, f ∞ in the CMIP5 ensemble falls on 1.923 [1.434, 2.411] W m−2 K−1. The mean of these two values is 1.923 W m−2 K−1. Based on the mean feedback sum f ∞ = 1.923 W m−2 K−1, the CMIP5 central estimate of climate sensitivity should have been 2.9 K, not 3.2 K.
Secondly, the simple model reveals that the climate sensitivity 3.3 [2.0, 4.5] K in AR4 should have fallen sharply to 2.2 [1.7, 3.7] K in AR5 commensurately with the reduction of the feedback-sum interval between the two reports (Fig. 3). For the variance between the CMIP3 and CMIP5 projections of climate sensitivity is inferentially confined to the feedback-sum interval. If the CMIP5 models took account of significant net-positive feedbacks not included in AR5, Fig. 9.43, in the chart of climate-relevant feedbacks (Fig. 3), it is not clear why that chart was not updated to include them. The sharp reduction of the feedback-sum interval in CMIP5 and hence in AR5 compared with the interval in CMIP3 and hence in AR4 mandates a sharp reduction in the climate-sensitivity interval, which, however, was instead increased somewhat.
Thirdly, the simple model shows that even the reduced feedback-sum interval in CMIP5 and hence in AR5 seems implausibly high when set against the thermostasis over geological timescales shown in [40]. In Fig. 5, g ≤ +0.1 is consistent with the inferred thermostasis. Charney sensitivity would then be 1.3 K or less—below even the lower bound of the climate-sensitivity interval [1.5, 3] K in AR5.
Fourthly, the simple model demonstrates that, in AR5, the estimates of global warming to 2100 under the four RCP scenarios (Table 5) project much more warming over the twenty-first century than they should. For instance, under the RCP 2.6 scenario, it is expected that there will be no more than 2.6 W m−2 radiative forcing to 2100, of which some 2.3 W m−2 had already occurred by 2011. Even adding IPCC’s estimate of 0.6 K committed but unrealized warming to the small warming yet to be generated by the 0.3 W m−2 forcing still to come by 2100 under this scenario, it is not easy to understand why IPCC’s upper-bound warming estimate on RCP 2.6 is as high as 1.7 K.
Fifthly, application of the simple model raises the question why AR5 adopted the extreme RCP 8.5 scenario at all. On that scenario, atmospheric CO2 concentration is projected to reach 936 ppmv by 2100 on the basis of two implausible assumptions: first, that global population will be 12 billion by 2100, though the UN predicts that population will peak at little more than 10 billion by not later than 2070 and will fall steeply thereafter; and secondly, that coal will contribute as much as 50 % of total energy supply, though gas is rapidly replacing coal in many countries, a process that will accelerate as shale gas comes on stream. Furthermore, the observed increase in CH4 concentration at a mean rate of 3 ppbv year−1 from 1990 to 2011, taken with the history of very substantial over-prediction of the CH4 growth rate, does not seem to justify IPCC in projecting that, on the RCP 8.5 scenario, the mean rate of increase in CH4 concentration from 2015 to 2100 will be 21 ppbv year−1, seven times the observed rate of increase over recent decades.
The utility of the simple model lies in identifying discrepancies such as those enumerated above. It should not be seen as a substitute for the more complex models, but as a simple benchmark against which the plausibility of their outputs may be examined.
11 Conclusion
Resolving the discrepancies between the methodology adopted by IPCC in AR4 and AR5 is vital. Once those discrepancies are corrected for, it appears that the impact of anthropogenic global warming over the next century, and even as far as equilibrium many millennia hence, may be no more than one-third to one-half of IPCC’s current projections.
Suppose, for instance, that the equilibrium response to a CO2 doubling is, as the simple model credibly suggests it is, <1 K. Suppose also that the long-run CO2 fraction proves to be as high as 0.9. Again, this possibility is credible. Finally, suppose that remaining affordably recoverable reserves of fossil fuels are as much as thrice those that have been recovered and consumed so far. Then, the total warming we shall cause by consuming all remaining recoverable reserves will be little more than 2.2 K, and not the 12 K imagined by IPCC on the RCP 8.5 scenario. If so, the case for any intervention to mitigate CO2 emissions has not necessarily been made: for the 2.2 K equilibrium warming we project would take place only over many hundreds of years. Also, the disbenefits of more extreme heat may well be at least matched by the benefits of less extreme cold. It is no accident that 90 % of the world’s living species thrive in the warm, wet tropics, while only 1 % live at the cold, dry poles. As a benchmark, AR5 estimates that adaptation to the 2–3 K global warming it expects by 2100 will cost 0.2 %–2.0 % of global GDP, broadly in line with the cost estimate of 0–3 % of GDP in Lord Stern’s report for the UK Government on the economics of climate change in 2006. However, the reviewed journals of economics generally report that the cost of mitigation today would be likely to exceed these low costs of adaptation to projected global warming, perhaps by as much as one or two orders of magnitude.
Under different assumptions, the simple model is of course capable of reaching conclusions more alarming (but arguably less reasonable) than those that have been sketched here. Be that as it may, the utility of the model lies in making accessible for the first time the distinction between the relative contributions of forcings and feedbacks; in exposing anomalies requiring clarification in the outputs of the general-circulation models, which seem to agree ever more closely with each other while departing ever farther from observation (Fig. 1); and, above all, in facilitating the rapid and simple estimation of both transient and equilibrium climate sensitivity under a wide range of assumptions and without the need either for climatological expertise or for access to the world’s most powerful computers and complex models. The simple model has its limitations, but it has its uses too.
References
IPCC FAR (1990) In: Houghton JT, Jenkins GJ, Ephraums JJ (eds) Climate change—the IPCC assessment (1990): report prepared for Intergovernmental panel on climate change by working group I. Cambridge University Press, Cambridge, New York
IPCC SAR (1995) In: Houghton JT, Meira Filho LG, Callander BA et al (eds) Climate change 1995—the science of climate change: contribution of WG1 to the second assessment report. Cambridge University Press, Cambridge, New York
IPCC TAR (2001) Climate change 2001: the scientific basis. In: Houghton JT, Ding Y, Griggs DJ et al (eds) Contribution of working group I to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, New York
IPCC AR4 (2007) Climate change 2007: the physical science basis. In: Solomon S, Qin D, Manning M et al (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change, 2007. Cambridge University Press, Cambridge, New York
IPCC AR5 (2013) Climate change 2013: the physical science basis. In: Stocker TF, Qin D, Plattner G-K et al (eds) Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, New York
Garnaut R (2011) The Garnaut climate change review: final report. Cambridge University Press, Cambridge
Hoyle F (1996) The great greenhouse controversy. In: Emsley J (ed) The global warming debate. The European Science and Environment Forum, London, pp 179–189
Legates DR, Soon WW-H, Briggs WM et al (2013) Climate consensus and “misinformation”: a rejoinder to “agnotology, scientific consensus, and the teaching and learning of climate change”. Sci Educ. doi:10.1007/s11191-013-9647-9
RSS (2014) Satellite-derived monthly global mean lower-troposphere temperature anomaly dataset: www.remss.com/data/msu/monthly_time_series/RSS_Monthly_MSU_AMSU_Channel_TLT_Anomalies_Land_and_Ocean_v03_3.txt. Accessed 1 July 2014
UAH (University of Alabama at Huntsville) (2014) Satellite MSU monthly global mean lower-troposphere temperature anomalies. http://vortex.nsstc.uah.edu/data/msu/t2lt/uahncdc_lt_5.6.txt. Accessed 1 July 2014
NCDC (2014) National Climatic Data Center monthly global mean land and ocean surface temperature anomalies, 1880-2013. https://www.ncdc.noaa.gov/cag/time-series/global/globe/land_ocean/p12/12/1880-2014.csv. Accessed 1 July 2014
Morice CP, Kennedy JJ, Rayner N et al (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J Geophys Res 117:D08101
GISS (2014) Goddard Institute for Space Studies monthly global mean land and sea surface temperature anomalies, 1880–2014. http://data.giss.nasa.gov/gistemp/tabledata_v3/GLB.Ts+dSST.txt. Accessed 1 July 2014
Soon WW-H, Baliunas S, Idso SB et al (2001) Modeling climate effects of anthropogenic carbon dioxide emissions: unknowns and uncertainties. Clim Res 18:259–275
Douglass DH, Pearson BD, Singer SF (2004) Altitude dependence of atmospheric temperature trends: climate models versus observation. Geophys Res Lett 31:L13208
Douglass DH, Christy JR, Pearson BD et al (2007) A comparison of tropical temperature trends with model predictions. Int J Climatol. doi:10.1002/joc.1651
McKitrick RR, Michaels PJ (2007) Quantifying the influence of anthropogenic surface processes and inhomogeneities on gridded global climate data. J Geophys Res (Atmos.) 112:D24S09
Tsonis AA, Swanson KL, Kravtsov S (2007) A new dynamical mechanism for major climate shifts. Geophys Res Lett. doi:10.1029/2007GL030288
Wentz FJ, Ricciardulli L, Hilburn K et al (2007) How much more rain will global warming bring? Science 317:233–235
Monckton of Brenchley C (2008) Climate sensitivity reconsidered. Phys Soc 37:6–19
Monckton of Brenchley C (2011) Global brightening and climate sensitivity. In: Zichichi A, Ragaini R (eds) Proceedings of the 45th annual international seminar on nuclear war and planetary emergencies, World Federation of Scientists. World Scientific, London
Paltridge G (2009) The climate caper. Connor Court, Sydney
Douglass DH, Christy JR (2009) Limits on CO2 climate forcing from recent temperature data of earth. Energy Environ 20:1–2
Douglass DH, Christy JR (2013) Reconciling observations of global temperature change. Energy Environ 24:415–419
Lindzen RS, Choi Y-S (2011) On the observational determination of climate sensitivity and its implications. Asia Pac J Atmos Sci 47:377–390
Loehle C, Scafetta N (2011) Climate change attribution using empirical decomposition of climatic data. Open Atmos Sci J 5:74–86
Spencer RW, Braswell WD (2011) On the misdiagnosis of surface temperature feedbacks from variations in Earth’s radiant-energy balance. Remote Sens 3:1603–1613
Tsonis AA (2011) Cycles in the major ocean oscillations. Lecture at the annual seminar on planetary emergencies, World Federation of Scientists. Erice, Sicily, August 23
Essex C (2013) Does laboratory-scale physics obstruct the development of a theory for climate? J Geophys Res. doi:10.1029/jgrd.50195
Zhang D, Lou T, Liu D et al (2014) Spatial scales of altocumulus clouds observed with collocated CALIPSO and CloudSat measurements. Atmos Res 148:58–69
Jiang DB, Lang XM, Tian ZP et al (2012) Considerable model-data mismatch in temperature over China during the mid-Holocene: results of PMIP simulations. J Clim 25:4135–4153
Myhre G, Highwood EJ, Shine KP et al (1998) New estimates of radiative forcing due to well-mixed greenhouse gases. Geophys Res Lett 25:2715–2718
Soden BJ, Held IM (2006) An assessment of climate feedbacks in coupled ocean–atmosphere models. J Clim 19:3354–3360
Hansen J, Lacis A, Rind D et al (1984) Climate sensitivity: analysis of feedback mechanisms. Meteorol Monogr 29:130–163
Kiehl JT (1992) Atmospheric general circulation modeling. In: Trenberth KE (ed) Climate system modeling. Cambridge University Press, Cambridge, pp 319–369
Hartmann DL (1994) Global physical climatology. Academic Press, San Diego
Colman RA (2003) A comparison of climate feedbacks in general-circulation models. Clim Dyn 20:865–873
Roe G (2009) Feedbacks, timescales, and seeing red. Ann Rev Earth Planet Sci 37:93–115
Solomon S, Plattner GK, Knutti R et al (2009) Irreversible climate change due to carbon dioxide emissions. Proc Natl Acad Sci USA 106:74–79
Jouzel J, Masson-Delmotte V, Cattani O et al (2007) Orbital and millennial Antarctic climate variability over the past 800,000 years. Science 317:793–796
Petit JR, Jouzel J, Raynaud D et al (1999) Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 399:429–436
Scotese CR, Boucot AJ, McKerrow WS (1999) Gondwanan paleogeography and paleoclimatology. J Afr Earth Sci 28:99–114
Zachos J, Pagani M, Sloan L et al (2001) Trends, rhythms and aberrations in global climate 65 Ma to present. Science 292:686–693
Schlesinger ME, Mitchell JFB (1987) Climate model simulations of the equilibrium climatic response to increased carbon dioxide. Rev Geophys 25:760–798
Kirk-Davidoff DB, Lindzen RS (2000) An energy balance model based on potential vorticity homogenization. J Clim 13:431–448
Hourdin F, Foujols M-A, Codron F et al (2013) Impact of the LMDZ atmospheric grid configuration on the climate and sensitivity of the IPSL-CM5A coupled model. Clim Dyn 40:2167–2192
Schmidt GA, Kelley M, Nazarenko L (2014) Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive. J Adv Model Earth Syst 6:141–184
Bode HW (1945) Network analysis and feedback amplifier design. Van Nostrand Reinhold, New York
Bódai T, Lucarini V, Lunkeit F et al (2014) Global instability in the Ghil-Sellers model. Clim Dyn. doi:10.1007/s00382-014-2206-5
Budyko MI (1969) The effect of solar radiation variations on the climate of the Earth. Tellus 21:611–619
Sellers WD (1969) A global climatic model based on the energy balance of the earth-atmosphere system. J Appl Meteorol 8:392–400
North GR (1975) Theory of energy-balance climate models. J Atmos Sci 32:2033–2043
Ghil M (1976) Climate stability for a Sellers-type model. J Atmos Sci 33:3–20
North GR, Cahalan RF, Coakley JA Jr (1981) Energy balance climate models. Rev Geophys Space Phys 19:91–121
North GR (1984) The small ice cap instability in diffusive climate models. J Atmos Sci 41:3390–3395
Lindzen RS, Farrell B (1977) Some realistic modifications of simple climate models. J Atmos Sci 34:1487–1501
Schneider EK, Lindzen RS (1977) Axially symmetric steady-state models of the basic state for instability and climate studies, part I, linearized calculations. J Atmos Sci 34:263–279
Conflict of interest
The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Monckton, C., Soon, W.WH., Legates, D.R. et al. Why models run hot: results from an irreducibly simple climate model. Sci. Bull. 60, 122–135 (2015). https://doi.org/10.1007/s11434-014-0699-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11434-014-0699-2