Skip to main content
SpringerLink
Log in

A practical parallel preprocessing strategy for 3D numerical manifold method

  • Article
  • Special Topic: Novel Technology and Numerical Method in Geotechnics
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

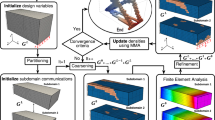
Abstract

Over the past three decades, the numerical manifold method (NMM) has attracted many researchers from geotechnical community because it unifies the solutions of continuous and discontinuous problems in the same framework. However, due to the lack of ready-made preprocessing tools, the development of three dimensional NMM (3DNMM) is still limited. A practical strategy to generate the discretized models for a 3DNMM analysis is proposed. In the proposed strategy, regular hexahedral meshes are uniformly deployed to construct the mathematical cover system. The physical meshes including the joints, material interfaces, and problem domain boundaries are adopted to cut the mathematical cover system into physical cover system and manifold elements (MEs). To improve the efficiency of the proposed strategy, the Intel threading building blocks (TBB) parallel library for CPU paralleling is adopted. Several typical examples are adopted to validate the proposed strategy. The results show that the proposed strategy can effectively generate the discretized 3D models of some geotechnical problems for 3DNMM calculations. The proposed strategy deserves a further investigation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zienkiewicz O C, Taylor R L. The Finite Element Method. 5th ed. Oxford: Butterworth-Heinemann, 2000

    MATH  Google Scholar 

  2. Mohammadnejad T, Khoei A R. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elem Anal Des, 2013, 73: 77–95

    Article  MathSciNet  MATH  Google Scholar 

  3. Yan F, Pan P Z, Feng X T, et al. The continuous-discontinuous cellular automaton method for elastodynamic crack problems. Eng Fract Mech, 2018, 204: 482–496

    Article  Google Scholar 

  4. Zhou S W, Zhuang X Y, Rabczuk T. A phase-field modeling approach of fracture propagation in poroelastic media. Eng Geol, 2018, 240: 189–203

    Article  Google Scholar 

  5. Shi G H. Manifold Method of Material Analysis. In: Transactions of the 9th Army Conference on Applied Mathematics and Computing. Minneapolis, 1992. 51–76

  6. Yang S, Cao M, Ren X, et al. 3D crack propagation by the numerical manifold method. Comput Struct, 2018, 194: 116–129

    Article  Google Scholar 

  7. Yang Y, Tang X, Zheng H, et al. Three-dimensional fracture propagation with numerical manifold method. Eng Anal Bound Elem, 2016, 72: 65–77

    Article  MathSciNet  MATH  Google Scholar 

  8. Xu D, Wu A, Li C. A linearly-independent higher-order extended numerical manifold method and its application to multiple crack growth simulation. J Rock Mech Geotechnical Eng, 2019, 11: 1256–1263

    Article  Google Scholar 

  9. Yang L, Yang Y, Zheng H, et al. An explicit representation of cracks in the variational phase field method for brittle fractures. Comput Methods Appl Mech Eng, 2021, 387: 114127

    Article  MathSciNet  MATH  Google Scholar 

  10. Zhou G L, Xu T, Konietzky H, et al. An improved grain-based numerical manifold method to simulate deformation, damage and fracturing of rocks at the grain size level. Eng Anal Bound Elem, 2022, 134: 107–116

    Article  MathSciNet  MATH  Google Scholar 

  11. Li W, Yu X, Lin S, et al. A numerical integration strategy of meshless numerical manifold method based on physical cover and applications to linear elastic fractures. Eng Anal Bound Elem, 2022, 134: 79–95

    Article  MathSciNet  MATH  Google Scholar 

  12. Yang Y T, Xu D D, Sun G H, et al. Modeling complex crack problems using the three-node triangular element fitted to numerical manifold method with continuous nodal stress. Sci China Tech Sci, 2017, 60: 1537–1547

    Article  Google Scholar 

  13. Yang Y, Xu D, Liu F, et al. Modeling the entire progressive failure process of rock slopes using a strength-based criterion. Comput Geotechnics, 2020, 126: 103726

    Article  Google Scholar 

  14. Chen L, Yang Y T, Zheng H. Numerical study of soil-rock mixture: Generation of random aggregate structure. Sci China Tech Sci, 2018, 61: 359–369

    Article  Google Scholar 

  15. Wu W, Yang Y, Zheng H. Hydro-mechanical simulation of the saturated and semi-saturated porous soil-rock mixtures using the numerical manifold method. Comput Methods Appl Mech Eng, 2020, 370: 113238

    Article  MathSciNet  MATH  Google Scholar 

  16. Yang Y, Sun G, Zheng H, et al. Investigation of the sequential excavation of a soil-rock-mixture slope using the numerical manifold method. Eng Geol, 2019, 256: 93–109

    Article  Google Scholar 

  17. Luo S, Zhang X, Cai Y. The variational principles and application of nonlinear numerical manifold method. Appl Math Mech, 2000, 21: 1401–1406

    Article  MATH  Google Scholar 

  18. Wang H, Yang Y, Sun G, et al. A stability analysis of rock slopes using a nonlinear strength reduction numerical manifold method. Comput Geotechnics, 2021, 129: 103864

    Article  Google Scholar 

  19. Jiang Q, Deng S, Zhou C, et al. Modeling unconfined seepage flow using three-dimensional numerical manifold method. J Hydrodyn, 2010, 22: 554–561

    Article  Google Scholar 

  20. Sun G, Wang W, Shi L. Steady seepage analysis in soil-rock-mixture slope using the numerical manifold method. Eng Anal Bound Elem, 2021, 131: 27–40

    Article  MathSciNet  MATH  Google Scholar 

  21. Zheng H, Liu Z J, Ge X R. Numerical manifold space of Hermitian form and application to Kirchhoff’s thin plate problems. Int J Numer Meth Engng, 2013, 95: 721–739

    Article  MathSciNet  MATH  Google Scholar 

  22. Li H F, Zhang G X, Shi G H, et al. Manifold cut and generation of three-dimensional manifold element under FEMESH cover (in Chinese). Chin J Rock Mech Eng, 2010, 29: 731–742

    Google Scholar 

  23. Shi G H. Contact theory. Sci China Tech Sci, 2015, 58: 1450–1496

    Article  Google Scholar 

  24. Li H, Zhang G. Researches on the generation of three-dimensional manifold element under FEM mesh cover. Math Problems Eng, 2014, 2014: 140180

    MathSciNet  MATH  Google Scholar 

  25. Yang S, Ren X, Zhang J. Generation of three-dimensional manifold element based on Boolean intersection operations (in Chinese). Rock Soil Mech, 2016, 37: 2706–2711+2720

    Google Scholar 

  26. Ke J, Wang S. A study on the block-cutting technique of three-dimensional numerical manifold method (in Chinese). Rock Soil Mech, 2020, 41: 3473–3480

    MathSciNet  Google Scholar 

  27. Wang W. Research on PRE-post processing and parallel computing of numerical manifold method. Dissertation for Master’s Degree. Wuhan: Changjiang River Scientific Research Institute, 2011

    Google Scholar 

  28. Jing L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int J Rock Mech Min Sci, 2003, 40: 283–353

    Article  Google Scholar 

  29. He L, An X M, Ma G W, et al. Development of three-dimensional numerical manifold method for jointed rock slope stability analysis. Int J Rock Mech Min Sci, 2013, 64: 22–35

    Article  Google Scholar 

  30. Akenine-Möllser T. Fast 3D triangle-box overlap testing. J Graphics Tools, 2001, 6: 29–33

    Article  Google Scholar 

  31. Si H. TetGen, a delaunay-based quality tetrahedral mesh generator. ACM Trans Math Softw, 2015, 41: 1–36

    Article  MathSciNet  MATH  Google Scholar 

  32. Robison A D. Intel® threading building blocks (TBB). In: Encyclopedia of Parallel Computing. Boston: Springer, 2011. 955–964

    Google Scholar 

  33. Schroeder W, Martin K, Lorensen W. The Visualization Toolkit: An Object-Oriented Approach To 3D Graphics. New York: Kitware, Inc., 2006

    Google Scholar 

  34. Liu Z, Zhang Y, Jiang Y, et al. Unfitted finite element method for fully coupled poroelasticity with stabilization. Comput Methods Appl Mech Eng, 2022, 397: 115132

    Article  MathSciNet  MATH  Google Scholar 

  35. Liu Z, Zhang P, Sun C, et al. Smoothed numerical manifold method with physical patch-based smoothing domains for linear elasticity. Int J Numer Methods Eng, 2021, 122: 515–547

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, 430071, China

    YongTao Yang & JunFeng Li

  2. University of Chinese Academy of Sciences, Beijing, 100049, China

    YongTao Yang & JunFeng Li

Authors
  1. YongTao Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. JunFeng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to YongTao Yang.

Additional information

This work was supported by the Youth Innovation Promotion Association CAS (Grant No. 2020327), the Young Top-notch Talent Cultivation Program of Hubei Province, and the National Natural Science Foundation of China (Grant No. 12072357).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y., Li, J. A practical parallel preprocessing strategy for 3D numerical manifold method. Sci. China Technol. Sci. 65, 2856–2865 (2022). https://doi.org/10.1007/s11431-022-2166-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-022-2166-5

Keywords

Search

Navigation