Skip to main content
SpringerLink
Log in

Effects of stick-slip on stress intensity factors for subsurface short cracks in rolling contact

  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

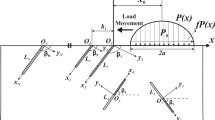
This paper theoretically investigates the effects of stick-slip in rolling contact zone on stress intensity factors (SIFs) for subsurface short cracks. New mathematical models for SIFs including stick-slip ratio are deduced in two cases. One is a subsurface short crack parallel to surface, and the numerical analysis shows that the value of K II increases with the increase of stick-slip ratio; the other is a subsurface short crack perpendicular to the surface, and the numerical analysis indicates that the positive value of K I decreases with the increase of stick-slip ratio. As ΔK I and ΔK II are necessary to evaluate the fatigue crack propagation rate or fatigue lifetime, the influences of stick-slip ratio on them are then discussed. It is found that the maximum variations of ΔK I and ΔK II are both around 3.0% due to stick-slip ratio variation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Half of the width of contact zone

a 1 :

Half of the width of stick zone

c :

x-coordinate value of the crack

\(\bar c\) :

c divided by a

f :

Friction coefficient of rollers in contact

h :

Depth of the crack

\(\bar h\) :

h divided by a

K I :

The model I stress intensity factor

K Imax :

The maximal positive value of K I

K DI :

K I for the lower crack tip

K UI :

K I for the upper crack tip

ΔK I :

Range of the stress intensity factor K I

ΔK DI :

ΔK I for the lower crack tip

ΔK UI :

ΔK I for the upper crack tip

ΔK Imax :

The maximal value of ΔK I

ΔK Imin :

The minimal value of ΔK I

K II :

The mode II stress intensity factor

ΔK II :

Range of the stress intensity factor K II

ΔK IImax :

The maximal value of ΔK II

ΔK IImin :

The minimal value of ΔK II

L :

Length of the crack

\(\bar L\) :

L divided by a

m(z i , L):

Weight function

p n :

Normal load per unit thickness

p t :

Tangential load per unit thickness

p z :

Normal force in contact zone

p x :

Tangential force in contact zone

s 1 :

Symbolic variable

\(\bar x,\bar x_1 ,\bar x_2\) :

x-coordinates divided by a

\(\bar z,\bar z_1 ,\bar z_2\) :

z-coordinates divided by a

σ x :

Stress component in x-direction

σ z :

Stress component in z-direction

τ xz :

Shear stress

τ c :

Net shear stress acted on crack faces

σ s :

Material yield stress in shearing direction

ξ :

Stick-slip ratio in contact zone

η :

Friction coefficient of crack faces

ψ I :

The maximum variation ratio of ΔK I

ψ DI :

ψ I for the lower crack tip

ψ UI :

ψ I for the upper crack tip

ψ II :

The maximum variation ratio of ΔK II

References

  1. Kalker J J. Three-dimensional Elastic Bodies in Rolling Contact. Dordrecht: Kluwer Academic Publishers, 1990. 40–62

    Book  MATH  Google Scholar 

  2. Suresh S, Ritchie R O. Propagation of short fatigue cracks. Int Mater Rev, 1984, 29(1): 445–475

    Google Scholar 

  3. Carter F W. On the action of a locomotive driving wheel. Proc Royal Soc London A, 1926, 112: 151–157

    Article  MATH  Google Scholar 

  4. Haines D J, Ollerton E. Contact stress distributions on elliptical contact surfaces subjected to radial and tangential forces. Proc Inst Mech Eng, 1963, 177(1): 95–114

    Article  Google Scholar 

  5. Haines D J. Contact stresses in flat elliptical contact surfaces which support radial and shearing forces during rolling. Proc Inst Mech Eng, 1964, 179(10): 154–168

    Google Scholar 

  6. Lee A J C, Ollerton E. A photoelastic investigation of contact stresses in equal spheres rolling together with spin. J Strain Anal Eng, 1969, 4(3): 219–227

    Article  Google Scholar 

  7. Johnson K L. The effect of a tangential contact force upon the rolling motion of an elastic sphere on a plane. J Appl Mech, 1958, 25: 339–346

    MathSciNet  MATH  Google Scholar 

  8. Kaneta M, Murakami Y, Okazaki T. Growth mechanism of subsurface crack due to Hertzian contact. J Tribol, 1986, 108: 134–139

    Article  Google Scholar 

  9. Keer L M, Bryant M D, Haritos G K. Subsurface and surface cracking due to Hertzian contact. J Lubr Technol, 1982, 104: 347–351

    Article  Google Scholar 

  10. Keer L M, Bryant M D. A pitting model for rolling contact fatigue. J Lubr Technol, 1983, 105: 198–205

    Article  Google Scholar 

  11. Murakami Y, Kaneta M, Yatsuzuka H. Analysis of surface crack propagation in lubricated rolling contact. ASLE Trans, 1985, 28(1): 60–68

    Article  Google Scholar 

  12. Glodez S, Ren Z. Modelling of crack growth under cyclic contact loading. Theor Appl Fract Mec, 1998, 30: 159–173

    Article  Google Scholar 

  13. Ren Z, Glodez S, Fajdiga G, et al. Surface initiated crack growth simulation in moving lubricated contact. Theor Appl Fract Mec, 2002, 38: 141–149

    Article  Google Scholar 

  14. Hu Y D, Hu Z Z, Cao S Z. Theoretical study on Manson-Coffin equation for physically short cracks and lifetime prediction. Sci China Tech Sci, 2012, 55(1): 34–42

    Article  MathSciNet  Google Scholar 

  15. Peng D, Jones R, Constable T, et al. The tool for assessing the damage tolerance of railway wheel under service conditions. Theor Appl Fract Mec, 2012, 57: 1–13

    Article  Google Scholar 

  16. Peng D, Jones R. The development of combination mechanical contact and thermal braking loads for railway wheel fatigue analysis. Theor Appl Fract Mec, 2012, 60(1): 10–14

    Article  Google Scholar 

  17. Guan M F, Yu H. In-situ investigation on the fatigue crack propagation behavior in ferrite-pearlite and dual-phase ferrite-bainite low carbon steels. Sci China Tech Sci, 2013, 56(1):71–79

    Article  MathSciNet  Google Scholar 

  18. Hearle A D, Johnson K L. Mode II stress intensity factor for a crack parallel to the surface of an elastic half-space subjected to a moving point load. J Mech Phys Solids, 1985, 33(1): 61–81

    Article  MathSciNet  Google Scholar 

  19. Sheppard S, Barber J R, Comninou M. Short subsurface cracks under conditions of slip and stick caused by a moving compressive load. J Appl Mech, 1985, 52: 811–817

    Article  Google Scholar 

  20. Liu J T, Du P A, Zhang Z Y. A general model of fatigue crack growth under variable amplitude loading. Sci China Tech Sci, 2012, 55(3): 673–683

    Article  MATH  Google Scholar 

  21. Ringsberg J W, Bergkvist A. On Propagation of short rolling contact fatigue cracks. Fatigue Fract Engng Mater Struct, 2003, 26(10): 969–983

    Article  Google Scholar 

  22. Kong X A, Jiang X Y. Solid Contact Mechanics (in Chinese). Beijing: China Railway Press, 1999. 28–29

    Google Scholar 

  23. Shang D G, Yao W X, Wang D J. A new approach to the determination of fatigue crack initiation size. Int J Fatigue, 1998, 20(9): 683–687

    Article  Google Scholar 

  24. Miller K J. The short crack problem. Fatigue Fract Engng Mater Struct, 1982, 5(3): 223–232

    Article  Google Scholar 

  25. Parker A P. Stress intensity factors, crack profiles, and fatigue crack growth rates in residual stress fields. In: Throop J F, Reemsnyder H S, eds. Residual Stress Effects in Fatigue. ASTM, STP, Phoenix, Ariz., 1982. 13–31

Download references

Author information

Authors and Affiliations

  1. Key Laboratory of Tribology, Department of Mechanical Engineering, Tsinghua University, Beijing, 100084, China

    WenTao Liu, Yun Zhang, ZhiJing Feng & JingShan Zhao

Authors
  1. WenTao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. ZhiJing Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. JingShan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to JingShan Zhao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, W., Zhang, Y., Feng, Z. et al. Effects of stick-slip on stress intensity factors for subsurface short cracks in rolling contact. Sci. China Technol. Sci. 56, 2413–2421 (2013). https://doi.org/10.1007/s11431-013-5307-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-013-5307-1

Keywords

Search

Navigation