Skip to main content
SpringerLink
Log in

Shape sensitivity analysis of flutter characteristics of a low aspect ratio supersonic wing using analytical method

  • Progress of Projects Supported by NSFC
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

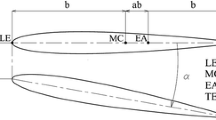
Shape sensitivities of flutter characteristics can predict the moving of flutter boundary as wing shape varies. The nonlinear relationship between mass, stiffness and damping matrices of aeroelastic systems and shape variables makes the flutter characteristics vary nonlinearly as shape variables change. The computation cost of finite difference method is high and it cannot solve precisely shape sensitivities. An analytic method is developed to compute sensitivities of flutter characteristics of low aspect ratio wings to shape parameters, which include aspect ratio, taper ratio, sweep angle, and area. On the basis of the equivalent plate model and piston theory, analytic sensitivities of mass, stiffness and damping matrices with respect to various shape parameters are computed. The equivalent plate model is a continuous aeroelasticity analysis model oriented toward wing design. The flutter equation is solved by tracking the root locus of the system state space model. Lancaster’s adjoint method is used to solve the eigenvalue derivatives and shape sensitivities of flutter characteristics. Linear Taylor approximation based on the analytic sensitivities is used to predict the variation of flutter speed with respect to shape variables. Comparison of these results with those from reanalysis indicates that Taylor approximation based on analytic sensitivities can precisely predict trends of flutter characteristics near the baseline configuration, but the applied neighborhood is small for sweep and area. The method can help designers make a judicious choice of wing shape parameters for preventing flutter in the preliminary design phase of aircraft.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wright J R, Cooper J E. Introduction to Aircraft Aeroelasticity and Loads. Chichester: John Wiley & Sons, Ltd., 2007

    Google Scholar 

  2. Lin M H, Sun X X. Integrated design of flexible structure/flutter active control law (in Chinese). Acta Aeron Astron Sin, 2001, 22: 30–34

    Google Scholar 

  3. Liu Y H, Kapania M. Modal response of trapezoidal wing structures using sencond order shape sensitivities. AIAA J, 2000, 38: 732–735

    Article  Google Scholar 

  4. Haftka R T, Gurdal Z. Elements of Structural Optimization. The Netherlands: Kluwer Academic Publishers, 1992. 255–304

    MATH  Google Scholar 

  5. Lv B, Tan S G, Yang C. Optimization design for aeroelastic dynamics of T-tail (in Chinese). J Beijing Univ Aeron Astro, 2007, 33: 409–413

    Google Scholar 

  6. Wu Q, Wan Z Q, Yang C. Design optimization of flutter scaled model considering structural dynamic and flutter constraints (in Chinese). Acta Aeron Astron Sin, 2011, 32: 1210–1216

    Google Scholar 

  7. Yang C, Xiao Z P. Aeroelastic optimization design for wing with maneuvor load uncertainties. Sci China Tech Sci, 2010, 53: 3102–3109

    Article  MathSciNet  Google Scholar 

  8. Gao P, Guan D. Integrated design of flexible structure/flutter active control law (in Chinese). Acta Aeron Astron Sin, 1995, 16: 521–527

    Google Scholar 

  9. Liu X N, Xiang J W. Study of aeroelastic tailoring of high aspectratio flexible composite wing (in Chinese). Acta Aeron Astron Sin, 2006, 32: 1403–1407

    Google Scholar 

  10. Singhvi S, Kapania R K. Shape sensitivities and approximation of modal response of laminated skew plates. J Aircraf, 1993

  11. Livne E. Analytical sensitivities for shape optimization in equivalent plate structural models. J Aircraf, 1994, 31: 961–969

    Article  Google Scholar 

  12. Livne E, Mineau D. Panel flutter constraints: analytic sensitivities and approximations including planform shape design variables. J Aircraf, 1997, 34: 558–568

    Article  Google Scholar 

  13. Giles G L. Equivalent plate analysis of aircraft wing box structures with general planform geometry. J Aircraf, 1986, 23: 859–864

    Article  Google Scholar 

  14. Livne E. Equivalent plate structural modeling for wing shape optimization including transverse shear. AIAA J, 1994, 32: 1278–1288

    Article  MATH  Google Scholar 

  15. Yang Y X, Wu Z G, Yang C. Flutter analyses of missile wing using equivalent plate model (in Chinese). Acta Aeron Astron Sin, 2011, 32: 833–840

    Google Scholar 

  16. Yang Y X, Wu Z G, Yang C, et al. An aeroelasticity analysis model oriented toward wing design (in Chinese). Acta Aeron Astron Sin, 2011, 32: 1860–1868

    Google Scholar 

  17. Chen G B, Zou C Q, Yang C. Elements of Aeroelastic Dynamics (in Chinese). Beijing: Beijing University of Aeronautics and Astronautics Press, 2004

    Google Scholar 

  18. Reissner E. The effect of transverse shear deformation on the bending of elastic plates. J Apppl Mech, 1945, 12: A69–A77

    MathSciNet  MATH  Google Scholar 

  19. Mindlin R D. Influence of rotatory interia and shear on flexural motions of isotropic, elastic plates. J Appl Mach, 1951, 18: 31–38

    MATH  Google Scholar 

  20. Murthy D V, Haftka R T. Survey of methods for calculating sensitivity of general eigenproblems. NASA CP-2457, 1987

  21. H. M W G H. The aerodynamic effects of aspect ratio and sweepback on wing flutter. ARC R&M 3011, 1955

Download references

Author information

Authors and Affiliations

  1. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Chao Yang, YouXu Yang & ZhiGang Wu

Authors
  1. Chao Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. YouXu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. ZhiGang Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to YouXu Yang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, C., Yang, Y. & Wu, Z. Shape sensitivity analysis of flutter characteristics of a low aspect ratio supersonic wing using analytical method. Sci. China Technol. Sci. 55, 3370–3377 (2012). https://doi.org/10.1007/s11431-012-4933-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-012-4933-3

Keywords

Search

Navigation