New existence of multi-spike solutions for the fractional Schrödinger equations

Abstract

We consider the following fractional Schrödinger equation:

$${\left( { - \Delta } \right)^s}u + V\left( y \right)u = {u^p},\,\,\,\,\,\,u > 0\,\,\,\,{\rm{in}}\,\,{\mathbb{R}^N},$$

((0.1))

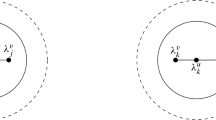
where s ∈ (0, 1), $1 < p < {{N + 2s} \over {N - 2s}}$, and V(y) is a positive potential function and satisfies some expansion condition at infinity. Under the Lyapunov-Schmidt reduction framework, we construct two kinds of multi-spike solutions for (0.1). The first k-spike solution u_k is concentrated at the vertices of the regular k-polygon in the (y₁, y₂)-plane with k and the radius large enough. Then we show that u_k is non-degenerate in our special symmetric workspace, and glue it with an n-spike solution, whose centers lie in another circle in the (y₃, y₄)-plane, to construct infinitely many multi-spike solutions of new type. The nonlocal property of (−Δ)^s is in sharp contrast to the classical Schrödinger equations. A striking difference is that although the nonlinear exponent in (0.1) is Sobolev-subcritical, the algebraic (not exponential) decay at infinity of the ground states makes the estimates more subtle and difficult to control. Moreover, due to the non-locality of the fractional operator, we cannot establish the local Pohozaev identities for the solution u directly, but we address its corresponding harmonic extension at the same time. Finally, to construct new solutions we need pointwise estimates of new approximation solutions. To this end, we introduce a special weighted norm, and give the proof in quite a different way.