Skip to main content
SpringerLink
Log in

Analysis of the nonlinear scheme preserving the maximum principle for the anisotropic diffusion equation on distorted meshes

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

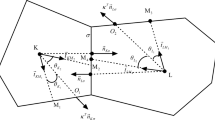
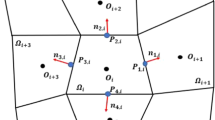
In this paper, a nonlinear finite volume scheme preserving the discrete maximum principle for the anisotropic diffusion equation on distorted meshes is described. We prove the coercivity of the scheme under some constraints on the cell deformation and the diffusion coefficient. Numerical results show that the scheme is indeed coercive and satisfies the discrete maximum principle, and the accuracy of this scheme is remarkably better than that of an existing scheme preserving the discrete maximum principle on random triangular meshes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Angelini O, Chavant C, Chenier E, et al. A finite volume scheme for diffusion problems on general meshes applying monotony constraints. SIAM J Numer Anal, 2010, 47: 4193–4213

    Article  MathSciNet  MATH  Google Scholar 

  2. Bertolazzi E, Manzini G. A second-order maximum principle preserving finite volume method for steady convection-diffusion problems. SIAM J Numer Anal, 2005, 43: 2172–2199

    Article  MathSciNet  MATH  Google Scholar 

  3. Blanc X, Labourasse E. A positive scheme for diffusion problems on deformed meshes. ZAMM Z Angew Math Mech, 2016, 96: 660–680

    Article  MathSciNet  Google Scholar 

  4. Burdakov O, Kapyrin I, Vassilevski Y. Monotonicity recovering and accuracy preserving optimization methods for postprocessing finite element solutions. J Comput Phys, 2012, 231: 3126–3142

    Article  MathSciNet  MATH  Google Scholar 

  5. Burman E, Ern A. Discrete maximum principle for Galerkin approximations of the Laplace operator on arbitrary meshes. C R Acad Sci Ser I Math, 2004, 338: 641–646

    MathSciNet  MATH  Google Scholar 

  6. Camier J S, Hermeline F. A monotone nonlinear finite volume method for approximating diffusion operators on general meshes. Internat J Numer Methods Engrg, 2016, 107: 496–519

    Article  MathSciNet  MATH  Google Scholar 

  7. Cances C, Cathala M, Le Potier C. Monotone corrections for generic cell-centered finite volume approximations of anisotropic diffusion equations. Numer Math, 2013, 125: 387–417

    Article  MathSciNet  MATH  Google Scholar 

  8. Chang L, Sheng Z, Yuan G. An improvement of the two-point flux approximation scheme on polygonal meshes. J Comput Phys, 2019, 392: 187–204

    Article  MathSciNet  MATH  Google Scholar 

  9. Chang L, Yuan G. Cell-centered finite volume methods with flexible stencils for diffusion equations on general nonconforming meshes. Comput Methods Appl Mech Engrg, 2009, 198: 1638–1646

    Article  MathSciNet  MATH  Google Scholar 

  10. Drăgănescu A, Dupont T F, Scott L R. Failure of the discrete maximum principle for an elliptic finite element problem. Math Comp, 2004, 74: 1–23

    Article  MathSciNet  MATH  Google Scholar 

  11. Droniou J. Finite volume schemes for diffusion equations: Introduction to and review of modern methods. Math Models Methods Appl Sci, 2014, 24: 1575–1619

    Article  MathSciNet  MATH  Google Scholar 

  12. Droniou J, Le Potier C. Construction and convergence study of schemes preserving the elliptic local maximum principle. SIAM J Numer Anal, 2011, 49: 459–490

    Article  MathSciNet  MATH  Google Scholar 

  13. Friis H A, Edwards M G. A family of MPFA finite-volume schemes with full pressure support for the general tensor pressure equation on cell-centered triangular grids. J Comput Phys, 2011, 230: 205–231

    Article  MathSciNet  MATH  Google Scholar 

  14. Gao Z, Wu J. A small stencil and extremum-preserving scheme for anisotropic diffusion problems on arbitrary 2D and 3D meshes. J Comput Phys, 2013, 250: 308–331

    Article  MathSciNet  MATH  Google Scholar 

  15. Gao Z, Wu J. A second-order positivity-preserving finite volume scheme for diffusion equations on general meshes. SIAM J Sci Comput, 2015, 37: A420–A438

    Article  MathSciNet  MATH  Google Scholar 

  16. Hoteit H, Mose R, Philippe B, et al. The maximum principle violations of the mixed-hybrid finite-element method applied to diffusion equations. Internat J Numer Methods Engrg, 2002, 55: 1373–1390

    Article  MathSciNet  MATH  Google Scholar 

  17. Huang W. Discrete maximum principle and a Delaunay-type mesh condition for linear finite element approximations of two-dimensional anisotropic diffusion problems. Numer Math Theory Methods Appl, 2011, 4: 319–334

    Article  MathSciNet  MATH  Google Scholar 

  18. Huang W, Wang Y. Discrete maximum principle for the weak Galerkin method for anisotropic diffusion problems. Commun Comput Phys, 2015, 18: 65–90

    Article  MathSciNet  MATH  Google Scholar 

  19. Jameson A. Analysis and design of numerical schemes for gas dynamics, 1: Artificial diffusion, upwind biasing, limiters and their effect on accuracy and multigrid convergence. Int J Comput Fluid Dyn, 1995, 4: 171–218

    Article  Google Scholar 

  20. Le Potier C. Finite volume monotone scheme for highly anisotropic diffusion operators on unstructured triangular meshes. C R Acad Sci Ser I Math, 2005, 341: 787–792

    MATH  Google Scholar 

  21. Le Potier C. A nonlinear finite volume scheme satisfying maximum and minimum principles for diffusion operators. Int J Finite Vol, 2009, 6: 1–20

    MathSciNet  MATH  Google Scholar 

  22. Li D, Shui H, Tang M. On the finite difference scheme of two-dimensional parabolic equation in a non-rectangular mesh. Chinese J Numer Methods Comput Appl, 1980, 4: 217–224

    Google Scholar 

  23. Lipnikov K, Manzini G, Svyatskiy D. Analysis of the monotonicity conditions in the mimetic finite difference method for elliptic problems. J Comput Phys, 2011, 230: 2620–2642

    Article  MathSciNet  MATH  Google Scholar 

  24. Lipnikov K, Shashkov M, et al. Monotone finite volume schemes for diffusion equations on unstructured triangular and shape-regular polygonal meshes. J Comput Phys, 2007, 227: 492–512

    Article  MathSciNet  MATH  Google Scholar 

  25. Lipnikov K, Svyatskiy D, Vassilevski Y. Interpolation-free monotone finite volume method for diffusion equations on polygonal meshes. J Comput Phys, 2009, 228: 703–716

    Article  MathSciNet  MATH  Google Scholar 

  26. Lipnikov K, Svyatskiy D, Vassilevski Y. A monotone finite volume method for advection-diffusion equations on unstructured polygonal meshes. J Comput Phys, 2010, 229: 4017–4032

    Article  MathSciNet  MATH  Google Scholar 

  27. Lipnikov K, Svyatskiy D, Vassilevski Y. Minimal stencil finite volume scheme with the discrete maximum principle. Russian J Numer Anal Math Modelling, 2012, 27: 369–385

    Article  MathSciNet  MATH  Google Scholar 

  28. Liska R, Shashkov M. Enforcing the discrete maximum principle for linear finite element solutions of second-order elliptic problems. Commun Comput Phys, 2008, 3: 852–877

    MathSciNet  MATH  Google Scholar 

  29. Lu C, Huang W, Qiu J. Maximum principle in linear finite element approximations of anisotropic diffusion-convection-reaction problems. Numer Math, 2014, 127: 515–537

    Article  MathSciNet  MATH  Google Scholar 

  30. Lu C, Huang W, Van Vleck E. The cutoff method for the numerical computation of nonnegative solutions of parabolic PDEs with application to anisotropic diffusion and lubrication-type equations. J Comput Phys, 2013, 242: 24–36

    Article  MathSciNet  MATH  Google Scholar 

  31. Nordbotten J, Aavatsmark I, Eigestad G. Monotonicity of control volume methods. Numer Math, 2007, 106: 255–288

    Article  MathSciNet  MATH  Google Scholar 

  32. Queiroz L, Souza M, Contreras F, et al. On the accuracy of a nonlinear finite volume method for the solution of diffusion problems using different interpolations strategies. Internat J Numer Methods Fluids, 2014, 74: 270–291

    Article  MathSciNet  MATH  Google Scholar 

  33. Schneider M, Agelas L, Enchery G, et al. Convergence of nonlinear finite volume schemes for heterogeneous anisotropic diffusion on general meshes. J Comput Phys, 2017, 351: 80–107

    Article  MathSciNet  MATH  Google Scholar 

  34. Sheng Z, Yuan G. A nine point scheme for the approximation of diffusion operators on distorted quadrilateral meshes. SIAM J Sci Comput, 2008, 30: 1341–1361

    Article  MathSciNet  MATH  Google Scholar 

  35. Sheng Z, Yuan G. The finite volume scheme preserving extremum principle for diffusion equations on polygonal meshes. J Comput Phys, 2011, 230: 2588–2604

    Article  MathSciNet  MATH  Google Scholar 

  36. Sheng Z, Yuan G. A new nonlinear finite volume scheme preserving positivity for diffusion equations. J Comput Phys, 2016, 315: 182–193

    Article  MathSciNet  MATH  Google Scholar 

  37. Sheng Z, Yuan G. Construction of nonlinear weighted method for finite volume schemes preserving maximum principle. SIAM J Sci Comput, 2018, 40: A607–A628

    Article  MathSciNet  MATH  Google Scholar 

  38. Terekhov K, Mallison B, Tchelepi H. Cell-centered nonlinear finite-volume methods for the heterogeneous anisotropic diffusion problem. J Comput Phys, 2017, 330: 245–267

    Article  MathSciNet  MATH  Google Scholar 

  39. Wang J, Zhang R. Maximum principles for P1-conforming finite element approximations of quasi-linear second order elliptic equations. SIAM J Numer Anal, 2012, 50: 626–642

    Article  MathSciNet  MATH  Google Scholar 

  40. Wang S, Yuan G, Li Y, et al. Discrete maximum principle based on repair technique for diamond type scheme of diffusion problems. Internat J Numer Methods Fluids, 2012, 70: 1188–1205

    Article  MathSciNet  MATH  Google Scholar 

  41. Yuan G. Diffusion schemes satisfying extremum principle on non-orthogonal meshes (in Chinese). Math Numer Sin, 2021, 43: 1–16

    MathSciNet  Google Scholar 

  42. Yuan G, Sheng Z. Monotone finite volume schemes for diffusion equations on polygonal meshes. J Comput Phys, 2008, 227: 6288–6312

    Article  MathSciNet  MATH  Google Scholar 

  43. Yuan G, Yu Y. Existence of solution of a finite volume scheme preserving maximum principle for diffusion equations. Numer Methods Partial Differential Equations, 2018, 34: 80–96

    Article  MathSciNet  MATH  Google Scholar 

  44. Zhou H, Sheng Z, Yuan G. A conservative gradient discretization method for parabolic equations. Adv Appl Math Mech, 2021, 13: 232–260

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant Nos. 12071045 and 11971069), the Foundation of CAEP (China Academy of Engineering Physics) (Grant No. CX20210042) and the Foundation of LCP (Laboratory of Computational Physics).

Author information

Authors and Affiliations

  1. Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China

    Zhiqiang Sheng & Guangwei Yuan

  2. HEDPS, Center for Applied Physics and Technology, and College of Engineering, Peking University, Beijing, 100871, China

    Zhiqiang Sheng

Authors
  1. Zhiqiang Sheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guangwei Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guangwei Yuan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sheng, Z., Yuan, G. Analysis of the nonlinear scheme preserving the maximum principle for the anisotropic diffusion equation on distorted meshes. Sci. China Math. 65, 2379–2396 (2022). https://doi.org/10.1007/s11425-021-1931-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-021-1931-3

Keywords

MSC(2020)

Search

Navigation