Abstract
The increasing use of digital learning tools and platforms in formal and informal learning settings has provided broad access to large amounts of learner data, the analysis of which has been aimed at understanding students’ learning processes, improving learning outcomes, providing learner support as well as teaching. Presently, such data has been largely accessed from discussion forums in online learning management systems and has been further analyzed through the application of social network analysis (SNA). Nevertheless, the results of these analyses have not always been reproducible. Since such learning analytics (LA) methods rely on measurement as a first step of the process, the robustness of selected techniques for measuring collaborative learning activities is critical for the transparency, reproducibility and generalizability of the results. This paper presents findings from a study focusing on the validation of critical centrality measures frequently used in the fields of LA and SNA research. We examined how different network configurations (i.e., multigraph, weighted, and simplified) influence the reproducibility and robustness of centrality measures as indicators of student learning in CSCL settings. In particular, this research aims to contribute to the provision of robust and valid methods for measuring and better understanding of the participation and social dimensions of collaborative learning. The study was conducted based on a dataset of 12 university courses. The results show that multigraph configuration produces the most consistent and robust centrality measures. The findings also show that degree centralities calculated with the multigraph methods are reliable indicators for students’ participatory efforts as well as a consistent predictor of their performance. Similarly, Eigenvector centrality was the most consistent centrality that reliably represented social dimension, regardless of the network configuration. This study offers guidance on the appropriate network representation as well as sound recommendations about how to reliably select the appropriate metrics for each dimension.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Research in computer-supported collaborative learning (CSCL) focuses on learning processes that take place through group practices and interactional processes mediated by computers (Stahl et al. 2014a, b). CSCL typically promotes collaboration where students can share, discuss, and exchange ideas via, for example, text-based discussion boards (Dillenbourg et al. 2009; Stahl et al. 2014; Weinberger and Fischer 2006). In many constructivist pedagogical approaches, including problem-based learning, students are expected to make joint decisions, negotiate roles, as well as regulate and modify learning strategies and group work through dialogue (Hennessy and Murphy 1999), which relates to the important participation and social dimensions of collaborative learning. Yet, organization of dynamic collaborative learning imposes several challenges and problems, especially in terms of the group dynamics and formation (Kreijns et al. 2013; Näykki et al. 2014). To be able to address these challenges, we need to better and more accurately understand various aspects of CSCL, and the present advances in the fields of learning analytics and social network analysis have proven to be valuable in this regard.
Scholars posit that the collaborative learning process in CSCL settings is a complex knowledge construction process that can be analyzed along several dimensions. For example, Kreijns et al. (2013) suggest that collaborative learning has both a cognitive dimension (e.g., acquisition of knowledge and skills) as well as a socioemotional dimension that underlies these cognitive processes (e.g., group interactions and dynamics). In other words, stimulating and building valuable as well as sound relationships serves as a catalyst for students’ cognitive gains. Others have operationalized collaborative learning through the following four dimensions: the participation dimension, the argumentative dimension, the epistemic dimension and the dimension of social modes of co-construction (Weinberger and Fischer 2006). While many studies involving the use of text-based discussion forums have examined argumentative and epistemic dimensions of collaborative learning (Fu et al. 2016), this study aims to contribute to a deeper understanding of the participation and the social dimensions and in particular, to the validation and reproducibility of the (computational) centrality methods to measure, understand, and reliably represent these dimensions of collaboration. This is critical, since the reproducibility of research findings regarding centrality measures is a problem stressed by many scholars (for more, see Sections 2.3 & 2.4).
As the effectiveness of CSCL depends both on participant and idea interaction, understanding of both the participation and the social dimensions is essential for creating good conditions that facilitate productive knowledge co-construction among students (Hong et al. 2010). To uncover the complex dynamics of these dimensions, this study takes advantage of the recent advances in: (1) the learning analytics (LA) field, which refers to the “measurement, collection, analysis and reporting of data about learners and their contexts, for purposes of understanding and optimizing learning and the environments in which it occurs” (Siemens and Long 2011, p. 34), and (2) social network analysis (SNA). In the context of CSCL, advances in SNA and LA have provided new tools to explore the collaborative learning processes by tracking, collecting, analyzing, and reporting data about how a student contributes to the joint activities, externalizes their own ideas, comments on and responds to peers (i.e., the participation dimension) and builds on the ideas and contributions of others in knowledge co-construction (i.e., the social dimension) (Berland et al. 2014; Fincham et al. 2018; Gaševi et al. 2015; Schneider and Pea 2014) Such improved understanding of the both dimensions provides researchers, teachers and students with fundamentally new, data-driven ways to: (1) view and support the critical phases of collaborative learning, (2) find evidence of critical moments of success or failure, and finally, and (3) to act upon this information to improve conditions for learning and collaboration (Noroozi et al. 2019).
The use of SNA in combination with LA requires researchers to make several critical decisions with respect to selected techniques for accurately measuring complex dynamics of participation and social interaction. However, despite the critical importance of using validated methods to measure collaborative learning, only few LA research studies have hitherto addressed the validity of the employed methods (see, e.g., Kovanovic et al., 2015; Fincham et al. 2018). Given the significance of the participation and the social dimensions of collaborative learning, this study seeks to extend the work on methodological choices by focusing on the validation of centrality measures (i.e., outdegree, indegree, closeness, betweenness and eigenvector centralities) in CSCL settings.
The study aims to answer the following research questions:
How do different network configurations influence the reproducibility and robustness of centrality measures as indicators of student learning in collaborative learning settings?
What are the most robust centrality measurements that are least sensitive to different network configurations?
What are course network structural factors that could explain the variability of findings?
This article starts by discussing the concept of centrality measures and how they have been operationalized to indicate students’ participatory efforts, to identify roles, predict learning gains, as well as monitor interactivity. Then, it presents a review of the issues with current methods and discusses how different network configurations influenced the reproducibility and robustness of centrality measures as indicators of student learning. The article concludes by arguing that the accurate representation of SNA centrality measures is vital for facilitating students’ participation and interaction, and also for understanding of the complex dynamics and patterns of participation in productive knowledge construction.
Background
Several studies have sought to automate the analysis of CSCL using computational methods. One such method is interaction analysis, which offers analysis of students’ posting behavior, comparative statistics or visualizations (e.g., Martínez-Monés et al. 2011; Rodríguez-Triana et al. 2013). SNA is another computational method that has been similarly implemented to analyze the participatory and the social dimensions of CSCL through indicators known as centrality measures. These measures have been used to: indicate students’ participatory efforts, monitor engagement, identify participatory roles (e.g., active, coordinators and isolated) or forecast learning gains. In the next sections, we will discuss the concept of centrality measures and how they have been operationalized to explain the participatory and social dimensions of CSCL. Finally, we conclude by discussing why methodical refinement is needed, and why the existing methods are insufficient.
The concept of centrality measures
Centrality is a concept used to indicate the importance, relevance, or value of an actor (e.g., the learner or the teacher) in a network It is computed from network representations using mathematical formulae. The concept of centrality was applied to human communications and dates back to late 1940s at MIT, where Bavelas and his colleagues studied the association between structural position and influence in group processes (Bavelas 1948). In his seminal article, Freeman (1978) stresses that an important actor in a network has more connections (i.e., higher degree centrality), can reach others (i.e., higher closeness centrality), and connects between others (i.e., high betweenness centrality). Since the concept of value or relevance may have different meanings in different learning settings, there are various centrality metrics that reflect this diversity (Borgatti and Everett 2006; Freeman 1978).
Operationalization of centrality measures in CSCL
Centrality measures have been used as indicators for several aspects of CSCL, including the participatory- and social dimensions. Measures of the participatory dimension include outdegree centrality, which is frequently calculated as the number of out-posts generated by a learner, or the number of the learner’s contacts. It serves as an indicator of quantity of participation in the collaborative knowledge (co)-construction (Cadima et al. 2012; Joksimovic et al. 2016). The pace of outdegree centrality has also been linked to self-regulation in learning and better achievement (Saqr et al. 2019a). Indegree centrality is commonly used to demonstrate the importance and worthiness of a learner contribution, prestige and authority in knowledge construction as well as the popularity of the learner. Indegree measures the times a learner has been responded to. In other words, it serves as an indicator of social interaction in which the learner connects, elaborates and integrates ideas by referring to contributions of the learning partners (Hershkovitz 2015; Hong et al. 2010; Reychav et al. 2018; Romero et al. 2013).
The measures that reflect the social dimension of CSCL include closeness centrality, betweenness centrality and eigenvector centrality. Closeness centrality refers to the degree to which an individual is close to all other members in a given network. It measures the engagement level of the learner, the distance to all others in the discourse, and closeness to the collaborators. It is often operationalized as the ease of reachability and the ease of access to information (e.g., Hernández-García et al. 2015; Liu et al. 2019; Osatuyi and Passerini 2016). Betweenness centrality represents learner engagement in the discourse. Higher values of betweenness reflect access to opportunities to control information exchange and diversity of information and its novelty (Cadima et al. 2012; De-Marcos et al. 2016; Reychav et al. 2018; Saqr et al. 2018b). It measures when a learner has been on the shortest path between others, or connected others. The last centrality measure used in this study is eigenvector centrality; it considers the centrality scores of the collaborators; therefore, it reflects the selectivity of the learner and quality of connections. Eigenvector centrality is expected to be higher in students engaged in discourse with active and engaged collaborators. It has frequently been operationalized as influence, connectedness and building significant social capital (De-Marcos et al. 2016; Liu et al. 2018; Putnik et al. 2016; Traxler et al. 2016).
The need for validated methods
Decades of research on social networks have contributed to several revisions and refinements of the centrality concept (Borgatti 2005; Borgatti and Everett 2006; Freeman 1978; Liao et al. 2017; Opsahl et al. 2010). In several research areas, to achieve more robust results, scholars were able to identify the relevant centrality measures optimal for specific problems, devise better computational algorithms, and develop standardized data operationalization techniques (e.g., Liao et al. 2017; Lü et al. 2016). A popular example is the development of the PageRank centrality used by Google to identify relevant search results (Liao et al. 2017). Nevertheless, many challenges remain, for example, which metrics are more efficient in ranking actors in a particular context, and how weighting affects node centrality (Liao et al. 2017; Lü et al. 2016). Each network representation method can result in a different network configuration and different centrality metrics. Consequently, it is important to identify which methods yield the representative and the most robust centrality measures of the dimension or phenomenon they are thought to represent. In this study, we in particular focus on the validation of the centrality measures – in terms of their reliability and consistency – used to measure and explain the important participatory and social dimensions of CSCL.
Issues with current methods
Variability of results
The variability of findings regarding centrality measures is a problem identified by many researchers (e.g., Agudo-Peregrina et al. 2014; Fincham et al. 2018; Hernández-García et al. 2015; Joksimovic et al. 2016; Rogers et al. 2016; Saqr et al. 2018a). In the context of CSCL, indegree centrality was, for example, reported to be positively correlated with learners’ performance in several studies (Hernández-García et al. 2015b; Liu et al. 2018; Saqr et al. 2018a; Wise and Cui 2018). Others have reported no significant correlations (Reychav et al. 2018; Saqr and Alamro 2019). Outdegree centrality was also found to correlate with learner performance (Hernández-García et al. 2015; Saqr et al. 2018; Saqr and Alamro 2019). However, others (Liu et al. 2018; Reychav et al. 2018) have shown no significant correlations. The problem extends to other centrality measures, such as closeness and betweenness centrality, that were indicated on the one hand to be positively correlated with performance (Hernández-García et al. 2015; Liu et al. 2018), but on the other hand were not (e.g., Reychav et al. 2018; Saqr and Alamro 2019). The reasons for this variability were attributed to contextual and network operationalization factors (Agudo-Peregrina et al. 2014; Fincham et al. 2018; Joksimovic et al. 2016), explained in the sections below.
Operationalization of data
There are three main factors in network representation to consider: (1) what a tie is, (2) what the weight (strength) of a tie is, and (3) how the whole network is aggregated (Lü et al. 2016; Opsahl et al. 2010). Few studies have been devoted to the examination of the role of different network configurations (Fincham et al. 2018; Wise et al. 2017) in the field of education. Recently, LA researchers have started to address this gap (Bergner et al. 2018). Fincham et al. (2018), for example, examined the influence of different tie extraction methods on a network structure and statistical metrics. The findings exhibit a significant influence of each tie extraction method and the information derived from the network. The authors also found that the correlation between centrality measures and academic performance varied significantly with each tie extraction method, and stressed the importance of transparency of the tie definition. For any SNA analysis, the definition of a tie is crucial since each definition carries with it a set of beliefs about the nature of social interactions: while most scholars define ties on the basis of direct replies, others rely on co-presence, where a tie within a network is explained as being present in the same part of the discussion (Fincham et al. 2018).
Equally important to the definition of the tie, is the weight assigned to the tie, and how duplicate ties or loops are dealt with to form the final configuration of the network (Opsahl 2009; Opsahl et al. 2010; Shafie 2015; Tsugawa et al. 2015; Wei et al. 2013). In CSCL – the focus of this study – a tie is usually considered when a learner replies to another learner and is operationalized as an edge from the source (the post writer) to the target (the replied-to).Footnote 1 Ties have been used to, for example, construct an aggregated network (Dado and Bodemer 2017). Forming such a network requires the researcher to make decisions on the aggregation of ties, such as duplicate ties (i.e., when two users exchange multiple interactions), the loops (i.e., when a user replies to self), the weight of the ties (i.e., whether the ties have a strength or not such as the size of the post), and lastly, whether to keep every tie or extract the backbone network (a sub-network with only important ties of a certain strength or threshold).
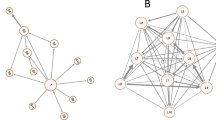
To demonstrate the network configuration, Fig. 1 introduces the same network with three representations. Figure 1a presents a multigraph network, where duplicate ties and loops are allowed. Figure 1b shows a simplified weighted network (loops and multiple ties removed); the thickness of the ties represents the weight of the tie. In the figure, the weight corresponds to the frequency of interactions among nodes. Figure 1c is a representation of a simplified network where all duplicate edges and loops were removed. Each of these configurations underscores a certain aspect. Multigraph configuration highlights quantity and effort. Weighted configuration emphasizes the tie strength or quality. The simplified graph highlights diversity over multiplicity (Opsahl 2009; Shafie 2015; Tsugawa et al. 2015).
Contextual factors
The contextual variability is a widely recognized aspect in the field of LA in general and in SNA studies in particular (Bergner et al. 2018; Joksimovic et al. 2016). Interactions between students, teachers and learning tools in a course frequently vary by context and/or instructional conditions (Gašević et al. 2016; Rogers et al. 2016). These variations result in a substantial heterogeneity of learners’ interactions (Lockyer et al. 2013). For instance, networks derived from a collaborative discussion among students are expected to be different from a question/answer forum with a teacher (Lockyer et al. 2013). In the former (collaborative discussion), outgoing interactions (outdegree), as well as incoming replies (indegree) are expected to correlate with students’ engagement in a collaborative learning activity. While in the latter (discussion with the teacher) outdegree matters more as it signifies students’ answers. One of the possible shortcomings is that the operationalization of ties and their relation to learning outcomes are not ‘measured.’ Furthermore, some ties might not be accurately defined, especially when students address each other directly in the text (by mentioning their names) or indirectly through addressing their contribution while replying.
Motivation for this study
Since LA relies on measurement as a first step of the process (Siemens and Long 2011), the robustness of selected techniques for measuring (collaborative) learning activities is critical for several reasons. First, adequate measurements help generalizability and replicability of research findings. Secondly, theory and measurement are interdependent. For a theory to advance our understanding of the complex nature of learning and teaching processes, there is an evident need for valid measurements and testable models that can deliver reproducible results (Loken and Gelman 2017; Smaldino and McElreath 2016). As stressed by Bergner et al. (2018), “It can safely be assumed that without foregrounding methodological choices in learning analytics we run the risk of generating more doubt” (p. 3).
Through the validated SNA measures applied to CSCL, scholars can uncover and explain better the participation and social dimensions of collaborative learning using the centrality measures of degree, closeness, betweenness and eigenvector centralities. These measures represent, for example, quantity, ego network size, diversity, positioning, sociability and role in information exchange (Rienties et al. 2009; Weinberger and Fischer 2006). Consequently, they are used, for instance, to monitor students’ engagement, forecast learning gains and identify roles in a learning network. Each of these centralities is expected to have a different value in each network configuration and with different weight choices (Fincham et al. 2018; Opsahl 2009; Shafie 2015; Tsugawa et al. 2015; Wei et al. 2013). Therefore, it is critical to examine the influence of different network configurations on the resulting network, and this study aims to fill this gap.
This study aims at establishing sound methodological guidelines regarding operationalizing of the important participatory (behavior) and social dimensions of CSCL using SNA to accurately reflect what it is supposed to measure. More importantly, we aim to examine the reliability and reproducibility of the frequently used measures. Results aim to guide the choice of adequate and robust methods for construct operationalization and better reproducibility. Given the importance of research on the methodological choices in SNA and LA in education, we argue that studies are needed to fill such a gap that helps to test the measurements, their reproducibility and their influence on findings. As Wise and Schwarz posit, the substantial question in using computational methods to understand CSCL is “how to develop practices and norms around their use that maintain the community’s commitment to theory and situational context” (Wise and Schwarz 2017, p. 448).
Method
Context
The study was conducted based on a dataset of four university courses (in medical higher education) over three iterations (12 courses in total) during the years 2016–2018 (Table 1). The courses were chosen so that we could compare different iterations of the same course by different students and compare the same students taking different courses. To minimize the effect of a specific learning design, the courses were chosen based on essentially the same design of problem-based learning (PBL), expecting students to engage in discussion forums with the same rules. The examined courses also had the same duration (i.e., eight weeks) and similar weight of credit hours (i.e., eight hours each).
In the targeted courses, students were assigned to small groups (five groups per course of seven to eleven students) with a tutor. On a weekly basis, they were offered a problem (online) aimed to act as a trigger for further discussions. The problems were real-life scenarios of complex patients’ problems that did not have any single direct solution. The problems were formulated to stimulate the discussion about gaps in students’ current knowledge and identify new topics they have to learn, collaboratively work together to learn these issues, share their understandings, argue, and comment on their work. By the end of the week, students were expected to: (1) have reached a common understanding of the problem, (2) have reflected on their collaborative work, and (3) have received feedback from their tutor and peers. The interactions took place online in the Moodle learning management system (LMS) forums. A thread was created for each group for each weekly problem. An abridged sample of the discussions from the course Principles of Dental Sciences 2016 is shown in Fig. 2.
The performance was measured by the grades given for a PBL task, consisting of a multiple-choice knowledge test that assessed students’ acquisition of the knowledge of the PBL objectives and the performance of the individual student as evaluated by the tutor. The tutor evaluated the students’ contributions based on three criteria: (1) their contributions to the discussions and presentation of their arguments, (2) their engagement with other peers in the group, as well as (3) their reflection on their performance. To minimize subjectivity, the evaluating tutor was unified for all groups for each week. Each knowledge exam is reviewed for quality by the assessment committee and a post-exam psychometric analysis; grades were adjusted accordingly.
Data collection and data analysis
Data were extracted from the LMS log system. The collected data included the username, the forum ID, the post ID, the post writer, the post target, the post content, the post subject, the thread ID, and the group ID. Posts that were outside the PBL discussions (i.e., news, announcements, social interactions) were excluded. The data were used to construct the networks by considering an edge as when a student replies to another student. As each online group was separate, a network was generated for each group.
Three types of networks were created:
Multigraph network, where all interactions were compiled, loops and multiple edges were retained.
The simplified network where loops and multiple edges were removed.
Weighted, where each edge was assigned the weight of the number of characters a student has posted.
For each student in each course, the five most-used centrality measures were calculated for each network.
Outdegree centrality: refers to the number of messages a student posted (multigraph), or the number of unique users a student contacted (simplified), or the total volume of text a student posted (weighted) (Liao et al. 2017; Opsahl et al. 2010; Stephenson and Zelen 1989; Wei et al. 2013). Outdegree is commonly operationalized as the effort and participation of a learner in forums (Hernández-García et al. 2015; Saqr et al. 2018a; Saqr and Alamro 2019).
Indegree centrality: refers to the number of replies a student gets (multigraph), or the number of unique users who have replied to the student (simplified), or the total volume of text a student has received from all contacts (weighted) (Csardi and Nepusz 2006; Liao et al. 2017; Opsahl et al. 2010; Stephenson and Zelen 1989; Wei et al. 2013). Indegree is always operationalized as prestige, leadership or worthiness of argument to discuss, debate or be replied to (Liao et al. 2017; Liu et al. 2018; Lu et al. 2017; Saqr et al. 2018a).
Betweenness centrality: is the number of times a student has connected to unconnected users (on the paths between them), the multigraph variant considers all interactions. While the simplified variant considers only the unique variant, the weighted variant is calculated as weighted by the post size (Lü et al. 2016; Stephenson and Zelen 1989). Students who have high betweenness centralities control the flow of information as well as have access to diverse perspectives and resources.
Closeness centrality: represents the closeness of a student to all others in a network (inverse distance). The multigraph variant takes into account all interactions; the simplified variant considers only the unique interactions, and the weighted variant is calculated as weighted by the post size (Lü et al. 2016; Stephenson and Zelen 1989). Closeness centrality is a sign of ease of accessibility to all others and reachability (Lü et al. 2016; Stephenson and Zelen 1989).
Eigenvector centrality: in contrast to degree centrality that counts only the number of contacts. Eigenvector centrality calculates the number of contacts and their cumulative strength; as such it is computed as the sum of all centralities of a student’s contacts. In a CSCL context, it reflects student positioning, selection of peers and relations. It is expected to be higher if a student interacts with others who are engaged in discourse and lower in students who interact with disengaged and/or isolated students. Therefore, Eigenvector centrality captures the social positioning of the students more reliably than the other centrality measures (De-Marcos et al. 2016; Liu et al. 2018; Putnik et al. 2016; Traxler et al. 2016).
For each network, we calculated the average degree as the mean number of edges that represent messages posted or received by a participant in the course, and we calculated the network density as the proportion of actual edges among students to the maximum possible. In this study, all centrality measures were calculated with the Igraph library (Csardi and Nepusz 2006) implemented in the R programming language version 3.52 (R Core Team 2018). Since centrality measures were estimated from groups with different sizes, two versions were calculated for each centrality measure: (1) A normalized centrality, i.e., the centrality measure is divided by the number of students to balance the influence of group size on the number of possible interactions in the group (Saqr et al. 2019b), and (2) an unmodified version, raw or non-normalized version, in which we report the centrality measure as it is, with no modification. Both methods are reported and compared to test the influence of group size on the robustness of the methods.
Ethics
The study was approved by the college ethical committee. Data utilized in this study were anonymized, and personal information was removed during analysis. The researchers of this study did not participate in teaching or grading the studied courses and the analysis started after courses ended.
Results
Participants
The study was performed on a dataset from 12 courses consisting of 13,428 interactions from 598 students. The number of students in each course ranged from 45 to 54, with a mean of 49.83 (Table 1). The median frequency of interactions in a course was 921.5 and ranged from 439 to 3134. The mean strength was 201.48 (SD 15.99); the mean degree was 9.36 (SD 4.02); the mean size of the post was 1096 characters, while the median was 329.
How do different network configurations influence the reproducibility and robustness of centrality measures?
Indegree centrality
The Spearman correlation between indegree centrality calculated with the multigraph method proved to be consistently positively correlated, and with higher strength of correlation coefficient with performance, in the 12 studied courses (Fig. 3). The correlation coefficient ranged from r = 0.54, p < 0.01 to r = 0.77, p < 0.01; the coefficient value was also stronger than the other configurations in eight courses. The simplified configuration was positively and significantly correlated with performance in nine courses, with a correlation coefficient that ranged from r = 0.42, p < 0.05 to r = 0.7, p < 0.01, while not correlated with three courses: C2 (r = 0.22, p = 0.13), C4 (r = 0.15, p = .33), C10 (r = 0.03, p = 0.85). The weighted configuration was positively correlated with 10 courses, with a correlation coefficient ranging from r = 0.29, p < 0.05 to r = 0.7, p < 0.05 and not correlated with two courses: C2 (r = 0.03, p = 0.83) and C10 (r = −0.05, p = 0.73).
Plot of indegree centrality correlation coefficient with performance in each course *Each significant correlation is plotted against the Y-axis in each course. Non-significant correlations are plotted as 0 on the Y axis. The plot shows the multigraph (blue line) is consistently positively and significantly correlated in the 12 studied courses in both plots (normalized and raw).
Similar results were obtained when the indegree centrality (multigraph) was normalized. However, the simplified and weighted variant were not correlated with the two courses (C4 & C10) and positively correlated with the remaining 10 courses. The notable difference is that C2 (in the simplified configuration) showed significant positive correlation (r = 0.41, p < 0.01) compared to (r = 0.22, p = 0.13) in the non-normalized version. These results indicate that the multigraph indegree (whether normalized or not) produces a consistent stronger correlation with grades regardless of the studied course or the batch. This also demonstrates that normalization offers some improvement as C2 became significantly correlated after normalization.
Outdegree centrality
Similar to the indegree centrality, the correlation between outdegree centrality (calculated with the multigraph method) proved to be consistently positively correlated with student performance in all courses, with a higher correlation coefficient in 10 courses compared to other configurations; the coefficient ranged from r = 0.57, p < 0.01 to r = 0.78, p < 0.01. In the simplified configuration, outdegree was correlated with six courses only (C1, C5–8, C11), with a correlation coefficient that ranged from (r = 0.34, p = 0.02) to (r = 0.73, p < 0.01). In the weighted configuration, the correlation was positively significant in six courses (C1, C 5–8 & C11), with a coefficient that ranged from r = 0.32, p = 0.02 to r = 0.78, p < 0.01, while negatively and significantly correlated in two courses C9 and C10 (Fig. 4).
A plot of outdegree centrality correlation coefficient with performance in each course *Each significant correlation is plotted against the Y-axis in each course. Non-significant correlations are plotted as 0 on the Y-axis. The plot shows the multigraph (blue line) is consistently positively and significantly correlated in the 12 studied courses in both plots (normalized and raw).
Similarly, when the outdegree was normalized, in the multigraph configuration, the correlation was consistently and significantly positive in all examined courses. In the simplified configuration, the correlation was relatively better than the ‘raw’ results and showed a positive correlation in eight courses, compared to six. The weighted variant demonstrated a positive correlation in six courses (C1, C5–8 & C11) and a negative correlation in C10. Both the simplified and weighted variant showed slightly better results in terms of the number of positive correlations.
In summary, the results show that the multigraph outdegree is the most robust and has the highest correlation with performance (Fig. 4). Normalization by group size improved other configurations.
Closeness centrality
An almost similar pattern to indegree and outdegree centralities was observed in closeness centrality. The multigraph configuration was positively and significantly correlated with student performance in eleven courses with a correlation coefficient that ranged from r = 0.57, p < 0.01 to r = 0.74, p < 0.01 except for C8 (r = −0.032, p = 0.82). The simplified configuration was positively correlated in seven courses (C1, C2–4, C9, C10 & C12), negatively and significantly correlated in C8 (r = −0.52, p < 0.01), and non-significant in four courses (C5–7, & C11).
However, the normalized closeness centrality was more consistent than the ‘raw’ methods. In the multigraph method, normalized closeness centrality was positively correlated with student performance in eleven courses (except for C8); the simplified configuration was statistically significant in nine courses (C1–7, C9 & C10), and non-significant in two courses (C8, C11), while negative in one course (C12). While the weighted variant was positively correlated with performance in four courses (C2–4, C10), it was negatively correlated in C12 and insignificant in the other courses. The raw centralities (Fig. 5) showed inconsistent results among courses except for the multigraph configuration. In summary, the multigraph configuration produces the most consistent results in most courses, especially when normalized by group size.
A plot of closeness centrality correlation coefficient with performance in each course. *Each significant correlation is plotted against the Y-axis in each course. Non-significant correlations are plotted as 0 on the Y axis. The plot shows the multigraph (blue line) is consistently positively and significantly correlated in the 12 studied courses in both plots (normalized and raw)
Betweenness centrality
Contrary to the previous centralities, betweenness centrality in all configurations was largely inconsistent, showing only C8 as positively and significantly correlated with student performance in the multigraph configuration (r = 0.35, p < 0.01) and similarly in the normalized multigraph configuration (r = 0.33, p = 0.02), while negatively and significantly correlated in C5, C7, C9 and C10 in the multigraph configuration, and similarly in the normalized variant in C5, C7 and C9. Other configurations showed either negative correlations (e.g., C2, C5 & C10) in the simplified configuration or insignificant correlation (C6–9). The simplified normalized betweenness centrality was statistically insignificant in all courses (Fig. 6).
Eigenvector
The eigenvector centrality was positively and statistically significant in 11 courses in the multigraph configuration, as well as the simplified configuration, except for C2. In the weighted example, it was statically and positively significant in 10 courses, except C2 and C8 (Fig. 7). Interestingly, regardless of the configuration, the normalized eigenvector centrality was statistically and positively correlated with performance in all courses, pinpointing the robustness and consistency of eigenvector centrality in different network configurations.
What are course network structural factors that could explain the variability of findings?
We plotted the centrality measures along with the course characteristics as it may offer a clue to why some predictions have not been accurate in some courses. As seen in Fig. 8, C2 had fewer interactions than all other courses (n = 439), as well as the insignificant correlations on simplified indegree, outdegree, and eigenvector centrality. It was also statistically insignificant in the weighted outdegree and Eigen centralities. In C10, which was mostly either insignificant or negatively correlated in most configurations, the count of interactions was also low (n = 567). One can see the mixed results for C4 as well with a low count of interactions (810).
Discussion and conclusions
SNA and LA methods are useful to uncover several aspects of the students’ collaborative roles, including cooperative behavior, brokerage of information, reach and sphere of influence, as well as mapping the relations to other collaborators (learners and teachers) through visualizations (Saqr et al. 2018a; Saqr et al. 2018c). The accurate identification and further adequate (in-time) learner support in CSCL settings can and should significantly enhance the success of the collaboration process, thus creating better conditions for students’ learning, ultimately leading to their improved academic performance. This study builds on previous research efforts (Fincham et al. 2018; Wise et al. 2017) and continues the line of methodological refinement. In doing so, we have investigated the methods that reflect an accurate view of students’ roles and interactions that constitute the relational aspect, a key component of both participation – and social dimensions of collaborative learning.
How do different network configurations influence the reproducibility and robustness of centrality measures as indicators of student learning in collaborative learning settings?
This study has examined how different network configurations influence the reproducibility and robustness of centrality measures as indicators of student learning – especially the participation and social dimensions of collaborative learning – in CSCL settings. Overall, our findings indicate that the multigraph configuration produces the most consistent and robust centrality measures, suggesting that these measures can be used to generalize relevant results across courses. One explanation to this finding is the fact that such a configuration retains the information about the frequency of students’ participation and hence presents a more accurate view of students’ efforts, especially in quantitative centrality measures (i.e., indegree and outdegree), compared to the weighted and simplified configurations. It is important, since the frequency of interactions among students bears valuable information about learner engagement (both static and continuous) and is “regarded as an important indicator of knowledge construction” (Weinberger and Fischer 2006, p. 73).
Moreover, research has shown that reciprocity is an important building block of social and learning networks: the frequency of reciprocal interactions are indicative of the strength of mutual trust and the perceived value of the interaction (Block 2015). Our results have shown that simplifying the network (i.e., removing multiple edges and loops) is reductionist. The simplified configuration came next in robustness. While it accurately reflects (and possibly rewards) the diversity and multiplicity of students’ connections, it turned out that it may have been over-simplifying and thus detrimental to the quality it is expected to represent (i.e., the participatory dimension of collaborative learning). These results are congruent with earlier research efforts, in which simplified network correlations between centrality and final grade were used (Traxler et al. 2016).
The findings have also demonstrated that post size was not a reliable weight. A possible explanation may be the possibility that students who posted large chunks of text tended to care less about text quality and/or they copy-pasted content from the Internet. Nonetheless, such posts received fewer interactions. Therefore, the indegree centrality (i.e., how students value the post and select to reply to it, giving rise to high indegree) is more important than the mere count. While we have tested the weighted network by post size, it may be useful to try other types of weight.Footnote 2
Similar results were found with closeness centrality. The multigraph configuration was found to be far more robust in most courses, confirming the idea that reducing networks may be at the cost of the consistency. Betweenness centrality showed the least consistent results among all centrality measures in all configurations. On the contrary, eigenvector centrality showed the most robust centrality across all configurations. Regardless of the configuration and the way it was represented, eigenvector centrality was positively correlated and statistically significant with student performance. As eigenvector centrality takes into consideration the strength of connections of all connections of a student, it samples both the size and the quality of the network of the students. Such a range of data makes the centrality more robust to changes compared to the local centrality measures (i.e., indegree and outdegree).
A learner who interacts with ten peers has the possibility to have a larger network size than another in a group of five, and consequently, a higher centrality measure. This imbalance requires researchers to carefully consider normalization when comparing students in groups or classes of different sizes. Our results have shown an improvement of centrality robustness with normalization and pinpoint that the number of interactions in a course may affect the robustness of the derived centrality measures. Consequently, caution should be exercised in interpreting centrality measures in courses with a small number of interactions or low engagement. However, it is important to note that eigenvector centrality was consistently positively correlated even in such small courses. Therefore, the answer to the first research question is: whereas closeness and betweenness centralities are more sensitive to network configuration methods, degree and eigenvector centralities are more robust measures, especially when calculated with the multigraph configuration. Our findings also support multigraph as the recommended configuration in general.
Is there guidance on which centrality to choose to better understand the participatory and social dimension in CSCL environments?
As discussed earlier, the degree centralities in the multigraph configuration reflect the efforts and contributions of students and, therefore, should be considered when evaluating the participatory dimension of collaborative learning. The eigenvector centrality was found to be a more reliable measure of the social dimension of CSCL because it considers both the number and the strength of relationships. Our results demonstrated that eigenvector centrality was the most consistent measure of the social dimension, demonstrating a consistently positive and significant correlation in all selected network configurations. These findings stress the robustness and the reliability of this method as an indicator of building sound and valuable social relationships that are considered as an essential element of the collaborative process. Kreijns et al. (2013) point out that although a focus on the social space might emphasize the structural aspects, “these structures must exist to some degree before a group may become a performing group” (p.234). In other words, stimulating and building valuable and sound relationships serves as a catalyst for achieving the promise and potential of CSCL. In summary, the following answers the study’s second research question: Whereas degree centralities are robust indicators of students’ participation in CSCL, eigenvector centrality reliably reflects students’ social positioning and relationships.
What course network structural factors could explain the variability of findings?
In our study, we found that courses with a low number of interactions had inconsistent results regarding the participatory dimension, but not so for the social dimension, as reflected by eigenvector centrality. This stresses the importance of active social interactions in the course before relying on SNA measures. Of course, this is not the only factor, the accuracy of students’ assessment as measured by test grades depends on students’ characteristics (e.g., knowledge, motivation and effort), task characteristics and assessment methods (e.g., exam difficulty, the standards and criteria of the assessment) as well as on teacher expertise and accuracy of teacher judgment (Südkamp, Kaiser and Möller 2012). Therefore, the inconsistency of results may be partly a reflection of the quality and accuracy of the assessment process. Further research may need to explore the reliability and validity of learning measures in combination with reliability and validity of interaction/social relation measures.
Implications
Centrality measures have been used to identify students’ roles (e.g., leaders, collaborators, animators or peripherals). Correctly identifying these roles is therefore critical to inform learners and their collaborative partners about their own and others’ participation on the one hand, and the teacher or instructor on the other. Similarly, centrality measures have been used to indicate students’ engagement and effort to build on peer contributions in knowledge co-construction. While contributions by the learners serve as an indicator of the effort of participation, some contributions may be connected, elaborated and synthesized more intensively than others (Hong et al. 2010). For example, the results of this study indicate that receiving interactions may be more indicative of the value of an interaction over the interaction size. Consequently, it is important to compute valid centrality measures and to select the appropriate measures that allow exploring complex dynamics and patterns between contributions in productive knowledge building. Another implication is that researchers aiming to implement a predictive algorithm in the context of CSCL could find guidance in the methods examined in this study (e.g., which centrality measures are replicable and which are robust against course variations). In summary, the study emphasizes that network centralities can be a reliable indicator for students’ participatory efforts, social relations as well as a predictor of their performance when calculated with appropriate methods (Kreijns et al. 2013).
The results emphasize the need for researchers who report on SNA to present in detail their methodological choices so that research is better able to be compared, replicated, and ultimately generalized. Based on this study’s results, we suggest that the following items should be reported:
Tie definition: what is considered to represent a tie and any assumption made for a tie definition;
Direction: whether the network is directed, undirected or mixed;
Network mode: e.g., unipartite or bipartite;
Weight: network is weighted, simplified or a backbone with a certain threshold;
Number of nodes, edges in each of the studied networks;
Aggregation method and duration of aggregation;
Software and version used for calculation of network centralities;
Software used for network visualization and layout;
Community finding method and parameters used.
Future research
In this study, we have used specific settings of problem-based learning design in medical higher education where research on LA is lacking (Saqr 2015, 2018). Since the contextual aspect is important in SNA studies (Gašević et al. 2016), we suggest that future research should replicate this study in other disciplines, with other kinds of learning designs, as well as in other educational levels and forms (e.g., K-12 education and MOOCs). This will enable better understanding of whether the multigraph configuration generates equally robust and consistent centrality measures of student learning across divers CSCL settings. Moreover, simulation is an area that has not been explored in education research. Consequently, it would be interesting to simulate different network structures and study how different simulations influence learning. Content analysis could be incorporated in graph measures as a weight for ties. It can also be used as a validation of the different assumptions inherent within different centrality measures.
In sum, while proving the multigraph configuration produces the most consistent and robust centrality measures of student learning, we call for further research to test other network configurations, apply other tie definitions, and verify our results in similar learning settings, or some others, and further build upon them to continue the line of methodological refinement in the fields of social network analysis and learning analytics.
Notes
There are other tie definitions too. For a review and methodological discussion, please see the study by Fincham et al. (2018)
An initial analysis of this study tested the weight as a function of number of duplicate links, which resulted in identical results for the indegree and outdegree centralities, and similar (but less robust) correlations for other centrality measures.
References
Agudo-Peregrina, Á. F., Iglesias-Pradas, S., Conde-González, M. Á., & Hernández-García, Á. (2014). Can we predict success from log data in VLEs? Classification of interactions for learning analytics and their relation with performance in VLE-supported F2F and online learning. Computers in Human Behavior, 31(1), 542–550. https://doi.org/10.1016/j.chb.2013.05.031.
Bavelas, A. (1948). A mathematical model for group structures. Human Organization, 7(3), 16–30.
Bergner, Y., Gray, G., & Lang, C. (2018). What does methodology mean for learning analytics? Journal of Learning Analytics, 5(2), 1–8. https://doi.org/10.18608/jla.2018.52.1.
Berland, M., Baker, R. S., & Blikstein, P. (2014). Educational data mining and learning analytics: Applications to constructionist research. Technology, Knowledge and Learning, 19(1–2), 205–220. https://doi.org/10.1007/s10758-014-9223-7.
Block, P. (2015). Reciprocity, transitivity, and the mysterious three-cycle. Social Networks, 40(October), 163–173.
Borgatti, S. P. (2005). Centrality and network flow. Social Networks, 27(1), 55–71. https://doi.org/10.1016/j.socnet.2004.11.008.
Borgatti, S. P., & Everett, M. G. (2006). A graph-theoretic perspective on centrality. Social Networks, 28(4), 466–484. https://doi.org/10.1016/j.socnet.2005.11.005.
Cadima, R., Ojeda, J., & Monguet, J. M. (2012). Social networks and performance in distributed learning communities. Educational Technology & Society, 15(4), 296–304 www.ifets.info/journals/15_4/25.pdf?
R Core Team. (2018). R: A language and environment for statistical computing. https://www.r-project.org
Csardi, G., & Nepusz, T. (2006). The igraph software package for complex network research. InterJournal, Complex Sy, 1695 http://igraph.org.
Dado, M., & Bodemer, D. (2017). A review of methodological applications of social network analysis in computer-supported collaborative learning. Educational Research Review, 22, 159–180. https://doi.org/10.1016/j.edurev.2017.08.005.
De-Marcos, L., Garciá-López, E., Garciá-Cabot, A., Medina-Merodio, J.-A. J. A., Domínguez, A., Martínez-Herraíz, J. J. J.-J., & Diez-Folledo, T. (2016). Social network analysis of a gamified e-learning course: Small-world phenomenon and network metrics as predictors of academic performance. Computers in Human Behavior, 60(PG-312-321), 312–321. https://doi.org/10.1016/j.chb.2016.02.052.
Dillenbourg, P., Järvelä, S., & Fischer, F. (2009). The Evolution of Research on Computer-Supported Collaborative Learning BT - Technology-Enhanced Learning: Principles and Products. In N. Balacheff, S. Ludvigsen, T. de Jong, A. Lazonder, & S. Barnes (Eds.), (pp. 3–19). Netherlands: Springer. https://doi.org/10.1007/978-1-4020-9827-7_1.
Fincham, E., Gašević, D., & Pardo, A. (2018). From social ties to network processes: Do tie definitions matter? Journal of Learning Analytics, 5(2), 9–28. https://doi.org/10.18608/jla.2018.52.2.
Freeman, L. C. (1978). Centrality in social networks conceptual clarification. Social Networks, 1(3), 215–239. https://doi.org/10.1016/0378-8733(78)90021-7.
Fu, E. L. F., van Aalst, J., & Chan, C. K. K. (2016). Toward a classification of discourse patterns in asynchronous online discussions. International Journal of Computer-Supported Collaborative Learning, 11(4), 441–478.
Gaševi, D., Dawson, S., & Siemens, G. (2015). Let ’ s not forget : Learning analytics are about learning course signals : Lessons learned. TechTrends, 59(1), 64–71. https://doi.org/10.1007/s11528-014-0822-x.
Gašević, D., Dawson, S., Rogers, T., Gasevic, D., Ga, D., Dawson, S., Rogers, T., Gasevic, D., Gasevic, D., Dawson, S., Rogers, T., Gasevic, D., Ga, D., Dawson, S., Rogers, T., & Gasevic, D. (2016). Learning analytics should not promote one size fits all: The effects of instructional conditions in predicting academic success. Internet and Higher Education, 28, 68–84. https://doi.org/10.1016/j.iheduc.2015.10.002.
Hennessy, S., & Murphy, P. (1999). The potential for collaborative problem solving in design and technology. International Journal of Technology and Design Education, 9(1), 1–36.
Hernández-García, Á., González-González, I., Jiménez-Zarco, A. I., & Chaparro-Peláez, J. (2015). Applying social learning analytics to message boards in online distance learning: A case study. Computers in Human Behavior, 47(PG-68-80), 68–80. https://doi.org/10.1016/j.chb.2014.10.038.
Hershkovitz, A. (2015). Towards data-driven instruction. Technology, Instruction, Cognition and Learning, 10, 1–4.
Hong, H.-Y., Scardamalia, M., & Zhang, J. (2010). Knowledge society network: Toward a dynamic, sustained network for building knowledge. Canadian Journal of Learning and Technology/La Revue Canadienne de l’apprentissage et de La Technologie, 36(1).
Joksimovic, S., Manataki, A., Gaševic, D., Dawson, S., Kovanovic, V., & De Kereki, I, F. (2016). Translating network position into performance: Importance of centrality in different network configurations. ACM international conference proceeding series, 25–29-Apri (PG-314-323), 314–323. https://doi.org/10.1145/2883851.2883928.
Kovanović V., Gašević D., Dawson S., Baker R. S., Hatala M., (2015). Does time-on-task matter? Implications for the validity of learning analytics findings. Journal of Learning Analytics, 2(3), 81–110. https://doi.org/10.18608/jla.2015.23.6
Kreijns, K., Kirschner, P. A., & Vermeulen, M. (2013). Social aspects of CSCL environments: A research framework. Educational Psychologist, 48(4), 229–242. https://doi.org/10.1080/00461520.2012.750225.
Liao, H., Mariani, M. S., Medo, M., Zhang, Y. C., & Zhou, M. Y. (2017). Ranking in evolving complex networks. Physics Reports, 689(April), 1–54. https://doi.org/10.1016/j.physrep.2017.05.001.
Liu, Z., Kang, L., Domanska, M., Liu, S., Sun, J., & Fang, C. (2018). Social network characteristics of learners in a course forum and their relationship to learning outcomes. CSEDU 2018 - proceedings of the 10th international conference on computer supported education, 1(PG-15-21), 15–21. https://doi.org/10.5220/0006647600150021.
Liu, S., Chai, H., Liu, Z., Pinkwart, N., Han, X., & Hu, T. (2019). Effects of proactive personality and social centrality on learning performance in SPOCs. CSEDU 2019 - proceedings of the 11th international conference on computer supported education, 2(PG-481-487), 481–487. https://doi.org/10.5220/0007756604810487.
Lockyer, L., Heathcote, E., & Dawson, S. (2013). Informing pedagogical action: Aligning learning analytics with learning design. American Behavioral Scientist, 57(10), 1439–1459. https://doi.org/10.1177/0002764213479367.
Loken, E., & Gelman, A. (2017). Measurement error and the replication crisis. Science, 355(6325), 584–585.
Lü, L., Chen, D., Ren, X. L., Zhang, Q. M., Zhang, Y. C., & Zhou, T. (2016). Vital nodes identification in complex networks. Physics Reports, 650, 1–63. https://doi.org/10.1016/j.physrep.2016.06.007.
Lu, O. H. T., Huang, J. C. H., Huang, A. Y. Q., & Yang, S. J. H. (2017). Applying learning analytics for improving students engagement and learning outcomes in an MOOCs enabled collaborative programming course. Interactive Learning Environments, 25(2), 1–15. https://doi.org/10.1080/10494820.2016.1278391.
Martínez-Monés, A., Harrer, A., & Dimitriadis, Y. (2011). An Interaction-Aware Design Process for the Integration of Interaction Analysis into Mainstream CSCL Practices BT - Analyzing Interactions in CSCL: Methods, Approaches and Issues. In S. Puntambekar, G. Erkens, & C. Hmelo-silver (Eds.), (pp. 269–291). US: Springer. https://doi.org/10.1007/978-1-4419-7710-6_13.
Näykki, P., Järvelä, S., Kirschner, P. A., & Järvenoja, H. (2014). Socio-emotional conflict in collaborative learning-a process-oriented case study in a higher education context. International Journal of Educational Research, 68, 1–14. https://doi.org/10.1016/j.ijer.2014.07.001.
Noroozi, O., Järvelä, S., & Kirschner, P. A. (2019). Introduction paper special issue computers in human behavior multidisciplinary innovations and technologies for facilitation of self-regulated learning. Computers in Human Behavior, 100, 295–297. https://doi.org/10.1016/j.chb.2019.07.020.
Opsahl, T. (2009). Structure and evolution of weighted networks. University of London Queen Mary College, 104–122. http://toreopsahl.com/publications/thesis/
Opsahl, T., Agneessens, F., & Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks, 32(3), 245–251. https://doi.org/10.1016/j.socnet.2010.03.006.
Osatuyi, B. J., & Passerini, K. (2016). Twittermania: Understanding how social media technologies impact engagement and academic performance of a new generation of learners. Communications of the Association for Information Systems, 39(1 PG-509–528), 509–528.
Putnik, G., Costa, E., Alves, C., Castro, H., Varela, L., & Shah, V. (2016). Analysing the correlation between social network analysis measures and performance of students in social network-based engineering education. International Journal of Technology and Design Education, 26(3 PG-413–437), 413–437. https://doi.org/10.1007/s10798-015-9318-z.
Reychav, I., Raban, D. R., & McHaney, R. (2018). Centrality measures and academic achievement in computerized classroom social networks: An empirical investigation. Journal of Educational Computing Research, 56(4), 589–618. https://doi.org/10.1177/0735633117715749.
Rienties, B., Tempelaar, D., Van den Bossche, P., Gijselaers, W., & Segers, M. (2009). The role of academic motivation in computer-supported collaborative learning. Computers in Human Behavior, 25(6), 1195–1206. https://doi.org/10.1016/j.chb.2009.05.012.
Rodríguez-Triana, M. J., Martínez-Monés, A., Asensio-Pérez, J. I., & Dimitriadis, Y. (2013). Towards a script-aware monitoring process of computer-supported collaborative learning scenarios. International Journal of Technology Enhanced Learning, 5(2), 151–167. https://doi.org/10.1504/IJTEL.2013.059082.
Rogers, T., Dawson, S., & Gašević, D. (2016). Learning analytics and the imperative for theory-driven research. The SAGE Handbook of E-, January 2016.
Romero, C., López, M. I., Luna, J. M., & Ventura, S. (2013). Predicting students’ final performance from participation in on-line discussion forums. Computers and Education, 68, 458–472. https://doi.org/10.1016/j.compedu.2013.06.009.
Saqr, M. (2015). Learning analytics and medical education. International Journal of Health Sciences, 9(4), v–vi.
Saqr, M. (2018). A literature review of empirical research on learning analytics in medical education. International Journal of Health Sciences, 12(2), 80–85.
Saqr, M., & Alamro, A. (2019). The role of social network analysis as a learning analytics tool in online problem based learning. BMC Medical Education, 19(1), 1–11. https://doi.org/10.1186/s12909-019-1599-6.
Saqr, M., Fors, U., & Nouri, J. (2018a). Using social network analysis to understand online problem-based learning and predict performance. PLoS One, 13(9), e0203590. https://doi.org/10.1371/journal.pone.0203590.
Saqr, M., Fors, U., & Tedre, M. (2018b). How the study of online collaborative learning can guide teachers and predict students’ performance in a medical course. BMC Medical Education, 18(1), 1–14. https://doi.org/10.1186/s12909-018-1126-1.
Saqr, M., Fors, U., Tedre, M., & Nouri, J. (2018c). How social network analysis can be used to monitor online collaborative learning and guide an informed intervention. PLoS One, 13(3), 1–22. https://doi.org/10.1371/journal.pone.0194777.
Saqr, M., Fors, U., & Nouri, J. (2019a). Time to focus on the temporal dimension of learning: A learning analytics study of the temporal patterns of students’ interactions and self-regulation. International Journal of Technology Enhanced Learning, 11(4), 398. https://doi.org/10.1504/ijtel.2019.10020597.
Saqr, M., Nouri, J., & Jormanainen, I. (2019b). A learning analytics study of the effect of group size on social dynamics and performance in online collaborative learning. In M. Scheffel, J. Broisin, V. Pammer-Schindler, A. Ioannou, & J. Schneider (Eds.), Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics): Vol. 11722 LNCS (pp. 466–479). Springer International Publishing. https://doi.org/10.1007/978-3-030-29736-7_35.
Schneider, B., & Pea, R. (2014). Toward collaboration sensing. International Journal of Computer-Supported Collaborative Learning, 9(4), 371–395.
Shafie, T. (2015). A multigraph approach to social network analysis. Journal of Social Structure, 16.
Siemens, G., & Long, P. (2011). Penetrating the fog: Analytics in learning and education. Educause Review, 46(5), 30.
Smaldino, P. E., & McElreath, R. (2016). The natural selection of bad science. Royal Society Open Science, 3(9), 160384. https://doi.org/10.1098/rsos.160384.
Stahl, G., Koschmann, T., & Suthers, D. (2014a). Cambridge handbook of the learning sciences. Computer-supported collaborative learning: An historical perspective. In Cambridge Handbook of the Learning Sciences (pp. 409–426). https://doi.org/10.1145/1124772.1124855.
Stahl, G., Koschmann, T., & Suthers, D. (2014b). Computer-supported collaborative learning. In R. K. Sawyer (Ed.), The Cambridge Handbook of the Learning Sciences (pp. 479–500). Cambridge University Press. https://doi.org/10.1017/CBO9781139519526.029.
Stephenson, K., & Zelen, M. (1989). Rethinking centrality: Methods and examples. Social Networks, 11(1), 1–37. https://doi.org/10.1016/0378-8733(89)90016-6.
Südkamp, A., Kaiser, J., & Möller, J. (2012). Accuracy of teachers’ judgments of students’ academic achievement: A meta-analysis. Journal of Educational Psychology, 104(3), 743–762. https://doi.org/10.1037/a0027627.
Traxler, A, L., Gavrin, A., Lindell, R, S., Traxler, A, L., Gavrin, A., & Lindell, R, S. (2016). CourseNetworking and community: Linking online discussion networks and course success. PHYS EDUC RES CONF, PG-352-355, 352–355. https://doi.org/10.1119/perc.2016.pr.083.
Tsugawa, S., Matsumoto, Y., & Ohsaki, H. (2015). On the robustness of centrality measures against link weight quantization in social networks. Computational and Mathematical Organization Theory, 21(3), 318–339. https://doi.org/10.1007/s10588-015-9188-7.
Wei, D., Deng, X., Zhang, X., Deng, Y., & Mahadevan, S. (2013). Identifying influential nodes in weighted networks based on evidence theory. Physica A: Statistical Mechanics and its Applications, 392(10), 2564–2575. https://doi.org/10.1016/j.physa.2013.01.054.
Weinberger, A., & Fischer, F. (2006). A framework to analyze argumentative knowledge construction in computer-supported collaborative learning. Computers and Education, 46(1), 71–95. https://doi.org/10.1016/j.compedu.2005.04.003.
Wise, A. F., & Cui, Y. (2018). Unpacking the relationship between discussion forum participation and learning in MOOCs: Content is key. In ACM international conference proceeding series, PG-330-339 (pp. 330–339). https://doi.org/10.1145/3170358.3170403.
Wise, A. F., & Schwarz, B. B. (2017). Visions of CSCL: Eight provocations for the future of the field. International Journal of Computer-Supported Collaborative Learning, 12(4), 423–467. https://doi.org/10.1007/s11412-017-9267-5.
Wise, A, F., Cui, Y., & Jin, W, Q. (2017). Honing in on social learning networks in MOOC forums. Proceedings of the Seventh International Learning Analytics & Knowledge Conference on - LAK ‘17, 383–392. https://doi.org/10.1145/3027385.3027446.
Funding
Open access funding provided by University of Eastern Finland (UEF) including Kuopio University Hospital.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saqr, M., Viberg, O. & Vartiainen, H. Capturing the participation and social dimensions of computer-supported collaborative learning through social network analysis: which method and measures matter?. Intern. J. Comput.-Support. Collab. Learn 15, 227–248 (2020). https://doi.org/10.1007/s11412-020-09322-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11412-020-09322-6