Abstract
Systemic liquidity risk, defined by the International Monetary Fund as “the risk of simultaneous liquidity difficulties at multiple financial institutions,” is a key topic in financial stability studies and macroprudential policy-making. In this context, the complex web of interconnections of the interbank market plays the crucial role of allowing funding liquidity shortages to propagate between financial institutions. Here, we introduce a simple yet effective model of the interbank market in which liquidity shortages propagate through an epidemic-like contagion mechanism on the network of interbank loans. The model is defined by using aggregate balance sheet information of European banks, and it exploits country and bank-specific risk features to account for the heterogeneity of financial institutions. Moreover, in order to obtain the European-wide topology of the interbank network, we define a block reconstruction method based on the exchange flows between the various countries. We show that the proposed contagion model is able to estimate systemic liquidity risk across different years and countries. Results suggest that our effective contagion approach can be successfully used as a viable alternative to more realistic but complicated models, which not only require more specific balance sheet variables with high time resolution but also need assumptions on how banks respond to liquidity shocks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The global financial crisis of 2007/08 has shown how fundamental is the role of liquidity risk in the stability of the financial system. Recently, an IMF Working Paper on macroprudential stress testing has pointed out that liquidity shocks can rapidly manifest and impact the whole financial system, while bank solvency concerns tend to take more time to build up (Jobst et al. 2017). On the same line, the Bank of England (Kapadia et al. 2012) has drawn attention to the fact that “although the failure of a financial institution may reflect solvency concerns, it often manifests itself through crystallization of funding liquidity risk.” Likewise, the ECB Task Force on Systemic Liquidity (Bonner et al. 2018) has recently released a paper on the monitoring framework for liquidity risk and the use of macroprudential liquidity tools in the banking system of the European Union.
Liquidity risk can be differentiated in two main categories: funding liquidity risk and market liquidity risk. The former is related to the fact that the bank is not able to meet its liquidity needs in case of a funding shock, while the latter refers to the case where an institution is not able to buy or sell securities without a huge price impact, usually measured by the bid–ask spread. The literature has shown that while distinct in nature, the increased reliance on wholesale bank funding has made the two liquidity risks strongly connected, with possible feedback and spiral effect between the two, especially during distress periods (Brunnermeier and Pedersen 2008; Cai and Thakor 2008; Brunnermeier 2009; Bonfim and Kim 2012a, b; Drehmann and Nikolaou 2013; Jobst et al. 2017). Additionally, funding shocks may originate not only from depositor run but from the interbank funding market as well, a clear example is the case of Northern Rock in 2012. Importantly, seminal research papers on the propagation of funding liquidity shocks (Cifuentes et al. 2005; Gai and Kapadia 2010; Gai et al. 2011) have shown that an initial shock affecting a single bank has the potential to generate a domino effect that may lead to a systemic financial collapse, because of the interconnectedness of financial institutions in the funding market.
Indeed, from the viewpoint of a single bank, it is convenient to diversify investments and have many counterparties in order to minimize individual risk. However, as we have learned the hard way from the global financial crisis, the resulting complex structure of interconnections allows for the propagation and amplification of financial shocks at the systemic level (Allen and Gale 2000; Diamond and Rajan 2001; Nier et al. 2007; Haldane 2009; Cont et al. 2013; Gai and Kapadia 2010; Beale et al. 2011; Haldane and May 2011; Glasserman and Young 2016). Since then, the academic community, as well as regulators, started to adopt complex networks as underlying models of interconnectedness between financial institutions. The advantage of the network representation is to clearly and conveniently figure out all the institutions involved in the market and the topological structure of their interconnections (Cocco et al. 2009; Battiston et al. 2010; Haldane 2013; Bardoscia et al. 2017, 2021). This has led to the rise of the “too-interconnected-to-fail” paradigm (Hüser 2015) and to the development of network-based models for financial shocks propagation (Rochet and Tirole 1996; Freixas et al. 2000; Eisenberg and Noe 2001; Furfine 2003; Gai et al. 2011; Upper 2011; Battiston et al. 2012; Elsinger et al. 2013; Rogers and Veraart 2013; Thurner and Poledna 2013; Bardoscia et al. 2015; Acemoglu et al. 2015; Amini et al. 2016; Barucca et al. 2020), while more attention has been devoted to the interplay between the shock spreading dynamics and the underlying topology of the network (Ramadiah et al. 2020). Note that despite its fundamental relevance in macroprudential policy and financial stability analysis, funding liquidity contagion has received much less attention in the literature than market liquidity or solvency contagion.
This work belongs to this line of research, by proposing an effective model for the propagation of liquidity shocks as an epidemic disease spreading over the interbank market network (Toivanen 2013; Philippas et al. 2015; Brandi et al. 2018). To this end, we have adapted the classical susceptible-infected (SI) compartment models of epidemiology to the framework of funding and market liquidity contagion. In particular, we have built on the model by Brandi et al. (2018), introducing banks’ heterogeneity in contagiousness and vulnerability depending on bank-specific properties (country of jurisdiction, size, loan volumes, and liquidity resilience). Our model only requires aggregated balance sheet exposure data, which are extracted for a set of European banks from the Bankscope dataset (Battiston et al. 2016). As another difference from previous attempts, we have modeled the interbank network at the European level using a block structure, with each community representing the internal market of a country and intra-community relations representing cross-border claims. Since interbank network data are typically privacy-protected and thus not available, we have employed a physics-inspired reconstruction method (Cimini et al. 2015; Squartini et al. 2018) that takes as input the aggregated balance sheet exposure data (again provided by Bankscope). We have developed a new improved technique to generate block networks, by imposing as additional constraints the aggregate cross-border banking claims that we extract from the Bank of International Settlement database.
The aim of the model is to assess systemic liquidity risk, defined by the IMF (Monetary and Capital Markets Department 2011) as “the risk of simultaneous liquidity difficulties at multiple financial institutions.” In a nutshell, model simulations for the time period 2006–2013 confirm that for the European interbank market, systemic funding liquidity risk started to build up during the global financial crisis but escalated in particular during the European sovereign debt crisis. We remark that our framework is to all effects an effective model, based on i) a simplification of liquidity shocks dynamics using a contagion process, and ii) an ensemble representation of the underlying interbank network. Both these ingredients require only aggregate balance sheet information, as well as a few model assumptions and parameters, similarly to, e.g., the approaches by Eisenberg and Noe (2001) and Battiston et al. (2012) that deal with solvency contagion. Data requirement in particular is indeed a major advantage of our model with respect to more sophisticated approaches (Krause and Giansante 2012; Manna and Schiavone 2012; Aldasoro et al. 2017; Halaj 2018; Smaga et al. 2018; Teply and Klinger 2019; Cont et al. 2020), which require not only more specific balance sheet variables (for instance, exposures split according to the seniority or type of contract—repurchase agreements, derivatives, CDS, and so on) with high time resolution, but also several assumptions to define an agent-based response of banks to shocks.
Let us also stress that the proposed model is intended to measure systemic risk in the market at a given time stemming from the structure of banks’ balance sheet and of the interbank network, regardless of whether or not a liquidity crisis occurred at that time. We do not aim at predicting the dynamics of a possible crisis unfolding in the interbank market, for two main reasons: i) we cannot predict when and where an exogenous shock would hit the market, and if its size would trigger a chain of contagion; ii) the model does not include the possibility that banks reallocate assets nor of external interventions by central banks or governments, which instead happen in reality reducing liquidity problems and thus contagion. Instead our model is appropriate for measuring potential losses in a worst-case scenario, similarly to regulatory stress tests.
The rest of the paper is structured as follows. Section 2 introduces the epidemic-like liquidity contagion processes. Section 3 illustrates the data used to inform the model, and Sect. 4 presents the network reconstruction method. Section 5 contains the results of both the reconstruction procedure and of the liquidity-driven dynamics. Section 6 is devoted to final remarks and conclusions.
2 Liquidity contagion model
The idea of using an epidemiological model to describe financial contagion derives from the conceptual similarity between the diffusion of a disease in a population and the spreading of financial losses within a market. As we know, in both cases, the process is heavily influenced by the topology of the underlying network of connections (Pastor-Satorras et al. 2015; Bardoscia et al. 2021). Adapting the toolkit of epidemic modeling to finance ultimately means assuming that financial shocks propagate as an epidemic disease over the interbank market. There are already a few studies in the literature that use this approach to model credit-driven (Toivanen 2013; Philippas et al. 2015) or liquidity-driven (Brandi et al. 2018) contagion. In this work, we focus on contagion due to banks’ liquidity hoarding causing liquidity shortages to their counterparties. We build on the model by Brandi et al. (2018), further enhancing it by considering banks’ heterogeneity. Indeed, each bank has a different financial structure and it operates in a specific country; both features are important in order to determine the bank’s riskiness and vulnerability to financial contagion. Before introducing the detailed model formulation, it is useful to explain how losses can spread in the interbank market.
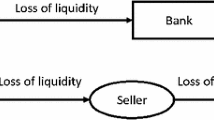
The primary function of the interbank market is to allow banks to cope with liquidity fluctuations by quickly getting funds through interbank lending (Iori et al. 2006; Finger et al. 2013; Gabbi et al. 2015). Such borrowed liquidity allows these banks to temporarily meet reserve requirements without having to sell their illiquid assets. While the typical duration of these loans is overnight (meaning that the borrower must repay the lender at the start of the next business day), usually banks’ liquidity shortages last longer than 1 day, so these overnight loans are rolled-over the day after. This mechanism generates roll-over risk: when for some reason a bank cannot find all the liquidity needed in the interbank market, it will stop lending to other banks, in turn causing further funding shortages. Additionally, distressed banks may be forced to sell their assets; large volumes of illiquid assets sales (the so-called fire sales) may then trigger further losses and sales, in a downward spiral of assets price (Diamond and Rajan 2011; Cont and Wagalath 2016). Besides, if other banks perceive these or other financial turmoils, they may start liquidity hoarding (particularly toward banks perceived as unhealthy) due to lack of trust and fear of contagion (Brunnermeier 2009; May and Arinaminpathy 2009). All these mechanisms can induce subsequent waves of liquidity shortages (Anand et al. 2012) and then to an overall reduction in bank funding supply on the interbank market. This is precisely what happened during the global financial crisis: the default of Lehman Brothers in 2008 triggered a chain of liquidity shocks that caused a market freeze and a liquidity drought.Footnote 1 Overall, researchers by Bank of England (Kapadia et al. 2012) identified five different channels that allow liquidity shocks to propagate in the interbank market—see Fig. 1:
-
1.
Reputations shocks and negative feedback loops;
-
2.
Liquidity hoarding;
-
3.
Asset prices depreciation (market liquidity risk);
-
4.
Confidence contagion (run on banks similar to defaulted ones);
-
5.
Counter-party credit risk.
Channels of liquidity risk in the interbank funding market. Source: Bank of England (Kapadia et al. 2012)
The model we are proposing in the paper is based on funding liquidity risk. This means that we do not consider credit risk (channel 5), while we do consider market liquidity risk (channel 3) as an amplification mechanism rather than a contagion channel.
The contagion process we present is an adaption of the SI (Susceptible-Infected) model with two different infectious compartments, corresponding to two levels of liquidity distress. Note that we do not consider the possibility of recovering, as we suppose the time scale of the contagion spreading to be much shorter than the time an infected bank would need to sort out its liquidity problems by, e.g., reallocating its assets.Footnote 2 In other words, an infected bank remains contagious because the recovery procedure needs longer times than the duration of the considered dynamics. Overall, we have an EDB (Exposed-Distressed-Bankrupted) compartment model, whose dynamics proceeds in discrete time steps. At each step t, a bank can be in one of the three possible states E, D, B. Susceptible (Exposed, E) banks are those that have obtained all the liquidity they need from the interbank market. Infected (Distressed, D or Bankrupted, B) banks instead are those that, due to liquidity shortages, have withdrawn some of their interbank lending. Contagion spreads from an infected (either D or B) lender i to an exposed (E) borrower j, since the withdrawn of i’s lending may cause liquidity issues for j, in which case j becomes distressed (D) and contagious for its lending counterparties. When liquidity issues become overwhelming, a bank i may turn from the distressed (D) to bankrupted (B) state.
Brandi et al. (2018) define the probability of contagion from a distressed or bankrupted bank i to an exposed bank j as follows:Footnote 3
where \(w_{ij}\) is the amount of the loan between the lender i and the borrower j, while \({\mathcal {B}}_i\) is the set of i’s borrowers. The economic rationale behind this contagion rate specification is that the probability that the funding shock is transmitted is proportional to the amount of money i lends to j with respect to i’s total interbank lending volume.
The bankruptcy rate of bank i (that is, the probability that a distressed i becomes bankrupt) instead depends on its current liquidity provision and is defined as follows:
where \({\mathcal {L}}_i\) is the set of lenders of i, while \({\mathcal {I}}_i(t)\) is the set of those lenders that are distressed and bankrupted at time step t. \(\mu _{i}(t)\) is thus the fraction of liquidity bank i needs that was previously lent by infected banks, and sums up the volume of shocks received by i. The underlying idea is that when liquidity losses are overwhelming, a bank goes bankrupt since it has no possibility to reallocate its assets and absorb quickly the losses.
Note that according to Eq. (1), the contagion rate is independent of the specific features of the involved banks. To make the model more realistic, we assume that liquidity shocks are more likely to originate from banks with higher liquidity risk and operating in countries with a more fragile economy (Panetta et al. 2011). To incorporate these features in the model, we redefine the contagion rate as follows:
where \(\gamma _i \in [-1,1]\) is a node-specific variable, introducing in the equation a dependence on the features of the infected lender bank i. The functional form of Eq. (3) ensures the contagion rate to be always bounded between 0 and 1 (since \(0<\lambda _{ij}\le 1\) by definition). In particular, the contagion rate tends to 1 as \(\gamma _i\rightarrow 1\), while it gets smaller as \(\gamma _i\rightarrow -1\).Footnote 4 In the neutral case \(\gamma _i=0\), we recover the contagion rate of Brandi et al. (2018), which we use as a benchmark model.
We define the node variable \(\gamma _i\) as a combination of a bank-specific liquidity risk measure and a country-specific risk measure. Regarding the former, we use the following liquidity indicator:
where \(T_i\), \(E_i\) and \(F_i\) are, respectively, the values of total assets, the equity and a proxy of banks’ liquid assets for bank i.Footnote 5 This indicator is inspired by the regulatory liquidity (coverage) ratio, or LCR, given by liquid assets over liabilities due to be repaid. As the LCR, the larger the liquidity indicator is, the better the liquidity position of the bank. Indeed, liquid assets are the first defense that banks have against liquidity shocks. Instead, regarding the country-specific risk, we use as a proxy the bid–ask spread \(\delta _P\) of government bonds, which is a popular measure of market liquidity:
where \(B_P\) is the bid price of the 10-year government bond, defined as the highest price that a buyer is willing to pay for the bond, while \(A_P\) is the ask price, that is, the lowest price that a seller is willing to accept in order to sell the bond. A high value of this measure indicates lower liquidity, while a lower value signals higher liquidity in the market. The European Central Bank has recently released a paper on systemic liquidity (Bonner et al. 2018), stating that such a measure “shows a clear distinction between periods of stress and periods of more benign market conditions.”
In order to combine \(Liq_i\) and \(\delta _P\) into a node variable \(\gamma _i\) defined in the interval \([-1,1]\), we use the following transformation:
where x is a generic variable and m(x) is the median of x. As x, we use the ratio between the country and the liquidity risk of bank i.Footnote 6 The motivation for using this ratio is to have an amplification mechanism between the country liquidity risk and the bank liquidity structure, so that a solid bank liquidity structure would imply a contraction of the country risk, while a fragile structure would magnify it. Overall, the node variable \(\gamma _i\) of bank i is thus defined as:
where the transformation \(f(\cdot )\) (which is symmetric around the median) allows to discern between banks that are more contagious from banks that are less contagious with respect to the benchmark model.
We further enrich our framework by considering a bankruptcy rate that depends on bank’s liquidity resilience. Indeed, the transition from the distressed to the bankrupted state depends not only on the volume of liquidity shocks received by the bank but also on the bank’s capability to absorb these shocks. We thus redefine the bankruptcy rate as follows:
where \(\nu _i \in [-1,1]\) represents the rescaled liquidity resilience indicator of bank i. The latter is defined as:
where \(L_i\) are the interbank liabilities and \(F_i\) is the liquidity proxy of bank i. This indicator thus quantifies the capability of a bank to absorb liquidity shocks using liquid assets. As for the contagion rate, the default rate is amplified when \(\nu _i>0\) and decreases when \(\nu _i<0\). Note that this model specification does not alter the asymptotic stage of the dynamics but only the speed at which this stage is reached.
As noted in an IMF Working Paper on macroprudential stress testing (Jobst et al. 2017), “liquidity crises are partly attributable to psychological factors or confidence effects.” As previously discussed, funding contagion can propagate from lenders to borrowers when lenders decide to stop funding their borrowers. This can happen not only because lenders are distressed and cannot lend liquidity, but also because borrowers are distressed and therefore lenders perceive them as too risky investments. While we model the former mechanism explicitly through Eq. (1), the latter is more tricky since it requires banks to know the state of their counterparties. We therefore consider this second mechanism as a global tendency to hoard liquidity, depending on the health state of the whole system. This is achieved by introducing the variable \(\theta (t)\), which we call systemic risk multiplier, capturing the pressure exerted by the presence of distressed or defaulted banks on the whole market:
where e(t), d(t), b(t) are the fraction of banks, respectively, in the exposed, distressed and bankrupted state at time step t, \(\beta _*\) is a tunable parameter (see Sect. 5.2.5 for further discussion), and the last equality derives from the identity \(e(t)+d(t)+b(t)=1\) \(\forall t\). The systemic risk multiplier enters in the equation for the contagion rate, making it dependent on the current global state of the market:Footnote 7
According to this equation, we have that when \(e(t)=e_*\equiv (1+\beta _*)^{-1}\), then \(\theta (t)=1\) and the contagion rate becomes \(\lambda _{ij}^{*}\) of Eq. (3). When distressed and bankrupted banks are many (so that \(e(t)<e^*\)), then we have a lower value of \(\theta <1\), which increases the contagion rate and speeds up the infection spreading. Conversely, when distressed and bankrupted banks are few (so that \(e(t)>e^*\)), then we have a higher value of \(\theta >1\) that corresponds to a smaller contagion rate and a slower infection spreading.
3 Data
In this section, we present the three data sources that we use in our model. In summary, banks’ balance sheets were collected from the Bankscope dataset; countries’ bid–ask spreads were obtained from Bloomberg; cross-border banks claims were collected from Bank of International Settlements.
3.1 Bankscope balance sheets
Bureau Van Dijk Bankscope database contains information on banks’ balance sheets and aggregate exposures. Here, we consider \(N=97\) anonymized European banks that were publicly traded between 2006 and 2013Footnote 8 (Battiston et al. 2016). For these banks, we have access to yearly values of total interbank assets, total interbank liabilities, total assets, equities, total customer deposits, total deposits, money market, short-term funding and derivatives, plus we know the country in which each bank is based. Overall, these 97 banks represent nine different EU countries: Austria (AT), France (FR), Germany (DE), Great Britain (GB), Greece (GR), Italy (IT), Portugal (PT), Spain (ES) and Sweden (SE). Figure 2 reports the number of banks in our dataset for each of these countries, while Fig. 3 reports the fraction of total asset, interbank assets and interbank liabilities aggregated for each country, in two representative years of the dataset (2007 and 2012). Notice that a higher number of banks for a specific country does not directly translate to a higher contribution of assets and liabilities in the market. For example, Great Britain has higher figures relative to Italy, even if it is represented by less than half of the banks. On the contrary, Germany seems to be under-represented in terms of total assets; this is probably due to the absence of the biggest German banks in our dataset.
Of the different balance sheet variables collected for each bank i, interbank assets \(A_i\) and liabilities \(L_i\) are crucial to reconstruct the individual exposures between banks (see Sect. 4 below). Additionally, these and other variables (total assets \(T_i\), equity \(E_i\), liquid assets \(F_i\)) are used to define the various bank-specific indicators we use in our model. Figure 4a reports the liquidity indicator \(Liq_i\) of Eq. (4), which together with the bid–ask spread (see below) affects the contagion rate. This indicator is close to one for most of the banks except four; a liquidity shock hitting these banks could easily spread the infection to their neighbors. Figure 4b instead reports the liquidity resilience indicator \(L_i/F_i\) (the variable entering into Eq. (9)), which can speed up or slow down the default of a bank. This indicator is consistently high for a few banks, which thus have a very small liquidity buffer to absorb liquidity shocks.
3.2 Bloomberg bid–ask spreads
Bid and ask prices of 10-year government bonds were collected from Bloomberg.Footnote 9 We have collected end-of-the-year values for the same set of countries and time periods of Bankscope data. The bid–ask spread of Eq. (5) is a widely adopted measure of market liquidity. In normal times, this spread mostly synthesizes market structural features, while during distress periods, it becomes a responsive indicator of liquidity tightness (market liquidity risk) (Kyle 1985; Iachini and Nobili 2016): a high spread indicates lower liquidity, while a lower spread indicates higher liquidity in the market. Figure 5 shows bid–ask spreads for the countries in our dataset. Some countries (the so-called PIGS: Portugal, Italy, Spain, Greece) consistently have higher spreads than others; banks locate in these countries suffer more from liquidity risk and they can more likely cause a systemic event through network contagion.
3.3 BIS cross-border claims
Cross-country interbank exposures, namely the aggregate exposures between the banking sectors of pairs of countries, are obtained using the consolidated banking statistics from the Bank for International Settlements (BIS)Footnote 10. In particular, BIS data consist of (quarterly) amounts of money that banks in country U have lent to banks in country V, hereinafter \(exp_{UV}\). Note that due to several missing values in the BIS dataset during 2006–2013 for the nine EU countries we consider, we use the exposure data of 2013-Q4, which is the quarter with fewer missing values.Footnote 11
Figure 6 reports the rescaled BIS volumes defined as follows:
This figure shows that (i) there is a strong home bias, as banks preferentially lend to banks of the same country rather than to foreign banks, and (ii) there is a large heterogeneity of foreign exposures among countries. As explained in the following section, we will incorporate countries’ preferential lending in the network reconstruction procedure, so to generate a network with a block structure where each block represents the exposure between two countries.
4 Network reconstruction
In this section, we explain how we deal with the problem of missing information on interbank networks. Indeed, data about the individual bilateral exposures in the market (who lends to whom and how much) is typically not available because of privacy issues. Several methods have thus been proposed to infer the network structure from the publicly available information, that is, the aggregated balance sheet variables—see Squartini et al. (2018) and Anand et al. (2018) for recent reviews of the topic.
4.1 Constrained maximum entropy and fitness model
Here, we will exploit the reconstruction methods that rely on the principle of constrained entropy maximization (Cimini et al. 2015). The rationale behind this approach is to maximize the Shannon entropy, which represents our ignorance on the system, while constraining the information that we know (in our case, the aggregate exposures of each bank). In this way, we follow the recipe provided by Information Theory and avoid making any unsupported assumption on the system (Cimini et al. 2019). However, as additional step in order to reconstruct a realistic and sparse network configuration, we need to find out how to estimate the actual number of bilateral exposures for each bank from its aggregate exposure volumes.Footnote 12 This step is achieved assuming a functional relationship (or at least a strong correlation) between the number of connections and total exposure volume of a bank—an approach known as fitness model (Caldarelli et al. 2002). Overall, the network reconstruction approach consists of the two following steps: (1) infer the binary network topology (that is, the presence of individual links) using constrained entropy maximization and fitness model, and (2) assign weights to realized links according to balance sheet constraints. These steps are summarized as follows (see Cimini et al. (2015); Squartini et al. (2017) for full model details).
Technically, to realize step (1), one needs to define an ensemble of directed networks with N nodes, and estimate the occurrence probability of each network within the ensemble. This is done by maximizing the Shannon entropy of this probability distribution, using as constraints the number of outgoing and incoming connections for each node i (respectively the out-degree \(k_i^{\rightarrow }\) and in-degree \(k_i^{\leftarrow }\) of each i). These constraints are enforced using a set of parameters known as Lagrange multipliers: for each node i, we have a multiplier \(\omega _i^{\rightarrow }\) for \(k_i^{\rightarrow }\) and a multiplier \(\omega _i^{\leftarrow }\) for \(k_i^{\leftarrow }\). At this point, in order to obtain the numerical values of the multipliers that define the ensemble, we need the empirical values of the degrees, which are unfortunately unavailable. Therefore, we make a fitness ansatz that these multipliers are linearly proportional to interbank assets and liabilities: these balance sheet variables are assumed to determine the bank’s connectivity. In mathematical terms, this ansatz translates to \(\omega _i^{\rightarrow }\propto A_i\) and \(\omega _i^{\leftarrow }\propto L_i\), where \(A_i\) and \(L_i\) are the interbank assets and liabilities of bank i, respectively. In this way, we can express the ensemble probability that a connection is established from lender bank i to borrower bank j simply as:
The value of the free parameter z is found imposing that the average connection probability between two nodes is equal to a tunable parameter \(\rho \) representing the density of the network (defined as the number of realized connections over the maximum number of allowed connections in the network):
Step (2) then consist in the numerical generation of weighted network configurations. In order to build a single network instance, for each ordered pair (i, j) of nodes, we draw a connection \(i\rightarrow j\) using Eq. (13):
where \(a_{ij}\) is the (i, j) element of the binary adjacency matrix of the network. At last, the weight \(w_{ij}\) of the connection \(i\rightarrow j\) (which is the input of the contagion model defined above) is estimated using the following degree-corrected gravity model recipe:
where \(W=\sqrt{(\sum _iA_i)(\sum _i L_i)}\) is a normalization term representing the total volume of the market. Note that in general the market is not “closed,” as banks can have external interbank exposures, in which case \(\sum _i A_i \ne \sum _i L_i\). Typically, total interbank liabilities are larger than total interbank assets. In order to fix this issue, we introduce in the system a ground bankFootnote 13 acting as an external lender, i.e., whose total interbank assets are given by \(A_{gb}=\sum _i (L_i-A_i)\ge 0\), while \(L_{gb}=0\). By adding the ground bank we have \(W=\sum _iA_i=\sum _i L_i\), whence Eq. (16) properly ensures that for each bank, the ensemble averages of interbank assets and liabilities sum up to their aggregate value as prescribed by the balance sheet:
Lastly, we note that the above relations are satisfied exactly only when the network admits self-loops, namely links that connect nodes with themselvesFootnote 14. To get rid of these self-loops, we employ the iterative proportional fitting algorithm (IPF) defined on top of the degree-corrected gravity model (Squartini et al. 2017). This method redistributes the diagonal terms \(\sum _i w_{ii}\) over the other realized connection in the network, in order to still preserve the constraints of total interbank assets and liabilities. Thanks to the IPF, such constraints are reproduced exactly (and not only on average) for each network in the ensemble.
In a recent paper, Anand et al. (2018) tested the performance of different reconstruction methods using a set of empirical bilateral data obtained from 25 markets spanning 13 jurisdictions (including interbank networks, payment networks, networks of repurchase agreements, foreign exchange derivatives, credit default swaps, and equities). They show that the method of Cimini et al. (2015) that we exploit here has a very high performance, and is “the clear winner among ensemble methods.”
4.2 Block reconstruction
Most of the reconstruction methods proposed so far (with the exception of Hałaj and Kok (2013)) were designed to infer the interbank market of a single jurisdiction. This happened because empirical data to test the goodness of the reconstruction are available only at the national level (for a few countries), while aggregate data broken down by country counterparties are available only for cross-border banking claims (source: BIS, see Sect. 3.3). Nevertheless, we have seen that at least for Europe, banks preferentially lends to counterparties of the same country, and this pattern results in an international interbank network with a marked block-diagonal structure.
In this section, we thus extend the reconstruction method discussed above to reproduce such country-specific blocks in the network. To this end, we will exploit the BIS volumes of inter- and intra-country exposures as additional constraints in the reconstruction procedure. So we split banks into groups corresponding to their home countries, and define network blocks that are reconstructed separately as illustrated below. Consider the block UV representing the lending relationship from banks of country U to banks of country V. From BIS data, we have \(exp_{UV}\), the aggregate amount of such exposures. We use this information to define the interbank assets and liabilities of bank i in the block UV as:
The rationale is that the exposures of the banks are rescaled according to the fractional exposure of home country U with respect to country V. Indeed, these relations satisfy \(\sum _V \tilde{A_i}^{UV}=A_i\) and \(\sum _U \tilde{L_i}^{UV}=L_i\). We can thus define the block-specific probability matrix and weight matrix, analogously to Eqs. (13) and (16):
where \(W^{UV}=\sqrt{(\sum _i\tilde{A_i}^{UV})(\sum _j \tilde{L_j}^{UV})}\). Again the free parameter z is found by solving the equation:
Note that imposing the same value of z in each block is the simplest assumption that requires only the average value of the network density \(\rho \). An alternative choice would be to use block-specific parameters \(z_{UV}\) found by \(\langle p^{UV}_{i\rightarrow j} \rangle _{i\in U,j\in V}=\rho ^{UV}\), an approach that however requires block-specific density values \(\rho ^{UV}\).
5 Results
We now present the results of the model. We first focus on how banks’ bilateral exposures are reconstructed from aggregated data. This is an important point to assess since such reconstructed networks constitute the underlying topology of the contagion spreading. Then, we present results of the epidemic-like contagion model under different scenarios and parameter choices. For the sake of readability, we report in the main text only plots related to two representative years, 2007 and 2012. Plots for other years in the period 2006–2013 are available in the electronic supplementary materials.
5.1 Reconstructed network
In order to generate the reconstructed network we have to assume a density value of the interbank network. We use \(\rho =0.3\)Footnote 15 assuming a constant value over the considered years 2006–2013. Using this density we generated, for each year, an ensemble of 1000 weighted directed networks.
Figure 7 shows the weighted adjacency matrices obtained as ensemble averages, for the standard reconstruction method (Eqs. (13) and (16)) and for the block reconstruction (Eqs. (19) and (20)). By sorting banks according to their size (as measured by total assets), the network exhibits a core-periphery structure, analogously to real interbank topology (Finger et al. 2013; Fricke and Lux 2015; Craig and Von Peter 2014). This sorting scheme however does not highlight the difference between the two reconstruction approaches.
Figure 8 shows instead the average link density of the network, when banks are grouped into country-specific blocks. While the overall density is fixed, block-specific values are not uniform due to the heterogeneity of bank and country constraintsFootnote 16. We can now see a very different pattern between the two reconstruction approachesFootnote 17. In the standard reconstruction, density values are much more uniform; in the block reconstruction, the addition of country-specific constraints allows the home lending bias to emerge.
In order to check whether the reconstruction methods are able to capture the empirical block pattern of country exposures shown in Fig. 6, we show in Fig. 9 the average rescaled cross-country volumes as of Eq. (12), computed on the reconstructed networks. As expected, a comparison between the figures clearly shows that countries’ preferential lending pattern is properly recovered only in the block reconstruction method.
Average lending volume of each block (rescaled as of Eq. (12)) for 2007 (left) and 2012 (right). Banks are sorted by country code
Finally, in order to quantify how much the reconstructed networks can reproduce the BIS cross-border claims of Fig. 6, we compute the Pearson correlation coefficient between the (logarithmic) rescaled cross-country volumes \(VOL_{UV}\) as of Eq. (12), computed on BIS data and on the reconstructed networksFootnote 18. Results for each year, shown in Fig. 10, confirm that the block reconstruction can effectively reproduce BIS cross-border exposure data (the correlation coefficients range from 0.80 to 0.88), much better than the standard reconstruction technique (whose coefficients range between 0.48 and 0.62).
Overall, results of this section show that the block reconstruction generates networks with a much more realistic structure; in the following, we will thus run the contagion model on these network configurations.
5.2 Systemic liquidity risk contagion
5.2.1 Contagion setting
As previously explained, for each year, we have generated an ensemble of 1000 weighted directed networks. For each of these networks, we run 97 stochastic SI contagion simulations, using in each run a different bank of the network as initial seed. The seed is put in the distressed state at the beginning of the simulation, which then stops when either there are no more banks in the distressed state, or 50 iterations of the contagion are reached. Unless stated otherwise, results reported below are averages over the 97000 contagion dynamics simulated for each year.
5.2.2 Contagion without node variable
In this scenario, we consider the functional form of the contagion rate \(\lambda \) already discussed in Brandi et al. (2018), i.e., the benchmark model of Eq. (1). Figure 11 shows the prevalence dynamics in 2007 and 2012, namely the fraction of banks that belong to each compartment at each time step of the contagion spreadingFootnote 19. Figure 11 reports also the asset-weighted prevalence, in which each bank weights according to the fraction of total assets owned in the considered year. The pattern of the contagion dynamics is indeed enhanced in the asset-weighted representation.
To better understand how systemic risk evolves during the years, we plot in Fig. 12 the dynamics of the bankruptcy fraction. This fraction is computed as the ratio of bankrupted banks or, in the asset-weighted case, as the fraction of total assets owned by bankrupted banks, at the end of the contagion. As the figure shows, there are only small differences among the various years. The asset-weighted fraction being around 90% means that on average the bigger banks default more frequently than the smaller ones. This is not an obvious result, since both contagion and bankruptcy rates depend on relative exposures and thus not on the bank size. However, bigger banks have higher connectivity (higher in- and out-degree): they are more prone to contagion because they are involved in several contagion paths. We recall that since our model is intended to measure potential systemic risk, the bankruptcy fraction is not intended to reproduce the number of banks that defaulted in a given year. Rather, it indicates that the structure of the market in that year had an inherent level of systemic risk capable of causing those defaults if a crisis would have broken out and spread freely.
Figure 13a reports the decomposition of the bankruptcy fraction with respect to the country in which banks are based. The plot shows that France, Italy and Great Britain are the ones that contribute the most to systemic risk. Notice that countries more represented in the dataset do not necessarily have more defaults. In fact, GB has less than half of the Italian banks and almost 50% banks less than Germany, but its contribution is comparable to the former and higher than the latter. This is because GB banks are more connected to foreign banks with respect to other countries’ banks. Moreover, Fig. 13b reports the decomposition of the asset owned by defaulted banks for each country. In this case, GB is the main contributor, even if it is not the biggest country in terms of assets and number of banks. This is because GB banks being on average big and central in the interbank market. Furthermore France, even with a large fraction of assets in defaulted banks, has an average figure per each bank smaller than other countries which are less represented in number but with a similarly consistent fraction of assets owned by bankrupted banks, e.g., Spain and Sweden. This result suggests that in some countries big banks are the ones at higher risk because of their centrality, while in other countries the risk is high for both central and peripheral banks irrespective of size.
Figure 14 shows the dynamics of the average bankruptcy rate \(\mu \) of Eq. (2), which can be interpreted as a measure of the market health. For each individual bank, \(\mu \) is defined as the fraction of liquidity the bank needs that was previously lent by infected banks. (The higher the value of \(\mu \), the larger the number of the infected lender of a bank and thus the probability to go bankrupt.) When averaged over the market, this rate provides information on the resilience of the whole system.
Dynamics of the distribution of the bankruptcy rate \(\mu \) as of Eq. (2) in 2007 and 2012. Contagion rate without node variable. The line is the mean, while the shaded area is constructed by using the box-plot whiskers’ formula, i.e., \(1^{st}\) and \(3^{rd}\) quartiles \(\pm 1.5 \times \)IQR, where IQR is the Interqurtile Range
5.2.3 Contagion with node variable
In this scenario, we consider the node variable in the functional form of the contagion rate \(\lambda \) as for Eq. (3).Footnote 20 In this way, we model heterogeneity in banks’ contagiousness, according to individual liquidity risk stemming from balance sheet structure and home country. Figure 15 shows the prevalence and the weighted prevalence dynamics in 2007 and 2012. With respect to the previous scenario (Fig. 11), the node variable caused a substantial change in the prevalence pattern. In particular, systemic risk is much higher for the unweighted case in 2012, as can be noticed by a higher fraction of bankrupted than healthy banks.
Node variable \(\gamma \) as of Eq. (7), 2006–2013
The evolution of the bankruptcy fraction over the years, shown in Fig. 16, is likewise very different from the benchmark case without node variable (Fig. 12). In particular the bankruptcy fraction, taken as a proxy of liquidity systemic risk, is much less constant over time, with a substantial increase in correspondence of the European sovereign debt crisis of 2011 (rather than of the global financial crisis of 2007–2008). This outcome can be attributed to the distribution of the node variable, reported in Fig. 17Footnote 21. Starting from 2008, the node variables on average moved upward to positive values (except for all GB and some DE banks), consequently increasing the contagion rate (mostly relevant for highly connected banks). After 2011, the bankruptcy fraction decreased in 2012, probably due to the ECB forward guidance pursued in that year to counteract the European sovereign debt crisis.
Figure 18a further shows the contribution of the various countries to the bankruptcy fraction. We can see that Italian banks provide the highest contribution to the potential systemic risk. This happens because banks operating in this country have both a high liquidity risk and a lot of interconnections, with domestic as well as foreign banks. Also France bears a large share of systemic risk, due to French banks having many links with risky banks. However, if we analyze the average risk contribution per-bank in each country (i.e., the share of bankruptcy fraction divided by the number of banks in the country), we find that Spain and Sweden are the riskiest countries, bearing a non-negligible fraction of systemic risk stemming from a small number of banks. On the contrary, with respect to the benchmark model, the contribution of GB banks is reduced. This happens because these banks have low liquidity risk. From what concerns the assets of defaulted banks decomposed by country, shown in Fig. 18b, similarly to the benchmark model, GB is the country with the highest share: even if not all the GB banks default, the ones which do are the biggest ones. Conversely for France, even if more banks default, these banks are of smaller size on average.
Moving further, Fig. 19 shows the dynamics of the bankruptcy rate \(\mu \) of Eq. (2), compared with the benchmark model of Fig. 14. We notice that during the simulation dynamics, such rate is higher for the benchmark model in 2007 but in 2012 the order is reversed. Thus, in 2012, the node variable speeds up the convergence of the dynamics: this can be due to more connected and riskier banks becoming more likely to default. Additionally, for both years, the width of the distribution increases: the bankruptcy rate is more heterogeneous across banks.
Overall, the node variables introduce heterogeneity in the model and as we have seen leading to results that are more in line with our expectations. We can conclude that both topology and country-bank features matters for a proper assessment of systemic liquidity risk.
5.2.4 Contagion and bankruptcy rates with node variable
In this scenario, we consider the liquidity resilience indicator in the functional form of the bankruptcy rate \(\mu \) as of Eq. (8). In this way, the spontaneous transition from the distressed state d to the bankrupted state b is also dependent on nodes’ feature as banks’ interbank liquidity resilience of Eq. (9). For long enough simulations, the systemic risk would result to be equal since without a recovery mechanism, distressed banks are set to remain in the distress compartment or to default and this node variable would only accelerate or decelerate the bankruptcies. For this reason, showing the systemic liquidity risk would not carry any additional information. What is important though, is not only the final state of the simulation but also its speed to convergence. In fact, if a policymaker is able to monitor a distress situation, it would intervene timely. For this reason, it is of crucial importance to understand if liquidity resilience of some banks (in topologically relevant positions) can indeed slow down the contagion process. If it is the case, a central bank would operate on banks which can help to stop the contagion rather than injecting liquidity directly to more central or more vulnerable banks. To see if we have any effect by the liquidity resilience indicator, we compare the dynamics of the average bankruptcy rate \(\mu \) before and after the introduction of the resilience indicator. The results are reported in Fig. 20. As it is possible to notice, the mean dynamic is almost the same. This is not unexpected. In fact, the resilience indicator is constructed to have a neutral median; hence, the central tendency should be quite similar. What is important however, is the variability, i.e., the heterogeneity, in the speed of the bankruptcy rate, especially in the initial time steps of the contagion. What we can notice, in fact, is that the variability in the scenario with the resilience indicator is higher in the initial time steps for both the years considered. From an economic viewpoint, even if the difference between the two curves is not huge in absolute terms when we look at the mean levels, focusing on heterogeneity of speed of bankruptcy can make the difference when preventing an additional bank to fail that can generate a domino effect is vital.Footnote 22
Dynamics of the average bankruptcy rate \(\mu \). The line-square line \(\mu (NV)\) refers to the model with node variable in the contagion rate, while the line-cross line refers to \(\mu ^*\), the model with liquidity resilience in the bankruptcy rate defined in Eq. (8). Line and shaded area as in Fig. 14
5.2.5 Contagion and bankruptcy rates with node variable and confidence dynamics
In this scenario, we employ the node variables in both the contagion and the bankruptcy rate; in addition, the contagion rate has a time-dependent confidence multiplier which makes the contagion rate intrinsically dynamic. In particular, the liquidity resilience indicator enters in the functional form of the bankruptcy rate \(\mu ^{*}\) as of Eq. (8), while the systemic risk multiplier \(\theta \) enters the dynamic of the contagion rate \(\lambda ^{+}\) as of Eq. (11).
The parameter \(\theta \), as described in Eq. (10), measures the health state of the system at each iteration and modifies the contagion rate accordingly. When the fraction of distressed and bankrupted banks grows, the fear of contagion and the lack of confidence increase in the interbank market. The consequence is that distressed banks are more likely to withdraw their lending, thus effectively increasing the contagion rate. As defined in Eq. (11), this “psychological” effect translates into an increase of the contagion rate once the threshold \(e_*=(1+\beta _*)^{-1}\) is reached: \(\lambda ^+>\lambda ^*\) when \(e<e^*\). In this context, the parameter \(\beta _*\in (0,1)\) determines the tipping point \(e_*\)Footnote 23: a higher value of \(\beta _*\) corresponds to a lower threshold \(e_*\) and vice versa.
Evolution of the bankruptcy fraction over the period 2006–2013. Contagion rate with node variable and confidence dynamics. Bankruptcy rate with liquidity risk multiplier. Mean over the all simulations with 95% confidence bands. On the left, the fraction of bankrupted banks at the end of the infection; on the right, the fraction of total assets owned by bankrupted banks at the end of the infection
Figure 21 shows in this scenario the bankruptcy fraction dynamics for different \(\beta _*\) specificationsFootnote 24. First of all, the peak in correspondence of the Euro sovereign debt crisis of 2011 is evident for any value of \(\beta _*\). With respect to the previous scenario \(\lambda ^*\) (same of Fig. 16), the presence of the parameter \(\theta \) has a strong impact on the dynamics. We can identify three regimes: slow-reversal (\(\beta _*\ge 0.5\)), fast-reversal (\(\beta _*=0\)) and a mixed-effect (\(\beta _*\in (0,0.5)\) ). For \(\beta _*=1\), i.e., the slowest reversal case among those we consider, the extent of the contagion decreases in every year but 2011. On the contrary, for very low values of \(\beta _*\), the contagion is more severe and more banks default with respect to the static contagion rate \(\lambda ^*\). These additional failures however concern mainly the small banks, as can be seen by the smaller difference of the share of assets owned by bankrupted banks (right panel). In between, the mixed-effect cases are more interesting. Indeed, these cases are more credible both ex-ante from an economical point of view and ex-post from the results we get.
Dynamics of the distribution of the bankruptcy rate \(\mu ^*\) of Eq. (8) in 2007 and 2012 for different \(\beta _*\) specifications. Mean over the all simulations with 95% confidence bands
We finally show in Fig. 22 the bankruptcy rate \(\mu ^*\) for different \(\beta _*\) specifications. While \(\mu ^*\) does not depend directly on \(\theta (t)\), the bankruptcy rate grows as the number of distressed lenders increases, and thus the effect of \(\beta _*\) on \(\mu ^*\) is analogous to the effect of \(\beta _*\) on the contagion rate. In 2007, the bankruptcy rate is rather flat for the slow-reversal specifications, while the fast-reversal case is very similar to the scenario without confidence contagion (\(\lambda ^*\)); mixed-effect specifications fall between these two regimes. In 2012, the dynamic of the bankruptcy rate for the mixed-effect specifications is much more interesting. For early stages of the simulation, we observe a default rate that is smaller than the rate of the no confidence contagion case; however, this rate grows at a faster pace, and thus after some simulation steps it becomes larger than the reference case \(\lambda ^*\): at the end of the simulations there are approximately \(15\%\) more defaults. This behavior suggests that contagion due to psychological effects has a twofold nature: it lessens systemic risk if tackled in time; otherwise, it can lead to a quicker systemic collapse.
6 Conclusions
In this paper, we proposed a stochastic epidemic-like model for the propagation of (funding) liquidity risk in the European interbank market. We built on the Exposed-Distressed-Bankrupted (EDB) contagion dynamics recently proposed by Brandi et al. (2018), enhancing it using bank-specific features related to liquidity risk. In particular, we used the bid–ask spread of the home country combined with liquidity indicators to characterize the contagion dynamics of each individual bank in the interbank network. Further, we employed the liquidity resilience indicator to model a heterogeneous probability of bank default. Finally, we introduced a confidence contagion channel depending on the health state of the interbank market. In order to run agent-based simulations of the model, we reconstructed the European interbank market generalizing the degree-corrected gravity model of Cimini et al. (2015) to account for the block structure of the system. In particular, we used data on cross-countries banking claims to inform the reconstruction method.
We found that our reconstruction approach generates interbank networks with realistic country-block structures. Concerning the results of the contagion model, we found that using bank features in the dynamics considerably improves the outcome in terms of systemic risk assessment. Importantly, we found that the interplay of market topology and contagion dynamics is non-trivial. For example, while Greece has the highest (country) market liquidity indicator, the default rate of Greek banks turns out to be less prominent, because these banks are not much connected to foreign banks as compared to, e.g., Italian banks. Overall our results highlight that a macroprudential policy targeted at the hubs of the interbank network (the big actors in the contagion dynamics) can be more effective than simply injecting money in the larger or in the more vulnerable banks.
As remarked in the introduction, our proposal represents a simple yet effective and flexible model to assess the potential systemic risk stemming from banks’ balance sheets and contagion driven by the interbank network structure. As such, our modeling approach can be useful when data to inform more refined models is not available. However, our model can be easily enriched with more parameters entering in the node variables \(\gamma \) and \(\nu \), or modified by changing the functional form of the contagion and bankruptcy rate in order to more accurately mimic specific financial mechanisms. An important limitation concerning data is however the incompleteness of BIS cross-country exposures: while we used the most complete snapshot (2013Q4), more realistic results would have been obtained from having at disposal data for each year. Another more general limitation of our model is the absence of contagion channels due to, e.g., credit risk and overlapping portfolios. A future step in the use of epidemic-like models for financial contagion is thus to couple the liquidity risk dynamics with these and other contagion channels. A model encompassing all contagion channels simultaneously could be implemented on a multilayer network, with spillover effects between layers.
Notes
Note that banks failures due only to losses in the interbank market have not been observed, possibly because a lack of liquidity generates solvency issues which in turn become the cause of default, or because of government interventions. A notable exception is the case of Northern Rock that defaulted in 2012 due to funding liquidity cuts in the interbank market and bank run. Indeed, systemic defaults in the interbank market seem to be possible even due to cash fluctuations alone (Smaga et al. 2018). In any event, assessing systemic risk in the interbank market is important because of its interplay with other channels of contagion (Hüser 2015).
If such a mechanism would be of economic relevance, the model could be easily adapted to an SIS (Susceptible-Infected-Susceptible) or SIR (Susceptible-Infected-Recovered) model, using a stochastic rate of recovery.
For the sake of simplicity, we consider the same contagion rate from distressed and bankrupted banks, but it is easy to adapt the contagion mechanism to more complex situation in which the two mechanisms differ.
Notice that the effect is not symmetric and that \(\gamma _i>0\) has a higher impact.
We will use the total deposits, money market and short-term funding as a proxy.
Other possibilities arise in this context. One can subtract the two variables, and then apply the \(f(\cdot )\) transformation, or can firstly transform each variable and then use the geometric or arithmetic mean between the rescaled variables, taking into account the interval in which \(\gamma _i\) should be defined. We tested for such alternatives and the results remain qualitatively similar.
It is also possible to generalize the formulation of the systemic risk multiplier \(\theta \) introducing a nonlinear transformation \(h(\theta ,\phi )\), where \(h(\cdot )\) is a nonlinear function, and \(\phi \) represents the strength of nonlinearity such that the feedback effect is stronger or weaker with respect to the systemic risk. We have tested different nonlinear specifications; results are available in the electronic supplementary information.
We use the subset of banks for which there was no missing information and that contains a minimum of 4 banks for each represented country.
Bloomberg, “Bid and ask price of the 10-year government bonds 12/30/06 to 12/30/13.”
BIS Statistics Warehouse, https://www.bis.org/statistics/index.htm.
We further need to impute the values for the pairs GB-GB, ES-ES, IT-AT and PT-PT. For the first three pairs, we use the lending exposures of 2014-Q1 for GB-GB and of 2014-Q4 for ES-ES and IT-AT, while for PT-PT, we use a value proportional to that of ES-ES (as ES and PT have proportionally similar exposures to other countries).
This step is needed because maximum entropy alone would distribute volumes as evenly as possible, leading to an almost fully connected network structure (Cimini et al. 2015) However dense networks are rather different from real interbank networks, both in terms of topological and systemic risk properties (Squartini et al. 2018; Anand et al. 2018) (see also Gai and Kapadia (2010); Ramadiah et al. (2020)).
The ground bank is not involved in the contagion dynamics.
Self-loops can be meaningful as internal exposures when a network node represents a bank group rather than an individual bank.
This density value is compatible with typical density values of European interbank networks (Anand et al. 2018). We obtain similar results also using lower densities.
We have only generated network topologies with a single weakly connected component so there are no isolated nodes.
In both schemes, we observe very high values of the Sweden block density. This happens because Swedish banks in our dataset are only four but are very big in terms of total interbank assets and liabilities; according to both Eqs. (13) and (19), this implies a huge probability of connection among themselves.
The matching between these quantities is not perfect, since we do not constrain BIS exposure but rather single-bank exposures rescaled proportionally to these volumes. Mismatches can thus arise because the composition of the BIS and BankScope datasets is different: BIS data are supposed to contain all banks of the considered countries, and indeed are much larger than what we can compute from our Bankscope data, which only has a subset of banks for each country. Further deviations from perfect correlation arise also because of the IPF algorithm: after reconstructing the network with the block constraints, we redistribute the weights of the matrix diagonal using a global IPF procedure that does not take into account the country-block structure.
We remark that the time step of the simulations has in principle nothing to do with real time. Indeed, we are not trying to model the unfolding of a real crisis but rather to measure the potential systemic risk in the market due to the structure of balance sheets and interconnections. Similarly to the Eisenberg and Noe (2001) or the DebtRank (Battiston et al. 2012; Bardoscia et al. 2015) dynamics, iterations of the algorithm are needed to obtain, respectively, finer refinements of the payment vectors and asset valuations at equilibrium.
We remark that the transformation of Eq. (6) is applied for all the variables in the model over the whole time span of the dataset. Implementing the transformation separately for each year would erase the dynamics of the variables over time.
Note that the individual contribution of the two components to the node variable is not equivalent: The country term, having stronger fluctuations over the years, drives the dynamic of the liquidity risk, while the bank component provides corrections that magnify or reduce the liquidity risk indicator.
For the sake of completeness, a figure showing the deviation between the two different bankruptcy rate scenarios for all the banks is reported in the electronic supplementary material.
We set \(\beta _*\in (0,1)\) according to the following argument. At the beginning of the dynamics, \(e\simeq 1\). If \(\beta _*=1\), we have \(\theta \gg 1\) and thus a much smaller contagion than in the benchmark model, even when e decreases: the presence of distressed and defaulted banks has a negligible psychological effect on the market. Instead, if \(\beta _*=0\), then \(\theta =1\) as in the benchmark model; however, as soon as e decreases, \(\theta \) becomes smaller than 1 and contagion is much higher than in the benchmark model: distressed and defaulted banks have a very strong psychological effect even if most of the banks are healthy. A reasonable value for \(\beta _*\) should therefore be in the range (0, 1), with small values having a stronger behavioral effect.
We show the results for different values of \(\beta _*\). Plots related to the nonlinear specification of the systemic risk multiplier are available in the electronic supplementary materials.
References
Acemoglu D, Ozdaglar A, Tahbaz-Salehi A (2015) Systemic risk and stability in financial networks. Am Econ Rev 105(2):564–608
Aldasoro I, Delli Gatti D, Faia E (2017) Bank networks: contagion, systemic risk and prudential policy. J Econ Behav Organ 142:164–188
Allen F, Gale D (2000) Financial contagion in the moment. J Polit Econ 108(1):1–33
Amini H, Cont R, Minca A (2016) Resilience to contagion in financial networks. Math Financ 26(2):329–365
Anand K, Gai P, Marsili M (2012) Rollover risk, network structure and systemic financial crises. J Econ Dyn Control 36(8):1088–1100
Anand K, van Lelyveld I, Banai Á, Friedrich S, Garratt R, Hałaj G, Fique J, Hansen I, Jaramillo SM, Lee H et al (2018) The missing links:a global study on uncovering financial network structures from partial data. J Financ Stab 35:107–119
Bardoscia M, Battiston S, Caccioli F, Caldarelli G (2015) Debtrank: a microscopic foundation for shock propagation. PLoS ONE 10(6):e0130406
Bardoscia M, Battiston S, Caccioli F, Caldarelli G (2017) Pathways towards instability in financial networks. Nat Commun 8:14416
Bardoscia M, Barucca P, Battiston S, Caccioli F, Cimini G, Garlaschelli D, Saracco F, Squartini T, Caldarelli G (2021) The physics of financial networks. Nat Rev Phys. https://doi.org/10.1038/s42254-021-00322-5
Barucca P, Bardoscia M, Caccioli F, D’Errico M, Visentin G, Caldarelli G, Battiston S (2020) Network valuation in financial systems. Math Financ 30(4):1181–1204
Battiston S, Glattfelder JB, Garlaschelli D, Lillo F, Caldarelli G (2010) The structure of financial networks. In: Network science. Springer, pp 131–163
Battiston S, Puliga M, Kaushik R, Tasca P, Caldarelli G (2012) Debtrank: too central to fail? financial networks, the fed and systemic risk. Sci Rep 2:541
Battiston S, Caldarelli G, D’Errico M, Gurciullo S (2016) Leveraging the network: a stress-test framework based on debtrank. Stat Risk Model 33(3–4):117–138
Beale N, Rand David G, Battey H, Croxson K, Robert M, Martin NA (2011) Individual versus systemic risk and the regulator’s dilemma. Proc Natl Acad Sci 108(31):12647–12652
Bonfim D, Kim M (2012a) Liquidity risk in banking: is there herding. Eur Bank Center Discuss Pap 24:1–31
Bonfim D, Kim M(2012b) Systemic liquidity risk. Financial Stability Report. Banco de Portugal
Bonner C, Wedow M et al (2018) Systemic liquidity concept, measurement and macroprudential instruments. Technical report. European Central Bank
Brandi G, Di Clemente R, Cimini G (2018) Epidemics of liquidity shortages in interbank markets. Physica A 507:255–267
Brunnermeier MK (2009) Deciphering the liquidity and credit crunch 2007–2008. J Econ Perspect 23(1):77–100
Brunnermeier MK, Pedersen LH (2008) Market liquidity and funding liquidity. Rev Financ stud 22(6):2201–2238
Cai J, Thakor AV (2008) Liquidity risk, credit risk and interbank competition. Credit risk and interbank competition (November 19, 2008)
Guido C, Andrea C, Paolo DL, Miguel R, Munoz A (2002) Scale-free networks from varying vertex intrinsic fitness. Phys Rev Lett 89(25):258702
Cifuentes R, Ferrucci G, Hyun SS (2005) Liquidity risk and contagion. J Eur Econ Assoc 3(2–3):556–566
Cimini G, Squartini T, Garlaschelli D, Gabrielli A (2015) Systemic risk analysis on reconstructed economic and financial networks. Sci Rep 5:15758
Cimini G, Squartini T, Saracco F, Garlaschelli D, Gabrielli A, Caldarelli G (2019) The statistical physics of real-world networks. Nat Rev Phys 1(1):58–71
Cocco JF, Gomes FJ, Martins NC (2009) Lending relationships in the interbank market. J Financ Intermed 18(1):24–48
Cont R, Wagalath L (2016) Fire sales forensics: measuring endogenous risk. Math Financ 26(4):835–866
Cont R, Moussa A, Santos EB (2013) Network structure and systemic risk in banking systems. Cambridge University Press, pp. 327–368
Cont R, Kotlicki A, Valderrama L (2020) Liquidity at risk: joint stress testing of solvency and liquidity. J Bank Finance 118:105871
Craig B, Von Peter G (2014) Interbank tiering and money center banks. J Financ Intermed 23(3):322–347
Diamond DW, Rajan RG (2001) Liquidity risk, liquidity creation, and financial fragility: a theory of banking. J Polit Econ 109(2):287–327
Diamond DW, Rajan RG (2011) Fear of fire sales, illiquidity seeking, and credit freezes. Q J Econ 126(2):557–591
Drehmann M, Nikolaou K (2013) Funding liquidity risk: definition and measurement. J Bank Finance 37(7):2173–2182
Eisenberg L, Noe TH (2001) Systemic risk in financial systems. Manage Sci 47(2):236–249
Elsinger H, Lehar A, Summer M (2013) Network models and systemic risk assessment. Handb Syst Risk 1:287–305
Finger K, Fricke D, Lux T (2013) Network analysis of the e-mid overnight money market: the informational value of different aggregation levels for intrinsic dynamic processes. CMS 10(2–3):187–211
Freixas X, Parigi BM, Jean-Charles R (2000) Systemic risk, interbank relations, and liquidity provision by the central bank. J Money Credit Bank 32(3):611
Daniel Fricke, Thomas Lux (2015) Core-periphery structure in the overnight money market: evidence from the e-mid trading platform. Comput Econ 45(3):359–395
Furfine CH (2003) Interbank exposures: quantifying the risk of contagion. J Money Credit Bank 111–128
Gabbi G, Iori G, Jafarey S, Porter J (2015) Financial regulations and bank credit to the real economy. J Econ Dyn Control 50:117–143
Gai P, Kapadia S (2010) Contagion in financial networks. Proc R Soc A: Math Phys Eng Sci 466(2120):2401–2423
Gai P, Haldane A, Kapadia S (2011) Complexity, concentration and contagion. J Monet Econ 58(5):453–470
Glasserman P, Peyton YH (2016) Contagion in financial networks. J Econ Lit 54(3):779–831
Halaj G (2018) Agent-based model of system-wide implications of funding risk. Working paper series 2121. European Central Bank
Hałaj G, Kok C (2013) Assessing interbank contagion using simulated networks. CMS 10(2–3):157–186
Haldane A (2009) Why banks failed the stress test. BIS Rev 18:2009
Haldane AG (2013) Rethinking the financial network. In: Fragile stabilität–stabile fragilität. Springer, pp 243–278
Haldane AG, May R (2011) Systemic risk in banking ecosystems. Nature 469(7330):351
Hüser A-C (2015) Too interconnected to fail: a survey of the interbank networks literature. SAFE working paper, 91
Iachini E, Nobili S (2016) Systemic liquidity risk and portfolio theory: an application to the italian financial markets. Span Rev Financ Econ 14(1):5–14
Iori G, Jafarey S, Francisco PG (2006) Systemic risk on the interbank market. J Econ Behav Organ 61(4):525–542
Jobst AA, Lian Ong L, Schmieder C (2017) Macroprudential liquidity stress testing in FSAPs for systemically important financial systems. International Monetary Fund
Kapadia S, Drehmann M, Elliott J, Sterne G (2012) Liquidity risk, cash flow constraints, and systemic feedbacks. In: Quantifying systemic risk. University of Chicago Press, pp 29–61
Krause A, Giansante S (2012) Interbank lending and the spread of bank failures: a network model of systemic risk. J Econ Behav Organ 83(3):583–608
Kyle AS (1985) Continuous auctions and insider trading. Econ: J Econ Soc, pp 1315–1335
Manna M, Schiavone A (2012) Externalities in interbank network: results from a dynamic simulation model. Bank of Italy Temi di Discussione (working paper), 893
May Robert M, Nimalan Arinaminpathy (2009) Systemic risk: the dynamics of model banking systems. J R Soc Interface 7(46):823–838
Monetary and Capital Markets Department (2011) Global financial stability report April 2011: durable financial stability: getting there from here. International Monetary Fund
Nier E, Yang J, Yorulmazer T, Alentorn A (2007) Network models and financial stability. J Econ Dyn Control 31(6):2033–2060
Panetta F, Correa R, Davies M, Di Cesare A, Marques J-M, Nadal F, de Simone F, Signoretti CV, Vildo S, Wieland M et al (2011) The impact of sovereign credit risk on bank funding conditions. BIS, CGFS papers no, p 43
Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A (2015) Epidemic processes in complex networks. Rev Mod Phys 87(3):925
Philippas D, Koutelidakis Y, Leontitsis A (2015) Insights into european interbank network contagion. Manag Financ 41(8):754–772
Ramadiah A, Domenico DG, Ruggiero Lo Sardo D, Macchiati V, Pham Minh T, Pinotti F, Wilinski M, Barucca P, Cimini G (2020) Network sensitivity of systemic risk. J Netw Theory Finance 5(3):53–72
Rochet J-C, Tirole J (1996) Interbank lending and systemic risk. J Money Credit Bank 28(4):733–762
Rogers LCG, Veraart LAAM (2013) Failure and rescue in an interbank network. Manage Sci 59(4):882–898
Smaga P, Wiliński M, Ochnicki P, Arendarski P, Gubiec T (2018) Can banks default overnight? Modelling endogenous contagion on the o/n interbank market. Quant Finance 18(11):1815–1829
Squartini T, Cimini G, Gabrielli A, Garlaschelli D (2017) Network reconstruction via density sampling. Appl Netw Sci 2(1):3
Squartini T, Caldarelli G, Cimini G, Gabrielli A, Garlaschelli D (2018) Reconstruction methods for networks: the case of economic and financial systems. Phys Rep 757:1–47
Teply P, Klinger T (2019) Agent-based modeling of systemic risk in the european banking sector. J Econ Interac Coord 14(4):811–833
Thurner S, Poledna S (2013) Debtrank-transparency: controlling systemic risk in financial networks. Sci Rep 3:1888
Toivanen M (2013) Contagion in the interbank network: an epidemiological approach. Bank Finland Res Discuss Pap (19)
Upper C (2011) Simulation methods to assess the danger of contagion in interbank markets. J Financ Stab 7(3):111–125
Acknowledgements
The authors thank Marco Bardoscia for useful discussions. We thank Bloomberg for providing the data. We would like to thank the anonymous referees who provided useful and detailed comments on a previous version of the manuscript. Their comment significantly improved the quality of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Macchiati, V., Brandi, G., Di Matteo, T. et al. Systemic liquidity contagion in the European interbank market. J Econ Interact Coord 17, 443–474 (2022). https://doi.org/10.1007/s11403-021-00338-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11403-021-00338-1