Abstract
We propose a model economy consisting of interdependent real, monetary and stock markets. The money market is influenced by the real one through a standard LM equation. Private expenditures depend on stock prices, which in turn are affected by interest rates and real profits, as these contribute to determine the participation level in the stock market. An evolutionary mechanism regulates agents’ participation in the stock market on the basis of a fitness measure that depends on the comparison between the stock return and the interest rate. Relying on analytical investigations complemented by numerical simulations, we study the economically relevant static and dynamic properties of the equilibrium, identifying the possible sources of instabilities and the channels through which they spread across markets. We aim at understanding what micro- and macro-factors affect the dynamics and, at the same time, how the dynamics of asset prices, which are ultimately influenced by the money market, behave over the business cycle. Starting from isolated markets, we show the effect of increasing the market interdependence on the national income, the stock price and the share of agents that participate in the stock market at the equilibrium. Moreover, we investigate the stabilizing/destabilizing role of market integration and the possible emergence of out-of-equilibrium dynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays it is well acknowledged that the rapid development of financial markets has led to an increased financial instability, which undoubtedly brings effects into the real side of the economy. The macroeconomic principles cannot neglect the effect of interactions among different markets, a fact that has already been highlighted in the last century by Keynes (1936), who emphasized the possible two-sided feedback between the real and financial sides of the economy. The contribution by Keynes (1936) provided a new stimulus to the investigation of the macro-interactions, on which basis Hicks (1937) proposed his investment saving–liquidity money (IS–LM) model, representing a first synthetic attempt to translate the Keynesian economy into a formal model. The literature that originated from this seminal contribution is wide and followed several directions. Among the different branches, there is one that led to the analysis of the market interactions, with the aim of understanding the origins of turmoil in the business cycle. In fact, the financial and economic turbulence of the recent years shed light on the interconnections between the stock market and the economic activity. The outcomes of stock markets have a relevant impact on the decisions of firms’ capital allocation. This occurs directly, by affecting the level of investments through financial returns (Chiarella et al. 2001), but also indirectly influencing the beliefs of agents through the information content embedded in stock prices (Chen et al. 2007). However, the backward connection from the financial to the real market is also of relevance, as a rise in stock prices can boost private investments.
It is against this background that, in recent years, a pretty large body of literature devoted its attention to the mutual relationships between the real economy and the stock market. Examples of these types of works are the ones by Chiarella et al. (2010), Westerhoff (2012), Lengnick and Wohltmann (2013), Naimzada and Pireddu (2015), Cavalli et al. (2018), Flaschel et al. (2018), Sordi and Davila-Fernandez (2020). Alongside these, we can mention the contributions proposed by Charpe et al. (2011), Asada et al. (2010), Bask (2011), which, considering an heterogeneous agents setting, mainly deal with policy rules (both fiscal and monetary) with the aim of improving the stability of the economy. Besides the different approaches and the various modeling techniques, all these papers share the common goal of deepening the understanding of the interactions between the real economy and the stock market.
Nonetheless, such strands of research have mostly neglected the formalization of the money market which, instead, is a channel that bears relevance for the transmission of turbulence between financial markets and the real economy. A consistent part of the financial market is certainly represented by the money (and eventually bonds) market. This is where, to a large extent, interest rates are determined, and their role is crucial for the course of the dynamics of the economic activity. In this respect, it is worth mentioning the paper by Lengnick and Wohltmann (2016) that develops a macro-finance interaction model in which the presence of a Central Bank is taken into account to investigate whether the financial sector changes the optimal policy rule, and to what extent the different interactive channels matter.
Moreover, the way the monetary sector exerts its influence and how it is affected by the other sectors of the economy can be ambiguous. In this regard, we can mention the work by Friedman (1988), who argued about the existence of two opposite and antagonistic effects of stock market price on the demanded quantity of money. In fact, he described a “wealth effect,” consisting in a positive influence on the nominal wealth of an increase in stock prices, and a “substitution effect” between money and investments in financial market, as a consequence of the rise of attractiveness of assets when prices increase. The reciprocal strength of such opposite components can change depending on the different economic contingency. Friedman, after highlighting that the wealth effect acts as the dominant one, suggested that such preeminence could not actually be the rule. In line with this, Dow and Elmendorf (1998) and Carlson and Schwarz (1999) have found evidence of a link between stocks and money in households’ management of their wealth portfolios over time. The study by Browne and Cronin (2012) highlights how, in the last two decades, the substitution effect has increasingly become prevalent with respect to the wealth effect.
The present paper builds on the aforementioned literature on the macro-interactions with a first aim of enriching it by taking explicitly into account the presence of the money market. The model we consider takes inspiration by the contribution of Blanchard (1981), who enriched the traditional IS–LM approach by considering a stock market, coupled with a simple and stable multiplier description of the output dynamics on the goods market. The key assumption and the novelty of the paper by Blanchard is the introduction of the interaction between asset values and output. In particular, the national income, through consumption and investments, is driven by the real activity as well as stock prices. The outcomes of the Blanchard macro-model exclude the existence of feedback mechanisms that can lead to an endogenous propagation of shocks. In that setting fluctuations are ruled out, unless unanticipated shocks occur, as is the case of many rational expectations models. In order to overcome this drawback, Chiarella et al. (2002) and Semmler (2011) modified the Blanchard model with the aim of recovering such feedback effects by considering gradual expectations adjustments, and thus imperfect substitutability, to the yield between stocks and money. In so doing, they take into account the stock price impact on the real activity but, differently from the Blanchard model, the stock price jumps to its stable paths are avoided by introducing gradual adjustments of stock prices, interest rates and output.
In the present paper, we do consider the relationships among stock prices, interest rates and output, but, unlike the aforementioned contributions, we introduce a price formation mechanism in the stock market that allows for a micro-level description of it in terms of agents’ heterogeneity, and for investors to split between the stock and the money market in an evolutionary perspective. In the contributions by Chiarella et al. (2002) and Semmler (2011), the way monetary and real sector influence the stock market is only sketched, neglecting both a modeling of the agents’ behavior and any selection mechanism of the market in which they operate. In a nutshell, the economy under investigation comprises a real sector, consisting in a Keynesian good market in which production modifies according to the aggregate demand, a money market regulated by the standard assumption of an LM equilibrium and a stock market where the price is adjusted by a market maker with respect to the current excess demand. The total excess demand depends on a time-varying population of agents that can decide to participate or not in the stock market. Agents choose to invest or not in the stock market on the basis of an evolutionary selection mechanism regulated by the comparison between the stock return and the interest rate. That agents have to make a choice about which market they will operate in is inspired by the works by Shiller (2015) and Aliber and Kindleberger (2017). The general idea behind this mechanism is that agents flow into the stock market when they glance at chances of realizing profits, for instance during phases of price booms because they do not want to lose the chance of getting profit opportunities. In the model economy we propose, as a consequence of the interconnections among the different sectors, we describe the attractiveness of the stock market not only in terms of the performance of the stock market itself, but it is affected by the performance of the money and real markets. In this way, we can account for a direct connection between the real and the financial side of the economy through the price of the asset, but also for an indirect link that comes from the participation mechanism which explicitly encompasses the features of the monetary sector.
Finally, we assume that our economy is populated by two types of agents, namely fundamentalists and chartists, which differ in their expectation formation mechanism. This allows us taking into account agents’ heterogeneity, which is a well-established feature that characterizes stock market participants, from both theoretical and empirical points of view. Therefore, the present paper fits also into the literature strand that attempts at explaining the dynamics of the economy (and of its interconnected sectors) by considering the effects of the behavior of heterogeneous and interacting agents. Among others, we would like to mention the contributions by Brock and Hommes (1998), Hommes (2011), Hommes (2013), Hommes (2006), Kirman and Zimmermann (2012), Chiarella et al. (2014), Onozaki (2018).
The three markets we consider are interconnected. The link between the real and the stock market is described by the dependence of the private expenditure with respect to the stock price, resembling the idea that the status of the households and firms is positively/negatively affected by the good/bad performance of the financial market. The national income affects expected returns and, through the money market equilibrium, the interest rate, which both determine the participation of agents in the stock market. Hence, both the real and the monetary sectors affect the stock market. The influence of the stock market on the money market occurs through the national income, in which private investments depend on the stock price. The link between real and monetary sectors is both direct, encompassed in the LM equilibrium, and indirect, through the stock market.
The model we end up with consists in a discrete time dynamical system that describes the interactions between the variables characterizing each sector. The market linkages have a twofold effect: On the one side, they act at a micro-level by influencing the agents’ market participation; on the other side, they act at a macro-level by affecting the dynamics of the stock price and the national income. The proposed approach allows us to investigate how the introduction of such two levels of interactions can alter the stability properties characterizing the different markets when isolated. From the dynamic viewpoint, beside the possibility that the system converges to the macroeconomic equilibrium, quasi-periodic dynamics resembling the business cycle fluctuations are also a relevant characteristic of the proposed model. Such persistent trajectories provide a representation of how the propagation of financial instability may affect the overall pace of the economic activity. Moreover, since agents are allowed to enter or leave the financial market chasing their most attractive investment opportunity, the continuous inflow and outflow of agents to and from the stock market is responsible for the occurrence and amplification of endogenous dynamics in the business cycle.
We test the relevance of the model also from the empirical side, being this a significant feature when addressing to macro-variables. In fact, even if the aim of the present paper is to provide a starting point for the (theoretical) analysis of market interactions within a stylized and analytically tractable macro-model, the proposed setup allows us testing the empirical relevance of the model, comparing the simulated results with the observed financial ones. When buffeted with noise, the proposed model is able to replicate the common stylized facts of financial markets (e.g., bubbles and crashes, excess volatility, serially uncorrelated returns, volatility clustering) as well as the qualitative behavior of the national income variable.
Finally, to test the robustness of the results about interaction among different market sectors, we consider a modified version of the model and we study it in “Appendix A” section, showing the consistency between the outcomes of the two models, from both the theoretical and simulative points of view.
The remainder of the paper is organized as follows: Section 2 outlines the baseline model that constitutes our framework for the analysis on the market interactions; Sect. 3 contains the analytical results on the existence of the unique macroeconomic equilibrium as well as its local stability conditions; Sect. 4 confirms the analytical results through numerical simulations in which we further highlight the role of the parameters linking the different sides of the economy; Sect. 5 explores the dynamics of the model when a stochastic component is introduced, while Sect. 6 concludes. In “Appendix A” section, we investigate an alternative version of the model in which we consider a different mechanism for the money market. Finally, “Appendix B” section collects all the proofs.
2 The baseline macro-model
We consider a closed economy made up by a real, a monetary and a stock market that are linked among each other. The setup for the real economy is as follows: The good market is characterized by the national income Y that adjusts with respect to the aggregate demand Z. More precisely, we have
where \(g_1:\mathbb {R}\mapsto \mathbb {R}\) is a differentiable strictly increasing function satisfying \(g_1(0)=0.\) According to (1), the production at time \(t+1\) increases when there is an excess of aggregate demand against production at time t, and vice versa. Function \(g_1\) describes the good market adjustment speed with respect to the deviation between demand and production and represents a possibly nonlinear reactivity function.
The aggregate demand is defined as
where C, I and G stand for consumption, investment and government expenditure, respectively.
We consider a constant government expenditure, while the private expenditure increases with the national income. Moreover, since the financial situation of the households and firms depends on the performance of the stock market, the private expenditure also increases with the stock price, denoted by P (see Blanchard 1981). In light of these considerations, we can write
which establishes the relation between consumption, investment, government expenditures, national income and stock price. The parameter \(K>0\) accounts for all the autonomous expenditures, while \(0<b<1\) and \(0<d<1\) represents the marginal propensity to consume and invest from current income,Footnote 1 and from current stock market wealth, respectively.
As concerns the money market, we adopt the standard assumption of an LM equilibrium, that is we consider combinations of interest rates and levels of real income for which the money market is in equilibrium. This reads as:
where \(\bar{M}\) denotes the exogenous money supply, \(\bar{p}\) represents the fixed price level, i is the interest rate and \(l>0\) represents the autonomous demand of money, \(k>0\) is the proportion of income that is kept for transactions purposes and \(h>0\) is the liquidity preference for speculative motives. From the equilibrium condition on the money market, we can write
where we have set \(m=\bar{M} / \bar{p}\).
The stock price is determined by a market makerFootnote 2 who adjusts the price with respect to the current excess demand. In particular, the market maker clears the market, adjusting the stock price for the next period on the basis of an offsetting long or short position. This translates into:
where \(N_t\) is the number of agents active in the stock market at time t (see, e.g., Agliari et al. 2018 and the references therein for a similar approach) and \(g_2:\mathbb {R}\mapsto \mathbb {R}\) is a differentiable and strictly increasing function satisfying \(g_2(0)=0.\) The possibly nonlinear function \(g_2\) represents the reactivity of the market maker to the market total excess demand, where the excess demand \(\varDelta _i\) of the ith agent is given by
and \(P_{i, t + 1}^e\) represents the price expectation at \(t + 1\) of the ith agent.
We assume that the market is populated by two different types of agents, namely fundamentalists (f) and chartists (c). Accordingly we have \(P_{i, t}^e\in \{P_{f, t}^e,P_{c, t}^e\}\) for any \(t\ge 0\). The two types of agents differ in their expectation formation mechanism. Fundamentalists know the fundamental value of the asset and believe that the market price, being anchored to it, will revert to such fundamental value in the long run, so that they form their expectations on this basis, i.e.,
where \(\xi _f >0\) is the fundamentalists’ reactivity parameter to the deviation between the fundamental valueFootnote 3F and the observed price.
On the contrary, chartists ground their expectations on the information obtained by observing the price time series and, accordingly, try to extrapolate the future dynamics, submitting buying (selling) orders if prices increase (decrease). This translates into
where \(\xi _c > 0\) is the chartists’ reactivity parameter to the price trend.
In each period, agents decide whether to enter the stock market. We assume that there exists a number \(N_0\) of agents that always operate within the stock market and maintain it active, while other investors can decide to participate in the stock market activity from time to time. We formalize this idea by introducing the total number of investors N of which the time-varying fraction \(\omega _t\in (0,1)\) participates to the market.Footnote 4 In so doing, we explicitly model the stock market participation as a significant ingredient for the stock demand and, ultimately, for the stock price determination. On the basis of the previous considerations, and taking into account (8) and (9), the total excess demand reads as:
where the exogenousFootnote 5 fraction of fundamentalists that populate the market is given by \(n_{f}=n\), while the fraction of chartists is \(n_{c}=1-n,\) so that the number of active fundamentalists and chartists is, respectively, given by \((N_0+N\omega _t) n\) and \((N_0+N\omega _t) (1-n)\), and indeed lie between \(N_0\) and \(N_0+N.\)
Agents decide whether to invest or not in the stock market on the basis of the difference between the interest rate \(i_{t}\) and the stock market return, in line with Chiarella et al. (2002) and Semmler (2011). The expected return of a stock is defined as:
where \(\pi _t = \alpha _0 + \alpha _1 Y_t\) represents the real profits and it is assumed to be an increasing function of the output Y (see Blanchard 1981; Semmler 2011), while \(P_{t+1}^e\) is the average expected price. Recalling the expectations of the two types of agents (8)-(9) into (11), we obtain:
Agents’ probabilities of entering the stock market is modeled through the well-known logit mechanism (see, e.g., Manski and McFadden 1981; Brock and Hommes 1998), so that the share of agents participating in the market results
where \(\beta >0\) represents the intensity of choice and measures how sensitive the agents are with respect to the profitability signals of the monetary and stock markets. In particular, when \(\beta =0\) both fractions are fixed over time and equal to 1/2, while when \(\beta \rightarrow +\infty \) we have that, at time t, either the maximum possible number of agents \(N+N_0\) are active in the stock market (if \(R_{t + 1}^e>i_t\)) or, conversely, the minimum possible number \(N_0\) (if \(R_{t + 1}^e<i_t\)).
Equation (12) allows us to define the attractiveness of the stock market
so that the share of market participants can be rewritten as
As a consequence, parameter \(\beta \) measures how much sensitive agents are toward the stock market attractiveness, so that with positive (respectively, negative) attractiveness \(A_t>0\) (respectively, \(A_t<0\)), the share of agents participating in the stock market is larger (respectively, smaller) than 1/2. We also would like to emphasize that the stock market attractiveness does not depend on elements that only relates to such a market, but it is also related to the monetary sector, through the interest rate i, and to the real sector, via the real profits \(\pi \).
In view of the subsequent analysis, it is useful to introduce \(Q_t = P_{t - 1}\). In so doing, we end up with the following three-dimensional discrete time dynamical system which describes the interaction between the variablesFootnote 6 characterizing the real, monetary and stock markets:
where \(\omega _t\) has been defined in (12).
Before studying the model in (15), it is worth summarizing the reciprocal influences among the three sectors that constitute our model economy and the related parameters governing the interactions. The real sector influences the monetary one through the dependence of the money demand on the national income, which is regulated by the parameter k, representing the proportion of income that is kept for transaction purposes. The stock market influences the real sector through the dependence of the private expenditures on stock prices, ruled by d. Finally, both the real and the money sectors affect the participation to the stock market: In fact, the attractiveness depends on interest rates and on real profits, whose endogenous component is affected by the performance of the sector with a proportionality described by the parameter \(\alpha _1.\) The intensity of choice \(\beta \) determines how strongly the stock market attractiveness affects the agents’ decision to participate or not in such a market.
Finally, it is worth observing that if private expenditures do not depend on the performance of the stock market (i.e., \(d=0\)), the turbulence of the stock market does not spread to the real or monetary sector, while those of the real sector extend to the monetary one and, in turn, to the stock market. Conversely, if we assume an exogenous participation in the stock market (i.e., \(\omega _{t}=\omega \)), endogenous instabilities can be transmitted to the real one and then to the money market, while a transmission in the opposite direction is indeed not possible.
3 Analytical results on existence and stability of the equilibrium
In this section, we study the static and dynamical properties of the model in (15). We shall show that a unique macroeconomic equilibrium exists and we shall provide its local stability conditions. In so doing, we will be able to identify the effect that the interactions and the reciprocal influence among sectors play on the (in)stability of the economy.
We start by studying the possible equilibria of the model in (15) and how they vary as long as the relevant parameters are modified. The next two propositions contain the results.
Proposition 1
The model in (15) owns a unique equilibrium \(S^{*} = (Y^{*}, P^{*}, Q^{*}) = \left( \frac{K + F d}{1 - b}, F, F \right) .\) At \(S^{*}\), the share of agents participating in the stock market is provided by
where \(\pi ^{*} = \alpha _0 + \alpha _1 Y^{*},\, i^{*} = \frac{l + k Y^{*} - m}{h}\) and \(A^{*}=\pi ^{*} / F- i^{*}\) are the real profits, the interest rate and the attractiveness at the equilibrium, respectively. Moreover, we have that \(\omega ^{*} > 1 / 2\) (resp. \(\omega ^{*} < 1 / 2\)) if and only if \(A^{*} >0 \) (resp. \(A^{*} < 0\)).
It is easy to see that when the influence of the stock market on the real sector is neglected (i.e., when \(d=0\)) the national income equilibrium value is the same as in the classical IS–LM model. Setting \(\beta =0,\) we remove the dependence of the stock market on the monetary and real sectors. In this case, the equilibrium participation relies on a random choice, and accordingly, we have \(\omega ^{*}=1/2.\) In what follows, the benchmark setting corresponding to \(\beta =d=0\) will be referred to as isolated real and stock markets.
The equilibrium level of the national income is positively affected by a growth in the dependence of private expenditures on stock market prices, in the autonomous expenditures and in the marginal propensity to consume from current income. Concerning the effect on \(\omega ^{*}\) of the parameters describing each sector of the economy, from (16) we observe that the share of agents participating in the stock market is positively related to the relative real profits, while it negatively depends on the interest rate, whose difference provides the equilibrium attractiveness of the stock market. Any factor having the effect to increase the profitability signal coming from the stock (resp. money) market then contribute to the growth (resp. fall) of the attractiveness and, hence, of the participation. The main drivers of the equilibrium participation variation that are consequences of market interdependence are investigated in the next proposition, which will be also crucial to understand the effects on the dynamics of market interactions.
Proposition 2
The equilibrium participation \(\omega ^{*}\) increases if
-
\(\alpha _1\) increases;
-
k decreases;
-
d increases and \(\alpha _1 / F - k / h > 0;\)
-
\(\beta \) increases and \(A^{*} > 0.\)
Reverting either the signs of inequalities or the monotonicity behavior of the parameters, we have that \(\omega ^{*}\) decreases.
The first three results reported in Proposition 2 allow us to understand how the linkages among the different sides of the economy determine the stock market attractiveness, while the last one clarifies to what extent agents take into account the attractiveness to determine their participation.
As the sensitivity of the real profits with respect to income changes (encompassed in \(\alpha _1\)) increases, the positive effect of the real market on the stock market grows, so that it results increasingly appealing and attracts agents, bolstering participation. Conversely, the participation is inversely related to the behavior of the money market. If agents earmark a smaller proportion of their income for transactive purposes (i.e., k decreases), the interest rate decreases as well and the preference for the liquid asset diminishes too, making the stock market more attractive with a subsequent increase in the participation level. The former outcome is related to the direct effect that the real market exerts on the stock one, while the latter one is ascribed both to the direct impact that the money sector has on the stock market, through interest rate, and to the indirect influence of the real sector on stock market attractiveness, mediated by the monetary one.
The third result described in Proposition (2) is related to the indirect effect that stock market exerts on its attractiveness, through its direct influence of the real one. An increased marginal propensity to invest from the stock market has a positive effect on the income level, which, as we already saw, directly and indirectly affects the attractiveness. However, the marginal effect on attractiveness of an increase in \(Y^{*}\) can be positive or negative and is quantified by the balancing of \(\alpha _1 / F\) and k/h. The former term represents the relative marginal returns when the stock market is at the equilibrium (i.e., the ratio between marginal real profits and the equilibrium price), so that, ceteris paribus, the more sensitive to an increase in \(Y^{*}\) real profits are, the more marginally attractive the stock market is. The marginal effect of \(Y^{*}\) on the monetary sector depends on the proportion of income k that is kept for transactions purposes with respect to its speculative counterpart h. As such ratio increases, the interest rate is more sensitive to changes of \(Y^{*}\) and hence an increase in the equilibrium national income reduces the marginal attractiveness of the stock market. The higher the proportion of income kept for transactional purposes is, the more the monetary sector is influenced by the real one and agents preference for liquid assets rises, the less attractive the stock market is, as the connection between the stock market and the real one increases. The comparison between the previous two effects determines the way attractiveness, and hence participation, changes. When the latter overcomes the former, the equilibrium participation in the stock market shrinks since agents are more attracted by liquid assets provided by the money market, while the opposite effect occurs when the former overcomes the latter.
Summarizing, the way stock market attractiveness is affected by the market interdependence depends on both non-marginal and marginal effects on it, which are a consequence of market interdependencies exerted either directly or indirectly through a chain of subsequent market linkages.
However, the actual participation that corresponds to a certain degree of equilibrium attractiveness strongly depends on how much agents take it into account, and this is regulated by the intensity of choice \(\beta .\) The smaller the evolutionary pressure is, the greater the number of agents that randomly decide whether to participate or not in the stock market is, thus resulting in a participation share that gets closer and closer to 1/2. Conversely, as the agents’ sensitivity to the stock market attractiveness increases, participation scenarios become more extreme. A positive attractiveness means that the profitability signal from the stock market is larger with respect to that from the monetary one. In this case, as the intensity of choice increases, agents are more receptive to the attractiveness of the stock market, and thus, the equilibrium participation increases. In the opposite situation, i.e., when \(A^{*}<0,\) agents mostly prefer the liquid asset and an increase in the intensity of choice has the effect of dwindling the stock market participation in equilibrium.
We now focus on the analysis of the dynamical properties of the equilibrium. The next couple of propositions deals with the stabilityFootnote 7 of the equilibrium \(S^{*}.\) We start by focusing on the role of agents’ reactivities. To this end, let us introduce \(\gamma =g_1'(0)\) and \(\sigma =g_2'(0),\) representing the market adjustment speed and the market maker’s reactivity at the equilibrium, respectively.
Proposition 3
The equilibrium \(S^{*}\) is locally asymptotically stable provided that
If the first or the second stability condition is violated, a flip bifurcation occurs, while a Neimark–Sacker bifurcation occurs if the last condition is violated.
On increasing the reactivity parameters related to fundamentalists, we can have an unconditionally unstable or a destabilizing scenario. Conversely, on increasing the reactivity parameters related to chartists we can have an unconditionally unstable, mixed or destabilizing scenario.
Finally, on increasing the share of fundamentalists, we can have stabilizing, destabilizing and mixed scenarios, in addition to those unconditional.
The first condition in (17) is related to the stability of the real sector alone and is common to similar models (see, e.g., Naimzada and Pecora 2017). Instabilities arise from the real sector only in the presence of a strong adjustment speed, at the equilibrium, between demand and production (there must necessarily hold \(\gamma > 2)\), provided that it is not counterbalanced by a suitably large marginal propensity to consume. In the rest of the analysis, we shall focus only on the case \(\gamma \le 2,\) under which condition the isolated real market is stable.Footnote 8
The remaining two conditions explain how instability can arise from the stock market. Firstly, we focus on the joint effect of the reactivity at the equilibrium of the market maker (\(\sigma \)) and of each kind of agent \(\xi _i\). We stress that the way the equilibrium turns unstable (and the consequent non-converging trajectories) changes depending on whether they are due to an overreaction of fundamentalists or chartists. This is a direct consequence of the different expectation mechanisms of the two kinds of agents. In the following comments, we make reference to the stability region of Fig. 1a referred to the \((\xi _c,\xi _f)\) parameter plane, in which the black lines highlight some relevant scenarios. If the reactivity of chartists is suitably small, on increasing \(\xi _f\) we may observe that an overreactive behavior of the fundamentalists can be the source of unstable dynamics, which, in agreement with Proposition 3, results in a period-doubling bifurcation (horizontal line D). However, as the reactivity of chartists increases, the threshold at which instability occurs increases, until such reactivity becomes too strong and the behavior of chartists is a source of instability itself (horizontal line UU). The role of chartists is more evident looking at scenarios depicted by the vertical lines. If the reactivity of fundamentalists is small, an overreaction of chartists with respect to the price trends indeed introduces instability, which, in agreement with Proposition 3, results in quasi-periodic trajectories (vertical line D). However, if the reactivity of fundamentalists is so large that may introduce instability, an intermediate reactivity of chartists could be beneficial as it can be able to counterbalance the endogenous unstable dynamics introduced by fundamentalists (vertical line M).Footnote 9 We stress that from Proposition 3, changing the way in which the agents that participate in the stock market distribute among fundamentalists or chartists can be very ambiguous. However, each scenario can be quite simply explained, recalling the role of the reactivity parameters related of each group. As we can see from the second and third relation in (17), the aggregated reactivity of the group of fundamentalists participating in the stock market at the equilibrium is given by \((N_0 + N \omega ^{*}) n \xi _f\), while that of chartists is \( (N_0 + N \omega ^{*}) \xi _c (1 - n)\). Ceteris paribus, if we increase the share of fundamentalists, the aggregated reactivity of the group of fundamentalists increases, while concurrently that of chartists decreases. The corresponding effects are comparable to those obtained by simultaneously increasing the reactivity of fundamentalists and decreasing that of chartists, keeping fixed their shares. We have already discussed that the effects of former change in the agents’ reactivity can destabilize the equilibrium, while the latter one can have either a stabilizing or a mixed effect.Footnote 10 Combining them, we simply have that each scenario due to an increase in the reactivity of fundamentalists alone or to a decrease in the reactivity of chartists alone can arise, depends on which is the group with the largest aggregated reactivity. Hence, the comments related to what happens when the reactivity parameters change can be rephrased to explain the scenarios occurring when the share of fundamentalists changes. We shall provide additional details taking into account a numerical example at the end of Sect. 4.
Moreover, from (17), we can see that the stability of \(S^{*}\) is affected by the number of agents active at the equilibrium in the stock market, i.e., by \(n_i (N_0 + N \omega ^{*}), i \in \{ f, c \}\) and in particular by the equilibrium participation share \(\omega ^{*}.\) The reason is simple: The more the agents participate in the stock market, the more the orders are placed, and depending on the price misalignment and/or trend, this increasingly affects the overall excess demand. This can lead to a substantial price adjustment that can result in endogenous oscillations around the fundamental, with sudden outburst of prices when a general optimism prevails, while a nervous mood can cause a sharp decline in asset prices.
As we have already seen, the participation at the equilibrium is a consequence of the attractiveness, which, among the others, is affected by the parameters that encompass the interaction effects. The next proposition makes explicit the final effect on stability of allowing for interconnection among markets, starting from scenarios in which markets are isolated.Footnote 11
Proposition 4
If the isolated stock market is stable, then the economy consisting of interconnected markets can become unstable on increasing
-
\(\beta \) if \(A^{*}>0,\) or
-
d if \(\alpha _1/F-k/h>0,\) or
-
\(\alpha _1,\)
or on decreasing k.
If the isolated stock market is unstable, then the economy consisting of interconnected markets can be stabilized on increasing
-
\(\beta \) if \(A^{*}<0,\) or
-
d if \(\alpha _1/F-k/h<0,\) or
-
k,
or on decreasing \(\alpha _1.\)
Stability regions in the \((\xi _f,\xi _c)\) parameter plane (a), \((k,\beta )\) plane (b) and \((d,\beta )\) plane (c–d). For all the reported regions we set \(\gamma =2, \sigma =1, A=8, \alpha _0=5, m=3, h=4.2, N=1, N_0=0.3, F=10\) and \(l=4,\) while the remaining parameters are reported atop each panel. White (resp. yellow) color is used for parameters’ combinations for which the equilibrium is stable (resp. unstable). Dashed and solid red lines represent the stability thresholds corresponding to the second and third conditions in (17), respectively. Dotted black lines highlight stabilizing (S), destabilizing (D), mixed (M), unconditionally stable (US) and unstable (UU) scenarios
The results of Proposition 4 are a dynamic reflection of those of Proposition 2 and can be understood in the light of the (marginal) effects of the parameters on the equilibrium attractiveness, which positively influences the participation. In short, any element that has the main effect of increasing the stock market attractiveness potentially leads to the emergence of instability inside the stock market, since it contributes to an increase in the participation. As a consequence, when agents are more (resp. less) prone to participate in the stock market, they can take positions that may render the dynamics unstable (resp. stable). In addition, the intensity of choice \(\beta \) enhances or minimizes the effect of the attractiveness of the stock market. The greater the evolutionary pressure is, the stronger the effect of large (resp. small) market attractiveness is. This results in a larger (resp. smaller) number of agents that participate in the stock market when it is strongly attractive (resp. unattractive). Accordingly, we observe that when the intensity of choice increases and the attractiveness of the stock market is positive, the equilibrium turns unstable as the effect of an increased mass of agents attracted by the profitability signal coming from the market.
To deepen the explanation of the results of Proposition 4, we make use of the scenarios reported in Fig. 1b–d in which, starting from isolated markets, we show the effect of introducing interconnection among them. We recall that the isolated real market is stable, thanks to the moderate good market adjustment speed.
Figure 1b, c both shows the \((d,\beta )\) parameter plane. In these scenarios, the lower boundary of the stability region (corresponding to \(d\rightarrow 0\)) depicts the situation in which the real market does not depend on the financial one, while the left boundary of the stability region (corresponding to \(\beta \rightarrow 0\)) portrays the case in which the stock market participation is independent on the attractiveness, and hence, the stock market behavior is not affected by the characteristics of the real and monetary ones. In the scenario reported in Fig. 1b, the isolated stock market is unstable, due to an overreaction in the behavior of chartists. Indeed, in this case turbulence only affects price dynamics. Introducing a whatever small dependence of private expenditures on prices has the immediate effect to spread price instability to the real and monetary sectors. If agents slightly rely on attractiveness in order to decide whether to participate or not, dynamics remain unstable (black dotted line denoted by UU), as participation is only slightly affected by the comparison of markets’ performance. However, if the intensity of choice increases, suitably increasing values of d can introduce a feedback effect on the stock market that leads to stabilization (horizontal black dotted line S). This can be understood by noting that the marginal effect of income is stronger on interest rate than on relative real profits (\(k/h=0.07>0.05=\alpha _1/F\)), so that the marginal effect of the monetary sector on the attractiveness is the dominant one. This means that if the coupling between stock and real market strengthens, the effect of the consequent increase in the income level is to reduce attractiveness, since the interest rate grows faster than the real profits. Indeed, if we considered the opposite case (i.e., \(k/h<\alpha _1/F\)), no positive feedback effect would be possible, as participation would increase the turmoil in the stock market. Note that the scenario studied in Fig. 1b is characterized by an equilibrium attractiveness that is always negative (\(A^{*}<-0.5\)), so a suitably large evolutionary pressure eventually leads to stability (vertical black dotted line S) and allows for unconditionally stable behaviors with respect to d ( horizontal black dotted line US). Both chances would be not possible if for some values of d the equilibrium attractiveness were positive.
The setting considered for Fig. 1c is such that the isolated stock market is stable, the marginal effect of income on interest rate is weaker than on relative real profits (\(k/h=0.12<0.3=\alpha _1/F\)) and the equilibrium attractiveness is always positive (\(A^{*}>2.6\)), so that the depicted scenario is the opposite with respect to that in Fig. 1b. As a consequence, the increase in the output level occurring when private expenditures are more and more positively affected by price has an opposite effect, since now real profits proportionally grow more than the interest rate. If a suitable relevance is assigned to the attractiveness, more and more agents follow the profitability signal coming from the stock market and participation increases, leading to the emergence of unstable dynamics (e.g., along the horizontal black dotted line denoted with D). Indeed, if attractiveness has a small influence on participation, the stability characterizing isolated market sectors is preserved even in the presence of large values of d. Conversely, as \(\beta \) increases, the positive equilibrium attractiveness drives more agents toward the stock market, which is the source of instability (vertical black dotted line S).
The previous comments allow us to understand the remaining results of Proposition 4 with respect to the parameters governing the influence of the real and monetary sectors on the stock market. As an example, in Fig. 1d we report a stability region referred to the \((k,\beta )\) parameter plane. Each isolated market is stable, but the economy can turn unstable in the presence of a sufficient agents’ responsiveness to the positive attractiveness that characterizes this scenario even in the presence of a weak effect of the real sector on the interest rate (\(k\rightarrow 0\)). If the dependence of the monetary sector on the real one increases (i.e., when k is sufficiently large), the interest rate increases, while the attractiveness of the stock market decreases, so the equilibrium remains unconditionally stable both when the intensity of choice is sufficiently low and on increasing \(\beta \) (the black dotted lines US). Instead, starting from a sufficiently high value of \(\beta \), an increase of k has a stabilizing effect (as highlighted by the dotted black line denoted with S) thanks to the augmented level assigned to the income detained for transactions purposes in consequence of which the stock market results less attractive. In conclusion, we would like to stress once more the fundamental role played by the monetary market to understand the dynamical behavior of the proposed economy.
4 Nonlinear dynamics and instabilities across markets
In this section, we carry out numerical investigations of the model dynamics, complementing the local stability analysis performed in the previous section, in order to get an insight of the possible dynamic behaviors arising when stability is lost. In particular, we shall focus on the nonlinear patterns and cross-dependencies occurring due to the interactions among different markets, and that arise for the relevant parameters \(d,\beta ,k\) and \(\alpha _1,\) whose role have been outlined in the analytical part. Before carrying out simulations, we need to provide specific expressions for functions \(g_1\) and \(g_2.\) In both cases, we choose linear expressions \(g_1(x)=\gamma x\) and \(g_2(x)=\sigma x,\) where \(\gamma \) and \(\sigma \), respectively, represents the constant good market adjustment speed and market maker’s reactivity.
All the following simulations have been obtained by setting \(A=8, F=10, \sigma =1, \alpha _0=5, N=1, N_0=0.3\) and \(h=4.2,\) while the remaining parameters are reported along with the related simulations. We set the initial conditions suitably close to the equilibrium. In the two-dimensional bifurcation diagrams, different colors are used to identify parameters’ combinations for which the trajectories converge to attractors consisting of a different number of points, according to the color bar placed on the right of the corresponding panel. (Black color is used for parameters’ combinations for which the variables assume non-feasible values.) In particular, the white area represents the region in which trajectories converge to the equilibrium. In the one-dimensional bifurcation diagrams as well as in the time series, we report the asymptotic behavior of the price and national income, depicted in red and blue, respectively, plotted against the left axis. In the same diagrams, we also display the proportions of individuals participating in the stock market, depicted in black and plotted against the right axis.
In Sect. 3, we have identified micro- and macro-factors that influence the stability of the equilibrium: In the former group, we have the agents’ reactivity, which also determines the type of bifurcation occurring, and the evolutionary pressure; in the latter one, we encompass the parameters describing the market interactions. Combining such elements in different ways, several scenarios can be obtained. In what follows, we limit our analysis to only some of them, nonetheless providing a comprehensive description of the possible economic phenomena.Footnote 12
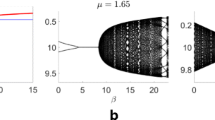
In the first couple of simulations reported in Figs. 2 and 4, we investigate the effect played by the variation of the parameter d, responsible for the direct link between the stock and the real market, and by the evolutionary pressure \(\beta \). Figure 2a shows a two-dimensional bifurcation diagram in the \((d,\beta )\) parameter space. The crossing of the bottom border of the white stability region leads to instability with the occurrence of quasi-periodic dynamics, as also confirmed by observing Fig. 2b, in which we report the bifurcation diagrams showing the asymptotic behavior of the price, the national income and of the proportions of individuals participating in the stock market. The present scenario is characterized by a marginal influence of the monetary sector on the stock market that is stronger than that exerted by the real one (\(k/h=0.23>0.2=\alpha _1/F\)) and by an unstable isolated stock market. As a consequence, increasing both d and \(\beta \) can have a stabilizing effect, as noticeable from Fig. 2b in which we show that on increasing d, the equilibrium can gain stability with a reduced level in the oscillations of dynamics of P, Y and \(\omega \). Moreover, an increased tightening between the two markets has also the effect of generating a stimulus in the economic activity, as demonstrated by the course of the national income, which exhibits an expansion.
Time series of P (red), Y (blue) and \(\omega \) (black), for the same parameters used for the one-dimensional bifurcation diagrams of Fig. 2 and \(d=0.5\)
When unstable, the dynamics of economic variables are characterized by quasi-periodic oscillations on a closed orbit, as a consequence of the Neimark–Sacker bifurcation. This is evident also looking at the time series reported in Fig. 3, corresponding to the value \(d=0.5\) in the bifurcation diagrams of Fig. 2b. The time series depict the occurrence of endogenous business cycle for both price and national income dynamics. The rationale for this scenario can be outlined as follows. For instance, let us look at a situation in which agents move to the stock market, as a result of a phase of negative price trend in which investors find more convenient to buy stocks in the hope of a future positive price trend. An increase in the stock market participation enhances a higher stock demand and thus pushes up stock prices. This has also a positive effect on the national income. At the same time, the other investors, perceiving a boom in stock markets, reduce their money demand for transactional purposes and prefer to participate to the stock market activity as well. This leads to a further rise of the stock price. However, this increases the interest rate more than expected returns, paving the way for a market’s trend change. In fact, since the majority of agents is already active in the stock market, a further increase in the market’s participation is unlikely. Additionally, investors may also perceive that this positive and continuous market trend is mirroring a stock market overvaluation, with prices and national income significantly above their equilibrium values. At this point, a wealth effect prevails thanks to the increased level of the national income that adds to the effect of the price misalignment, which is stronger than the price trend. Therefore, investors will eventually change their behavior and exit the stock market, preferring to sell the stocks and detain a more liquid asset, causing a reversal in the dynamics, with the national income that follows the same path. In this phase, due to the reduced stock market participation, the total excess demand is smaller in absolute value, so that \(P_t\) and, in turn, \(Y_t\) change more slowly than in the previous phase. Stock prices keep declining until the stock market features a phase of undervaluation, which generates another change in the market direction and the story repeats, yet in a cyclical manner.
Differently from Fig. 2, in Fig. 4 we consider a setting characterized by a significant reactivity of fundamentalists and by a marginal influence of the real sector on the stock market stronger than that exerted by the monetary sector (\(k/h=0.07<0.1=\alpha _1/F\)), while the isolated stock market is stable. In Fig. 4a, we observe that when the boundary of the white stability region is crossed from below, the equilibrium undergoes a period-doubling bifurcation from which a stable 2-cycle arises. Such a cycle, in turn, goes through a cascade of period-doubling bifurcations leading to the occurrence of cycles of higher periodicity and, finally, chaos. Figure 4b reports a one-dimensional bifurcation diagram on increasing the intensity of choice \(\beta \), showing that the impact of a more and more strong intensity of choice is destabilizing. Such destabilization occurs through a cascade of period-doubling bifurcations which opens the onset of chaotic dynamics. It is worth noting that an initial increase in the value of \(\beta \) makes the stock market participation increase as well, due to the positive equilibrium attractiveness that characterizes the stock market (\(A^{*}=2.04>0\)). Nonetheless, if the intensity of choice keeps increasing, the inflow of agents generates instability in the dynamics of both price and national income and, accordingly, in the market participation.
Time series of P (a), Y (b) and \(\omega \) (c), obtained for the same parameters adopted in the one-dimensional bifurcation diagrams of Fig. 4 and \(\beta =2.\)
Again, we can focus on a particular time series to better understand the way endogenous oscillations arise in the stock market and spread across the others. The setting is such that the marginal effect of the national income on the attractiveness is positive, in a way that the participation in the stock market is positively correlated with the growth and drop of the real sector. Figure 5 shows examples of time series generated beyond the flip bifurcation boundary. The three panels refer to the dynamics of the price, national income and fractions of agents participating in the stock market, respectively. The time series show phases characterized by sequences of low prices, with a few oscillations, followed by phases characterized by sharp hikes and larger oscillations. The national income time series follows the same path, while, in the right panel, we observe that in general large participation tends to be followed by large participation, with the exception of the phases in which the participation drops.
The model reveals that investors’ tendency to move from the stock market to the money market, or vice versa, may set endogenous stock and national income dynamics in motion. Let us try to explain how this occurs. The initial state of the economy is characterized by a price below the fundamental \(F=10,\) a real sector that outperforms the equilibrium \(Y^{*}=22\) and a low participation to the stock market. In the next period, the participation greatly increases, due to the strong attractiveness of the stock market induced by a high level of the national income. Simultaneously, price slightly jumps above the fundamental, as a consequence of the augmented participation, while the national income level is negatively influenced by the low prices of the previous period, so that it strongly decreases below the equilibrium. The reduced misalignment at \(t=2\) between \(P_t\) and \(Y_t\) and the corresponding equilibrium values triggers a sequence of small amplitude oscillations, which arise in the stock market, spread with a lag to the real one and, from this latter, to the monetary one. Small oscillations can be observed in the stock market participation as well, even if it keeps at a high level thanks to the large component of real profits in expected returns that exceeds the possible loss arising from price oscillations. This phenomenon can be also related to the preponderance of a substitution effect over a wealth effect, in which agents are attracted toward the stock market thanks to higher real profits. The significant reactivity of the fundamentalists together with the persistent large participation leads to increasingly large price oscillations (\(t=3,\dots ,11\)), which eventually end up with a fall in the participation, since the real profits component is no more able to prevent expected returns to become negative due to the significant drop in expected prices. At this point (\(t=12\)), we have a situation very similar to the initial one, and the sequence of phenomena keeps repeating. To sum up, in this scenario instabilities arise in the stock market, since the influence of the real sector on the stock market, which in this case is more significant than that of the monetary one, sustains instability as it fosters stock market participation. Then, turbulence spread to the real and monetary sectors.
We would like to stress that an increasing reactivity of chartists can initially compensate this effect as a consequence of their different expectation mechanism, and eventually lead to an overall stabilization. In fact, chartists form their expectations on the basis of the price pattern which, in the presence of oscillating prices, induces to place orders that are opposite to those of fundamentalists. For instance, at \(t=10\) the price is low and fundamentalists would buy. Conversely, on the basis of the decreasing trend between the two last prices, chartists would sell. With suitable reactivities, the two different orders can balance out and result in a reduced excess demand, thus stabilizing the market dynamics. However, if chartists overreacts to the signals arising from the price trend, then the dynamics turns unstable with quasi-periodic trajectories.
In the last simulation reported in Fig. 6, we show a two-dimensional bifurcation diagram in the \((k,\alpha _1)\) plane. As shown in Sect. 3, both the proportion of income that is kept for transactions purposes and the sensitivity of real profits to income variations have unambiguous effects on the equilibrium stability. The former, related to the monetary sector, has a potential stabilizing role since it decreases the marginal effect of national income on attractiveness. Conversely, the latter acts in the opposite way. The parameters setting identifies a scenario characterized by a significant reactivity of fundamentalists. For such reason, we can see that along the boundary of the white stability region, instability occurs by means of a flip bifurcation. Indeed, if we considered larger reactivity for chartists, we would have a very similar scenario in which the unique difference would be the occurrence of a Neimark–Sacker bifurcation.
Similar phenomena can occur when we change the share of fundamentalists n. In Fig. 7, we report a couple of two-dimensional bifurcation diagrams obtained on varying the share of fundamentalists and the reactivity of chartists, so that we are able to control the effects of both increasing and decreasing the aggregated reactivity of the each group of agents.
For both simulations, we set \(\gamma = 2, d = 0.3, \beta = 1, \alpha _1 = 2, k = 1, m = 3\). In the left and right panels, we, respectively, report the simulations obtained setting \(\xi _f = 1\) and \(\xi _f = 6\), i.e., respectively, considering a small and large reactivity for fundamentalists. From both panels, we can see that when the reactivity of chartists is low and the share of fundamentalists is small, the equilibrium is stable. Increasing the share of fundamentalists can lead to emergence of unstable dynamics if their reactivity is sufficiently large (right panel), while the equilibrium stability is not affected if their reactivity is small enough (left panel). If instability occurs, consistently with the previous comments on the role of \(\xi _f\), it arises through a period-doubling. Conversely, if we consider larger reactivity for chartists, so that the equilibrium is unstable if the share of fundamentalists is small, an initial increase of n can have a stabilizing effect (both left and right panels). This is a consequence of the aggregated overall reactivity of the group of chartists, which reduces as n increases. However, if we keep increasing the share of fundamentalists and their reactivity is suitably large, instability can again arise (right panel). We stress that, consistently with the comments about the role of the reactivity of chartists, if we decrease the share of fundamentalists, instability occurs by means of a Neimark–Sacker bifurcation.
5 Stochastic dynamics
The evolution of any economic system is characterized by periods of intense expansion in output which alternates with periods of reduction in economic growth. In Fig. 8a, we report the time series of the detrended and normalized US GDP (quarterly data related to years 1975-2019), from which it is evident the emergence of a business cycle consisting of alternating periods of growth and decline. At the same time, the dynamics of the stock markets is also characterized by a plethora of well-known stylized facts, such as bubbles and crashes, excess volatility, serially uncorrelated returns and volatility clustering. It is then reasonable that, at least qualitatively, the model could explain and reproduce such features observed in the economic activity of real and financial markets. In Fig. 8b, we report the Dow Jones Industrial Average index (monthly index related to years 2005–2019), from which it is evident its erratic behavior. The real data reported in Fig. 8 may serve as a mean of comparison between the real course of the data and the simulated dynamics emerging from our benchmark model.Footnote 13
In the rest of this section, we present a stochastic version of the deterministic model (15)–(12), in which we introduce a shock in order to test the capability of the model to reproduce a set of stylized facts that characterize real time series of national income and stock prices. Since the goals of the present contribution are mainly theoretical, and we do not aim at developing a highly specialized model that takes into account all the possible sources of stochastic perturbations, we only introduce a single shock on the fundamental value. This allows us to test whether an even simple model, in which the essential elements to establish an interconnection between monetary, stock and real markets are introduced, is able to reproduce the typical stylized facts of time series such as bubble and crashes, autocorrelation of absolute returns and deviation from normality.
To this end, following De Grauwe and Kaltwasser (2012) and Blaurock et al. (2018), we let the fundamental value F follow the random walk
where \(\{ \varepsilon _t \}\) are normally distributed random variables with zero mean and standard deviation \(s_1 > 0\). The introduction of this component can be motivated by the fact that the fundamental value of a stock can change as a result of new information that hinders an instantaneous and complete adjustment of the actual prices to the new fundamental value (see Fama 1995). Accordingly, the resulting stochastic model is then obtained adding Eq. (18) to model (15)–(12), in which F is also replaced by \(F_t\).
We present the results related to the parameter configuration used for the simulation reported in the right panel of Fig. 4, and in which we additionally set \(s_1 = 0.06\) for the standard deviation of the stochastic component. We stress that we checked the meaningfulness of the value assumed by all the economic variables during the whole simulation. Moreover, even if the following results are related to a specific parameter setting, we thoroughly tested their robustness repeating simulations for different parameter settings. In Fig. 9, we report a time series for the national income, in which we can observe the emergence of a business cycle with phases of a stronger growth in the national income alternating with phases of lower growth.
Concerning the stock market behavior, in the left and right panels of Fig. 10 we report couple typical simulated time series referred to prices and returns, defined as \(R_t=100(\log (P_t)-\log (P_{t-1})).\) From both panels, it is evident that the stock price fluctuates quite erratically, with phases of price appreciations and depreciations, resembling the boom and bust behavior of the real stock indexes. Moreover, the corresponding returns behavior highlights the presence of volatility clustering and occasional volatility outbursts. A further evidence of volatility clustering is provided by the significant and slowly decaying autocorrelation coefficients of the absolute and squared returns (see panels (a) and (b) of Fig. 11), together with the essentially uncorrelated coefficients for returns (Fig. 11c).
Returns distribution exhibit a relevant deviation from the normality, summarized by a leptokurtic distribution with a kurtosis equal to 6.9. We stress such deviation grows significantly as the complexity of endogenous dynamics due to equilibrium instability increases. Referring to simulation reported in the right panel of Fig. 4, kurtosis deviates from 3 as \(\beta \) increases. Finally, the standard deviation of returns distribution is 0.13, which is in good agreement with those of the considered real stock market (i.e., 0.11 for the Dow Jones Index between 2005 and 2019).
6 Concluding remarks
The proposed model allowed us to highlight some elements that have to be taken into account for the understanding of the macroeconomic implications of an economy with interacting markets. Indeed, a turbulence that originates within a particular market can spread to the others. Endogenous fluctuations can be ascribed to elements proper of a market, such as the agents’ reactivity, which also determines the type of dynamics. But more importantly, the dynamics that originate from our simple model are the consequence of the factors regulating the interaction across markets, which would be otherwise stable when considered as independent. In this respect, crucial elements are those related to market interconnections that can be realized at both micro- and macro-levels, and affect the level of the attractiveness and the marginal effects on it. When the economy consists of multiple interacting sub-systems, the attractiveness of a single market does not only depends on the performance and on the characteristics of that market alone, but it has unavoidably to depend on the other markets with which it interacts. In the proposed model, the participation in the stock market is introduced through an evolutionary mechanism, which is directly or indirectly influenced by the behavior of all the interacting markets. Indeed, the attractiveness depends on the interest rates, the expected stock price variation and the real profits. In this regard, the role of the money market is crucial to explain the significant channels through which instabilities originate, transmit or extinguish throughout the whole economy. The money market is also responsible for determining the amount of the stock market participation, by directly influencing its attractiveness. It is the joint role played by the wealth and substitution effects of money, which alternatively may dominate that determines the stock market participation. This is the key element that makes agents rush toward one market or another, and finally be the trigger for the course of the economic activity. The present paper can be extended along several directions: A first way would be to refine the modeling of the stock market, with the introduction of different and more sophisticated market designs that may better describe the real functioning of financial markets (e.g., the Walrasian market clearing, the order book or the batch auction), in order to obtain a comparison among their performances; a second possibility would be the introduction of a mixture of monetary and fiscal policies in order to investigate whether the intervention of the public authorities can stabilize the economy; a more refined, endogenous modeling of the fundamental value as well as of the consumption and investment functions would also add more realism, with investments based on the acceleration principle, for instance; and finally, several stock interacting markets could be introduced by inserting a network structure within our setup.
Notes
In agreement with Blanchard (1981) and in line with our research aims, we keep the modeling of aggregate demand at a simple level. A more refined version taking into account, for example, the different marginal propensities, would be more in line with the observed course of consumption and investment.
There exist several approaches for designing the price formation mechanism in financial markets, ranging from the Walrasian market clearing to the batch auction and the order book. The Walrasian setting is a standard theoretical tool to model the market clearing process, but it requires infinite information from the agents and therefore is hardly implementable in practice. This problem can be solved under the market maker scenario which is a price-driven protocol, by announcing a single trading price at the beginning of the trading session.
Several modeling techniques have been proposed for the fundamental value: This can be fixed to an exogenous value, it can be time-varying, it can follow a random process, it can be linked to the real part of the economy, etc. (see, among others, De Grauwe and Kaltwasser 2012; Gori and Ricchiuti 2018; Blaurock et al. 2018; Ascari et al. 2018). Our choice is to set the fundamental value of the stock price as constant, assuming that it is common knowledge, which is in line with other papers that encompass heterogeneous agents in asset pricing models, from both a theoretical and an experimental point of view (see, e.g., Noussair et al. 2001; Tramontana et al. 2010; Schmitt and Westerhoff 2017). In Sect. 5, we will introduce a stochastically perturbed version of the present model in which the fundamental value follows a random walk.
Throughout the paper, we consider a unitary population of agents that can participate or not in the market, and \(N_0\) is therefore normalized.
In the present contribution, the focus is on market interdependencies, and the modeling of the stock market is then kept simple. In particular, the share of each group of agents is exogenously set. An evolutionary mechanism for an endogenous share formation is indeed possible, but it would not add further insight to the economic rationale of the effects of market interactions, as shown by preliminary numerical investigations we performed on such a more refined setting.
We stress that for some parameters’ settings and initial conditions, the trajectories generated by (15) can exit the feasible regions (e.g., Y, P or Q can become negative, as well as interest rates defined in (5)). For all the analytical results in Sect. 3, we implicitly restrict to settings that provide economically significant values, while we have numerically checked that this holds for all the reported simulations of Sect. 4.
Hereinafter, we establish that a parameter z has a stabilizing effect if the equilibrium is unstable for \(z < z_1\) and stable for \(z > z_1\) (stabilizing scenario), a destabilizing effect if the equilibrium is stable for \(z < z_1\) and unstable for \(z > z_1\) (destabilizing scenario) and a mixed effect if the equilibrium is unstable for \(z < z_1\) or for \(z > z_2\) and stable for \(z_1< z < z_2\), for some \(z_1\) and \(z_2\) (mixed scenario). Finally, we state that a parameter has a neutral effect if the equilibrium stability/instability is not affected by a change in the parameter (unconditionally stable/unstable scenarios).
We stress that the instability arising in the isolated real market cannot be removed by market interactions and hence simply spreads to the other sectors of the economy. Instability could be hindered by the adoption of suitable fiscal and/or monetary policies. However, this is not the scope of the present contribution.
As already noted, such behavior is also described and commented in Agliari et al. (2018), to which we refer for more details.
Indeed, we discussed the destabilizing or mixed effect of increasing the reactivity of chartists. If we decrease it, we simply have to “read” the scenario from right to left.
In Proposition 4, we avoid to make explicit situations in which the change of a parameter does not affect the equilibrium stability. Unconditionally stable/unstable scenarios will be briefly discussed in the subsequent comments. Moreover, for the sake of shortness, we state that an isolated market and the economy are stable/unstable when the corresponding steady state is locally asymptotically stable/unstable.
All the remaining scenarios can be understood with the help of the same comments and explanations provided for the selected simulations.
The different time span of the two series is due to the different reporting method for the two types of data. Nonetheless, the two reported series contain the same number of observations.
We stress that the simulations in which k is changed correspond to the simulations in which both \(\delta \) and \(i^{*}\) are moved. However, it still holds that a simulation obtained for a particular value of k can be reproduced by a suitable parameters’ configuration in the modified model.
References
Agliari A, Naimzada A, Pecora N (2018) Boom-bust dynamics in a stock market participation model with heterogeneous traders. J Econ Dyn Control 91:458–468
Aliber RZ, Kindleberger CP (2017) Manias, panics, and crashes: a history of financial crises. Springer, Berlin
Asada T, Chiarella C, Flaschel P, Mouakil T, Proaño CR, Semmler W (2010) Stabilizing an unstable economy: on the choice of proper policy measures. Econ Open Access E J 4
Ascari G, Pecora N, Spelta A (2018) Booms and busts in a housing market with heterogeneous agents. Macroecon Dyn 22(7):1808–1824
Bask M (2011) Asset price misalignments and monetary policy. Int J Financ Econ 17(3):221–241
Blanchard OJ (1981) Output, the stock market, and interest rates. Am Econ Rev 71(1):132–143
Blaurock I, Schmitt N, Westerhoff F (2018) Market entry waves and volatility outbursts in stock markets. J Econ Behav Organ 153:19–37
Brock WA, Hommes CH (1998) Heterogeneous beliefs and routes to chaos in a simple asset pricing model. J Econ Dyn Control 22(8–9):1235–1274
Browne F, Cronin D (2012) The new dynamic between US stock prices and money holdings. World Econ 13(1):137–156
Carlson JB, Schwarz JC (1999) Effects of movements in equities prices on M2 demand. Tech. Rep. 35, Economic Review-Federal Reserve Bank of Cleveland
Cavalli F, Naimzada AK, Pecora N, Pireddu M (2018) Agents’ beliefs and economic regimes polarization in interacting markets. Chaos Interdiscip J Nonlinear Sci 28(5):055911
Charpe M, Flaschel P, Hartmann F, Proaño C (2011) Stabilizing an unstable economy: Fiscal and Monetary policy, stocks, and the term structure of interest rates. Econ Model 28(5):2129–2136
Chen Q, Goldstein I, Jiang W (2007) Price informativeness and investment sensitivity to stock price. Rev Financ Stud 20(3):619–650
Chiarella C, Flaschel P, Semmler C (2001) Real-financial interaction: a reconsideration of the Blanchard model with state-of-market dependent reaction coefficient. Tech. rep., Working Paper, School of Finance and Economics, UTS
Chiarella C, Semmler W, Mittnik S, Zhu P (2002) Stock market, interest rate and output: a model and estimation for US time series data. Stud Nonlinear Dyn Econ 6(1):1–39
Chiarella C, Giansante S, Sordi S, Vercelli A (2010) Financial fragility and interacting units: an exercise. In: Decision theory and choices: a complexity approach. Springer, pp 117–126
Chiarella C, He XZ, Zwinkels RC (2014) Heterogeneous expectations in asset pricing: empirical evidence from the s&p500. J Econ Behav Organ 105:1–16
De Grauwe P, Kaltwasser PR (2012) Animal spirits in the foreign exchange market. J Econ Dyn Control 36(8):1176–1192
Dow JP, Elmendorf DW (1998) The effect of stock prices on the demand for money market mutual funds. Tech. rep., Division of Research and Statistics, Division of Monetary Affairs, Federal Reserve Board
Fama EF (1995) Random walks in stock market prices. Financ Anal J 51(1):75–80
Flaschel P, Charpe M, Galanis G, Proaño CR, Veneziani R (2018) Macroeconomic and stock market interactions with endogenous aggregate sentiment dynamics. J Econ Dyn Control 91:237–256
Friedman M (1988) Money and the stock market. J Polit Econ 96(2):221–245
Gori M, Ricchiuti G (2018) A dynamic exchange rate model with heterogeneous agents. J Evolut Econ 28(2):399–415
Hicks JR (1937) Mr. Keynes and the classics; a suggested interpretation. Econ J Econ Soc 5(2):147–159
Hommes C (2011) The heterogeneous expectations hypothesis: some evidence from the lab. J Econ Dyn Control 35(1):1–24
Hommes C (2013) Behavioral rationality and heterogeneous expectations in complex economic systems. Cambridge University Press, Cambridge
Hommes CH (2006) Heterogeneous agent models in economics and finance. Handb Comput Econ 2:1109–1186
Keynes JM (1936) The general theory of employment, interest and money. Palgrave Macmillan, London
Kirman A, Zimmermann JB (eds) (2012) Economics with heterogeneous interacting agents. Springer, Berlin
Lengnick M, Wohltmann HW (2013) Agent-based financial markets and New Keynesian macroeconomics: a synthesis. J Econ Interact Coord 8(1):1–32
Lengnick M, Wohltmann HW (2016) Optimal monetary policy in a New Keynesian model with animal spirits and financial markets. J Econ Dyn Control 64:148–165
Manski CF, McFadden D et al (1981) Structural analysis of discrete data with econometric applications. MIT Press, Cambridge
Medio A, Lines M (2001) Nonlinear dynamics: a primer. Cambridge University Press, Cambridge
Naimzada A, Pecora N (2017) Dynamics of a multiplier-accelerator model with nonlinear investment function. Nonlinear Dyn 88(2):1147–1161
Naimzada A, Pireddu M (2015) Real and financial interacting markets: a behavioral macro-model. Chaos Solitons Fract 77:111–131
Noussair C, Robin S, Ruffieux B (2001) Price bubbles in laboratory asset markets with constant fundamental values. Exp Econ 4(1):87–105
Onozaki T (2018) Nonlinearity, bounded rationality, and heterogeneity. Springer, Berlin
Schmitt N, Westerhoff F (2017) Heterogeneity, spontaneous coordination and extreme events within large-scale and small-scale agent-based financial market models. J Evolut Econ 27(5):1041–1070
Semmler W (2011) Asset prices, booms and recessions: financial economics from a dynamic perspective. Springer, Berlin
Shiller RJ (2015) Irrational exuberance: revised and expanded, 3rd edn. Princeton University Press, Princeton
Sordi S, Davila-Fernandez MJ (2020) Investment behaviour and bull & bear dynamics: modelling real and stock market interactions. J Econ Interact Coord
Tramontana F, Westerhoff F, Gardini L (2010) On the complicated price dynamics of a simple one-dimensional discontinuous financial market model with heterogeneous interacting traders. J Econ Behav Organ 74(3):187–205
Westerhoff F (2012) Interactions between the real economy and the stock market: a simple agent-based approach. Discret Dyn Nature Soc 2012
Acknowledgements
We wish to thank two anonymous referees for their valuable comments and suggestions.
Funding
Open access funding provided by Università Cattolica del Sacro Cuore within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
An alternative monetary policy rule
The main goal of the present contribution has been to investigate in depth the role of interaction between different market sectors. In particular, we focused on the role of the presence of a monetary and of a stock market, being the latter characterized by agents’ heterogeneity, with investors allowed to split between the stock and the money market under an evolutionary mechanism. To this end, the literature originated by the seminal paper by Blanchard (1981) and then retrieved and developed by Chiarella et al. (2001), Chiarella et al. (2002) and Semmler (2011) represented the ideal starting point for the proposed model. Indeed, many other benchmark models and approaches could be taken into account, and enriched, proceeding as we proposed in Sect. 2. In this section, we want to test the reliability of the results we have found in Sect. 3 by considering a different formulation for the monetary policy rule. Instead of considering the standard LM relation, obtained by the equality from money demand and supply, we assume that the interest rate is set according to the following rule
This rule resembles the way modern Central Banks target the monetary policy and allows the regulation of the macroeconomic activity by choosing the interest rate based on an assumed equilibrium interest rate and on the deviation between the national income and its equilibrium level. In so doing, the money supply does not serve as the policy instrument directly, but, instead, is the interest rate that is tuned in order to stabilize the pace of the economic activity.
Both the real and the stock market are modeled as in Sect. 2, with the only difference in the final expression of the fraction of agents participating in the financial market. Such share \(\omega _t\) is still determined through the logit mechanism by \(\omega _t = \frac{e^{\beta R_{t + 1}^e}}{e^{\beta R_{t + 1}^e} + e^{\beta i_t}}\), but in which \(i_t\) is defined by (19) and instead of (5). The resulting expression is
and the model is described by System (15), in which \(\omega _t\) is defined by (20) instead of (12).
In the remainder of this section, we show how each Proposition of Sect. 2 changes when the alternative monetary policy rule is taken into account. We omit proofs, since they are very similar to those related to model (15)-(12), from which they can be easily rephrased. We start by studying the model equilibrium.
Proposition 5
The model in (15) owns a unique equilibrium \(S^{*} = (Y^{*}, P^{*}, Q^{*}) = \left( \frac{K + Fd}{1 - b}, F, F \right) \). At \(S^{*}\), the share of agents participating in the stock market is provided by
where \(\pi ^{*} = \alpha _0 + \alpha _1 Y^{*}\) and \(A^{*} = \pi ^{*} / F - i^{*}\) are the real profits, the interest rate and the attractiveness at the equilibrium, respectively. Moreover, we have that \(\omega ^{*} > 1 / 2\) (resp. \(\omega ^{*} < 1 / 2\)) if and only if \(A^{*} > 0\) (resp. \(A^{*} < 0\)).
The previous proposition is essentially the same as Proposition 1, with the only difference that now \(i^{*}\) is exogenous, and hence, it does not depend any more on \(Y^{*}\). Consequently, the comments following Proposition 1 still applies to the model introduced in the present section, in particular those about the role of \(i^{*}\) and \(\pi ^{*}\) on equilibrium attractiveness and therefore on the equilibrium participation. Then, we investigate the role of the parameters governing market interdependence on the equilibrium participation.
Proposition 6
The equilibrium participation \(\omega ^{*}\) increases if
-
\(\alpha _1\) increases;
-
d increases or \(i^{*}\) decreases;
-
\(\beta \) increases and \(A^{*} > 0\).
Reverting either the signs of inequalities or the monotonicity behavior of the parameters, we have that \(\omega ^{*}\) decreases.
With respect to Proposition 2, in Proposition 6 the result about k is missing (since it is no more a parameter in the model) as well as that about d, since as we already observed that in model (15)–(20) the equilibrium interest rate \(i^{*}\) is exogenous, and is no more influenced by \(Y^{*}\). The only remarkable difference is then the unambiguous role of d in Proposition 6, which is a direct consequence of the independence of \(i^{*}\) with respect to \(Y^{*}\). In this case, since there is not direct influence of the real market on the equilibrium interest rate, the marginal effect of a change in \(Y^{*}\) is null on \(i^{*}\) This scenario can be connected to the third of Proposition 2 in which we assume that k/h is very small with respect to \(\alpha _1 / F,\) so that the role of marginal propensity to consume and invest in model (15)–(20) results unambiguous.
However, the economic rationale of Proposition 6 is essentially the same of that of Proposition 2: We still have that the attractiveness of the financial market is strongly affected by the interdependence between markets and by their non-marginal and marginal influence on attractiveness.
Concerning the stability, recalling that we set \(\gamma = g_1' (0)\) and \(\sigma = g_2' (0)\), we have that Proposition 3 still holds as is for model (15)–(20), too. When then have that from the local asymptotic stability point of view, all the comments that follow Proposition 3 are valid to explain the dynamic behavior of model (15)–(20).
Finally, we discuss the role of market interdependence on stability.
Proposition 7
If the isolated financial market is stable, then the economy consisting of interconnected markets can become unstable on increasing
-
\(\beta \) if \(A^{*} > 0\), or
-
d, or
-
\(\alpha _1\),
or on decreasing \(i^{*}\).
If the isolated financial market is unstable, then the economy consisting of interconnected markets can be stabilized on increasing
-
\(\beta \) if \(A^{*} < 0\)
or on decreasing \(\alpha _1\).
Also in this case, we have minimal differences between Propositions 4 and 7, due to the exogenous \(i^{*}\) in model (15)–(20), and the consequent unambiguous role of the influence of d. Again, the economic explanation of the effects of market interdependence on the stability changes is basically the same and can be understood in terms of the non-marginal and marginal influence on the attractiveness of market linkages. Therefore, we refer to the comments about Proposition 4, which can be straightforwardly rephrased for Proposition 4, also in light of the considerations about the role of d on comparative statics that is described after Proposition 6.
Finally, we would like to state that we limit to describe in detail the theoretical results of the model (15)–(20) since its numerical investigation (both deterministic and stochastic) would lead to exactly the same scenarios reported in Sects. 4 and 5. From the mathematical point of view, dynamical systems (15)–(12) and (15)–(20) are in one-to-one correspondence if we set \(\delta = k / h\) and \(i^{*} = (l - m) / h + \delta (A + F d) / (1 - b)\). Thus, each single simulation reported in Sects.Footnote 144 and 5 can be obtained from a suitable parameter configuration of model (15)–(20), and consequently, all subsequent comments and economic explanations reported in those Sections still hold, as well as the capability of the model to reproduce stylized facts.
Proofs of Propositions
Proof
(Proposition 1) We \(\omega ^{*} = \omega _{t + 1}, P_t = P_{t + 1} = P^{*}, Q_{t + 1} = Q_t = Q^{*}\) and \(Y_t = Y_{t + 1} = Y^{*}\) and we recall that functions \(g_1\) and \(g_2\) are strictly increasing, so that \(g_i(x)=0,\;i=1,2\) just for \(x=0.\) In (15), we find \(Q^{*} = P^{*}\) from the last equation, which used in the second one provides \(Y^{*} = F\). Plugging \(Y^{*} = F\) in the first equation provides the corresponding expression of \(P^{*}\). Using the equilibrium values in the expression of \(\omega _{t + 1}\), we find (16).
Proof
(Proposition 2) Since \(\omega ^{*}\) positively depends on \(A^{*}\), the comparative statics of \(\omega ^{*}\) with respect to \(\beta \) is straightforward. Moreover, since \(\partial \omega ^{*} / \partial Y^{*} = \partial \omega ^{*} / \partial A^{*} \cdot \partial A^{*} / \partial Y^{*}\), the behavior of \(\omega ^{*}\) on varying \(Y^{*}\) is determined by the sign of \(\partial A^{*} / \partial Y^{*}\). Finally, we have \(\partial \omega ^{*} / \partial F = \partial \omega ^{*} / \partial A^{*} \cdot \partial A^{*} / \partial F\) where
which concludes the proof.
Proof
(Proposition 3) The Jacobian matrix of System (15) is
where
in which we set \(S = e^{- \beta \left( \frac{\alpha _0 + Y \alpha _1 - \xi _c (P - Q) (n - 1) + n \xi _f (F - P)}{P} - \frac{l - m + Yk}{h} \right) }\).
Evaluating J at the equilibrium, we find
where \(\omega ^{*} = \frac{1}{e^{\beta \left( m^{*} - \frac{\pi ^{*}}{F} \right) } + 1}\)
The spectrum of matrix \(J^{*}\) consists of eigenvalue \(1 - \gamma (1 - b) < 1\) and of the eigenvalues of
To guarantee stability, we have to impose that \(1 - \gamma (1 - b) > - 1,\) which provides the first condition in (17), and that the eigenvalues of M belongs to the unitary circle (see, e.g., Medio and Lines 2001), namely
Noting that \(1 + {{\,\mathrm{tr}\,}}(M) + \det (M)\) provides the first condition in (17), \(1-{{\,\mathrm{tr}\,}}(M) + \det (M) = 2 - (N_0 + N \omega ^{*}) \sigma n \xi _f > 0\) always hold, and from \(1 - \det (M)\), we have the last condition in (17) concludes the proof.
Proof
(Proposition 4) In order to study situations in which stability is lost or recovered on increasing a parameter, we assume that for \(\omega ^{*} = 0,\) the last two conditions in (17) are fulfilled, while when \(\omega ^{*} = 1\) at least one of such conditions is violated. From the mathematical viewpoint, this translates into the following conditions
Let \(B_f = 2 / (\sigma n \xi _f - 2 \sigma \xi _c (1 - n))\) and \(B_c = 1 / \sigma \xi _c (1 - n)\). The second and third condition in (17) can be rewritten as \(\omega ^{*} < \bar{\omega }\), where if \(B_f > 0\), we have \(\bar{\omega } = \min \{ \bar{\omega }_f, \bar{\omega }_c \}\), with \(\bar{\omega }_i = B_i / (N ) - N_0 / N, i \in \{ f, c \}\), while if \(B_f \le 0\) we have \(\bar{\omega } = \omega _c\)
Thanks to (22), we have \(0< \bar{\omega } < 1\). Note that if (22) does not hold, we have unconditionally stable/unstable scenarios that are already encompassed in the scenarios arising in the remaining part of the proof for the case of \(0< \bar{\omega } < 1\), so no other situations are actually possible.
Since \(\omega ^{*} = \frac{1}{e^{- \beta A^{*}} + 1}\), the previous relation can be rewritten as
in which the right-hand side is positive (resp. negative) for \(\bar{\omega } > 1 / 2\) (resp. \( \bar{\omega } < 1 / 2)\). Let us focus on the role of \(\beta \). If \(A^{*} > 0\) and \(\bar{\omega } \le 1 / 2\), then the right-hand side in (23) is negative, while the left-hand side is positive, so (23) never holds. Conversely, if \(\bar{\omega } > 1 / 2\), condition (23) is fulfilled only below a certain threshold, so \(\beta \) has a destabilizing effect. If \(A^{*} < 0\) and \(\bar{\omega } \ge 1 / 2\), then the right-hand side in (23) is positive, while the left-hand side is negative, so (23) always holds. Conversely, if \(\bar{\omega } < 1 / 2\), condition (23) holds for \(\beta \) above a certain threshold, so \(\beta \) has a stabilizing effect.
Now we consider k, in a feasibility range for which \(i^{*} > 0\). Recalling the expressions of \(i^{*}\) and \(\pi ^{*}\), condition (22) can be rearranged as
which is a decreasing line, so k can have a neutral or stabilizing effect. The previous inequality also describes the role of \(\alpha _1\), which, since the left-hand side is an increasing line, is neutral or destabilizing.
Rearranging the last inequality and putting in evidence \(Y^{*}\) and collecting, we have
Recalling that \(Y^{*}\) positively depends on d we can conclude that it has a neutral or destabilizing role if \(\alpha _1 / F - k / h > 0\), while it has a neutral or stabilizing role if \(\alpha _1 / F - k / h < 0\).
Collecting the previous results, we have the scenarios reported in the proposition.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cavalli, F., Naimzada, A. & Pecora, N. A stylized macro-model with interacting real, monetary and stock markets. J Econ Interact Coord 17, 225–257 (2022). https://doi.org/10.1007/s11403-021-00320-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11403-021-00320-x