A neural network-based approach for variable admittance control in human–robot cooperation: online adjustment of the virtual inertia

Abstract

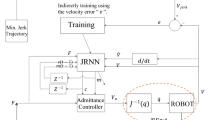
This paper proposes an approach for variable admittance control in human–robot collaboration depending on the online training of neural network. The virtual inertia is an important factor for the system stability, and its tuning is investigated in improving the human–robot cooperation. The design of the variable virtual inertia controller is analyzed, and the choice of the neural network type and their inputs and output is justified. The error backpropagation analysis of the designed system is elaborated since the end-effector velocity error depends indirectly on the multilayer feedforward neural network output. The proposed controller performance is experimentally investigated, and its generalization ability is evaluated by conducting cooperative tasks with the help of multiple subjects using the KUKA LWR manipulator under different conditions and tasks than the ones used for the neural network training. Finally, a comparative study is presented between the proposed method and previous published ones.

Appendix

1.1 First part: derivation of the part $\frac{\partial V }{\partial m }$

Equation (22) is derived in the following equations;

Equation (21) can be rewritten as,

$$\begin{aligned} \frac{\partial V\left( s \right)}{\partial m} & = \left( {\frac{ - 1}{{m^{2} }}} \right)\left( {\left( {F\left( s \right)} \right)\left( {\frac{1}{{\left( {s + \frac{c}{m}} \right)}}} \right) - \left( {\frac{c}{m}} \right)\left( {F\left( s \right)} \right)\left( {\frac{1}{{\left( {s + \frac{c}{m}} \right)^{2} }}} \right)} \right) \\ & = \left( {\frac{ - 1}{{m^{2} }}} \right)\left( {P_{1} \left( s \right) - \left( {\frac{c}{m}} \right)P_{2} \left( s \right)} \right) \\ \end{aligned}$$

(A.1)

By taking the inverse of Laplace Transform for (A.1) and using the convolution theorem, we can get,

$$\begin{aligned} P_{2} \left( t \right) & = \mathop \int \limits_{0}^{t} F\left( u \right) G_{1} \left( {t - u} \right){\text{d}}u \\ & = \mathop \int \limits_{0}^{t} F\left( u \right)\left( {t - u} \right)e^{{\frac{ - c}{m}\left( {t - u} \right)}} {\text{d}}u \\ \end{aligned}$$

(A.2)

It is known from convolution theorem that $\mathop \int \nolimits_{0}^{t} F\left( u \right) G_{1} \left( {t - u} \right){\text{d}}u = \mathop \int \nolimits_{0}^{t} F\left( {t - u} \right) G_{1} \left( u \right){\text{d}}u$, so (A.2) is converted to

$$\begin{aligned} P_{2} \left( t \right) & = \mathop \smallint \limits_{0}^{t} F\left( {t - u} \right)G_{1} \left( u \right){\text{d}}u \\ & = \mathop \smallint \limits_{0}^{t} F\left( {t - u} \right)ue^{{\frac{{ - c}}{m}u}} {\text{d}}u \\ \end{aligned}$$

(A.3)

Based on the approach proposed by Mirsepassi [53], where a graphical evaluation of a convolution integral was presented, if the interval [0, t] is divided into small segments from 0 to $n\Delta t$ where $t = n\Delta t$, (A.3) can be given as

$$P_{2} \left( t \right) = \mathop \int \limits_{0}^{t} F\left( {t - u} \right) G_{1} \left( u \right){\text{d}}u = \left[ {\mathop \int \limits_{0}^{\Delta t} F_{n} G_{1} \left( u \right){\text{d}}u + \mathop \int \limits_{\Delta t}^{2\Delta t} F_{n - 1} G_{1} \left( u \right){\text{d}}u + \cdots + \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} F_{n - i + 1} G_{1} \left( u \right){\text{d}}u + \cdots + \mathop \int \limits_{{\left( {n - 1} \right)\Delta t}}^{n\Delta t} F_{1} G_{1} \left( u \right){\text{d}}u} \right]$$

(A.4)

Equation (A.4) is rewritten as follows,

$$\begin{aligned} P_{2} \left( t \right) & = \mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} G_{1} \left( u \right){\text{d}}u \\ & = \mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} ue^{{\frac{ - c}{m}u}} {\text{d}}u \\ \end{aligned}$$

(A.5)

where the part $\mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} ue^{{\frac{ - c}{m}u}} {\text{d}}u$ is calculated using the “Integration by parts” as

$$\begin{aligned} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} ue^{{\frac{ - c}{m}u}} {\text{d}}u & = \left[ {\frac{ - m}{c}u e^{{\frac{ - c}{m}u}} - \left( {\frac{m}{c}} \right)^{2} e^{{\frac{ - c}{m}u}} } \right]_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} \\ & = \frac{ - m}{c}i\Delta te^{{\frac{ - c}{m}i\Delta t}} - \left( {\frac{m}{c}} \right)^{2} e^{{\frac{ - c}{m} i\Delta t}} - \frac{ - m}{c}\left( {i - 1} \right)\Delta t e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} + \left( {\frac{m}{c}} \right)^{2} e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} \\ & = \frac{ - m}{c}\left( {i\Delta te^{{\frac{ - c}{m}i\Delta t}} + \frac{m}{c}e^{{\frac{ - c}{m} i\Delta t}} - \left( {i - 1} \right)\Delta t e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} - \frac{m}{c}e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} } \right) \\ \end{aligned}$$

(A.6)

By substituting (A.6) into (A.5), then we get

$$P_{2} \left( t \right) = \frac{ - m}{c}\mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \left( {i\Delta te^{{\frac{ - c}{m}i\Delta t}} + \frac{m}{c}e^{{\frac{ - c}{m} i\Delta t}} - \left( {i - 1} \right)\Delta t e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} - \frac{m}{c}e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} } \right)$$

(A.7)

The inverse of the Laplace Transform for $P_{1} \left( s \right)$ is calculated as

$$\begin{aligned} P_{1} \left( t \right) & = \mathop \int \limits_{0}^{t} F\left( {t - u} \right) G_{2} \left( u \right){\text{d}}u \\ & = \mathop \int \limits_{0}^{t} F\left( {t - u} \right) e^{{\frac{ - c}{m}u}} {\text{d}}u \\ \end{aligned}$$

(A.8)

Equation (A.8) is calculated in the same way used before for (A.3), so

$$\begin{aligned} P_{1} \left( t \right) & = \mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} G_{2} \left( u \right){\text{d}}u \\ & = \mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} e^{{\frac{ - c}{m}u}} {\text{d}}u \\ \end{aligned}$$

(A.9)

The part $\mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} e^{{\frac{ - c}{m}u}} {\text{d}}u$ is calculated easily as

$$\begin{aligned} \mathop \int \limits_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} e^{{\frac{ - c}{m}u}} {\text{d}}u & = \frac{ - m}{c}\left[ {e^{{\frac{ - c}{m}u}} } \right]_{{\left( {i - 1} \right)\Delta t}}^{i\Delta t} \\ & = \frac{ - m}{c}\left( {e^{{\frac{ - c}{m}i\Delta t}} - e^{{\frac{ - c}{m}\left( {i - 1} \right)\Delta t}} } \right) \\ \end{aligned}$$

(A.10)

By substituting (A.10) into (A.9), we get

$$P_{1} \left( t \right) = \frac{ - m}{c}\mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \left( {e^{{\frac{ - c}{m}i\Delta t}} - e^{{\frac{ - c}{m}\left( {i - 1} \right)\Delta t}} } \right)$$

(A.11)

By substituting (A.7) and (A.11) into the inverse Laplace transform of (A.1), then we get

$$\begin{aligned} \frac{\partial V}{\partial m} & = \left( {\frac{ - 1}{{m^{2} }}} \right)\left( {P_{1} - \left( {\frac{c}{m}} \right)P_{2} } \right) = \left( {\frac{ - 1}{{m^{2} }}} \right)P_{1} + \left( {\frac{c}{{m^{3} }}} \right)P_{2} \\ \frac{\partial V}{\partial m} & = \frac{1}{{m^{2} }}\mathop \sum \limits_{i = 1}^{i = n} F_{n - i + 1} \left( {\left( {i - 1} \right)\Delta t e^{{\frac{ - c}{m} \left( {i - 1} \right)\Delta t}} - i\Delta t e^{{\frac{ - c}{m}i\Delta t}} } \right) \\ \end{aligned}$$

(A.12)

The way to implement the algorithm of (A.12) or (22) in real time is illustrated in the “second part”.

1.2 Second part: algorithm for Eq. (22)

From Eq. (22) or (A.12), it is noted that after many n loops, some sum terms can be neglected since they are very small (approximately zero). It is difficult to calculate this equation online using huge n loops, because the calculation time will be very long and the robot will stop so we should neglect the terms that approximating zero. To identify at which loop the error will be very small if we neglect these terms, real data with different determined loops (n) are used to calculate the equation. The equation is calculated from i = 1 to i = n and if the terms from i = n − z to i ≥ n that have very small values (approximately close to zero) are ignored then the error percentage is calculated. Figure 14 shows some results of this process for Eq. (22) which calculate $\frac{\partial V}{\partial m}$ and as presented from the diagrams with increasing n the error percentage decreases. It should be noted that in our experiments, we calculate this equation using n = 20 where the error percentage is low (3.75%) in order to shorten the calculation time, so the robot can move smoothly.

Fig. 14

The error percentage by ignoring the small parts from Eq. (22) that calculate $\frac{\partial V}{\partial m}$ after many n loop