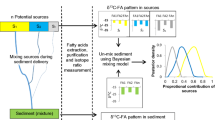
Abstract
Purpose
Accelerated soil erosion poses a global hazard to soil health. Understanding soil and sediment behaviour through sediment fingerprinting enables the monitoring and identification of areas with high sediment delivery. Land-use specific sediment source apportionment is increasingly determined using the Bayesian mixing model MixSIAR with compound-specific stable isotopes (CSSI). Here, we investigate CSSIs of fatty acid (FA) tracer selection with a novel method to identify and investigate the effect of non-informative tracers on model performance.
Methods
To evaluate CSSI tracer selection, mathematical mixtures were generated using source soils (n = 28) from the Rhine catchment upstream of Basel (Switzerland). Using the continuous ranked probability (CRP) skill score, MixSIAR’s performance was evaluated for 11 combinations of FAs and 15 combinations of FAs with δ15N as a mixing line offset tracer. A novel scaling and discrimination analysis (SDA) was also developed to identify tracers with non-unique mixing spaces.
Results
FA only tracer combinations overestimated pasture contributions while underestimating arable contributions. When compared to models with only FA tracers, utilizing δ15N to offset the mixing line resulted in a 28% improvement in the CRP skill score. δ15N + δ13C FA26 was the optimal tracer set resulting in a 62% model improvement relative to δ15N + all δ13C FAs. The novel SDA method demonstrated how δ13C FA tracers have a non-unique mixing space and thus behave as non-informative tracers. Importantly, the inclusion of non-informative tracers decreased model performance.
Conclusions
These results indicate that MixSIAR did not handle non-informative CSSI tracers effectively. Accordingly, it may be advantageous to remove non-informative tracers, and where feasible, all combinations and permutations of tracers should be assessed to optimize tracer selection. Application of these tracer selection steps can help improve and advance the performance of sediment fingerprinting models and ultimately aid in improving erosion mitigation and management strategies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Accelerated soil erosion and sedimentation is a widely recognized global problem that reduces water quality and agricultural output (Bakker et al. 2004; Issaka and Ashraf 2017). Comprehensive and economically feasible mitigation plans are required to reduce accelerated soil erosion. Therefore, effective mitigation plans need to be founded on the accurate identification of erosion sources (Collins and Walling 2004; Walling 2005; Owens et al. 2016).
Sediment source fingerprinting helps identify and apportion the main erosion sources in a catchment. Tracing sediments back to their original sources (e.g., from soils with different land uses), provides a direct, field-based approach that holds the potential to identify the relative contribution of different soil erosion sources to sediment transported downstream in various waterways (Collins et al. 1996; Gibbs 2008; Cooper et al. 2015). The technique uses various properties of the soils and sediments as fingerprints to differentiate the main erosion sources (Collins et al. 1997a, 2001; Walling 2013; Smith et al. 2018). For properties to be able to effectively fingerprint sediment sources, they need to discriminate between sediment sources and remain constant through detachment, transport and deposition processes, or vary in a measurable and predictable way (Motha et al. 2002; Koiter et al. 2013; Belmont et al. 2014; García-Comendador et al. 2023). Essentially, properties of the eroded sediment should remain constant or any variation during these processes must be reproducible.
Sediment fingerprinting has been applied to a wide range of fluvial sediment types including: lacustrine sediment cores (le Gall et al. 2016; Lavrieux et al. 2019), flood plains (Pulley et al. 2015; Kemper et al. 2022), dam reservoir samples (Nosrati et al. 2011; Ben Slimane et al. 2013), and riverine systems (Collins et al. 2001; Bispo et al. 2020; Upadhayay et al. 2018b). A wide range of parameters have been employed to trace sediment sources, including but not limited to radionuclides (Evrard et al. 2013), elemental geochemistry (Batista et al. 2019), compound-specific stable isotopes (Hirave et al. 2021), colour (Martínez-Carreras et al. 2010), diffuse Reflectance Infrared Fourier Transform Spectroscopy (Evrard et al. 2013), ultraviolet–visible absorbance (Lake et al. 2022), and eDNA (Evrard et al. 2019) among others. For more information on the sediment fingerprinting technique, please consult some of the reviews in the literature (Haddadchi et al. 2013; Koiter et al. 2013; Owens et al. 2016; Collins et al. 2017, 2020).
Sediment source apportionment is generally determined by unmixing sediment and soil fingerprints typically using linear equations (Collins et al. 1997b). The reliability of the model outputs is dependent on the mixing model used (Batista et al. 2022), the number of sources, the number of tracers and the dominate source contributing to the sediment load (Vale et al. 2022). Specifically, the accuracy of the apportionment increases when the primary source is well discriminated regardless of the discrimination of the other sources (Vale et al. 2022). Bayesian (e.g., MixSIAR), (Stewart et al. 2015; Stock et al. 2018) and frequentist models (Collins et al. 1997a; Pulley and Collins 2018) have the potential to provide robust and reliable erosion source information fundamental to targeting sediment management practices (Cooper and Krueger 2017; Evrard et al. 2022; Xu et al. 2022).
The compound-specific stable isotopes (CSSI) of plant-derived biomarkers such as fatty acids (FA) and n-alkanes have been used to apportion sediment source contributions from different land uses (Gibbs 2008; Alewell et al. 2016; Upadhayay et al. 2018b; Lavrieux et al. 2019; Hirave et al. 2021). The CO2 fixation routes (C3, C4, or CAM) of plants generate distinct isotopic patterns with the effect being more pronounced in C4 plants than in C3 plants (Reiffarth et al. 2016). Even though they are not species specific, CSSI isotopic values can further distinguish between some plant groups, for example, angiosperms and gymnosperms (Collister et al. 1994; Chikaraishi et al. 2004). Additionally, biological and environmental factors (e.g., altitude and rainfall patterns) can induce variation in the isotopic value (Reiffarth et al. 2016).
The exclusion of short, medium, and non-saturated FAs helps reduce the uncertainty related to input from non-terrestrial plant-derived FAs (Alewell et al. 2016; Reiffarth et al. 2016; Lavrieux et al. 2019). Ultimately, the 13C FA fingerprint of the sediment mixture is determined by source mixing proportions and two parameters in each source: FA concentration and δ13C FA (Upadhayay et al. 2018a). Therefore, the non-linear mixing of the isotopic tracers in the mathematical mixtures requires the incorporation of FA concentration dependency. Additionally, the use of FA isotopes as tracers requires the transformation of unmixing isotopic values to the unmixing sediment. The use of the concentration dependency of FA isotopes incorporates this transformation into the model and therefore requires no additional post organic matter corrections (Alewell et al. 2016).
Fingerprinting with FA CSSIs has limitations, where source values regularly plot along a linear mixing line (Alewell et al. 2016; Lavrieux et al. 2019). Importantly, having sources plot along a mixing line can result in modelled contributions from the central source(s) being misclassified as a contribution from the sources located at the mixing line endpoints. The misclassification has previously been resolved by grouping sources with the subsequent apportionment occurring only between the two grouped sources (Alewell et al. 2016), with the drawback of not being able to distinguish between three or more sources.
The highly correlated δ13C of FA tracers and the resultant linear mixing line are a product of the biosynthesis of very long chain fatty acids (VLCFA, FA22:0—FA30:0). The elongation of long chain fatty acids (LCFA, FA16:0- FA20:0) to VLCFA proceeds with a cyclic four-step process of condensation, reduction, dehydration, and reduction (Erdbrügger and Fröhlich 2020). The elongation of FAs occurs with a δ13C depletion with increasing alkyl length (Chikaraishi et al. 2004). As this relationship is assumed to be similar for VLCFA of different plant groups, this may result in the δ13C FA tracers of different alkyl lengths having a non-unique mixing space and possibly acting as non-informative tracers.
CSSI tracers have been combined with geochemical tracers in an attempt to improve the discrimination between different land covers using non-land-use specific tracers (Lizaga et al. 2022). As geochemical tracers are not land-use specific, they require significant geological differences between land uses and low variability of lithology within land uses (Blake et al. 2012; Hancock and Revill 2013). δ15N has been used previously as a tracer for land-use-specific sediment source apportionment (Papanicolaou 2003; Fox and Papanicolaou 2007; Mukundan et al. 2010). However, the conservativeness of δ15N is questionable (Laceby et al. 2017). Here, we nonetheless use δ15N to expand the δ13C FA mixing line to a mixing polygon for mathematical mixtures (also known as: virtual mixtures and artificial mixtures). When investigating model behaviour using mathematical mixtures, the conservativeness of tracers is less relevant as sediment tracer values are calculated from source soil values and are not subject to degradation and possible isotopic fractionation effects.
Mathematical mixtures using non-concentration dependent tracers (e.g., geochemical tracers) were reported to be equivalent to laboratory mixtures (Batista et al. 2022). Although mathematical mixtures do not fully represent what happens during mixing processes in nature (e.g., signal degradation, tracer alteration in case of non-conservativeness, isotope fractionation, particle size transport selectivity), they are fundamental to understanding and evaluating model performance, and characterizing the uncertainty of the unmixing process (Haddadchi et al. 2014; Batista et al. 2019; Vale et al. 2022).
Currently, there is a limited application of mathematical mixtures to concentration-dependent tracers, in which tracer values of the mixture (e.g., isotopic signatures) are dependent on another parameter in source soils (e.g., the concentration of isotopic tracer). Until recently the validation of concentration-dependent unmixing models has been reliant on the generation of a small number of time-consuming laboratory mixtures (Bravo-Linares et al. 2018) or the over-simplification by the removal of the concentration dependency by assuming that isotopic tracers mix linearly (Collins et al. 2019; Bahadori et al. 2019). However, recently concentration dependent mathematical mixtures have been explored and utilised (Lizaga et al. 2022; Vale et al. 2022) for investigating model parameters.
The deficiency of suitable evaluation tools and metrics for CSSI tracer selection steps has resulted in the legacy of two commonly used assessments: a Kruskal Wallis test to optimize model performance and a polygon/boxplot range test to identify non-conservative tracers. When using a large number of tracers (e.g., geochemical tracers), linear discrimination analysis (LDA) has also been applied to reduce the suite of tracers to an optimal number with maximum discrimination (Gellis and Noe 2013; Walling 2013; Laceby et al. 2015). The LDA tracer reduction step is not commonly included when using CSSIs due to the limited number of CSSI tracers relative to the number of sources being discriminated. Upadhayay et al. (2018b) used LDA with CSSI tracers to remove bulk 13C from the VLCFA tracer suite as bulk 13C did not improve source LDA reclassification. Lizaga et al. (2021) also used LDA as a tracer selection step for mixtures from different time points in an attempt to optimise tracer selection for each mixture. An argument for not including the LDA when using MixSIAR is the hypothesis that the covariance structure of MixSIAR (Stock et al. 2018) effectively handles conservative non-informative tracers resulting in a null or a beneficial impact (Smith et al. 2018). The model's output should accurately reflect the real-world scenarios, without being reduced in the interest of enhancing model performance. An additional argument for maximising the number of tracers is to reduce the potential influence of possible non-conservativeness within the tracer set.
Land use-specific sediment source apportionment with CSSIs has been determined with all tracers that pass the two prerequisites without further validation of tracer selection. Consensus ranking (Lizaga et al. 2020) and consistent tracer selection (Latorre et al. 2021) methods have been recently applied to remove non-conservative tracers and tracers which have non-consistent results. Others have argued that tracer selection should be made on a robust bio-physical–chemical foundation (Laceby et al. 2015; Batista et al. 2019), with adjustments to the tracer set aimed at supporting the reliability and accuracy of the model.
We hypothesize that the relationship between δ13C depletion and increasing alkyl length is similar for all land uses. If this is true, the mixing space for each FA tracer may be seen as a direct isometry translation of each other (i.e., every point of the mixing shape is moved the same distance and in the same direction), resulting in additional FA tracers having non-unique mixing spaces and being non-informative. This effect may result in the inclusion of additional δ13C FA tracers being seen as essentially comparable to the addition of non-informative clone tracers (i.e., an exact copy of a tracer included as an additional tracer). In this study, clone tracers are used as a standard example of tracers which have identical mixing spaces and therefore can potentially be seen as non-informative tracers. In particular, clone tracers are used to determine the capacity of the mixing model to handle non-informative tracers. The comparison of model performance using additional FA tracers and non-informative clone tracers helps to quantify the information gained by using an additional FA tracer.
Further evaluation and optimization of CSSI tracer selection in sediment source fingerprinting research is critical to increase the reliability of apportionment estimates and as a result the development of appropriate sediment management practices. In this study, we present the results for all combinations of δ13C FA (n = 11) and FA tracer sets including δ15N (n = 15) using concentration-dependent mathematical mixtures. Using a novel scaling and discrimination analysis (SDA), non-informative tracers that have a non-unique mixing space are identified. Importantly, we test the hypothesis that the covariance structure of MixSIAR can adequately handle non-informative tracers using clone tracers.
2 Materials and methods
2.1 Site description and sampling
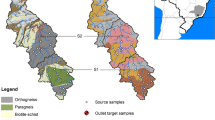
The study was conducted using source soils from the Rhine catchment upstream of Basel (10,687 km2) (draining northern Switzerland and parts of southern Baden-Württemberg, Germany) and downstream of the large lakes (i.e., Konstanz, Zürich, Hallwil, Sempach, and Biel) (Fig. 1). Land use within the catchment area was mainly classified as arable land (28%), mixed forest (20%), and pasture (13%).
The Basel Rhine catchment was divided into four sub-catchments: The Birs catchment, the Aare catchment, a Rhine catchment downstream of the Aare entering the Rhine, and a Rhine catchment upstream of the Aare entering the Rhine (Fig. 1). Each sub-catchment contained 3–8 sites of the major land-use classes: arable, pasture, and forest. With the aid of a connectivity model by Borselli et al. (2008), land-use specific sample locations within each sub-catchment were selected based on their high likelihood to contribute suspended sediment to the watercourses. To reduce analytical costs while maintaining the representativeness of the source samples, composite samples were generated from four individual samples located 2 m apart using a soil extraction cylinder (diameter 5.5 cm, length 5 cm). As suggested by Laceby et al. (2017) and Evrard et al. (2022), the size fraction of source soils analysed (< 100 µm), was selected based on particle size analysis of flood sediment from wider research project. Information on the sediment collection and size analysis is included in Online Resource 1.
2.2 Laboratory analysis
Lipids were extracted from 0.5–1.5 g of soil using CH2Cl2: MeOH (9: 1 v∕v) in an Accelerated Solvent Extractor (Dionex ASE 350) with the addition of FA19:0 as an internal standard. The total lipid extract was separated into polar, neutral, and acidic fractions using solid-phase extraction on aminopropyl bonded silica as described in Jacob et al. (2005). The acidic fractions were eluted using 1% formic acid in diethyl ether on a pre-acidified column. The acidic fraction was subsequently methylated at 60 °C for 1 h using 1 ml of 14% BF3 in MeOH. Fatty acid methyl esters were extracted from the solution by agitating it four times with 2 mL hexane in the presence of 1 mL of 0.1 M KCl. The δ13C FA isotopic ratio was measured using a Trace 1310 GC instrument interfaced online through a GC-Isolink II to a Conflo IV and Delta V Plus isotope ratio mass spectrometer (Thermo Fisher Scientific) as described by Lavrieux et al. (2019). Nitrogen concentrations and δ15N values for source soils were measured by Flash EA (Thermo Finnigan Delta plus XP mass spectrometer coupled with Flash EA 1112 series elemental analyser supplied by Thermo Finnigan, Waltham, MA, USA). Carbon and nitrogen stable isotope ratios were reported in delta notation, per mil deviation from Vienna Pee Dee Belemnite (VPDB) and atmospheric nitrogen (AIR) respectively.
2.3 Mathematical mixtures
Mathematical mixtures were generated using the mean stable isotopic ratio and mean concentration of tracers (i.e., bulk N, FA (24, 26, 28, 30)) for arable (n = 10), pasture (n = 7), and forest (n = 11) soil samples. Proportions of source contributions were created using a random number generator sampling from a Dirichlet distribution between 0 and 100 with the condition that the sum of source proportions must equal 1. The python script used to generate mathematical mixtures is appended in the Online Resource 2 (an excel version of the mathematical mixture formulation is appended as Online Resource 3). To ensure evenly distributed mixing proportions of each source, 150 mathematical mixtures were generated (the mean of each source proportion of 150 mixtures was ~ 33%). Concentration-dependent mathematical mixtures were generated as shown in Eq. (1).
Where V is the mean isotopic value of the tracer t, C refers to the mean concentration for all (\(\forall )\) tracers in a set (\(\in )\) of tracers T in source S. SO refers to the number of sources and P refers to the known proportions of the mathematical mixtures.
2.4 End member mixing model
Mathematical mixtures were modelled using the open-source MixSIAR R package (Stock et al. 2018). MixSIAR was run with concentration dependency utilising the concentration of both FAs and N, transforming the unmixing of isotopes to the unmixing sediment/mixtures. Therefore, an organic matter correction was not applied post hoc to prevent a secondary transformation. Priors were set to uninformative and all MixSIAR runs used the same model parameters: chains = 3, chain length = 3,000,000, thin = 500, burn = 2,700,000 with a ‘very long’ run time. The convergence of the mixing model was assessed by using the Gelman-Rubin diagnostic, with model output being rejected if variables scored > 1.0. The R script used for all models is appended in the Online Resource 4.
While the ‘residual x process’ error structure has been applied appropriately to multiple mixture samples (Cooper et al. 2015; Smith et al. 2018; Upadhayay et al. 2018b; Blake et al. 2018; Vale et al. 2022), likely the high cost and processing time of the analysis of CSSI has led to the predominant use of ‘process only’ error structure using single mixture samples (Gateuille et al. 2019; Reiffarth et al. 2019; Liu and Han 2021). As such, a single sample of each mixture proportion was unmixed in MixSIAR using the “process only” error structure, in which the variation in the mixtures is assumed to be fully dependent on the variation in the sources (Smith et al. 2018).
2.4.1 Model evaluation
The probabilistic output of MixSIAR should be evaluated using probabilistic metrics rather than deterministic metrics such as mean absolute error (Batista et al. 2022). The continuously ranked probability score (CRPS) (Matheson and Winkler 1976) is a generalization of the mean absolute error toward a probabilistic perspective and can be thought of as the total displacement needed to move the output distribution density to the observed single outcome or known mixture proportion. CRPS is negatively orientated with smaller values equating to better model performance. A perfect score of 0 represents the entire density of the output placed exactly on the outcome value. Deviation from the perfect score results from a lower density of probability around the observed value. CRPS has provided a useful metric to account for both accuracy and precision of unmixing models and has been suggested to be particularly applicable for model comparison and tracer selection analysis (Batista et al. 2022). CRPS was calculated using the python package ‘properscoring’ and is used to report on individual model performance.
The CRPS of all tracer combinations are further used to evaluate the accuracy of using LDA for tracer selection. Using the R package ‘KlaR’, the model performance of the tracer section by a stepwise forward variable selection using the Wilk's Lambda criterion (niveau = 0.1) is compared to the empirically selected optimal tracer combination with the lowest CRPS.
Model comparisons are then evaluated by the continuously ranked probability skill score (CRP skill score) shown in Eq. (2) (Pedro et al. 2018). The CRP skill score is a comparative metric of the accuracy and precision between two mode outputs. Where CRPSm and CRPSref are the CRPS of the new model (the model compared, e.g., δ15N + δ13C all FA’s) and the reference model (the model compared against, e.g., only δ13C all FA’s.) respectively.
Negative CRP skill score values indicate the new model does not outperform the reference model as the newer model requires more displacement of output distribution density to be shifted onto the known value than the reference model. A value of one indicates that the newer model has a perfect skill score compared to the reference model (Pedro et al. 2018).
2.4.2 Tracer selection and prediction bias analysis (PBA)
The unmixing performance of ideal tracers should be independent of the source contribution, as contribution-dependent model performance is an indication of prediction bias. Predictive bias and dominant source effects on model output have been previously recognised and suggested to be an effect of poor tracer source discrimination (Vale et al. 2022). The hypothesis that FA tracers have similar and non-informative mixing spaces infers that additional FA tracers provide minimal additional source discrimination information. If the hypothesis is true, predictive bias will be decreased by reducing the number of tracers with a non-unique mixing spaces (e.g., FA tracers) as any added source uncertainty is removed. To assess if apportionment estimates occur with predictive bias, known source proportions of mathematical mixtures are plotted against the model performance (CRPS) for each source (predictive bias analysis-PBA). Two tracer sets (δ15N + all δ13C FAs and δ15N + δ13C FA26) were used to illustrate the effect of reducing the number of tracers on predictive bias.
2.4.3 Non-informative tracers – scaling and discrimination analysis (SDA)
MixSIAR uses the relative source-sediment-source positions for un-mixing. Therefore, tracers that exhibit differences in their mixing space by only direct isometry translation, can be seen mathematically, as being identical and potentially non-informative. To evaluate if δ13C FA tracers have non-unique mixing spaces and are direct isometry translations of each other, a novel scaling and discrimination analysis (SDA) was developed. Scikit-learn’s MinMaxScaler package (Pedregosa et al. 2011) was used to scale tracer values between 0 and 1 across all sources. Scaling retains the relative location, shape, and distribution of the sources for each tracer, enabling comparison of relative source locations between tracers. A Kruskal Wallis H-test (p < 0.05) was used to evaluate the similarity between the relative source locations of the scaled tracers. Scaled tracers depicting a non-significant difference in source locations will consequently have mixing spaces which are direct isometry translations and can therefore be seen as non-informative.
2.4.4 Non-informative tracers – clone tracer analysis
To evaluate MixSIAR's effectiveness to model tracers with non-unique mixing spaces, δ13C FA26 was utilized as a non-informative clone tracer (an exact copy of a tracer used as an additional tracer). This clone tracer was then added three times to the δ15N + δ13C FA26 tracer set. Each addition of FA26 was evaluated individually by CRPS to identify the effect of additional non-informative tracers. The comparison of model performance using additional FA tracers and non-informative clone tracers is then used to quantify the information gained by using an additional FA tracer.
3 Results and discussion
3.1 Source tracer values
To reduce errors associated with input from non-terrestrial plant-derived FAs, only VLCFAs (FA22:0- FA30:0) (hereby referred to as FAs) were considered (Alewell et al. 2016; Reiffarth et al. 2016; Upadhayay et al. 2017; Lavrieux et al. 2019). Forest sources contained the highest concentration of FAs (mean: 19.4 µg g−1, SD: 5.0 µg g−1) and the most δ13C enriched isotopic values for all FA tracers (mean δ13C: -33.4 ‰, SD: 1.3 ‰), (Tables 1 and 2, Fig. 2). Pasture sources had the most δ13C depleted isotopic values for all FAs (mean δ13C: -36.2 ‰, SD: 1.4 ‰) and mid-ranged FA concentrations (mean: 11.9 µg g−1, SD: 1.9 µg g−1). Arable sources contained the lowest concentration of FAs (mean: 7.7 µg g−1, SD: 1.1 µg g−1) and mid-ranged FA isotopic values (mean δ13C: -35.0 ‰, SD: 1.7 ‰). The δ13C FA values for these land uses are similar to previous findings in fresh biomass (Chikaraishi et al. 2004) and soils from the same land use classification in similar geographic and climate regions (Alewell et al. 2016; Lavrieux et al. 2019; Hirave et al. 2021).
The δ15N value of soil reflects the isotopic signature of nitrogen inputs, outputs and internal processes of the system (Amundson et al. 2003). δ15N values ranged from a mean of 6.3 ‰ (SD 0.9 ‰) in arable land to 4.0 ‰ (SD 0.9 ‰) in pasture and 0.0 ‰ (SD 1.6 ‰) in forest soil. Nitrogen concentrations ranged from a mean 0.5 mg g−1 (SD 0.1 mg g−1) in pasture to a 0.4 mg g−1 (SD 0.1 mg g−1) in forest and 0.3 mg g−1 (SD 0.1 mg g−1) in arable soil (Tables 1 and 2, Fig. 2). The δ15N values are comparable to previous results of similar land uses (Fox and Papanicolaou 2007; Mukundan et al. 2010). Source tracer distribution are similar to those in the literature (Fox and Papanicolaou 2007; Mukundan et al. 2010; Alewell et al. 2016; Lavrieux et al. 2019; Hirave et al. 2021). As such, we found the samples representative of their land use classification and therefore are suitable for the mathematical mixture analysis of this study. However, we suggest that further source soil sampling should be done for the reliable unmixing of real suspended sediment. The full source value data set is appended in the Online Resource 5.
3.2 Source discrimination and mixing line origins
The discriminative power of the isotopic tracers between each possible source pair was tested before MixSIAR modelling. 93% of all tracers significantly discriminated between all pairs of sources (Kruskal Wallis, p < 0.05). Only δ13C FA24:0 did not discriminate between arable and forest sources (Fig. 2). All land uses displayed similar δ13C depletion with increasing alkyl chain length (x̄ = -1.1 ‰ δ13C per two additional carbon atoms, SD = 0.13 ‰) (Fig. 3).
The results are consistent with the literature that suggests a depletion of up to -2.7 ‰ in C3 plants from FA24:0 to FA32:0 (Agrawal et al. 2014; and references within). The small variation of δ13C enrichment and alkyl chain length (SD = 0.13) between all sources suggests the δ13C enrichment during FA elongation is not land-use dependent. The similar enrichment of the mean δ13C FAs with increasing alkyl length (forest: R2 = 0.999, arable: R2 = 0.952 and pasture: R2 = 0.995) (Fig. 3) results in a mixing line for all FA tracers (Fig. 4) with the isotopic value of forest and pasture located at either end of the mixing line.
Iso plots of δ15N and δ13C FA with colours indicating land use type. δ13C FA tracers present the mixing line problem that occurred using FA tracers only. It is unlikely that there will be a perfect 1:1 mixing line when there are multiple samples for each source. Nonetheless, the central location of one source consistently between two other source end members will create challenges (i.e. central source(s) being misclassified as a contribution from endpoint sources) during the modelling process. The addition of δ15N expands the mixing line/space to more of a mixing polygon that provides the source discrimination necessary for more accurate and less uncertain model results
3.3 The mixing line problem
The FA mixing line illustrated in Fig. 4 is present in δ13C FA sediment fingerprinting studies with a similar land-use classification of sediment sources (Alewell et al. 2016; Lavrieux et al. 2019). The linear mixing line problem is not confined to isotopic tracers. Colour (Barthod et al. 2015) and geochemical tracers (Bouchez et al. 2011) have also presented a linear mixing line. The similar alkyl length—δ13C relationship of the different land uses is a result of the same mechanistic process of FA elongation for all land uses. Interestingly, this effect is not observed in all reported cases of arable, pasture and forest land uses (Upadhayay et al. 2020; Lizaga et al. 2021). Deviation from this relationship and the absence of a mixing line could indicate that the previous land use or crop type contained a higher concentration of a specific FA, which is now more present in the current soil compared to other legacy FAs. Conservative tracers, such as FAs, can persist in the soil after a change in land management (Upadhayay et al. 2020). Swales and Gibbs (2020) demonstrated that isotopic shifts occur during a land use transition, and therefore, past land use management should be considered when grouping source soils. This legacy effect has the potential to increases the uncertainty in source distributions and reduce source discrimination and subsequent unmixing performance. However, the legacy effect can potentially be used beneficially for fingerprinting if sources are grouped by their crop cycle rather than the current crop.
3.4 Evaluation of mathematical mixtures
All possible permutations and combinations of δ13C FA tracers (n = 11) were evaluated using 150 concentration-dependent mathematical mixtures (Fig. 5A). Results demonstrated a general increase in CRPS of all sources as the number of δ13C FA tracers is increased (2 FAs mean CRPS: 0.165, 3 FAs: 0.188, 4 FAs: 0.195). A summary of all tracer combination CRPS is appended in the Online Resource 1.
The elevated errors for the arable source contributions (mean CRPS: 0.260) are probably directly related to the location of arable FAs in the mixing space, resulting in the underreporting of arable sources with their contributions likely being misclassified as pasture. Misclassification of the arable source contribution potentially results in the over-estimation of pasture contributions, as suggested by pasture having the second highest CRPS value (mean CRPS: 0.209) for all δ13C FA tracers sets. Strong discrimination of forest sources resulted in a relatively low CRPS value (mean CRPS: 0.058) for all sets of tracers. Forest apportionment estimates were relatively independent of the number of δ13C FA tracers, suggesting that any additional source-based uncertainty induced by additional δ13C FAs was out-weighed by the beneficial source discrimination gained. This collaborates with the iso plots that display low source uncertainty of the forest using any δ13C FA tracer (Fig. 4). Although, our findings differ from those of Vale et al. (2022), who reported that the forest source apportionment had the highest mean absolute error (MAE) among all sources. Both studies demonstrate that the sources with a higher source discrimination have increased model performance. This indicates the ability to discriminate between sources is likely a crucial factor in model performance. Nonetheless, there is a necessity for catchment specific apportionment validation as source discrimination is highly variable even with similar land use groups. Overall, the performance of the model is more dependent on the number of δ13C FA tracers rather than the selection of individual tracers due to mixing space similarities.
Including δ15N to offset the mixing line for all combinations of tracers (n = 15) increased the performance of the model of all sources (FA combinations mean CRPS: 0.175, δ15N + FA combinations mean CRPS: 0.091) (Fig. 5B). Importantly, pasture and arable source apportionment estimates decreased in performance with additional δ13C FA tracers (Pasture mean CRPS: δ15N + 1 FA 0.073,2 FAs CRPS: 0.102, 3 FAs: 0.161, 4 FAs: 0.184 and arable mean CRPS: δ15N + 1 FA 0.079,2 FAs CRPS: 0.109, 3 FAs: 0.172, 4 FAs: 0.184) suggesting any beneficial source discrimination by additional δ13C FA tracers is out-weighted by the increase in source-based uncertainty. Further evidence supporting these results is the iso plots that depict a large intersection between the arable and pasture source groups for all δ13C FA tracers (Fig. 4). Consequently, the mixing space shifts from a mixing line to a mixing polygon with the inclusion of δ15N, reducing pasture-arable misclassification.
3.5 Tracer selection by the analysis of all combinations
The benefit of using δ15N as a mixing line offset tracer is presented in Fig. 6 with the solid line indicating perfect fit (i.e., estimated proportion equals the known proportion). Figure 6(A) highlights the only δ13C FA tracer set’s inaccurate and underestimated apportionment of arable contribution and the overestimation of pasture contribution. Again, the inaccuracy can be attributed to the central location of arable in the mixing space for all δ13C FA tracers, causing an underestimation of arable contributions as they are misclassified as pasture contributions. This centralised source location challenge and misclassification has been presented previously by Alewell et al. (2016) and Lavrieux et al. (2019).
The inclusion of the δ15N tracer reduced the overestimation of pasture and the underestimation of the contribution of arable sources (Fig. 6B). Using the CRP skill score as a comparative model performance metric, the expansion of the mixing space using δ15N had a mean 18% (median 22%) CRP skill score model improvement compared to using only δ13C FAs. The improvement of the model output using δ15N as an additional tracer was expected by the expansion of the δ13C FA linear mixing line into a more suitable mixing polygon.
When examining all potential tracer combinations, δ15N + δ13C FA26 (Fig. 5C) had the best model performance for all permutations with a mean 16% (median 62%) improvement compared to δ15N + all δ13C FAs (Fig. 5B). The offset between mean and median is a result of the model predicting low contributions for all arable mixture proportions, at these low arable contributions, the model is likely correct for the wrong reasons. The increase in the accuracy and uncertainty of estimated source apportionment using δ15N + δ13C FA26 (Fig. 6C) results in the known source proportions being bracketed by the estimated values. The increase in uncertainty of the model compared to using δ15N + all δ13C FA tracers suggests that a reduction in the number of δ13C FA tracers increases the number of possible solutions to the unmixing equation.
Although LDA is commonly used to optimise the power of discrimination when handling a large number of tracers, it is used irregularly for CSSI tracer selection. The accuracy of using LDA for tracer selection was investigated with a stepwise forward variable selection using the Wilk's Lambda criterion (niveau = 0.1), which selected δ15N + δ13C FA24 + δ13C FA26 as the optimal tracer set (LDA reclassification score 89%). Interestingly, the model performance of the LDA selected tracers decreased by 24% compared to δ15N + δ13C FA26. The poor performance of the LDA selected tracers may be attributable to the mixing model's inclusion of concentration dependency, which is ignored by the LDA.
3.6 Tracer selection and prediction bias analysis (PBA)
Predictive bias and the impact of the dominant source on model output has been identified previously in sediment fingerprinting and been described as a product of the source discrimination (Vale et al. 2022). Ideal tracers should contain enough discrimination power for null predictive bias; however, this is not the case with real tracers. To assess if predictive bias effects are reduced by the removal of tracers which have non-unique mixing spaces, known source proportions of mathematical mixtures are plotted against the model performance (CRPS) for each source (predictive bias analysis-PBA) (Figs. 7 and 8). PBA of δ15N + all δ13C FA and δ15N + δ13C FA26 was used to illustrate the effect of reducing source uncertainty by removing non-informative tracers.
The prediction bias analysis of δ15N and δ13C FA26 shows how the model's performance for each source is impacted by different source proportions, with the contribution of each source plotted against the mean model's performance (where higher CRPS values indicate lower performance). By comparing the linear regression slope to Fig. 7, it is clear that that there is a decrease in predictive bias with less non informative tracers
PBA of the δ15N + all δ13C FA tracer set illustrates the decrease in arable and pasture performance with increasing arable contribution (Fig. 7). The extremely similar and linear relationship between arable and pasture CRPS is strong evidence for the misclassification of arable and pasture as the model underestimates and overestimates contributions from arable and pasture respectively. The clear discrimination of the forest source for all tracers (Fig. 4) resulted in the performance of the forest estimates being not affected by different source contributions. The PBA of the δ15N + δ13C FA26 tracer set depicts a reduction in the linear regression slope indicating a reduction in predictive bias effects (Fig. 8). It can be assumed that this is the result of a reduction in source uncertainty, when using a single FA tracer. The PBA highlights the balance between the source uncertainty error and the discriminative information gained by additional tracers.
3.7 Identifying non-informative tracers by scaling and discrimination analysis (SDA)
The tracers' balance of source discrimination and source uncertainty is determined on a regular basis using boxplots and a Kruskal Wallis test (Fig. 2). However, tracers are not independent factors and work in the mixing model simultaneously. The current approach to tracer selection is to see if individual tracers can distinguish between sources. As an alternative, we investigated whether it is possible to distinguish various FA tracers based on mixing space.
The majority of δ13C FA tracers (94%) had significantly different source distributions (p < 0.05) (except δ13C FA28 –FA30 in arable) (Fig. 9A, Table 3, Left). This can lead to the assumption that each tracer has valuable information for the model. However, the difference between absolute source distributions of each tracer (distance of source distribution from 0) is caused by each FA tracer being depleted by approximately -1.1 ‰ δ13C per two additional carbon atoms (similarly shown by Chikaraishi et al. 2004) (Fig. 3). Considering that MixSIAR uses relative (source-source) tracer vales rather than the absolute tracer value, tracers which demonstrate modification of all source distributions by direct isometric translation (e.g., every point/source of the mixing shape is moved in the same distance and in the same direction) can be considered mathematically non-unique in terms of mixing space.
A δ15N and δ13C FA grouped by source, demonstrating the linear relationship of δ13C FA and alkyl chain length B δ15N and δ13C FA tracers scaled and grouped by source allows comparison of relative source-source distributions for each tracer. Tracer values are scaled using the max and minimum value of each tracer over all land uses
To provide an alternative and more robust line of evidence of non-unique mixing spaces of FA tracers, the tracer values were scaled between 0 and 1 across all sources. Scaling retains the relative location, shape, and distribution of the sources for each tracer, enabling comparison of the relative source locations of different tracers using Kruskal Wallis test and as such is a suitable tool for evaluating if tracers have significantly different mixing spaces.
The scaled value of δ15N was shown to be significantly different (p < 0.05) to all δ13C FAs for all land uses (Fig. 9B, Table 3, Right). In contrast, only 17% of FA tracers had significant differences between any of the scaled source values. Pasture had no significant differences between any scaled δ13C FA. Forest and arable only had a significant difference between two and one pair of scaled tracers, respectively (Forest: δ13C FA26 – FA30:0 and δ13C FA28 – FA30. Arable: δ13C FA24 – FA30) (Fig. 9B). The minimal but present uniqueness of mixing space for 20% of the FAs in the forest source can be assumed to be caused by a more biodiverse FA input, while the non-uniqueness of 10% of FAs in arable sources could be a result of the legacy tracer signal from crop rotation (Upadhayay et al. 2020). δ13C depletion during the FA elongation processes appears to be similar for all land uses, with any land-use-specific isotopic variation during FA elongation being negligible when compared to the intra-source variability. The linear relationship between δ13C and FA alkyl length causes FA tracers to be direct isometry translations of each other and consequently, there is minimal significant differences between the relative source locations of each FA tracer (Fig. 9B) and as such, the mixing space can be thought of as being non-unique for all δ13C FA tracers. The similarities between scaled source values for all tracers are illustrated in Fig. 10. δ15N is depicted to have to have non-translation transformations of the mixing shape compared to FAs. The similarities in the mixing shape for all FAs indicate that direct isometry translation is present between different FAs, making multiple FA tracers non-unique and non-informative.
Scaled δ15N and δ13C FA tracer values used to compare the relative source distributions for each tracer. Tracer values are scaled using the max and minimum value of each tracer over all land uses. The mixing space is shown to be similar for all FAs while δ15N mixing space is shown to be modified by non-isometry translations
Considering MixSIAR uses the relative source-sediment-source positions for un-mixing, any modification of the mixing space by only direct isometry translation has a null effect on the mixing space. Therefore, any tracer with a mixing space that is a direct isometry translation of another tracer can be seen as almost identical and either one of the tracers is non-informative.
3.8 Non-informative tracers – clone tracer analysis
To assess MixSIAR’s performance when using tracers with identical mixing spaces, a non-informative clone tracer (an exact copy of a tracer used as an additional tracer) was used as a direct approach to test non-informative tracer behaviour. Three sequential additions of the clone tracer δ13C FA26 were added to the δ15N + δ13C FA26 tracer set (Fig. 11A). Increasing the number of clone tracers decreased the model performance (δ15N + 1 × δ13C FA26 CRPS: 0.034, 2 × FA26: 0.181, 3 × FA26: 0.199, 4 × FA26: 0.202). This effect can be attributed to the lack of any additional beneficial information when using tracers with non-unique mixing spaces, whilst the source uncertainty error induced by adding multiple clone tracers is propagated. In this study, these results disagree with the notion that MixSIAR handles non-informative tracers sufficiently (Smith et al. 2018).
Comparison between model performance using A additional clone tracers (δ13C FA26) and B additional different δ13C FA tracers to the δ15N + δ.13C FA26 tracer set. The mean CRPS of all tracer combinations with the same number of tracers is used for additional FA tracers to improve the representative of results (higher CRPS indicates lower performance)
Optimizing model performance strives to balance new beneficial source discrimination and the additional source uncertainty brought to the model by each additional tracer. Figure 11A indicates that when using a clone tracer, the source uncertainty is propagated until the addition of a fourth tracer. The difference in CRPS between clone tracers and different FAs was used as a measure of information gain when using additional FA tracers. The mean CRPS of different FA tracer combinations with the same number of tracers displayed a similar trend to that when adding additional clone tracers (δ15N + 1 × δ13C FA CRPS: 0.060, 2 × FA: 0.081, 3 × FA: 0.124, 4 × FA: 0.138) (Fig. 11B). Small non-translation modifications of FA mixing spaces resulted in the CRPS using additional different FA tracers being generally lower (mean 22%) than additional clone tracers. Therefore, from a mathematical perspective, different FAs are not completely non-informative. Although, from a practical perspective additional FA tracers are essentially non-informative, as any beneficial information gained is outweighed by the error added from the propagation of source uncertainty.
Indeed, this approach is highly experimental, and it is unlikely that you will have truly identical tracers in the field. Nonetheless, this method demonstrates that non-informative tracers can add bias to a model, as additional FA tracers may bring limited additional information for unmixing. When using different FAs, our results demonstrate that the error gained by mixing spaces translation effects outweighs the information gained from non-translation modification. This, however, may not be the case for all catchments and tracers.
An intriguing area of investigation is how the balance of source discrimination and tracer mixing space similarities effect model performance. CSSI of FAs have a relatively narrow range of possible source values (ca. 10–40 ‰) compared to other tracers (e.g., geochemistry). When tracers with a higher degree of source discrimination, though identical mixing spaces, are modelled, the propagation of source uncertainty may be out weighted and potentially result in improved model performance.
4 Conclusion
Using mathematical mixtures, the addition of δ15N to expand the CSSI FA mixing line, improved the model by 22% compared to using only δ13C FAs. The evaluation of possible combinations of tracers indicated that δ15N + δ13C FA26 was the optimal tracer set and had a 62% improvement compared to δ15N + all δ13C FAs. LDA tracer selection is regularly used in the literature to select the optimal suite of tracers to increase model performance. However, in this case, the tracers selected by the LDA did not provide the optimal tracer selection. Additional δ13C FA tracers had a negative influence on model performance, indicating that increasing the number of conservative tracers does not necessarily result in improved performance, as previously suggested when using a Bayesian framework. However, the reduction in number of tracers will increase the influence of any non-conservative tracers. As mathematical mixtures, by definition, do not contain non-conservative tracers, the potential influence of non-conservative tracers needs careful consideration when apportioning sediment sources.
Our results indicated there is a reduction of predictive bias when using a single FA tracer. Using a novel SDA test, additional FAs were shown to have non-unique mixing spaces. Considering MixSIAR uses the relative source-sediment-source positions for un-mixing, any tracer which exhibits a non-unique mixing space can be seen as non-informative. Using a clone tracer to evaluate MixSIAR’s performance handling non-informative tracers resulted in strong evidence of MixSIAR’s insufficient handling of tracers with non-unique mixing spaces. In particular, model performance decreased when using additional FA as well as clone tracers.
Land-use-specific sediment source apportionment using FA CSSIs requires a supplemental offset tracer that is not dependent on the C3-C4 discrimination pathway. Since a single FA CSSI had the best performance with an additional offset tracer, an alternative single tracer to FA CSSIs that uses the C3-C4 discrimination pathway for source discrimination such as bulk isotopes may be more accessible and have similar unmixing performance. However, the conservativeness and unmixing performance of these tracers need to be explored further; the latter can be evaluated confidently by using mathematical mixtures. Even though adding δ15N as a tracer in this study outperformed the combination of several FA CSSI, δ15N may be prone to isotopic fractionation during the degradation of molecules and thus may not meet the requirement of a conservative tracer under real world situations, where molecules are subject to transport and possible degradation. δ15N may be useful in scenarios where the balance between beneficial information gained by improving source discrimination outweighs any effect of modification or fractionation of the tracer during sediment mobilization, transport and deposition processes. Here, we capitalized on the availability of δ15N data (which is analysed simultaneously with bulk δ13C) to demonstrate the utility of additional tracers that have an alternative mixing space.
In fingerprinting applications, additional tracer selection steps should be considered, including: 1) checking the uniqueness of tracer mixing spaces by SDA, with the removal of tracers that show non-unique mixing spaces, and 2) where feasible, analysing all combinations and permutations of tracers using mathematical mixtures to further optimize tracer selection. Although computationally intensive, it can help identify the optimal tracer suite for modelling. Even though this method is applied to FA CSSI and δ15N tracers in this study, this method is potentially appropriate for broader application to identify non-informative tracers. This includes multiple fingerprinting parameters (e.g. fallout radionuclides, spectra and geochemical tracers) in which the co-linearity of tracers is not uncommon. However, we suggest further exploration of mathematical mixtures to determine the effect of different error structures on model performance and the validity of organic matter or particle size corrections. We anticipate that the use of mathematical mixtures and tracer combinations as a decisive tracer selection step will enable a wider range of applications for sediment fingerprinting, improve our knowledge of the dynamics of soil and sediment in the environment, and enhance soil erosion mitigation techniques.
Data availability
The authors confirm that the data supporting the findings of this study are available within the Online Resources.
References
Agrawal S, Galy V, Sanyal P, Eglinton T (2014) C4 plant expansion in the Ganga Plain during the last glacial cycle: Insights from isotopic composition of vascular plant biomarkers. Org Geochem 67:58–71. https://doi.org/10.1016/j.orggeochem.2013.12.007
Alewell C, Birkholz A, Meusburger K et al (2016) Quantitative sediment source attribution with compound-specific isotope analysis in a C3 plant-dominated catchment (central Switzerland). Biogeosciences 13:1587–1596. https://doi.org/10.5194/bg-13-1587-2016
Amundson R, Austin AT, Schuur EAG et al (2003) Global patterns of the isotopic composition of soil and plant nitrogen. Global Biogeochem Cycles 17: https://doi.org/10.1029/2002GB001903
Bahadori M, Chen C, Lewis S et al (2019) A novel approach of combining isotopic and geochemical signatures to differentiate the sources of sediments and particulate nutrients from different land uses. Sci Total Environ 655:129–140. https://doi.org/10.1016/j.scitotenv.2018.11.084
Bakker MM, Govers G, Rounsevell MDA (2004) The crop productivity-erosion relationship: An analysis based on experimental work. CATENA 57:55–76. https://doi.org/10.1016/j.catena.2003.07.002
Barthod LRM, Liu K, Lobb DA et al (2015) Selecting color-based tracers and classifying sediment sources in the assessment of sediment dynamics using sediment source fingerprinting. J Environ Qual 44:1605–1616. https://doi.org/10.2134/jeq2015.01.0043
Batista PVG, Laceby JP, Evrard O (2022) How to evaluate sediment fingerprinting source apportionments. J Soils Sediments 22:1315–1328. https://doi.org/10.1007/s11368-022-03157-4
Batista PVG, Laceby JP, Silva MLN et al (2019) Using pedological knowledge to improve sediment source apportionment in tropical environments. J Soils Sediments 19:3274–3289. https://doi.org/10.1007/s11368-018-2199-5
Belmont P, Willenbring JK, Schottler SP et al (2014) Toward generalizable sediment fingerprinting with tracers that are conservative and nonconservative over sediment routing timescales. J Soils Sediments 14:1479–1492. https://doi.org/10.1007/s11368-014-0913-5
Ben Slimane A, Raclot D, Evrard O et al (2013) Fingerprinting sediment sources in the outlet reservoir of a hilly cultivated catchment in Tunisia. J Soils Sediments 13:801–815. https://doi.org/10.1007/s11368-012-0642-6
Bispo DFA, Batista PVG, Guimarães DV et al (2020) Monitoring land use impacts on sediment production: a case study of the pilot catchment from the Brazilian program of payment for environmental services. Rev Bras Cienc Solo 44. https://doi.org/10.36783/18069657rbcs20190167
Blake WH, Boeckx P, Stock BC et al (2018) A deconvolutional Bayesian mixing model approach for river basin sediment source apportionment. Sci Rep 8:13073. https://doi.org/10.1038/s41598-018-30905-9
Blake WH, Ficken KJ, Taylor P et al (2012) Tracing crop-specific sediment sources in agricultural catchments. Geomorphology 139–140:322–329. https://doi.org/10.1016/j.geomorph.2011.10.036
Borselli L, Cassi P, Torri D (2008) Prolegomena to sediment and flow connectivity in the landscape: A GIS and field numerical assessment. CATENA 75:268–277. https://doi.org/10.1016/j.catena.2008.07.006
Bouchez J, Gaillardet J, France-Lanord C et al (2011) Grain size control of river suspended sediment geochemistry: Clues from Amazon River depth profiles. Geochem Geophys Geosyst 12. https://doi.org/10.1029/2010GC003380
Bravo-Linares C, Schuller P, Castillo A (2018) First use of a compound-specific stable isotope (CSSI) technique to trace sediment transport in upland forest catchments of Chile. Sci Total Environ 618:1114–1124. https://doi.org/10.1016/j.scitotenv.2017.09.163
Chikaraishi Y, Naraoka H, Poulson SR (2004) Hydrogen and carbon isotopic fractionations of lipid biosynthesis among terrestrial (C3, C4 and CAM) and aquatic plants. Phytochemistry 65:1369–1381. https://doi.org/10.1016/j.phytochem.2004.03.036
Collins AL, Blackwell M, Boeckx P et al (2020) Sediment source fingerprinting: benchmarking recent outputs, remaining challenges and emerging themes. J Soils Sediments 20(12):4160–4193. https://doi.org/10.1007/s11368-020-02755-4
Collins AL, Burak E, Harris P et al (2019) Field scale temporal and spatial variability of δ13C, δ15N, TC and TN soil properties: Implications for sediment source tracing. Geoderma 333:108–122. https://doi.org/10.1016/j.geoderma.2018.07.019
Collins AL, Pulley S, Foster IDL et al (2017) Sediment source fingerprinting as an aid to catchment management: A review of the current state of knowledge and a methodological decision-tree for end-users. J Environ Manage 194:86–108. https://doi.org/10.1016/j.jenvman.2016.09.075
Collins AL, Walling DE (2004) Documenting catchment suspended sediment sources: Problems, approaches and prospects. Prog Phys Geogr 28:159–196. https://doi.org/10.1191/0309133304pp409ra
Collins AL, Walling DE, Leeks GJL (1997a) Source type ascription for fluvial suspended sediment based on a quantitative composite fingerprinting technique. CATENA 29:27
Collins AL, Walling DE, Leeks GJL (1996) Composite fingerprinting of the spatial source of fluvial suspended sediment: a case study of the Exe and Severn River basins, United Kingdom. Géomorphologie Relief Processus Environnement 2:41–53. https://doi.org/10.3406/morfo.1996.877
Collins AL, Walling DE, Leeks GJL (1997b) Fingerprinting the origin of fluvial suspended sediment in larger river basins: Combining assessment of spatial provenance and source type. Geogr Ann Ser B 79:239–254. https://doi.org/10.1111/j.0435-3676.1997.00020.x
Collins AL, Walling DE, Sichingabula HM, Leeks GJL (2001) Suspended sediment source fingerprinting in a small tropical catchment and some management implications. Appl Geogr 21:387–412
Collister JW, Rieley G, Stern B et al (1994) Compound-specific ~3C analyses of leaf lipids from plants with differing carbon dioxide metabolisms. Org Geochem 21:619–627
Cooper RJ, Krueger T (2017) An extended Bayesian sediment fingerprinting mixing model for the full Bayes treatment of geochemical uncertainties. Hydrol Process 31:1900–1912. https://doi.org/10.1002/hyp.11154
Cooper RJ, Pedentchouk N, Hiscock KM et al (2015) Apportioning sources of organic matter in streambed sediments: An integrated molecular and compound-specific stable isotope approach. Sci Total Environ 520:187–197. https://doi.org/10.1016/j.scitotenv.2015.03.058
Erdbrügger P, Fröhlich F (2020) The role of very long chain fatty acids in yeast physiology and human diseases. Biol Chem 402:25–38
Evrard O, Batista PVG, Company J et al (2022) Improving the design and implementation of sediment fingerprinting studies: summary and outcomes of the TRACING 2021 Scientific School. J Soils Sediments 22:1648–1661. https://doi.org/10.1007/s11368-022-03203-1
Evrard O, Laceby JP, Ficetola GF (2019) Environmental DNA provides information on sediment sources: A study in catchments affected by Fukushima radioactive fallout. Sci Total Environ 665:873–881. https://doi.org/10.1016/j.scitotenv.2019.02.191
Evrard O, Poulenard J, Némery J et al (2013) Tracing sediment sources in a tropical highland catchment of central Mexico by using conventional and alternative fingerprinting methods. Hydrol Process 27:911–922. https://doi.org/10.1002/hyp.9421
Fox J, Papanicolaou A (2007) The use of carbon and nitrogen isotopes to study watershed erosion processes. J Am Water Resour Assoc 43(4):1047–1064
García-Comendador J, Martínez-Carreras N, Fortesa J et al (2023) In-channel alterations of soil properties used as tracers in sediment fingerprinting studies. Catena 225:107036. https://doi.org/10.1016/j.catena.2023.107036
Gateuille D, Owens PN, Petticrew EL et al (2019) Determining contemporary and historical sediment sources in a large drainage basin impacted by cumulative effects: the regulated Nechako River, British Columbia, Canada. J Soils Sediments 19:3357–3373. https://doi.org/10.1007/s11368-019-02299-2
Gellis AC, Noe GB (2013) Sediment source analysis in the Linganore Creek watershed, Maryland, USA, using the sediment fingerprinting approach: 2008 to 2010. J Soils Sediments 13:1735–1753. https://doi.org/10.1007/s11368-013-0771-6
Gibbs MM (2008) Identifying source soils in contemporary estuarine sediments: A new compound-specific isotope method. Estuaries Coasts 31:344–359. https://doi.org/10.1007/s12237-007-9012-9
Haddadchi A, Olley J, Laceby P (2014) Accuracy of mixing models in predicting sediment source contributions. Sci Total Environ 497–498:139–152. https://doi.org/10.1016/j.scitotenv.2014.07.105
Haddadchi A, Ryder DS, Evrard O, Olley J (2013) Sediment fingerprinting in fluvial systems: review of tracers, sediment sources and mixing models. J Sediment Res 28:560–578
Hancock GJ, Revill AT (2013) Erosion source discrimination in a rural Australian catchment using compound-specific isotope analysis (CSIA). Hydrol Process 27:923–932. https://doi.org/10.1002/hyp.9466
Hirave P, Glendell M, Birkholz A, Alewell C (2021) Compound-specific isotope analysis with nested sampling approach detects spatial and temporal variability in the sources of suspended sediments in a Scottish mesoscale catchment. Sci. Total Environ 755. https://doi.org/10.1016/j.scitotenv.2020.142916
Issaka S, Ashraf MA (2017) Impact of soil erosion and degradation on water quality: a review. Geology, Ecology, and Landscapes 1:1–11. https://doi.org/10.1080/24749508.2017.1301053
Jacob J, Disnar JR, Boussafir M et al (2005) Pentacyclic triterpene methyl ethers in recent lacustrine sediments (Lagoa do Caçó, Brazil). Org Geochem 36:449–461. https://doi.org/10.1016/j.orggeochem.2004.09.005
Kemper JT, Rathburn SL, Friedman JM et al (2022) Fingerprinting historical tributary contributions to floodplain sediment using bulk geochemistry. Catena 214. https://doi.org/10.1016/j.catena.2022.106231
Koiter AJ, Owens PN, Petticrew EL, Lobb DA (2013) The behavioural characteristics of sediment properties and their implications for sediment fingerprinting as an approach for identifying sediment sources in river basins. Earth Sci Rev 125:24–42
Laceby JP, Evrard O, Smith HG et al (2017) The challenges and opportunities of addressing particle size effects in sediment source fingerprinting: A review. Earth Sci Rev 169:85–103
Laceby JP, McMahon J, Evrard O, Olley J (2015) A comparison of geological and statistical approaches to element selection for sediment fingerprinting. J Soils Sediments 15:2117–2131. https://doi.org/10.1007/s11368-015-1111-9
Lake NF, Martínez-Carreras N, Shaw PJ, Collins AL (2022) High frequency un-mixing of soil samples using a submerged spectrophotometer in a laboratory setting—implications for sediment fingerprinting. J Soils Sediments 22:348–364. https://doi.org/10.1007/s11368-021-03107-6
Latorre B, Lizaga I, Gaspar L, Navas A (2021) A novel method for analysing consistency and unravelling multiple solutions in sediment fingerprinting. Sci Total Environ 789. https://doi.org/10.1016/j.scitotenv.2021.147804
Lavrieux M, Birkholz A, Meusburger K et al (2019) Plants or bacteria? 130 years of mixed imprints in Lake Baldegg sediments (Switzerland), as revealed by compound-specific isotope analysis (CSIA) and biomarker analysis. Biogeosciences 16:2131–2146. https://doi.org/10.5194/bg-16-2131-2019
le Gall M, Evrard O, Foucher A et al (2016) Quantifying sediment sources in a lowland agricultural catchment pond using 137Cs activities and radiogenic 87Sr/86Sr ratios. Sci Total Environ 566–567:968–980. https://doi.org/10.1016/j.scitotenv.2016.05.093
Liu J, Han G (2021) Tracing riverine particulate black carbon sources in Xijiang River Basin: insight from stable isotopic composition and Bayesian mixing model. Water Res 194. https://doi.org/10.1016/j.watres.2021.116932
Lizaga I, Bodé S, Gaspar L et al (2021) Legacy of historic land cover changes on sediment provenance tracked with isotopic tracers in a Mediterranean agroforestry catchment. J Environ Manage 288. https://doi.org/10.1016/j.jenvman.2021.112291
Lizaga I, Latorre B, Gaspar L, Navas A (2022) Combined use of geochemistry and compound-specific stable isotopes for sediment fingerprinting and tracing. Sci Total Environ 832. https://doi.org/10.1016/j.scitotenv.2022.154834
Lizaga I, Latorre B, Gaspar L, Navas A (2020) Consensus ranking as a method to identify non-conservative and dissenting tracers in fingerprinting studies. Sci Total Environ 720. https://doi.org/10.1016/j.scitotenv.2020.137537
Martínez-Carreras N, Krein A, Gallart F et al (2010) Assessment of different colour parameters for discriminating potential suspended sediment sources and provenance: A multi-scale study in Luxembourg. Geomorphology 118:118–129. https://doi.org/10.1016/j.geomorph.2009.12.013
Matheson JE, Winkler RL (1976) Scoring rules for continuous probability distributions. Manag Sci 22:1087–1096
Motha JA, Wallbrink PJ, Hairsine PB, Grayson RB (2002) Tracer properties of eroded sediment and source material. Hydrol Process 16:1983–2000. https://doi.org/10.1002/hyp.397
Mukundan R, Radcliffe DE, Ritchie JC et al (2010) Sediment fingerprinting to determine the source of suspended sediment in a Southern Piedmont stream. J Environ Qual 39:1328–1337. https://doi.org/10.2134/jeq2009.0405
Nosrati K, Govers G, Ahmadi H et al (2011) An exploratory study on the use of enzyme activities as sediment tracers: biochemical fingerprints? J Sediment Res 26:136–151
Owens PN, Blake WH, Gaspar L et al (2016) Fingerprinting and tracing the sources of soils and sediments: Earth and ocean science, geoarchaeological, forensic, and human health applications. Earth Sci Rev 162:1–23
Papanicolaou T (2003) Soil fingerprinting in the Palouse Basin, USA, using stable carbon and nitrogen isotopes. Int J Sediment Res 18:278–284
Pedregosa F, Michel V, Grisel O et al (2011) Scikit-learn: Machine learning in Python. J Machine Learning Res 12:2825–2830
Pedro HTC, Coimbra CFM, David M, Lauret P (2018) Assessment of machine learning techniques for deterministic and probabilistic intra-hour solar forecasts. Renew Energy 123:191–203. https://doi.org/10.1016/j.renene.2018.02.006
Pulley S, Collins AL (2018) Tracing catchment fine sediment sources using the new SIFT (SedIment Fingerprinting Tool) open source software. Sci Total Environ 635:838–858. https://doi.org/10.1016/j.scitotenv.2018.04.126
Pulley S, Foster I, Antunes P (2015) The application of sediment fingerprinting to floodplain and lake sediment cores: assumptions and uncertainties evaluated through case studies in the Nene Basin, UK. J Soils Sediments 15:2132–2154. https://doi.org/10.1007/s11368-015-1136-0
Reiffarth DG, Petticrew EL, Owens PN, Lobb DA (2016) Sources of variability in fatty acid (FA) biomarkers in the application of compound-specific stable isotopes (CSSIs) to soil and sediment fingerprinting and tracing: A review. Sci Total Environ 565:8–27
Reiffarth DG, Petticrew EL, Owens PN, Lobb DA (2019) Spatial differentiation of cultivated soils using compound-specific stable isotopes (CSSIs) in a temperate agricultural watershed in Manitoba, Canada. J Soils Sediments 19:3411–3426. https://doi.org/10.1007/s11368-019-02406-3
Smith HG, Karam DS, Lennard AT (2018) Evaluating tracer selection for catchment sediment fingerprinting. J Soils Sediments 18:3005–3019. https://doi.org/10.1007/s11368-018-1990-7
Stewart HA, Massoudieh A, Gellis A (2015) Sediment source apportionment in Laurel Hill Creek, PA, using Bayesian chemical mass balance and isotope fingerprinting. Hydrol Process 29(11):2545–2560
Stock BC, Jackson AL, Ward EJ et al (2018) Analyzing mixing systems using a new generation of Bayesian tracer mixing models. PeerJ. https://doi.org/10.7717/peerj.5096
Swales A, Gibbs MM (2020) Transition in the isotopic signatures of fatty-acid soil biomarkers under changing land use: Insights from a multi-decadal chronosequence. Sci. Total Environ 722. https://doi.org/10.1016/j.scitotenv.2020.137850
Upadhayay HR, Bodé S, Griepentrog M et al (2017) Methodological perspectives on the application of compound-specific stable isotope fingerprinting for sediment source apportionment. J Soils Sediments 17:1537–1553
Upadhayay HR, Bodé S, Griepentrog M et al (2018a) Isotope mixing models require individual isotopic tracer content for correct quantification of sediment source contributions. Hydrol Process 32:981–989. https://doi.org/10.1002/hyp.11467
Upadhayay HR, Griepentrog M, Bodé S et al (2020) Catchment-wide variations and biogeochemical time lags in soil fatty acid carbon isotope composition for different land uses: Implications for sediment source classification. Org Geochem 146. https://doi.org/10.1016/j.orggeochem.2020.104048
Upadhayay HR, Smith HG, Griepentrog M et al (2018b) Community managed forests dominate the catchment sediment cascade in the mid-hills of Nepal: A compound-specific stable isotope analysis. Sci Total Environ 637–638:306–317. https://doi.org/10.1016/j.scitotenv.2018.04.394
Vale S, Swales A, Smith HG et al (2022) Impacts of tracer type, tracer selection, and source dominance on source apportionment with sediment fingerprinting. Sci Total Environ 831. https://doi.org/10.1016/j.scitotenv.2022.154832
Walling DE (2005) Tracing suspended sediment sources in catchments and river systems. Sci Total Environ 344:159–184. https://doi.org/10.1016/j.scitotenv.2005.02.011
Walling DE (2013) The evolution of sediment source fingerprinting investigations in fluvial systems. J Soils Sediments 13:1658–1675
Xu Z, Belmont P, Brahney J, Gellis AC (2022) Sediment source fingerprinting as an aid to large-scale landscape conservation and restoration: A review for the Mississippi River Basin. J Environ Manage 324:116260. https://doi.org/10.1016/j.jenvman.2022.116260
Acknowledgements
The authors would like to express their appreciation to Simon Scheper for creating the land use maps and two anonymous reviewers for their constructive feedback. We are also grateful for scientific discussions with Pedro Batista and his input in developing the concentration-dependent mathematical mixtures.
Funding
Open access funding provided by University of Basel.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Responsible editor: Olivier Evrard
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cox, T., Laceby, J.P., Roth, T. et al. Less is more? A novel method for identifying and evaluating non-informative tracers in sediment source mixing models. J Soils Sediments 23, 3241–3261 (2023). https://doi.org/10.1007/s11368-023-03573-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11368-023-03573-0