1 Introduction

Hydro-morphological processes in rivers, lakes, and reservoirs strongly depend on the sediment supply from the catchment area. Hence, information on sediment load is required as an upstream boundary condition for long-term predictions of bathymetric changes with deterministic hydro-morphodynamic numerical models (Haun et al. 2013; Mouris et al. 2018; Hanmaiahgari et al. 2018; Olsen and Hillebrand 2018). In addition, engineering interventions, such as implementing sustainable reservoir operations, require accurate predictions of sediment load, at sufficiently high temporal resolution. To this end, a model chain for assessing sediment dynamics typically starts with a parametric characterization of the catchment to estimate the sediment yield, defined as the amount of sediment load passing the outlet of the catchment. Yet, modeling soil erosion and sediment transport processes in the catchment area relies on subjective decision-making, which results in partially non-measurable uncertainty (Melsen et al. 2019). Thus, objectively calculated sediment loads are rarely available and the uncertainties of final outputs are often unknown (Song et al. 2011).

Soil erosion and sediment transport processes can be described by a variety of models that involve, for instance, conceptual, empirical, or physical-deterministic approaches (Benavidez et al. 2018). The choice of a suitable modeling approach depends on the spatio-temporal scales of input data, the quality of available data, and the target model output (Nearing 2013; Alewell et al. 2019). However, more complex process-based physical models do not necessarily reduce uncertainty compared to simple empirical models (Brazier 2013; de Vente et al. 2013; Alewell et al. 2019) because the quality or gaps of available measurement data play a superordinate role for large-scale applications (> 1 km2) (Tan et al. 2018; Haun and Dietrich 2021; Borrelli et al. 2021). Thus, simple empirical soil erosion models are often preferred to complex models in areas with limited data availability (Efthimiou et al. 2017; Benavidez et al. 2018). A performance evaluation of different empirical soil erosion models in mountainous Mediterranean catchments showed that the Revised Universal Soil Loss Equation (RUSLE) (Renard et al. 1991; Renard 1997) yields the best results, in particular for investigating long-term trends (Efthimiou et al. 2017). This is why we adapted the RUSLE in this study along with the SEdiment Delivery Distributed (SEDD) model (Ferro and Porto 2000) to estimate the suspended sediment load in a region where data are only sparsely available. Still, the RUSLE involves sketchy empirical parameters and subjective decision-making. For instance, the RUSLE uses a rainfall-runoff factor that does not distinguish between precipitation in the form of rain or snow (Renard 1997; Alewell et al. 2019), which may lead to an overestimation of erosion during the event, as snowfall is not erosive. For this reason, recent studies ignore precipitation (i.e., consider it a non-erosive) that occurs at temperatures below 0 °C (Meusburger et al. 2012; Schmidt et al. 2016). The subsequent snowmelt, which can be highly erosive (Lana-Renault et al. 2011; Wu et al. 2018), however, is neglected in these approaches (Alewell et al. 2019), resulting in an underestimation of eroded sediments. Thus, Yin et al. (2017) propose that future research should focus on the effect of snowmelt on erosion. This study aims to close this gap by vetting approaches that neglect snow against novel techniques that consider the effects of snowfall and snowmelt on suspended sediment loads in a Mediterranean catchment. In addition, to overcome challenges related to subjective decision-making and snow-driven erosion processes in mountainous Mediterranean catchments, this study has the goal to establish an objective workflow for generating monthly suspended sediment loads. Another challenge in many regions of the world is a lack of measurement data on catchment characteristics and hydro-climatic processes, including precipitation. Thus, the superordinate research question in this study is as follows: How can viable and objective sediment loads from mountainous Mediterranean catchments and sparse data be generated? To answer this question, this study develops a series of algorithms, which constitute an objective workflow. The algorithms combine the RUSLE and the SEDD model to predict monthly suspended sediment loads coming from the Devoll catchment (Southeast Albania, Fig. 1) with mostly free data. The SEDD model estimates sediment transport and delivery, while the RUSLE calculates the spatial distribution of the gross soil erosion in the catchment. In particular, to leverage re-using the workflow in other data-sparse regions, the approach involves testing the relevance of free global datasets (e.g., satellite imagery and hydro-climatic parameters from reanalysis datasets). A core element of the methods is an algorithm that takes into account both the non-erosivity of snowfall and the erosivity of snowmelt by introducing a seasonal memory into the RUSLE. The results feature the output of the novel algorithmic workflow.

Fig. 1
figure 1

Location of the study area. a) European context, b) national context, and c) the catchment of the Banja reservoir with indication of the Kokel monitoring station, the Devoll river network, the subcatchment of the monitoring station, and the Banja Reservoir in the Northwest (datasource: EU-DEM v1.1)

Full size image

2 Materials and methods

The methods feature study site characteristics, challenges associated with data-sparse regions, and a comprehensive literature review on the RUSLE and the SEDD model. Thus, this section describes step by step the implementation of modular research products, related hypotheses, and the pathway to validate the hypotheses in a novel algorithmic workflow.

2.1 Study area

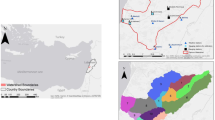
This study focuses on the upper catchment of the Banja Reservoir at the Devoll River in the Southeast of Albania (Fig. 1). The 1875 km2 large catchment is surrounded by up to 2390 m a.s.l-high mountains, a highland plain in the Southeast where the Devoll River has its source, and the, in 2016, commissioned Banja Reservoir in the Northwest. Downstream of its source, in the Gramos Mountains near the Greek border, the Devoll River flows toward the Northwest, passing the Korçë plain, and falls into a narrow v-shaped canyon section. A monitoring station (close to the village of Kokel, red dot in Fig. 1) at the downstream end of the canyon section has been measuring sediment concentration and discharge instantaneously, but not consistently since March 2016. Downstream of the Kokel monitoring station, the Devoll River passes into a braided river section that leads into the Banja Reservoir.

Approximately 30% of the catchment area is forested, 25% is covered by scrubs and herbaceous vegetation, and 25% is used for agriculture (Copernicus Land Monitoring Service 2018). Other minor but non-negligible land cover types are pasture, natural grasslands, and sparse vegetation. The soils are mainly composed of Eutric Regosol (37%), Calcic Cambisol (30%), Calcaric Lithosol (12%), and Orthic Luvisol (11%) (Fischer et al. 2008; Hiederer 2013).

The catchment of the Banja reservoir is divided into two climatic zones (Kottek et al. 2006; Beck et al. 2018). The Eastern (upstream) part of the catchment, including the sub-catchment of the Kokel monitoring station, is characterized by a warm-summer Mediterranean climate (Csb according to the Köppen climate classification). The Western (downstream) part of the catchment is characterized by a hot-summer Mediterranean climate (Csa according to the Köppen climate classification). Both parts of the catchment typically experience dry and hot summers and humid winters, but the precipitation amounts decrease with increasing distance from the coast (i.e., moving in the Eastern direction). Thus, the Eastern part receives an average of 660 mm year−1, while the Western part receives up to 1600 mm year−1 (Almestad 2015). In winter, snowfall is frequent in elevations higher than 1000 m a.s.l. Hence, the flow regime of the Devoll River and its tributaries are driven by precipitation, and also by snowfall and snowmelt.

As a part of geographical Mediterranean Europe, the Devoll catchment is an erosion hotspot (Walling and Webb 1996; Borrelli et al. 2017b, 2020), where high soil loss occurs because of a combination of high precipitation erosivity and steep topography.

2.2 Revised Universal Soil Loss Equation (RUSLE)

The RUSLE has been developed based on worldwide datasets and has already been applied on various spatial scales ranging from local case studies (e.g., Yang 2015; Koirala et al. 2019; Schmidt et al. 2019; Chuenchum et al. 2019) to continental (Panagos et al. 2015c; Teng et al. 2016) and global assessments (Yang et al. 2003; Borrelli et al. 2020). The RUSLE computes soil loss A (t ha−1 year−1) as the product of six erosion risk factors:

$$A\hspace{0.25em}=\hspace{0.25em}R\cdot K\cdot C\cdot LS\cdot P$$
(1)

where \(R\) is a rainfall-runoff erosivity factor (MJ mm ha−1 h−1 year−1), \(K\) is a soil erodibility factor (t h MJ−1 mm−1), \(LS\) is a combined dimensionless topographic factor of slope length \(L\) (-) and steepness \(S\) (-), \(C\) is a cover and management factor (-), and \(P\) is a support practice factor (-).

The following sections briefly describe the factors and hypotheses made in this study to yield a possibly objective sediment load calculation.

2.2.1 Rainfall-runoff erosivity factor R

The rainfall-runoff erosivity factor (\(R\) factor) estimates the erosive forces of precipitation and the resulting surface runoff. The \(R\) factor accounts for the combined effect of duration, strength, and intensity of every precipitation event. The rainfall erosivity of an event is the product of its kinetic energy and its maximum 30-min intensity (Brown and Foster 1987; Renard 1997). The original approach introduces the annual \(R\) factor as the sum of the rainfall erosivities during a defined period divided by the number of years. However, high temporal resolution (< 0.5 h) precipitation data are not available in many regions of the world, including the Devoll catchment. To overcome high-resolution data shortage, empirical regression equations have been developed to correlate the \(R\) factor with any available precipitation data resolution, such as daily, monthly, or annual totals. Such region-specific regression equations calculate the \(R\) factor with sufficient accuracy and have been successfully applied in various case studies (Arnoldus 1980; de Santos and de Azevedo 2001; Torri et al. 2006; Diodato and Bellocchi 2010; Diodato et al. 2013). The so-called rainfall erosivity model for complex terrains \({REM}_{DB}\) (Diodato and Bellocchi 2007) is one of the most recent developments for calculating the \(R\) factor and is used in this study for the Devoll catchment. The choice was made because the \({REM}_{DB}\) is the most suitable regarding the available data (temporal and spatial resolution) and it was developed to estimate the monthly erosivity factor (\({R}_{m}\)) in the geographically closely located Italy, which shares similar topographic (range of elevations) and hydro-climatic conditions with Albania (Beck et al. 2018). In addition to the monthly precipitation \({p}_{m}\) (mm month−1), the approach considers the elevation, latitude, and seasonal characteristics of precipitation (Diodato and Bellocchi 2007):

$${R}_{m}=0.207\hspace{0.25em}\cdot {\left[{p}_{m}\cdot \left(f\left(m\right)+f\left(E,L\right)\right)\right]}^{1.561}$$
(2)

where \(f\left(m\right)\) is a monthly sinusoidal function and \(f\left(E,L\right)\) is a parabolic function expressing the influence of site elevation \(E\) and the latitude \(L\).

The erosive forces of runoff from snowmelt are typically not included in the \(R\) factor (Renard 1997), though their importance was recognized in the RUSLE’s predecessor’s \(R\) factor by estimating the snowmelt erosivity based on precipitation totals in winter months (Wischmeier and Smith 1978; McCool et al. 1982; Schwertmann et al. 1987; Banasik et al. 2021). Expanding on the insights from the past, this study tests a novel method to account for snowfall and snowmelt in the \(R\) factor. This method accounts for non-erosive snowfall and snowmelt that becomes erosive weeks to months after the precipitation event. The method calculates a monthly total \(R\) factor \({R}_{m,\mathrm{total}}\) (MJ mm ha−1 h−1 month−1) as the sum of the monthly \({R}_{m, \mathrm{rain}}\) factor resulting from the erosive forces of rainfall and monthly \({R}_{m, \mathrm{snowmelt}}\) factor resulting from the erosive forces of snowmelt.

$${R}_{m,\mathrm{total}}= {R}_{m, \mathrm{rain}}+{R}_{m, \mathrm{snowmelt}}$$
(3)

where \({R}_{m, \mathrm{snowmelt}}= 2 \frac{MJ}{ha \cdot h}\cdot {SWE}_{\mathrm{snowmelt}}\) and \({SWE}_{\mathrm{snowmelt}}\) denote the snow water equivalent of the melted snow (mm month−1). The amount of melted snow is derived from satellite-based snow cover detection and the analysis of temperature and precipitation data.

This study tests a novel method for calculating the snow-cover-dependent monthly \(R\) factor to improve the accuracy of predicted monthly sediment yield in mountainous Mediterranean regions.

2.2.2 Soil erodibility factor K

The soil erodibility factor (\(K\) factor) describes the susceptibility of soils to be mobilized by the impact of precipitation and surface runoff. In this study, the most used and cited equation to calculate soil erodibility from Wischmeier and Smith (1978) was applied. The equation calculates the soil erodibility as a function of organic matter content, soil structure, soil permeability, and soil texture (Wischmeier and Smith 1978). In addition, the erodibility of soils reduces in the presence of cobbles, which can be accounted for by a correction factor (Panagos et al. 2014). This study uses the correction for the \(K\) factor and derives soil parameters from the free soil information of the European Soil Database (Hiederer 2013) and the Harmonized World Soil Database (Fischer et al. 2008). The here-presented approach is suitable for data-sparse regions but does not account for seasonal changes and therefore, it should only be used when local data is not available. Further details are provided in the supplementary information SI 1.

2.2.3 Land cover and management factor C

The land cover and management factor (\(C\) factor) describes the ratio of long-term soil loss from vegetated areas and the soil loss from bare grounds (fallow land) with a defined gradient and length (Renard 1997). The \(C\) factor is a function of land cover and takes values between 0 and 1, where 1 corresponds to a reference condition of an area of clean-tilled fallow land. \(C\) factor values can be derived from land cover classes (Jain and Kothyari 2000; Märker et al. 2008; Vente et al. 2009; Borrelli et al. 2014) or satellite imagery (de Asis and Omasa 2007; Schönbrodt et al. 2010; Teng et al. 2016). This study combines both approaches by first defining a plausible range for the \(C\) factor for every land cover class and second, by calculating seasonal \(C\) factors for winter and summer months based on satellite imagery and using the normalized difference vegetation index (NDVI), as proposed by Gianinetto et al. (2019).

For non-arable land, this study calculates the \(C\) factor as a function of 20 different land cover classes (Copernicus Land Monitoring Service 2018), which stem from a summary of the most cited European studies (Panagos et al. 2015a). The land cover classes are derived from the satellite imagery-based CORINE Land Cover database (Copernicus Land Monitoring Service 2018). For arable land, we calculate the \(C\) factor range as a function of cultivated crop types and tillage practices. Thus, the arable-land \(C\) factor is the weighted average of crop types and their share of a region unit, multiplied by a tillage factor (Panagos et al. 2015a). Satellite imagery serves to calculate seasonal \(C\) factors that account for seasonal dynamics of vegetated land cover classes (e.g., forests, grasslands, or croplands). The \(C\) factors of the land cover classes that are not influenced by seasonality (e.g., urban fabric) remain constant. Since satellite imagery and satellite-based land cover products are globally available, this approach is applicable worldwide. The implemented \(C\) factors and calculation details can be found in the supplementary information SI 2.

2.2.4 Slope length and steepness LS

The dimensionless factors slope length (\(L\) factor) and slope steepness (\(S\) factor) are typically combined into the \(LS\) factor that accounts for topographic landscape characteristics. The slope length \(L\) is defined as “the distance from the point of origin of the overland flow to the point where each slope gradient decreases enough for the beginning of deposition or when the flow comes to concentrate in a defined channel” (Wischmeier and Smith 1978). To account for flow accumulation from complex topographies, the slope length is substituted by the upslope drainage area per unit of contour length (Desmet and Govers 1996). The slope steepness \(S\) can be calculated with empirical equations as a function of the slope angle \(\theta\) (Wischmeier and Smith 1978; McCool et al. 1987; Liu et al. 1994; Nearing 1997).

This study builds upon the latest development for calculating \(LS\) with a multi-flow direction algorithm as a function of slope, aspect, and downhill flow direction using the LS-Tool (Zhang et al. 2017). The herein-used approach considers both flow convergence based on the contributing surface and slope cutoff conditions according to Griffin et al. (1988).

2.2.5 Support practice factor P

The support practice factor (\(P\) factor) accounts for artificial soil stabilization measures (e.g., contouring, strip-cropping, or terrace farming) that reduce the erosion potential by altering surface runoff paths, patterns, and hydraulic forces (Wischmeier and Smith 1965; Renard et al. 1991; Panagos et al. 2015b).

In many studies, the \(P\) factor predominantly expresses the influence of contouring on soil erosion also for larger areas. Contouring (i.e., contour farming) is the practice of planting and tilling along contours that are perpendicular to the flow direction of the runoff. This practice decreases the runoff velocity and leaves more time for infiltration (Stevens et al. 2009). The effectiveness of this method depends on the slope and is applied exclusively to agricultural land (Haan et al. 1994; Morgan and Nearing 2010). Also, in this study, satellite imagery indicates that in the region of interest, farmers are contouring the landscape to reduce soil erosion. Thus, the \(P\) factor values are calculated as a function of the slope and the land cover class (SI Table 3).

2.3 SEdiment Delivery Distributed (SEDD) model

The RUSLE only assesses the spatial distribution of the gross soil loss \({A}_{i}\), and this is why an additional sediment routing is needed to estimate the sediment yield \({Y}_{b}\) of a catchment. The sediment yield \({Y}_{b}\) is defined as the sediment mass per unit time or sediment load that passes a defined boundary, such as the outlet of a (sub-)catchment (here, the Kokel monitoring station) or a hillslope (ASCE 1982; White 2006). In addition, the ratio between the sediment yield \({Y}_{b}\) (t) and the gross soil erosion of the catchment \({A}_{b}\) (t) represents the catchment’s sediment delivery ratio \({SDR}_{b}\) (-). Without this additional equation, the soil loss \({A}_{i}\) calculated with the RUSLE cannot be applied to compute suspended sediment loads (e.g., for comparison with measured data). Hence, this study uses the Sediment Delivery Distributed (SEDD) model for calculating the net sediment delivery on a catchment scale, where the catchment’s sediment yield \({Y}_{b}\) is the sum of the sediment yield \({Y}_{i}(t)\) of morphological units (i.e., grid pixels) (Ferro and Porto 2000):

$${{Y}_{b}={SDR}_{b}\cdot {A}_{b} = \sum_{i=1}^{{n}_{u}}{Y}_{i}}_{\hspace{0.25em}}=\hspace{0.25em}\sum_{i=1}^{{n}_{u}}SD{R}_{i}\cdot {A}_{i}\cdot S{U}_{i}$$
(4)

where \(SD{R}_{i}\) (-) is the pixel-wise sediment delivery ratio, \({A}_{i}\) (t ha−1) is the soil loss resulting from the RUSLE, \(S{U}_{i}\) (ha) denotes the area of a pixel \(i\), and \({n}_{u}\) is the total number of pixels where every pixel is considered a morphological unit that has length, steepness, and aspect attributes. The pixel-specific parameter \(SD{R}_{i}\) can be calculated as follows (Ferro and Minacapilli 1995):

$$SD{R}_{i}=\mathrm{exp}\left(-\beta \cdot {t}_{i}\right)$$
(5)

where \({t}_{i}\) is the travel time along the flow path to the closest river channel and \(\beta\) is a catchment-specific parameter that depends on the time scale. Thus, the \(SD{R}_{i}\) represents “a measurement of the probability that the eroded particles from the entire upland area arrive into the nearest stream reach” (Ferro and Minacapilli 1995). Moreover, the travel time \({t}_{i}\) is the sum of pixel-specific travel times along hydraulic pathways crossing \({n}_{p}\) pixels (Jain and Kothyari 2000):

$${t}_{i}=\sum_{i=1}^{{N}_{p}}\frac{{l}_{i}}{{v}_{i}}=\sum_{i=1}^{{N}_{p}}\frac{{l}_{i}}{\sqrt{{s}_{i}}\cdot {d}_{i}}$$
(6)

where \({l}_{i}\) (m) is the length of a pixel \(i\) along the flow path and \({v}_{i}\) is the pixel-specific flow velocity (m s−1) that can be calculated by multiplying the square root of the slope \({s}_{i}\) of a pixel and the surface roughness coefficient \({d}_{i}\), which is a function of land cover classes (Haan et al. 1994). A minimum pixel slope of \({s}_{i, min}=0.3\)% is required to ensure sediment routing.

This study implements the SEDD model to calculate monthly suspended sediment loads in the Devoll catchment with an algorithmic model chain. A model calibration is performed that involves the modification of the catchment-specific \(\beta\) parameter to fit the output of the SEDD model to measure suspended sediment data monitored at the Kokel monitoring station (Ferro and Porto 2000; Porto and Walling 2015).

2.4 Data

2.4.1 Available ground truth

To evaluate the soil loss and the resulting sediment yield from the catchment, the Kokel monitoring station (Fig. 1) continuously recorded discharge and suspended sediment concentrations between May 2016 and April 2018, when the water depth exceeded 1 m (387 of 730 days). Measurements were performed with two side-mounted H-ADCPs (horizontal-acoustic Doppler current profilers) and the mean and maximum concentrations (averaged over 1 h) in the observation period were 1 g L−1 and 11.6 g L−1, respectively (Aleixo et al. 2020). Figure 2 plots the measured sediment concentrations against the discharge where no strong correlation is visible. For small discharge values, a large scattering can be seen, whereas for higher discharges, almost uniform suspended sediment concentrations were recorded. One reason for the large scatter in Fig. 2 can be the hysteresis effects of single events that cannot be reproduced in the absence of a time dimension (Aleixo et al. 2020). The highest discharges (above 150 m3·s−1) occurred during one single event in March 2018. In addition, the low concentration of suspended load might be attributed to snowmelt runoff subjected to pronounced dilution effects (Lana-Renault et al. 2011). Thus, commonly used sediment rating curves, such as a power-law function (e.g., Asselman 2000; Vercruysse et al. 2017), are not suitable for sediment load prediction.

Fig. 2
figure 2

Discharge versus suspended sediment concentration at the Kokel monitoring station, recorded for the time period from March 2016 to May 2018

Full size image

2.4.2 Data sparsity and interpolation methods

Soil erosion and sediment transport processes are functions of complex parameter sets that result from hydro-climatic conditions, topography, land cover types, soil types, and erosion control practices. Such complex datasets are rarely available without gaps, and therefore, this study tests to what extent incomplete datasets can be filled with interpolation methods using free climate reanalysis datasets and satellite imagery.

The Kokel monitoring station provides suspended sediment load measurements during high and average flows only. Furthermore, single values are missing within the observed period due to a low signal-to-noise ratio (Aleixo et al. 2020). However, the model chain in this study requires seamless sediment load data for calibration. Hence, interpolation methods are applied for filling in temporal measurement gaps, and missing single values are linearly interpolated. Concentrations at water levels less than 1 m (below the measuring threshold) cannot be objectively calculated and used for calibration because higher sediment concentrations may occur even during low-flow periods, after single rainfall events.

Climate reanalysis datasets are an alternative to in situ measurements (ground truth) of precipitation or temperature (among other parameters). A climate reanalysis uses observations and weather forecasting models to produce a globally complete and consistent dataset of the past weather and climate. In this process, observations from satellites and ground-based radars are used along with in situ measurements, for example, from weather stations, aircraft, ships, or buoys (Hersbach et al. 2020). To estimate precipitation patterns, this study employs the ERA5 reanalysis dataset that provides atmospheric, land, and hydro-climatic data with a spatial resolution of 30–31 km and an hourly time resolution since 1950 (Hersbach et al. 2020). In addition, temperature reanalysis datasets serve for the differentiation of rainfall and snowfall. However, the original calculation of the rainfall-runoff erosivity (\(R\)) factor builds on 30-min data (Brown and Foster 1987) and cannot be derived from reanalysis datasets. Thus, we correlate reanalysis precipitation data through an empirical regression with the \(R\) factor by applying Eq. (2) (Mouris et al. 2021d).

Satellite imagery involves spectral bands and enables the classification of land cover or vegetation on a catchment scale (e.g., Teng et al. 2016; Borrelli et al. 2017a; Gianinetto et al. 2019). For instance, the CORINE Land Cover for Europe (Copernicus Land Monitoring Service 2018), the Dynamic Land Cover Dataset for Australia (Thackway et al. 2013), or the worldwide Global Land Cover Characterization (Earth Resources Observation and Science Center 2017) provide classification data. Such satellite imagery also enables tracking seasonal and other time-dependent changes in land use or vegetation and generates digital elevation models (Mulder et al. 2011). Furthermore, snow-covered areas can be detected on satellite imagery where the spectral band ratio called Normalized Difference Snow Index (NDSI) enables to differentiate between cloud and snow cover, even though snow cannot be detected below clouds (Gafurov and Bárdossy 2009). The NDSI assumes that snow absorbs light in the ShortWave InfraRed region (\(SWIR\), e.g., band 11 of Sentinel 2 satellite imagery) and reflects light in the visible wavelength region (e.g., the green band 3 of Sentinel 2 satellite imagery) whereas most cloud types reflect both infrared and visible wavelengths. Pixels with an NDSI larger than a threshold value (typically 0.4, published values range from 0.18 to 0.7) are considered a snow and the NDSI is calculated as follows (Riggs et al. 1994; Härer et al. 2018):

$$NDSI= \frac{\left(\mathrm{Green}-SWIR\right)}{(\mathrm{Green}+SWIR)}$$
(7)

This study involves testing for an optimum NDSI threshold to detect snow cover. Snow cover thickness in the form of snow water equivalent is calculated by summing up the pixel-specific snowfall based on reanalysis temperature and precipitation data.

2.4.3 Summary of available data

The input data used in this study involve data from the Kokel monitoring station, data from public and free databases, and satellite imagery. Table 1 lists all data types, their sources, and their purpose in this study.

Table 1 Input data used for the model chain to compute soil loss and suspended sediment load
Full size table

2.5 Model chain for calculating sediment loads

Figure 3 shows a flowchart of the model chain used in this study where satellite imagery, precipitation, soil data, topographic data, and land cover information are mandatory input data (white boxes), while temperature data is only needed when applying the modified \(R\) factor from this study (gray box), which enables the detection of snowfall and snowmelt. In the case that observed suspended load measurements are available, those can be used for calibration by defining them as an optional argument in the workflow. The model chain starts with input rasters to calculate the spatial distribution of soil loss, suspended sediment load, and, optionally, bedload at monthly resolution using the RUSLE, the SEDD model, and interpolation methods to fill in data gaps. The following sections explain the workflow modules in detail.

Fig. 3
figure 3

Flowchart of the model chain for calculating soil loss and sediment loads. Input data in the upper part of the flowchart require user interaction while the tasks within the dashed box are fully automated in Python algorithms (Mouris et al. 2021b)

Full size image

2.5.1 Pre-processing

The fully automated core of the model chain (dashed box in Fig. 3) requires the alignment of input data in the form of pre-processing, which, in contrast, cannot be meaningfully automated because of varying data formats.

A digital elevation model (see Table 1) with sufficient spatial resolution (i.e., maximum pixel size of 50 m) describes the catchment topography and serves to identify the river network (SI 4). The Python algorithms (Mouris et al. 2021a) calculate the travel time from every raster pixel to the nearest channel reach by summing up pixel-specific travel times along the flow path (Eq. (6)). The pixel values for the \(C\), \(LS\), \(P\), and \(K\) factors are assigned to the corresponding rasters as described in the section on the RUSLE. Every pixel represents a raster pixel and its size remains constant in the entire model chain, which is defined and achieved in the pre-processing along with coherent coordinate reference systems and no data values. The spatial interpolation of data pixels (e.g., to ensure equal raster resolutions) uses the nearest neighbor method for discrete (categorical) data, such as land cover classes or soil types. Inverse distance weighting with a combination of elevation-dependent regression and distance-based interpolation is applied for continuous data, such as precipitation or temperature.

2.5.2 Combination of RUSLE, SEDD, snowfall, and snowmelt recognition

The calculation of the sediment load at the outlet of a (sub-)catchment (here, the Kokel monitoring station) is fully implemented in a ready-to-use Python code (Mouris et al. 2021b) that performs the tasks in the dashed box in Fig. 3. The sediment delivery ratio and the RUSLE factors \(K\), \(LS\), \(C\), and \(P\) represent constant input parameters in the form of rasters. The \(R\) factor is calculated at monthly resolution and represents a variable input parameter that makes the workflow using either the standard \({REM}_{DB}\) (Eq. (2)) or the modified approach that additionally considers snowfall and snowmelt (Eq. (3)). The snowfall and snowmelt options require additional climate reanalysis and satellite imagery, respectively, and the \(R\) factor is calculated as illustrated in Fig. 4 (Mouris et al. 2021c). In particular, the algorithm uses precipitation and temperature rasters with an hourly or daily (here daily) resolution to calculate the spatial distributions of monthly rainfall intensity and snow water equivalent (SWEmonth) of snow cover. For this purpose, a temperature threshold of 0 °C is used in this study to define when precipitation falls as snow.

Fig. 4
figure 4

Simplified flowchart of the modified R factor calculation, also accounting for snowfall and snowmelt

Full size image

To detect the size of snow-covered areas at the end of every month, the snow detection algorithm uses three spectral bands of Sentinel-2 imagery, notably blue (band 2), green (band 3), and the Short-Wave InfraRed band 11 (\(SWIR\)). The green and the \(SWIR\) bands are used to calculate the NDSI (Eq. (7)) to detect snow for every raster pixel, which takes a value of 1 when snow is present and 0 without snow (binary value). In addition, a threshold value for the blue band is implemented to avoid false snow detection from water pixels (mainly turbid lakes and rivers). Subsequently, the snow cover rasters are multiplied by the SWE of the snow cover where unmelted snow did not have an erosive effect in the considered month. The SWE raster accumulates newly fallen snow. Snow-covered pixels that are no longer covered at the end of the considered month generate erosive snowmelt. Thus, the algorithm has a seasonal memory, which should not be applied for a single-month analysis only. Ultimately, the algorithm implemented in the Python code processes precipitation and optionally temperature raster files to calculate the resulting monthly \(R\) factor for every raster pixel. It outputs soil loss and sediment yield rasters with monthly resolution along with a table of monthly averages of soil loss, sediment yield, and suspended sediment load at the outlet of the catchment. In addition, the monthly bedload fraction can be optionally computed and written to the output table using an empirical equation that estimates bedload transport from suspended transport rates (Turowski et al. 2010). A comparison of the approaches without snow recognition (“no snow,” where precipitation is considered erosive rain), with snow recognition only (“snowfall,” where snowfall is considered non-erosive), and with combined snowfall-snowmelt (“snowfall + snowmelt,” where snowfall is considered non-erosive, but snowmelt is considered erosive) consideration enables to quantify the importance and necessity of snow-related processes for sediment load prediction in this study. Thus, we test for the relevance of the consideration of snowfall and snowmelt in mountainous Mediterranean regions at a monthly resolution.

2.5.3 Calibration

The RUSLE parameters are calibrated in this study with respect to the effect of snowmelt in the \(R\) factor only, which is a core novelty in this study. All other parameters stem from the databases listed in Table 1. The calibration of satellite imagery band (NDSI and blue) thresholds for snow detection relies on expert assessment of true-color satellite imagery and overlays of snow cover delineation from the code and elevation contour lines. All pixels with values above the blue band threshold are considered snow-covered if also the NDSI is above the threshold value. In the calibration processes, the NDSI threshold is changed in 0.1-steps (i.e., increased and decreased by 0.1) starting from an initial threshold value of 0.4, which corresponds to the literature recommendation (Riggs et al. 1994). If the algorithm wrongly recognizes clouds or other pixels as snow, the NDSI threshold is increased by 0.1 and decreased if snow-covered pixels are not recognized. The additional blue band threshold is set to the highest blue band values of water pixels to avoid false snow detection, especially in turbid river stretches.

To obtain objective suspended sediment loads on a monthly resolution, the catchment-specific \(\beta\) parameter in the SEDD model is calibrated to measured suspended sediment loads at the Kokel monitoring station for the observation period between May 2016 and April 2018. The calibration of the model chain varies the catchment-specific \(\beta\) parameter by coupling the soil erosion and sediment transport model with the parameter estimation software PEST (Doherty 2001). In this process, the weighted squares of the residuals between monthly computed and observed suspended sediment loads are minimized by using a Gauss-Levenberg–Marquardt algorithm in the model chain (Levenberg 1944; Marquardt 1963; Shoarinezhad et al. 2020). The \(\beta\) parameter requires re-calibration for every model combination. Hence, the \(\beta\) parameter is calibrated in this study for the model chain without snow recognition, with snow recognition, and with combined snow recognition and additional snowmelt using the entire 10 months of observations embracing two wet seasons with inherently different hydro-climatic pattern. For comparison, we split the 10-month period additionally into two separate 5-month periods for calibration and validation, respectively. A complementary leave-one-out cross-validation is carried out to evaluate the model performance of the three different approaches to attempt an assessment of the consequences of limited data availability from two wet seasons only.

2.6 Synthesis of hypothesis testing

Testing the hypotheses starts with the calibration of the model chain (Fig. 3) to the catchment-specific \(\beta\) parameter for all scenarios (“no snow” without the recognition of snow, “snowfall” with snow recognition only, and “snowfall + snowmelt” with combined snowfall and snowmelt). When snowmelt recognition is activated in the model chain, an additional calibration of threshold values for snow cover detection on the satellite imagery is required with respect to the \(R\) factor (Fig. 4). After the calibration, the model chain runs the three snow scenarios to verify and refine hypotheses related to the superordinate research question of generating viable monthly suspended sediment loads from mountainous Mediterranean catchments with sparse data availability. In particular, the model chain results serve to verify the following hypotheses: (1) data interpolation with climate reanalysis and satellite imagery enables viable suspended sediment load predictions in data-sparse regions, (2) the accuracy of a model chain that relies on satellite and reanalysis data improves with the consideration of snowfall in the \(R\) factor, and (3) the accuracy of the model chain that relies on satellite and reanalysis data improves with the consideration of snowmelt in the \(R\) factor.

3 Results

Figure 5 shows the average monthly precipitation totals (post-processed reanalysis data) in the catchment, the observed monthly suspended sediment loads, and the computed monthly suspended sediment loads at the Kokel monitoring station for all three scenarios. The distribution of the observed monthly suspended sediment loads is heterogeneous and varies significantly with the monthly precipitation. Even though months without continuous data (water level < 1 m) were excluded and not used for calibration, the monthly observed loads cover a wide range from 25,800 t month−1 in June 2016 to 497,859 t month−1 in March 2018, whereas the average is 154,615 t month−1. In addition, Fig. 6 compares the observed and computed monthly suspended sediment loads in the entire observation period (10 months) for all three scenarios, whereas the dashed line describes the hypothetic perfect model accuracy. A calibration with the split observation data (i.e., 5 months) yields similar predicted suspended loads that are 2% lower in average. The detailed results with the 5-months calibration are provided with the supplementary information (SI 5). The results of the leave-one-out cross-validation are presented in the SI 6. The following subsections describe the results and figures in detail and illustrate the differences between the scenarios. In the following, we will use the 10-month calibration procedure to avoid parameter overfitting regarding one particular season only.

Fig. 5
figure 5

Average monthly precipitation totals in the catchment, the observed monthly suspended sediment loads, and the computed monthly suspended sediment loads at the Kokel monitoring station for all three scenarios

Full size image
Fig. 6
figure 6

Scatter plot of the observed and computed monthly sediment loads during the calibration period. The dashed line represents the hypothetic perfect model accuracy

Full size image

3.1 Sediment load prediction without snowfall recognition

3.1.1 Calibration of the β parameter

Figure 7 plots the model accuracy in the form of Nash–Sutcliffe efficiency (NSE) as a function of the catchment-specific \(\beta\) parameter at monthly resolution. The figure shows that the most accurate result (NSE= 0.78) is yielded with a catchment-specific \(\beta\) parameter (Eq. (5)) of 0.85 where the monthly catchment’s sediment delivery ratios \({SDR}_{b}\) (Eq. (4)) range between 25 and 39%.

Fig. 7
figure 7

Plot of Nash–Sutcliffe efficiency (NSE) against \(\beta\) parameter for the sediment load prediction without snow recognition

Full size image

3.1.2 Sediment load prediction

Figure 5 shows the computed monthly suspended sediment loads without snow recognition (“no snow”) in gray. The distribution of monthly computed suspended sediment loads is heterogeneous and varies to a large extent with monthly precipitation. The average computed monthly sediment load amounts to 71,900 t month−1, and the sum of February and March 2018 represents 48% (823,000 t) of the total computed suspended sediment load in the 2-year observation period. Furthermore, because of the seasonal variability involved in the \(C\) factor and \(R\) factor for Mediterranean regions, the same amount of precipitation results in different suspended sediment loads depending on the month. For instance, precipitation in December is less erosive than precipitation in February and March and smaller sediment loads tend to be underestimated, whereas the absolute deviations are the largest in the 3 months with the highest loads (12/17, 02/18 and 03/18). The model predicts similar loads for February and March 2018, but the measurements indicate a difference of more than 200,000 t. Ultimately, Fig. 5 suggests that the model qualitatively reproduces observed sediment loads well, where the mean absolute error between computed and measured monthly loads is 51,190 t month−1.

Figure 6 compares observed and computed monthly suspended sediment loads in the calibration period and indicates a larger deviation with increasing sediment loads. For instance, when the model predicts 4.1 × 105 t month−1, the measurements vary between 2.9 × 105 t month−1 and 5.0 × 105 t month−1, which stems from the aforementioned seasonal effects. The overall model accuracy corresponds to a Pearson’s correlation coefficient \(r\) of 0.92 and the Nash–Sutcliffe efficiency (NSE) is 0.78.

3.2 Sediment load prediction with snowfall recognition

3.2.1 Calibration of the β parameter

Since snowfall is not erosive, the \(\beta\) parameter requires a new calibration at a monthly resolution, which follows the approach underlying Fig. 7. The re-calibration results in an optimum catchment-specific \(\beta\) parameter of 0.58 for the model chain when snow recognition is implemented.

3.2.2 Sediment load prediction

Figure 5 shows the computed suspended load in the observation period using the modified \(R\) factor considering the non-erosivity of snowfall in red (“snowfall”). The most significant difference compared to the simulations without snow recognition (“no snow”) is that the suspended sediment load is 36,300 t smaller in February 2018 and 55,000 t larger in March 2018. As a result, the significant errors in February 2018 (44%) and March 2018 (18%) reduce to 31% and 7%, respectively. The influence of snowfall recognition is less significant in the other months of the observation period, but the sediment load also decreases in other months with significant snowfall (January 2017 and February 2018). Moreover, the smaller \(\beta\) parameter causes the monthly catchments sediment delivery ratios \({SDR}_{b}\) (Eq. (4)) to increase by an average of 9%, resulting in an increase in suspended sediment load during months without any snow influence. By considering snowfall, the overall mean absolute error reduces from 51,190 t month−1 to 35,090 t month−1.

Figure 6 compares observed and computed monthly suspended sediment loads in the calibration period with the recognition of snowfall (“snowfall”), based on temperature reanalysis datasets. Compared to the simulations without snow recognition (“no snow”), the deviations are significantly lower. The improvements can mainly be attributed to the distinction between snow and rain in February 2018 and March 2018. The Pearson’s correlation coefficient \(r\) increases to 0.96 and the Nash–Sutcliffe efficiency (NSE) increases to 0.89.

3.3 Sediment load prediction with snowfall and snowmelt recognition

3.3.1 Calibration of the R factor and NDSI threshold

Figure 8 shows an exemplary true-color satellite image (March 2018) that served for the expert assessment to identify the snow cover when calculating the \(R\) factor in the model chain (Fig. 4). The detected snow-covered areas are highlighted in green. The above-introduced expert verification (see chapter 2.5.3) of the snow cover algorithm with an overlay of elevation contour lines yields best results with an NDSI threshold of 0.4 in combination with a threshold of 1800 (top of atmosphere reflectance) for the blue band of Sentinel-2 satellite imagery.

Fig. 8
figure 8

True-color satellite image from March 2018 a) without and b) with detected snow cover in light green and c) topography with detected snow cover

Full size image

3.3.2 Calibration of the β parameter

Since snowmelt is erosive (unlike snowfall), the \(\beta\) parameter again requires a new calibration at a monthly resolution, which follows the approach underlying Fig. 7. The re-calibration results in an optimum catchment-specific \(\beta\) parameter of 0.63 for the model chain when snow recognition and snowmelt are implemented.

3.3.3 Sediment load prediction

Figure 5 shows the computed suspended load in the observation period using the modified \(R\) factor for consideration of snowfall and snowmelt (“snowfall + snowmelt”). The most significant difference compared to the simulations without snow recognition (“no snow”) is that the suspended sediment load is 44,100 t smaller in February 2018 and 72,000 t larger in March 2018 compared to the model without any snow recognition. As a result, the significant errors in February 2018 (44%) and March 2018 (18%) reduce to 29% and 3%, respectively, and compared with the model without any snow recognition. Compared to the case of snowfall consideration only (“snowfall”), the errors decrease by an additional 2% in February and 4% in March 2018. In April 2018, the error decreases by a further 6% because of significant snowmelt. The general trend indicates that the suspended sediment load decreases in the months with high snowfall (2017–01, 2018–02) and increases in the months with significant snowmelt (2017–02, 2018–03, and 2018–04). The \(\beta\) parameter causes the monthly catchment’s sediment delivery ratios \({SDR}_{b}\) (Eq. (4)) to increase by an average of 7% compared to the approach without snow recognition. This results in an increase in suspended sediment load during months without snow. By considering snow-related effects, the overall mean absolute error reduces from 51,190 t month−1 to 32,860 t month−1.

Figure 6 compares observed and computed monthly suspended sediment loads in the calibration period with the combined consideration of snowfall and snowmelt. The accuracy further increases compared to the simulations without snow recognition (“no snow”) and with snowfall recognition only (“snowfall”). The improvements can mainly be attributed to the time-shifted erosion in the spring seasons 2017 and 2018. Erosion attenuates in January 2017 and February 2018 because of the above-introduced snowfall and amplifies in the spring months February 2017, March 2018, and April 2018 because of additional runoff from snowmelt. The combined consideration of snowfall and snowmelt ultimately yields slightly higher accuracy compared to the snowfall-only case with a Pearson’s correlation coefficient \(r\) of 0.97 and a Nash–Sutcliffe efficiency (\(NSE\)) of 0.90.

4 Discussion

4.1 Snow cover detection

The satellite imagery indicates that most of the precipitation in February 2018 fell in the form of snow, which was confirmed by an additional analysis of the temperature data. Figure 9 shows the percentage of snow coverage of the catchment area over the entire observation period with two peaks at the beginning of February 2017 and the beginning of March 2018. The significantly lower snow covers in the following months make that the model chain predicts higher erosion in February 2017 and the spring months of March 2018 and April 2018. In particular, the superpositioning of daily precipitation and temperature data results in 40% of the February 2018 precipitation as snowfall, leading to an average snow water equivalent of 60 mm across the catchment. In contrast, only 7% of the March 2018 precipitation was snowfall. Furthermore, the analysis of satellite imagery reveals that snow cover in the catchment reduced from over 80% to less than 20% from the beginning of March 2018 to the beginning of April 2018, indicating snowmelt processes. In February and March 2018, the largest deviation of the RUSLE approach without considering snow effects (e.g., 44% overestimation in February 2018, see Fig. 5) can be observed. The resulting erosion patterns are significantly different, in particular with regard to peak events. To ensure reliable results, any long-term analysis (e.g., of climate change scenarios) should not neglect snow-related effects. Although only a few months (December to March) of the hydrological year might be affected by snow and snowmelt in mountainous Mediterranean regions, this study shows that their consideration is essential.

Fig. 9
figure 9

Percentage of snow cover of the catchment area between 05/2016 and 04/2018 using the satellite-imagery-based snow detection algorithm

Full size image

4.2 Improvement of the RUSLE

The original approach for calculating the \(R\) factor (Brown and Foster 1987; Renard 1997) in the RUSLE requires precipitation data with at least a 30-min resolution at every grid pixel. However, such data are not available in many regions of the world and the spatio-temporal resolution of reanalysis and climate forecast data underestimate the intensity of locally heavy rainfall events because of scale effects resulting from coarse spatial resolution (Chen and Knutson 2008). Without adjusting the \(R\) factor, every precipitation event (rain and snow) is considered to be erosive. Hence, the predicted suspended sediment transport is significantly overestimated in February 2018 since snowfall is not taken into account. The 74% higher suspended sediment load in March 2018 (compared to February 2018) cannot be modeled without considering snow in the \(R\) factor, because the precipitation (rain and snow) in March was 10% lower than in February 2018. This known limitation of the RUSLE has already been identified in previous studies (Alewell et al. 2019). This study indicates that the results improve significantly when a temperature threshold is set to consider snowfall in the \(R\) factor where the NSE increased by 14% to 0.89.

Thus, the results confirm the existing recommendations to set a temperature threshold for snow detection (Meusburger et al. 2012; Schmidt et al. 2016) by comparing modeled and observed suspended sediment loads. The RUSLE also does not consider snowmelt (Yin et al. 2017; Alewell et al. 2019) and this study shows that implementing snowmelt in the RUSLE’s \(R\) factor results in a further accuracy improvement (NSE increases to 0.90). In regions where snow plays a more important role or where the time shift between snowfall and snowmelt is larger, an even greater influence of the novel approach can be expected.

4.3 Sediment delivery ratio

This study shows that the average sediment delivery ratio \({SDR}_{b}\) of the catchment is higher than indicated in the literature (Boyce 1975; Walling 1983). However, the RUSLE does not reproduce all types of erosion. Thus, an underestimation of erosion because of gully erosion, fluvial erosion, or mass movement is a possible explanation. Since the model is calibrated to measured suspended sediment load and not to soil loss in the catchment area, the erosion may be underestimated. To compensate for the underestimated erosion, the \({SDR}_{b}\) increases. For example, Borrelli et al. (2014) found that rill and interrill erosion, which are included in the RUSLE, are not the dominant processes contributing to the sediment yield of a Mediterranean mountainous catchment in Italy. As a result, the RUSLE significantly underestimates the observed sediment yield.

To verify the consistency of soil erosion and sediment transport, the soil loss and sediment yield can be mapped to identify sediment source areas where absolute soil erosion rates should be considered rather the best available hypotheses than exact predictions (Borrelli et al. 2021). Figure 10 shows the annual soil loss and the annual specific sediment yield per hectare for the catchment area of the Kokel monitoring station for the observation period from May 2016 to April 2018. In particular, the pixels with high slopes near the river network have both high soil erosion and high \(SD{R}_{i}\) s, which leads to a high sediment yield. Because these areas are close to the outlet of the catchment, a larger catchment area does not necessarily result in a reduction of the catchment’s \({SDR}_{b}\). For instance, the mean annual soil loss in Italy is the highest in Europe (8.46 t ha−1) and stems from a combination of high rainfall erosivity and steep topography (Panagos et al. 2015c). In comparison, the average annual soil loss in the Kokel catchment was 12.8 t ha−1 year−1 in the observation period, whereas the highest values occurred at pixels with a steep slope and sparsely vegetated or agricultural areas. Remote areas with steep slopes close to the Korca plain (i.e., with a larger distance to the channel network) only have little effect on the catchment’s sediment yield, even though the pixels show high local erosion rates (Fig. 10).

Fig. 10
figure 10

Annual soil loss (left) and annual specific sediment yield (right) in the catchment area of the Kokel monitoring station for the observation period from May 2016 to April 2018

Full size image

4.4 SEDD

The SEDD model does not account for erosion and deposition processes in the river network. The simplified assumption of an unlimited river transport capacity (i.e., all supplied suspended sediments in the river network are transported to the outlet of the catchment) is only valid for long-term observations. Thus, daily or event-based dynamics can solely be modeled in small catchments with an ephemeral channel network (Ferro and Porto 2000; Burguet et al. 2017). In addition, mass wasting and fluvial erosion are not considered in the presented approach, which opens the door for future research to better encompass the boundary conditions for numerical models of rivers and reservoirs with the required complexity.

The SEDD model may be replaced with alternative models when sub-monthly data and analysis are the focus of a study. These can be runoff-driven Modified Universal Soil Loss Equation (MUSLE) approaches, such as the Soil & Water Assessment Tool (SWAT) (Arnold et al. 2012; Prabhanjan et al. 2015), physics-based models, such as the Water Erosion Prediction Project (WEPP) model (Flanagan and Nearing 1995), or the improved Morgan approach (Tan et al. 2018). However, physics-based models require a larger amount of data than empirical models, which is rarely available at large temporal and spatial scales (Nearing 2013). For example, WEPP requires more than 100 parameters for the full application of a hillslope model (Brazier 2013). MUSLE-based approaches use storm-based runoff volumes and peak flows to simulate erosion and sediment yield. Whereas these approaches rely on calibrated hydrological models, the RUSLE only requires precipitation data to calculate erosive energy. Still, even with good data availability, SWAT does not always result in a reliable prediction of sediment load due to the high degree of complexity involved where, in particular, the high temporal resolution (daily data) is challenging (Prabhanjan et al. 2015).

4.5 Merits and challenges of free data

This study uses climate reanalysis and satellite data to calculate the \(R\) and \(C\) factors, which requires the availability of appropriate datasets for the region. This is the case almost everywhere in the world, by virtue of global reanalysis datasets and the availability of satellite imagery. Thus, climate reanalysis data enable the implementation of regression equations for determining the monthly and the annual rainfall-runoff erosivity factor \(R\) in the RUSLE for all climatic regions (Naipal et al. 2015; Benavidez et al. 2018). However, the quality or the suitability of available regression equations can significantly influence the quality of the results. For instance, the uncertainty of the \(R\) factor is considerable when the selected regression equation does not correctly reflect physics-driven trends in the data.

Even without snow recognition, the high NSE (0.78) demonstrates that the presented workflow is a viable method to calculate monthly suspended sediment loads by using free and accessible data when no precipitation data in high spatio-temporal resolution are available. The computed suspended sediment loads mainly depend on total precipitation, seasonal dynamics of vegetated land cover, and seasonal erosivity characteristics of rainfall, which is in line with theoretical expectations (Perks et al. 2015; Vercruysse et al. 2017). For instance, Ranzi et al. (2012) also simulated monthly sediment loads in the Lo watershed in Vietnam and obtained a lower NSE of 0.45 using directly measured precipitation.

4.6 Limitations of the model chain

The uneven distribution of the measurement data in this study additionally involves uncertainty concerning transport processes at low flow conditions. For instance, measurements in the dry summer months are scarce because the water depth rarely exceeded the measurement criterion of at least 1 m. Hence, the influence of intense but short rainfall events in the summer (e.g., thunderstorms) cannot be analyzed in this study. However, most erosion in Mediterranean catchments occurs during the wet season and the influence of low-flow periods is almost negligible (Rovira and Batalla 2006). More observations of snowfall may aid to confirm the validity of the modified approach of this study. For instance, Eq. (3) used to calculate \({R}_{m, \mathrm{snowmelt}}\) requires additional data for accurate calibration and transferability to other studies.

The here-presented method accumulates snow over months and assumes that the snow cover thickness corresponds to the accumulated monthly snowfall since the last time that a pixel was not snow-covered. Snowmelt is only detected when a formerly snow-covered pixel is not covered anymore in the month under consideration. Thus, snowmelt corresponds to the total accumulated amount of snow that has fallen before, but partial snowmelt (i.e., variation in snow cover thickness) cannot be detected. Although this approach yields good results in this study, it cannot be applied to regions permanently covered with snow where snow-driven runoff predominantly is a function of snow cover thickness variation. For permanently snow-covered regions, temperature-dependent snowmelt models (e.g., Hock 2003) are more suitable than the here shown approach.

4.7 Validity of hypotheses

The hypotheses made in this study can be partially verified and show that the presented model chain, based on free datasets, represents a viable approach.

The presented methods rely on empiric formulae that wrap complex processes into a simplified workflow. In a perfectly documented world, precise deterministic models would yield better results, but in the absence of omnipresent precise data, model uncertainty in simple empirical models is not larger than in deterministic models (Brazier 2013). Thus, the here-presented approach is a reasonable tradeoff between applicability and reliability of monthly sediment load predictions, where readily available climate reanalysis datasets serve as input data. Hence, the gridded climate reanalysis data can be considered suitable input data and may also be used to simulate historical scenarios and for long-term predictions of sediment load.

The expert-based refinement of threshold values for the NDSI and the blue band of Sentinel-2 satellite imagery contributes to a substantial increase in the overall accuracy of the model chain. In addition, the plot of monthly snow cover (Fig. 9) indicates that the used band thresholds provide reasonable estimates. Hence, it can be concluded that the proposed strategy for deriving snow cover by using thresholds for the NDSI and the blue band of Sentinel-2 satellite imagery represents a viable and reusable approach. Thus, the hypothesis that data interpolation with climate reanalysis and satellite imagery enables viable sediment load predictions in data-sparse regions is accepted.

Adding snowfall as a function of interpolated temperature yields an increase in Pearson’s \(r\) between modeled and observed sediment loads at the Kokel monitoring station from 0.92 to 0.96 and the Nash–Sutcliffe efficiency (NSE) increases from 0.78 to 0.89. The increase in the accuracy of the model chain considering snowfall is most prominent comparing computed monthly suspended sediment loads with and without snowfall recognition (Fig. 5). The additional consideration of snowmelt results in a further increase in Pearson’s \(r\) and NSE to 0.97 and 0.90, respectively. Figure 5 confirms that the trend of statistics corresponds to observations. Thus, the novel model chain represents a major improvement for mountainous Mediterranean catchments with sparse measurement data, which is also confirmed by the 5-month split model calibration and validation (SI 5) and leave-one-out cross-validation (SI 6). Ultimately, the improved overall model accuracy and the strong capacities of the model chain to account for snowfall and snowmelt make this novel approach that combines the RUSLE and the SEDD model, a viable method in mountainous Mediterranean regions. Thus, we accept the hypotheses that the accuracy of the model chain improves with the consideration of snowfall and snowmelt in the \(R\) factor.

4.8 Bedload

Beyond total sediment load, estimates of bedload are crucial for hydro-morphodynamic studies in fluvial systems. Yet, bedload is often ignored (Milliman and Syvitski 1991; Wright et al. 2010) or estimated as an overly simplified constant fraction of suspended load (Galy and France-Lanord 2001; Grams et al. 2013). This approach is not recommended because bedload can be a significant fraction of the total load and can vary relatively to suspended load because of changing suspension conditions (Ashley et al. 2020). Since none of the existing models for calculating the bedload fraction has been accepted yet as universally valid, an empirical equation is used to estimate bedload transport rates from suspended transport rates (Turowski et al. 2010). The algorithm in this study enables guesstimating bedload. However, this feature is not presented here because the validity of the bedload estimates cannot be evaluated in the absence of bedload measurement data. A more accurate estimate requires the consideration of hydro-morphodynamic processes in the river network and measurement data.

5 Conclusions

The good agreement between predicted and observed suspended sediment loads demonstrates that the combination of the RUSLE and the SEDD model is a viable approach to objectively estimate monthly sediment loads in data-scarce regions. The here-presented novel approach involves a model chain that requires one gauging station for calibration and most of the input data are interpolated from freely available satellite imagery and climate reanalysis data. To this end, Sentinel-2 satellite imagery and climate reanalysis precipitation data are relevant data sources.

Especially in mountainous Mediterranean regions, the implemented snowfall and snowmelt processes significantly increase the model accuracy, which can be clearly attributed to an improved reproduction of physical processes, enabling objective predictions with monthly resolution. The snow-related processes are incorporated in the rainfall-runoff erosivity (\(R\)) factor of the RUSLE where temperature data informs about snowfall and satellite imagery enables the detection of snow cover and snowmelt.

Ultimately, the presented seasonal snow memory methods represent a major improvement in the prediction of soil erosion and sediment transport in mountainous Mediterranean catchments with limited measurement data availability. As a result, information on suspended sediment load is available at a resolution that enables the prediction of hydro-morphological processes in rivers, lakes, and reservoirs. The approach may also be used in the future to investigate climate change scenarios. For this purpose, the historical climate reanalysis data are to be replaced by predicted data from climate projections.