Abstract
Purpose
Environmental assessments of efforts to reduce vehicle fuel consumption require scientifically sound and robust fuel consumption models. The purpose of this paper is to introduce a novel method and model for calculating fuel consumption.
Method
This paper presents a method of powertrain modeling that is based on driving and powertrain physics, such as a net force approach to calculate force demand at the tire patch, and the use of engine maps to model engine efficiency.
Results
The presented method provides parsimonious open-source powertrain modeling to the environmental assessment community, thus an alternative to existing approaches. The modeling results are in agreement with existing values, while the modeling method is more flexible and avoids unnecessary approximations.
Conclusions
Existing fuel consumption modeling consists of very detailed and complex powertrain simulation models, typically not available for environmental vehicle assessments, or streamlined equation-based methods that use a mix of physical laws, engineering approximations, and sometimes accounting principles. The presented modeling method and open-source model provide a valuable alternative.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over 80% of global passenger vehicle sales are now subject to proposed or existing fuel economy or greenhouse gas emission standards for light duty vehicles (ICCT n.d.). To meaningfully support these environmental efforts, environmental assessments of light duty vehicles require careful and sound description of the use phase, which includes scientifically robust fuel consumption models. Especially change-oriented assessments, such as consequential life cycle assessments, require rigorous fuel consumption modeling, in particular of changes in fuel consumption due to changes in vehicle design (Modaresi et al. 2014; Das et al. 2016; Serrenho et al. 2017; Palazzo and Geyer 2019). However, even accounting-type assessments, which compare different given vehicle designs rather than explicitly model the consequences of vehicle design changes, require fuel consumption models, since they frequently compare a baseline vehicle design with a version that would result from one or more design changes (Sullivan and Cobas-Flores 2001; MacLean and Lave 2003; Geyer 2016).
An example of such a design change is vehicle mass reduction, frequently with the explicit intent to reduce fuel consumption. There are many different design strategies for vehicle mass reduction. One that has been subject to many environmental assessments over the last decades is material substitution, e.g., replacing steel with aluminum or fiber-reinforced composites (Kim and Wallington 2013a). The history of automotive material substitution studies reveals the evolution of fuel consumption modeling in environmental assessments.
Most of the early vehicle mass reduction studies used the concept of a mass elasticity of fuel consumption (in liter/100 km) or fuel economy (in km/l or miles per gallon), which is the ratio of relative fuel savings over relative mass savings, ∆FC · VM/FC · ∆VM or ∆FE · VM/FE · ∆VM. This ratio of percentage changes is typically assumed to be a constant, e.g., 0.5, which means that a 10% reduction in vehicle mass results in a 5% reduction in fuel consumption or a 5% increase in fuel economy (Saur et al. 1995; Stodolsky et al. 1995; IAI 2002; Das 2000; Field et al. 2001; Birat et al. 2004). As we pointed out in 2008, this approach is not scientifically sound for at least two reasons (Geyer 2008). First, the approach yields different results, depending on whether fuel consumption or fuel economy is used. Second, functions with constant elasticity are of the form f(x) = axb, with b being the elasticity, so any elasticity other than b = 1 would yield a non-linear relationship between vehicle mass and fuel consumption.
A more robust approach is to abandon the concepts of fuel economy and mass elasticity and express the relationship between a change in vehicle mass and the resulting change in fuel consumption in absolute terms, i.e., ∆FC/∆VM given in liters/(100 km · 100 kg). This is a widely used approach today, and ∆FC/∆VM is frequently called fuel reduction value (FRV) (Kim and Wallington 2013a).
Fuel consumption and fuel reduction values for specific vehicles and mass reductions can be determined empirically, e.g., through coast down and roller bench tests (ANL n.d.). They can also be determined through detailed powertrain simulation models, which require many input parameters and careful calibration and tend to be fairly black boxes (Wohlecker et al. 2007). Both methods are very labor and cost intensive and thus not available for most environmental assessments. They also yield only one fuel consumption or fuel reduction value per experiment or simulation and would have to be either extrapolated or repeated for each new studied vehicle design.
In 2010, Koffler and Rohde-Brandenburger introduced a streamlined approach to FRV calculation, which is much more grounded in physics than the mass elasticity approach (Koffler and Rohde-Brandenburger 2010). To achieve a useful balance between simplicity and technical fidelity, several simplifications were deliberately included in their model. One is the linear decomposition of force demand due to rolling resistance, aerodynamic drag, and acceleration. The so-called mass induced work required at the tire patch to move a vehicle through a driving cycle is then defined as the sum of rolling resistance work for time steps with non-negative acceleration and acceleration work for time steps with positive acceleration. However, it is the net of all three forces that determines whether the engine needs to provide torque or not. Separate treatment of the three forces introduces the possibility of error, since it can no longer be observed whether the net force is positive or negative. In fact, calculating the total energy demand at the tire patch for the NEDC driving cycle using the linear decomposition and the net force approach shows that the former is 3–6% different from the latter. The net force approach is also necessary to model regenerative braking, which is standard in hybrid electric vehicles.
A second simplification is the use of so-called Willans lines (engine fuel consumption [l/h] as function of power output [kW] at constant engine speed [rpm]) to argue that one constant “differential” efficiency is sufficient to describe how a change in engine power demand due to mass reduction affects engine fuel demand. However, this assumes that the slopes of all Willans lines are constant and equal, which they are not, and that mass reduction changes engine power output without changing engine speed. Again, these assumptions introduce the possibility of error. Furthermore, this simplified approach provides no theoretical framework to account for the fact that mass reduction may enable powertrain adjustments such as the use of downsized engines.
The approaches introduced by Kim and Wallington a few years later also use linear decomposition of force demand, the concept of mass-induced fuel consumption, and many other mathematical decomposition and allocation steps (Kim and Wallington 2013b; Kim and Wallington 2015). One example is the linear decomposition of engine efficiency using constant thermal efficiency and friction loss. Another is the allocation of powertrain conversion losses to “mass-induced” work required at the tire patch.
The recent exchange between Koffler and Rohde-Brandenburger and Kim and Wallington shows that their approaches, which are based on a mix of physical laws, engineering approximations, and even accounting principles in some instances, still provide ample opportunity for controversy (Koffler and Rohde-Brandenburger 2018; Kim et al. 2019; Koffler and Rohde-Brandenburger 2019).
This paper presents a third approach to powertrain modeling that lies between the complex and comprehensive simulation studies and the streamlined equation-based methods mentioned above. We present a powertrain simulation model that is based on two modeling principles. The first is to rely entirely on driving and powertrain physics and not use any engineering rules of thumb or approximations (Ross 1997; Heywood 1988; Waters 1972). The second is to obtain accurate fuel consumption results with a minimal number of vehicle and powertrain parameters. The latter objective aims at finding the sweet spot between model accuracy and modeling effort and complexity, a modeling approach sometimes called parsimonious. It also enables a model that is completely transparent and can be used by non-experts.
2 Methods and data
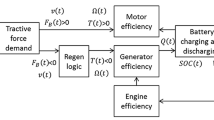
Vehicle energy demand is given in MJ of fuel per 100 km and calculated by moving a vehicle through a so-called driving cycle, which specifies vehicle velocity v(t) (in meters per second) as a function of time t, typically given in time increments of 1 s ti. The approach to powertrain modeling presented in this paper is to calculate the net tractive force demand FT at the vehicle’s tire patch for each time increment ti and then determine the operating point of the powertrain that provides the required force under realistic operating conditions. The operating point of the powertrain, in turn, determines the fuel demand of the internal combustion engine, called brake-specific fuel consumption (BSFC) and given in gram per kWh. For a given driving cycle, the energy demand of the vehicle is obtained simply by summing up the energy demands of each time increment ti and normalizing the result to 100 km. All model calculations are implemented in an Excel workbook. The modeled powertrain components are shown in Fig. 1.
2.1 Force demand at tire patch and secondary loads
The first step is to calculate the net tractive force that is required at the tire patch in each time step in order to move the vehicle through the drive cycle. In addition to the driving cycle v(t), the minimal set of input parameters required to calculate tractive force demand are mass M, frontal area AF, and aerodynamic drag coefficient cD of the vehicle, as well as the rolling resistance coefficient of the tires fR. The force demand at time ti due to rolling resistance is calculated as FR(ti) = Ma = MgfR, with \( g=9.81\frac{m}{s^2} \) being the acceleration due to gravity. The force demand at time ti due to aerodynamic resistance is calculated as \( {F}_D\left({t}_i\right)=\frac{1}{2}\rho {c}_D{A}_Fv{\left({t}_i\right)}^2 \), with \( \rho =1.225\frac{kg}{m^3} \) being the density of air. The force demand at time ti due to acceleration/deceleration is calculated as \( {F}_A\left({t}_i\right)= Ma=M\left(\frac{v\left({t}_i\right)-v\left({t}_{i-1}\right)}{t_i-{t}_{i-1}}\right) \). Net force demand at the tire patch is calculated as FT(ti) = FR(ti) + FD(ti) + FA(ti) and can be positive or negative, since the negative force of deceleration can be larger than the sum of the always positive rolling resistance and aerodynamic drag forces. A negative value of FT indicates that frictional or regenerative braking is required to meet the velocity demanded by the driving cycle.
There are two secondary loads in addition to the primary tractive force demand, which are included in the powertrain model. They are the rotary inertia of rotating vehicle components and the spin loss of the drive train. As the vehicle moves forward, rotational inertias such as tires, wheels, and driveline components must also be rotationally accelerated. This rotary inertia can be described as an additional term of the translational inertia, i.e., FR = M(1 + ε)a, where Mε is the effective additional inertia mass due to rotating components.
Spin loss is a resistance force proportional to vehicle speed. An empirical way to measure the forces resisting forward motion is to estimate the coefficients in equation \( M\frac{dv}{dt}=A+ Bv+C{v}^2 \) through coast down tests. A is identical with the rolling resistance force A = FR = MgfR. C is due to aerodynamic drag and thus calculated as \( C=\frac{1}{2}\rho {c}_D{A}_F \). Spin loss coefficient B is related to the viscous forces generated in the drivetrain and determined empirically.
The resulting net force required during time increment ti in order to move a vehicle through driving cycle v(ti) is now calculated as \( {F}_T\left({t}_i\right)= Mg{f}_R+ Bv\left({t}_i\right)+\frac{1}{2}\rho {c}_D{A}_Fv{\left({t}_i\right)}^2+M\left(1+\varepsilon \right)\frac{v\left({t}_i\right)-v\left({t}_{i-1}\right)}{t_i-{t}_{i-1}} \). The final part in this first modeling step is to convert translational speed v(ti) (in meter per second) and force demand FT(ti) (in Newton) into rotational tire speed ΩT(ti) (in rad per second) and axle torque demand TT(ti) (in Newton meter) according to the equations TT = r · FT and ΩT = v/r, with r being the rolling radius of the tire.
An interesting and useful intermediate result is the total energy demand at the tire patch, which is calculated as EDT = ∑iFT(ti) · v(ti) for all FT(ti) > 0 and given in MJ per km or 100 km.
2.2 Torque demand at engine shaft
The next step is to model the drive train components between the tires and the engine. A minimal set of components that needs to be modeled is the differential, the transmission, and the torque converter (Chana et al. 1977; Kim et al. 2007). The model calculations follow the powertrain backwards, or from left to right in Fig. 1. The differential and transmission gears are defined by their gear ratios and their torque/energy conversion efficiencies, which are used to convert the required torque and rotational speed output (in Nm and rad/s) into the corresponding torque and rotational speed input (Genta and Morello 2009; Flamand et al. 1998). Required torque input into the differential is thus calculated as TD − in = TT/(ηD · RD), with ηD being the energy/torque conversion efficiency, RD being the gear ratio of the differential, and TD − out = TT. Speed input into the differential is calculated as ΩD − in = RD · ΩD − out = RD · ΩT.
The function of the transmission is to convert the required output torque and speed to corresponding values of engine torque and speed that allow efficient and smooth operation of the engine. For each gear, required torque and speed input to the transmission are calculated in the same way, i.e., \( {T}_{Tr- in}^n={T}_{D- in}/\left({\eta}_n{R}_n\right) \) and \( {\Omega}_{Tr- in}^n={R}_n{\Omega}_{D- in} \), with ηn being the energy/torque conversion efficiency of gear n, Rn being the ratio of gear n, \( {T}_{D- in}={T}_{Tr- out}^n \), and \( {\Omega}_{D- in}={\Omega}_{Tr- out}^n \).
The function of the torque converter is to allow non-zero engine speed when the vehicle is at rest and to match torque needs at low vehicle speeds. A simple, yet reasonable model of the torque converter is to assume that the torque output over input ratio is a linear function of the speed output over input ratio, i.e., \( \frac{T_{Tr- in}}{T_{TC- in}}=-\frac{STR}{EXT}\frac{\Omega_{Tr- in}}{\Omega_{TC- in}}+ STR+1 \). Here STR is the stall torque ratio, and EXT (called extension) is the point at which the lockup clutch directly connects engine and transmission without slippage, i.e., \( \frac{T_{Tr- in}}{T_{TC- in}}=1\ for\ \frac{\Omega_{Tr- in}}{\Omega_{TC- in}}\ge EXT \). By far the largest torque converter slippage occurs in first gear. Therefore, slippage is only modeled there and not in any of the higher gears. This means that in the vast majority of time steps TTC − in = TTr − in.
For each time step ti the model needs to determine which gear the car is operated in. To do that, the brake torque TB(ti) = TTC − in(ti) and engine speed ΩB(ti) = ΩTC − in(ti) required at each time step to move the vehicle through the driving cycle is calculated for every gear. In other words, for each time step ti n pairs of required brake torque TB(ti) and engine speed ΩB(ti) are calculated by the powertrain model.
2.3 Fuel demand
The final step of the powertrain model is to convert the torque demand at the engine shaft into fuel demand. This step is complicated by the fact that brake-specific fuel consumption (BSFC), i.e., fuel consumption rate per power output, is a complex function of engine torque and engine speed. The relationship has to be determined empirically, through engine tests, and the resulting data is stored and visualized in so-called engine maps. BSFC is essentially the energy conversion efficiency of the engine at a given operating point, i.e., torque and speed, and typically given in g/kWh. Simplified powertrain models used in environmental assessments typically use a constant BSFC, or other simplifications, even though the conversion efficiency of a typical engine varies from single digits to close to 40%.
For each time step ti and gear, the powertrain model looks up the BSFC that matches the required brake torque and engine speed. The engine maps in the powertrain model are data tables with 10 Nm torque and 100 rpm speed intervals. To increase model precision, linear interpolation is used to calculate the BSFC of each engine operating point. It is possible that, for some time steps of the driving cycle, certain gears would require brake torque and engine speed combinations that are not feasible with the chosen engine map. For each time step, the powertrain model needs to select one of the feasible gears. Many different gear shifting logics could be implemented. In the current version, the powertrain model simply chooses the gear with the lowest BSCF. For the time steps in which the net force demand FT(ti) is zero or negative, idle fuel consumption is selected, which is another data input given in liter gasoline or diesel per second and liter engine displacement. The last step is to calculate the fuel consumption during each time step as FC(ti) = BSFC(ti) · ΩB(ti) · TB(ti)/ρfuel, with ρfuel being the density of the used fuel in grams per liter, which is another data input to the model. The fuel consumption for the specified vehicle and driving cycle (in liters of fuel per 100 km), without accessory load, is now calculated as FC = ∑iFC(ti)/(0.01 · LDC), with LDC = ∑iv(ti)/1000 being the length of the driving cycle in km.
An additional source of fuel demand is accessory load AL, which is also a data input to the model and given in Watt of mechanical power demand. The additional fuel demand due to accessory load is thus calculated as ALFC(ti) = BSFC(ti) · AL/ρfuel. Total fuel consumption including accessory load is TFC = ∑i(FC(ti) + ALFC(ti))/(0.01 · LDC). FC and TFC are both given in liters per 100 km. Multiplying fuel consumption values with the energy density of the fuel yields the energy demand ED for the specified vehicle and driving cycle (in MJ fuel per 100 km).
2.4 Vehicle performance and engine resizing
Comparative environmental assessments of vehicles need to make sure that functionally equivalent cars are compared. One pertinent example is that, all other things being equal, the acceleration performance of a vehicle will increase when its mass is reduced. The resulting question is now if, or to what extent, the original vehicle should be compared to the mass-reduced version, which has at least somewhat different driving characteristics. A common approach to reestablishing functional equivalence is to downsize the engine of the mass-reduced vehicle, so that it has the same 0–60 miles per hour (mph) acceleration time as the baseline car.
To implement such engine resizing, the powertrain model calculates the 0–60 mph acceleration time for the vehicle specified by the model user. It does so by calculating the time intervals it takes to accelerate the vehicle by 1 mph increments. For each speed increment, x mph → x + 1 mph, the model selects the gear that provides the maximum torque, converts this engine torque into force at the tire patch, and uses the net force demand equation to calculate the time it takes to increase vehicle speed by one mile. The time it takes to accelerate from 0 to 60 mph is simply the sum of the 60 time increments. The model also accounts for torque converter slip in first gear, tire slip beyond a set maximum force, and the time it takes to shift gear.
The resizing of the engine is modeled using a torque scaling factor, Tresized/Tbase. This approach takes advantage of the fact that engine torque is directly proportional to the area of the piston heads, i.e., Tresized/Tbase = Aresized/Abase, given that all other engine characteristics, such as number of cylinders, stroke, thermal, mechanical, and volumetric efficiencies remain the same (Anderson 2003). As a result, the powertrain model simulates engine resizing by taking an engine map and scaling the torque axis by a constant factor, while leaving everything else the same. The assumption that all other engine characteristics stay the same is a reasonable approximation for incremental changes to the piston head area. Large changes will have a higher impact on some characteristics, such as mechanical and thermal efficiencies. It would be valuable to include such secondary effects of engine resizing in future versions of the presented powertrain model. For the time being, using torque scaling to model engine resizing should be limited to incremental changes. Large changes are better modeled using two engine maps.
In the powertrain model, all engine maps can be resized manually. The process of engine resizing after vehicle mass reduction to achieve equal performance is as follows: Enter all input data for the baseline vehicle and note the calculated 0–60 mph acceleration time. Reduce vehicle mass input data; the calculated 0–60 mph time will decrease as a result. Use the Excel goal seek function to set the 0–60 mph time back to the baseline value by changing the torque scaling factor, i.e., simulating a downsizing of the engine. The result is a mass-reduced vehicle with the same 0–60 mph acceleration as the baseline vehicle.
3 Results and discussion
The presented powertrain model has 30 input parameters and therefore enables many different analyses. This results section will focus on the impact of key vehicle characteristics on fuel consumption for different driving cycles and 0–60 mph acceleration times. Those vehicle characteristics are vehicle mass M, frontal area AF, aerodynamic drag coefficient cD, rolling resistance coefficient fR, and engine map.
3.1 Fuel consumption and key vehicle characteristics
Figure 2 depicts fuel consumption as a function of vehicle mass M, frontal area AF, and rolling resistance coefficient fR. It does this for two driving cycles, NEDC, a so-called modal driving cycle, and Hyzem, an example of transient driving cycles, which involve more speed variation and are thus more representative of on-road driving. All three vehicle characteristics are varied by ±10 % , ± 20 % , ± 30 % , and ± 40% around baseline values typical for a compact ICV-G. The engine size was not adjusted for constant acceleration performance.
The response of fuel consumption to all three vehicle characteristics is not exactly, but close to, linear. All three characteristics enter the equation for net force at the tire patch FT(ti) in a linear fashion. The aerodynamic drag coefficient cD enters the net force equation in the same way as frontal area AF and is therefore omitted in the analysis. That the relationships are not exactly linear is due to the fact that changing vehicle characteristics has a small impact on the selected set of engine operating points, which, in turn, determines the overall engine efficiency. The ratio EDT/ED denotes the overall powertrain efficiency η for a given vehicle and driving cycle. In the simulations shown in Fig. 2, η increases slightly as M, AF, and fR increase. This means that the overall powertrain efficiency (calculated over the entire driving cycle) depends on the driving cycle and the entire vehicle configuration, and not just the engine alone.
Hyzem generates a consistently higher fuel consumption than NEDC due to higher speeds and more acceleration events. The smallest difference in fuel consumption between NEDC and Hyzem occurs at minimal frontal area AF. The fuel consumption in Hyzem is most sensitive to frontal area, while the fuel consumption in NEDC is most sensitive to vehicle mass. Both are least sensitive to the rolling resistance coefficient. Most and least sensitive is defined here in terms of equal percentage variations of the vehicle characteristics. It should be noted that the same engine map (inline 4 cylinder 1.2 l 85 kW gasoline) was used for all simulations in Fig. 2, and thus some of the underlying vehicle configurations may yield somewhat unrealistic car designs.
3.2 Impact of vehicle mass on fuel consumption and acceleration time
For many environmental vehicle assessments, the impact of vehicle mass on fuel consumption is of particular interest. Figure 3 shows fuel consumption for five different driving cycles and 0–60 mph acceleration times for a typical compact ICV-G configuration. Again, the functional relationship between fuel consumption and vehicle mass is not exactly, but highly, linear. The same is true for the relationship between 0−60 mph acceleration and vehicle mass. It can be seen that different driving cycles generate varying absolute levels of fuel consumption, with HWFET generating the lowest and Hyzem the highest. These results are obtained regardless of the engine map and fuel type used in the simulation. The sensitivity of fuel consumption to vehicle mass varies from driving cycle to driving cycle, shown to be the varying gradients of the lines in Fig. 3.
As should be expected, the FTP, which simulates city driving in the USA with lots of stop and go, has the highest sensitivity, and HWFET, which simulates highway driving in the USA, has the lowest. The development of the presented powertrain model was motivated by the long-standing controversy about the best way to quantify changes in vehicle fuel economy due to vehicle mass reduction, e.g., through the use of light-weight materials. The next section will therefore take an even closer look at the response of fuel consumption to vehicle mass reduction.
3.3 Change of fuel consumption due to change in vehicle mass
Table 1 shows the fuel reduction value FRV in liters per 100 km driven and 100 kg mass reduction. In Table 1, FTP and HWFET are averaged to yield the US Combined driving cycle. Vehicle mass reduction can be considered and modeled as a stand-alone design change or combined with an adjustment of the powertrain. A frequently considered powertrain adjustment is the downsizing of the engine in order to obtain equal acceleration between original and mass-reduced vehicle. Table 1 therefore shows fuel reduction values for each driving cycle and engine with and without engine resizing, which is done as described in Section 2.4. Vehicle parameters have been chosen in order to match the engine size and thus yield realistic vehicle configurations. A few basic vehicle characteristics are also shown in Table 1.
The table shows results from a limited set of simulations rather than a comprehensive analysis of the powertrain model. Nevertheless, some patterns are noteworthy and consistent with theory and existing literature. FRVs for diesel engines are consistently smaller than FRVs for gasoline engines. This reflects the higher efficiency of diesel engines relative to similar gasoline engines. FRVs without engine resizing are consistently smaller than FRVs with engine resizing. The reason for this is systematic changes in powertrain efficiency shown in Table 2 and discussed below. The rank ordering of FRVs with regard to driving cycles is very consistent across engine sizes. US Combined and Hyzem generate the smallest FRVs, while NEDC yields the largest FRVs. WLTP 3b mostly generates values in the middle range.
As mentioned in Section 3.1, vehicle mass reduction not only impacts energy demand at the tire patch EDT, but also the overall powertrain efficiency η = EDT/ED. FRVs conflate these two effects, and it is thus useful to conduct decomposition analysis.
A useful way to decompose the fuel reduction value FRV is to separate the change in energy demand at the tire patch EDT from the change in powertrain efficiency η = EDT/ED according to the following identity:
The equation shows FRV as the sum of the change in energy demand at the tire patch EDT at fixed powertrain efficiency and the change in powertrain efficiency at fixed energy demand at the tire patch. Subscript 1 denotes the vehicle design before mass reduction, while 2 stands for the vehicle after mass reduction.
Table 2 shows the decomposition of the FRVs from Table 1. It can be seen that vehicle mass reduction reduces the energy demand at the tire patch, but also changes the powertrain efficiency. In the examples shown in the table, mass reduction without powertrain resizing consistently reduces powertrain efficiency (η1 > η2), while the same mass reduction with engine resizing increases it (η1 < η2). The changes in powertrain efficiency are small, with |(η1 − η2)/η1| < 2%. The effect of the changes in powertrain efficiency, \( {\mathrm{ED}}_{T2}\left(\frac{1}{\eta_1}-\frac{1}{\eta_2}\right) \), is substantially smaller than the effect of the changes in EDT, \( \left({\mathrm{ED}}_{T1}-{\mathrm{ED}}_{T2}\right)\frac{1}{\eta_1} \). Nevertheless, it still reaches up to 40% of \( \left({\mathrm{ED}}_{T1}-{\mathrm{ED}}_{T2}\right)\frac{1}{\eta_1} \) in the examples shown in Table 2 and is thus significant. Table 2 is also a reminder that the difference between FRVs with and without engine resizing (all other things being equal) are entirely due to a change in powertrain efficiency, since engine resizing has no impact on the energy demand at the tire patch EDT.
The FRV values shown in Table 1 all fall in the range of values reported in the recent literature (Kim and Wallington 2013a; Koffler and Rohde-Brandenburger 2010; Kim and Wallington 2013b; Kim and Wallington 2015). They are also very close to FRVs generated by much more complex and detailed powertrain simulations that use the same vehicle and driving input data. Table 3 compares FRV values found in literature with values derived from the presented powertrain model. The values from (19) and (20) are generic FRVs. In contrast, the values reported in (FKA 2011) are from detailed powertrain simulations, which where replicated in the presented powertrain model to the extent possible. Using the presented powertrain model to derive fuel reduction values has several advantages. One is the use of actual engine maps to model engine efficiency, which avoids the need for approximations or simplifications. A second is the transparency of the model calculations, which allows for detailed analyses as shown in Figs. 2 and 3. This helps environmental practitioners build confidence in the soundness of the model results. It also facilitates more in-depth research into the physics of vehicle fuel consumption as shown in Table 2. Another advantage is that the model can easily be updated to include additional driving cycles and engine maps. Finally, the need to use generic FRVs is avoided, since fuel consumption and reduction values for specific vehicle configurations and driving cycles can be readily generated by non-experts. All this makes parsimonious powertrain models like the one presented here a useful alternative to the existing approaches to fuel consumption modeling and calculations.
3.4 Limitations and outlook
This paper introduces a powertrain modeling method and an open-source model implementation for gasoline- or diesel-powered ICVs. The computational transparency and the use of driving cycles, a net force demand, and engine maps make this method a valuable complement to the existing models and approaches. The LCA community will benefit from having multiple resources available for such an important aspect of environmental vehicles assessments. While the main purpose of this paper is to introduce the modeling approach, the implementation of the approach in the accompanying Excel workbook is not just a proof of concept, but a fully functional model. The open-source nature of the Excel spreadsheets allows users to modify and update the model, e.g., by adding driving cycles and engine maps. This is facilitated by the increasing public availability of engine maps. One example is the engine maps and the engine mapping tool provided by the US EPA (U.S. EPA n.d.).
One limitation of the current model implementation is the way in which engine resizing is simulated (see Section 2.4). The current approximations are reasonable for incremental changes in engine size, but need to be revisited for larger changes. Future improvements of the presented method should thus include a more refined simulation of engine resizing, such as adjusting thermal and mechanical efficiencies. It is important to keep in mind, though, that redesigning a vehicle in the real world is done by exchanging an existing engine with another one, which is ideally modeled by swapping out engine maps in the powertrain simulation. Another worthwhile future development would be to adapt the powertrain model to heavy-duty vehicles.
References
Anderson M (2003) Powertrain design and integration lecture, vehicle systems integration course AUTO501, University of Michigan, May 19, 2003
ANL (n.d.) Argonne National Laboratory (ANL); Downloadable Dynamometer Database; https://www.anl.gov/es/downloadable-dynamometer-database
Birat J, Guérin V, Rocchia L, Tuchman M (2004) Ecodesign of automobiles based on the environmental properties of body materials. SAE Technical Paper 2004-01-0250; https://doi.org/10.4271/2004-01-0250
Chana H, Fedewa W, Mahoney J (1977) An analytical study of transmission modifications as related to vehicle performance and economy. SAE Technical Paper 770418. https://doi.org/10.4271/770418
Das S (2000) The life-cycle impacts of aluminum body-in-white automotive material. J Miner Met Mater Soc 52:41–44. https://doi.org/10.1007/s11837-000-0173-2
Das S, Graziano D, Upadhyayula VKK, Masanet E, Riddle M, Cresko J (2016) Vehicle lightweighting energy use impacts in U.S. light-duty vehicle fleet. Sustain Mater Technol 8:5–13. https://doi.org/10.1016/j.susmat.2016.04.001
Field AF, Kirchain R, Clark J (2001) Life cycle analysis and temporal distributions of emissions: developing a fleet-based analysis. J Ind Ecol 4:71–91. https://doi.org/10.1162/108819800569816
FKA (2011) Determination of weight influence on the energy consumption according to US regulations. Report 105620. Forschungsgesellschaft Kraftfahrwesen mbH, Aachen
Flamand L, Dalmaz G, Dowson D, Childs THC, Berthier Y, Georges JM, Lubrecht A, Taylor CM (eds) (1998) Tribology for Energy Conservation, 1st edn. Elsevier, Amsterdam
Genta G, Morello L (2009) The automotive chassis, volume 1-components design. Springer, Berlin
Geyer R (2008) Parametric assessment of climate change impacts of automotive material substitution. Environ Sci Technol 42(18):6973–6979. https://doi.org/10.1021/es800314w
Geyer R (2016) The Industrial Ecology of the Automobile. In: Clift R, Druckman A (eds) Taking Stock of Industrial Ecology. Springer, Berling, p 331
Heywood JB (1988) Internal combustion engine fundamentals. McGraw-Hill, NY
IAI (2002) Aluminium applications and society – Life cycle inventory of the worldwide aluminium industry with regard to energy consumption and emissions of greenhouse gases; Paper 1 – Automotive; International Aluminium Institute (IAI): London
ICCT (n.d.) The International Council on Clean Transportation(ICCT).Chart library: Passenger vehicle fuel economy. https://www.theicct.org/chart-library-passenger-vehicle-fuel-economy
Kim H, Wallington TJ (2013a) Life-cycle energy and greenhouse gas emission benefits of lightweighting in automobiles: review and harmonization. Environ Sci Technol 47(12):6089–6097. https://doi.org/10.1021/es3042115
Kim H, Wallington TJ (2013b) Life cycle assessment of vehicle lightweighting: a physics-based model of mass-induced fuel consumption. Environ Sci Technol 47(24):14358–14366. https://doi.org/10.1021/es402954w
Kim H, Wallington TJ (2015) Life cycle assessment of vehicle lightweighting: novel mathematical methods to estimate use-phase fuel consumption. Environ Sci Technol 49(16):10209–10216. https://doi.org/10.1021/acs.est.5b01655
Kim D, Peng H, Bai S, Maguire J (2007) Control of integrated powertrain with electronic throttle and automatic transmission. IEEE Trans Control Syst Technol 15(3):474–482. https://doi.org/10.1109/TCST.2007.894641
Kim H, Wallington TJ, Sullivan JL, Keoleian GA (2019) Commentary on “Correction to: on the calculation of fuel savings through lightweight design in automotive life cycle assessments” by Koffler and Rohde-Brandeburger (2018). Int J Life Cycle Assess 24:397–399. https://doi.org/10.1007/s11367-019-01584-z
Koffler C, Rohde-Brandenburger K (2010) On the calculation of fuel savings through lightweight design in automotive life cycle assessments. Int J Life Cycle Assess 2010(15):128–135. https://doi.org/10.1007/s11367-009-0127-z
Koffler C, Rohde-Brandenburger K (2018) Correction to: On the calculation of fuel savings through lightweight design in automotive life cycle assessments. Int J Life Cycle Assess 2018(123):1525–1526. https://doi.org/10.1007/s11367-018-1474-4
Koffler C, Rohde-Brandenburger K (2019) Reply to Kim et al. (2019): Commentary on “Correction to: on the calculation of fuel savings through lightweight design in automotive life cycle assessments” by Koffler and Rohde-Brandenburger (2018). Int J Life Cycle Assess 2019, 2019:400–403. https://doi.org/10.1007/s11367-019-01585-y
MacLean HL, Lave LB (2003) Life cycle assessment of automobile/fuel options. Environ Sci Technol 37(23):5445–5452. https://doi.org/10.1021/es034574q
Modaresi R, Pauliuk S, Løvik AN, Mu DB (2014) Global carbon benefits of material substitution in passenger cars until 2050 and the impact on the steel and aluminum industries. Environ Sci Technol 48:10776–10784
Palazzo J, Geyer R (2019) Consequential life cycle assessment of automotive material substitution: Replacing steel with aluminum in production of north American vehicles. Environ Impact Assess Rev 75:47–58. https://doi.org/10.1016/j.eiar.2018.12.001
Ross M (1997) Fuel efficiency and the physics of automobiles. Contemp Phys 38(6):381–394. https://doi.org/10.1080/001075197182199
Saur, K.; Schuckert, M.; Beddies, H.; Eyerer, P. 1995 Foundations for life cycle analysis of automotive structures - the potential of steel, aluminium and composites. SAE Technical Paper 951844. https://doi.org/10.4271/951844
Serrenho AC, Norman JB, Allwood JM (2017) The impact of reducing car weight on global emissions: the future fleet in Great Britain. Philos Trans R Soc A Math Phys Eng Sci 375:20160364. https://doi.org/10.1098/rsta.2016.0364
Stodolsky F, Vyas A, Cuenca R, Gaines L (1995) Life-cycle energy savings potential from aluminum-intensive vehicles. SAE Technical Paper:951837. https://doi.org/10.4271/951837
Sullivan JL, Cobas-Flores E (2001) Full vehicle LCAs: a review. SAE Technical Paper 2001-01-3725. https://doi.org/10.4271/2001-01-3725
U.S. EPA (n.d.) Engine mapping process document. Available at: https://www.epa.gov/regulations-emissions-vehicles-and-engines/advanced-light-duty-powertrain-and-hybrid-analysis-alpha#engine-mapping. Accessed February 2, 2020
Waters W (1972) General purpose automotive vehicle performance and fuel economy simulator. SAE Technical Paper 720043, https://doi.org/10.4271/720043
Wohlecker R, Johannaber M, Espig M (2007) Determination of weight elasticity of fuel economy for ICE, hybrid and fuel cell vehicles. SAE Technical Paper 2007-01-0343; https://doi.org/10.4271/2007-01-0343
Acknowledgments
We thank the World Auto Steel for partial funding of this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geyer, R., Malen, D.E. Parsimonious powertrain modeling for environmental vehicle assessments: part 1—internal combustion vehicles. Int J Life Cycle Assess 25, 1566–1575 (2020). https://doi.org/10.1007/s11367-020-01774-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11367-020-01774-0