Assessing life cycle impacts from changes in agricultural practices of crop production

Abstract

Purpose

This paper presents an improved methodological approach for studying life cycle impacts (especially global warming) from changes in crop production practices. The paper seeks to improve the quantitative assessment via better tools and it seeks to break down results in categories that are logically separate and thereby easy to explain to farmers and other relevant stakeholder groups. The methodological framework is illustrated by a concrete study of a phosphate inoculant introduced in US corn production.

Methods

The framework considers a shift from an initial agricultural practice (reference system) to an alternative practice (alternative system) on an area of cropland A. To ensure system equivalence (same functional output), the alternative system is expanded with displaced or induced crop production elsewhere to level out potential changes in crop output from the area A. Upstream effects are analyzed in terms of changes in agricultural inputs to the area A. The yield effect is quantified by assessing the impacts from changes in crop production elsewhere. The field effect from potential changes in direct emissions from the field is quantified via biogeochemical modeling. Downstream effects are assessed as impacts from potential changes in post-harvest treatment, e.g., changes in drying requirements (if crop moisture changes).

Results and discussion

An inoculant with the soil fungus Penicillium bilaiae has been shown to increase corn yields in Minnesota by 0.44 Mg ha⁻¹ (~ 4%). For global warming, the upstream effect (inoculant production) was 0.4 kg CO₂e per hectare treated. The field effect (estimated via the biogeochemical model DayCent) was − 250 kg CO₂e ha⁻¹ (increased soil carbon and reduced N₂O emissions) and the yield effect (estimated by simple system expansion) was − 140 kg CO₂e ha⁻¹ (corn production displaced elsewhere). There were no downstream effects. The total change per Mg dried corn produced was − 36 kg CO₂e corresponding to a 14% decrease in global warming impacts. Combining more advanced methods indicates that results may vary from − 27 to − 40 kg CO₂e per Mg corn.

Conclusion and recommendations

The present paper illustrates how environmental impacts from changes in agricultural practices can be logically categorized according to where in the life cycle they occur. The paper also illustrates how changes in emissions directly from the field (the field effect) can be assessed by biogeochemical modeling, thereby improving life cycle inventory modeling and addressing concerns in the literature. It is recommended to use the presented approach in any LCA of changes in agricultural practices.

Introduction

As the world population continues to expand, along with its demands for feed, food, fuel, and fiber, the necessity in achieving sustainable agricultural production is of urgent concern. To do so, several agricultural practices and concepts have been introduced, e.g. organic farming (Rigby and Cáceres, 2001), sustainable intensification (Pretty 1997), no/low tilling (Tebrügge and Düring, 1999), and precision agriculture (Bongiovanni and Lowenberg-DeBoer 2004). Potentially, changes in agricultural practices can lead to trade-offs (burden shifting) as well as “upstream effects” (e.g., due to changes in the use of agricultural inputs such as seeds, fertilizers, pesticides, etc.). Life cycle assessment (LCA) is the obvious choice of methodology to study the environmental implications of such effects. However, the LCA literature contains surprisingly little guidance on how to systematically and consistently evaluate the change in environmental impacts of crop production following from a change in agricultural practices.

Brentrup et al. (2004) presented an extended version of the general LCA approach to assess the environmental impacts of crop production. This allowed for a better characterization of the environmental impacts from different agricultural “stand-alone systems” but the methodology did not focus on the change in environmental impacts from a shift from one agricultural practice to another.

Caffrey and Veal (2013) discussed various challenges and perspectives in agricultural LCA at a generic level but did not give detailed guidance to the LCA practitioner.

Meier et al. (2015) reviewed 34 studies comparing organic and conventional farming based on LCA. The authors pointed out several challenges relating to data as well as methods and called for a better differentiation between nitrogen fluxes in different agricultural systems as well as the use of consequential LCA (including system expansion) to account for differences in analyzed farming systems. This need for improved methodology to assess nutrient flows and soil carbon dynamics in agricultural LCAs was also highlighted by Goglio et al. (2015).

Jiang et al. (2014) discussed the use of biogeochemical models for informing LCA of energy crops but did not consider changes in management practices and their potential impact on production elsewhere.

Numerous case studies compare agricultural practices by use of LCA (e.g., Keyes et al. 2015, Goossens et al. 2017, Houshyar and Grundmann 2017, Tricase et al. 2018). The common approach is to divide environmental impacts related to a fixed area of cropland by the yield of that land—thereby allowing for comparison across practices based on the same functional unit. While this approach is intuitive, it fails to capture potential changes elsewhere driven by a potential change in output (yield) from the cropland studied. This further supports the need for methodological guidance.

The purpose of consequential LCA is to estimate the environmental consequences of a specific change (Weidema 2003), e.g., a change in crop demand or a change in cropping systems. This may involve changes in agricultural inputs, changes in soil nutrient flows, and changes in crop yields. If crop yields are changed, while there are no changes in demand, the change in crop supply will in turn affect production elsewhere (to balance out the change in crop supply). This must be considered in consequential LCA.

The tools and concepts to assess changes in environmental impacts from changes in agricultural practices are already available but broadly applicable guidelines for their combined and consistent use in LCA have been lacking. The purpose of this paper is to demonstrate how concepts such as system equivalence, biogeochemical modeling, system expansion and/or modeling of indirect land use change (ILUC) can be combined to assess the environmental impacts from changes in agricultural practices and, thereby, relative changes in environmental impacts from the crops grown in the analyzed cropping systems. The main focus will be on global warming impacts. The purpose is also to categorize changes in impacts according to where they occur. The paper describes a generic approach and illustrates options at different levels of sophistication to derive LCA results. The paper seeks to give detailed guidance on how to use results from biogeochemical models and ILUC models in agricultural LCA but it is beyond the scope of the paper to also give detailed guidance on how to run such supporting models. Finally, the use of the suggested approach is exemplified with a novel case study of a phosphate-solubilizing microbial inoculant introduced in US corn production.

Methods

The methodological description takes its point of departure in an area of cropland (A) to which a change is introduced. From here, this change will be referred to as the alternative agricultural practice or just the alternative practice. To analyze the consequences of introducing an alternative practice, a reference system is defined. The reference system is the area A with the functional output Q (quantity of crop). The alternative system (with the alternative practice introduced on the area A) must provide the same functional output to allow for direct comparison to the reference system (the principle of system equivalence; Hauschild et al. 2018). When this has been ensured, the impacts from introducing the alternative practice can be quantified by analyzing the differences between the reference system and the alternative system.

To illustrate how different aspects of the alternative practice (e.g., change in inputs, change in field emissions, and change in yield) influence the environmental impacts from producing a certain quantity of crop (Q), the change in impacts is divided into four categories (upstream, field, yield, and downstream), which will be discussed in the subsequent sections. The change resulting from a shift in agricultural practice within each category is defined as an “effect.” Note that each of the four effects cover all impact categories considered and thereby can have multiple dimensions. Some of the effects may be assessed in different ways with different methodological sophistication. The paper introduces an overview of such published methods to provide the reader with different choices and to allow for sensitivity analyses to test the influence of these choices.

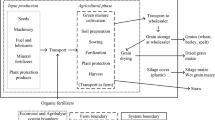
Figure 1 illustrates the reference system and the alternative system. The area A (the field) receives agricultural inputs such as fertilizers and pesticides. Agricultural inputs also cover fuel and machinery for field work (sowing, harvesting, etc.). These inputs are associated with upstream life cycle impacts, i.e., emissions and resource use taking place prior to crop cultivation on the field. Fuel combustion during field work is the exception as that takes place during cultivation but is counted as an upstream impact because it is related to the fuel produced off the field (i.e., fuel production and combustion is counted in the same category). Fuel combustion is relevant because different agricultural practices may require different levels of field work and therefore different quantities of fuel.

Fig. 1

Illustration of the reference system and the alternative system producing the same functional output (Q) with different environmental impacts. The index sys refers to either the reference system (ref) or the alternative system (alt). Agricultural inputs represent upstream life cycle impacts, field emissions represent impacts stemming directly from the field, system expansion represents impacts “elsewhere,” and post-harvest treatment represents downstream life cycle impacts

As shown in Fig. 1, there are also direct emissions from the field. These include (but are not limited to) carbon dioxide (CO₂) from changes in soil organic carbon (SOC), nitrous oxide (N₂O) from microbial soil processes as well as nitrate (NO₃⁻) leaching to the aquatic environment. After harvest, the fresh crop may need to go through post-harvest treatment (e.g., drying to meet moisture specifications) before it is ready for sale as an agricultural commodity (referred to as crops to market in Fig. 1). In case the alternative agricultural practice results in a yield change, it is necessary to consider the impact on crop production elsewhere (system expansion) as illustrated in Fig. 1 (represented by crop cultivation on the area B). As mentioned above, the environmental consequences of introducing the alternative agricultural practice can be divided into four different effects, which will be discussed in detail in the following sections. One of these effects (the field effect) needs special attention if the alternative agricultural practice is applied to a crop, which is grown in rotation with another crop. This special case has been discussed in Sect. S1 of the Electronic Supplementary Material item 1 (ESM 1).

Upstream effects

The shift in agricultural practice may involve a change in agricultural inputs (fertilizer, pesticides, etc.) to the area A. For instance, if shifting from conventional tilling to a no-till practice, there is a reduced need for fuel (for tilling). The environmental impacts from changes in agricultural inputs to the area A will be referred to as upstream effects.

The upstream effects are simply characterized by summing up the difference in impacts from the agricultural inputs used on the area A in the reference system and the alternative system. This can be expressed as described in Eq. 1.

$$ {E}_{up,j}={\sum}_{i=1}^n\left({m}_{i, alt}-{m}_{i, ref}\right).{I}_{i,j} $$

(1)

where

• E_{up, j} is the upstream effect for impact category j

• m_{i, alt} is the quantity of agricultural input i to the area A in the alternative system

• m_{i, ref} is the quantity of agricultural input i to the area A in the reference system

• I_{i, j} is the life cycle impact for the impact category j for one unit of the input i

• n is the total number of agricultural inputs

The field effect

Field emissions from the area A (cf. Fig. 1) are likely to change when an alternative agricultural practice is introduced. This can happen for several reasons. If there are changes in the amount or type of fertilizers applied or if the crop yield is affected, the nutrient flows in the field will be impacted. Changes in yield can also impact emissions related to crop residues as well as soil organic carbon (SOC), e.g., due to larger crop roots. The impacts from changes in field emissions from the area A will be referred to as the field effect. Note that this effect covers emissions (incl. nutrient losses to the aquatic environment) associated with soil processes only. Hence, indirect emissions of N₂O following from leaching and volatilization of N should also be included (aggregated default values of respectively 1.1% and 1.0% suggested by IPCC 2019) but emissions from field work (e.g., life cycle impacts from fuel production and use) are considered part of the upstream impacts (cf. explanation in the beginning of Sect. 2). Note also that the field effect relates only to the area A (i.e., the area where the change in agricultural practice occurs). Field emissions from the area B are considered part of the yield effect (see separate section). This distinction has been made to allow farmers and other agricultural stakeholders to separate effects taking place “on site” (where the new agricultural practice is introduced) and effects taking place elsewhere (“off site”).

The assessment of the field effect requires establishment of consistent life cycle inventories for different agricultural practices. As pointed out by Meier et al. (2015), this can be challenging. It is therefore recommended to apply biogeochemical models such as Century (Paustian et al. 1992), DayCent (Del Grosso et al. 2001), or DNDC (Li et al. 1992). Biogeochemical models (sometimes also referred to as soil-crop models) are designed to characterize nutrient flows in cropping systems as well as the impact of management changes on nutrient cycling and productivity in these systems. Hence, they are useful in the assessment of the field effect. Goglio et al. (2018) indicates that biogeochemical models, in comparison to simpler empirical equations, are particularly helpful in deriving reliable results for N₂O emissions from cropping systems, thereby addressing some of the concerns mentioned in the introduction, e.g., those raised by Meier et al. (2015). The substances that should be accounted for as field emissions depend on the considered impact categories. N₂O and CO₂ from SOC changes will typically be the most important for global warming whereas leaching and run-off of N and P will be important for nutrient enrichment. For these substances, biogeochemical models are very practical. Meanwhile, biogeochemical models also have limitations in terms of scope and assessment capabilities. Hence, issues such as leaching of heavy metals and active ingredients in pesticides may need to be modeled separately (if relevant for the impact categories considered in a specific LCA study).

Once a biogeochemical model has been set up to simulate the soil processes on the area A in the reference system and the alternative system, field emissions from the two systems can be estimated (cf. Fig. 1). This is done by simulating production of the relevant crop over a modeling period long enough to determine representative average emissions, usually a few decades. On this basis, the field effect can be quantified by use of Eq. 2.

$$ {E}_{field,j}={\sum}_{i=1}^m\left({e}_{i, alt}-{e}_{i, ref}\right).{P}_{i,j} $$

(2)

where

• E_{field, j} is the field effect for impact category j

• e_{i, alt} is the quantity of field emission i from the area A in the alternative system¹

• e_{i, ref} is the quantity of field emission i from the area A in the reference system¹

• P_{i, j} is the specific characterization factor for the impact category j for one unit of the field emission e_i

• m is the total number of different field emissions

While biogeochemical models can be used to estimate annual, average field emissions from the area A (which can then be inserted in Eq. 2), one specific output requires special attention, namely CO₂ emissions derived from changes in SOC. These CO₂ emissions are different from other GHG emissions from the field because they are governed by long-term changes in soil carbon stock. Hence, they must be treated different than, for example, annual emissions of N₂O stemming from the addition of nitrogen to the field. First, a change in SOC must be converted to a corresponding amount of CO₂ by use of stoichiometry, i.e., 1 kg of C corresponds to − 44/12 kg CO₂. The negative sign indicates that a positive change in SOC (carbon sequestration) corresponds to a negative CO₂ emission (binding of carbon from the atmosphere). Secondly, it must be considered how to assign an appropriate amount of SOC-related CO₂ emissions to the output from the area A. This is challenging because SOC levels adjust slowly to changes in practices (moving towards an equilibrium state, which matches inputs and outputs of carbon). Hence, estimates of SOC changes will depend on the time perspective applied creating the need for a well-considered approach to time accounting. Currently, there is no well-defined procedure for how to account for SOC changes in LCA (Goglio et al. 2015) but the following sections outlines two approaches that have both previously been used in the literature. The methods will be presented with an increasing level of sophistication.

SOC modeling: 20-year annualization

One option to account for SOC-related CO₂ emissions from the area A is to calculate an annual average based on the first 20 years of the modeling period applied in the biogeochemical modeling. Specifically, e_{CO2, alt} in Eq. 2 then becomes the change in SOC in the alternative system during the first 20 years multiplied by − 44/12 kg CO₂ per kg C and divided by 20. The same approach is applied to determine e_{CO2, ref} in Eq. 2.

While the 20-year annualization approach builds on an arbitrary period, there is some precedence for its use. It has been applied in the life cycle GHG accounting method in the European Renewable Energy Directive (EC 2009) and in LCA studies by Knudsen et al. (2010) and Hamelin et al. (2012). Note that a different choice of annualization period would yield substantially different results. A 100-year period could reduce the result by a factor of 5 and a 1-year period could increase the result by a factor of 20.

If the 20-year annualization approach is applied, it is important to interpret the SOC results from the biogeochemical modeling carefully. Due to their intended complexity in representing SOC dynamics, these models are able to estimate the inter-annual changes in SOC and crop carbon inputs as influenced by year to year climate variability that can sometimes be difficult to detect in measurements. Hence, there can be a need to smooth out the yearly SOC changes over time to derive an appropriate 20-year trend in SOC change. There are several options for doing that. One of them is described by VandenBygaart et al. (2008) where they fit the output from the CENTURY model to a first-order exponential equation.

SOC modeling: time-independent approach

Another option to account for SOC-related CO₂ emissions has been described by Petersen et al. (2013). This approach does not rely on an arbitrary time horizon (annualization period) and will therefore be referred to as the time-independent approach or just time-independent approach (TIA). The time-independent approach is based on the change in radiative forcing related to a single event with impact on SOC. In the present paper, such an event would be the introduction of a new agricultural practice during one growth cycle for a crop grown on the area A. This “one-time intervention” would impact the subsequent development of SOC because a change in SOC in 1 year provides a different starting point for subsequent years. The alternative temporal development in SOC can be compared to the temporal development in the reference system (the “baseline”). By conversion of the differences in SOC into radiative forcing, the global warming potential (GWP) can be determined for any given accounting period. This approach is easier to reason scientifically than the more arbitrary annualization approach but may also be more challenging to apply.

The aim is to derive a value, which represents (${e}_{C{O}_2, alt}-{e}_{C{O}_2, ref}$) in Eq. 2. To do this, a biogeochemical model can be set up to characterize a single year of the alternative agricultural practice followed by 99 years of the previous practice. As a reference (baseline), 100 years of the initial practice (i.e. the practice applied in the reference system) is also modeled. This procedure will allow for the tracking of the differences in SOC (year-by-year) between the alternative system and the reference system over the full accounting period (100 years if GWP100 is used as the global warming metric). To derive representative results, this curve (difference in SOC over time) should be smoothed out by use of an exponential fit function. This gives a generalized picture of the difference in SOC between the two systems in each year of the accounting period. Hence, the difference in CO₂ emissions can be calculated for each year (stoichiometric conversion). The difference in CO₂ emissions in a given year is then multiplied with a characterization factor, which assigns a certain weight to the emission. This is based on CO₂’s atmospheric decay function and the timing of the emission in the accounting period as described by Petersen et al. (2013) and further elaborated by Schmidt and Brandão, (2013, Sect. 3.1). The emission in year one will have a characterization factor of 1 while characterization factors for the end of the accounting period will be close to zero (because a late emission will have little impact within the accounting period). The time dependent characterization factors are available in Sect. S2 of ESM 1. The difference in CO₂ emissions for each year is multiplied with the corresponding time dependent characterization factor and results for all years are summed up to provide an estimate of (${e}_{C{O}_2, alt}-{e}_{C{O}_2, ref}$), which can then be used in Eq. 2.

Note that the described approach is not dependent on an arbitrary annualization period because it relates SOC changes directly to one ‘batch’ of output from the area A. Thereby, the CO₂ field effect can be viewed in isolation for one growth cycle of crop production (as with all the other emissions covered by the present methodological proposal).

Yield effect

If the studied alternative practice changes the crop yield on the area A (cf. Fig. 1), it will impact crop production elsewhere through market-mediated effects. This is because the overall demand for crops is not affected by the introduction of an alternative practice. If the crop yield on the area A increases, the additional output (ΔQ in Fig. 1) will displace crop production elsewhere (Schmidt 2008). In case of a reduction in yield (if shifting to a less intensive practice), farmers elsewhere will be incentivized to fill the supply gap. The environmental impacts from changes in crop production elsewhere will be referred to as the yield effect.

To account for the yield effect, the alternative system must be expanded to ensure that it produces the same amount of crop (or an equivalent quantity of other crops with the same functional characteristics, e.g. same feed value in terms of nutritional composition) as in the reference system. If the change in output from the area A in the alternative system (as compared to the reference system) is ΔQ, the system is expanded (as shown in Fig. 1) with an area B, which produces a quantity of the crop c equal to -ΔQ. This ensures that the two systems have the same functional output (system equivalence) because any change in output from the area A is leveled out by a corresponding change (with the opposite sign) in crop production on the area B. Hence, the yield effect is determined by the impacts of a change in the quantity of crop production elsewhere. This has been described in Eq. 3.

$$ {E}_{yield,j}=-\Delta Q.{I}_{c,j} $$

(3)

where

• E_{yield, j} is the yield effect for impact category j

• ΔQ is the change in output of crops to market from the area A

• I_{c, j} is the life cycle impact for the impact category j for one unit of crops to market (c) displaced or induced elsewhere. I_{c, j} should exclude potential impacts from post-harvest treatment (see below).

As mentioned in the definitions above, I_{c, j} should not include impacts from potential post-harvest treatment. This is because the overall need for post-harvest treatment in the two systems is unrelated to potential yield changes on the area A. The reason is that the two systems compared (cf. Fig. 1) produce the same quantity of crops (Q). Only if the composition of the fresh crop (cf. Fig. 1) is different in the alternative system and the reference system (e.g., different moisture contents) could there be changes in impacts related to post-harvest treatment. Such changes will be referred to as downstream effects (see Sect. 2.4).

The estimation of I_{c, j} in Eq. 3 requires an assessment of how crop production is affected elsewhere when the output from the area A changes. This can be approached in different ways. In the following, several options are discussed with increasing levels of sophistication but also increasing requirements for the LCA practitioner. A table with a simple overview of the different approaches is available in Sect. 2.3.5.

Simple system expansion

The simplest option to deal with the expansion of the alternative system is to assume that the crop production affected elsewhere is conventional production. For instance, if the alternative practice is improving wheat yields on the area A, the additional output can be assumed to displace conventional wheat production on the area B.

LCI data for conventional crop production is often readily available in the literature and in LCA databases, at least for developed countries. In case the reference system (cf. Fig. 1) is characterized by conventional crop production, data from that system can be used to estimate I_c,j in Eq. 3. This approach will be referred to as simple system expansion and I_{c, j} will, for this particular approach, be referred to as I_{c, j, s}. Note that I_{c, j, s} refers to impacts from the specific crop c on the area B.

If the applied inventory data for the crop c on the area B includes CO₂ emissions (positive or negative) from ongoing changes in SOC, it is suggested to exclude this aspect in the estimation of I_{c, j, s}. The reason is that gradual SOC changes in a continuous cropping system do not reflect a situation where crop production on the area B is either initiated or seized as a result of changes on the area A. Hence, the use of inventory data for SOC changes could give misleading results. The exclusion of SOC-related CO₂ changes in the estimation of I_{c, j, s} can be seen as a “corrective simplification.” Note that more sophisticated approaches are also discussed in the following sections.

While it may sound complicated to establish I_{c, j, s} without post-harvest treatment (as discussed above) and without SOC-related CO₂ emissions, it can be quite simple. If an LCI is available for the crop to market (produced from the area B), it is only necessary to neglect any inputs from post-harvest treatment and any potential CO₂ emissions from changes in SOC.

Simple system expansion (although not necessarily dubbed as such) is applied in several LCA studies of grain-based bioethanol, which is co-produced with protein feed (also known as distillers’ grains with solubles or DGS). Both Cai et al. (2013) and Wang et al. (2012) assumed that DGS would displace equivalent amounts of conventionally produced crops. Another example is found in a study by Nielsen and Oxenbøll (2007), who assessed the environmental impacts from enzyme production. One of the inputs studied was wheat starch, which is co-produced with wheat protein. To account for additional protein production (driven by the use of wheat starch), system expansion was used to consider displacement of conventional protein production elsewhere.

Marginal system expansion

In a slightly more sophisticated approach, it may be considered whether it is possible to determine a marginal type of crop production, which is affected by a change in output from the area A. It might not be standard, conventional crop production, which is affected but instead a less competitive supplier, which is squeezed out of the market if yields are improved on the area A. For some crops and other agricultural products, the literature already describes suggested marginal suppliers. For instance, Weidema (1999) demonstrated how 1 kg of protein by-product from food production could be assumed to displace 3.9 kg soybeans and Schmidt and Weidema (2008) suggested that palm oil took over from rapeseed oil as the marginal vegetable oil on the world market around the year 2000. Another example of marginal system expansion in agricultural LCA can be found for a comparison of conventional and organic milk production by Flysjö et al. (2011). Here, system equivalence in terms of milk production and co-produced calf meat was ensured by expanding one of the milk production systems to include displaced marginal meat production elsewhere. Schmidt (2015) utilized marginal system expansion in consequential LCA in a comparative assessment of rapeseed and palm oil suggesting that the marginal suppliers of displaced fodder protein and energy were Brazilian soybean and Canadian barley producers, respectively.

In summary, if a relevant marginal crop can be identified, a corresponding LCI can be established and I_{c, j} in Eq. 3 can be determined based on marginal system expansion. For marginal system expansion, I_{c, j} will be referred to as I_{c, j, m}. Note that I_{c, j, m} refers to impacts from the specific crop c on the area B. Further guidance on the identification of marginal suppliers is available in Weidema et al. (2009). As for simple system expansion, SOC-related CO₂ emissions and post-harvest treatment should be excluded (cf. discussion above).

As mentioned above, marginal system expansion is an attempt to identify the type of crop production ultimately affected by a change in output from the area A. In that sense, marginal system expansion seeks to by-pass the many market-mediated steps between the initial “supply shock” (the change in output from A) and the crop production affected in the end. The alternative to this ‘short-cut’ is actual economic equilibrium modeling, which has been applied in recent years when assessing land use changes caused by changes in crop demand (see, e.g., Hertel et al. 2010, Kløverpris et al. 2010). This topic is addressed in the next sections.

ILUC option 1: yield effect fully based on ILUC modeling

The concept of indirect land use change (ILUC) covers market-mediated land use changes caused by changes in crop demand or crop supply. Such a change can be driven by the use of crop-based products (affecting crop demand) or by the introduction of yield-changing agricultural practices (affecting crop supply). Various methods and models to estimate ILUC and associated GHG emissions have been developed (De Rosa et al. 2016), but there is still no scientific consensus on how to address the issue (de Bikuña et al. 2018; Woltjer et al. 2017). However, the topic is highly relevant for agricultural practices with impacts on crop yields. Hence, two possible options for including ILUC as part of the yield effect will be discussed here. The best choice of option will need to be determined in relation to the specific LCA study in question and the characteristics of the ILUC model applied. The advanced ILUC options are more complex and demanding than simple or marginal system expansion but also theoretically more correct.

With ILUC option 1, the impacts driven elsewhere by a change in yield on the area A are entirely based on ILUC modeling. In other words, I_{c, j} in Eq. 3 is estimated solely by use of an ILUC model. This option is feasible if the applied ILUC model not only covers impacts from land use change but also impacts from changes in crop intensity. Further explanation follows below.

ILUC modeling can in itself be viewed as a complex and sophisticated form of system expansion where cropland and other land uses can displace each other as a result of a studied change. In general, markets can react to a change in crop supply from a specific area in three ways (Kløverpris et al. 2008, Schmidt et al. 2015). (1) Crop production can be adjusted by changes in production intensity, i.e., adjustment of agricultural inputs to match a new supply situation (adjusting crop yields to a new economic optimum). (2) Crop production can also be adjusted by bringing new land into production or taking existing cropland out of production. (3) Changes in crop supply can lead to changes in crop use patterns, i.e., certain uses of crops may be either reduced or increased. The interplay between the three above-mentioned effects (change in intensity, change in land use, and change in use patterns) determines the total impact from the studied change. If the applied ILUC model incorporates both the intensity and land use aspect, it can be used to assess the impact of producing one additional unit (or one unit less) of ‘crop to market’ on the area A (cf. Fig. 1). In other words, the ILUC model can be used to derive an estimate of I_{c, j} (here denoted I_{c, j, ILUC1}) in Eq. 3 encompassing the full market response and associated impacts from a change in crop supply from the area A (cf. Fig. 1).

Results of ILUC models are typically related to an area of land occupied for production of an item under study (e.g. an area required for bioenergy crops). This land occupation triggers the indirect land use change. In the present paper, however, the triggering land use occupation could be either positive or negative depending on the yield impact from the alternative agricultural practice. If the output from the area A increases by ΔQ, it means that the initial production (Q) could be maintained on an area smaller than A. It is this initial land saving that triggers the indirect land use change, which ultimately reduces pressure on land elsewhere. The initial reduction in land occupation can be quantified as the fraction of the area A no longer needed to maintain the production of Q. On this basis, Eq. 3 can be re-written as follows (specific to ILUC option 1) into Eq. 4.

$$ {E}_{yield,j, ILUC1}=-\Delta Q.{I}_{c,j, ILUC1}=-\frac{\Delta Q}{Q+\Delta Q}.A.T.{I}_{ILUC,j,A} $$

(4)

where

• E_{yield, j, ILUC1} is the yield effect expressed on the basis of ILUC option 1

• ΔQ is the change in output of crops to market from the area A

• I_{c, j, ILUC1} is the ILUC impact in impact category j per unit of additional output (crops to market) from the area A

• Q is the output of crops to market from the area A in the reference system (cf. Fig. 1)

• A is the area where the alternative practice is introduced (cf. Fig. 1)

• T is the time of land occupation on the area A, i.e. the effective duration of the full crop cycle

• I_{ILUC, j, A} is the ILUC impact in impact category j per unit of land occupation² in the region where A is located³

It follows from Eq. 4 that I_{c, j, ILUC1} is equal to $\frac{A\bullet T}{Q+\Delta Q}.{I}_{ILUC,j,A.}$

Note that I_{ILUC, j, A} needs to be estimated by use of an ILUC model. Meanwhile, some ILUC models may be able to estimate I_{c, j, ILUC1} directly, which then simplifies the application of ILUC option 1. Due to the variety of existing ILUC models, it is not feasible to provide formulas for all cases in the present paper.

The advanced ILUC approaches (both options 1 and 2) avoid the complexities relating to SOC changes on the area B in Fig. 1 (cf. discussion in Sect. 2.3.1). This is because the approach considers general market effects in terms of land use and intensification whereby effects are not confined to a single specific area (B in Fig. 1). To be consistent with the principle of system equivalence (same output from compared systems), option 1 is only feasible with an ILUC model that assumes a fully elastic market response in the long run where a change in supply or demand is fully compensated through changes in intensification and land occupation (i.e., where there are ultimately no changes in sectorial crop use patterns).

ILUC option 2: yield effect partially based on ILUC modeling

With ILUC option 2, an estimate of impacts from indirect land use change is added to the impacts from crop production on the area B (determined by simple or marginal system expansion). In other words, the land occupation associated with the crop(s) displaced (or induced) is used as a starting point for estimating ILUC impacts. These impacts are then added to the other emissions associated with crop production on the area B. Hence, the ILUC estimate is added to (and thereby becomes part of) I_{c, j} in Eq. 3. This can be expressed as follows from Eq. 5. Note that ILUC option 2 is particularly relevant when applying an ILUC model that only considers land use impacts (and not intensification).

$$ {E}_{yield,j, ILUC2}=-\Delta Q.{I}_{c,j, ILUC2}={E}_{yield,j,x}-B.T.{I}_{ILUC,j,B}=-\Delta Q.{I}_{c,j,x}-B.T.{I}_{ILUC,j,B} $$

(5)

where

• E_{yield, j, ILUC2} is the yield effect expressed on the basis of ILUC option 2

• ΔQ is the change in output of crops to market from the area A

• I_{c, j, ILUC2} is the ILUC impact in impact category j per unit of additional output (crops to market) from the area A

• I_{c, j, x} is the life cycle impact for the impact category j for changes in crop production elsewhere modeled via system expansion where x denotes either simple (s) or marginal (m)

• B is the area where production of crop c is induced or displaced⁴ (cf. Fig. 1)

• T is the time of occupation on the area B, i.e. the effective duration of the full crop cycle

• I_{ILUC, j, B} is the ILUC impact in impact category j per unit of land occupation⁵ in the region where B is located⁶

The last term in Eq. 5 constitutes the addition of ILUC to the environmental impacts from crop cultivation on the area B. The term simply expresses land occupation (the area B multiplied by the time T) multiplied with the ILUC impact per unit of land occupation. Any type of ILUC model could be used with this approach (also ILUC models that do not assume full elasticity of supply) because system equivalence is ensured by displaced or induced production on the area B and then ILUC follows as an “add-on effect.”

It follows from Eq. 5 that I_c,j,ILUC2 is equal to $\left({I}_{c,j,x}+\frac{B.T.{I}_{ILUC,j,B}}{\Delta Q}\right)$.

The way to interpret this approach (ILUC option 2) is that the intensification aspect is covered by the (induced or avoided) agricultural inputs to the area B (assuming no change in SOC on the area B) and the land use aspect is covered by the ILUC modeling, which also includes the SOC component (cf. discussion in Sect. 2.3.1). It is important that the LCI for the crop production on the area B does not include any emissions from direct land transformation (as this would result in double-counting of land use emissions).

Overview of approaches to assess the yield effect

Table 1 seeks to provide an overview of the four approaches outlined for estimation of the yield effect or, more specifically, determination of I_{c, j} in Eq. 3.

Table 1 Overview of approaches to estimation of the yield effect

Downstream effects

As previously discussed, the collective inputs to post-harvest treatment of the fresh crop (cf. Fig. 1) will be unchanged when shifting to an alternative agricultural practice—unless the characteristics of the fresh crop (e.g., moisture content) is impacted by the shift in practice. As this will probably be unusual in most agricultural LCAs, it has been decided to handle the topic in ESM 1 (Sect. S3). Any potential impacts in post-harvest treatment following from the introduction of the alternative practice will be referred to as downstream effects.

Total effects

The change in impacts from introducing a new agricultural practice on the area A for impact category j (E_{total, j}) can be summed up by use of Eq. 6.

$$ {E}_{total,j}={E}_{up,j}+{E}_{fiel\mathrm{d},j}+{E}_{yield,j}+{E}_{down,j} $$

(6)

Once the total change in impacts is known, the change in impact per unit of crops to market for impact category j (ΔI_{c, j}) can be estimated by use of Eq. 7.

$$ \varDelta {I}_{c,j}={E}_{total,j}/Q $$

(7)

If the impact of the crops produced in the reference system is known (I_{c, j, ref}), the relative change in impacts per unit of crops to market following from the studied shift in practice (ΔI_{c, j, rel}) can be quantified via Eq. 8.

$$ \varDelta {I}_{c,j,r\mathrm{e}l}=\varDelta {I}_{c,j}/{I}_{c,j, ref} $$

(8)

Case study results: introduction of microbial phosphate inoculant in corn production in Minnesota

The approaches described in Sect. 2 are exemplified by a case study available as Electronic Supplementary Material item 2 (ESM 2). The study has not previously been published but has undergone critical review by three independent experts in accordance with the ISO 14040 standards for LCA (ISO 2006a; ISO 2006b). The study formed the pre-cursor to the general method described in the present paper.

The case study considers the introduction of a new practice in corn production in Minnesota and North Dakota, USA. The present paper focuses on Minnesota. The new practice consists of the introduction of a yield-enhancing microbial inoculant, which contains spores of the naturally occurring soil fungus called Penicillium bilaiae (P. bilaiae or P.b.). The inoculant is added to corn seeds prior to seeding. When the corn grows, the fungus colonizes the roots. P. bilaiae solubilizes minerally bound phosphorus by secretion of organic acids leading to an increase in nutrient uptake for corn plants. Penicillium bilaiae is available in the agricultural inoculant called JumpStart® and as an integrated part of the seed inoculant called Acceleron® B-300 SAT.

To determine the impact of the new agricultural practice, a reference system and an alternative system is defined in accordance with Fig. 1. The area A is defined as 1 ha and calculations are performed on this basis while final results are expressed per Mg of dried corn kernels, which is the functional unit of the case study. In the reference system, corn is cultivated and the fresh crop is harvested and then dried (post-harvest treatment) to meet the market requirements of approximately 14% moisture. The alternative system receives the same inputs on the area A as the reference system and, in addition, the inoculant is applied to the corn seeds. This leads to a higher output of corn from the area A as documented by Leggett et al. (2015). The case study considers corn grown after corn (continuous corn rotation). The data applied for continuous corn is shown in Table 2.

Table 2 Yield and input data applied in the case study for corn production in Minnesota, USA

The yield data in Table 2 is based on the field trials described by Leggett et al. (2015). Total application of macronutrients (N, P, and K) is also based on Leggett et al. (2015) and the share of each nutrient applied by the specific fertilizers in Table 2 is based on the ratio between fertilizers in the dataset for US corn (consequential model) in the ecoinvent LCI database version 3.0 (ecoinvent 2014). More detail available in Sect. 3.2 of ESM 2. Seeds, pesticides, and field work data is also based on ecoinvent (2014). The inoculant dose is based on the report available as ESM 2. Lime has been omitted in the table since lime only impacts LCA results from corn production with less than 0.25% in all impact categories, based on the applied corn process from ecoinvent 2014) and the applied LCIA method (see below). Irrigation has been left out since the corn fields were not irrigated during field trials (Leggett et al. 2015). The measured average yield increase when applying P. bilaiae on corn in Minnesota is 0.44 Mg ha⁻¹. This does not fully appear from Table 2 because yields are only shown with three significant digits. A detailed discussion of the data in Table 2 is found in Sect. 5 in ESM 2.

The case study considers the following six environmental impact categories: global warming (gw), acidification (ac), nutrient enrichment (ne), photochemical ozone formation (po), fossil energy resources (fe), and land occupation (lo). The impact assessment method called CML-IA baseline (version 3.01) was used. While this method is now superseded, it was still commonly used when the LCA study in ESM 2 was initiated. As the choice of LCIA method is of little relevance for the exemplification of the methodological recommendations in the present paper, and to stay consistent with the case study in ESM 2, it has been decided to stick to the CML method in this case study section. This has a minor impact for the characterization of global warming impacts from N₂O emissions but it does not impact the overall conclusions of the case study (cf. end of Sect. 2.2.7 in ESM 2). Ideally, a newer and regionalized LCIA method had been applied.

The base case is based on 20-year amortization of CO₂ from changes in SOC (field effect) and simple system expansion (yield effect). Equally relevant results of the more advanced methods are also presented and discussed.

The approach outlined in the method section will be demonstrated for the impact category global warming (gw) and for corn grown after corn (continuous corn rotation) in Minnesota. Results for remaining considered impact categories will also be presented but not exemplified by calculations.

Upstream effects from inoculant production

As shown in Table 2, the agricultural inputs to the area A (cf. Fig. 1) are the same in the reference system and the alternative system, except for the use of the P.b. inoculant. The spores from P. bilaiae are produced via “solid state fermentation” and mixed with other ingredients. The exact inventory is proprietary but contained in an internal LCA report, which has been subject to critical review in accordance with the ISO standards for LCA (ISO 2006a; ISO 2006b). Additional detail is available in Sect. 3.4 of ESM 2.

The impacts from the inoculant (I_{inoc, j}) are shown in Table 3.

Table 3 Contribution to environmental impact categories from production of 1 kg P.b. inoculant, cf. Sect. 3.4 in ESM 2

The global warming impacts from inoculant production (I_{inoc, gw}) of 69 kg CO₂e kg⁻¹ (see Table 3) is potentially overestimated because a worst-case scenario for disposal of organic waste, mainly from the fermentation process, was assumed (maximum conversion to methane in a landfill). This accounts for almost 30% of I_{inoc, gw}. In addition, some uncertainty relates to heating and electricity use, which together account for roughly one-third of I_{inoc, gw}. As impacts from inoculant production turn out to have low influence on final results, above-mentioned uncertainties and potential over-estimation are not considered critical.

The dose of the inoculant amounts to 5.7 g ha⁻¹ (cf. Table 2). By use of Eq. 1, the upstream effect in terms of global warming can thereby be estimated as follows.

$$ {E}_{\mathrm{up},\mathrm{gw}}=\left({m}_{\mathrm{inoc},\mathrm{alt}}-{m}_{\mathrm{inoc},\mathrm{ref}}\right).{I}_{\mathrm{inoc},\mathrm{gw}}=\left(0.0057\ \mathrm{k}\mathrm{g}\ \mathrm{inoc}.\right).69\ \mathrm{k}\mathrm{g}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e}\ \mathrm{k}{\mathrm{g}}^{-1}\ \mathrm{inoc}.=0.39\ \mathrm{k}\mathrm{g}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e} $$

Field effect from inoculant use

In the present case study, the biogeochemical model DayCent (Del Grosso et al. 2001) was applied to model field emissions from the different corn production systems. The DayCent model simulates crop growth, nutrient flows, soil carbon, and trace gas emissions in cropping systems. Additional detail (including sources for climate data, etc.) is available in Sect. 2.2.6.3 of ESM 2. The yield and fertilizer data in Table 2 was applied to calibrate the DayCent model and characterize the effect of the inoculant. A more detailed description of this procedure can be found in Sect. 3.1 in ESM 2.

All field emissions and nutrient losses from the area A, except SOC-related CO₂ emissions, were estimated as averages over a 40-year modeling period for the corn production systems. A sufficiently long modeling period was chosen to be able to smooth out inter-annual variations and derive generally representative results. Results are available in Table 4. Methane emissions have been left out because they were unaffected by the new practice. More detail is available in Sect. 4.1 in ESM 2.

Table 4 Annual field emissions to air and water from continuous corn production in Minnesota with and without the use of P. bilaiae (P.b.) as modeled using DayCent (average based on a modeled 40-year time horizon)

Field effect with SOC-related CO₂ emissions based on 20-year annualization

Based on the DayCent results, the change in SOC over a 20-year period corresponded to emissions of − 13.7 Mg and − 17.3 Mg of CO₂ in the reference system and the alternative system, respectively. Applying the 20-year annualization approach described in Sect. 2.2.1, the SOC-related CO₂ emissions from the area A in the reference system and the alternative system is respectively − 686 and − 864 kg CO₂ (appears in Table 4 in Mg CO₂). Note that the CO₂ emissions are negative, indicating that the two systems are building up SOC and thereby sequestering CO₂ from the atmosphere. Further discussion is available in Sect. 2.2.6.3 in ESM 2. Indirect N₂O emissions from leaching and volatilization of N were not covered in the original case study (ESM 2) but have been estimated for this publication as laid out in ESM 1 Sect. S4.1.1.

The field effect for global warming (gw) based on annualized SOC emissions (E_{field, gw}) can now be estimated based on Eq. 2.

$$ {E}_{field, gw}=\left({\mathrm{e}}_{\mathrm{CO}2,\mathrm{alt}}-{\mathrm{e}}_{\mathrm{CO}2,\mathrm{ref}}\right).{\mathrm{P}}_{\mathrm{CO}2,\mathrm{gw}}+\left({\mathrm{e}}_{\mathrm{N}2\mathrm{O},\mathrm{alt}}-{\mathrm{e}}_{\mathrm{N}2\mathrm{O},\mathrm{ref}}\right).{\mathrm{P}}_{\mathrm{N}2\mathrm{O},\mathrm{gw}} $$

$$ =-179 kg\ C{O}_2.1 kg\ C{O}_2e\ k{g}^{-1}C{O}_2+\left(-0.25 kg\ {N}_2O\ \right).298 kg\ C{O}_2e\ k{g}^{-1}{N}_2O=-254\ kg\ C{O}_2e $$

Note that nitrous oxide is the only greenhouse gas in the modeled field emissions (cf. Table 4) and therefore the only contributor to the field effect for global warming besides CO₂ from SOC changes.

Field effect with SOC-related CO₂ emissions based on TIA

This section provides a summary of how the approach described in Sect. 2.2.2 was applied in the inoculant LCA study. A more elaborate description is available in ESM 1 Sect. S4.2.1.

By modeling 1 year of inoculant use in DayCent within a 100-year timeframe and a reference with no inoculant use, it was possible to estimate differences in SOC over time between the two systems. On this basis, (e_{CO2, alt} − e_{CO2, ref}) in Eq. 2 was estimated at − 129 kg CO₂. Inserting this in Eq. 2 gives an estimated field effect for global warming of − 204 kg CO₂e, i.e., 20% lower in numeric terms than with the 20-year annualization approach. As for SOC-related CO₂ emissions specifically, the field effect is 28% lower (− 129 kg CO₂ vs. − 179 kg CO₂), also in numeric terms. Interestingly, a 30-year annualization period gives an estimate of SOC-related CO₂ emissions quite close to the TIA estimate (8% higher in numeric terms). Thirty-year annualization is often applied in US ILUC studies (see, e.g., US EPA 2010 and Hertel et al. 2010).

Yield effect from inoculant use

Based on Leggett et al. (2015), the use of P. bilaiae on corn in Minnesota gives an average increase in corn output of ΔQ = 0.44 Mg on the area A (defined as 1 ha). On this basis, the yield effect was estimated by simple system expansion (cf. Sect. 2.3.1) and by system expansion with ILUC modeling (cf. Sects. 2.3.3 and 2.3.4).

Yield effect based on simple system expansion

It was assumed that the corn displaced on the area B had the same characteristics as the corn in the reference system (cf. discussion in Sect. 2.3.1). The impacts from the corn in the reference system (I_{c, j}) were estimated based on the agricultural inputs in Table 2 and the field emissions in Table 4. SOC changes in Table 4 where however excluded for the reasons discussed in Sect. 2.3 (and Sect. 4.2 in ESM 2). On this basis, the global warming impact from reference corn (I_{c, gw, s}) was estimated at 312 kg CO₂e. Hence, the yield effect for global warming can be estimated as follows on the basis of simple system expansion and Eq. 3.

$$ {E}_{yield, gw}=-\Delta Q.{I}_{c, gw}=-0.44\ \mathrm{M}\mathrm{g}.312\ \mathrm{kg}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e}\ \mathrm{M}{\mathrm{g}}^{-1}=-137\ \mathrm{kg}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e} $$

Yield effect based on system expansion with ILUC modeling

The ILUC model by Schmidt et al. (2015) was used to assess the indirect land use implications of the increased corn yield obtained with P. bilaiae. According to the model, the occupation of 1 ha of cropland in Minnesota generates a global warming impact of 2050 kg CO₂e. There are two options for how to interpret and apply this result (cf. Sects. 2.3.3 and 2.3.4).

Option 1 assumes a direct market response to the change in yield on the area A. Based on Eq. 4, the yield effect for global warming can thereby be estimated as follows (details available in Sect. S4.2.2 of ESM 1).

$$ {E}_{yield, gw, ILUC1}=-\frac{0.44\ \mathrm{Mg}}{10.7\ \mathrm{Mg}+0.44\ \mathrm{Mg}}.1\ \mathrm{ha}.1\ y.2050\ \mathrm{kg}\ {\mathrm{CO}}_2\mathrm{e}\ {\mathrm{ha}}^{-1}{y}^{-1}=-81\ \mathrm{kg}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e} $$

Option 2 assumes initial displacement of adjacent crop production on the area B, which is then accompanied by an ILUC response. In the specific case of P. bilaiae. Applied on continuous corn in Minnesota, the area B equals 411 m² and, by use of Eq. 5, the yield effect for global warming can be estimated as follows.

$$ {E}_{yield, gw, ILUC2}=-137\mathrm{kg}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e}-\frac{411\ {\mathrm{m}}^2y}{10\ 000\ {\mathrm{m}}^2\mathrm{h}{\mathrm{a}}^{-1}}.2050\ \mathrm{kg}\ {\mathrm{CO}}_2\mathrm{e}\ {\mathrm{ha}}^{-1}{y}^{-1}=-221\ \mathrm{kg}\ \mathrm{C}{\mathrm{O}}_2\mathrm{e} $$

Option 1 reduces (numerically) the estimated yield effect for global warming by 41% as compared to simple system expansion. This indicates that the combined land use and intensification response to the yield increase from the inoculant (as modeled with the ILUC model) is less pronounced in terms of GHG emissions than the direct one-to-one displacement of agricultural inputs assumed with simple system expansion.

Option 2 increases (numerically) the estimated yield effect for global warming by 61% as compared to simple system expansion. The increase occurs because the ILUC emissions are added on top of the emissions estimated via simple system expansion.

Use of option 1 requires an ILUC model, which can model the full market response in terms of land use change and intensification whereas option 2 can be applied with models that only capture the land use aspect (cf. Sects. 2.3.3 and 2.3.4). Besides, the choice of option depends on interpretation of ILUC dynamics. As scientific consensus is still lacking, the present study leaves both options open. The calculations for the two ILUC options have been further explained and discussed in Sect. S4.2.2 of ESM 1.

Downstream effects

The downstream effects from using P. bilaiae (changes in transport and drying) are negligible since the corn from the reference system has the same characteristics as the corn from the alternative system. Hence, there is no net change in the need for post-harvest treatment and E_{down, j} thereby equals zero for all impact categories (j). Additional detail is available in ESM 2 (e.g., Sect. 4.2).

Total effects from inoculant use

Based on Eq. 6, the total global warming effect of introducing P. bilaiae on 1 ha of corn in Minnesota (E_total,gw) is − 390 kg CO₂e for the base case (applying simple system expansion and 20-year annualization of SOC) and respectively − 284 and − 424 kg CO₂e for the advanced methods with ILUC options 1 and 2 (TIA for SOC).

The change in impact per Mg corn produced with P. bilaiae (ΔI_{c, gw}) can be calculated by use of Eq. 7 (Q = 10.7 Mg) and amounts to − 36 kg CO₂e Mg⁻¹ corn in the base case and respectively − 27 kg CO₂e Mg⁻¹ corn (ILUC option 1) and − 40 kg CO₂e Mg⁻¹ corn (ILUC option 2). Additional detail is available in Sect. S4.2.3 of ESM 1 and a breakdown of results is available in Fig. 2.

Fig. 2

Global warming results (change in greenhouse emissions per unit of corn produced) in the base case and as assessed with the time-independent approach (TIA) for soil organic carbon (SOC) combined with option 1 and 2 for indirect land use change (ILUC)

The changes in field emissions (CO₂ and N₂O) contribute the most to GHG savings in the base case. These savings are reduced by 20% when applying the time-independent approach for SOC in the advanced methods (N₂O unchanged). The yield effect is also important in the base case, making up 40% of the total global warming impact. The numeric impact of the yield effect decreases when modeled as ‘ILUC only’ in accordance with ILUC option 1 in the advanced methods. On the other hand, the impact of the yield effect increases with ILUC option 2 because (avoided) ILUC emissions are added on top of the (avoided) emissions from displaced production. The difference in results between ILUC option 1 and 2 (cf. Fig. 2) shows the need for further research in this field.

With a global warming impact of conventional corn of roughly 260 kg CO₂e Mg⁻¹ (see Table 8 in ESM 2), the relative reduction in global warming impact per Mg of corn (ΔI_{c, gw, rel}) is 14% in the base case and respectively 10% and 15% with the advanced methods applying ILUC option 1 and 2 (based on Eq. 8). Table 5 shows the effects of introducing the inoculant in all assessed impact categories per Mg of corn produced for the base case. Note that the advanced SOC method (TIA) only affects global warming results. Results per hectare treated with Penicillium bilaiae can be found in Sect. S4.1 in ESM 1.

Table 5 Change in environmental impacts and resource use per Mg corn when P. bilaiae is introduced in a continuous corn rotation in Minnesota (base case: simple system expansion and 20-year SOC annualization)

As discussed above, methodological choices influence the results. In addition, there is uncertainty related to the parameters in the calculations. This has been further discussed in Sect. 5.1 of ESM 2. The largest parameter uncertainty is related to the modeling of agricultural N₂O emissions. For the results based on simple system expansion, the relative 95% confidence interval (CI) was estimated at − 28%/+ 25%. Meanwhile, this does not consider potential covariance in some of the parameters, so the actual CI is likely somewhat lower.

Section S4.3 of ESM 1 illustrates the outlined approach for corn grown after soybeans (corn-soybean rotation).

Discussion

The approach laid out in the present paper has “the field” as the focal point. The upstream effect, the downstream effect, and the field effect represent changes within the supply chain of the crop grown on the field. The yield effect represents changes in other supply chains; changes caused by market signals driven by yield changes on the field (A). The equations for estimation of the four effects contain multiple indices required to generalize the methodology but the calculations are trivial in an LCA context. Meanwhile, the breakdown of results into the four effects should be applied systematically in all LCA studies of new agricultural practices. The breakdown makes it easier to explain the environmental impacts caused by a change in agricultural practice and, more importantly, where these changes occur. This allows for a more informed discussion with relevant stakeholders. In addition, different sustainability schemes have different criteria for recognition of environmental benefits. If a farmer shifts from conventional tilling to no till, the total change in impacts would be comprised of all four effects from a product LCA perspective whereas only the “CO₂ field effect” would count in some of the carbon trading schemes with carbon credits for no till. The approach laid out in the present paper makes it easy to break down results as needed. The approach is also useful in demonstrating the consequences of yield changes. In that sense, it can be a useful tool to inform the discussion about conventional vs. organic crop production. From an optimization perspective, the approach can be useful in determining where in the supply chain the biggest improvement opportunities are situated and this may in turn guide development of better agricultural practices.

Another important aspect of the present paper is the proposal to utilize biogeochemical modeling for estimation of the yield effect. As discussed earlier, LCA studies of agricultural practices often fail to assess these impacts comprehensively for nutrient flows, which can hinder the formulation of clear conclusions and decision support recommendations. The utilization of biogeochemical modeling, as part of agricultural LCA, helps to address this concern. Meanwhile, it also increases the level of expertise required to conduct LCAs of crop production. Whether this added level of comprehensiveness is worthwhile will need to be judged on a case-by-case basis but the marriage between LCA and biogeochemical modeling can certainly provide improved LCA results.

As also discussed, CO₂ emissions resulting from changes in SOC can be modeled at different degrees of sophistication with a notable impact on the results. Ideally, advanced methods where the temporal changes are estimated over time should be applied to best reflect the environmental impacts from changes in agricultural practices. Meanwhile, the case study in the previous section illustrates that simpler methods can, in certain cases, provide results that are in a similar range as the more sophisticated methodologies. Hence, a pragmatic approach may sometimes be adequate to show tendencies and guide decision making.

The case study also illustrates that the field effect can be very important if a new practice can improve nutrient efficiency in the field. If this comes in tandem with improved yield, there is a double benefit. Interestingly, the base case results for P.b. on continuous corn and corn after soy in Minnesota and North Dakota were quite similar despite of the different rotations and locations (see ESM 2). The average change in GHG emissions for the four scenarios were − 37 kg CO₂e Mg⁻¹ corn, i.e., very close to the − 36 kg CO₂e Mg⁻¹ corn estimated for continuous corn in Minnesota (base case). This is partly explained by the fact that the relative yield increase obtained with P. bilaiae in Minnesota and North Dakota was more or less the same (Leggett et al. 2015). In the report (ESM 2), average results were used for a crude extrapolation to a general US scenario with a somewhat lower yield increase, thereby estimating a total GHG saving potential of 3.9 million Mg CO₂e if P.b. were applied on all US corn fields. This illustrates how the approach laid out in the present paper can be used to estimate full potentials of new agricultural practices.

Conclusions

Changes in environmental impacts from shifts in agricultural practices can be logically categorized according to where in the life cycle they occur. The categorization is helpful when assessing and explaining the environmental implications of introducing a new practice. Upstream effects caused by changes in agricultural inputs can be assessed by standard LCA procedure as can potential downstream effects related to post-harvest treatment. Changes in emissions from the field where the change in practice occurs (the field effect) can be assessed by biogeochemical modeling, thereby improving life cycle inventory modeling and addressing concerns raised in the literature. Finally, changes in impacts from production elsewhere (the yield effect) can be assessed via system expansion, potentially supplemented by ILUC modeling.

The outlined approach has been shown to be applicable to the introduction of the phosphate-solubilizing microbe P. bilaiae on corn fields in the USA. It was found that induced environmental impacts from production of the microbial inoculant (the upstream effect) were overshadowed by the environmental impacts avoided in terms of the field effect (reduced emissions of N₂O, increased sequestration of carbon, and reduced nitrogen losses) and the yield effect (avoided crop production elsewhere). In other words, the impacts from producing the spore-containing inoculant was small compared to the positive effects obtained when P. bilaiae colonizes corn roots and facilitates improved nutrient uptake in the crops. It was also shown that the yield effect can vary substantially depending on modeling choices and interpretation of system dynamics. This is not a weakness of the approach laid out in the present paper but rather a reflection of the ongoing scientific developments in ILUC modeling. In addition, the variation in results (specifically for the yield effect) did not alter the overall conclusions in the case study.

It is recommended that the outlined approach be applied to other assessments for changes in agricultural practices, such as switching from conventional to organic farming and from conventional tilling to no or low till. It may also be considered to integrate price rebound effects in the approach to account for potential changes in cost of agricultural production when switching from one practice to another.