A tool to operationalize dynamic LCA, including time differentiation on the complete background database

Abstract

Purpose

The objective is to demonstrate an operational tool for dynamic LCA, based on the model by Tiruta-Barna et al. (J Clean Prod 116:198-206, Tiruta-Barna et al. 2016). The main innovation lies in the combination of full temporalization of the background inventory and a graph search algorithm leading to full dynamic LCI, further coupled to dynamic LCIA. The following objectives were addressed: (1) development of a database with temporal parameters for all processes of ecoinvent 3.2, (2) implementation of the model and the database in integrated software, and (3) demonstration on a case study comparing a conventional internal combustion engine car to an electric one.

Methods

Calculation of dynamic LCA (including temporalization of background and foreground system) implies (i) a dynamic LCI model, (ii) a temporal database including temporal characterization of ecoinvent 3.2, (iii) a graph search algorithm, and (iv) dynamic LCIA models, in this specific case for climate change. The dynamic LCI model relies on a supply chain modeling perspective, instead of an accounting one. Unit processes are operations showing a specific functioning over time. Mass and energy exchanges depend on specific supply models. Production and supply are described by temporal parameters and functions. The graph search algorithm implements the dynamic LCI model, using the temporal database, to derive the life cycle environmental interventions scaled to the functional unit and distributed over time. The interventions are further combined with the dynamic LCIA models to obtain the temporally differentiated LCA results.

Results and discussion

A web-based tool for dynamic LCA calculations (DyPLCA) implementing the dynamic LCI model and temporal database was developed. The tool is operational and available for testing (http://dyplca.univ-lehavre.fr/). The case study showed that temporal characterization of background LCI can change significantly the LCA results. It is fair to say that temporally differentiated LCI in the background offers little interest for activities with high downstream emissions. It can provide insightful results when applied to life cycle systems where significant environmental interventions occur upstream. Those systems concern, for example, renewable electricity generation, for which most emissions are embodied in an infrastructure upstream. It is also observed that a higher degree of infrastructure contribution leads to higher spreading of impacts over time. Finally, a potential impact of the time window choice and discounting was observed in the case study, for comparison and decision-making. Time differentiation as a whole may thus influence the conclusions of a study.

Conclusions

The feasibility of dynamic LCA, including full temporalization of background system, was demonstrated through the development of a web-based tool and temporal database. It was showed that considering temporal differentiation across the complete life cycle, especially in the background system, can significantly change the LCA results. This is particularly relevant for product systems showing significant environmental interventions and material exchanges over long time periods upstream to the functional unit. A number of inherent limitations were discussed and shall be considered as opportunities for further research. This requires a collegial effort, involving industrial experts from different sectors.

Introduction

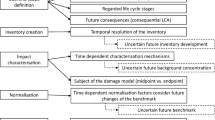
In the quest to assess the environmental impacts of a production-consumption system, life cycle assessment (LCA) is usually performed without adequate consideration of temporal differentiation (ISO 14 040 and 14 044). In conventional LCA, Life Cycle Inventory (LCI) and intermediary flows are assumed to occur simultaneously. Life Cycle Impact Assessment (LCIA) is mostly based on steady-state modeling and time-integrated indicators. Nonetheless, time differentiation along the framework could have a significant impact on the LCA results and on decision support, as is conceptually explained in Fig. 1 through a simple example.

Fig. 1

Importance of time dependence in the calculation of the climate change impact of 1 kg methane emission (from Shimako et al. 2018)

Consider an instantaneous emission of 1 kg of methane to air as an LCI result. This generates a climate change impact of 28 kg of CO₂ equivalents using GWP₁₀₀ as an LCIA characterization factor (IPCC- 2013, Table 8.A.1.). Consider now two emission profiles (A and B) for the same emission content. These two impact results provide quite different information than the other case.

Extrapolating this exercise to all LCIs, the effects of temporal differentiation can propagate exponentially. At the LCI level, such an extrapolation shall result from knowing when each process of the life cycle actually occurs. At the LCIA level, impacts are also dependent on the timing of emissions. For example, volatile organic compound emissions have a higher influence on ozone and smog formation (Cheremisinoff 2002) during NO_x peak levels. A temporal differentiation of impacts over time is also relevant as, from an ethical perspective, future impacts could be regarded as less relevant (Levasseur et al. 2011; Schaubroeck and Rugani 2017). The common cut-off for climate change at 100 years is not only interpretable from a convenience perspective but also from an ethical perspective, in the sense that the impact on the globe after 100 years is completely discarded. A more gradual decrease in the importance of future effects could also be achieved using a discount factor as done by Levasseur et al. (2010) for global warming.

In principle, time-differentiated LCA results can be beneficial for different decision contexts. For example, bio-products could contribute to lowering radiative forcing thanks to the carbon stored (Røyne et al. 2016) on condition that the end of life of these products is consciously designed and scheduled in time. This is a concern not only when a bio-product is the object of a study, but also when it is used in the background of a product system. A more detailed discussion and literature examples of the ins and outs of a dynamic approach in LCA and of the main developments was provided by Beloin-Saint-Pierre et al. (2014) and Cardellini et al. (2018).

The methods and tools employed to perform dynamic LCA (DLCA) strongly evolved during the last decade, from a simplified spreadsheet-based temporalization of LCA results to a conceptualization accompanied by models and software development. However, operational tools capable of calculating time-differentiated inventories and impacts are still lacking, and this issue is therefore the subject of the present work.

At the LCI level, we distinguish between two kinds of temporalization. The first one concerns the changes in an inventory during the lifetime of a system, which can be described by defining several scenarios with distinct LCIs, occurring at distinct points in time. Some examples, not exhaustive, are the works of Hellweg et al. (2005), Penth (2006), or Collinge et al. (2013a, 2013b), with case studies from different fields of activity. In these works, the system’s inventory was built up at moments in time when significant modifications of the material and energy flows occurred, as for example the increasing energy demand during the lifetime of a building.

Practitioners need to “manually” build many inventories; they have to trace back which process and/or environmental intervention occurs at which time. As a result, this approach could be interpreted as repeating static inventories for several scenarios, each one representative of a given time period; it does not actually provide a dynamic model for LCA. In practical terms, it is also more feasible for the foreground system of an inventory than for the background system. Changes in background processes are excluded because of the complexity of the network, which cannot be processed manually.

The second type of temporalization aims to distribute the processes, flows, and LCI of a system over time, based on the evidence that the linked processes of the life cycle are time-deferred. Combined with appropriate impact calculation methods, the time-differentiated LCI is the first requirement for a consistent DLCA approach. The first attempts at temporalized inventories were proposed for the foreground part of the life cycle in order to calculate climate change impacts as a function of GHG-emission timing and to understand the role of biogenic CO₂ on the impact (Levasseur et al. 2010; Cherubini et al. 2011; Kendall (2012); Ericsson et al. 2013; Levasseur et al. 2012; Laratte et al. 2014, Laratte and Guillaume 2014; Lecompte et al. 2017). All these works focused on the impact generated by a few emissions related to foreground processes and did not propose a structured model for dynamic LCI. The emissions were “manually” distributed in time thanks to a precise knowledge of the studied foreground system.

In this vein, Beloin-Saint-Pierre et al. (2014) proposed a framework centered on the temporal characterization of processes and elementary (resource and emission) flows. The timeline of the LCI is then automatically derived through the interlinkages between inventory processes. The convolution operation is used to this end. A case study was done on domestic hot water production (Beloin-Saint-Pierre et al. 2016), applying a temporal differentiation for the foreground system only (energy production/consumption). The authors acknowledged that a huge effort was necessary to provide the necessary information for the background system.

Pinsonnault et al. (2014) applied this same framework to 22% of the processes of the ecoinvent 2.2 database, for which the authors defined temporal characteristics by sector of activity (e.g., infrastructure, forestry). The analysis was performed for the climate change impact category, also considered as a criterion for selecting significant intermediary and elementary flows for calculation. However, this first model for dynamic LCI calculation lacks a structured definition of the temporal characteristics needed for processes, flows, and supply chain representation (i.e., what is the physical meaning of the distribution functions?). From a theoretical point of view, using the convolution operation will introduce an intrinsic dependence of the processes in the network, that is to say, a producer process will adapt its temporal characteristics (e.g., not only the timing but also the emission profile) following the consumer process, which is not the case in a real-life scenario (for more information, see Tiruta-Barna et al. (2016)—supplementary information document). A clear definition of the necessary temporal characteristics and an associated database are lacking for a framework operationalization.

Tiruta-Barna et al. (2016) presented a modeling approach akin to supply chain modeling practices, by considering temporal characteristics of processes and supply chains, which can be leaned back against LCA databases (e.g., ecoinvent). In this approach, a limited set of temporal parameters have to be defined for each process and its exchanges with directly linked processes. A time-distributed LCI is calculated by combining the model with a graph search algorithm. The capability to link the temporalized LCI to dynamically calculated impacts was also demonstrated (Shimako et al. 2016, 2017, 2018).

More recently, Cardellini et al. (2018) proposed a tool for performing dynamic LCA based on a graph search algorithm combined with the convolution operation between emissions of the producer process and production of the consumer process, like in Beloin-Saint-Pierre et al. (2014). To do so, temporal distributions for emissions must be defined. As a demonstration, the dynamic LCI was coupled with GWP characterization factors for climate change. However, the approach lacks a parameterized model with a clear reference to process and supply chain functioning, as well as a proper temporal database linked to the background LCI, as is the case for the previous methods.

As our present work focuses on dynamic LCI calculation, the temporal aspects in LCIA are not presented extensively. Instead, the main realizations in this field are only briefly introduced hereafter, for comprehension of the developed framework.

Global warming is the impact category most considered in DLCA. Levasseur et al. (2010) proposed an approach based on the calculation of characterization factors (CF) for discrete time steps (1 year). This dynamic model uses radiative forcing as a physical parameter, but contrary to the classical approach, no fixed time horizon is needed. Similarly, this line of reasoning was applied to derive CFs (pre-calculated for fixed 1-year intervals) for the freshwater ecotoxicity of metals by Lebailly et al. (2014).

An alternative to pre-calculated CF is proposed in Shimako et al. (2016, 2017, 2018). Here, a flexible LCIA modeling approach was proposed to be directly coupled with the temporal differentiated LCI results obtained using the model of Tiruta-Barna et al. (2016). Coupling was done for climate change and toxicity/ecotoxicity impacts. Dynamic impact indicators and their cumulative values are calculated in function of time, taking advantage of a temporalized LCI with a time resolution going from hours to years.

The objective of the present work is to develop an operational tool for dynamic LCI calculation, based on the modeling approach presented by Tiruta-Barna et al. (2016). To this extent, we aim to provide an improved artifact that can better address a research problem and achieve a fully temporally differentiated LCA, in line with the design and development-centered approach of Peffers et al. (2007). In particular, the following issues are addressed in our work: (1) development of a database with temporal parameters for all processes in ecoinvent 3.2, in order to completely consider the background processes in DLCA; (2) implementation of the model and database in an integrated software; and (3) demonstration with a case study (comparing a fossil driven and an electric car) of the feasibility of a complete DLCA, in particular by considering the background LCI.

The novelty of the approach adopted here lies especially in points 1 and 2; therefore, this work aims to demonstrate the feasibility of such an approach for complete DLCA.

Methods

In the following, the principles of the dynamic LCI model are briefly recalled. Then, the development of the new database for the temporal parameters of the ecoinvent processes is presented, followed by the method of integration of the LCI model, database, and LCIA dynamic models into the global framework. Besides the case study, a more simplified and didactic example to understand the framework behind the tool can be found in the work of Tiruta-Barna et al. (2016).

Principles of the dynamic LCI model

The dynamic LCI model was initially developed by Tiruta-Barna et al. (2016). The reader is invited to refer to this and to the SI1 for a detailed presentation. Here, we recall the main features of the model that are important to understand the following steps. The model relies on the classical LCI structure (technology A and environmental intervention B matrices). It introduced a fundamental novelty with the adoption of a process/supply chain modeling perspective instead of an accounting point of view. The unit processes composing the life cycle inventory (foreground and background) are considered as operations having a proper functioning over time. The reference unit and the material/energy interventions of each have a distinct temporal profile. Furthermore, the intermediary exchanges among unit processes are positioned over a timeline depending on specific supply models, e.g., continuous, intermittent, and single punctual supply. As a result, mass and energy quantities listed in the dataset of a specific activity are no longer considered average quantities for a reference flow in a representative time period. Instead, the model allows the following to be calculated, the quantity requested by an activity, when and for how long it will be supplied to that activity, when and for how long it is stored before or after delivery, and when and for how long it was produced by the supplier.

Production and supply are described by temporal parameters and functions (also shown in Table S1 and Fig. S1 in SI1—Electronic Supplementary Material). All processes are characterized by (i) a production function α(t) for the reference flow and an emission profile β(t), which can be discrete values or functions of time; (ii) parameters r, the duration of an activity between the raw material input and the product output, T, the lifetime of the infrastructure supporting an activity, and t₀, the starting time of an activity. The supply is defined through parameters: δ, a no-activity period, and τ, the frequency of a product supply. These temporal parameters can be manually defined for the foreground processes, but a database must be developed for background processes, and this is presented in the following section. The model was implemented in DyPLCA, a web-based tool, which was then used in the works of Shimako et al. (2016, 2017, 2018). This tool is a very first version, modified and adapted in the present work for integrating the ecoinvent database with a temporal database of all processes, and coupling it with LCIA dynamic models.

Temporal database development

The temporal database was developed in an ecospold format for the Default, Consequential and Recyc system models of ecoinvent 3.2 from SimaPro. A representative sample of the database is provided in SI2. The rules and simplifications below apply.

Rules for the choice of the time parameters

(i) Functions α(t) (for production flows) and β(t) (for environmental interventions) are defined for the period r. Period T is a multiple of r. Functions can be constant or variable over time; they are replicated identically for all periods r covering the T lifetime. In the current version of the database, for the sake of simplification, α and β are defined once for each activity, i.e., they apply to all inputs and outputs of that activity, although the framework supports a specific definition for each individual flow.

(ii) Production functions that are calendar-dependent are defined over 1 year, starting in January, regardless of whether the activity starts at another moment. For example, if a product whose production takes a year (r = 1 year) is requested in October, the production process starts in October of the previous year. In this case, the specific activity intensity at that moment in time is considered. A potential issue is that a process often involves a series of consecutive steps. For example, in agricultural processes, sowing occurs before maintaining, which precedes harvesting. Applying the calendar dependence, sowing would start after harvesting, which does not make sense. This issue does not apply, however, as long as α is the same for all material and energy inputs/outputs of a process, which is the case in the current version of the database.

(iii) Supply scheduling and frequency is defined by δ (delay period) and τ (interval between supplies). These parameters shall be defined per material/energy flow, per product type, and combination of processes (supply and demand), as presented in Tiruta-Barna et al. (2016). These relationships are complex as they depend on supply and demand in the real market. For the sake of simplification, in the temporal database, those parameters were attributed to each supplier (or producer) process. Three types of supply profiles were defined: (1) Continuous, the product is supplied without interruption; for example, this is the case with an electricity supply. Here, τ is set equal to r meaning that the interval between production batches is the same as the production time. (2) Intermittent, when products are supplied in series of equal intermittent batches. τ specifies the duration of these time intervals. In general, τ is set equal to T of the consumer process if it is supplied once per lifetime (e.g., an infrastructure). It is set equal to δ for consumables that are frequently supplied but can be stored. It can also be set equal to either r of the producing process if production, and thus supply, are seasonal; or r of the consuming process, for example, in the case of frequently supplied consumables that are directly consumed at each production cycle of the consumer process. (3) Services, whenever the activity starts at the same time or later than the activity of the consumer process (t₀). This is the case of services occurring during the consumer process, e.g., “Fertilising, by broadcaster {RoW}| processing | Alloc Def, “U” for agriculture.” Services occurring at different moments (but with equal periods) are also considered, for example, mowing may occur at different moments during agricultural processes. In general, two types of processes are considered as services: (a) waste treatment processes (assuming that waste is generated and treated while the process is running) and (b) the majority of the processes that end with “processing” in their names. Services processes hold an ID (“S”) in the database.

Exceptions to the general rule are:

• Processes used by other processes, e.g., “Beverage carton converting {GLO}| processing,” “Wood preservation service, logs, pressure vessel, preservative not included {RER}| processing,” and “rock crushing.”

• Services not occurring simultaneously with other processes; namely all the vehicle and machinery maintenance processes, e.g., “Maintenance, barge {RER}| processing.”

• Services encompassing the complete production period, e.g., “Polystyrene foam slab for perimeter insulation {CH}| processing,” “Router, internet {CH}| processing” and “Wire drawing, copper {RER}| processing.”

• Transport processes, e.g., “Transport, freight train {AT}| processing.”

• Services that are performed afterwards, e.g., “Venting of argon, crude, liquid {GLO}| processing.”

• Waste treatment (including out of order equipment, machinery), e.g., “Used lorry, 16 metric ton {CH}| treatment of”

• “Sowing {CA-QC}| sowing,” which is considered as a service (for plant cultivation) even though “processing” is not mentioned in its title.

Further specific rules adopted for some of the ecoinvent processes are given in SI1, Section 2.5.

Processes without temporal profile

In ecoinvent 3.2, several processes do not reflect actual physical activities. For example, “market” processes gather several products without any physical transformation, i.e., there are no emissions, waste generation, and consumed resources or products. These processes are considered to occur instantaneously and hold an ID in the database (“M”); no temporal characteristics are needed for these.

Market processes (and exceptions)

These include market mixes and/or transport. For example, a process where different alternative production processes are given as inputs with their relative share as quantity. Sometimes, “market for” is not specified in the process name; for example, “Cement, unspecified {CH}| production.” Exceptions to the rule are (i) electricity markets including the activity of electricity transmission, for which temporal characterization is required. This means that this transportation activity is not covered by another process. The specific case of processes transforming high voltage to medium voltage is an exception of the exception. Temporal characterization is not needed; the material for the activity is already included in the medium voltage market processes containing the activity of transmission. (ii) a few fossil fuel markets, such as natural gas markets or imports; these include natural gas transportation, which must be characterized. Diesel markets (e.g., “Diesel {RoW}| market for” and “Diesel {CH}| market for”) also include the transportation of the diesel.

Processes only linking with other processes/markets

Two families of processes are considered (i) obsolete processes, without any function and link to other processes. The description often contains the following statement: “This process is no longer part of the ecoinvent 3 database and will not be updated. Please, choose another process.” An example is “Hard coal ash (waste treatment) {RoW}| cement production, pozzolana and fly ash 11–35%, non-US.” Waste treatment processes are also concerned. (ii) Non-obsolete processes, linking other processes together without any activity involved (1) processes substituting another process in the consequential version, e.g., “Sodium hydroxide, without water, in 50% solution state {GLO}| sodium hydroxide to generic market for neutralising agent.” The latter translates an extra demand of sodium hydroxide in an extra demand of neutralizing agent (e.g., sodium carbonate); consequently, it makes a link with its production dataset, which requires characterization. (2) Import processes, e.g., “Aluminium, primary, ingot {IAI Area, EU27 & EFTA}| aluminium, ingot, primary, import from Africa.” (3) Processes linking with one or several processes under one name, e.g., “Heat and power co-generation unit, 50 kW electrical, common components for heat+electricity {RER}| construction.” Another example is “Heat pump, 30 kW {RER}| production.”

Empty processes

This is the case, for example, for waste treatment products in the Recyc version of the database, to which cut-off is applied. Examples are “Digester sludge {GLO}| digester sludge, Recycled Content cut-off” or “Inert waste {CH}| clinker production | Alloc Def, U.”

Development of the integrated framework

Principles of computation of temporally differentiated LCI results

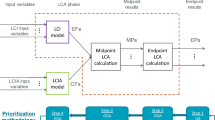
The objective is to obtain the life cycle environmental interventions (β functions) scaled to the functional unit (FU) and distributed over time. Further integration of the functions over time shall yield the static LCI results. This is achieved by combining (i) the conventional LCI inventory datasets from ecoinvent, (ii) the temporal parameters and functions associated with these datasets, and (iii) implementing an efficient graph search algorithm.

The combination was achieved practically in the web-based tool named DyPLCA, as a new, extended version of the initial tool cited by Tiruta-Barna et al. (2016) and Shimako et al. (2016, 2017, 2018). The algorithm works on a network of processes created based on the topology of matrix A, starting from the FU. A backward timeline is first defined, starting with the delivery of the FU. Then, the graph search implementation of the dynamic LCI model provides the amount of reference units for each process as well as its position along the timeline. Practically, a case study is first modeled in LCA software (SimaPro or OpenLCA) in a static manner. Then, matrices A and B are exported and further imported into DyPLCA in order to retrieve the values of intermediary and elementary flows. The temporal database is used to associate the temporal parameters to all the background processes used. In the foreground, the links between activities and the temporal parameters associated are directly added by the practitioner through the DyPLCA web interface (more details are given in SI1 – Electronic Supplementary Material).

The algorithm is computationally intensive; therefore, calculation time is critical. Memory usage during the computation and the size of the datasets has to be carefully addressed to avoid disruptive latencies. To this end, the search algorithm uses thresholds and stop conditions. Discretization steps are considered in order to accommodate the continuous dynamic LCI model to discrete time-series.

In the following, the functioning of the algorithm is detailed.

Implementation of the graph search algorithm

Once a project is properly configured (as described in SI1 - Electronic Supplementary Material), it can be computed. First, the “search” step resolves the start date and material quantity for each activity in the project. Then, the “distribution” step computes the distribution over time for the interventions for each activity. The distribution step is computed right after each activity gets resolved during the search step.

Search step

Life cycle processes are linked together by a producer/supplier-consumer/user relationship, based on matrix A. This is formally the adjacency matrix to a network where processes are nodes and producer-consumer relations are links. Although possibly large (15000 processes for ecoinvent 3.2), this material network remains a compact graph. Each link represents all the possible activities between a producer and a consumer. In order to obtain the complete list of activities concerned by one specific case study, one needs to obtain the complete activity network. This is an extended graph including, for each activity, its start date and material quantity over the timeline. In order to produce the activity network, a search is performed in the material network. The links indicate the flow of material or service between a producer and a consumer. This search starts from the final consumer (the FU), follows incoming links backwards to the producer, and finally, computes the start time and material quantities. The main issue to address here is that the network of processes involves loops that require a no-end graph and search algorithm. Indeed, the algorithm goes from one process to another in the loops without end, as the quantities exchanged by the processes (over time) are smaller and smaller but not null. This effect is not seen when the time dimension is ignored, as the quantities are calculated by matrix inversion to obtain the solution directly. A similarity can be drawn with the resolution of an integral by power series expansion. The solution can only be approximated as the expansion goes to infinity without reaching it.

In order to resolve this issue, the search algorithm uses boundary parameters. Once reached, these stop the search. The time limit parameter defines the maximum number of years the search algorithm can go back. This corresponds to an end time date of the timeline that was set in the past. Activities starting earlier than this date are excluded from the search. The threshold parameter defines a cut-off ratio on the quantities of the reference unit requested for each activity. Whenever the requested quantity is below the cut-off, that part of the network is discarded from the search (Table S2 in SI1 - Electronic Supplementary Material).

Distribution step

As long as the search algorithm proceeds, environmental interventions associated with each activity are computed. They are further associated to a given moment in the timeline with a specific discrete resolution. This generates large data tables containing the time series of the different environmental intervention types over the timeline. This step is controlled by two parameters. The step size parameter (Table S2 in SI1 - Electronic Supplementary Material) defines the interval of time between each data point of the time series. The smaller the step size, the bigger the size of the resulting time series. There is virtually no limit to how small the step size can be. However, the tool sets a threshold on the step size based on the available memory during the calculation. The numerical precision parameter (Table S2 in SI1 - Electronic Supplementary Material) is used during the computation of mathematical integrals for the α functions. This precision defines the step used for the numerical integrations. Integrals are computed over an interval equal to r (Table S3 in SI1 - Electronic Supplementary Material). Therefore, the precision should be orders of magnitude lower than r in order to render realistic values.

Linking temporally differentiated LCI results to dynamic LCIA models

Temporally differentiated LCI results are obtained as:

- β_{k, i, j} functions per substance k and intermediary flow (i,j) between processes i and j;

- γ_k functions, representing the emission profile of a substance k over the life cycle.

Results are obtained in the form of discrete values over time and can be used with dynamic LCIA models. Final outputs are impact indicators calculated at each time step along the timeline, which results from the combination of the dynamic LCI and LCIA models. These results can be obtained individually per process and substance, per substance on the life cycle, aggregated per impact category, etc.

Climate change, human toxicity, and ecotoxicity models have been implemented, based on Shimako et al. (2016, 2017, and 2018). As these methods were presented in the cited articles, they are not described extensively here.

Climate change impact is assessed by two indicators (based on IPCC models, 2007, 2013): (1) radiative forcing, which is instantaneous and cumulated in time—it replaces the conventional global warming potential GWP; (2) global mean temperature change as a function of time—it replaces the global temperature potential GTP.

Toxicity and ecotoxicity models are based on USEtox (Rosenbaum et al. 2008; Mackay 2002). Human toxicity (cancer and non-cancer) and ecotoxicity indicators are calculated as instantaneous and cumulated indicators, both as a function of time.

The main differences with respect to temporal climate change and toxicity from literature (Levasseur et al. 2010; Lebailly et al. 2014) are (1) the impact models are implemented in their initial dynamic form in order to directly obtain indicators in function of time and in order to avoid the use of characterization factors (otherwise a huge number of CF values would have to be calculated). The models were resolved in full dynamic conditions with the emission function β_{k, i, j} and γ_k as input data. (2) The approach is flexible, allowing the use of different time steps and adaptation to the granulometry of LCI.

The use of dynamic LCIA models allows us to exploit the full potential of the full temporally differentiated LCI results. The resolution of LCI results can be as high as permitted by the calculation time or can be chosen in accordance with the impact category (e.g., higher resolution for toxicity, lesser for climate change, Shimako et al. 2018).

Moreover, conventional LCIA indicators and dynamic CF can also be used over limited time intervals.

At this stage, the outcomes only present curves of impacts over time. Being able to provide single values would characterize the overall impact over time and allow for comparison and possibly decision support. To this end, the integration of these results over a given time period should be undertaken, as it has been done for the GWP₁₀₀ over 100 years. As already mentioned in the introduction, additionally, a discounting of impact over time can be considered, implying the lesser valuing of impacts later over time. This is commonly done using a constant annual periodic factor of x%, in which the impact diminishes over time with a factor 1/(1+year)^x. Such an approach was applied by Levasseur et al. (2010) and will be exemplified with the case study.

Case study: battery electric vehicle (EV) vs. internal combustion engine vehicle (ICEV)

A case study was performed to demonstrate the DyPLCA tool and the feasibility of a full dynamic LCA. In particular, the effect of implementing time differentiation in the background LCI is evaluated. To this end, a battery electric vehicle (EV) and an internal combustion engine vehicle (ICEV, EURO5 diesel) were compared. The two processes from ecoinvent 3.2 (the cut-off version) “Transport, passenger car, electric {GLO}| processing” and “Transport, passenger car, medium size, diesel, EURO 5 {RoW}| transport, passenger car, medium size, diesel, EURO 5” were considered.

Three different approaches to calculating the instant radiative forcing and dynamic global temperature were compared. The fully dynamic approach harnesses the full capabilities of DyPLCA. All foreground and background processes are given temporal parameters. The fully static approach is the opposite approach. It assumes that all emissions occur at the time the FU was provided. This is the most common situation adopted in LCA case studies and that can be obtained using standard LCA software tools. The dynamic foreground only relies on the assumption that the demand for passenger vehicle transportation occurs over 10 years for the given system. Therefore, only the foreground system is given a temporal profile. All first-tier activities, i.e., direct inputs to the functional unit, are accounted for in a static manner.

Figure 2 and Fig. 3 report on (i) the emission profile of fossil carbon dioxide, (ii) the instant radiative forcing, and (iii) the dynamic increase in global temperature that the profile generates, for all three modeling approaches. The fully static causes are a pulse emission, an instant peak in radiative forcing, and a fast increase of the dynamic global temperature potential at the exact time of fulfillment of the final demand. Both the fully static and dynamic foreground only lead to accounting for practically the same amount of emissions. A sensible difference in terms of the total amount of carbon dioxide emitted occurs in the fully dynamic, especially for the EV. The explanation is straightforward: static background inventories are compiled using the Leontief inverse. This accounts for the entirety of the (infinitely long) chain of activities. However, the search algorithm cannot cover 100% of biosphere intervention, for computational reasons. Truncation occurs in the fully dynamic approach, in which not all the carbon dioxide emitted can be accounted for.

Fig. 2

Carbon dioxide emission profile, instant radiative forcing, and dynamic temperature increase for the internal combustion engine vehicle system

Fig. 3

Carbon dioxide emission profile, instant radiative forcing, and dynamic temperature increase for the electric vehicle system

The earliest significant emissions tracked by the search algorithm start 20 years before the final demand is fulfilled. In particular, the process “Petroleum combustion, in drilling tests {GLO}” is identified. It is used as an input for onshore well construction and petroleum extraction. This is a precursor to many energy carriers pervading the system through, e.g., heavy fuel oil demand in shipping, diesel demand in road freight, and indirectly in electricity production.

It was observed that a higher degree of infrastructure contribution leads to a higher spreading of impacts over time. Systems showing more direct emissions in the foreground are significantly affected by time differentiation. However, the more upstream emissions occur, the higher the difference between fully dynamic and fully static results. Delays and production functions indeed compound along the supply chain. This contributes to flattening the emission profile and the radiative forcing effect.

As a result, it is fair to say that temporally differentiated LCI in the background offers little interest for activities with high downstream emissions. It can provide insightful results when applied to life cycle systems where significant environmental interventions occur upstream. Those systems concern, for example, renewable electricity generation, for which most emissions are embodied in an infrastructure upstream.

The graph search algorithm considers two conditions to stop the search: (1) if an intervention occurs prior to the time cut-off (using the time limit introduced in Section 2.3.2) and (2) if a product exchange is lower than a given threshold (using the threshold variable of Section 2.3.2). The first condition keeps the results in a reasonable period. However, it might lead to processes with very long lifetimes being neglected, for example, carbon sequestration in hardwood trees with production functions being defined over 140 years. Regarding the second condition, a scaling vector is calculated for each product exchange in the inventory. The vector contains the static LCI results, which represent the total emission values. A value between 0 and 1 is set as the threshold. The graph will then stop the search if a product exchange between two processes is lower than the product of the threshold and the process total output from the scaling vector (a_i,j s_j).

The trade-off between accuracy and computational time is investigated in Fig. 4. Carbon dioxide flows are considered, with a threshold of 10⁻⁴ leading to a coverage of 79%. It is estimated that 90% coverage would require more than 5 h of computation and 95% almost nine full days. Further optimization is needed to improve the coverage of emissions and to close the gap between numerical and analytical results.

Fig. 4

Time-differentiated flows of carbon dioxide, cumulated, and broken down by origin and sub-compartment, for the functional unit 1 pkm of “transport, passenger car, electric {GLO}” of ecoinvent 3.2 with a threshold of 10^-4

Results and discussion

The integrated framework for the dynamic LCA developed here is a flexible tool:

• A reduced number of temporal parameters can describe generic supply chains and can be evaluated for a huge number of processes; a temporal database can be built up for any other LCA database;

• LCA case studies can be performed as usual, with, e.g., Simapro software, completed by a simulation with DyPLCA tool;

• LCA case studies can also be defined directly on the web application if the number of processes is not huge or via an Excel file template to be filled in with temporal information;

• The dynamic LCI is obtained as discrete values in time, with time steps defined by the user. The time steps are not imposed and any dynamic LCIA can be coupled with these LCI results.

• Impact calculation can be done with dynamic LCIA models resulting in temporalized indicators, or with dynamic CFs, or static CF with or without flow integration over time.

Discussion of results from the case study

The results of the case study were integrated over time, or more precisely, summed over time. This has been done using a time window of 100 years, as this is a commonly considered time horizon, and a discount factor of 3%, which is the largest considered by Levasseur et al. (2010). See Table 1 for an overview of the results.

Table 1 Cumulated global dynamic radiative forcing (dynamic AGWP) in 10^-16 W/m²year for 1 vkm is shown at a 100-year time horizon with a discount factor (r) of or 3%

These single scores point out that the life cycle of the diesel car is characterized by a higher environmental impact than that of the electric car in all considered combinations. Since the distribution of environmental impacts do not differ much (see curves depicted in Figs. 2 and 3), the effect of time integration on the comparison is limited. However, the ratios between electric and diesel car impact differ when considering time differentiation for the foreground system and even more so for the fully dynamic system. Concerning the influence of discounting, the ratios alter more considerably. This exemplifies the potential impact of the time window and discounting on comparison and decision-making. Time differentiation as a whole may thus influence the conclusions of a study.

Limitations and further research on the temporal database

In the current version of the database, data consistency primes on accuracy. Possible improvements are detailed below.

The temporal database should ideally include a specific temporal profile for product exchange and environmental intervention. Currently, supply-demand parameters are provided per producer process; the same temporal profile (β function) is considered for all environmental interventions of a process. These simplifications can be alleviated by manually inputting the desired functions into the web interface of the tool, which is feasible for processes with significant contributions.

In ecoinvent, some types of processes are highly aggregate, hampering a sequentialization of the incoming flows in a process. In transportation processes, the lack of sequentialization is striking as the transported goods and the goods themselves are both inputs. In ecoinvent, transportation is an input in the consumer process in the same way as the production process of the transported goods. In reality, the production of the goods precedes their transport. Another example is the consideration of storage processes, which are often integrated into the production process, e.g., crop storage is considered a 1-year process, till the next harvesting.

The subdivision of the process into several sub-processes can be a pragmatic solution for the foreground system. However, it is not a feasible systematic solution for the complete database.

As shown in the results of the case study, the outcomes may easily span several decades. However, the process inventories differ over time. For example, the electricity mix has changed over time. Ideally, database inventories should be developed over time or following given socio-economic/technology evolution scenarios when it comes to future predictions. Although this issue is outside the scope of this work, the developed tool allows scenarios to be defined with different processes in the inventory (as mentioned in Section 1), and for example, to consider a different electricity mix by periods. However, scenarios can be defined in a reduced number and for a few processes.

Another limitation concerns the lack of information on freight transport distances, thus on the duration of transport processes. The functional unit of freight transportation is expressed as the product of weight and distance (tkm). The duration of transportation depends on the distance covered. This cannot be inferred from such an aggregated indicator. For example, 100 tkm could imply that 1 t is transported over 100 km; or that 100 t are transported over 1 km. The time it takes to transport these quantities differs significantly. To mitigate this issue, average r values were assigned to freight transportation processes. These represent the average transportation duration derived from literature. This issue does not apply to passenger transportation: it is assumed that only one person is transported and therefore the amount reflects the distance.

In future versions of LCI databases, it would be helpful to integrate temporal information right from the start of the development, as was already done for spatial information (Wernet et al. 2016). The structure of the database itself should be revised, based on the considerations above, to accommodate temporal information.

Further research on tool development

The specific developments of the tool could consist of the following:

• Including the option to fix the temporal profile of processes to specific calendar timing. For example, to fix the start of agricultural production at the right time of the season.

• To model supply-demand, only an intermittent, regular supply pattern has been considered so far for the sake of simplification. A non-constant intermittent period (τ - bridging the gap between supply and demand) should also be included. For example, in the seasonal agricultural products, delays between supply and demand should be higher in the period of the year that is furthest from the harvesting season.

• Increasing the calculation speed and making the tool compatible with other LCA software (e.g., OpenLCA) and databases.

• Coupling with other dynamic LCIA modules.

• Improving user-friendliness, namely the visualization of the outputs.

Further research on the time-differentiated LCA

Enlarging the scope of the current dynamic LCA could be envisaged from the following perspectives. An exploratory development would consider novel integrated modeling approaches for sustainability assessment (Schaubroeck 2018; Schaubroeck and Rugani 2017). A framework to differentiate industrial chains and related environmental interventions over time is crucial when coupling with nonlinear consequential models of earth or technosphere. After all, these are the only other impact models in which cause-effect chains are nonlinear and differentiated over time. Arvesen et al. (2018) point out this importance by providing factors derived from LCAs (with some minor temporal differentiation) to be used in such integrated assessment models.

By introducing full time-differentiation, the timing of FU delivery shall also be considered to ensure the comparability among different product systems. If the FU consists of a product, assuming t₀ as the point of product provision, this implies that the production of the product occurs in the relative past whereas its usage and disposal occur in the relative future. This could be interpreted as an attributional LCA viewpoint, despite attributional studies following future product scenarios also being possible. From a consequential LCA perspective, a variation of demand of a process (reflecting a decision taken) is assumed to trigger a change in the economy. In this case, t₀ would correspond to the moment at which the decision is taken; the demand variation occurs at a specific process in the supply chain. From this viewpoint, the choice of the activities actually requested after the decision is made according to the consequential approach and inventory database. The adaptation of the temporally differentiated framework of this paper to the attributional and consequential dimension goes far beyond the scope of this paper and deserves to be treated consistently in future studies.

Similarly, the integration of spatial information is a development opportunity that deserves further attention. This includes the actual location of processes, environmental interventions, and impacts. A few literature sources have already focused on the integration of spatial aspects in LCA, in particular on how to prioritize the addition of spatial information in the LCI database in order to reduce the computation time (e.g., Mutel et al. 2011; Yang and Heijungs 2017). However, a combination of spatial and temporal characterization was not addressed. In principle, integration can be relevant in some situations. Consider, for example, that a toxic compound is emitted twice in a short time at the same location. Its effect might be much greater than if it is emitted at different locations in the same short time duration. The graph search approach adopted in this work could also be applied to spatial differentiation. To this end, full spatial characteristics of processes and environmental interventions shall be added and further used when tracing back the processes along the life cycle network.

The main aim of this work was to provide an improved artifact that can be of use in further studies. Despite having already investigated our tool through a case study and parameter evaluation (see Section 3 in the Electronic Supplementary Material), further research is needed to increase the value of its impact in the field.

Conclusions

An operational approach and tool to assess the fully time-differentiated LCA results of a product life cycle were developed. The main feature of these is to implement the full temporal differentiation of background LCI processes. A supply chain model is implemented with a graph search algorithm. Temporal characterization was achieved for about 15000 processes of ecoinvent 3.2. The temporal database is used by the tool as a stand-alone web application. The tool was designed to work with case studies imported from Simapro or OpenLCA. The temporally differentiated LCI are further processed with dynamic LCIA models for climate change and toxicity, to gather the final temporally differentiated LCA results. As of now, the tool software is freely available online (http://dyplca.univ-lehavre.fr/) for testing purposes; the temporal database is protected by intellectual property rights.

The feasibility of a full dynamic LCA was tested with a case study on mobility. The case study showed that considering temporal differentiation across the complete life cycle, especially in the background system, can significantly change the results and interpretation of comparative LCA results. Therefore, the additional sophistication introduced by full temporal differentiation is valuable. This is particularly the case for product systems, which show significant environmental interventions and material exchanges over long time periods upstream to the FU.

This work provides the first operational framework to conduct fully temporally differentiated LCA. The inherent limitations outlined shall be considered as opportunities for further research on the temporal model and in particular on the temporal database to refine the temporal characterization of background processes. This requires a collegial effort, in particular involving the different industrial experts from the different sectors.