Advertisement

Assessing the merits of bioenergy by estimating marginal climate-change impacts

  • Miko U.F. Kirschbaum
Open Access
CARBON FOOTPRINTING
First Online:
Received:
Accepted:

Abstract

Purpose

Climate-change impacts can be mitigated through greater use of bioenergy, but the extent to which specific options actually reduce overall impacts needs to be assessed. Most bioenergy assessments have used proxy measures for assessing its merits. Here, a new approach is presented, whereby the contribution of bioenergy use is assessed through quantifying marginal changes in climate-change impacts that result from the implementation of a bioenergy option.

Methods

Marginal climate-change impacts were calculated for one specific example of a bioenergy option, conversion of an unutilised mature forest into a production forest harvested repeatedly for bioenergy over successive 25-year rotations. The overall benefit of the option was assessed by including stand-level carbon dynamics, global carbon-cycle feedback, progressively changing radiative efficiency and marginal impact sensitivity of warming. It also includes a differentiated assessment of three kinds of climatic impacts: direct-warming, rate-of-warming and cumulative-warming impacts. Marginal impacts were calculated and summed over 100 years to assess the overall marginal impact of this bioenergy option.

Results and discussion

Bioenergy use in this specific example led to a large initial loss of biomass carbon followed by an ongoing and accumulating benefit through fossil-fuel substitution. This caused adverse climatic impacts over the first two rotations as the effects of the on-site carbon loss dominated the overall impact, but the option became increasingly beneficial over longer time frames as the benefit of fossil-fuel substitution accrued and eventually dominated. Summed over 100 years, the bioenergy option reduced direct-temperature and rate-of-warming impacts whilst increasing cumulative-warming impacts. The average of the three kinds of impacts showed a slight mitigation benefit by reducing overall impacts. In the particular example, bioenergy use was assessed to have a more beneficial effect if the analysis was carried out under the assumption of higher-emission concentrations pathways, or if it assumed a steeper relationship between climate perturbations and impacts.

Conclusions

The usefulness of any climate-change mitigation option ultimately relates to the marginal climate-change impacts it can avert. It is shown here that marginal impacts can be calculated in routine operation and that they can provide an objective and methodologically consistent assessment of the mitigation potential of bioenergy use.

Keywords

Bioenergy C cycle Fossil fuel Global warming potential Impacts Mitigation Radiative efficiency Temperature 

1 Introduction

The atmospheric CO2 concentration reached about 400 μmol mol−1 by 2015 and continues to increase by about 2 μmol mol−1 yr−1 (Hartmann et al. 2013). The increasing CO2 concentration in the atmosphere, together with increases in other greenhouse gases, have begun to have noticeable impacts both on the natural world and on human livelihoods and well-being (Cramer et al. 2014). Hence, there is an urgent need to reduce anthropogenic emissions of greenhouse gases to curtail further climatic changes.

Reducing the emissions from fossil fuel use is the most urgent need, and it can be facilitated through the use of bioenergy that can produce useable energy without attendant fossil fuel emissions. Biomass already supplies about 10 % of global energy needs, and its use could be expanded to supply an even greater share of global energy (Hall 1997; REN21 2012). Bioenergy has, therefore, been supported as a strategy to mitigate climate change (e.g. EC 2003; Brandão et al. 2013; Creutzig et al. 2015).

However, there are a number of problems with its use. First, substitution efficiencies may be very low. Substitution efficiency is defined here as the units of fossil fuel substituted by a unit of bioenergy (also called ‘displacement factor’; Schlamadinger and Marland 1996), and it is one of the key determinants of the overall benefit of using bioenergy. Substitution efficiencies can potentially vary over a wide range of relevant values depending on biomass moisture content, the ease of collection and transport to a site of use, the type of fossil fuel being substituted, whether there are associated changes in the net emissions of non-CO2 greenhouse gases and whether extra fertilisers need to be supplied to sustain biomass productivity. Biomass use typically involves extra greenhouse gas emissions in harvesting and transport that tend to be higher than for fossil fuels. The decentralised nature of biomass production usually incurs additional emissions in transport to a power plant, or biomass has to be utilised in small-scale local power plants with low conversion efficiencies.

Substitution efficiency tends to be particularly low if the substituted energy type involves some complex conversion processes, such as for the production of transport fuels from lignocellulosic materials (e.g. Ioelovich 2015). Substitution efficiencies can be somewhat higher for the conversion of sugar to ethanol or vegetable oils into biodiesel (Davis et al. 2009; Lopez-Bellido et al. 2014). Higher substitution efficiencies can be obtained when biomass is simply burnt either directly for space heating (e.g. Paul et al. 2006; Koyuncu and Pinar 2007; Georges et al. 2013) or for electricity generation, particularly when electricity generation can be combined with heat cogeneration (e.g. Gustavsson et al. 1995; González et al. 2015).

Some fossil fuels, especially natural gas, also tend to have lower carbon emissions per unit of end-use energy than biomass, although that benefit can be lost if there is high methane leakage in the production-consumption chain (e.g. Hausfather 2015). If the replaced alternative energy source is wind, hydroenergy or solar energy, its ‘fossil-fuel’ substitution efficiencies can be very low so that the use of bioenergy might not save any fossil-fuel emissions at all.

Second, the production of bioenergy inevitably requires the use of land, making that land unavailable for other potential uses, such as food or fibre production. If the demand for those other products persists, bioenergy production may lead to indirect land use change (iLUC) where land in some other parts of the world may be converted to meet the demand for those products (e.g. Searchinger et al. 2009, 2015; Palmer and Owens 2015; Panichelli and Gnansounou 2015; de Rosa et al. 2016). Indirect land use change can only be quantified through models, but different models have given a wide range of estimates (e.g. Edwards et al. 2010), leaving it uncertain to what extent iLUC may negate any climate benefits of using bioenergy. However, if agricultural produce is used as the bioenergy source, the role of iLUC in reducing any mitigation benefits must always be considered in an overall assessment.

The present work addresses a third kind of problem that relates to the carbon-stock changes associated with bioenergy production that principally arise when forest systems are involved (e.g. Schlamadinger and Marland 1996; Schlamadinger et al. 1997; Helin et al. 2013). Forests can potentially store carbon that is the equivalent of any fossil-fuel substitution benefits of many years’ worth of bioenergy production. Carbon-stock changes can, therefore, considerably change the overall greenhouse gas balance of bioenergy systems (Fargione et al. 2008) and need to be considered when bioenergy is produced from production forests harvested over successive rotations. Relevant carbon-stock changes include the fluctuations in carbon stocks over each rotation and any losses of biomass or soil carbon if existing forests are converted to bioenergy production systems. For determining the benefits of bioenergy usage, it is, therefore, always necessary to define a baseline that quantifies the carbon-stock changes, if any, that would have occurred without the bioenergy project under consideration.

In principle, carbon-stock changes can contribute to the overall greenhouse gas balance either positively or negatively. If the alternative to a bioenergy production forest (the baseline) is a carbon-rich established forest, there can be an initial loss in carbon stocks, sometimes referred to as a ‘carbon debt’ (Fargione et al. 2008; Cherubini et al. 2013), which can substantially reduce the overall benefit of using bioenergy. Conversely, if the baseline land cover consists of vegetation with low carbon stocks, and if the bioenergy production system itself maintains higher average carbon stocks between harvests than the baseline, then the change in average carbon stocks can add to the benefit of using bioenergy.

The focus of the present work is on the accounting methodology that can be used to quantify the different positive and negative contributions that bioenergy use might entail. For carbon accounting in policy evaluation or life cycle assessments, there is currently no agreed procedure to account for differences in the timing of emissions and removals (Brandão et al. 2013) even though many of the basic issues had been identified in previous work (e.g. Schlamadinger et al. 1997). It is clear that the current default metric, the use of global warming potentials (GWPs), does not adequately reflect the importance of the timing of emissions and removal. This makes it necessary to find and adopt a broadly acceptable new accounting approach that appropriately reflects the effect of bioenergy options on modifying climate-change impacts.

The current work presents a simple bioenergy scenario to highlight the issues that need to be addressed in an objective assessment of the merits of specific bioenergy options. It gives one specific case for bioenergy use and should not be used to draw general conclusions about the desirability of using bioenergy. This scenario only serves for illustrative purposes. The focus of the present work is on presenting appropriate methodology that should be used for assessing the benefits of specific bioenergy options. The work thus presents the consecutive stages that need to be considered to calculate ultimate marginal climate-change impacts due to the bioenergy option considered.

The chosen scenario was selected as one that could most starkly highlight and contrast the positive and negative aspects of bioenergy use. As a baseline, the scenario assumed an established old-growth forest with constant carbon stocks and that produced no bioenergy. This baseline condition was then compared with an option where the management of the forest was changed to produce bioenergy over successive rotations. That change in the production system caused changes in forest carbon stocks relative to baseline conditions. This allowed consideration of gains and losses in carbon stocks and of the increasing bioenergy availability that allowed fossil-fuel substitution from which global temperature changes and resultant climate-change impacts could be calculated.

The work presents the series of necessary steps to move from carbon-stock changes in a forest stand plus fossil-fuel substitution benefits from the use of bioenergy to ultimate global climate-change impacts. It builds on the work of Kirschbaum (2003a, 2003b, 2006), who explicitly accounted for carbon-cycle feedback in the assessment of different biospheric carbon-management options. That earlier work was further refined through the development of climate-change impact potentials (CCIPs) as a greenhouse gas-accounting metric in more recent work (Kirschbaum 2014). The work presented here includes carbon-cycle feedback (following Joos et al. 2013), changing radiative efficiency with changing background greenhouse gas concentrations (see Reisinger et al. 2011), a differentiated assessment of three kinds of temperature-related climatic impacts (e.g. Fuglestvedt et al. 2003; Kirschbaum 2014) and the changing sensitivity of climatic impacts per unit climate perturbation with changing background conditions (Kirschbaum 2014).

The accounting approach is illustrated here with an example that considers only carbon dynamics. In principle, other greenhouse gases (Kirschbaum 2014) or albedo changes (Kirschbaum et al. 2013) can be readily incorporated into the assessment. The key end point of the presented accounting framework is the calculation and comparison of marginal climate-change impacts under different management options.

2 Calculation steps

The calculations of changes in forest biomass, fossil-fuel substitution, resultant changes in atmospheric CO2 concentration, radiative forcing and global temperature are described in detail in Electronic supplementary material. Temperatures up to 2010 were based on the data compilation of Jones et al. (2012). Temperature variations from 2010 onwards were calculated based on atmospheric CO2 concentrations under different representative concentration pathways (RCPs; van Vuuren et al. 2011) with modifications of net emissions through the bioenergy scenarios used as outlined in Electronic supplementary material. These global temperatures were then used to calculate marginal impacts.

Separate impacts were calculated for direct-temperature, rate-of-warming and cumulative-warming impacts (Kirschbaum 2014). First, the perturbations underlying the three different kinds of impacts were calculated. The perturbation P y,T in year y, underlying direct-temperature impacts, was calculated as
$$ {P}_{y,T}={T}_y{\textstyle \hbox{-} }{T}_p $$
(1)
where T y and T p are the temperatures in year y and a pre-industrial year p, with temperatures in 1900 taken to represent pre-industrial conditions.
For any year, the rate of temperature change, P y,Δ, was calculated as the temperature increase over the preceding 100 years as
$$ {P}_{y,\varDelta }=\left({T}_y{\textstyle \hbox{-} }{T}_{y-100}\right)/100 $$
(2)
Cumulative temperature, P y,Σ , was calculated as the sum of temperatures above pre-industrial temperatures as
$$ {P}_{y,\varSigma }={\displaystyle \sum_{j=p}^y\left({T}_j-{T}_p\right)} $$
(3)
where T j is the temperature in every year j from the pre-industrial year p (1900) to year y.
Impacts, I, were then calculated for each year and impact as
$$ {I}_{y,i}={P_{y,i}}^s $$
(4)
where i refers to one of the three kinds of impacts and s is an impact-severity term. Kirschbaum (2014) used a more complex exponential function for relating impacts to their underlying climate perturbations, but a power function was used here for greater simplicity and transparency. A value of s = 3 was used as default (a cubic function), with impacts also calculated for different values of s as shown below.
Total marginal impacts, I t , attributable to the bioenergy option, were then calculated for each of the three kinds of impacts as the sum of impacts over 100 years from 2010 to 2109 as
$$ {I}_{t,i}={\displaystyle \sum_{y=2010}^{2109}{I}_{y,i}} $$
(5)

These numbers can be expressed as ratios between different options, such as the ratio of calculated impacts resulting from the generation of a unit of energy from fossil fuels versus generation of the same unit of energy by using bioenergy as calculated in the steps shown here. Similar ratios were used by Kirschbaum (2014) for comparing pulse emissions of different greenhouse gases.

3 Results and discussion

3.1 Stand-level carbon balance

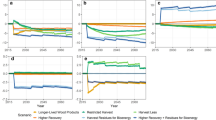
The baseline for the bioenergy scenario was a carbon-rich forest that maintained a high and steady level of carbon stocks (Fig. 1a). Although the forest was not sequestering any additional carbon, the large existing carbon store constituted a valuable environmental asset. In 2010, with the start of the bioenergy scenario, this forest was harvested, with 75 % of above-ground biomass burnt for bioenergy use, whilst 25 % of biomass were assumed to be unsuitable for harvesting and collection and were, instead, left as slash on the forest floor from where it slowly decayed over subsequent years. This included stumps, bark, leaves, cones and small branches and twigs. Soil carbon was assumed not to be affected by forest management (Johnson and Curtis 2001).
Fig. 1

Changes in different carbon pools over time, plus the cumulative CO2 savings from the substitution of bioenergy for fossil-fuel use (a) and the combined cumulative C flux considering the stand-level carbon balance plus cumulative fossil-fuel savings (b). All pools are expressed relative to the baseline condition

When trees are harvested, their roots die and start to decay, with rates of decay and consequent carbon loss depending on species and environmental conditions. Coarse roots can typically account for 20–30 % of total tree biomass (Mokany et al. 2006). After harvesting the old forest, new trees were planted for a new forest rotation. After some time, here assumed to be 25 years, the new rotation forest could also be harvested, and the sequence could repeat itself. It was assumed that forest growth was sustainable in the sense that each rotation could achieve the same growth rate and carbon sequestration as the preceding one.

Figure 1 thus represents all changes to the carbon cycle that resulted from the decision to convert an established but non-productive forest into one used for bioenergy production. This firstly included changes at the stand level in various pools that responded to harvesting and subsequent regrowth, above-ground biomass, live and dead roots and slash on the forest floor. The wood available at each harvest could be used as bioenergy source. Without the use of bioenergy, end-use energy would have been generated from the use of fossil fuels, leading to an ongoing depletion of this global reservoir. Compared with that baseline, the saving of fossil fuels through substitution by bioenergy constituted a positive difference. From an atmospheric perspective, that saving was equivalent to carbon accumulation in a physical pool. It is therefore represented in Fig. 1a in the same units as the various stand-level pools. This is a useful way of using common units and a single diagram to summarise all relevant changes resulting from a bioenergy project.

Following Kirschbaum (2003b), the calculations here assumed a 50 % substitution efficiency. It means that 1 tC in harvested biomass could generate the same amount of end-use energy as could be generated by using 0.5 tC of fossil fuel. This value accounts for conversion efficiencies and all associated carbon emissions and energy losses incurred in the production chain of both fossil fuels and bioenergy. The 50 % substitution efficiency used here was relevant to one specific combination of the relevant factors. The usefulness of using bioenergy would be assessed differently under different conditions characterised by different substitution efficiencies. However, the present work focuses on the methodology that can be used for assessing the usefulness of bioenergy use. The parameters used here are simply an example selected to illustrate the application of the relevant accounting methodology.

The carbon contained in all forest carbon pools plus cumulative fossil-fuel savings could then be summed to result in the net carbon flux that ultimately affected atmospheric concentrations (Fig. 1b). Under the assumptions made here, there was no net biospheric carbon flux before the stand was harvested as the stand was assumed to have a zero carbon balance, and there was no fossil-fuel substitution. When the forest’s use for bioenergy began, 90 tC was initially burnt for bioenergy use. That was offset by a 45 tC ha−1 saving through fossil-fuel substitution resulting in a net emission of 45 tC ha−1.

In subsequent years, there was a further carbon efflux to the atmosphere from decaying slash and coarse roots. That efflux was balanced by carbon gain through the regrowth of new wood. At the end of the first rotation, the cumulative carbon balance nearly reached the zero line when the stand-level growth of new biomass carbon added to previous fossil-fuel savings. The next harvest turned the system into carbon deficit again, but from the end of the second rotation, the accruing fossil-fuel savings had shifted the system towards an overall positive carbon balance. It became negative immediately after each harvest, but from the fourth harvest onwards, it retained a positive carbon balance even through the periods immediately after each harvest.

3.2 Atmospheric CO2 and radiative forcing

The combined changes in stand-level carbon stocks plus fossil-fuel savings then constituted the combined CO2 load to the atmosphere. Changes in atmospheric CO2 concentrations (Fig. 2a) largely mirrored stand-level carbon changes (Fig. 1b), but the magnitude of changes was slightly reduced through global-carbon cycle feedback (Joos et al. 2013).
Fig. 2

Changes in atmospheric CO2 concentration (a), radiative forcing under RCP6 (b) and cumulative radiative forcing (c), calculated under either RCP 6 or constant CO2 concentrations (400 μmol mol−1) as indicated in the figure

In essence, any increase in atmospheric CO2 concentration increases the effective concentration difference between the atmosphere and other global carbon reservoirs, principally the oceans. That increased concentration difference increases CO2 uptake by the oceans and reduces the amount remaining in the atmosphere. The addition of 1 tC to the atmosphere, therefore, leads to an eventual increase in atmospheric CO2 by less than 1 tC. Changes in atmospheric CO2 concentrations are therefore smaller than the underlying changes in stand-level carbon stocks (Korhonen et al. 2002; Kirschbaum 2003a, b).

These changes in atmospheric CO2 concentration then cause radiative forcing (Fig. 2b), but the proportionality between CO2 concentration and radiative forcing diminishes over time because radiative efficiency of CO2 diminishes with increasing background CO2 concentrations (Reisinger et al. 2011). This is further illustrated in Fig. 3, which shows radiative efficiency of CO2, defined as the radiative forcing per unit of atmospheric CO2, over the next 100 years under four different RCPs. Under RCP 6, radiative efficiency approximately halved over the next 100 years, with an even larger change under RCP 8.5. Reducing radiative efficiency significantly affects the warming calculated under future CO2 concentrations.
Fig. 3

Radiative efficiency of CO2 calculated under four different RCPs

Radiative forcing was then summed over 100 years to generate a simple estimate of the effect of the chosen bioenergy scenario (Fig. 2c). Different sums were obtained for calculations done with constant background CO2 concentrations (as is done for GWP calculations) and under changing background concentrations according to RCP 6. This pattern resulted because bioenergy use increased radiative forcing over the first 50 years and reduced radiative forcing over the next 50 years (Fig. 2b). As radiative efficiency decreased with increasing background CO2 concentrations (Fig. 3), it diminished the importance of the negative radiative forcing over the second 50-year period compared to that of the increased radiative forcing over the first 50-year period. Calculations under constant background CO2 concentrations therefore resulted in lower cumulative radiative forcing than calculations that included changing radiative efficiency with changing background concentrations (Fig. 2c).

3.3 Climate-change impacts

However, radiative forcing itself does not constitute an impact per se. Instead, it constitutes a perturbation of the Earth’s energy balance that leads to temperature changes, which are more closely related to ultimate impacts. As discussed by Fuglestvedt et al. (2003), Kirschbaum (2003a, 2014) and Tanaka et al. (2010), at least three different kinds of climate-change impacts can be categorised based on their functional relationship to increasing temperature as follows:

  • The impact related directly to elevated temperature

  • The impact related to the rate of warming

  • The impact related to cumulative warming

Impacts related directly to temperature are the relevant measure for impacts such as heat waves and other extreme weather events. The rate of warming relates to impacts such as maladaptation of both natural and socio-economic systems, with slower rates of change allowing time for migration or other adjustments, whilst faster rates of change provide less scope for adjustments and equate to more severe impacts. Cumulative warming is related to impacts such as sea level rise, because sea level rise is related to both the magnitude of warming and the duration over which oceans and ice sheets are exposed to increased temperatures (see Kirschbaum 2014 for further discussion).

Radiative forcing (Fig. 2b) changed surface temperatures (Fig. 4a), from which rates of warming (data not shown) and cumulative warming (Fig. 4b) could be derived. Temperature changes followed radiative forcing but with additional delays due to the thermal inertia of the global climate system. Bioenergy use thus added to global warming over the first 50 years due to the large initial carbon loss, followed by cooling over the subsequent 50 years as cumulative fossil-fuel substitution increasingly began to dominate the combined carbon balance (see Fig. 1).
Fig. 4

Calculated changes in temperature (a) and cumulative temperature (b) under the bioenergy scenario analysed here. Cumulative warming in b is simply the integral of the temperature changes shown in a. All temperature changes here are calculated under RCP 6

That initial warming led to a broad peak in cumulative warming from about 2050 to 2070 (Fig. 4b). Subsequent cooling from about 2070 reduced cumulative warming, but it remained positive to the end of the 100-year assessment period. The patterns of temperature change and cumulative warming were similar to radiative forcing (Fig. 2b) and cumulative radiative forcing (Fig. 2c), respectively, but peaks were smoothed and shifted towards later periods by the thermal inertia of the global climate system. Thermal inertia also caused cumulative warming to remain positive up to 2110 (Fig. 4b), even though cumulative radiative forcing had already become negative by then (Fig. 2c).

The perturbations in temperature (Fig. 4a), rate of warming (data not shown) and cumulative warming (Fig. 4b) were then used to calculate impacts at corresponding times. However, units of additional perturbations had different impacts under different background conditions (Fig. 5). In essence, when background conditions are relatively mild, any marginal perturbation has little marginal impact, but when background conditions are more severe, the same marginal perturbation can have a proportionately much larger impact. Marginal warming impacts increased sharply over the 100-year assessment period, especially under RCP 8.5 (Fig. 5a). Changes were less extreme under RCP 6, but marginal impacts per unit of warming still increased more than sixfold between 2010 and 2109, whilst changes under RCP 4.5 were only moderate.
Fig. 5

Relative marginal impacts per unit of marginal warming (a) or per unit cumulative warming (b) under four different RCPs, calculated with a cubic impact-perturbation relationship. All data are expressed relative to marginal impacts in 2010

Under higher RCPs, any marginal temperature change in the latter part of the next 100 years, therefore, had a much greater overall impact than the same marginal temperature change over the earlier parts of the next 100 years. This was important as bioenergy use in the specific illustrative scenario shown here effectively traded warming in one period against cooling in another. The pattern was even more extreme for cumulative-warming impacts than for direct-warming impacts, with the sensitivity of marginal impacts increasing more steeply towards the end of the assessment period (Fig. 5b). There were strong increases in marginal impacts from marginal increases in cumulative warming even under RCP 3. These increases in cumulative warming occurred because even though temperatures might stabilise under RCP 3, they are expected to stabilise at a level above pre-industrial values. This continued elevation of temperature continued to add to cumulative warming, leading to increasing sensitivity of marginal impacts to any further cumulative warming even under RCP 3.

For the calculation of marginal impacts at different times, the shape of the impact-perturbation relationship is thus critically important. Whilst it is generally accepted that impacts increase more than proportionately with their underlying perturbations, there is no consensus on the steepness of that relationship (Nordhaus 1994; Hammitt et al. 1996; Roughgarden and Schneider 1999; Tol 2012; Weitzman 2012, 2013; Lemoine and McJeon 2013; Kirschbaum 2014). For the work shown here, a relatively steep perturbation-impact function (a cubic relationship) was used to reflect the strongly non-linear nature of climate-change impacts (Weitzman 2012, 2013).

The shape of the perturbation-impact function therefore has a strong bearing on future impact assessments. A steep perturbation-impact relationship shifts the importance of extra warming to times when background temperatures are already high. This has also been shown to have a strong influence on the relative importance of CH4 and CO2, with steeper perturbation-impact relationships increasing the relative importance of long-lived greenhouse gases (Kirschbaum 2014). The steepness of the perturbation-impact relationship also influenced the marginal impacts caused by emissions/removals at different times. As bioenergy use affects the timing of emissions and removals, changing impact sensitivity has a strong bearing on ultimate calculated marginal impacts.

Calculated temperature changes (from Fig. 4) were then combined with relative impacts per units of warming (from Fig. 5) to calculate marginal impacts under the bioenergy scenario over the next 100 years for each of the three distinct kinds of climatic impacts (Fig. 6). Marginal impacts were primarily driven by positive or negative temperature changes (Fig. 4), but their magnitude was modified by changing marginal impact sensitivity over time (Fig. 5).
Fig. 6

Marginal impacts over the next 100 years under the bioenergy scenario studied here. Shown are the marginal changes in direct-temperature impacts (T), rate-of-warming impacts (Δ) and cumulative-warming impacts (Σ). All data have been expressed relative to the largest (positive or negative) relative impacts calculated over the next 100 years

Consequently, even though the warming caused by the carbon release from the initial harvest was greater than the cooling calculated at the end of the 100-year period (Fig. 4a), the impact of the later cooling was about five times as large as the warming impact over the first two rotations. Rate-of-warming impacts followed a similar pattern, but positive and negative impacts were more similar because their impact sensitivity is not expected to increase as steeply as those underlying direct-warming impacts because of lesser changes in the underlying perturbations (data not shown).

Cumulative-warming impacts remained positive to the end of the 100-year assessment period (Fig. 6). Even though the cumulative warming attributable to the bioenergy project was decreasing sharply by the end of the century (Fig. 4b), its impact was still increasing up to about 2095 because its marginal impact sensitivity increased more strongly (Fig. 5b) than the decrease in the underlying perturbation.

3.4 Integrated climate-change impacts

Marginal impacts were then summed over 100 years to give the total change in impacts over a 100-year assessment period (Table 1). The base conditions used RCP 6 and a cubic impact-perturbation function. Impact sums were also calculated under different RCPs and for different impact-perturbation functions as shown in the table.
Table 1

The 100-year sums of radiative forcing, marginal impacts under the three kinds of impacts and their average, climate-change impact potential (CCIP), as a result of the bioenergy scenario described above

 

Impacts

Radiative forcing

Direct warming

Rate of warming

Cumulative warming

Average (CCIP)

RCP 3, I = P 3

−22

−5

38

44

26

RCP 4.5, I = P 3

−9

−33

−10

47

1

RCP 6, I = P 3

1

−49

−33

49

−11

RCP 8.5, I = P 3

15

−59

−54

54

−20

RCP 6, I = P 2

1

−17

−9

58

11

RCP 6, I = P 4

1

−78

−55

43

−30

All sums are expressed relative to that of the emission of 1 tCO2 in 2010, with positive numbers indicating an increase in impacts. A number of +10, for example, would mean that the bioenergy scenario had the same marginal impact as burning 10 tCO2 in 2010. Calculations are shown under four different RCPs and with three different functions relating impacts (I) to changes in the underlying perturbations (P). The base conditions used here are shown in bold

Under the base conditions (RCP 6, I = P 3), total radiative forcing was increased by the equivalent of burning only enough fossil-fuel carbon to produce just 1 tCO2 in 2010. That means that the extra radiative forcing over the first 50 years through the loss of forest biomass was almost exactly balanced by the negative radiative forcing through accumulating fossil-fuel substitution benefits over the second 50-year period (Fig. 2b, c). The effect became more positive under higher-concentration RCPs because radiative efficiency decreased more sharply under higher RCPs (Fig. 3), rendering the later period of negative radiative forcing less effective than under lower RCPs.

In terms of direct-temperature and rate-of-warming impacts, the bioenergy scenario reduced impacts under the base conditions by the equivalent of −49 and −33 tCO2 ha−1, respectively. Even though the 100-year sum of radiative forcing was virtually unchanged under the bioenergy scenario, warming impacts were reduced because the cooling occurred at a time with much greater marginal impact sensitivity to changes in the underlying perturbations. This pattern was further heightened under higher-concentration RCPs because the increase in marginal impact sensitivity became stronger under higher background concentrations (Fig. 5).

In contrast to direct-temperature and rate-of-warming impacts, cumulative-warming impacts increased under the bioenergy scenario, with an increase in impacts by the equivalent of about 50 tCO2 ha−1 with similar values under all RCPs and impact-perturbation relationships (Table 1). The calculated impact was relatively insensitive to the underlying RCP because highest cumulative warming occurred at an intermediate length of time (Fig. 4b) so that the positive and negative effects of increasing impact sensitivity over time largely cancelled out in the calculation of total cumulative-warming impacts.

Taking an average of the three individual impacts (CCIPs; Kirschbaum 2014) resulted in a combined impact that ranged from increasing impacts by the equivalent of 26 tCO2 ha−1 under RCP 3 to reducing them by −20 tCO2 ha−1 under RCP 8.5, and with impacts becoming more negative with increasing steepness of the perturbation-impact relationship. The changes in CCIPs with RCPs and steepness in the impact-perturbation relationship were due to changes in direct-warming and rate-of-warming impacts, whilst cumulative-warming impacts changed little with RCP or steepness of the impact-perturbation relationship.

These differences are important because they show that an assessment of the merits of bioenergy must be made within the context of specific assumptions about likely background future concentration pathways. The same bioenergy option may increase climate-change impacts under a sustainable concentration pathway whilst usefully helping to reduce impacts under higher-concentration pathways. Similarly, the bioenergy scenario will increase impacts if an appropriate impact-perturbation relationship is judged to be fairly flat (I = P 2), given that warming and cooling at different times contribute similarly to the total. If a steep relationship (I = P 4) is used, instead, it would be concluded that bioenergy can usefully reduce impacts because the cooling contribution towards the end of the 100-year assessment period is weighted more heavily than the warming contribution at the beginning of the period.

4 General discussion

Ultimately, a meaningful assessment of the merits of using bioenergy must rest on an explicit or implicit assessment of the relative marginal changes in climatic impacts that would result from its use. That must include consideration of changes of on-site carbon stocks and the accumulating benefit of fossil-fuel substitution. Such marginal impacts were quantified in the present work. They involved a few critical assumptions and a small number of calculation steps that could be easily carried out in any analysis. Those calculation steps included consideration of carbon-cycle feedback, changes in radiative efficiency, a dependence of the sensitivity of marginal impacts on background conditions and a separate assessment of the three kinds of climatic impacts.

The assessment needs to start with calculation of stand-level changes in biospheric carbon stocks relative to an appropriate baseline and cumulative fossil-fuel substitution. Together, they constituted the overall change in carbon stocks attributable to the adoption of a specific bioenergy production system. These carbon-stock changes then change atmospheric CO2, with actual changes in atmospheric CO2 concentrations modified through global carbon-cycle feedbacks (Joos et al. 2013). These are important adjustments for the assessment of net effects of any biospheric carbon-stock changes as they reduce the change in atmospheric CO2 per unit carbon-stock change on the ground (Korhonen et al. 2002; Kirschbaum 2003a, 2006).

Changes in atmospheric CO2 cause radiative forcing, but radiative forcing is affected not only by changes in CO2 but also by radiative efficiency, which decreases with increasing background CO2 concentrations (Reisinger et al. 2011). Under the highest RCPs, radiative efficiency of CO2 can be reduced by more than 50 % over the coming century, which makes inclusion of changing radiative efficiency quantitatively important.

Radiative forcing then leads to temperature changes. Temperature changes lag changes in radiative forcing due to the thermal inertia of the global climate system. Temperature lags are of the order of months for the atmosphere and land surface, about 5 years for the mixed-layer upper ocean and decades to centuries for adjustments in the deep ocean layers (e.g. Meinshausen et al. 2011). Different authors have used different approaches to describe these time lags in simplified calculation schemes, typically using one or two simple time constants (e.g. Hasselmann et al. 1993; Watterson 2000; Li and Jarvis 2009; Jarvis and Li 2011; Meinshausen et al. 2011). The implications of using different time constant were discussed by Kirschbaum (2003a), and in line with the approach adopted then, a single time constant of 10 years was used here. These time lags shift temperature patterns to later dates than the underlying patterns in radiative forcing, so that in the scenario studied here, peak cumulative warming (Fig. 4b) was reached at a later date than peak cumulative radiative forcing (Fig. 2c).

Temperature changes were then used to calculate the relevant perturbations underlying the three different kinds of impacts, direct-temperature, rate-of-warming and cumulative-warming impacts (Kirschbaum 2014), which were differently affected by the bioenergy scenario. Temperatures (Fig. 4a) and rates of warming (data not shown) increased over the first two rotations in response to the initial loss of forest carbon but decreased over the last two rotations due to accumulating fossil-fuel substitution benefits. Cumulative warming increased over the first half of the assessment period in line with increasing temperatures. It decreased from its peak over the second half of the assessment period as temperature changes became negative, but that was not sufficient to fully negate the earlier accumulation of warming units. Cumulative warming therefore remained positive up to the end of the 100-year assessment period (Fig. 4b).

To translate these temperature perturbations into impacts required consideration of background climatic changes. Because impacts increased more than linearly with their underlying perturbations, the same marginal changes in perturbations caused disproportionately larger changes in marginal impacts if they occurred at a time with larger background perturbations (Fig. 5). This was important in the case of the studied bioenergy scenario since it essentially traded off increasing temperature impacts over the first 50 years against decreasing impacts over the second 50 years. As the first 50 years had lower background temperature increases than the second 50 years, the period of increasing marginal impacts mattered less than the later period with decreasing marginal impacts (Fig. 6). Direct-temperature and rate-of-warming impacts showed similar patterns over time but differed in their relative magnitude.

That pattern was different for cumulative-temperature impacts. As cumulative temperatures remained elevated to the end of the assessment period (Fig. 4b), there was no trade-off between periods of increasing and decreasing impacts. Marginal impacts remained positive (increasing impacts) throughout the assessment period (Fig. 6). There was thus an important difference between the temporal patterns of direct and rate-of-warming impacts on the one hand, and cumulative-warming impacts on the other. This difference had also been noted in previous assessments that made an explicit distinction between these kinds of impacts (e.g. Kirschbaum 2003a, b, 2006, 2014). Since all three kinds of impacts are important, a comprehensive impact assessment cannot be undertaken without explicitly accounting for all three kinds of impacts. It also means that metrics like GWPs (a variant of cumulative-warming impacts) and global temperature change potentials (GTP; a variant of direct-temperature impacts) ignore part of the impacts that matter, thereby providing a biased assessment of the relevant totality of impacts.

Marginal impacts were then summed over 100 years to give 100-year total marginal impacts attributable to the bioenergy scenario (Table 1). The average of the three kinds of impacts typically consisted of both positive and negative contributions driven by corresponding fluctuations in direct-warming and rate-of-warming impacts (Fig. 6). All these contributions mattered, and the ultimate net impact could only be assessed when the various positive and negative contributions were explicitly considered and included in the analysis.

Calculated impacts under the bioenergy scenario analysed here depended strongly on assumed background conditions, with the bioenergy option becoming increasingly more favourable under higher-emission RCPs and with increasing steepness of the impact-perturbation relationship. Assessed impacts depended on the selected background conditions as they critically determined radiative efficiency and impact sensitivity. Whilst radiative efficiency decreased with increasing background RCP, a quantitatively more important factor was the increasing marginal impact sensitivity with increasing RCP. Hence, whilst a given change in forest carbon led to less radiative forcing and a smaller temperature change under a higher RCP, that smaller temperature change nonetheless had a larger impact because of sharply increasing impact sensitivity. These differences were quite marked so that full impact assessments could only be provided under a given assumed RCP.

This leads to the uncomfortable realisation that there can be no universal answer to the question of the desirability of using bioenergy as the same scenario may mitigate climate-change impacts under one possible background condition and worsen it under another. This makes it more difficult to decide on the desirability of supporting specific mitigative actions, but that is the reality. If the interaction between the desirability of using bioenergy and relevant background conditions is not considered, it may lead to support for bioenergy even under conditions where such support may not be warranted or, conversely, a failure to support it under conditions where support might be warranted. If the desirability of using bioenergy changes with changing background conditions, then a comprehensive analysis of the desirability of using bioenergy must explicitly include these interactions.

The assessment of bioenergy scenarios also depended on assumptions about the steepness of the impact-perturbation relationship. Temperature perturbations can be calculated on the basis of physical principles, but temperature perturbations do not equate to impacts. Instead, impacts increase disproportionately with increases in the underlying perturbations, but there is no consensus on the steepness of that relationship (Kirschbaum 2014). Some authors opted to describe the impact-perturbation relationship with a fairly flat relationship, like a quadratic equation (e.g. Nordhaus 1994; Roughgarden and Schneider 1999; Tol 2012). These choices are often based on damages that are quantifiable in economic assessments. However, these readily identifiable factors do not constitute the totality of relevant impacts, and a steeper impact-perturbation relationship needs to be used to account for non-economic factors or for the possibility of low-probability impacts with catastrophic consequences (e.g. Hammitt et al. 1996; Weitzman 2012, 2013; Lemoine and McJeon 2013).

The calculations described here applied the same relative importance to impacts occurring at any time over the next 100 years. Alternatively, impacts in a more distant future could be discounted in some way. In economic analyses, it is common practice to discount future costs or benefits, but in environmental assessments, it is more defensible to apply very low discount rates (e.g. Stern 2006), or zero discount rates, as is effectively done in calculating GWPs. Sterner and Persson (2008) argued that negative discount rates might be even more appropriate in climate-change assessments. Whilst these arguments all have merit, the work here followed the approach adopted in the calculation of GWPs and applied a 100-year assessment horizon with no discount rates.

A comparison of different mitigation options, such as between different energy production systems, should be based on an assessment of marginal impacts caused by these different options. There are various metrics that have or could be used for the assessment of bioenergy projects (e.g. Brandão et al. 2013). Most metrics strive for simple analyses in which the link between the initial perturbation of the carbon cycle and ultimate climate impacts is only implicit. They typically rely on calculating carbon-stock changes that are combined with a representation of carbon-cycle feedback to provide some weighting or adjustment of carbon-stock changes (e.g. Fearnside et al. 2000; Cherubini et al. 2011; Pingoud et al. 2016). However, as shown here, even two of the most widely considered impacts, direct-temperature and cumulative-warming impacts, showed dramatically different responses to the same underlying scenario (Fig. 6 and Table 1).

Different greenhouse gas-accounting metrics are also usually based on quantifying only one kind of impact (such as cumulative warming—GWP) or another (direct-temperature impacts—GTP). Both kinds of impacts are important, as are rate-of-warming impacts that are usually not considered at all (other than by Peck and Teisberg 1994). However, an appropriate assessment of ultimate climate-change impacts should not select one of these measures and ignore the others. Instead, it should explicitly consider all relevant kinds of impacts together, as is done with climate-change impact potentials (Kirschbaum 2014). For any assessment metric to be useful, it is important that it captures the totality of impacts to assess the true mitigative contribution of bioenergy use.

This is important for both life cycle assessments and policy evaluation. Biospheric carbon-stock management can be characterised by a sequence of gains and losses of carbon, and a full assessment of its ultimate consequences requires the timing of greenhouse gas concentrations, their radiative forcing and ultimate climate-change impacts to be explicitly assessed. The complexity of possible interactions (i.e. see Fig. 6) precludes the use of simple indices, as the timing of emissions is important as well as its quantity. In all case, it comes down to an explicit evaluation of marginal climate-change impacts under a set sequence of net emissions of relevant greenhouse gases over time.

5 Conclusions

An objective assessment of the merit of bioenergy use in specific production systems requires an assessment of the ultimate marginal change in climate-change impacts through the use of bioenergy. The assessment must use a set of assumed background conditions that describe the climate-change dynamics within which bioenergy use is assessed. This assessment must include consideration of changing on-site carbon stocks and cumulative fossil-fuel savings through bioenergy substitution. The present work provided such an assessment that took the analysis closer to a quantification of actual marginal impacts than had been provided in previous assessments of bioenergy use. In addition to calculated stand-level carbon dynamics and fossil-fuel substitution benefits, the assessment included global carbon-cycle feedback, changing radiative efficiency, quantification of future marginal warming, changing marginal impact sensitivity and a differentiated assessment of three kinds of climatic impacts. Marginal impacts were calculated as the 100-year sums of annually calculated changes in marginal impacts.

The example bioenergy option analysed here was characterised by a large initial loss in stand-level carbon stocks and an accumulating benefit through fossil-fuel substitution. Putting all factors together resulted in slightly negative overall marginal impacts (reducing climate-change impacts). The study also found that this assessment depended on assumed background conditions, with more beneficial outcomes obtained under higher-concentration pathways. The present assessment included only carbon dynamics, but albedo changes and non-CO2 greenhouse gases could be readily incorporated into the same assessment framework. There is thus no unique answer to the question of the merit of using bioenergy, but it can only be assessed within specifically defined background conditions. Specifying such underlying assumptions about background conditions must therefore be an integral part of any assessment of the merits of using bioenergy.

Notes

Acknowledgments

With thanks to the International Energy Agency Bioenergy Task Force 38 for facilitating the ongoing work on the refinement of relevant accounting methodology. I would also like to thank Suzie Greenhalgh, Kevin Tate and three anonymous referees for their useful suggestions on the manuscript and Anne Austin for scientific editing.

Supplementary material

11367_2016_1196_MOESM1_ESM.pdf (287 kb)
ESM 1 (PDF 287 kb)

References

  1. Brandão M, Levasseur A, Kirschbaum MUF, Weidema BP, Cowie AL, et al. (2013) Key issues and options in accounting for carbon sequestration and temporary storage in life cycle assessment and carbon footprinting. Int J Life Cycle Assess 18:230–240CrossRefGoogle Scholar
  2. Cherubini F, Bright RM, Strømman AH (2013) Global climate impacts of forest bioenergy: what, when and how to measure? Environ Res Lett 8, Article no. 014049Google Scholar
  3. Cherubini F, Peters GP, Berntsen T, Strømman AH, Hertwich E (2011) Emissions from biomass combustion for bioenergy: atmospheric decay and contribution to global warming. GCB Bioenergy 3:413–426CrossRefGoogle Scholar
  4. Cramer W, Yohe GW, Auffhammer M, Huggel C, Molau U, da Silva Dias, MAF, Solow A, Stone DA, Tibig L (2014) Detection and attribution of observed impacts. In: Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC, Girma B, Kissel ES, Levy AN, MacCracken S, Mastrandrea PR, White LL Climate change 2014: impacts, adaptation, and vulnerability. Part a: global and sectoral aspects. Contribution of working group II to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 979–1037Google Scholar
  5. Creutzig F, Ravindranath NH, Berndes G, et al. (2015) Bioenergy and climate change mitigation: an assessment. GCB Bioenergy 7:916–944CrossRefGoogle Scholar
  6. Davis SC, Anderson-Teixeira KJ, DeLucia EH (2009) Life-cycle analysis and the ecology of biofuels. Trends Plant Sci 14:140–146CrossRefGoogle Scholar
  7. De Rosa M, Knudsen MT, Hermansen JE (2016) A comparison of land use change models: challenges and future developments. J Clean Prod 113:183–193CrossRefGoogle Scholar
  8. EC (2003) Directive 2003/30/EC of the European Parliament and of the Council of 8th May 2003 on the Promotion of the use biofuels or other renewable fuels for transport. Official Journal of the European Union L123: 42–46, European Commission, BrusselsGoogle Scholar
  9. Edwards R, Declan Mulligan D, Marelli L (2010). Indirect land use change from increased biofuels demand—comparison of models and results for marginal biofuels production from different feedstocks. Publication Office of the European Union, Luxembourg, 145 ppGoogle Scholar
  10. Fargione J, Hill J, Tilman D, Polasky S, Hawthorne P (2008) Land clearing and the biofuel carbon debt. Science 319:1235–1238CrossRefGoogle Scholar
  11. Fearnside PM, Lashof DA, Moura-Costa P (2000) Accounting for time in mitigating global warming through land-use change and forestry. Mitig Adapt Strateg Glob Chang 5:239–270CrossRefGoogle Scholar
  12. Fuglestvedt JS, Berntsen TK, Godal O, Sausen R, Shine KP, Skodvin T (2003) Metrics of climate change: assessing radiative forcing and emission indices. Clim Chang 58:267–331CrossRefGoogle Scholar
  13. Georges L, Skreiberg Ø, Novakovic V (2013) On the proper integration of wood stoves in passive houses: investigation using detailed dynamic simulations. Energy Build 59:203–213CrossRefGoogle Scholar
  14. González A, Riba JR, Puig R, Navarro P (2015) Review of micro- and small-scale technologies to produce electricity and heat from Mediterranean forests’ wood chips. Renew Sust Energ Rev 43:143–155. doi: 10.1016/j.rser.2014.11.013
  15. Gustavsson L, Borjesson P, Johansson B, Svenningsson P (1995) Reducing CO2 emissions by substituting biomass for fossil fuels. Energy 20:1097–1113CrossRefGoogle Scholar
  16. Hall DO (1997) Biomass energy in industrialised countries—a view of the future. For Ecol Manag 91:17–45CrossRefGoogle Scholar
  17. Hammitt JK, Jain AK, Adams JL, Wuebbles DJ (1996) A welfare-based index for assessing environmental effects of greenhouse-gas emissions. Nature 381(6580):301–303Google Scholar
  18. Hartmann DL, Klein Tank AMG, Rusticucci M, Alexander LV, Brönnimann S, Charabi Y, Dentener FJ, Dlugokencky EJ, Easterling DR, Kaplan A, et al. (2013) Observations: atmosphere and surface. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge UK, and New York, NY, USA, Warming Potentials, pp. 159–254Google Scholar
  19. Hasselmann K, Sausen R, Maier-Reimer E, Voss R (1993) On the cold start problem in transient simulations with coupled atmosphere-ocean models. Clim Dyn 9:53–61CrossRefGoogle Scholar
  20. Hausfather Z (2015) Bounding the climate viability of natural gas as a bridge fuel to displace coal. Energ Policy 86:286–294CrossRefGoogle Scholar
  21. Helin T, Sokka L, Soimakallio S, Pingoud K, Pajula T (2013) Approaches for inclusion of forest carbon cycle in life cycle assessment—a review. GCB Bioenergy 5:475–486CrossRefGoogle Scholar
  22. Ioelovich M (2015) Recent findings and the energetic potential of plant biomass as a renewable source of biofuels—a review. Bioresources 10:1879–1914Google Scholar
  23. Jarvis A, Li S (2011) The contribution of timescales to the temperature response of climate models. Clim Dyn 36:523–531CrossRefGoogle Scholar
  24. Johnson DW, Curtis PS (2001) Effects of forest management on soil C and N storage: meta analysis. For Ecol Manag 140:227–238CrossRefGoogle Scholar
  25. Jones PD, Lister DH, Osborn TJ, Harpham C, Salmon M, Morice C P (2012) Hemispheric and large-scale land-surface air temperature variations: an extensive revision and an update to 2010. J. Geophys. Res. 117 Art. No. D05127. doi:10.1029/2011JD017139Google Scholar
  26. Joos F, Roth R, Fuglestvedt JS, Peters GP, Enting IG, von Bloh W, Brovkin V, Burke EJ, Eby M, Edwards NR, Friedrich T, Frölicher TL, Halloran PR, Holden PB, Jones C, Kleinen T, Mackenzie FT, Matsumoto K, Meinshausen M, Plattner G-K, Reisinger A, Segschneider J, Shaffer G, Steinacher M, Strassmann K, Tanaka K, Timmermann A, Weaver AJ (2013) Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis. Atmos Chem Phys 13:2793–2825CrossRefGoogle Scholar
  27. Kirschbaum MUF (2003a) Can trees buy time? An assessment of the role of vegetation sinks as part of the global carbon cycle. Clim Chang 58:47–71CrossRefGoogle Scholar
  28. Kirschbaum MUF (2003b) To sink or burn? A discussion of the potential contributions of forests to greenhouse gas balances through storing carbon or providing biofuels. Biomass Bioenergy 24:297–310CrossRefGoogle Scholar
  29. Kirschbaum MUF (2006) Temporary carbon sequestration cannot prevent climate change. Mitig Adapt Strateg Glob Chang 11:1151–1164CrossRefGoogle Scholar
  30. Kirschbaum MUF (2014) Climate change impact potentials as an alternative to global warming potentials. Environ Res Lett 9, Article #034014Google Scholar
  31. Kirschbaum MUF, Saggar S, Tate KR, Thakur K, Giltrap D (2013) Quantifying the climate–change consequences of shifting land use between forest and agriculture. Sci Total Environ 465:314–324CrossRefGoogle Scholar
  32. Korhonen R, Pingoud K, Savolainen I, Matthews R (2002) The role of carbon sequestration and the tonne-year approach in fulfilling the objective of climate convention. Environ Sci Pol 5:429–441CrossRefGoogle Scholar
  33. Koyuncu T, Pinar Y (2007) The emissions from a space-heating biomass stove. Biomass Bioenergy 31:73–79CrossRefGoogle Scholar
  34. Lemoine D, McJeon HC (2013) Trapped between two tails: trading off scientific uncertainties via climate targets. Environ Res Lett 8(3):034019. doi: 10.1088/1748-9326/8/3/034019
  35. Li S, Jarvis A (2009) Long run surface temperature dynamics of an A-OGCM: the HadCM3 4×CO2 forcing experiment revisited. Clim Dyn 33:817–825CrossRefGoogle Scholar
  36. Lopez-Bellido L, Wery J, Lopez-Bellido RJ (2014) Energy crops: prospects in the context of sustainable agriculture. Eur J Agron 60:1–12CrossRefGoogle Scholar
  37. Meinshausen M, Raper SCB, Wigley TML (2011) Emulating coupled atmosphere-ocean and carbon cycle models with a simpler model, MAGICC6—part 1: model description and calibration. Atmos Chem Phys 11:1417–1456CrossRefGoogle Scholar
  38. Mokany K, Raison RJ, Prokushkin AS (2006) Critical analysis of root: shoot ratios in terrestrial biomes. Glob Change Biol 12:84–96CrossRefGoogle Scholar
  39. Nordhaus WD (1994) Expert opinion on climatic change. Am Sci 82:45–51Google Scholar
  40. Palmer J, Owens S (2015) Indirect land-use change and biofuels: the contribution of assemblage theory to place-specific environmental governance. Environ Sci Pol 53:18–26CrossRefGoogle Scholar
  41. Panichelli L, Gnansounou E (2015) Impact of agricultural-based biofuel production on greenhouse gas emissions from land-use change: key modelling choices. Renew Sust Energ Rev 42:344–360CrossRefGoogle Scholar
  42. Paul KI, Booth TH, Elliott A, Kirschbaum MUF, Jovanovic T, Polglase PJ (2006) Net carbon dioxide emissions from alternative firewood-production systems in Australia. Biomass Bioenergy 30:638–647CrossRefGoogle Scholar
  43. Peck SC, Teisberg TJ (1994) Optimal carbon emissions trajectories when damages depend on the rate or level of global warming. Clim Chang 28:289–314CrossRefGoogle Scholar
  44. Pingoud K, Ekholm T, Soimakallio S, Helin T (2016) Carbon balance indicator for forest bioenergy scenarios. GCB Bioenergy 8:171–182CrossRefGoogle Scholar
  45. Reisinger A, Meinshausen M, Manning M (2011) Future changes in global warming potentials under representative concentration pathways. Environ Res Lett 6, Article Number: 024020. doi: 10.1088/1748–9326/6/2/024020
  46. REN21 (2012) Renewables 2012—global status report. Renewable Energy Policy Network for the Twenty-First Century. REN21 Secretariat, Paris, France, 176 ppGoogle Scholar
  47. Roughgarden T, Schneider SH (1999) Climate change policy: quantifying uncertainties for damages and optimal carbon taxes. Energ Policy 27:415–429CrossRefGoogle Scholar
  48. Schlamadinger B, Marland G (1996) The role of forest and bioenergy strategies in the global carbon cycle. Biomass Bioenergy 10:275–300CrossRefGoogle Scholar
  49. Schlamadinger B, Apps M, Bohlin F, Gustavsson L, Jungmeier G, Marland G, Pingoud K, Savolainen I (1997) Towards a standard methodology for greenhouse gas balances of bioenergy systems in comparison with fossil energy systems. Biomass Bioenergy 13:359–375CrossRefGoogle Scholar
  50. Searchinger T, Edwards R, Mulligan D, Heimlich R, Plevin R (2015) Do biofuel policies seek to cut emissions by cutting food? Science 347:1420–1422CrossRefGoogle Scholar
  51. Searchinger TD, Hamburg SP, Melillo J, Chameides W, Havlik P, Kammen DM, Likens GE, Lubowski RN, Obersteiner M, Oppenheimer M, Robertson GP, Schlesinger WH, Tilman GD (2009) Fixing a critical climate accounting error. Science 326:527–528CrossRefGoogle Scholar
  53. Sterner T, Persson UM (2008) An even sterner review: introducing relative prices into the discounting debate. Rev Environ Econ Pol 2:61–76CrossRefGoogle Scholar
  54. Tanaka K, Peters GP, Fuglestvedt JS (2010) Policy update: multicomponent climate policy: why do emission metrics matter? Carbon. Manage 1:191–197Google Scholar
  55. Tol RSJ (2012) On the uncertainty about the total economic impact of climate change. Environ Resour Econ 53:97–116CrossRefGoogle Scholar
  56. van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, et al. (2011) The representative concentration pathways: an overview. Clim Chang 109:5–31CrossRefGoogle Scholar
  57. Watterson IG (2000) Interpretation of simulated global warming using a simple model. J Clim 13:202–215CrossRefGoogle Scholar
  58. Weitzman ML (2012) GHG targets as insurance against catastrophic climate damages. J public. Econ Theory 14:221–244Google Scholar
  59. Weitzman ML (2013) A precautionary tale of uncertain tail fattening. Environ. Res Econ 55:159–173CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Landcare ResearchPalmerston North 4442New Zealand

Personalised recommendations