1 Introduction

Co-product allocation is defined in the ISO series of international standards on LCA as “partitioning the input or output flows of a process or a product system between the product system under study and one or more other product systems” (International Organisation for Standardisation 2006a; International Organisation for Standardisation 2006b). Originating from practices in economics and other management sciences, co-product allocation is a key concept within life cycle assessment (LCA) (Frischknecht 2000; Suh et al. 2010) and is one of the most discussed methodological issues in the field (Heijungs and Frischknecht 1998; Finnveden et al. 2009; Guinée et al. 2011; Hanes et al. 2015). Recently, there has been a considerable effort by researchers and industry-funded committees (such as the FAO Livestock Environmental Assessment and Performance (LEAP) Partnership) to establish the most appropriate allocation methodology for LCA studies of livestock production (International Dairy Federation 2010; FAO 2014a; FAO 2014b; FAO 2014c). This has been part of wider efforts to unify methodologies adopted by those developing LCA models of agricultural and in particular livestock systems to ensure they are comparable in their approach since it is obvious that the use of different allocation rules in LCA studies comparing different aspects of agricultural systems can lead to different conclusions (Nguyen et al. 2011; Eady et al. 2012; Brankatschk and Finkbeiner 2014).

The allocation of environmental impacts to co-products based on their economic value is the most commonly used allocation method in agricultural LCA studies, particularly for crop production and the livestock feed supply chain (Ardente and Cellura 2012; Brankatschk and Finkbeiner 2014; Van Der Werf and Nguyen 2015). However, several new allocation methodologies have been proposed for LCA studies of agricultural systems based on physical relationships between co-products. These methodologies are often referred to as “biophysical” allocation (International Dairy Federation 2010; Eady et al. 2012; Thoma et al. 2013; Gac et al. 2014; Van Der Werf and Nguyen 2015; Wiedemann et al. 2015). Draft guidelines on carbon footprinting in livestock systems issued by the FAO have also recommended that biophysical allocation should be adopted for models of the on-farm stages of livestock production (FAO 2014a; FAO 2014c), although currently not in the feed supply chain (FAO 2014b). These developments have followed from the ISO standard of requirements and guidelines for LCA, which state that co-product allocation based on underlying physical relationships between the material flows of a system and its products or functions is preferable to allocation based on other relationships, such as economic value (International Organisation for Standardisation 2006b).

The methodological trend towards biophysical allocation in agricultural LCA raises obvious and wider questions: what can be considered an underlying physical relationship between material flows and productive outputs in LCA? Are such relationships easily related to the outputs of agricultural systems which are useful from a human perspective? Ultimately, is biophysical allocation an appropriate approach for LCA of agricultural systems? The aims of this paper were to (1) examine whether researchers have been able to identify underlying physical relationships between the material and energy flows of agricultural systems and their products and (2) assess whether the trend towards biophysical allocation in agricultural LCA is feasible from a methodological perspective. Two key components of agricultural systems which involve co-product allocation were used to provide examples of current methodological practices and issues namely (1) the crop production chain and (2) the multiple co-products produced by livestock.

2 Co-product allocation and its use in agricultural LCA

ISO 14044 is the international standard of requirements and guidelines for best practice in conducting LCA (International Organisation for Standardisation 2006b). Part of the standard sets out a hierarchy for the methodological choices available regarding co-product allocation in LCA:

4.3.4.2 Allocation procedureThe study shall identify the processes shared with other product systems and deal with them according to the stepwise procedure presented below.a) Step 1: Wherever possible, allocation should be avoided by1) dividing the unit process to be allocated into two or more sub-processes and collecting the input and output data related to these sub-processes, or2) expanding the product system to include the additional functions related to the co-products, taking into account the requirements of 4.2.3.3.b) Step 2: Where allocation cannot be avoided, the inputs and outputs of the system should be partitioned between its different products or functions in a way that reflects the underlying physical relationships between them; i.e. they should reflect the way in which the inputs and outputs are changed by quantitative changes in the products or functions delivered by the system.c) Step 3: Where physical relationship alone cannot be established or used as the basis for allocation, the inputs should be allocated between the products and functions in a way that reflects other relationships between them. For example, input and output data might be allocated between co-products in proportion to the economic value of the products. (International Organisation for Standardisation 2006b).

 

The ISO standard suggests that co-product allocation is to be avoided wherever possible in LCA decision making. However, the adoption of either system separation or system expansion throughout entire LCA models can require large amounts of extra data to model either additional sub-processes or marginal systems (Parker 2008; Curran 2015), as most processes modelled in LCA are multi-output (Frischknecht 1994). Aside from the practical issue of obtaining extensive datasets, these large complex models also run the risk of being less transparent and using inaccurate assumptions (Ekvall 1999; Curran 2007). While system expansion is generally associated with consequential LCA modelling, it is also utilised in many attributional models (Finnveden et al. 2009). For example, many attributional livestock LCAs have used system expansion to account for nutrients in manure replacing the need for inorganic fertilizers when spread on fields for crop production (Williams et al. 2006; Reckmann 2013; Cherubini et al. 2015). There are, however, wider concerns as to whether implementing system expansion throughout LCA models to avoid co-product allocation is feasible or desirable (Finnveden et al. 2009). In theory, multi-functional processes could be added to LCA studies ad infinitum in order to fully implement this methodology for every aspect of an LCA (Lundie et al. 2007). Unlike the example of manure replacing inorganic fertilizer, there are many areas of LCA models of livestock systems where such “what if” exercises are purely speculative. For example, when utilising co-products such as corn or wheat dried distillers grains with solubles from bioethanol production in animal feed, there are a multitude of pathways for such material to be used if not included in the diets for the particular livestock system modelled. Expanding the model with a what if scenario to predict the replacement pathway for a particular ingredient when this cannot be predicted with any confidence means that the modelling exercise strays further away from using known facts (Heijungs and Guinée 2007). With this in mind, it is not possible or desirable to use system expansion as a general rule to eliminate allocation problems throughout LCA models of agricultural systems.

In cases where co-product allocation is necessary, step 2 of the hierarchy advises that inputs and outputs to a system are partitioned in a way that reflects the underlying (or causal) relationships beneath them (Azapagica and Clift 1999a; Ekvall and Finnveden 2001). This recommendation of the ISO standard is a significant reason why many of the new biophysical methodologies for allocation discussed below have been proposed as preferable to allocation based on the economic value of co-products. In this sense, the hierarchy followed the recommendations of a number of papers on the subject which used industrial processes (Azapagica and Clift 1994; Clift et al. 1996) and was the outcome of recommendations made by the working groups of bodies, such as the Society of Environmental Toxicology And Chemistry (SETAC) (SETAC 1994). Similar recommendations regarding a hierarchy for allocation methodologies in agricultural LCA can be found in reports from an EU working group on methodology harmonisation (Audsley et al. 1997).

3 Allocation using underlying physical relationships in an industrial setting

Many of the conventional guidelines and practices within the field of LCA should be viewed in the context of its early history during which it was mainly used as a tool to measure energy use and resource consumption from industrial processes (European Environment Agency 1999). Large industrial production sites typically have large amounts of instrumentation and data on the exact inputs and outputs from production processes. The causal mechanisms behind these production processes are in many cases well known and can be defined by process engineers. Example 1, originally presented by Azapagica and Clift (1999a), briefly describes an allocation methodology based on causal physical relationships approach being applied to a mineral processing facility producing five boron co-products using linear programming to model system behaviour.

3.1 Example 1—allocation in the boron co-product system (Azapagica and Clift 1999a)

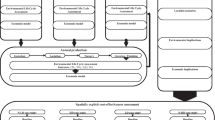
The boron production system shown in Fig. 1 has five boron co-products: (1) disodium terraborate decahydrate (Na2B4O710H2O) “10 Mol”, (2) disodium terraborate pentahydrate (Na2B4O74.67H2O) “5 Mol”, (3) boric acid (H3BO3) “BA”, (4) anhyrdrous borax (Na2B4O7) “AB” and (5) anhyrdrous boric acid (B2O3) “ABA”. As shown in Fig. 1, the LCA was split into a “foreground system”, which was the boron mine and production plant, and a “background system”, which comprised all other activities from material extraction to delivery to the foreground system. In the foreground system, the minerals borax and kernite are extracted from the mine, crushed and transported to an adjacent plant. 10 and 5 Mol borates are produced by dissolving borax and kernite in water. BA is produced separately by reacting kernite ore with sulphuric acid, and AB and ABA are produced in high-temperature furnaces from 5 Mol borate and BA, respectively. All products are then shipped from the factory gate. Electricity and steam for the system are provided by the on-site natural gas co-generation plant. All activities except the disposal phases of these products are considered in this cradle-to-gate LCA (Azapagica and Clift 1999a).

Fig. 1
figure 1

Flow diagram of the boron production system adapted from Azapagica and Clift (1999a)

Full size image

Azapagica and Clift used linear programming (LP) to model physical relationships in the boron system so that infinitesimal variations in the functional outputs were modelled to determine “marginal allocation coefficients”. The relationships which described the system behaviour were modelled using constraints in the LP algorithms. Upon providing a solution, the LP model also showed marginal values indicating the contribution of each constraint to the total burdens. Where a constraint limited the behaviour of the system, it had a marginal value greater than 0; non-active constraints had marginal values of 0 and were thus modelled as not contributing to the burdens resulting from the system. In this case, the authors assigned environmental impacts to constraints related to co-product outputs which are considered to be active and thus contributing to the environmental burdens. Any limits imposed by aspects of the production process were ignored. The marginal approach allowed the model to allocate the environmental impacts on the basis of the expected increase in emissions or resource input required to produce additional yield of each co-product. In this system, most of the CO2 emissions were allocated between AB and ABA as increasing production of either of these co-products requires large energy inputs to a furnace as well as further production of 5 Mol and BA, respectively. Further analysis by the authors using alternative co-product allocation methodologies showed that co-product allocation on the basis of mass flow produced the same results as those from marginal allocation using the LP model. As such, the authors were able to show that allocation using this simple physical property was appropriate to represent the causal mechanisms at work in the production system. However, they were only able to select the appropriate property using a holistic model of system behaviour, rather than selecting arbitrarily.

4 Biophysical allocation in agricultural LCA

While “causal physical relationships” between the material inputs and the outputs in LCA have been modelled in industrial processes, the question is whether such an approach can be easily related in the biological systems, which underpin agricultural production. At the organism level, the biological systems do not function with the goal of producing the items which humans deem to be economically valuable (and consider as co-products of the system). In order to establish physical causality between functional units and environmental burdens, it must be possible to change the functional outputs of the product system independently (Azapagica and Clift 1999b; Ekvall and Finnveden 2001). In the following, the functioning and relationships of different sub-processes in both crop and animal production are demonstrated and discussed within the context of physical causalities.

Figure 2 is a simplified representation of the energy flow and other causal relationships in animals in livestock production systems. It can be seen in the figure that biological processes involved in animal production form a complex network of interactions and that none of the functional outputs can be considered independently from other outputs or the inputs to the system. All the energy directly utilized by the animals in the production process enters the systems in the form of chemical energy obtained from the feed. This energy can then be considered to be partitioned to different outputs, some of which can be seen as useful, i.e. economically valuable products such as meat (containing proteins and lipids), products obtained when the animal is alive (e.g. eggs and milk), manure (used as fertilizer or as fuel) and animal by-products (i.e. parts of the slaughtered animal not used for human consumption). Other outputs can be unwanted and considered as “waste” and include methane (from enteric fermentation) and energy as heat from metabolic processes. These unwanted outputs cannot be ignored when exploring the “causal” relationships between the biological processes of animal production. For example, the metabolic heat production can be seen as construction cost without which the production of useful animal products would not be possible.

Fig. 2
figure 2

A simplified schematic of energy flow and other causal relationships in animals in livestock production systems. Inputs to the system are indicated in italics while potential co-products are in red bold font

Full size image

Furthermore, it should be also noted that feed (as a source of energy) is not the only input that is directly involved in animal production, especially when the LCA modelling framework is considered. Growing the animal especially in indoor conditions requires a considerable amount of other energy inputs, needed for example for heating, ventilation and feeding. Such inputs may have effects on the biological processes of the animal (e.g. regulating environmental conditions through heating/ventilation can affect the animal heat production), but it is quite clear that there is no straightforward method to relate such inputs to the metabolic energy flow/partitioning within the animal.

Figure 3 represents a simplified schematic of the crop production system, including growth of plants, the flow of the energy within the system, its partitioning to various co-products and the complicated interactions between these processes. Unlike in the animal production systems, in crop production all energy involved in biological processes enters the system in the form of solar radiation and is then transferred to chemical energy (sugars) through the process of photosynthesis. The energy is subsequently partitioned to other compounds, including starch, lipids and proteins, which then are used to construct structural organs, which are necessary to support other functions such as formation of reproductive organs and new leaves which are required for photosynthesis. Some of these organs are readily useful for human consumption or animal feed, and some of them can also be considered as raw materials of further refined co-products such as oils and protein meals. Interestingly, the solar energy input is something that is normally not considered in agricultural LCA modelling as an accountable input to the system. Furthermore, other resources considered as inputs in LCA models, such as fossil fuels used in field operations or fertilizers which provide necessary nutrients for the crops, cannot be directly linked to the physical process of energy flow and partitioning within the plants.

Fig. 3
figure 3

A simplified schematic of energy flow and other causal relationships in crop production. Inputs to the system are indicated in italics while potential co-products are in red bold font

Full size image

In general, Figs. 2 and 3 demonstrate the complexity of biological systems, multiple animal- and plant-based co-products originating from the systems and the need for allocation of the environmental burdens between these co-products. Below, we present and discuss some examples of recent attempts to solve these problems through proposed biophysical allocation methodologies specifically developed to address this modelling issue in agricultural systems.

4.1 Example 2—allocation methodologies for co-products from dairy systems

The three outputs to which environmental impacts are generally allocated within allocation frameworks for dairy systems are meat from culled cows, meat from veal calves and milk (Gac et al. 2014). In some countries, manure from dairy systems may also be an output, but this is generally excluded from allocation frameworks for dairy farming systems. Generally, these methodologies are based on defining the feed intake required by animals to produce the respective outputs which are defined as co-products. For example, the International Dairy Federation (IDF) (2010) methodology proposes that the allocation factor between meat and milk is based on the empirical relationship shown in Eq. (1).

$$ \mathrm{A}\mathrm{F} = 1-5.77\mathrm{R} $$
(1)

where AF = allocation fraction for milk and R kg beef/kg milk where kg milk is corrected to 4 % fat and 3.3 % protein.

This empirical equation is used to represent the feed requirement of the animal for the production of milk and meat based on the idea that “feed energy available for growth, for a given feed, is more readily available than that available for milk production”. According to the authors, the allocation methodology represents the “causal connection” between the feed, the major farm input and the products (International Dairy Federation 2010). The authors acknowledge that Eq. (1) is empirical, but justify that it was based on data from a larger trial, which related feed intake to the “net energy content” of the feed and the subsequent production of milk and beef in a causal manner. However, the net energy value of feed is an empirical representation itself of the underlying relationships which govern the energy value of feed for animals (Ferrell and Oltjen 2008) and was developed in order to predict feed intake and animal performance while applying many empirical adjustments for different production stages, genotypes, etc. The principles of the IDF methodology have since been adopted in subsequent LCA studies of dairy systems (Flysjö et al. 2011; Dollé and Gac 2012; Thoma et al. 2013) and is now being recommended in the LEAP guidelines on carbon footprinting in small ruminant systems (FAO 2014c). Thoma et al. (2013) collected data from US farms and concluded that allocation between milk and meat, based on the energy requirement to produce them, was best represented in simplified form as in Eq. (2):

$$ \mathrm{A}\mathrm{F} = 1-4.39\mathrm{R} $$
(2)

where AF = allocation fraction for milk and R = kg beef/kg milk where kg milk is corrected to 4 % fat and 3.3 % protein. It should be noted that, in this proposed framework, leather is not considered as a co-product.

The discrepancy between this equation and the IDF methodology arises from the empirical nature of the underlying equations and concepts being used. Similar differences are seen when applying the methodology of Dollé and Gac (2012) to French dairy systems compared to the IDF methodology, with the former allocating 73 % of impacts to milk production and the latter 82 %. Dollé and Gac (2012) consider that the animal has requirements for five functions—maintenance, activity, growth, gestation and lactation—and use a mix of system separation and allocation based on energy requirement to allocate the environmental impact of animal production between meat, milk and veal calves (Gac et al. 2014). Allocation between milk and meat in dairy systems has also been carried out on the basis of the energy and protein requirement to produce meat and milk respectively (Cederberg and Mattsson 2000; Basset-Mens et al. 2009; O’Brien et al. 2012). However, it is questionable whether “causality” is or can be demonstrated in any of these methodologies (see Fig. 2). For example, it is not possible for milk to be produced without the feed input to raise heifers into adulthood. Furthermore, any maternal growth taking place during lactation would not be possible without the energy and nutrient flow from feed to milk production (Houdijk et al. 2001; Friggens et al. 2004). Therefore, it is not possible to model causality in the system simply by modelling the flow of energy input from the feed to the various functions of the animal as these cannot be varied independently.

4.2 Example 3 manure as a “co-product” in egg production systems

Recent FAO guidelines on the environmental impact modelling in livestock systems specifically advise that manure is considered a co-product in cases where it has economic value (FAO 2014a; FAO 2014c). Here, we examine the example of allocation in an egg production system provided in the LEAP guidelines on poultry systems (FAO 2014a). In this example, the overall environmental impacts were allocated between three co-products: eggs, spent hens for slaughter and manure sold to a nearby power plant to be used as fuel. The burdens of the production system were allocated to these three product streams based on the amount of feed (or feed energy) proposed to be consumed for each stream.

As a starting point, the guidelines use the equation specified by the National Research Council (National Research Council 1994), which was originally developed to predict the metabolizable energy (ME) requirement of laying hens (Eq. (3)).

$$ \mathrm{ME} = {\mathrm{W}}^{0.75}\left(173-1.95\mathrm{T}\right) + 5.5\Delta \mathrm{W} + 2.07\mathrm{E}\mathrm{M} $$
(3)

where W = hen weight (kg), T = temperature (°C), ΔW = body weight change (g/day) and EM = egg mass produced (g/day). Although this equation is purely empirical and aimed to be used for predictive purposes only, the FAO guidelines (FAO 2014a) interpret its three terms to represent the energy partitioning between “maintenance”, growth and egg production respectively and suggest that these indicate the causal relationships to be used in the co-product allocation.

The biophysical allocation based on Eq. (3) considers only two co-products, meat (represented by the “hen weight”) and eggs. In order to consider the third co-product, namely manure, the guidelines (FAO 2014a) break down the maintenance term to different components based on the proposed sources of the heat produced by the animal, and one of these components is then interpreted to represent the biophysical processes behind manure production. In these guidelines, this component is called the “heat increment of maintenance feeding” and is quantified using an empirical equation originally presented by Emmans (1994). This equation is claimed to describe the “utilization of feed energy for the purpose of processing feed into useful nutrients and creating the excreta” and describes the “heat increment of maintenance feeding” as a multiple linear function of three variables, namely faecal organic matter content, urine nitrogen content and methane production. It is likely that these variables were used in the original model by Emmans (1994) in order to have some measurable quantities that can be easily applied to predict the energy use of the animals, so the original idea was not to use them as representation of any “causal” relationships between inputs and outputs. In any case, it is very difficult to see any causality in these variables.

According to the example calculations following the above principles and shown in the FAO guidelines (FAO 2014a), in a standard egg production system, the “heat increment of maintenance feeding” is found to be 9.1 % (25,276 kcalFootnote 1) of the total ME fed in the diet (277,767 kcal). The ME required for growth and egg production is then calculated using the relevant parts of Eq. (3). In the example, total ME required for growth is 17,820 kcal and ME for egg production 48,231 kcal. Finally, the allocation factors were calculated according to the relative size of these three flows of ME (which oddly appears to make up only 32 % of the total ME content in the diet fed according to the numbers provided). In this example, the allocation factors of 52.8, 19.5 and 27.7 % were obtained for eggs, hens (meat) and manure, respectively.

In the FAO guidelines, it is recommended that these allocation factors are used to “assign the whole operation emissions to the three co-products” (FAO 2014a). This last statement seems to be at odds with the principles of biophysical allocation; it is hard to understand why parts of the life cycle inventory (LCI) such as direct energy use on farm should be allocated on the basis of feed energy partitioning by the birds. There would not appear to be any quantifiable biophysical relationship between these two activities (Fig. 2). Furthermore, the FAO methodology demonstrates an odd situation where LCA practitioners are allocating a proportion of the impacts from feed based on the “energy required to produce” manure. However, the report acknowledges that “physiologically speaking … the purpose is to break down the feed ingredients so that they can be absorbed and used by the animal”. An example calculation where a farmer is selling poultry manure for the use as fuel to generate heat or electricity allocates 27.7 % of the burdens of the whole poultry production chain to the manure as a co-product (FAO 2014a). Where manure is not considered to have any economic value, 0 % of any environmental impacts associated with poultry production would be allocated to manure, despite the fact that the flow of physical inputs and outputs to and from the bird remains unchanged. In general, the case of manure as a co-product in animal production systems presented here highlights some major issues for utilising biophysical allocation methodologies in agricultural production systems.

4.3 Example 4—“The construction cost of plants”

Across all LCA studies of livestock systems which are not based solely on grazing, allocation issues arise in compiling an LCI of the feed supply chain, and similar issues are also valid in crop production for human consumption. Recently, a new allocation methodology for co-products from crop production has been proposed, which looks to define the energy involved in the “construction” of different categories of biomass contained within a plant (Van Der Werf and Nguyen 2015). Plant material components are categorised as carbohydrate, protein, lipid, lignin or mineral. The construction cost is then calculated using the following Eqs. (4) and (5),

$$ \mathrm{C}\mathrm{c} = \left(-1.041+5.077*{\mathrm{C}}_{\mathrm{om}}\right)*\left(1-\mathrm{M}\right) + \left(5.325*\mathrm{Norg}\right) $$
(4)

where Cc = the total cost to produce 1 g of plant biomass (g glucose/g dry weight)

Com = the carbon content of the biomass (g/g dry matter)

M = the mineral content of the biomass (g/g dry matter)

Norg = the organic N content of the biomass (g/g dry matter)

and

$$ {\mathrm{C}}_{\mathrm{om}} = 0.44\ *\ \mathrm{carbohydrates} + 0.535\ *\ \mathrm{protein} + 0.774\ *\ \mathrm{lipids} + 0.667\ *\ \mathrm{lignin} $$
(5)

Environmental impacts from the production of crops in the field are then allocated according to the construction costs of the material contained in the outputs from crop processing, such as vegetable oils and protein meals (Van Der Werf and Nguyen 2015).

However, the examples given in the paper ignore large sections of the plant which are not classed as co-products; all other plant materials except the bean, seed or grain are ignored in the methodology (Fig. 3). These appear not to be considered in the methodology on the grounds that they are not economically valuable although this is not explicitly stated. Straw is not mentioned in the presentation of the methodology, but one would have to expect that this methodology would be extremely sensitive to whether straw was considered a co-product of production in the field. If so, a large proportion of the impacts resulting from crop production would be allocated to straw, the construction of which would require a high input of solar energy.

In theory, the approach presented above can be seen to describe the physical energy flow in the crops, i.e. certain amount of absorbed solar radiation is needed to produce a certain amount of glucose, which is subsequently transformed to other compounds such as carbohydrates, lipids and proteins, and in the case of the protein (or organic nitrogen, as expressed in Eq. (4)), a correction is made to represent the higher construction cost of this compound. However, it is not clear how considering only the solar energy input to plant growth can be interpreted to represent all causal input/output relations in crop production. The methodology does not model any interaction with the nutrients (or inputs as fertilizers) available from the soil or the availability of water (and potential irrigation input), both of which are potential limiting factors on crop yields (Gregory et al. 1997). Therefore, a model which could account for these inputs would need to be used in order to develop an allocation methodology which would describe the causal relationship between the actual inputs and outputs of crop production. By definition, any causal methodology would have to consider how changes in these inputs would affect the composition of the whole plant and establish how this would alter the chemical composition of grains, beans or other products. Whether such a model, with a sufficient consistency to be generally used in a variety of LCA studies for crop production, could be ever constructed remains an open question.

5 Discussion and conclusions

There has been an obvious need to develop a consistent co-product allocation method to account for the environmental impact of agricultural products. As discussed above, several biophysical allocation methodologies have been proposed by LCA practitioners. To meet their own objectives, biophysical allocation methodologies must be based on causal relationships within the system established, and in practise, this can be often quantified only through mathematical modelling.

In this paper, we have examined whether researchers have been able to identify underlying physical relationships between the material and energy flows in agricultural systems and their products. The biophysical allocation methodologies detailed above have not adequately explained how the physical parameters chosen in each case represent causal physical mechanisms in these systems. The premise of many recent attempts at biophysical allocation methodologies in agricultural LCA has been to define relationships which describe how inputs to agricultural systems (usually in terms of energy) are partitioned between co-products. However, such models do not necessarily reflect the system behaviour in a mechanistic way. The methodologies discussed above for plant and animal production systems do not deal with causality in the same way as LCA models of industrial processes such as that for the boron production facility in example 1. In addition, the interconnectivity between co-products where one cannot exist without the other is often ignored. Allocation based on either physical causation or an arbitrary choice can be based on a physical parameter. Although the former option can be seen preferable as it is recommended by the ISO standards, it comes with a burden to prove how causation within the system has been modelled (Finnveden et al. 2009).

It can be argued that allocation methodologies which use arbitrary physical properties (without modelling causality) of co-products are less desirable than those using non-physical causal relationships, such as economic value (Ekvall and Finnveden 2001). However, following the argument of Ayer et al. (2007) that “economic allocation was not appropriate for LCA of seafood production, as it did not reflect the biophysical flow of materials and energy between the inputs and outputs of the production system”, many researchers have favoured allocation based on physical properties within the field of agricultural LCA (Van Der Werf and Nguyen 2015). Despite attempts to achieve these methodological requirements, it appears that common physical properties which simply reflect a functional output of co-products have commonly been used and described as biophysical allocation without justification of how they reflect causal relationships within the system modelled, as demonstrated in the examples above.

Outputs from a production process are typically defined as co-products rather than residual or waste if they have economic value (directly or indirectly). This leads to a bizarre situation where LCA practitioners justify the use of allocation methodologies based on physical properties or relationships as preferable to economic allocation on the basis that they are more “scientific”, while still applying economic criteria to determine whether a mass flow is classed as a co-product. Whole sections of the mass balance in a model of an agricultural system are included in or excluded from biophysical allocation systems on the basis of economic value. We see this paradox clearly in example 3 where on the basis of having economic value or not, manure from laying hens can be allocated either 27.7 or 0 % of the impacts of the system. In this sense, the biophysical allocation methodologies for agricultural systems to date do not resolve the problem of mixing socioeconomic causality with physical causality, which has been identified as a significant criticism of allocation based on economic value (Pelletier and Tyedmers 2011). In order to resolve this, allocation methodologies based only on physical relationships in a biological system must adopt a different definition for co-products based on physical properties.

Despite its well-documented disadvantages, a major advantage of economic allocation (which in fact can be considered to be based on non-physical causal relationships) is the ability to apply it with methodological consistency across models of complex systems (Eady et al. 2012). As co-products are still defined as such based on their economic value, alternative allocation methodologies may include or exclude outputs from an agricultural system which are identical in the physical sense. Due to the complex nature of the mechanisms which underpin agricultural systems and high levels of interconnectivity between their outputs, it is unlikely that modellers will be able to consistently apply the principles of “underlying physical relationships” in allocation across agricultural LCA models. Researchers should acknowledge that in many cases the choice of allocation methodology is essentially arbitrary and present this openly in cases where systems are too complex to model causal mechanisms adequately.