Abstract
Purpose
The environmental performance of products or services is often a result of a number of key decisions that shape their life cycles (e.g., techology choices). This paper introduces a modular LCA approach that is capable of reducing the effort involved in performing scenario analyses and optimization when several key choices along a product’s value chain lead to many alternative life cycles.
Methods
The main idea is that the value chain of a product can be divided into interconnected but exchangeable modules, which together represent a full life cycle. A module is comprised of unit processes from the practitioner’s LCI database. The inputs, outputs, and system boundaries of each module can be tailored to the context of the studied system. Alternatives arise whenever multiple modules produce substitutable products. Unlike in conventional LCI databases, no copies are necessary to represent the same process with different inputs. A module-product matrix is used to store this information. It can be used as a basis for an automated scenario analysis of all alternatives or as an input to an optimization model.
Results and discussion
Our approach is illustrated in two case studies: (1) Passenger car fuel choices are modeled by 15 modules representing 33 alternative value chains for diesel, petrol, natural gas and electric cars. The automated comparison of LCA results indicates that electric mobility is often the preferable option from a climate perspective, but impacts depend strongly on the electricity source. (2) A dynamic optimization model including stocks is built from eight modules to analyze the optimal use of wood for material and energy applications. Results indicate that although direct substitution benefits are higher for energy applications, cascading use of wood can maximize environmental performance over the entire life cycle.
Conclusions
The modular LCA approach permits an efficient modeling and comparison of alternative product life cycles, enabling practitioners to focus on key decisions. It can be applied to exploit a potential that is hidden in LCI databases, which is that they contain many specific inventories but not all useful combinations in the context of scenario analyses. The user-defined level of abstraction that is introduced through modules can be helpful in the communication of LCA results. The modular approach also facilitates the integration of LCA and optimization as well as other industrial ecology methods. An open source software is provided to enable others to apply and further develop our implementation of a modular LCA approach.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The application of life cycle assessment (LCA) ranges from accounting-type studies (e.g., environmental product declarations) to explorative studies that assess different options to improve production processes or product value chains. A typical characteristic of explorative LCA studies is that technology choices may arise in several places along a life cycle, resulting in a considerable number of alternative value chains. For example, if the interest of a study is to analyze the options for generating heat from biomass, these choices may include the biomass source (A), the transport of the biomass (B), different storage options (C), alternative furnaces (D), or heat distribution systems (E) (Fig. 1). The resulting number of alternative value chains can be calculated by multiplying the number of alternatives at each life cycle stage. It can be considerably higher than the number of processes in the system. For example, if A = 2, B = 3, C = 2, D = 4, and E = 3, the number of alternative value chains to produce heat is 144, whereas 14 activities are in principle sufficient to describe this system.
a Compact representation of 144 alternatives to produce “heat, at consumer” through 14 processes and 5 products where processes and products are truly distinguished and substitutable products allowed. b In LCI databases, each process input must come from a specific upstream process. Therefore, 212 copies of the processes in a, but with different inputs, would be required to represent all alternatives
Although LCA practitioners often face situations similar to this example, it is usually quite cumbersome to model all the alternatives present in such systems using standard LCA software. A main reason for this is that the mathematical structure that is generally used to represent the supply chains described in LCI databases is not well designed for extensive scenario analyses. It relies on a process-process linking, as each process input along the supply chain of a product must come from a clearly defined upstream process in order to perform LCA calculations (Heijungs and Suh 2002; Suh and Huppes 2005). This mathematical structure (often referred to as the technology matrix) requires process copies to represent the same process with inputs from different upstream suppliers, as shown in Fig. 1b. In situations where choices between substitutable products accumulate over several steps along a value chain, the number of processes that are required to represent this grows exponentially. This means that to describe all 144 alternatives in Fig. 1a, a total of 212 processes would be necessary (Fig. 1b).Footnote 1
Instead of modeling all alternatives within an LCI database, it is, in this case, probably more efficient to first calculate the LCA results of the individual life cycle stages, and then the corresponding sums for each alternative value chain. Such modular LCA approaches have been applied previously, e.g., to the modeling of food supply chains (Jungbluth et al. 2000) and in the context of type III environmental labeling (ISO 2006a, b) and environmental product declarations (EPD) (Buxmann et al. 2009; Rebitzer 2005). Modules describe gate-to-gate processes or life cycle stages, which can be modeled by unit processes. However, their system boundaries are usually larger than that of a single unit process due to energy generation, production of ancillaries, as well as recycling and waste-management processes that are linked to a certain life cycle stage (Rebitzer 2005). Strategic choices regarding the system boundaries of the modules can thereby lead to a simplified life cycle representation reflecting the decision factors (key choices) that are relevant to a given actor, e.g., a company or a policy maker (Buxmann et al. 2009). However, the possibilities for modeling alternative value chains based on combinations of interchangeable modules are currently rather limited in existing LCA software. Therefore, practitioners regularly model such systems manually (i.e., copying and reconnecting inventories) or switch to other modeling environments, if the number of alternatives is larger. Both approaches are associated with considerable extra work, which highlights the need for more streamlined scenario assessments tools.
A different, but complementary, approach is to treat the underdetermined system described in Fig. 1a as an optimization problem with the objective to minimize its environmental impacts. A benefit of using optimization techniques is the possibility of considering additional constraints, such as limited raw material supplies or production capacities. LCA and linear programming have been combined since the 1990s (Azapagic and Clift 1998) for applications ranging from process design (Gassner and Maréchal 2009; Guillén-Gosálbez et al. 2007) to regional resource management (Saner et al. 2014; Vadenbo et al. 2014) and the optimization of large-scale systems (You et al. 2012). A potential advantage of using optimization approaches is also that solutions have been proposed regarding typical LCA problems, e.g., multiple objectives (Azapagic and Clift 1999; Guillén-Gosálbez 2011; Tan et al. 2008) and uncertainties (Guillén-Gosálbez and Grossmann 2010; Tan 2008), leading possibly to more robust results than standard LCA.
In this paper, we present a tool to model and analyze scenarios for key choices along product value chains based on a modular LCA approach (case study transportation). Further, building upon work by Saner et al. (2014), we show how modules can be used as a direct input to an optimization problem (case study wood). In addition, a tool that enables the creation and linking of modules as well as automated scenario analyses is provided as free open source software (Steubing 2014).
2 Methods
2.1 General approach
As described in the introduction, the fundamental idea is to use interconnected, but exchangeable, modules to model the life cycle of products. Modules can be understood as user-defined life cycle stages with product inputs and outputs. Several modules can be linked based on their inputs and outputs to complete value chains. Alternative value chains arise whenever several modules produce the same, substitutable product. Each module is described by unit processes from an LCI database. These unit processes can be both processes modeled by the practitioner as well as processes that come with background LCI databases, such as ecoinvent (Ecoinvent 2015). As unit processes usually have inputs from other unit processes, the supply chain of a module can be as complex as the supply chain of any other unit process in an LCI database. However, user-defined cutoffs may need to be introduced to specify the upstream system boundaries of modules in order to avoid overlaps and double counting. When modules are linked, several partial value chains are combined to represent the full life cycle of a product.
For example, the module “natural gas production, region 1” produces natural gas and is described in the LCI database by the process “natural gas, high pressure, at consumer [CH],” as shown in Fig. 2 (step 1). The entire supply chain of this process is included, which means that the module relates to the life cycle of “natural gas, high pressure, at consumer [CH]” as modeled in ecoinvent. The downstream module “transport, natural gas car” produces transport and consumes natural gas for this. Based on their common input/output, these two modules can be linked to form a value chain for transport. However, the module “transport, natural gas car” links to the ecoinvent inventory “transport, passenger car, natural gas,” which includes by default in its supply chain the production of natural gas. In order to avoid a double counting when combining the two modules into a value chain, a cutoff is introduced in the module “transport, natural gas car.”
Description of our modular LCA approach: (1) modules describe user-defined life cycle stages based on unit processes from an LCI database (ecoinvent). Cutoffs define upstream boundaries and avoid double counting. All other upstream inputs are by default included (gray dashed lines). (2) Modules are linked based on product inputs and outputs, which can be represented as a graph or matrix. The linked modules represent alternative value chains for which LCA results can be calculated (3a) and/or which can be used within an optimization problem (3b)
The linking of modules is based on product inputs and outputs. This can be described by a (possibly non-square) matrix, which we call module-product matrix (see Fig. 2, step 2). It is different from the (square) technology matrix of LCI databases, which describes the linking of processes, in the sense that it truly distinguishes between modules (processes) and products and allows the same, substitutable, product to be the input or output of several modules. The drawback and reason why such matrices are not used in LCI databases is that they describe possible alternatives instead of predetermined value chains, which prohibits traditional approaches to solve the inventory problem and perform LCA calculations (Heijungs and Suh 2002; Suh and Huppes 2005).
Figure 2 (step 2) shows all the alternatives when connecting the modules. It includes two technology choices, with two alternatives each, resulting in a total of four different value chains for transport: the choice of natural gas from region 1 or region 2, and the choice of a combustion engine car versus an electric vehicle. The corresponding module-product matrix is non-square, as it includes alternative suppliers for the substitutable products natural gas and transport.
In order to model and compare alternative value chains, the main work of the practitioner consists of defining suitable modules and their inputs and outputs (step 1), which depends on the study context. Steps (2) and (3a), the linking of modules and LCA calculations, can be performed by software for all alternative value chains (provided that each module produces one output only, see 0). In addition, the system of linked modules can be directly integrated into an optimization model step (3b) (see 0). All steps in Fig. 2, except for 3b, are supported in our open source modeling environment (Steubing 2014).
2.2 The link between modules and the LCI database
If the supply chain of a module consists of unit processes from an LCI database, it can be specified by a final demand vector f. The latter determines the scaling vector s for a given technology matrix A, as in Eq. (1). The scaling vector describes the necessary activity level for each process in the supply chain to meet the final demand and is the basis for further LCA calculations (see Heijungs and Suh (2002) for a comprehensive introduction to matrix-based LCA).
For example, the technology matrix A in Table 1 describes the inputs and outputs of the four processes shown in Fig. 2 for the module “transport, natural gas car” (data from ecoinvent v2.2, which includes 4087 interlinked processes; all other processes are excluded here for simplicity). The module refers to the supply chain for “transport, passenger car, natural gas [CH],” which is expressed by the demand vector f 1 . As all processes are scaled to an output of one (diagonal values), the scaling vector s 1 informs us directly about the upstream inputs (see also Fig. 2): For example, we need 1.89 MJ of “natural gas, high pressure, at consumer [CH]” to produce one person-kilometer of transport (0.63 × 0.064 × 46.9 = 1.89). However, with this demand vector, the module includes the production of natural gas. In order to define the desired upstream system boundary and avoid double counting, a cutoff needs to be implemented.
2.3 Cutoff implementation
To cutoff the production of natural gas and make the module represent a life cycle stage (as opposed to a full life cycle), the amount of natural gas that is required for one person-kilometer of transport is subtracted from the demand vector f 2 as in Table 1. As a result, the scaling factor of the process “natural gas, high pressure, at consumer [CH]” becomes zero, which corresponds to a cutoff. In order to assure that the necessary input of natural gas is delivered by another module, it is stored in the module-product matrix (see Fig. 2).
2.4 LCA of a module
The environmental impacts related to a module can be calculated as shown in Eq. (2), where h is the environmental impact score of a module, B is the biosphere matrix containing environmental interventions (e.g., emissions), and Q is the characterization matrix that specifies the environmental impact per environmental intervention, see also Heijungs and Suh (2002).
2.5 Comparing alternative value chains
The module-product matrix in Fig. 2 describes alternative value chains whenever it contains several modules that produce substitutable products. While this is an efficient representation of alternatives, it does not allow regular LCA calculations directly, as suppliers cannot be uniquely identified (e.g., in Fig. 2, it would be unclear whether natural gas would be delivered from region 1 or region 2). Therefore, an intermediate step is required: For each alternative value chain contained in the module-product matrix, a smaller, square matrix needs to be constructed that uniquely links modules (as in conventional LCI databases). Based on this, LCA results can be calculated and compared for each alternative value chain.
2.5.1 Determining all alternatives
As shown in Fig. 2, the module-product matrix has a graph representation that distinguishes two types of nodes: modules and products. A recursive depth-first graph traversal algorithm is used to determine all possible value chain combinations contained in a module-product matrix. Its general logic is as follows: starting at the demanded product, the algorithm goes back through the value chains defined in the graph. When a product has multiple upstream producers, each of them will be considered in an alternative value chain. In contrast, when a module has several product inputs, all of them must be delivered simultaneously. The algorithm and a figure describing this logic are provided in the Electronic Supplementary Material.
2.5.2 LCA calculations
For each alternative value chain, the module-product matrix is reduced to a smaller matrix that contains only those modules and products present in the alternative value chain. The result is a square module-product matrix where each module produces a unique product. The scaling vector for each module-product matrix can therefore be determined as in Eq. (3) (like in a regular LCI database). In the example of Fig. 2, if the value chain consists of the modules “NG production, region 1” and “transport, natural gas car,” the module-product matrix A′ represents itself as in Table 2. The module “NG production, region 1” produces one MJ of natural gas and does not have an input from the module-product matrix. The module “transport, natural gas car” produces one person-kilometer of transport and uses 1.89 U of natural gas for this. This is reflected in the scaling vector s′ for a demand f′ of one person-kilometer transport.
In order to do LCA calculations, we need to translate the demand f′ from the system of linked modules to a scaling vector s of the technology matrix. The demand vectors f that correspond to the individual modules can be summarized in a demand matrix F, which has one column for each module and as many rows as there are processes in the LCI database. Assuming that the order of columns and rows in F corresponds to the columns in A′ and A, respectively, the translation of a product demand from the module-product matrix to a scaling vector for the LCI database can be realized as in Eq. (4).
There is also a faster way to perform LCA calculations for many alternatives: It consists of first calculating the LCA results for each module and then summing these up based on the scaling factors provided in s′. In this case, the number of required LCA calculations scales with the number of modules instead of the number of alternative value chains.
2.6 Multifunctional modules
Some processes produce several products, such as refineries or combined heat and power plants. The integration of multifunctional processes in LCI databases may result in non-square, overdetermined technology matrices, for which traditional methods fail to solve the inventory problem (Heijungs and Suh 2002). This problem is conventionally solved by system expansion or allocation (ISO 2006a, b). Both approaches lead to square technology matrices where each coproduct can be demanded independently. While these approaches could also be applied to multifunctional modules and the module-product matrix, it may, in some cases, be preferable to model multifunctional processes as they are in reality, i.e., considering their entire impacts, as well as the ratios of coproducts. For example, when designing chemical plants or energy systems, it is important to consider the integration of coproducts to avoid suboptimal outcomes.
Multifunctional modules can be based on multioutput processes from unallocated versions of LCI databases. If such inventories are unavailable, multifunctional modules can be designed by combining allocated processes to resemble the original multifunctional process. Suppose that we have a technology matrix A that contains two allocated processes that deliver heat and electricity from a joint production, as in Eq. (5). Let us further assume that for every unit of energy input, 50 % is converted to useful heat and 20 % to electricity. By specifying a demand vector f for heat and electricity in the same ratio as in the original process, we can reproduce the inventory of the original process before allocation. At the same time, the products can be distinguished within the module-product matrix. Any demand of electricity from this module will then automatically result in a coproduction of heat and vice versa. Mathematically speaking, valid solutions for the scaling vector s′, expressed as A′s′ = f′, are now limited to linear combinations of the outputs of the module, e.g., 1 unit of heat and 0.4 units of electricity. Also, A′ is now non-square and Eqs. (3) to (4) cannot be applied anymore. The use of multifunctional modules represents thus a trade-off: While additional information can be included to represent a system more realistically, other methods are required to identify feasible operating conditions for these systems. A method that is well suited to solve systems with such constraints is linear programming (Heijungs and Suh 2002).
2.7 Using linked modules in optimization problems
LCA calculations for alternative value chains can be done efficiently as described above, as long as the described system does not include multioutput processes. If it does, or if other constraints shall be considered, a frequently used method to identify optimal solutions is to describe the system as an optimization problem. While optimization problems can be very sophisticated, our intention here is to show how modules can be used as an input to an optimization problem in a straightforward way. Several authors have shown that a basic formulation of an LCA-based optimization problem may look like the following (Azapagic and Clift 1998; Heijungs and Suh 2002; Saner et al. 2014; Tan et al. 2008):
Subject to
Equation (6), where B and Q are matrices for environmental interventions and their characterization, respectively, formulates the goal of the optimization—to minimize environmental impacts—and thereby provides a metric for choosing between alternatives. Eq. (7) determines the constraints of the system. It differs from matrix-based LCA by requiring the system’s output to be greater or equal than the final product demand f. This means that the solution may include product surpluses in cases where multioutput activities do not generate outputs in exactly the necessary ratios to satisfy the final demand. The decision variable in this context is the scaling vector s, which represents the use of technologies. An algorithm, such as the simplex algorithm, is usually applied to solve the optimization problem and identify the set of technologies that satisfy the product demand with minimal environmental impacts.
In the case of modules, it is theoretically possible to replace s in Eq. (7) by Eq. (4) to include both the module-product and the technology matrix in the optimization problem. However, there is no direct benefit in this, as the LCI database normally does not contain any decision variables. Instead, we suggest to pre-calculate the environmental impacts h m for each module using Eq. (2). The optimization problem can then be formulated as in Eqs. (8) and (9), where the total environmental impacts h are the sum of the impacts of each module h m multiplied by the process-specific scaling factor s′ m , which is the decision variable.
Subject to
While this is the basic optimization model for modules, case-specific constraints may need to be added. An application of this model with additional constraints to a case study of the optimal use of wood is described in 3.2.
3 Application in case studies
3.1 Comparison of alternative scenarios for passenger car transport
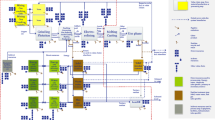
In order to illustrate some of the advantages of using modules, a strategic case study was developed around the topic of individual mobility by extending the example in Fig. 2. As shown in Fig. 3, transportation, the functional unit of the system, can be provided by means of conventional combustion engines (diesel, petrol, and natural gas) as well as by electric cars. Crude oil and natural gas have been considered as energy carriers, which can be converted either to transportation fuels or to electricity. Electricity can be generated with two different technologies for each energy carrier (for electricity from oil ecoinvent 2.2 distinguishes country averages; for electricity from natural gas, an average and a state-of-the art natural gas combined cycle power plant are used). Additionally, we assume that the import source of the energy carriers can be influenced and for each imports from three different producing countries are included. Figure 3 shows the product inputs and outputs for each module and the resulting system (details for each module are provided in the Electronic Supplementary Material).
The system contains 15 modules and 4 products. A total number of 33 alternative scenarios can be calculated automatically, as shown in Fig. 4. While no inventories have been specifically adapted for this illustration, this comparison based on ecoinvent 2.2 data shows that there are considerable differences regarding the climate impact of these transportation systems. As we distinguish products and modules, impact contributions along the value chain of each alternative can be expressed according to either one (Fig. 4).
LCA performance of all alternative value chains that deliver one person-kilometer of transport as described by the system of linked modules in Fig. 3
It can be observed that electric cars tend to perform better in this illustrative case study than cars with combustion engines. While the smaller electric city car performs better than the larger electric car, another important influence is the source of electricity, which can also lead to higher GHG emissions than combustion engines. In the case of combustion engines, diesel cars outperform petrol and natural gas cars. For the natural gas car, the source of natural gas plays an important role, due to differences in transportation distance and methane leakage.
Combustion engine-driven cars emit GHG emissions mainly at the transportation stage, while the main source of GHGs for electric cars is at the electricity generation stage. The observed GHG emissions at the transportation stage for electric cars arise from the fact that this stage also includes the road infrastructure and maintenance. While this could easily have been excluded or modeled as a “road” input, we leave it here at this to remind the reader that the definition of what a module comprises and how its products are called is case-specific and up to the practitioner.
3.2 Optimal use of wood in a cascading system
3.2.1 Model description
In order to illustrate how modules (including multioutput ones) can be used within an optimization problem, we devised a linear programming case study around the use of forest wood for material and energy applications. The central question raised is whether it is environmentally beneficial to use wood in cascades, i.e., first for a material applications and then for energy. As the case study is of illustrative nature, we limit the discussion to GHG emissions, although other impact categories could be assessed with the same model.
In an attempt to capture the most important processes, the wood value chain was simplified to include the following modules (Fig. 5): The process “wood harvest” describes everything from tree planting, forest maintenance and harvest to the production of round wood. Round wood can be further processed in a “sawmill” to timber. Timber can be used to construct “wood buildings.” The modules “wood harvest,” “sawmill,” and “wood building” are modeled as multioutput modules as each of them also produces residual wood (forest and sawmill residues as well as residual wood from the wood building at its end-of-life). The process “chipping, residual wood” can produce wood chips from residual wood, which can be used in a “wood chips heating” to produce heat. Alternatively, wood chips can be produced directly from round wood, i.e., without a previous material use, by the process “chipping, round wood.” Inventories for the modules are based on ecoinvent 2.2, except for the wood and concrete buildings, which are based on Gustavsson et al. (2006) (details are provided in the Electronic Supplementary Material).
We assume that the demand from this system is 2 buildings and 20 TJ heat, which represent, respectively, material and energy applications of wood. A supply constraint applies for the harvest of forest wood, which is assumed to be limited to 1000 m3 (as round wood and residual wood are coproduced at a ratio of 0.65 to 0.35, respectively, their supplies are limited to 650 and 350 m3). Due to this constraint, wood alone is insufficient to meet the product demand. To provide conventional alternatives, the processes “concrete building” and “fuel oil heating” are included.
We also extend the optimization model with time periods and two types of stocks: one for harvestable wood in the forest and one for timber in buildings. The harvestable wood stock increases each period by 1000 m3, and we assume that wood left in the forest can be harvested in later periods without losses. Timber in buildings on the other hand has a discrete lifespan: once the building is demolished, it becomes residual wood. For the sake of simplicity, our model includes two time periods of the length of a building lifespan (e.g., 60 years). After each period, all of the previously stored timber becomes residual wood and is burned to produce energy.
The model objective is to minimize the environmental impacts h, which are the sum of the impacts of the individual modules times their use over all time periods (10) (see Table 3 for nomenclature). The constraints are the following: The demand (D) needs to be satisfied by the product flows during each time period (11). The product flows (PF) are the result of the scaling of the modules in the system and the flows to and from stocks (ST) (12). Note that due to the introduction of stocks, the product flows may temporally differ from the flows as prescribed by the modules. Product lifetimes (L) are specified for each module in a matrix. The values of L are used in Eq. (13) to add or remove products from the stock, depending on the current and previous use of processes where storage occurs. In this case study, only wood in buildings is added to the stock and removed one period later. Finally, the harvestable wood stock (hws) is modeled as the difference of previously available and newly added harvestable wood (hw, 1000 m3 per period) and its use in the process “wood harvest” as described by Eq. (14). Neither the scaling factors of modules nor the amount of products stored can become negative in reality, which is expressed by Eq. (15). The model was solved using the GAMS software (GAMS 2013).
Subject to
3.2.2 Results
As shown in Fig. 5, the building and heating demand can only partly be satisfied by wood. The remainder is delivered by means of conventional technologies. The model was set up like this to reflect the fact that wood is a scarce resource in many countries. As wood cannot fully supply the product demand, the optimization model uses it for those applications with the highest environmental leverage. As a result, round wood is used entirely for material applications in period 1, whereas it is used entirely for direct energy purposes in period 2. The reason for this behavior is that the substitution of fuel oil for heating yields a higher benefit per unit wood used than the use of wood in buildings. The reason why round wood is used in a material way despite lower direct benefits is the fact that the end-of-life residual wood from buildings can be reused energetically in period 2. Since there are only two periods, round wood in period 2 is directly used for energy.
4 Discussion
4.1 Modular LCA approach
4.1.1 Areas of application
Modules, as described in this paper, can serve different purposes in different types of LCA studies (Fig. 6). An immediate benefit is a simplified representation of product value chains according to the system boundaries of the modules, which may reflect those aspects that are relevant to a specific actor. This may help practitioners to effectively analyze the implications of key choices and communicate LCA results. In contrast to system processes, where the whole supply chain is aggregated into a single inventory, modules do not prohibit contribution analyses from underlying unit processes.
In the context of explorative studies, the modular LCA approach offers a powerful tool to model and compare alternative value chains, possibly reducing the necessary time investment (see also 4.1.1.). A key element is the module-product matrix that links modules based on product inputs and outputs. It is a compact representation of alternative value chains, without the need for additional copies of datasets for alternative suppliers as in conventional LCI databases. However, it relies on the assumption that products from alternative suppliers are in fact substitutable. It is the responsibility of the practitioner to check whether this can be justified in a given context. As modules are most likely tailored to a specific context, a drawback is that they may not be reusable in a different context.
Modules can also be used in optimization models. This provides the possibility to add aspects that are not included in a standard LCA, such as multifunctional modules or constraints. Further, the temporal dimension (Beloin-Saint-Pierre et al. 2014; Finnveden et al. 2009; Levasseur et al. 2010) and the change of material stocks are important parameters that are generally not considered in LCA studies (Cherubini et al. 2011; Levasseur et al. 2012; Pauliuk and Müller 2014). The case study illustrates that six equations are sufficient to formulate an optimization problem that extends the LCA model with a simple temporal dimension, stocks, and supply and demand constraints. The use of modules could therefore potentially facilitate the combination of LCA with other industrial ecology methods such as material flow analysis (MFA). Modules could also be used in combination with input-output analysis (IOA) to describe the environmental impacts related to economic sectors with consistent system boundaries (i.e., cutoffs).
4.1.2 Unlocking the hidden potential of LCI databases
While LCI databases contain many specific inventories, they are designed to describe average value chains as opposed to all possible alternatives. For example, ecoinvent version 3 (Ecoinvent 2015) contains different inventories for the generation of electricity, depending on the energy source, but then combines all producers of electricity in a geographical region into a market to represent a production volume weighted average electricity mix (Treyer and Bauer 2014; Weidema et al. 2013). Downstream consumers are by default linked to the market mix, while direct links to specific electricity producers are the exception. Therefore, many alternative value chains—for which inventories exist—are not readily available to the practitioner. The transportation case study is a good example showing how modules can help to unlock the additional potential of inventories that are contained in LCI databases. Naturally, it is the responsibility of the practitioner to combine inventories in a meaningful way. Version 3 of ecoinvent has made an interesting development supporting this by formally distinguishing between processes and products. As a result, the same product (e.g., “electricity, high voltage”) may now be produced by several activities. This facilitates the search for alternative producers of substitutable products and, therefore, the design of modules.
4.1.3 Do practitioners gain time?
LCA studies are usually done under time constraints. Using modules to perform, e.g., scenario analyses, is associated with an up-front time investment. From our experience, much of it is related to developing a better system understanding, which enables the definition of suitable system boundaries to capture the key choices in modules. At the same time, modeling alternatives in conventional LCA software may be equally time-consuming or even limiting, e.g., if 212 processes need to be modeled like in the example of Fig. 1. A further consideration is that error corrections or sensitivity analyses can be realized much quicker in a small number of modules than with many processes. A clear advantage of the modular approach is also that the LCA calculation time scales with the number of modules and not with the number of alternatives (i.e., using the example of the introduction, 14 calculations instead of 144). As LCA is usually an iterative procedure, this can be relevant. Nevertheless, whether practitioners save time by applying the modular approach depends on the complexity of the system, the practitioner’s knowledge and modeling skills, and the LCA software itself.
4.1.4 Software implementation
In order to perform the individual modeling steps, we have developed the Activity Browser (Steubing 2014), which is an open source LCA software with a graphical user interface that builds upon the brightway2 LCA framework (Mutel 2015). The source code and documentation are provided online for the LCA community to apply and further develop the presented approach or to include it in other LCA software.
4.2 Case studies
Two case studies illustrate the application of the module framework for modeling and comparing alternatives as well as for extending an LCA problem to include constraints, a temporal dimension, and stocks. While they are mainly of illustrative nature, they are based on inventories from the ecoinvent database, which are regularly used as a reference within the LCA community and beyond. The comparison of 33 passenger car transportation alternatives showed that electric cars could significantly reduce GHG emissions compared to cars using conventional fuels. However, the size of the car, the battery, and the electricity source have substantial influence on environmental performance and may also make electric cars perform worse than conventional ones.
Regarding the optimal use of wood, we show that using wood in a use cascade, i.e., first for material and then for energy applications, may be advantageous for mitigating climate change. However, the potentially significant time gap between the material and the energy use (as much as a building’s life time) adds ambiguity to this conclusion as it is difficult to predict what will be the alternative (substitution) to wood energy in the future (Gärtner et al. 2013). Further, the assumption that wood substitutes other material or energy sources needs to be carefully examined (Gustavsson and Sathre 2011). These and other factors, such as the relation between product design, recycling efficiencies, and end-of-life energy substitution (Höglmeier et al. 2015), should be further investigated to better understand the conditions for an environmentally beneficial cascading of wood.
5 Conclusions
A modular LCA approach is presented with the potential to considerably reduce the effort involved in comparing alternative products life cycles, especially in situations, where numerous alternatives along the value chain lead to many possible scenarios. The fundamental idea is to represent the individual life cycle stages and their alternatives through modules and then recombine these into alternative value chains. While modules link to processes in LCI databases, their interdependencies and the way they can be combined are described in a separate module-product matrix. The latter describes the product inputs and outputs of each module, which are customized to a specific context by the practitioner. Alternatives arise whenever several modules produce substitutable products. Unlike in conventional LCI databases, no copies are necessary to represent the same process with different inputs. Further, the modular LCA approach can be used to exploit the hidden potential of LCI databases, which provide many specific inventories, but not all useful combinations in the context of scenario analyses, as illustrated by the transportation case study.
The modular approach can also serve other purposes, such as yielding a simplified the representation of a life cycle for communication purposes. The use of modules to formulate an optimization model enables the consideration of constraints and acts as a potential bridge to other industrial ecology methods, such as MFA and IOA.
The creation of modules and an automated scenario analysis are supported within an open source LCA software. However, the approach is generic and could be implemented in other software as well.
Notes
Technically, it is sufficient that LCI databases record the product inputs of processes, instead of specific suppliers (ISO 14048 2002). Therefore, systems as in Fig. 1a can be described in an LCI database. However, an additional step, involving possibly additional information and linking rules, is necessary to link the process inventories to uniquely determined supply chains and perform LCA calculations. Ecoinvent, for example, exploits this as of version 3 to produce different database versions (termed “system models”) for attributional and consequential LCA from a common, underlying LCI database. In practice, LCA software providers and practitioners have mainly worked with these process-linked LCI database versions. Due to their mathematical structure, separate processes are necessary to represent the same process with different product suppliers. In the following, the term “LCI database” is used as a synonym for process-linked versions of LCI databases.
References
Azapagic A, Clift R (1998) Linear programming as a tool in life cycle assessment. Int J Life Cycle Assess 3:305–316
Azapagic A, Clift R (1999) Life cycle assessment and multiobjective optimisation. J Clean Prod 7:135–143
Beloin-Saint-Pierre D, Heijungs R, Blanc I (2014) The ESPA (Enhanced Structural Path Analysis) method: a solution to an implementation challenge for dynamic life cycle assessment studies. Int J Liffe Cycle Assess 19:861–871
Buxmann K, Kistler P, Rebitzer G (2009) Independent information modules-a powerful approach for life cycle management. Int J Life Cycle Assess 14:S92–S100
Cherubini F, Peters GP, Berntsen T, Strømman AH, Hertwich E (2011) CO 2 emissions from biomass combustion for bioenergy: atmospheric decay and contribution to global warming. GCB Bioenergy 3:413–426
Ecoinvent (2015) The ecoinvent LCA database, http://www.ecoinvent.ch/
Finnveden G, Hauschild MZ, Ekvall T, Guinée JB, Heijungs R, Hellweg S, Koehler A, Pennington D, Suh S (2009) Recent developments in Life Cycle Assessment. J Environ Manage 91:1–21
GAMS (2013) GAMS Development Corporation. General Algebraic Modeling System (GAMS) Release 24.2.1., Washington, DC, USA, http://www.gams.com/
Gärtner S, Hienz G, Keller H, Müller-Lindenlauf M (2013) Gesamtökologische Bewertung der Kaskadennutzung von Holz – Umweltauswirkungen stofflicher und energetischer Holznutzungssysteme im Vergleich. Institut für Energie- und Umweltforschung (IFEU), Heidelberg, Germany
Gassner M, Maréchal F (2009) Methodology for the optimal thermo-economic, multi-objective design of thermochemical fuel production from biomass. Comput Chem Eng 33:769–781
Guillén-Gosálbez G (2011) A novel MILP-based objective reduction method for multi-objective optimization: application to environmental problems. Comput Chem Eng 1469–1477
Guillén-Gosálbez G, Grossmann I (2010) A global optimization strategy for the environmentally conscious design of chemical supply chains under uncertainty in the damage assessment model. Comput Chem Eng 42–58
Guillén-Gosálbez G, Caballero JA, Esteller LJ, Gadalla M (2007) Application of life cycle assessment to the structural optimization of process flowsheets. In: Serban AP (ed) Valentin P. Elsevier, Computer Aided Chemical Engineering, pp 1163–1168
Gustavsson L, Sathre R (2011) Energy and CO2 analysis of wood substitution in construction. Climatic Change 129–153
Gustavsson L, Pingoud K, Sathre R (2006) Carbon dioxide balance of wood substitution: comparing concrete- and wood-framed buildings. Mitig Adapt Strateg Glob Chang. 667–691
Heijungs R, Suh S (2002) The computational structure of life cycle assessment. Kluwer, Dordrecht, The Netherlands
Höglmeier K, Steubing B, Weber-Blaschke G, Richter K (2015) LCA-based optimization of wood utilization under special consideration of a cascading use of wood. J Environ Manage:158–170.
ISO (2006a) ISO 14040. Environmental management - Life cycle assessment - Principles and framework. International Standardization Organization, Geneva, Switzerland, pp 28
ISO (2006b) ISO 14025. Environmental labels and declarations - type III environmental declarations - Principles and procedures. ISO/TC 207/SC3. International Organization for Standardization, Brussels
ISO 14048 (2002) Environmental management — Life cycle assessment — Data documentation format. International Organization for Standardization (ISO), Geneva
Jungbluth N, Tietje O, Scholz RW (2000) Food purchases: impacts from the consumers’ point of view investigated with a modular LCA. Int J LCA 134–142
Levasseur A, Lesage P, Margni M, Deschěnes L, Samson R (2010) Considering time in LCA: dynamic LCA and its application to global warming impact assessments. Environ Sci Technol 3169–3174
Levasseur A, Lesage P, Margni M, Brandão M, Samson R (2012) Assessing temporary carbon sequestration and storage projects through land use, land-use change and forestry: comparison of dynamic life cycle assessment with ton-year approaches. Climatic Change 759–776
Mutel C (2015) A new open source framework for advanced life cycle assessment calculations., http://brightwaylca.org/
Pauliuk S, Müller DB (2014) The role of in-use stocks in the social metabolism and in climate change mitigation. Glob Environ Chang 132–142. doi:10.1016/j.gloenvcha.2013.11.006
Rebitzer G (2005) Enhancing the application efficiency of life cycle assessment for industrial uses. Int J LCA: 446. doi: 10.1065/lca2005.11.005
Saner D, Vadenbo C, Steubing B, Hellweg S (2014) Regionalized LCA-based optimization of building energy supply: method and case study for a swiss municipality. Environ Sci Technol 7651–7659
Steubing B (2014) Activity Browser - A free and extendable LCA software., https://bitbucket.org/bsteubing/activity-browser
Suh S, Huppes G (2005) Methods for life cycle inventory of a product. J Clean Prod 687–697
Tan RR (2008) Using fuzzy numbers to propagate uncertainty in matrix-based LCI. Int J LCA 585–592
Tan RR, Culaba AB, Aviso KB (2008) A fuzzy linear programming extension of the general matrix-based life cycle model. J Clean Prod. 1358–1367
Treyer K, Bauer C (2014) Life cycle inventories of electricity generation and power supply in version 3 of the ecoinvent database-part II: electricity markets. Int J LCA 1–14
Vadenbo C, Hellweg S, Guillén-Gosálbez G (2014) Multi-objective optimization of waste and resource management in industrial networks - Part I: model description. Resour Conserv Recy 52–63
Weidema B, Bauer C, Hischier R, Mutel CL, Nemecek T, Reinhard J, Vadenbo CO, Wernet G (2013) Overview and methodology. Data quality guideline for the ecoinvent database version 3. ecoinvent Centre
You F, Tao L, Graziano DJ, Snyder SW (2012) Optimal design of sustainable cellulosic biofuel supply chains: multiobjective optimization coupled with life cycle assessment and input–output analysis. AlChE J 1157–1180
Acknowledgments
This research was funded within the National Research Programme “Resource Wood” (NRP 66, www.nfp66.ch) by the Swiss National Science Foundation (project no. 136612). We would like to thank the two anonymous reviewers as well as Carl Vadenbo for their valuable input.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Adriana Del Borghi
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(DOCX 432 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Steubing, B., Mutel, C., Suter, F. et al. Streamlining scenario analysis and optimization of key choices in value chains using a modular LCA approach. Int J Life Cycle Assess 21, 510–522 (2016). https://doi.org/10.1007/s11367-015-1015-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11367-015-1015-3