Consistent characterisation factors at midpoint and endpoint relevant to agricultural water scarcity arising from freshwater consumption

Abstract

Purpose

The shortage of agricultural water from freshwater sources is a growing concern because of the relatively large amounts needed to sustain food production for an increasing population. In this context, an impact assessment methodology is indispensable for the identification and assessment of the potential consequences of freshwater consumption in relation to agricultural water scarcity. This paper reports on the consistent development of midpoint and endpoint characterisation factors (CFs) for assessing these impacts.

Methods

Midpoint characterisation factors focus specifically on shortages in food production resulting from agricultural water scarcity. These were calculated by incorporating country-specific compensation factors for physical availability of water resources and socio-economic capacity in relation to the irrigation water demand for agriculture. At the endpoint, to reflect the more complex impact pathways from food production losses to malnutrition damage from agricultural water scarcity, international food trade relationships and economic adaptation capacity were integrated in the modelling with measures of nutritional vulnerability for each country.

Results and discussion

The inter-country variances of CFs at the midpoint revealed by this study were larger than those derived using previously developed methods, which did not integrate compensation processes by food stocks. At the endpoint level, both national and trade-induced damage through international trade were quantified and visualised. Distribution of malnutrition damage was also determined by production and trade balances for commodity groups in water-consuming countries, as well as dependency on import ratios for importer countries and economic adaptation capacity in each country. By incorporating the complex relationships between these factors, estimated malnutrition damage due to freshwater consumption at the country scale showed good correlation with total reported nutritional deficiency damage.

Conclusions

The model allows the establishment of consistent CFs at the midpoint and endpoint for agricultural water scarcity resulting from freshwater consumption. The complex relationships between food production supply and nutrition damage can be described by considering the physical and socio-economic parameters used in this study. Developed CFs contribute to a better assessment of the potential impacts associated with freshwater consumption in global supply chains and to life cycle assessment and water footprint assessments.

Introduction

Demand for freshwater has been increasing due to population and economic growth, while freshwater resources are limited. The severity of this limitation varies among regions because of differences in the physical availability of water resources and in local socio-economic conditions. In addition, the uneven distribution of freshwater availability and demand is responsible for various types of environmental impacts (World Water Assessment Programme 2009). Global supply chains of products and services also contribute to the potential environmental risks related to water use, but these are hidden in material and service flows. Nevertheless, the importance of assessing the impacts of water use in life cycle assessment (LCA) has been recognized in recent years (Köehler 2008; Bayart et al. 2010; Berger and Finkbeiner 2012; Boulay et al. 2013; Kounina et al. 2013; Motoshita 2013; Tendal et al. 2013).

Many methods for assessing the impacts of water use in LCA have been developed (Kounina et al. 2013). According to the previously described impact pathway of freshwater use (Bayart et al. 2010; Kounina et al. 2013), freshwater deficits will result in impacts on human life and on biotic and abiotic environments. Specifically, damage related to water issues has been estimated to represent up to 9.1 % of total human health damage (Prüss-Üstün et al. 2008). This is the same level as the total health damage caused by cardiovascular diseases (WHO 2008). Thus, health damage in human populations resulting from water use should be a key concern of human society. Appropriate indicators for assessing the impacts on human health related to freshwater consumption need to be developed.

The primary impact factors leading to human health problems can be found in domestic/agricultural/aquacultural water scarcity (Bayart et al. 2010; Kounina et al. 2013). Specifically, agriculture is responsible for almost 70 % of freshwater use in the world (FAO 2010a). Thus, freshwater consumption may result in large impacts on agricultural water users. Several methods for assessing freshwater scarcity (Frischknecht et al. 2006; Pfister et al. 2009; Ridoutt and Pfister 2010; Hoekstra et al. 2011; Boulay et al. 2011) have been developed at the midpoint level. However, indicators clearly focusing on the impact for each water user have not been proposed to date. At the endpoint level, methods for assessing human health damage due to freshwater consumption have been developed (Pfister et al. 2009; Motoshita et al. 2010; Boulay et al. 2011). In the context of agricultural water scarcity, two models developed by Pfister et al. (2009) and Boulay et al. (2011) assess malnutrition damage resulting from freshwater consumption in the context of consideration of physical water availability and social vulnerability (human development index (HDI) and economic adaptation capacity). Models for assessing the impact of agricultural water scarcity can be improved by considering more direct factors relevant to vulnerability to food supply shortages (such as food stock and distribution of nutritional conditions within a population). In addition, the international trade in food may compensate for and/or shift food shortages to other countries.

This study aimed to develop appropriate indicators for assessing agricultural water scarcity due to freshwater consumption at the midpoint and endpoint. At the midpoint, the robustness of an indicator is one of the most critical aspects. Thus, indicators were proposed based on physical water stress and the consideration of region-specific factors addressing the extent of agricultural water demand and vulnerability to food supply shortage. At the endpoint, human health damage from malnutrition was modelled to improve previous models by incorporating economic adaptation capacity and the effects of the international food trade to reflect the total damage from food production losses.

Methods

Outline of agricultural water scarcity modelling

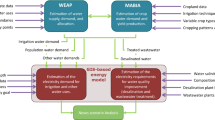
According to Bayart et al. (2010) and Kounina et al. (2013), excessive freshwater consumption will lead to irrigation water scarcity and result in health damage from malnutrition. Malnutrition may also result from infectious diseases that decrease nutrient absorption (World Water Assessment Programme 2009; Boulay et al. 2011). On the other hand, only malnutrition damage from food deprivation was considered in this study as a straightforward and robust endpoint resulting from agricultural water scarcity. The cause-effect chain in this modelling process is defined as shown in Fig. 1.

Fig. 1

The cause-effect chain in the modelling of water scarcity impact

Freshwater consumption will potentially lower water availability for agriculture and agricultural production, but the severity of this depends on irrigation intensity and societal capacity for compensation. Depending on absolute levels of water scarcity, a shortage of irrigation water might be compensated for by inputting additional water from other available freshwater resources and food stocks. In this context, alternative freshwater resources and food stocks can represent physical and socio-economic vulnerability to water scarcity, respectively, and were therefore included in characterisation factors (CFs) at the midpoint.

On the other hand, food production shortages may not be fully compensated for within a local system. Any local production shortages may also be spread through international food trade. As a result, food supply shortages due to agricultural water scarcity can cause health damage as a major endpoint impact. However, the spread effects of shortages in food production will depend on the commodity balance of water consumers, the vulnerability of economy and food stocks in food-importing countries. In addition, the significance of food supply shortages will also be controlled by overall nutritional conditions and their variability in each region. Suitable characterisation factors at the endpoint were developed by integrating these parameters.

As mentioned above, physical factors such as freshwater resources and social factors relating to food production and consumption were included in the modelling at both the midpoint and endpoint. However, the availability of statistical data for many socio-economic indices is often limited to the national level. Therefore, the geographic resolution of both the midpoint and endpoint was set at the scale of individual countries, even if some factors could be analysed at higher spatial resolution. Details of the modelling methodology are described in the following sections.

Midpoint modelling

While current midpoint indicators can be applied in different types of formulation, they commonly express the relationship of freshwater use (withdrawal or consumption) to the total amount of available freshwater resources (Kounina et al. 2013). However, agricultural water scarcity is not only determined by the total amount of water consumed. The severity of agricultural water scarcity will also be influenced by the level of dependency on irrigation for agricultural production. Agricultural food production losses may also be compensated for by additional food stocks from the viewpoint of social vulnerability. In this context, characterisation factors for agricultural water scarcity at the midpoint (CF_{Agr_Midpoint,i} ) should be defined by combining physical compensation capacity with the extent of agricultural water demand, dependency on irrigation water and social compensation capacity as follows:

$$ {\mathrm{CF}}_{\mathrm{Agr}\mathrm{Midpoint},i}=\underset{\kern1em \left(\mathrm{Irrigated}\kern0.5em \mathrm{crop}\kern0.5em \mathrm{production}\kern0.5em \mathrm{vulnerability}\right)}{\underbrace{R_{\mathrm{Agr},i}\cdot {\mathrm{IDR}}_i}}\cdot \underset{\kern1em \left(\mathrm{Physical}\kern0.5em \mathrm{vulnerability}\right)}{\underbrace{\left(1-{\mathrm{PCF}}_i\right)}}\cdot \underset{\begin{array}{l}\kern1em \mathrm{Social}\\ {}\mathrm{vulnerability}\end{array}}{\underbrace{\left(1-{\mathrm{SCF}}_i\right)}} $$

(1)

where R _Agr,i [dimensionless] is the ratio of agricultural water use to total water withdrawal in country i, IDR _i [dimensionless] is the irrigation dependency ratio for crop production in country i, PCF _i [dimensionless] expresses the physical compensation capacity of country i, and SCF _i [dimensionless] expresses the social compensation capacity of country i.

The meaning of the CFs at the midpoint is the ratio of potential “net” production loss of irrigated crops resulting from freshwater consumption. Based on the hypothesis that all water users are proportionally affected and that production loss is proportional to irrigation loss, the product of R _Agr,i and IDR _i expresses the potentially lost share of agricultural production. The gross value is converted to the net loss by considering vulnerability of physical (in terms of water resources) and social (in terms of food stocks) aspects.

R _Agr,i was calculated based on the amount of agricultural water use and total water withdrawal for each country (FAO 2010a). The dependence of agriculture on irrigation IDR _i was quantified by calculating the weighted average of the ratio of irrigation water volume to total water volume consumed (evapotranspiration) by commodity group (based on the metric of dietary energy). For physical vulnerability (1 − PCF _i ), midpoint indicators (the so-called water scarcity index (WScI)) expressing water scarcity at the national level developed by previous studies (Frischknecht et al. 2006; Pfister et al. 2009; Boulay et al. 2011) can be applied without any modifications. For the compensation capacity (SCF) using additional food stocks, the ratio of average surplus food stocks and total production for the last 10 years (to derive more robust results) was calculated for each commodity. Target commodities for calculating crop production loss (45 items) were determined (the specific lists in Tables S1 and S2 of the Electronic Supplementary Material) in accordance with the agricultural commodity classification in FAOSTAT (FAO 2013). The weighted average of the ratio by commodity production (based on the metric of dietary energy) was applied as SCF _i .

$$ {\mathrm{IDR}}_i={\displaystyle {\sum}_j\left\{{\mathrm{AID}}_{ij}/{\displaystyle {\sum}_j{\mathrm{ATD}}_{ij}}\cdot \underset{\mathrm{Weighting}\ \mathrm{on}\ \mathrm{production}}{\underbrace{\left({\mathrm{AFP}}_{ij}/{\displaystyle {\sum}_j{\mathrm{AFP}}_{ij}}\right)}}\right\}} $$

(2)

$$ {\mathrm{PCF}}_i = 1-{\mathrm{WScI}}_i $$

(3)

$$ {\mathrm{SCF}}_i = \kern1em \left\{\begin{array}{l}\kern1em 1\kern19em ,{\mathrm{AFP}}_{ij}<{\mathrm{AFS}}_{ij}\hfill \\ {}1-{\displaystyle {\sum}_j\left\{\left({\mathrm{AFP}}_{ij}-{\mathrm{AFS}}_{ij}\right)/{\mathrm{AFP}}_{ij}\cdot \underset{\mathrm{Weighting}\kern0.5em \mathrm{on}\kern0.5em \mathrm{production}}{\underbrace{\left({\mathrm{AFP}}_{ij}/{\displaystyle {\sum}_j{\mathrm{AFP}}_{ij}}\right)}}\right\},{\mathrm{AFP}}_{ij}\ge {\mathrm{AFS}}_{ij}}\hfill \end{array}\right. $$

(4)

where WScI _i is the scarcity index expressing a function of the ratio of water use to available water resources, AID _ij [m³/year] expresses the annual demand of irrigation water for producing commodity j in country i, ATD _ij [m³/year] expresses the annual total demand (including irrigation and rain) of water for producing commodity j in country i, AFP _ij [kcal/year] means the average annual production of commodity j in country i for 10 years (from 2000 to 2009), and AFS _ij [kcal/year] is the average annual stock of commodity j in country i for 10 years (from 2000 to 2009). For calculating AFP _ij and AFS _ij , the amounts of annual production and stocks in metric tons were converted into dietary energy based on FAOSTAT data (FAO 2013). Details of calculation of AID _ij , ATD _ij , AFP _ij and AFS _ij are described in Section 2.3.1.

Endpoint modelling

Malnutrition damage at the endpoint will occur when agricultural water scarcity causes losses of crop production and food supply cannot be locally compensated for. Consequences of crop production loss may be spread to other countries through international trade in food. Any resulting shortage of food in each country (not only water consumer but also food-importing countries) may cause malnutrition damage. For these reasons, the modelling incorporates three modules (food production loss assessment, food supply shortage assessment and health damage assessment) as described in the following sections.

The food production loss assessment module

The extent of agricultural water scarcity due to freshwater consumption was assessed based on the agricultural water use share. However, the vulnerability of crop production relevant to freshwater consumption needs to be distinguished among individual commodities, because irrigation water demand for each unit amount of crop production depends on the nature of specific commodities. In addition, the commodity balance of production and consumption in each country will control the types of agricultural commodities influenced by agricultural water scarcity. Thus, agricultural water scarcity needs to be allocated to each commodity by considering commodity balances in each country. Crop yield per unit of irrigation water should also be identified for specific commodities and countries. In this context, crop production loss (CPL _ij ) for each commodity was calculated by modifying the midpoint CFs (Eq. (1)) for each country and commodity to reflect the differences in water demand and food stock capacity of each commodity j:

$$ {\mathrm{CPL}}_{ij}={R}_{\mathrm{Agr},i}\cdot {\mathrm{IDR}}_{ij}\cdot \left(1-{\mathrm{PCF}}_i\right)\cdot {\mathrm{CY}}_{ij}\cdot \left(1-{\mathrm{SCF}}_{ij}\right) $$

(5)

where CPL _ij [ton/m³] indicates the amount of production loss of commodity j in country i, IDR _ij [dimensionless] expresses the demand ratio of irrigation water for commodity j to total irrigation water demand in country i, CY _ij [ton/m³] means the crop yield of commodity j in country i per unit irrigation water input, and SCF _ij [dimensionless] is the social compensation capacity of commodity j in country i.

The relationship IDR _ij allocates a unit volume of agricultural water scarcity to each commodity based on the ratio of the annual irrigation water demand of each commodity to the total annual agricultural water demand. The annual agricultural water (irrigation and rain) demand for each commodity was calculated by dividing the annual production amount of all crops produced in each country (FAO 2013) by the crop yield per unit volume of water consumption (CY _ij ) based on Mekonnen and Hoekstra (2010). AID _ij was calculated by multiplying ATD _ij with the ratio of irrigation water to total water consumption. IDR _ij and SCF _ij are described by the following:

$$ {\mathrm{IDR}}_{ij}={\mathrm{AID}}_{ij}/{\displaystyle \sum_j}{\mathrm{ATD}}_{ij} $$

(6)

$$ {\mathrm{SCF}}_{ij}=\kern1em \left\{\begin{array}{l}1\kern9.5em ,{\mathrm{AFP}}_{ij}<{\mathrm{AFS}}_{ij}\hfill \\ {}1-\left({\mathrm{AFP}}_{ij}-{\mathrm{AFS}}_{ij}\right)/{\mathrm{AFP}}_{ij},\ {\mathrm{AFP}}_{ij}>{\mathrm{AFS}}_{ij}\hfill \end{array}\right. $$

(7)

The amount of crop production loss in terms of dietary energy supply is not necessarily the same for all crops, because the dietary energy obtained from the same unit weight of production can be different for different crops. In addition, some part of each produced crop may be used as feed for producing animal food commodities which leads on average to a 7.22 times lower dietary energy supply (Boulay et al. 2011). Conversion factors for each commodity from weight to dietary energy and feed production ratio to total crop production were calculated based on data supplied by FAOSTAT (FAO 2013). Dietary energy loss of each crop production was separated into food and feed. Dietary energy loss of feed was allocated to each animal food commodity (ten types of meat and dairy products in accordance with the classification of FAOSTAT shown in Table S3 of the Electronic Supplementary Material), based on the ratio of the annual production amount of each animal food in dietary energy to the total annual animal food production. The food production loss of agricultural and animal food commodities was determined using the following equations:

$$ {\mathrm{FPL}}_{ij}=\left\{\begin{array}{l}{\mathrm{CPL}}_{ij}\cdot \underset{\begin{array}{l}\mathrm{Conversion}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{dietary}\kern0.5em \mathrm{energy}\end{array}}{\underbrace{{\mathrm{DEC}}_{ij}}}\cdot \underset{\begin{array}{l}\mathrm{Allocation}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{agricultural}\kern0.5em \mathrm{food}\end{array}}{\underbrace{\left(1-{\mathrm{FPR}}_{ij}\right)}}\kern3.1em ,j: agricultural\kern0.5em \mathrm{food}\kern0.5em \mathrm{commodities}\hfill \\ {}{\mathrm{CPL}}_{ij}\cdot \underset{\begin{array}{l}\mathrm{Conversion}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{dietary}\kern0.5em \mathrm{energy}\end{array}}{\underbrace{{\mathrm{DEC}}_{ij}}}\cdot \underset{\begin{array}{l}\mathrm{Allocation}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{animal}\kern0.5em \mathrm{food}\end{array}}{\underbrace{{\mathrm{FPR}}_{ij}\cdot {\mathrm{AFPR}}_{ij}}}\kern1em ,j:\mathrm{animal}\kern0.5em \mathrm{food}\kern0.5em \mathrm{commodities}\hfill \end{array}\right. $$

(8)

where FPL _ij [kcal/m³] expresses the food production loss of commodity j in country i (in terms of dietary energy), DEC _ij [kcal/ton] means the unit conversion factor of food from metric weight to dietary energy, FPR _ij [dimensionless] is the ratio of feed production amount to total crop production amount, and AFPR _ij [dimensionless] is the ratio of each type of animal food commodity to total animal food (both in terms of dietary energy).

Food supply shortage assessment module

These losses in food production may result in a shortage of food supplies inside the water consumer country. However, the water consumer country can avoid these by decreasing food exports (in case of a net exporter of a commodity) or by importing food. Therefore, the shortages in food supplies will differently affect water consumer countries based on the dependency ratio of domestic food supplies to total supplies (including the net amount of imports). If the water consumer country is a net exporter of a particular commodity, all of the food production loss is assumed to affect the net importers. Net importer countries share a part of the food shortage based on their individual ratios of net imports of each commodity to total net imports in the world. In international trade, economic power for purchasing commodities can be the biggest determining factor for decreasing the sharing ratio of food supply shortage. Thus, economic adaptation capacity is considered in the estimation of the sharing ratio. The actual food supply loss for each commodity in water consumer and other importer countries can be described using the following equations, respectively:

$$ {\mathrm{FSL}}_{ij}=\left\{\begin{array}{l}{\mathrm{FPL}}_{ij}\cdot {\mathrm{DSR}}_{ij}\cdot \underset{\begin{array}{l}\mathrm{Economic}\\ {}\mathrm{vulnerability}\end{array}}{\underbrace{\left(1-{\mathrm{EAC}}_i\right)}}\kern2em ,i:\mathrm{water}\kern0.5em \mathrm{consumer}\kern0.5em \mathrm{coutnry}\hfill \\ {}\underset{\begin{array}{l}\mathrm{Trade}-\mathrm{induced}\kern0.5em \mathrm{food}\kern0.5em \mathrm{loss}\\ {}\mathrm{in}\kern0.5em \mathrm{importer}\kern0.5em \mathrm{countries}\end{array}}{\underbrace{\left({\mathrm{FPL}}_{\mathrm{WC},j}-{\mathrm{FSL}}_{\mathrm{WC},j}\right)}}\cdot {\mathrm{ISR}}_{ij}\kern1em ,i:\mathrm{other}\kern0.5em \mathrm{importer}\kern0.5em \mathrm{countries}\hfill \end{array}\right. $$

(9)

where FSL_{WC, j} [kcal/m³] expresses the supply shortage of commodity j in the water consumer country, DSR_{WC, j} [dimensionless] indicates the ratio of the domestic supply amount of commodity j to the total supply in the water consumer country, EAC_WC [dimensionless] describes the economic adaptation capacity in the water consumer country, FPL_{WC, j} [kcal/m³] is the production loss of commodity j in the water consumer country, FSL _ij [kcal/m³] is the supply shortage of commodity j in country i, ISR _ij [dimensionless] is the import sharing ratio of commodity j in country i, and EAC _i [dimensionless] is the economic adaptation capacity in country i.

For the calculation of the import sharing ratio for each commodity ISR _ij , data on the net import amount of each commodity j in country i was obtained from FAOSTAT for all countries (FAO 2013):

$$ {\mathrm{ISR}}_{ij}=\left\{\left({\mathrm{NIA}}_{ij}\cdot \left(1-{\mathrm{EAC}}_i\right)\right)/{\displaystyle \sum_i}\left({\mathrm{NIA}}_{ij}\cdot \left(1-{\mathrm{EAC}}_i\right)\right)\right\} $$

(10)

where NIA _ij [kcal] expresses the net import amount of commodity j in country i.

The economic adaptation capacity EAC _i was defined by referring to the method by Boulay et al. (2011) based on income level classifications supplied by the World Bank (World Bank 2014a). Equations for calculating ISR _ij and EAC _i are as follows:

$$ {\mathrm{EAC}}_i=\left\{\begin{array}{l}1\kern12.5em ,\ \mathrm{G}\mathrm{N}\mathrm{I}\ \mathrm{per}\ \mathrm{capita}>12,615\kern0.5em \mathrm{US}\$\hfill \\ {}\left({\mathrm{GNI}}_i-1035\right)/\left(12,615-1035\right)\kern1em ,1035<\mathrm{G}\mathrm{N}\mathrm{I}\ \mathrm{per}\ \mathrm{capita}<12,615\kern0.5em \mathrm{US}\$\hfill \\ {}0\kern12.4em ,\mathrm{G}\mathrm{N}\mathrm{I}\ \mathrm{per}\ \mathrm{capita}<1035\kern0.5em \mathrm{US}\$\hfill \end{array}\right. $$

(11)

where GNI _i [current US$;] is the per-capita gross national income of country i reported by the World Bank (2014b).

The health damage assessment module

Loss of food supplies will result in a prevalence of undernourished populations. While the size of the undernourished population also depends on many aspects of nutrition in each country, we chose average dietary energy supply per capita as the main parameter for describing fundamental nutrient conditions at the national level. Additionally, a gap in nutrient conditions in each country was assumed to be a potential factor in the creation of an undernourished population (Thompson and Meerman 2010). Therefore, the level of the undernourished population in each country was modelled using two parameters of nutrient conditions (average dietary energy supply per capita and the Gini coefficient of dietary energy consumption). Non-linear multiple regression analysis was applied to model the relationship between the undernourished population and the above two parameters in accordance with the procedures described in Motoshita et al. (2010). Details of the analysis procedure and results are found in the Electronic Supplementary Material of this paper. Fundamental data on the above two explanatory variables was collected from the FAO database (FAO 2010b, 2013).

The following equation was obtained from the multiple regression analysis as follows (R ²* = 0.92, N = 171):

$$ {\mathrm{RUP}}_i=\begin{array}{lll}\underset{\begin{array}{l}\mathrm{Undernourished}\kern0.5em \mathrm{population}\\ {}\kern3em \mathrm{o}\mathrm{wing}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{average}\kern0.5em \mathrm{dietary}\;\mathrm{condition}\end{array}}{\underbrace{1.53\times {10}^3\cdot {e}^{-0.193\cdot {\mathrm{ADES}}_i}}}+\hfill & \underset{\begin{array}{l}\mathrm{Undernourished}\kern0.5em \mathrm{population}\\ {}\kern4em \mathrm{o}\mathrm{wing}\kern0.5em \mathrm{t}\mathrm{o}\\ {}\mathrm{gap}\kern0.5em \mathrm{condition}\kern0.5em \mathrm{o}\mathrm{f}\kern0.5em \mathrm{dietary}\kern0.5em \mathrm{energy}\end{array}}{\underbrace{0.878\cdot {\mathrm{GC}}_i}}\hfill & -20.1\hfill \end{array} $$

(12)

where RUP _i [%] expresses the rate of undernourished population in country i, ADES _i [kcal/capita/day] is the average daily dietary energy supply per capita in country i, and GC _i [dimensionless] is the Gini coefficient of dietary energy consumption per capita in country i.

The response factor (RF) describes changes in the undernourished population rate caused by changes in unit average daily dietary energy supply and can be described by deviating Eq. (12) in terms of ADES _i as follows:

$$ {\mathrm{RF}}_i=\varDelta {\mathrm{RUP}}_i/\varDelta {\mathrm{ADES}}_i=-2.96\times {10}^2\cdot {e}^{-0.193\cdot {\mathrm{ADES}}_i} $$

(13)

The level of health damage (disability adjusted life years (DALYs)) from malnutrition on a per case basis (HDM _i [DALY/case]) was calculated for each country by dividing total health damage from malnutrition in each country by the level of undernourished population (WHO 2008; FAO 2010b). By multiplying predicted undernourished population increases due to food supply shortages with the level of health damage of malnutrition per individual case, any increases in health damage from undernourishment caused by food supply shortages can be estimated. A point of notice is the limitation that the shortages in food supply are assumed to affect all population equally without considering the depth of lacking dietary energy for a specific part of the population. Thus, health damage calculated from Eq. (13) only describes the impact on all population at an average nutrient condition in each country.

The characterisation factor at the endpoint level

The characterisation factor [DALY/m³] of agricultural water scarcity on human health inside water consumer countries (national damage) and other influenced countries (trade-induced damage) can be separately calculated by integrating the above equations as follows:

$$ \begin{array}{l}{\mathrm{CF}}_{\mathrm{Agr}\_\mathrm{Endpoint}\_\mathrm{H}\mathrm{H},i}=\\ {}\left\{\begin{array}{ll}\kern1em \left({\displaystyle {\sum}_j{\mathrm{FSL}}_{ij}}\right)/\left({P}_i\cdot 365\right)\cdot {\mathrm{RF}}_i\cdot {\mathrm{HDM}}_i\hfill &, \mathrm{damage}\kern0.5em \mathrm{in}\kern0.5em \mathrm{water}\kern0.5em \mathrm{consumer}\kern0.5em \mathrm{country}\hfill \\ {}{\displaystyle {\sum}_i\left\{{\displaystyle {\sum}_j{\mathrm{FSL}}_{ij}}/\left({P}_i\cdot 365\right)\cdot {\mathrm{RF}}_i\cdot {\mathrm{HDM}}_i\right\}}\hfill &, \mathrm{trade}\hbox{-} \mathrm{induced}\kern0.5em \mathrm{damage}\kern0.5em \mathrm{in}\kern0.5em \mathrm{other}\kern0.5em \mathrm{countries}\hfill \end{array}\right.\end{array} $$

(14)

where P _i [capita] expresses the population of country i.

The impact on freshwater consumption from agricultural water scarcity can be separately identified for national and trade-induced damage by using these characterization factors at the endpoint (specific characterisation factors are shown in Annex A2 in the Electronic Supplementary Material).

Results of the development of characterisation factors

Comparison with characterization factors of previous models at the midpoint

Characterisation factors for each country at midpoint level are calculated based on Eq. (1). Currently proposed scarcity indicators (Frischknecht et al. 2006; Pfister et al. 2009; Boulay et al. 2011; Hoekstra et al. 2012) have the potential to be applied to the equations describing characterisation factors as WScI. In terms of geographical scale and comprehensiveness in target countries, two methods (Pfister et al. 2009; Boulay et al. 2011) were applied for obtaining CFs for agricultural water scarcity at the midpoint. To focus on agricultural water scarcity, the ratio of agricultural water use and food stock compensation capacity were considered in this modelling (a user-specific approach) differently from the previous midpoint indicators for unspecified users in the generic approach. For the analysis of the differences between the CFs in both approaches, the ranking of CFs from both the generic approach (WSI: Pfister et al. 2009) and the user-specific approach (this study) is mapped in Fig. 2.

Fig. 2

Map of the ranking of midpoint CFs of generic approach (WSI: Pfister et al. 2009) and user-specific approach (this study based on WSI by Pfister et al. 2009)

According to the distribution map of CF ranking (Fig. 2), the sensitivity to freshwater consumption in each country documents the differences in the CFs based on the generic and user-specific approaches. Some countries in North Africa, the Mediterranean, South-East Asia and South America recorded a lower ranking (are less sensitive) from the user-specific approach and a higher one from the generic approach. In addition, the differences in CFs among countries were larger in the user-specific approach (coefficient of variance = 3.38) than in the generic approach (coefficient of variance = 1.14). These differences can be attributed to the complexities in agricultural water demand and food compensation capacity in each country. However, no significant differences could be found in either cases when applying the water scarcity indices of WSI derived from Pfister et al. (2009) and those of Alpha obtained from Boulay et al. (2011) (details are found in the Electronic Supplementary Material).

In addition to the two WScI methods described above, the methods constructed by Frischknecht et al. (2006) and Hoekstra et al. (2012) may be made applicable by modifying the geographical scale and coverage of countries. Basically, a space for the inclusion of WScI in Eq. (2) is left for the users of this midpoint indicator when assessing the impact of freshwater consumption (Annex A3 and A4 in the Electronic Supplementary Material). However, it was pointed out in a previous study (Boulay et al. 2014) that the modelling choices of each indicator might lead to significant differences in analytical results. Actually, differences among CFs based on the two water stress indices (Pfister et al. 2009; Boulay et al. 2011) in the present analysis are found in some countries (Fig. S2 in the Electronic Supplementary Material), but the trends seem to be fairly similar on the whole. Thus, the default choice of WScI is discussed in the following section to achieve consistency in the endpoint assessment.

Comparison with characterization factors of previous models at the endpoint

Characterisation factors for each country at endpoint level were calculated based on Eq. (14). As the measure of the physical compensation capacity of water resources, WScI derived from the two methods described above (Pfister et al. 2009; Boulay et al. 2011) was applied to the calculation of CFs at the endpoint. As mentioned in the introduction, two endpoint models on agricultural water scarcity have been developed (Pfister et al. 2009; Boulay et al. 2011). For the comparison of endpoint CFs in this study with these previous models, data from each country calculated using the three methods (Pfister et al. 2009; Boulay et al. 2011; this study) were mapped as in Fig. 3. We adapted the marginal CFs for agricultural users from Boulay et al. (2011) (where agricultural users are the only ones deprived from lower water availability) by multiplying the ratio of agricultural water use to total water withdrawal (FAO 2010a) for a consistent comparison of the models.

Fig. 3

Maps of endpoint CFs derived by the three methods (Pfister et al. 2009; Boulay et al. 2011; this study)

As shown in Fig. 3, the CFs derived by Pfister et al. (2009) were relatively lower (average, 0.305 × 10⁻⁶ [DALY/m³]) on the whole than for the other two methods (the average of Boulay et al. (2011), 8.71 × 10⁻⁶ [DALY/m³]; the average of this study, 5.75 × 10⁻⁶ [DALY/m³]). The reason for the lower CFs in Pfister et al. (2009) can be found in the lower impact factor of health damage resulting from the shortage of a unit of agricultural water (Boulay et al. 2014). The regional relative vulnerability of CFs in these two models showed some similarities throughout (generally vulnerable in South American, South-East Asian, Mediterranean and African countries), even though the scale of the CFs in both models was different. On the other hand, the CFs derived in the present study seemed to be similar in scale to those of Boulay et al. (2011), but regional relative vulnerability was different from those derived in the first two methods. Developed countries in North America, Oceania, Asia and Europe also showed relatively high CFs in this study. In Fig. 3, both national and trade-induced damage in other countries caused by water consumer countries result in relatively higher CFs in developed countries than CFs of the other two models.

To analyse the effects of international food trade more clearly, the breakdown of CFs were mapped for four characteristic countries (Switzerland, Germany, China and India) (Fig. 4). The characterisation factors of Germany and Switzerland were very similar in total (Germany, 4.90 × 10⁻⁶ [DALY/m³]; Switzerland, 3.18 × 10⁻⁶ [DALY/m³]). Both countries showed no national damage due to their high economic adaptation capacity and consequently that the shortage of food production due to agricultural water scarcity is spread to more vulnerable countries. However, the affected countries and their damage were different in both cases. The main agricultural commodities differ in Germany (wheat, barley, maize) compared to Switzerland (cereal, potatoes, peas). In the case of China and India, damaged third-party countries were also different, while the CFs of both countries were similar (China, 1.53 × 10⁻⁵ [DALY/m³]; India, 2.46 × 10⁻⁵ [DALY/m³]). National damage in the cases of China was 12 % and even 94 % in India, because of the relatively low economic adaptation capacity in these countries (EAC in China 0.40, in India 0.05, and in Germany and Switzerland 1). In addition, the domestic supply ratios of food commodities (DSR) were higher in India (0.85 on average) than in China (0.51 on average). Therefore, the shortage of food production due to water consumption mainly causes national damage in India, while trade-induced damage spreads to other countries in the case of water consumption in China.

Fig. 4

Shares of national and trade-included damage in the CFs derived for this study for water consumption in four countries

Discussion

Verification of the assessment model

Estimation approach of malnutrition damage related to freshwater consumption

To check the validity of the assessment model, the malnutrition damage caused by total global freshwater consumption was estimated based on the CFs developed in this study. Data on the amount of consumed freshwater on a country scale were obtained from Chapagain and Hoekstra (2004). However, these CFs are valid for marginal water use (i.e. at current water stress level), and therefore, multiplying total water consumption by these factors is overestimating the impact, as discussed and quantified in Pfister and Bayer (2014). We therefore analysed the relations between any shortfall in agricultural water and actual water consumption to assess the actual impact of freshwater consumption. Current agricultural water supply shortages can be determined by assessing the difference between the supplied amount of water for agricultural use (including both rainwater and irrigation water) and the minimum required for agricultural production. The annual amount of supplied rain and irrigation in each country was estimated from AQUASTAT data (FAO 2010a). The minimum water demand for agriculture to avoid malnutrition damage was set to 1350 [m³/capita/year] as indicated by Falkenmark and Rockstorm (2004). The amount of freshwater shortage (AFS _i ) and human health damage from malnutrition due to freshwater consumption (HH_{Malnutrition,i} ) is therefore calculated as follows:

$$ \begin{array}{l}{\mathrm{AFS}}_i=\left\{\begin{array}{l}0\kern5.5em ,{\mathrm{WS}}_i>{\mathrm{MD}}_i\\ {}{\mathrm{WC}}_i\kern4.1em ,\ {\mathrm{WS}}_i<{\mathrm{MD}}_i,\kern0.75em {\mathrm{WC}}_i<{\mathrm{MD}}_i-{\mathrm{WS}}_i\ \\ {}{\mathrm{MD}}_i-{\mathrm{WS}}_i\kern1.86em ,\ {\mathrm{WS}}_i<{\mathrm{MD}}_i,\kern0.75em {\mathrm{WC}}_i>{\mathrm{MD}}_i-{\mathrm{WS}}_i\end{array}\right.\\ {}\end{array} $$

(15)

$$ {\mathrm{HH}}_{\mathrm{Malnutrition},i}={\mathrm{AFS}}_i\cdot {\mathrm{CF}}_{\mathrm{Agr}\_\mathrm{Endpoint}\_\mathrm{H}\mathrm{H},i} $$

(16)

where AFS _i [m³] expresses the amount of freshwater shortage in country i, WS _i [m³] indicates the amount of total water supply (rain and irrigation) for agriculture in country i, MD _i [m³] means the minimum demand of agricultural water, WC _i [m³] is the amount of consumed freshwater in country i, and HH_{Malnutrition,i} [DALY] is the health damage of malnutrition due to freshwater consumption in country i.

The results of estimated malnutrition damage

The human health damage of malnutrition was estimated based on the CFs derived from three endpoint models (this study, Pfister et al. (2009) and Boulay et al. (2011)) based on the estimation approach in Section 4.1.1 This is shown at the regional scale in Table 1, using WHO (2008) reported data on damage from nutritional deficiencies. The amount of freshwater shortages for agriculture was estimated as shown in Table S5 in the Electronic Supplementary Material.

Table 1 Estimated annual damage from malnutrition due to total global freshwater consumption

The estimated damage based on the CFs reported in previous models showed big variations with the damage of nutritional deficiencies reported by WHO. Specifically, no damage was estimated in Southeast Asia and the West Pacific because many countries in these regions showed no shortage of agricultural water (see Eq. (15) and Table S5 in the Electronic Supplementary Material). On the other hand, the estimated damage based on the CFs developed in this study showed relatively higher levels of damage on the whole. In addition, some damage was estimated in Southeast Asia and the West Pacific even though no shortage of agricultural water was found in these locations. In these regions, some countries were affected by the levels of water consumption in other countries through international food trade as a result of their lower economic adaptation capacities, even though their direct demand for freshwater for agriculture may be satisfied under current supply situations.

As shown in Table 1, the estimated damage based on the CFs developed in this study also showed some differences with the total damage from nutritional deficiencies as revealed by the WHO (2008). However, nutritional deficiencies will not be caused only by agricultural water scarcity. Other socio-economic factors (poverty gap, a coincidence of infectious disease damage) could increase both the number of cases and the level of damage from nutritional deficiencies (World Water Assessment Programme 2009; Boulay et al. 2011). Additionally, other agricultural production factors on production management (such as land availability, fertilizer, pesticide management and harvesting efficiencies) and environmental change (due to climate change and soil conditions) have a significant contribution to malnutrition. Finally, processing and distribution of food and related losses is another important factor. Therefore, all the damage from nutritional deficiencies is not necessarily explained by the estimated damage from agricultural water scarcity. At the country scale, the estimated damage based on the CFs derived from this study showed a fairly good correlation with the total damage from nutritional deficiencies, while for some cases (Senegal, Mauritania, Gambia, Swaziland, Comoros, El Salvador, Solomon Islands, Maldives), too high factors resulted (Fig. 5). Characterisation factors for some countries could not be developed because of the data availability, which resulted in overload of food shortage to vulnerable countries and overestimation of damage as mentioned above. Finally, the cause-effect modelling has several limitations, such as the assumptions that agriculture is affected by water scarcity in proportion to their water use share, which could also be assumed to be irrelevant as it might be considered more vulnerable because of low water prices paid for agriculture (Boulay et al. 2011) or the fact that the severity of malnutrition is not more specifically addressed. However, the endpoint model in this study improves the description of human health damage due to agricultural water scarcity by considering physical/social adaptation capacities and trade-induced damage from international relations.

Fig. 5

The relationship between estimated damage from malnutrition due to agricultural water scarcity (based on the CFs derived by this study) and total damage from nutritional deficiencies (WHO 2008) at a country scale

Choices of water scarcity index

In the model developed in this study, the choice of water scarcity index (physical stress on water resources) can be left up to the users of CFs at both midpoint and endpoint depending on the scope of the assessment. On the other hand, the choices of water scarcity index may significantly affect the result of the assessment (Boulay et al. 2014). As mentioned above, two indices of water stress (Pfister et al. 2009; Boulay et al. 2011) can be applied to the model at the midpoint and endpoint in terms of geographical relevance and coverage in order to derive sensitivities of the results. Table 2 shows the correlation coefficients between the estimated damage based on CFs with water scarcity index and total damage from nutritional deficiencies at the regional scale. The correlation coefficients are not high in both cases because damage of nutritional deficiency is determined by not only agricultural water scarcity but other several factors as mentioned in Section 4.1.2. But the case that applied water stress index from Pfister et al. (2009) showed a relatively higher correlation with the total damage from nutritional deficiencies in all regions. This can be explained by the binarity of results suggested by Boulay et al. (2011) with most results presenting regions as “stressed” (value of 1) or “non-stressed” (value of 0), thus affecting the correlation calculation. The characterisation factors determined based on the water stress index from Pfister et al. (2009) were set as default CFs in this study (Annex A1 and A2 in the Electronic Supplementary Material).

Table 2 Correlation coefficients of estimated malnutrition endpoint damage with two water stress indices and the total damage from nutritional deficiencies on a regional scale

Conclusions

Agricultural use of freshwater is generally the largest proportion of total freshwater demand for human activities. Food production shortages due to agricultural water scarcity may cause severe effects on human health in terms of a region’s nutritional conditions. On the other hand, the shortage of food production in a water consumer country can be compensated for by accumulating food stocks and/or spread to other countries through the international trade in food. These adaptation and trade-induced effects are now quantified in our model.

At the midpoint level, characterisation factors were developed in a manner consistent with those derived in the modelling of the endpoint by focusing on physical and social compensation factors (water resource availability, agricultural irrigation demand and food stock compensation capacity). At the endpoint level, malnutrition damage was assessed as a more specific result of freshwater consumption, along with consideration of the complex linkages among countries owing to commodity balance and economic vulnerability within the international food trade. As a consequence, characterisation factors could then reflect the actual social situation in describing the impacts of agricultural water scarcity. Specifically, the completeness of the assessment improved by specifying the impacts of national and trade-induced damage in the endpoint model. Achieving consistency between the CFs at midpoint and endpoint is expected to make the results of assessing the potential impacts of water use in worldwide supply chains more reliable.

In terms of water use for agriculture, the regional scale and temporal variations are very significant factors. These aspects have been integrated in midpoint models (Ridoutt and Pfister 2010; Hoekstra et al. 2012; Pfister and Bayer 2013). More specific modelling in terms of differences in regional and temporal resolutions is left as a future task, while the modelling in this study was performed at a country and annual scale due to limitations in the background data required for the analysis. The depth of lacking dietary energy for a specific part of the population may affect the severity of health damage of each malnutrition case, while the aspect was excluded in this analysis. This point is also expected to be discussed in future analyses for improving the endpoint modelling.