1 Introduction

Within life cycle impact assessment (LCIA), the study of noise impacts is an underdeveloped field (ILCD 2010). The sheer nature of sound and noise has limited the possibility of developing a methodology usable for the evaluation of impacts determined by any source of noise, and in principle, expandable to the analysis of impacts on other species than humans. The dearth of data in other fields than transportation noise stimulated the focus of researchers on this only field. Ad hoc methodologies developed solutions that are scarcely linked to the LCA practice commonly adopted for other pollutants and, in general, for impact assessment and which are based on the consideration of a specific traffic situation rather than on the evaluation of noise emissions which are explicitly linked to activities in the life cycle of a specific functional unit. Fundamental concepts in LCA such as system boundaries and functional unit seem to fall into the background of the analysis. The proposed models lack the required flexibility to expand them from impacts on humans to other target subjects.

The intent of this paper is to propose a new framework for the evaluation of noise impacts (Section “3”), after briefly reviewing the literature in the field of LCA and noise and having assessed what the impacts of noise from an epidemiological perspective (Section “2”) are. Whilst Section “2” is based on existing reviewed knowledge, Section “3” aims at assembling and expanding it to a new framework which may help towards the modelling and operalisation of noise impact assessment for human health and possibly to the health of other species.

Basing on the approach taken in human and environmental risk assessment and the approaches commonly adopted in LCIA for other impact categories, the framework goes beyond the only consideration of transportation and road noise and aims at developing a comprehensive cause–effect chain methodology usable for the evaluation of any source of noise. Even though transportation noise can, in fact, represent a main source of noise impact in the life cycle of some products, in some others, e.g., construction works, it can represent a minor source of impact. The proposed framework will be the skeleton for the future modelling activity which will be presented, together with the necessary developments in the field, in the research agenda section of this paper (Section “4”).

2 Fundamentals of sound and noise

2.1 Generation of a sound wave

If an object is moved at one place in a medium, e.g., air, there is an appreciable disturbance which travels through the medium, which we can refer to as vibration or sound. In the case of air as medium, a sudden movement of the object compresses the air causing a change of pressure which pushes on additional air, which in turn is compressed leading to extra pressure and to the propagation of the generated (sound) wave. To obtain a sound wave, it is necessary that molecules moving from a region with higher density and higher pressure move, transmitting momentum to the ones at lower density and pressure in the adjacent region (see, for example, Feynman et al. (1966) for a complete description). Audition is not static: something in the world has to happen to produce a sound, meaning that a sound source has to be involved in a physical action for the production of what is defined as a sound event or multiple types of sound events (Niessen 2010). The recognition of a sound event by human listeners (auditory event) determines their cognitive representation of it (auditory episode) and, therefore, their reaction to it; when intolerable, unwanted, annoying or completely disruptive of the daily sonic experience of individuals, a sound becomes noise.

2.2 Sound, noise and noise impacts

Since ancient times sleep disturbance and annoyance were already considered main issues for the life of citizens (Ouis 2001). Chariots in ancient Rome, for instance, were banned from night circulation, since their wheels clattered on paving stones (Goines and Hagler 2007). Growing attention of research on noise impacts has emerged in the last century as a consequence of ever increasing levels of intensity of unwanted noise: in 1994 almost 170 million Europeans were found to be living in zones that did not provide acoustic comfort to residents (Miedema 2007), requiring a close evaluation of the increasing magnitude of the presence and role of noise amongst ambient stressors.

In the 1960s, noise had already been identified as a health stressor, and most of its public health impacts had been recognised (Ward and Fricke 1969). They were later reviewed scientifically and confirmed in the 1970s to provide policy makers with recommendations (Health Council of the Netherlands 1971; US EPA 1974). Evidence has, since then, been found to corroborate the existence of a causal relationship between noise and specific effects on human beings and also with respect to other forms of living creatures, affecting their ability to communicate when noise masks their communication sounds, e.g., birds or marine species or also directly threatening their survival and reproduction (Brumm 2004; Slabbekoorn et al. 2010).

The definition of noise as unpleasant, unwanted sound makes the evaluation of its perception quite subjective and less prone to a scientific and robust modelling of its health burdens, indicating the need to employ more than physical measures for operational purposes (Shepherd 1974). Personal traits influence the reaction of people to noise as well as what is commonly defined as their subjective sensitivity to noise or attitude to noise in general (Stansfeld 1993). A complete and literature-summarising definition of noise sensitivity is found in Job (1999): “Noise sensitivity refers to the internal states (be they physiological, psychological [including attitudinal], or related to life style or activities conducted) of any individual which increase their degree of reactivity to noise in general”. It is then clearly indispensable to evaluate the subjective component of noise when evaluating its impacts on human health: some individuals can express more annoyance than their neighbours to a particular level of noise (Griffiths and Langdon 1968; Bregman and Pearson 1972; Stansfeld 1993) and some others high in trait anger might show stronger emotional reactions when disturbed by noise (Miedema 2007). Moreover, the concept of soundmarks, i.e., sounds to which a certain community associate a specific feeling of recognition (Adams et al. 2006), and keynote sounds (Schafer 1994), i.e., sounds heard by a particular society frequently enough to constitute the background against which any other sound is perceived, contributes to making the local situation where a sound event takes place fundamental to understand the relative impact of noise.

Scientific evidence confirms that it is clear that noise pollution is widespread and imposes long-term consequences on health (Ising and Kruppa 2004; Babisch 2006). Following, in fact, the WHO (1947, 1994) definition of health as “a state of complete physical, mental and social wellbeing and not merely the absence of disease and infirmity”, it is clearly understandable that noise impacts human health in manifold ways, which can be more easily detectable and linkable to the source as in the case of hearing loss but less evidently in causing other more subtle health effects. Moreover, it appears from the application of the available computational assessment models to case studies that not only is noise more directly perceived as disturbing by humans in comparison to chemical emissions or resource uses, but it objectively represents, for some processes in a life cycle, the most relevant of the health burdens. Considering, for instance, the overall health impacts of transportation within a life cycle, it is possible to conclude that the impact from noise-related health burdens, evaluated using common metrics (see Section “2.5”), are of the same order of magnitude or higher than those that are attributable to other emissions (Doka 2003; Muller-Wenk, 2004). It has to be noted that the assumption of linearity and the implication of averaging conditions could, however, have led to an overestimation bias and a misdjudgement of the overal health impacts due to noise (Franco et al. 2010).

2.3 Noise exposure and non-physiological effects on humans

Disturbance of activities, sleep, communication and cognitive and emotional response usually leads to what is generally referred to as annoyance. Miedema (2007) defines this as a primary influence of noise and, as reported by Job (1999), it may include other more specific effects such as “apathy, frustration, depression, anger, exhaustion, agitation, withdrawal, and helplessness”. Annoyance is certainly the most well-documented response to noise, seen as an avoidable source of harm.

Several effects on the sleeping activity have been associated with nocturnal noise. Physiological reactions lead to primary sleep disturbances, distressing the normal functioning of individuals during daytime and potentially disrupting personal circadian rhythm with consequential effects on health and well-being (Pirrera et al. 2010). A clear relationship has been found between transportation noise and altered aspects of the sleeping process and the quality of it, in terms, amongst others, of increased body motility (Williams et al. 1964), sleep stage redistribution (Pirrera et al. 2010) and self-reported sleep disturbance (Miedema 2007).

In the context of verbal interactions of people, exceeding levels of noise cause frustration of communications, implying the necessity of raising the voice of the speaker to allow conversations and free speech, altering the social capabilities of individuals and leading to problems such as uncertainty, fatigue, lack of self-confidence, misunderstandings and stress reactions. The impact on vulnerable groups “such as children, the elderly, and those not familiar with the spoken language” (Goines and Hagler 2007) is significant.

Prolonged exposure to noise sources negatively affects processes which require attention and concentration. Experiments demonstrated a direct altering of memory and comprehension functions of individuals exposed to noise, especially sensitive subjects such as children (Clark and Stansfeld 2007), with the manifestation of semantic errors, text comprehension errors, errors in the strategy selection for carrying out tasks, or reduction in connections between long-term memory and working memory (Hamilton et al. 1997; Enmarker 2004).

2.4 Noise exposure and physiological response of humans

The direct exposure to continuous and loud sources of noise, especially if prolonged, and the synergic combination of the stressors previously described can lead to predictable physiological responses. Direct exposure to noise leads to hearing impairment caused by a mechanical damage to the ear or in some cases by the interference of noise with the basic functions of the auditory cells (Chen et al. 1999). Hearing loss is dependent on a number of variables such as type, duration, intensity and frequency of the noise (Rao and Fechter 2000), but also to be considered are other factors such as periods between noise exposures (Henselman et al. 1994) and, of course, the previously mentioned noise sensitivity and individual variability. Hearing impairment can be associated with abnormal loudness perception, distortion and temporary or prolonged tinnitus (Berglund and Lindvall 1995; Axelsson and Prasher 2000).

The exposure to noise levels at or above 85 dB (e.g., the noise of a heavy truck traffic on a busy road) for an 8-h time-weighted average working day over a lifetime is associated to a hearing impairment at 4,000 Hz of about 5–10 dB for most workers (Lusk et al. 1995). It is generally considered that a hearing impairment that exceeds 30 dB, averaged over 2,000 and 4,000 Hz at both ears, can constitute a social handicap (Passchier-Vermeer and Passchier 2000). Noise-induced hearing loss is one of the most common occupational diseases (National Institute for Occupational Safety and Health 2000). The example of construction workers, who usually do not only operate in a single working setting but move around job sites, being exposed not only to the noise coming from tools or equipment of their own but also to the noise of those owned by the surrounding workers (Lusk et al. 1995) is interesting.

The so-called leisure noise (usually exceeding 120 dB) has been closely studied epidemiologically and can be a cause of hearing impairment (Axelsson and Prasher 2000), with young adults being the category of people mostly exposed, in environments such as clubs or discotheques. WHO (1994) recommends a maximum of 4 h of exposure, for a maximum of four times per year, to unprotected leisure noise levels exceeding 100 dB. The identified threshold for pain is 140 dB; even the shortest exposure at levels greater than 165 dB can cause immediate acute cochlear damage (Berglund and Lindvall 1995). Effects of somatic nature include stress-related cardiovascular disorders. It is important to underline how studies on this type of effects are complicated because of the different sensibility, susceptibility and genetic predisposition of individuals to the impairment, and because of the difficulty in evaluating precisely past noise exposure of the subjects under study (Passchier-Vermeer and Passchier 2000). The most complete studies available in the literature are generally focused on the exposure to traffic noise and aircraft noise with a dearth of data in the other fields of noise exposure, apart from limited studies in the field of occupational noise (Rai et al. 1981; Fogari et al. 2001).

In-bedroom and laboratory studies (Hofman et al. 1995) found that sound peaks due to transportation noise caused an increase in heart rates as a direct response to the stimulus in individuals living along highways with high traffic density. Sleep disturbance has been directly associated with collateral cardiovascular effects including increased blood pressure, increased pulse amplitude, vasoconstriction, cardiac arrhythmias (Verrier et al. 1996) as well as increased use of sleep medication and cardiovascular medication (Franssen et al. 2004).

Babisch et al. (2005) and Babisch (2006, 2008) found evidence to support the hypothesis that chronic exposure to traffic noise increases the risk of myocardial infarction especially in male individuals with predisposition to high systolic and diastolic pressure in the range between 45 and 55 years of age, as confirmed by de Kluizenaar et al. (2007) and also in young adults aged 18–32 years (Chang et al. 2007). Less evidence of association was found by Babisch and van Kamp (2009) in the case of aircraft noise. However, a Swedish study confirmed that hypertension was higher amongst people exposed to time-weighted energy-averaged aircraft noise levels of at least 55 dB(A) or maximum levels above 72 dB(A) around the Arlanda airport, in Stockholm (Stansfeld and Matheson 2003).

Exposure to noise also activates the sympathetic and endocrine systems, intervening with the excretion of hormones. Increased levels of catecholamine were found in people exposed to road traffic noise as a response to stress levels (Babisch et al. 2001) and also in workers of a textile factory in Vietnam (Sudo et al. 1996). Irregular excretion of corticosteroids, adrenalin and noradrenalin (Slob et al. 1973) was found in laboratory tests on men as well as upon laboratory animals.

In the context of this article, we are interested in analysing those effects that have been confirmed to have an impact on human health and which can be possibly modelled for their analysis in LCA and specifically in the life cycle impact assessment (LCIA) phase.

2.5 Sound and noise metrics and rating indices

The physical quantity which is of interest for the quantification of noise is sound pressure, defined as the incremental pressure due to the passage of the sound wave in the air, oscillating above and below ambient pressure (Ouis 2001). Sound pressure level (Lp) is defined as:

$$ Lp = 10log\left( {\frac{{{P^2}}}{{P_{\text{ref}}^2}}} \right) = 20log\left( {\frac{P}{{{P_{\text{ref}}}}}} \right) $$
(1)

where P is the sound pressure in pascal. The logarithmic unit is used to account for the large scale of the human sound pressure sensitivity and P ref, which is equal to 2 * 10−5 Pa, usually considered as the lowest sound pressure detectable by the human ear (Lp = 0 dB). In other media (e.g., underwater), a different reference might be used. The sound pressure level is a dimensionless quantity (the logarithm of the ratio of two pressures), but the unit-like indication decibel (dB) is added to indicate the logarithmic scale. The multiplication by 10 is related to the choice for decibel instead of bel and it is then multiplied by a factor 2 following common properties of the logarithm function.

In subsequent elaborations, Lp has been refined to take into account the time-dependent character of noise, with differences of impact on human health and in response to noise identifiable with nocturnal and diurnal noise, and also to take into account the duration of the noise itself.

The so-called A-weighting mode, expressed in A-weighted decibels (dB(A)), is the type of scale introduced to account for the subjective nature of noise exposure, which represents sound pressure levels at different frequencies comparable to that of the human hearing organ and its lower sensitivity to high and low frequencies (Passchier-Vermeer and Passchier 2000). Together with the A-weighting mode, a scale of octave bands frequencies or one-third octave band frequencies is commonly selected, taking into account a specific range of frequencies, with a lower cutoff frequency and an upper cutoff frequency selected according to the specific objective of the measurement (e.g., target subject).

The Equivalent Continuous Sound Pressure Level (Leq) measures the A-weighted sound pressure level over a specified time of measurement T, which can be taken as 1, 8 (i.e., working day), 12 or 24 h:

$$ Leq = 20log\left\{ {{{{\left[ {\left( {\frac{1}{T}} \right)\int\limits_0^T {{P_{\text{A}}}(t)dt} } \right]}} \left/ {{{P_{\text{ref}}}}} \right.}} \right\} $$
(2)

where P A(t) represents the instantaneous A-weighted sound pressure in pascal and T is a specified time interval. Penalties are introduced by other measures to account for exposures happening at specific times of the day. This is the case of Ldn, which represents the day–night level and accounts for an increased penalty of 10 dB(A) between 11 PM and 7 AM. Similarly, Lden, the day–evening–night level, uses an analogous construction but sound levels during the evening, between 7 PM and 11 PM, are increased by 5 dB(A), and those between 11 PM and 7 AM are increased by 10 dB(A).

For single noise events, the preferred measure is the sound exposure level (SEL), which is the equivalent sound level during an event (e.g., the overflight of a plane) normalised to a period of 1 s (Passchier-Vermeer and Passchier 2000). In general, as established with the Directive on Assessment and Control of Environmental noise EC-2002/49 (European Commission 2002a), Lden proved to be a good indicator for long-term effects and especially annoyance.

The study of noise levels, exposure and human health led to the definition of synthesis curves that quantify the exposure–response relationship of subjects exposed to variable levels of noise. Relations for which sufficient quantitative data are available typically regard transportation noise. Miedema and Vos (1998) integrated the results from 55 different datasets on noise and established summarising functions to quantify the relationship between annoyance and the incidence of noise, developing a measure of the percentage of highly annoyed people (%HA) as a function of the Lden level. Criticism has been raised in the past (Probst 2006) over the use of the percentage of highly annoyed people (%HA) as a measure of the effect of noise on humans with the consideration that the metric provides a weak weighting of noise levels and does not reflect the perception of the local communities over the noise level experienced. However, a position paper of the European Commission (European Commission 2002b) and a guide on good practices on noise exposure and effects by the European Environment Agency (2010) included the percentage of highly annoyed people (%HA) as a suitable measure but considered also a larger number of endopoints with a dose–effect relationship. Noise-induced behavioural awakenings, chronic increase of motility, self-reported sleep disturbance, learning and memory difficulties and increased risk of hypertension were found to have sufficient evidence of dose–effect relations or of a threshold value.

Monetised estimates of health damages, also referred to as external costs or externalities (Navrud 2002; ExternE 1995), are commonly used to associate an economic value to the impact of a xenobiotic substance or a pollutant (e.g., noise) onto human health and quantify a loss in life quality in monetary units. Cost–benefit analysis represents a form of evaluation in which the health and non-health aspects of the exposure to a pollutant are evaluated in monetary terms. The procedure allows for an easier inclusion of non-health aspects for the evaluation of criteria such as well-being, personal life satisfaction and productivity (de Hollander 2004). These analyses include the willingness to pay (WTP) of households for a reduction of the noise level in a specific area, measured in euro per decibel per household per year and the willingness to accept (WTA), related to the acceptance level of individuals of the risk to which they are exposed, with the focus often oriented to evaluate productivity loss and health care use as a consequence of health impairment or non-health burdens (Krupnick and Portney 1991; de Hollander et al. 1999).

Health-adjusted years (HALYs) are generally the human health metrics used to transform any type of morbidity including health issues from noise exposure into an equivalent number of life years lost (Hofstetter and Hammitt 2002). To the macro-category of HALYs belong quality-adjusted life years (QALYs) and disability-adjusted life years (DALYs). QALYs measure the actual health quality integrated over time, which usually requires variations and adjustments for the time preference of individuals or societes (Hofstetter and Hammitt 2002; see Pliskin et al. 1980 for a theoretical basis of the measure). DALYs refer to the loss in health that an individual would be exposed to in the case of a morbidity compared to a hypothetical profile of perfect health which would have died at a standard expected age; they are the sum of years of life lost (YOLL) and the number of years lived with a disability (YLD).

Both cost-based and health-adjusted life years find methodological objections (Diener et al. 1998) in the literature, which usually include the consideration of the limited reliability of questionnaire-based surveys and the consideration of health as an economic good (de Hollander 2004) as well as the substantial uncertainty related to the measures even though it was found to be less than one order of magnitude (Burmaster and Anderson 1994). Equity principles and morale often come into the argument of one choice to be made over the other or to exclude both of them on the basis of various reasons. For the context of this article, a detailed exemplification of the pros and cons of the methodologies described is not considered beneficial towards the improvement of the state-of-science in the field of LCA and noise, since both measures provide a useful framework for the explicit evaluation and comparison of health impairments associated with environmental exposures (de Hollander 2004).

3 Sound and noise in LCA

3.1 The current situation

Compliance to the ISO standards is often seen as a fundamental measure of quality for LCA studies. ISO 14'040 (2006) and ISO 14'044 (2006), together with the setting of the standards for LCA, specified the feature and the phases of the analysis including the description of the life cycle inventory (LCI) and of the life cycle impact assessment (LCIA) phases. Also, according to the ISO standard requirements, the addition of the effects on human health due to exposure to noise should—whenever possible—be assessed in the LCIA phase, and data regarding noise included in LCI. Nevertheless, in the words of Franco et al. (2010), “several methodological shortcomings still hinder the inclusion of transport noise as an established impact category within life cycle assessment” and “earlier attempts […] yielded valuable results […], but these were of limited use in the context of everyday LCA practice”. This remark highlights two main aspects of how research in the field of noise and LCA has progressed.

The investigation of possible ways of incorporating the evaluation of noise into LCA has considered primarily and almost exclusively “transport noise” (or traffic noise as it is often referred to) losing the focal point that noise effects in LCA need to relate to the functional unit,which is the transport and not the traffic situation (Althaus et al. 2009a). The two terms, “traffic” and “transport”, seem to overlap in the literature, whilst a distinction should be made to stick to the process causing the noise and not to the situation in which the event takes place. It is necessary to evaluate, for each specific life cycle under investigation, what sources of noise are preponderant and to develop a method that could be applicable to any noise situation relevant to the LCA practice.

The second element emerging from the words of Franco et al. (2010) is the limited use in the everyday LCA practice of the results so far available in the field, still not allowing for a revision of already available LCA analyses. Characterisation factors of the impact category noise are still not included in the main LCIA systems, and few studies have developed models and software of limited use in common practice and that do not yet provide application to upscaled and larger systems at a European and World level (LC-IMPACT 2010), nor do LCI databases which do not include data on noise. Back in 1993, Fava et al. already concluded that “a few processes—blasting minerals, for example—require attention, and certain products—for example, gasoline-powered lawn mowers, leaf blowers, edging tools […] should be included in an LCA if feasible”.

Althaus et al. (2009a) reviewed the methodology and state-of-science for the integration of traffic noise in LCA. Strengths and weaknesses of 66 LCA case studies were studied and combined with data regarding the study of LCA and traffic noise to define a set of requirements, thus, a “profile for noise inclusion methods for LCA” (see p.564, Althaus et al. 2009b). Even though the profile was seemingly not directly referring to a specific type of noise, but generally to “noise inclusion”, the list is specific to the traffic/transportation noise inclusion in LCA. Five different methodologies were analysed in detail to check for their coherence with the explained requirements, covering the whole spectrum of methods available in the field of study of traffic noise and LCA: CML guide for LCA (Guinée et al. 2001; Heijungs et al. 1992), Ecobilan method (Lafleche and Sacchetto 1997), Danish LCA guide method (Nielsen and Laursen 2005), Swiss EPA method (Muller-Wenk, 2002; 2004) and Swiss FEDRO method (Doka 2003). Amongst these methods, only the CML guide for LCA seems to focus on the consideration of the physical nature of sound/noise and on the construction of an indicator that could be used for any stationary source of noise. Althaus et al. (2009b) also propose a framework, which is consistent with the requirement profile individuated and based on the Swiss EPA method. The method is adequate for the consideration of “generic and specific road transport” and, following Muller-Wenk's method (2004), focuses on the consideration of additional noise emissions due to additional vehicles based on the official Swiss emission model SonRoad (Heutschi 2004). The proposal allows for a specific consideration of various vehicles, contexts and traffic situations in terms of space, time, speed and volume, but it does not take into account noise from mixed transportation (Lam et al. 2009). Percentage of highly annoyed individuals (%HA or frequently disturbed or instantaneously disturbed) and DALYs are the measures commonly used in the methods for the evaluation of impacts on human health at various levels of noise.

Franco et al. (2010), who moved on the same line, expanded on the work of Muller-Wenk by incorporating state-of-the-art noise emission models of the series of “improved methods for the assessment of the generic impact of noise in the environment” (IMAGINE 2005, 2007a, 2007b). In the above-mentioned methodologies, background is dealt with (or not as in Guinée et al. (2001); Heijungs et al. (1992) and Doka (2003)) in various manners, and commonly, the background situation defines a baseline condition and starting point from which the calculations develop. The Danish LCA guide method (Nielsen and Laursen 2005) explicitly considers the impact of noise on humans as a function of the part of the noise exceeding the background noise level (Althaus et al. 2009a). Muller-Wenk (2002; 2004) evaluates the background noise situation through the use of data calculated by available computer models using pre-existent traffic intensities and ground properties at specific locations. Franco et al. (2010) take background noise into account and incorporate it in their developed methodology by comparing the impacts of various specific traffic scenarios with or without (i.e., with the sole consideration of the background noise level) the consideration of a specific traffic flow. Lafleche and Sacchetto (1997) consider calculated or measured noise levels along roads as their starting point for the calculation of the area affected by a noise level above a defined threshold (Althaus et al. 2009a).

On the impact side, the impact of noise on human health is quantified in terms of the number of annoyed people using solely annoyance as a comprehensive indicator of impact and Lden as a descriptor of noise levels. The methods presented in the review by Althaus et al. (2009a) and the work by Franco et al. (2010) represent the full spectrum of methods currently available in the field of LCA and noise.

One approach needs to be highlighted. Meijer et al. (2006) describe how the LCA of dwellings could incorporate health effects of traffic, not as part of the life cycle of these dwellings (so not relating to the transport for the materials of the house), but for other life cycles, which just happen to have impacts for the residents of these dwellings.

3.2 Requirements for the assessment of noise in LCA

Ensuring the wide applicability of noise evaluation models in LCA (Althaus et al. 2009b) means that we should allow for the consideration of any type of noise which is proved to cause harm to human health. We can translate this into the following fundamental requirements:

  1. 1.

    Consideration of generic and specific sources of noise in LCA,

  2. 2.

    Separate treatment of different routes of noise emission within an LCA analysis,

  3. 3.

    Accounting for noise emissions from activities in different geographic contexts and evaluation of differences in noise treatment policies,

  4. 4.

    Accounting for different temporal and spatial contexts of noise emission and impact on human health,

  5. 5.

    Accounting for all the activities in the life cycle which can be associated with a noise emission, with particular attention to cases of noise levels above a given threshold and

  6. 6.

    Extendibility to other target organisms.

The first requirement ensures the accuracy of data included in LCA studies, with the focus placed on considering any source of noise. Separate treatment of emission routes ensures that all the possible routes of noise emission, deriving from the transportation of a product from A to B or from the laying of the groundwork of a building, are considered in a complete LCA. Different noise levels from activities also have to be considered amongst the characteristics and configuration of the context where the emission takes place. Spatial differentiation is fundamental in the context of noise in order to have a clear view of the measures in place at different locations (e.g., noise barriers) to protect citizens from being exposed to a source of noise and to account for the vicinity of the listener to the source when a noise event takes place. The temporal importance of the evaluation of noise levels has already been stressed in the previous sections, given the increased level in annoyance and stress levels verifiable in the occasion of a nocturnal noise event. Requirement 5 confirms the necessity of treating noise emissions as any other emissions in the life cycle. The flexibility (requirement 6) highlights what has been considered as a lack of already developed noise assessments available in the literature: in the future it should be possible to investigate, provided specific modelling adjustments, the impacts of noise on other organisms than humans.

The approach commonly in use in the context of LCA for chemical emissions can then be expanded to evaluate noise impacts, following the above-described requirements. In the procedure below, this parallel is described in detail using a multi-step approach, which takes into account the reviewed epidemiology of noise, the LCA and noise work previously analysed, and the theory described in the previous section of this paper.

3.3 Noise compared to emissions into the environment

For a comprehension of noise in the context of emissions, it is fundamental to investigate useful areas of commonalities with, and distinct from, toxic compounds. Given the physical nature of sound, noise obeys to the law of radiation, meaning that its intensity decreases as the distance from the source increases, with an effect localised in the immediate vicinity of the source itself, soon disappearing after the sound is produced (Muller-Wenk, 2002). On the contrary, typical distances between an emission source of a compound and its location of deposition can amount to several hundreds of kilometres (Potting et al. 1998). Phenomena that are typical of other compounds, in fact, such as dispersion, dilution, accumulation/bio-accumulation, sedimentation and deposition, adsorption or degradation assume different characteristics in the case of noise. Moreover, besides the energy content of a specific sound emitted by a source, it is essential to ponder other important pieces of information such as the frequency structure, the volume over time and the site-specific factors (e.g., presence of sensitive groups or keynote sounds) that can influence its impact and magnitude. For toxic releases, the emission compartment is quite important. For noise, we can restrict the discussion to air in the case of human health impacts, although a further refinement of the air compartment into urban and rural will be made, and an additional temporal specification (e.g., day and night) will be introduced. For a future extension to aquatic organisms (Anderson et al. 2011), we may need to include other compartments as well.

The LCA framework introduces a major break between inventory analysis and impact assessment. Inventory analysis looks at the elementary flows (or stressors or environmental interventions), i.e., the physical things taken from or introduced into the environment. It does so, first, on a per unit process basis, and later on, aggregates them across the life cycle. In the context of toxics, the emission in kilogram per type of pollutant (phenol, benzene, etc.) per compartment (air, water, etc.) is what is specified here. Additional descriptors may then be needed (e.g., distinguishing Cr(III) and Cr(VI), or rural and urban emissions). In the context of noise, the physical intervention is the sound level (e.g., in decibel or in energy units), with a possible addition of other descriptors (day or night, rural or urban, high or low frequency, etc.).

The impact assessment takes the inventory results as a starting point. Typical methods for the assessment of human toxicity in impact assessment are based on a causality chain (Udo De Haes and Lindeijer 2002) used to depict the changes in the quality of a natural environment. In principle, the same type of chain can be applied to the evaluation of noise impacts.

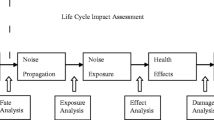
Four phases are considered in human toxicology as parts of a full causality chain. As correctly suggested by Muller-Wenk (2002; 2004), the same scheme can be adapted for use in the context of the evaluation of noise emissions:

  • Fate analysis refers to the change in concentration of a specific pollutant caused by a given emission. In the context of noise impact evaluation, the purpose of the analysis is to determine the increase of sound pressure levels if one or more processes in the life cycle determine noise production.

  • Exposure analysis investigates the number of individuals (humans or other target subjects) affected by the change in concentration identified in the fate analysis. An increase in the sound pressure levels identified in the fate analysis has an impact on a quantifiable number of individuals.

  • Effect analysis shows the effect of the increased concentration of a pollutant if humans (or other target subjects) are exposed to it for a given time lapse. The increase in the concentration of sound emissions (i.e., the marginal increase of sound levels above the background level) has various impacts on humans (or other target subjects), both psychologically and physiologically (see Section “2”), which are quantified at this stage of the analysis.

  • Damage analysis describes the total measurable damage represented by the health effects considered in the previous analysis. The damages caused by the exposure to the noise sources/noisy processes in the life cycle are, in this phase, evaluated to identify what type of diseases are identifiable on humans (or other target subjects).

3.4 General framework for sound emissions and noise impacts

3.4.1 Method overview

The framework here presented builds upon the considerations and the information commented in the previous sections. The breakdown of the various parts of the model starts by proposing a way in which sound can be dealt with in an inventory analysis, overcoming the issues of the common use of the logarithmic unit decibel. A methodological proposal follows, which provides a theoretical way of calculating characterisation factors for the impact category noise using a fate and effect factor (Pennington et al. 2004).

The methodology is based on the consideration of the variation of background sound levels at the emission compartment as a consequence of the presence of one—or more—sound-emitting sources in the life cycle, which consequently determines a variation in the effect on humans at the exposure compartment where the sound propagates.

3.4.2 The inventory part for sound

The first question to address is regarding attaching sound to a unit process in such a way that an aggregation across the life cycle can provide a starting point for the impact assessment. Even though sound is usually measured in decibel, the sound pressure level is obviously not the right quantity to present, as it does not allow for an aggregation over the life cycle. Moreover, it lacks the aspect of duration of the sound.

Heijungs and Huijbregts (2004) stressed the necessity of translating a sound from decibel into an additive scale and of incorporating the duration of the relative sound emission into an aggregate measure and proposed the use of pascal-squared seconds. Similarly, in the field of occupational noise exposure, Drott and Bruce (2011) propose to use the pascal-squared seconds or pasques. Pasques is an additive measure of sound exposure; therefore, it is not suitable for the inventory of sound in a life cycle.

In common practice, a unit process is usually represented in number per unit output. This means that all data are related to that reference. When dealing with a permanently running steelworks which produces 500 kg/h steel and needs 600 kg/h iron, one typically converts the output of steel to 1 kg, thereby the input of iron is changed from 600 kg/h into 1.2 kg of iron. It must be observed that not only the numerical value changes but also the unit changes from a flow (kilogram per hour) into an amount (kilogram). If the process emits 10 kg/h of a pollutant, this converts into 0.02 kg, and when it covers 800 m2, this converts into 1.6 m2 h. If the process in question produces a sound output of a certain frequency (say, 1 kHz) of 90 dB, it does not make sense to convert this into 90/500 = 0.18 dB h. Rather, the sound power level of the source must be calculated and then converted to a quantity that can be added.

The sound power level calculated in dB is obtained by applying Eq. 3:

$$ Lw = 10log\left( {\frac{W}{{{W_0}}}} \right) $$
(3)

where Lw is the sound power level in decibels and W is the sound power in watt produced by the source referred to a reference sound power (W ref) of 1 pW (10–12 W; ISO, 1996), which is normally considered as the lowest sound discernible by a person with a good hearing.

Thus, by back transforming the value of the sound power level in decibel to the sound power, or more precisely to its energy per unit of time, it is possible to obtain an addable quantity. This proceeds by:

$$ W = {W_{\text{ref}}} \times {10^{{{{Lw}} \left/ {{10}} \right.}}}{.} $$
(4)

The analysis of the sound power of a process commonly requires, with the intent of reducing the calculation and time efforts, and given the wide variety of frequencies the human ear is subject to (i.e., from about 20 Hz to 20 kHz), the selection of a scale of frequencies, from f n to f n + 1, determining a set of values of W and Lw to be contemporaneously evaluated (e.g., W fn … fn + 1). A scale of octave bands, meaning a frequency band with each progressive band having double the bandwidth of the previous, is usually considered handy for the analysis of the sound power level and, in general, of noise levels.The centre frequencies assigned for the bands covering the full range of human hearing are commonly the frequencies from 63 Hz to 8 kHz (ISO, 1996), which can be conveniently numbered from 1 to 8. The assignment of frequencies to octave bands, thus, proceeds according to Table 1.

Table 1 Definition of the octave bands (Ford 1970)
Full size table

Thus, back to the previous example, the steelworks produce energy per unit of time of 0.001 J/s at, for instance,1 kHz, so in octave band 5. Applying the conversion to the per kilogram of steel and then expressing it in joule further transforms this into:

$$ \matrix{{*{20}{c}} {\left( {0.00{\text{1 J}}/{\text{s}}} \right)/\left( {{5}00{\text{ kg}}/{\text{h}}} \right) = } \hfill \\ { = \left( {0.00{1}\,{\text{J}}/{\text{s}}} \right)/\left( {{5}00\,{\text{kg}}/{3},{6}00\,{\text{s}}} \right) = } \hfill \\ { = \left( {\left( {0.00{1}\,{\text{J}}} \right)*{3},{6}00} \right)/\left( {{5}00\,{\text{kg}}} \right) = } \hfill \\ { = \left( {\left( {000{1}/{5}00} \right)*{5}00} \right){\text{J}} = {7}.{2}0*{1}{0^{ - {3}}}{\text{J}}.} \hfill \\ } $$

Normal LCI routines are further applicable to scale these numbers to the functional unit and to aggregate them for every unit process across the entire life cycle. This can be done for different categories of sound, e.g., for the sound of high frequency during the night in an urban location, for the sound of medium frequency during the evening in a forest, etc.

Thus, the inventory table contains sound items defined for the scale of eight frequency bands selected, expressed in joule. Following the usual conventions in LCI, one can symbolise these by m 1, m 2, etc., where m i indicates the emitted amount of type i, or alternatively by m 1,1, m 1,2, m 2,1, etc., where the first subscript refers to the type of emission (benzene, daytime frequency noise, etc.) and the second subscripts to the emission compartment (e.g., air, sea water, etc.) or further specify the sound items classifying the attributes considered (e.g., day, night, rural, etc., as in the example in Table 2).

Table 2 Example of an inventory table including also sound energy emissions in J per octave band centre frequencies for a hypothetical life cycle
Full size table

3.4.3 The characterisation factor

The characterisation factor (CF) for the assessment of noise emissions can be calculated using a fate and effect factor, Eq. 1, according to the classical LCIA characterisation scheme (Pennington et al. 2004), as in Eq. 5:

$$ C{F_{i,c}} = \sum\limits_f {\left( {F{F_{i,c,f}} \times E{F_{i,f}}} \right)} $$
(5)

where FF is the fate factor and EF, the effect factor, i is the inventory item in compartment c and f, the final compartment after the fate step, where the target(s) is assumed to be exposed. Thus, the fate factor FF models how inventory item i moves from compartment c to compartment f and the effect factor EF, how serious the effect is for the population living at f and exposed to i. Below, we elaborate the two steps of fate and effect for the conceptual sound–noise model.

3.4.4 The fate factor

In the context of toxics, the fate factor for a substance i is defined as the factor that measures how a change of continuous release to compartment c (Φ i,c ) will result in a change of the steady-state concentration in compartment f (C i,f ):

$$ F{F_{i,c,f}} = \frac{{\partial {C_{i,f}}}}{{\partial {\Phi_{i,c}}}}{.} $$
(6)

Multi-media fate models such as EUSES (Vermeire et al. 1997), contain expression for C i,f (Φ i,c ). The fate factors will embody aspects of fugacity (how willing is a chemical to move from one compartment to another one) and degradability (how stable is a chemical in a specific compartment).

In the noise context, the development of theoretical models for the measurement of sound propagation from sources to receivers at various distances, impedances and contour characteristics (Boulanger et al. 1997; IMAGINE 2005,2007a, 2007b), and that of methods aiming at evaluating the attenuation of noise with distance (Delany et al. 1976), together with the specialist production in sound propagation manuals (see for instance Ford 1970) are a consolidated science of acoustics. For the purpose of LCA, ISO 9613-2 (ISO 1996) provides a more flexible and practical engineering method that can be ussed for predicting the long-term average sound pressure level under defined conditions from a source of known sound power emission. Any source is defined as a point source or as an assembly of point sources, moving or stationary, making the standard suitable for overcoming methodological limitations in assessing noise impacts in LCA and able to follow the requirements defined (Section “3.2”). At this stage of the development, the ISO standard allows for the development of a generic structure that is able to encompass any situation of emission and propagation, being determined by a single source or by an assembly of point sources each with directivity or propagation properties and, in principle, contributing to the overall sound emission. The model will be, in the future, supported for the determination and calculation of specific variables and components (Table 3) by findings of the international project IMAGINE (2007a, 2007b).

Table 3 Values and possible sources for the parameters of the characterisation factor
Full size table

We propose, therefore, to use the long-term average sound pressure level (Lp) per octave band i, as specified by ISO 9613-2, as a basis for the modelling of fate, adapting the notation when needed for disambiguation purposes. For the quantification of the Lp, in decibel, we follow the procedure suggested by the ISO standard. We start by calculating the equivalent continuous octave band sound pressure level at the final compartment f from Eq. 7:

$$ L{p_{i,f}} = L{w_{i,c}} + {D_{i,c,f}} - {A_{i,c,f}}{.} $$
(7)

Here, Lw i,c is the sound power level as described in Eq. 3. D i,c,f is the directivity correction, in decibels, that describes to what extent a deviation of sound pressure level occurs in a specified direction from the source of sound power level Lw i,c . The directivity correction D is 0 dB for an omnidirectional sound emitting source. A i,c,f in Eq. 7 is the octave band-specific attenuation, in decibels, occurring during the propagation of sound from source to receiver, and it is given by the contemporary consideration of several attenuation factors, which include geometrical divergence, atmospheric absorption, meteorological variation, presence of barriers, miscellaneous other effects, etc. The methodology can be adapted to be used for any generic source of sound including that generated by transportation, with the introduction of transportation means-specific attenuation and propagation parameters. Given that Lp is expressed in decibel, a conversion will be needed to have the sound pressure expressed in pascal and, therefore, comparable with the sound power emission (W) gathered in the inventory phase. Recalling the definition of sound pressure level as presented in Section “2.5”, in Eq. 1 and that of sound power level in Eq. 3, we obtain:

$$ \begin{gathered} {P_{i,f}} = {P_{\text{ref}}} \times {10^{{{{L{p_{i,f}}}} \left/ {{20}} \right.}}} = \hfill \\ = {P_{ref}} \times {10^{{{{\left( {L{w_{i,c}} + {D_{i,c,f}} - {A_{1,c,f}}} \right)}} \left/ {{20}} \right.}}} = \hfill \\ = {P_{\text{ref}}} \times {10^{{{{\left( {L{w_{i,c}}} \right)}} \left/ {{20}} \right.}}} \times {10^{{{{\left( {{D_{i,c,f}} - {A_{1,c,f}}} \right)}} \left/ {{20}} \right.}}} = \hfill \\ = {P_{\text{ref}}} \times \sqrt {{\frac{{{W_{i,c}}}}{{{W_{\text{ref}}}}}}} \times {10^{{{{\left( {{D_{i,c,f}} - {A_{1,c,f}}} \right)}} \left/ {{20}} \right.}}} = \hfill \\ = \frac{{{P_{\text{ref}}}}}{{\sqrt {{{W_{\text{ref}}}}} }} \times \sqrt {{{W_{i,c}}}} \times {10^{{{{\left( {{D_{i,c,f}} - {A_{1,c,f}}} \right)}} \left/ {{20}} \right.}}}{.} \hfill \\ \end{gathered} $$
(8)

Here, P i,f is the sound pressure, in pascal, in octave band i at compartment f relative to a reference sound pressure, P ref, of 2 * 10−5 Pa (ISO, 1996), whilst W i,c is the sound power, in watt, in octave band i at compartment c. The factors D i,c,f and A i,c,f , thus, serve to translate how much sound power from a source at c reaches a target at f.

The fate factor is now defined as the marginal increase of the sound pressure at f due to a marginal increase of the sound power at c, evaluated at the background level W i,c  = Wamb i,c :

$$ \begin{gathered} F{F_{i,c,f}} = {\left( {\frac{{\partial {P_{i,f}}}}{{\partial {W_{i,c}}}}} \right)_{{W_{i,c}} = Wam{b_{i,c}}}} = \hfill \\ = \frac{{{P_{\text{ref}}}}}{{\sqrt {{{W_{\text{ref}}}}} }} \times \frac{1}{{2\sqrt {{Wam{b_{i,c}}}} }} \times {10^{{{{\left( {{D_{i,c,f}} - {A_{i,c,f}}} \right)}} \left/ {{20}} \right.}}}{.} \hfill \\ \end{gathered} $$
(9)

The fate factor is measured at c given the ambient condition before the functional unit under investigation is introduced into the system; therefore, the fate factor reflects the marginal increase in the total ambient sound power at c.

As P ref and W ref are given, this reduces to

$$ F{F_{i,c,f}} = \frac{{{C_{\text{ref}}}}}{{\sqrt {{Wam{b_{i,c}}}} }} \times {10^{{{{\left( {{D_{i,c,f}} - {A_{i,c,f}}} \right)}} \left/ {{20}} \right.}}} $$
(10)

where C ref is 20 Pa W−1/2. The unit of the fate factor is pascal per watt: it brings about the conversion of a source sound power in watt to a target sound pressure in pascal. Therefore, a sound power “emitted” by a generic source in the life cycle at compartment c (e.g., rural day), being it a machine, a truck, a train, etc. or their combination is diffused into air and propagates through the medium and reaches compartment f, attenuated by the direction of emission from the source and by a series of attenuation factors (e.g., meteorological, physical, etc.) which determine a variation of sound pressure at f. It has to be noticed that the fate factor is a function of the sound power Wamb i,c . This is not the case for the linear multi-media models that are used for toxicity assessment, but it is not strange in itself. Toxicity models in LCA often employ a non-linear dose–response relation for the effect factor (Huijbregts et al. 2011), but not for the fate factor. We should understand the Wamb i,c as the background level to which a marginal change is added. So, it is not case-dependent, but it obviously depends on the compartment (location) of emission c and on the octave band i. Background levels of sound pressure may be obtained from noise maps, where noise exposure data by different noise sources and noise assessment data at a European level have been collected for most European countries (EEA-ETC LUSI, 2010).

3.4.5 The effect factor

In LCIA, the effect model transforms the results of the exposure step (the dose) into a measure of impact. For toxics, a usual way to do so is to divide the dose for a chemical by a critical level, say the EC50 or HC5, of that chemical. In that way, different types of chemical are “normalised”. This can be interpreted as a conversion step transforming the dose into an “effective” dose, where the intrinsic harmfulness of the chemical is used to establish the relative weight of a chemical.

For the effect step in the noise model, we do a similar thing. The effect of the exposure to noise depends on three aspects:

  • The aspect of the frequency–dependency of perception by humans;

  • The aspect of the time of the day of the exposure; and

  • The aspect of the number of humans that are exposed in the target area.

Because the effect indicator we develop corrects the sound levels at a target location into “effective” sound levels, the unit of the category indicator results will still be pascal-like, so looking like an exposure indicator but, in fact, representing an effect indicator.

Following the specifications above, the sound pressure level in octave band i at compartment f, Lp i,f , is perceived differently for different octave bands. The A-weighting provides standardised weighting factors for this (Fletcher and Munson 1933; ANSI 2001).The A-scale weighting factors for octave band i is denoted as α i and is added to Lp i,f to obtain the frequency-corrected sound pressure level Lpf i,f , (for which the “unit” A-weighted decibels (dB(A)) is typically used):

$$ Lpf = L{p_{i,f}} + {\alpha_i}{.} $$
(11)

To account for the fact that sound emissions influence the life of individuals differently according to the time of the day the emission takes place, the value of Lpf i,f is further corrected by a penalty that is zero for daytime and non-zero in the evening and at night (Ouis 2001; see Section “2.5” of this article). Thus, Eq. 11 transforms as:

$$ Lpf{t_{i,f}} = L{p_{i,f}} + {\alpha_i} + {\beta_f} $$
(12)

where β f represents the time weighting of the sound. For the frequency- and time-corrected pressure, Pft, back transforming the decibel into pascal applying the definition of sound pressure level, we thus obtain

$$ \begin{gathered} Pf{t_{i,f}} = {P_{\text{ref}}} \times {10^{{{{Lpf{t_{i,f}}}} \left/ {{20}} \right.}}} = \hfill \\ = {P_{\text{ref}}} \times {10^{{{{\left( {L{p_{i,f}} + {\alpha_i} + {\beta_f}} \right)}} \left/ {{20}} \right.}}} = \hfill \\ = {P_{\text{ref}}} \times {10^{{{{\left( {L{p_{i,f}}} \right)}} \left/ {{20}} \right.}}} \times {10^{{{{\left( {{\alpha_i} + {\beta_f}} \right)}} \left/ {{20}} \right.}}}{.} \hfill \\ \end{gathered} $$
(13)

The third aspect of the number of targets is introduced by multiplying the total value of Pft at f by the number of people living in compartment f, N f :

$$ PP = \sum\limits_f {\left( {{N_f} \times \sum\limits_i {Pf{t_{i,f}}} } \right)} $$
(14)

where PP is interpreted as the person-pressure of sound, which is measured in person-Pa.

The effect factor is introduced as the marginal change in person-pressure due to a marginal change in the sound pressure of octave band i at compartment f:

$$ E{F_{i,f}} = \frac{{\partial PP}}{{\partial {P_{i,f}}}}{.} $$
(15)

As the complete formula for “dose–response” is

$$ PP = \sum\limits_f {\left( {{N_f} \times \sum\limits_i {\left( {{P_{\text{ref}}} \times {{10}^{{{{\left( {L{p_{i,f}}} \right)}} \left/ {{20}} \right.}}} \times {{10}^{{{{\left( {{\alpha_i} + {\beta_f}} \right)}} \left/ {{20}} \right.}}}} \right)} } \right)} $$
(16)

the effect factor becomes

$$ E{F_{i,\,f}} = {N_f} \times {10^{{{{\left( {{\alpha_i} + {\beta_f}} \right)}} \left/ {{20}} \right.}}}{.} $$
(17)

The effect factor is thus strikingly simple: it contains just the A-scale weighting for octave band i (α i ), the day/night weighting (β f ) and the number of people living in compartment f (N f ). The unit of the effect factor is person; thus, it represents, given the population at f, the number of people that are exposed to a variation in sound pressure at compartment f corrected according to the sensitivity to the frequency composition of the emission and the time of the day of the exposure.

3.4.6 The midpoint characterisation factor and its use in LCIA

For midpoint characterisation, the usual structure applies. The characterisation factor is

$$ C{F_{i,c}} = \frac{{{C_{\text{ref}}}}}{{\sqrt {{Wam{b_{i,c}}}} }} \times \sum\limits_f {{{10}^{{{{\left( {{D_{i,c,\,f}} - {A_{i,c,\,f}}} \right)}} \left/ {{20}} \right.}}}} \times {N_f} \times {10^{{{{\left( {{\alpha_i} + {\beta_f}} \right)}} \left/ {{{20}}} \right.}}}{.} $$
(18)

The summation over the emission compartment f allows for the evaluation of the total impact of the sound emission on the target subjects living at f. The compartment can be spatially indentified and defined as urban, rural or offshore or, with a finer grain of definition, which is further divided to incorporate a higher level of detail.

The unit of the characterisation factor is person-Pa/W. It is applied in an LCA by means of

$$ HN = \sum\limits_i {\sum\limits_c {C{F_{i,c}} \times {m_{i,c}}} } $$
(19)

where HN represents the noise impact to humans. As the sound emission m i,c is measured in joule, the impact NH has the unit person-Pa/W J = person-Pa * s. It can be interpreted as the number of people that are exposed to a certain sound pressure for a certain period of time.

The characterisation factor looks complicated, so let us see what is needed to tabulate lists of such factors, as has been done for established impact categories like global warming and toxicity. We need to specify the archetypical emission and exposure compartments c and f. For instance, one could choose here to define three spatial and three temporal situations: urban, rural and offshore, and day, evening and night. For the frequencies i, we already chose for the eight frequency bands of Table 1. Six sets of numbers have to be listed (see Table 3).

Some of the data present in Table 3 requires the combination and gathering of various sources of information. Some of the data in question is usually available in the form of GIS maps with a variable level of grid mesh. This is the case of the number of people living at the exposure compartment, N f , and of the background noise levels, Wamb i,c , available in the form of noise maps. The values of A i,c,f and D i,c,f depend on the location of emission and exposure and can be derived from the application of the ISO9613-2 and of the findings of the IMAGINE project (2007a, 007b) to the archetypical compartments to be developed. With a choice of three spatial and three temporal compartments and eight octave bands, there are no more than 72 characterisation factors. In this way, applying the characterisation step requires a simple and concise recipe.

4 Discussion and conclusion

4.1 Noise impact model development and future research agenda

The structural framework presented in Section “3” represents the first step of a development process which will culminate in the creation of a working mathematical model, together with its elaboration and application to case studies, which will possibly allow for the determination of a noise footprint of a life cycle. The flexibility of the framework structure will allow for its expansion and adaptation for the incorporation of previous work and new contributions in the field, with particular attention to results obtained by international EU projects which have obtained significant results in proposing suitable methods for the measurement of sound propagation from various sources. The proposed model allows for the measurement of the sound emission from a single sound-emitting source or multiple sources present at the emission compartment. However, as in the case of models dealing with the combined emission of chemicals, the summation of multiple sources can lead to an extremely high noise concentration in the studied environment. At this stage of development, the model does not discriminate between possible synergistic, antagonistic or interference effects of the emitting sources but logarithmically treats their impacts.

The overall uncertainty of the model has not been tackled in this contribution, although it is of fundamental importance to deal with uncertainty in any LCA contribution. Given the complexity and the extension of such analysis, we reserve to conduct it in our follow up research. The use of techniques such as global or local sensitivity analysis (Heijungs and Huijbregts 2004; Saltelli et al. 1999) can help to perfect the model performance and applicability. The study of the impact of the variation of the model input, which considered the methodological, temporal and geographical variability of the model, will ensure the study of how uncertainty of the input propagates to the variance of the model output and will allow to propose accurate characterisation factors for noise impacts. Similarly, the risk of underestimation of the impact, which applies to all data systems, will be taken into account in the characterisation of noise. In the case of noise measurement, average values could portray a modelled system which, in reality, has a much higher impact on the health of the exposed population. Blast noises, for instance, which are common in the mining or construction sectors, are the result of sudden emissions which follow a moment of silence. Therefore, averaging a value over time could underestimate the effective proportion of the impact.

For the noise impact on humans, in contrast to many traditional impact categories, we have not introduced a dimensionless potential like the global warming potential (relative to CO2 to air) and the human toxicity potential (relative to, e.g., dichlorobenzene to air). For reasons of consistency, it would be reasonable to do the same and reformulate the characterisation as

$$ HN{P_{i,c}} = \frac{{C{F_{i,c}}}}{{C{F_{{\text{re}}{{\text{f}}_i},{\text{re}}{{\text{f}}_c}}}}} $$
(20)

where HNP represents the human noise potential, related to a unit of sound emission in a predefined reference octave band and in a predefined reference compartment, for instance, 1 kHz at urban daytime. The result of the characterisation would, in that case, not be expressed in person-Pa s, but in joule equivalent of the reference sound, just as the GWP yields a result in kilogram equivalent of CO2.

Our idea, at this moment, is not to use the dimensionless potential for noise but to use the (admittedly abstract) person-Pa/W for the characterisation factors and the person-Pa s for the characterisation results.Furthermore, in order to develop a methodological solution for the quantification of noise impacts, it is fundamental to gather information about the background or ambient condition of the area where the sound event takes place. The importance of the specific location of exposure has been stressed in Section “2.2”, where auditory cognition concepts as soundmarks and keynote sounds have also been defined. Key elements of the location of emission (e.g., time of day) have to be defined to incorporate the subjective impact of noise in the analysis. The characterisation factor developed allows for the evaluation of location-specific features of the emission. LCA tries to measure marginal changes, on a background situation subject to environmental interventions, even in circumstances in which they are relatively small and diminishing with increasing distance from the source (Verones et al. 2010). In our framework, the fate factor is calculated considering that the emission compartment is already sonically perturbed and that the increase of pressure at the exposure compartment is dependent on the increase of power at the emission compartment. As for the effect on humans, corrections have been applied to the sound pressure calculation to make it as adherent as possible to the human perception of sound/noise as identified in common epidemiological practice.

The calculation of the CF for noise impacts on human subjects allows for a midpoint characterisation, though a possible extension of the framework from midpoint to endpoint levels could be applied, with specificities to be further investigated with respect to the relationship between DALYs and the morbidities highlighted in the Sections “2.3” and “2.4” of this article.

WHO (2011) selected (amongst the outcomes earlier reported) cardiovascular disorders, cognitive impairment, sleep disturbance, tinnitus and annoyance as consequences of noise to focus research on, giving details on appropriate measures and indexes to be used case by case and with detail of DALY estimates, when possible. Estimated DALYs for western European countries were, respectively: 60,000 years for ischaemic heart disease, 45,000 years for cognitive impairment of children, 903,000 years for sleep disturbance, 21,000 years for tinnitus and 587,000 years for annoyance. All impacts in total ranged between 1.0 and 1.6 million DALYs. WHO data should be further analysed in details. If DALYs caused by environmental noise are compared with those from other pollutants, it is important to take into account the approximations and assumptions made in the calculation process.There are, in fact, several uncertainties, limitations and challenges which have to be taken into account for the selection of health effects. Unfortunately, the quality and the quantity of the evidence and data are not the same across the different health outcomes and derived from a limited pool of studies. Possible confounding factors should be taken into account in the analysis. These include age, gender, smoking, obesity, alcohol use, socioeconomic status, occupation, education, family status, military service, hereditary disease, use of medication, medical status, race and ethnicity, physical activity, noisy leisure activities, stress-reducing activities, diet and nutrition, housing condition and residential status (WHO 2011). Other stressors like air pollution and chemicals might be considered in the context of combined exposure with noise. A further point to consider with respect to variability is that psychoacoustical variations (see, for example, Moore 1989) should be taken into account for the analysis to be, as much as possible, reflective of the effective perception of noise by humans and should possibly be included in future expansions of the framework. A-weighting and temporal corrections, in fact, do not fully cover the complete range of variations of human perception and relative response to a sonic event. Events with similar sonic features and similar sources that produce them can be perceived differently by different individuals and determine different stimuli and sensations (e.g., at equal contour conditions, a modern and fast train is pleasant, whilst an old and ugly one is unpleasant). The extent to which this is feasible is, at this stage, not clear.

As described in Section “2.5” of this paper, dose–effect curves for a generic noise health effect supported by quantitative data are commonly available for effects attributable to Lp determined by transportation noise. Curves can be reset and converted to pascal and variation of dose–effect relationships calculated per variation of sound pressures in pascal. Further research, also taking into account the precautions mentioned, is needed for other sources than transport-related ones.

Given the stochastic nature of noise effects on humans, meaning that we have statistical evidence of the existence of some effects but we lack a deterministic link between severity/effect and exposure (Bare et al. 2002), uncertain estimates need to be made to move to an endpoint level. Potting, in Bare et al. (2002), suggests that a combination of “the spatial differentiated or site-dependent midpoint modelling with the site-generic endpoint modelling” would be desirable. In the context of noise, the midpoint could then be translated, bearing in mind the introduction of extra uncertainty into the system, into an endpoint, requiring the calculation of a damage factor for human health, by using the DALY scale and a convenient health damage model.

Given the number of people, N, living at compartment f, we can evaluate through PP the number of people who are exposed to a sound pressure in pascal. Individuals will be exposed to a different noise-related morbidity to which a year of life lost, or a fraction of it, can be associated. The morbidity could be intended as a statistically defined function linking the person-pascal at compartment f to the disability-adjusted years given the composition of the population. At this stage, the damage factor is just touched on and will be further developed in our future work.

Advancements in the modelling of noise impacts still require the development of research in some key fields. On the inventory side, there is a lack of sound emission data for unit processes outside the highly analysed transportation field. At a midpoint level, impacts can already be highlighted through the framework but dose–response curves need to be reset. Furthermore, research should be oriented towards translating new epidemiological findings, where possible, into dose–response relationships, in turn translatable, if necessary, into the DALY scale. For the expansion of research to the evaluation of the impacts of noise on the quality of ecosystems and other subjects than humans, it would be necessary to incorporate in the analysis epidemiological data on ecosystems, which has not been systematically organised yet, in order to stress similarities and singularities of impacts on humans and impacts on ecosystems. As reported in Section “2”, ongoing studies are already investigating the field with interesting results that could be incorporated in the model. In principle, the framework provided could be adapted with minor changes (e.g., different frequency corrections) to non-human populations, providing the basis for future work in the field of LCA and noise impacts on the survival of ecosystems.