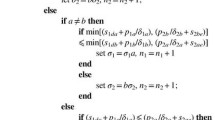Introduction

The global population growth, which has resulted in an exponential increase in industrial activities, and the worsening environmental situation over the past few decades highlight the need for sustainable industrial development. Global energy consumption is projected to grow by nearly 50% between 2018 and 2050, which is expected to reach a high of 910.7 quadrillion BTU. The industrial sector, including mining, manufacturing, agriculture, and construction, accounts for the largest share of global energy consumption.Footnote 1

To respond to the growing energy demands and alleviate the grid’s burden during peak hours, many countries introduced time-dependent energy prices that can vary during the day and across seasons. As a prime example, manufacturing enterprises are asked to shift all or parts of their activities to the off-peak periods to reduce the load on the system to manage the energy crisis. Purchasing energy-efficient machines, updating product designs, and process optimization are some of the other measures to tackle the energy consumption problem. Production scheduling is a relatively affordable and effective solution to help manage operations in the quest for cleaner production (Dai et al. 2013).

As a generalization of the classic flow-shop and parallel-machine scheduling, the hybrid flow-shop scheduling problem (HFSP) consists of at minimum two processing stages with at least one of them having two or more parallel machines (Ruiz and Vázquez-rodríguez 2010). Machines in the production stages can be identical, uniform, unrelated, or a combination, and the jobs flow through the shop floor in the same direction (Linn and Zhang 1999). The wide industrial needs have motivated production researchers to extend the HFSP for various shop floor configurations. Salvador (1973) for the first time applied the HFSP in practical settings, i.e., nylon polymerization production context for minimizing the maximum completion time—makespan. In the packaging industry context, Adler et al. (1993) developed a robust scheduling system that meets the due date and maximizes plants’ throughput. Minimizing makespan and buffer queueing in semiconductor manufacturing, Wittrock (1988) applied an adaptable scheduling algorithm to handle the dynamics of the shop floor. Jin et al. (2002) developed a scheduling approach for three-stage printed circuit board production line optimization, aiming to minimize the total completion time of all jobs over a finite planning horizon. Other practical applications of HFSP include the iron and steel industry (Tang and Wang 2011), ion plating cell production, container handling systems in a maritime terminal (Chen et al. 2007), and textile, glass, paper, furniture, and plastic-making industries (Lin et al. 2021).

Incorporating the technical and operational requirements into the basic HFSP, like setup time (Zandieh et al. 2006), machine eligibility (Ruiz and Maroto 2006), the machine turn-off-turn-on decisions (Mouzon et al. 2007), the transfer time of jobs (Pan et al. 2013), a limited buffer between production stages (Wardono and Fathi 2004), and work-center space constraints (Moghadam et al. 2018), has facilitated its industry reach. Most of the existing scheduling problems overlooked human considerations. Considering the impact of workers’ capabilities on energy efficiency (Zhang and Dornfeld 2007), simultaneously incorporating these factors helps to account for the possible interactions and improves the optimization outcomes. Inspired by this practical need, the main contribution of this study is to incorporate an energy consumption model into the HFSP formulation while considering workers’ performance and sequence dependent setup time (SDST) between the processing of consecutive jobs. Such an extension increases the scheduling complexity and calls for effective solution approaches. A multi-objective metaheuristic algorithm is extended and tested to contribute to the scheduling literature.

The rest of this manuscript is organized into four sections. The “Research gap” section reviews the relevant literature and highlights the research gap. The “Mathematical formulation” section is devoted to problem description and mathematical model formulation. The adjusted multi-objective genetic algorithm (AMOGA) optimization algorithm for solving the model is presented in the “Solution method” section. The “Computational experiments” section presents the computational experiments and analyzes the results considering different instances. Finally, the study is concluded and summarized in the “Conclusions” section.

Research gap

Maximizing the shop floor efficiency has been the central optimization objective in the production scheduling literature (Ruiz and Vázquez-rodríguez 2010; Ribas et al. 2010; Lee and Loong 2019). To tackle up-to-date manufacturing concerns for environmental sustainability and energy security, the energy consumed on the shop floor should also be taken into consideration. A growing number of studies are investigating this paradigm shift. Early studies on energy-efficient scheduling were limited to optimizing energy consumption using execution time variables (Dai et al. 2013; Tang et al. 2016; Yan et al. 2016; Li et al. 2018). More recent studies considered energy consumption models under time-of-use electricity tariffs. Such energy models are more practical and can more effectively address energy efficiency.

Luo et al. (2013) investigated scheduling under time-of-use electricity tariffs while minimizing makespan and electric power costs. Applying the right-shift procedure to reduce the estimated production cost, they found that as the length of each electricity price period increased, the electric power cost decreased. They suggested that it is more energy efficient to consider a mix of high-power and low-power machines rather than having the same number of machines with middle power. In a closely relevant study, Zhang et al. (2019) developed a bi-objective optimization model with the presence of time-of-use electricity tariffs for scheduling flexible flow-shops consisting of machines with heterogeneous energy consumption but did not account for the workers’ capabilities and setup times despite their relevance to the energy consumption context. They used the strength Pareto evolutionary algorithm (SPEA2) for solving the multi-objective optimization problem. Wang et al. (2020) proposed augmented epsilon-constraint and evolutionary algorithms for solving various variants of two-stage flow-shops under time-of-use energy tariffs, minimizing makespan and total energy consumption considering a case from the glassmaking industry. Most recently, Xue and Wang (2023) developed a multi-objective discrete differential evolution algorithm for scheduling under time-of-use electricity tariffs in two-stage flow shop environments.

To improve the practicability of the scheduling problems, direct human involvement should also be considered along with machine-related resource constraints. Industry 5.0 calls for this addition to the production planning and control models. Dual resource constraints have seen some developments in the job shop scheduling literature. Zheng and Wang (2016) proposed a knowledge-guided fruit fly optimization algorithm to solve dual resource-constrained flexible job shops with a single objective of minimizing the makespan. A flexible job shop with dual-resource constrained was studied by Yazdani et al. (2019) where two evolutionary algorithms were developed to minimize the makespan, critical machine workload, and total workload of machines altogether.

As a relevant variant of dual-resource constrained feature, workers’ flexibility considers the number of machines a worker can operate. An illustrative example of this scheduling variant is presented in Fig. 1, where identical machines with different power consumption operate with the help of different skilled workers. In this example, worker flexibility is considered in the first stage, meaning that any of worker 1 or worker 2 can be assigned to perform the setup operations.

Fig. 1
figure 1

The real-world illustration of a hybrid flow-shop with worker flexibility

Full size image

Gong et al. (2018a) investigated a multi-objective variant with flexible workers aiming to minimize total worker cost and makespan while maximizing green production indicators using an improved genetic algorithm. Gong et al. (2018b) developed a memetic algorithm to solve multi-objective flexible job shops with flexible workers, aiming at the minimization of makespan, maximum machines workload, and total workload of all machines. Gong et al. (2020) addressed flexible flow-shops with worker flexibility. They proposed a hybrid evolutionary algorithm to minimize three objectives of makespan, total worker cost, and green production indicators. They also developed a multi-objective memetic algorithm aiming to minimize the makespan, and total tardiness while accounting for a balanced workers’ workload in an HFSP with dual resource constraints. In their proposed model, operations are processed by both machines and workers with predefined processing times. Gong et al. (2021) developed a non-dominated ensemble fitness ranking algorithm for multi-objective flexible job-shop scheduling problem considering worker flexibility. Most recently, Luo et al. (2023) developed a Pareto-based two-stage evolutionary algorithm considering workers’ flexibility in flexible job shop production environments.

There are limited scheduling models that consider the workers’ flexibility and energy efficiency. Meng et al. (2019) proposed two mixed-integer linear programming models, an effective variable neighborhood search algorithm is utilized, and two energy-saving strategies, namely postponing strategy and turning off/on strategy to minimize total energy consumption in HJSP with worker flexibility. Meng et al. (2023) developed a variable neighborhood search algorithm for the optimization of energy-conscious flexible job shop scheduling problem with workers’ flexibility. The flow shop studies that consider dual resource conditions and workers’ flexibility are quite limited.

The research on HFSP predominantly considered machines as a sole resource. On the shop floor, different resources are required to complete the products. The most important resources are (1) machines (and robots), which are used to process the planned operations and can be one resource type like in a spool fabrication shop (Moghadam et al. 2014) or a combination of all types of resources like in car manufacturing industries; (2) energy, which is available in forms of electricity, gasoline, and coal, to provide power for process machines, handling systems, auxiliary equipment, lighting, and so forth; and (3) workers that operate machines and/or adjust tools for undertaking different jobs. Depending on the machine shop, a worker may be assigned to only one machine at a time to act as an operator that remains busy until the operation of a specific job is over. Otherwise, they may work on more than one identical or unrelated machine that should be adjusted and/or prepared for starting the next operation. In the latter case, the worker/operator remains busy for the duration of the setup operations. Given the worker’s role in these operations, human-related considerations, in particular their capabilities, should be incorporated into production planning to account for the social aspect of sustainability.

The next section extends the formulation developed by Zhang et al. (2019) to integrate the major social and environmental aspects of sustainability into the multi-objective HFSP, that is, simultaneously accounting for the energy consumption model as well as the human-related and setup constraints to account for sustainability in the scheduling problem.

Mathematical formulation

To provide a formal description of the problem, let us assume that \(n\) jobs should flow through \(s\) successive production stages in the same direction. In each stage, there are one or more identical machines featured with different power consumption and workers’ assignment when machines are in the setup state. Workers are required to perform preparational activities, like tools adjustment and cleaning, while the number of workers is limited, and the workers have different skill sets. In this situation, the objective is to arrange the operations in a time interval considering both objective functions. A schedule is feasible only if (a) every job is processed by only one machine and in only one stage; (b) each machine processes only one operation at a given time; (c) each worker can operate only one machine at a time and when the machine is in its setup state; (d) jobs are independent of each other; (e) machines are independent of each other; (f) workers are independent of each other; (g) operations are not interrupted after started; (h) every operation is processed only after its preceding operations are completed. It is also assumed that the moving time between the operations of machines is negligible, and the processing times corresponding to the operations and the SDST between different operations are predefined and deterministic.

The following indices, sets, parameters, and decision variables are used in the mathematical formulation of the problem.

Indices

\(j,\mathcal{I}\)

Job index, where \(j=\mathrm{1,2}, \dots , {n}_{j}\)

\(m\)

Machine tag, where \(m=\mathrm{1,2}, \dots ,{n}_{m}\)

\(s\)

Index of stages, where \(s=\mathrm{1,2}, \dots ,{n}_{s}\)

\(w\)

Workers’ index, where \(w=\mathrm{1,2}, \dots ,{n}_{w}\)

\(k\)

Sequential index of operations processed on the same machine,\(k=\mathrm{1,2}, \dots ,{n}_{l}\)

\(q\)

Sequential index of operations processed by the same worker,\(q=\mathrm{1,2}, \dots ,{n}_{l}\)

Parameters

\({n}_{j}\)

Number of jobs

\({n}_{m}\)

Number of machines

\({n}_{s}\)

Number of stages

\({n}_{w}\)

Number of workers

\({AM}_{s}\)

The set of available machines in stage \(s\)

\({AW}_{s}\)

Available worker set in stage \(s\)

\({C}_{ms}\)

Availability time of machine \(m\) in stage \(s\)

\({C}_{ws}\)

Availability time of worker \(w\) in stage \(s\)

\(ActW\)

Active worker

\({nm}_{s}\)

Number of machines in stage \(s\)

\({nw}_{s}\)

Number of workers in stage \(s\)

\({O}_{js}\)

Operation of job \(j\) in stage \(s\)

\({P}_{jsm}\)

Processing time of \({O}_{js}\) processed on machine \(m\)

\({C}_{js}\)

Completion time of \({O}_{js}\)

\({SC}_{js}\)

Sorted set of \({O}_{js}\) in stage s

\({C}_{j}\)

Completion time of job \(j\)

\({ST}_{jsm}\)

Start time of processing job j in stage \(s\) on machine \(m\)

\({st}_{j\mathcal{I}s}\)

Setup time between jobs \(j\) and its predecessor in stage \(s\)

\({pf}_{w}\)

Performance factor of worker \(w\)

\({S}_{w}\)

Base salary of worker \(w\) per minute

\({Pc}_{jsm}\)

Processing cost of \({O}_{js}\) on machine \(m\)

\({TEC}_{jsm}\)

Energy consumption when \({O}_{js}\) is processed on machine \(m\)

\(L\)

A large positive number

Variables

\({X}_{jsmk}\)

Binary variable; \(=1\), if \({O}_{js}\) is processed in position \(k\) on machine \(m\); \(=0\), otherwise

\({Q}_{jswq}\)

Binary variable; \(=1\), if setup of \({O}_{js}\) is processed in position \(q\) by worker \(w\); \(=0\), otherwise

\({y}_{jismw}\left(t\right)\)

Binary variable; \(=1\), if there is an adjustment from job \(j\) to job \(i\) in stage \(s\) on machine \(m\) by worker \(w\) at moment \(t\); \(=0\), otherwise

\({x}_{j,s,m}\left(t\right)\)

Binary variable; \(=1\), if job \(j\) in stage \(s\) is processed on machine \(m\) at moment \(t\); \(=0\), otherwise

\({z}_{m}\left(t\right)\)

Binary variable; \(=1\), if machine \(m\) is idle at moment \(t\); \(=0\), otherwise

\(\rho \left(t\right)\)

Power cost counter,\(=\left\{\begin{array}{c}cp1, t1 \le t < t2\\ cp2, t2 \le t < t3\\ \dots \\ cpp, tp \le t < tp+1\end{array}\right.\)

Objective functions

The first objective is to minimize the makespan, \({C}_{max}\): this refers to the completion time of the last job, to be computed using Eq. (1).

$$min {C}_{max}= max {C}_{j} : \forall j=\mathrm{1,2},\dots , {n}_{j};$$
(1)

The second objective is to minimize the total cost, \(TC\): this consists of total electricity consumption and workers’ costs as shown in Eq. (2).

$$min TC={TEC}_{cost}+{TW}_{cost}$$
(2)

These objectives are conflicting in nature; that is, minimizing one objective may increase the magnitude of the other objective. The objective function is subject to the following constraints.

Constraints

In the first stage, when jobs are not pre-processed, and there are no predecessor jobs on a machine, the completion time can be regulated using Eq. (3).

$$\begin{array}{c}{C}_{\mathcal{I}1m}=max\left({C}_{j},{C}_{m1},{C}_{w1}\right)+\left({st}_{\mathcal{I},\mathcal{I}1}\times {pf}_{w}\right)+\left({P}_{\mathcal{I}1m}.{x}_{\mathcal{I}1m}\right)\\ \forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{1}; w\in {AW}_{1}\end{array}$$
(3)

When jobs are not pre-processed, but preparations are required on a machine, the completion time can be described using Eq. (4).

$$\begin{array}{c}{C}_{\mathcal{I}1m}=max\left({C}_{j},{C}_{m1},{C}_{w1}\right)+\left({st}_{j,\mathcal{I}1}\times {pf}_{w}\right)+\left({P}_{\mathcal{I}1m}.{x}_{\mathcal{I}1m}\right)\\ \forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{1}; w\in {AW}_{1}\end{array}$$
(4)

In other stages, when jobs are pre-processed, but there are no antecedents on the machine, Constraint (5) will be the basis for calculating the completion time using Eq. (6). Constraint (5) indicates that the difference between the completion times must be larger than or equal to the required setups.

$${C}_{j\left(s-1\right)}-{C}_{ws} \ge {st}_{\mathcal{I},\mathcal{I}s}\times {pf}_{w}$$
(5)
$${C}_{\mathcal{I}sm}={C}_{j\left(s-1\right)}+{P}_{\mathcal{I}sm}\times {x}_{\mathcal{I}sm}$$
(6)

where \(\forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{s}; w\in {AW}_{s}\). Otherwise, if Constraint (7) applies, Eq. (8) calculates the completion time. Constraint (7) requires that the time difference between completing consecutive tasks is less than the associated setups.

$${C}_{j\left(s-1\right)}-{C}_{ws} <{st}_{\mathcal{I},\mathcal{I}s}\times {pf}_{w}$$
(7)
$${C}_{\mathcal{I}sm}={C}_{ws} +{st}_{\mathcal{I},\mathcal{I}s}\times {pf}_{w}+{P}_{\mathcal{I}sm}\times {x}_{\mathcal{I}sm},\forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{s}; w\in {AW}_{s}$$
(8)

Alternatively, when jobs are pre-processed, there are predecessor jobs on the machine, and conditions in Constraints (9) and (10) are both true, the completion time can be calculated using Eq. (11).

$${C}_{j\left(s-1\right)}>{C}_{ws} >{C}_{ms}$$
(9)
$${C}_{j\left(s-1\right)}-{C}_{ws} \le {st}_{j,\mathcal{I}s}\times {pf}_{w}$$
(10)
$${C}_{\mathcal{I}sm}={C}_{ws} +{st}_{j,\mathcal{I}s}\times {pf}_{w}+{P}_{\mathcal{I}sm}\times {x}_{\mathcal{I}sm},\forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{s}; w\in {AW}_{s}$$
(11)

In other cases, when jobs are pre-processed and there are antecedents on the machine, the completion time when Constraints (9) and (12) are both true is defined as Eq. (13).

$${C}_{j\left(s-1\right)}-{C}_{ws} >{st}_{j,\mathcal{I}s}\times {pf}_{w}$$
(12)
$${C}_{\mathcal{I}sm}={C}_{j\left(s-1\right)}+{P}_{\mathcal{I}sm}\times {x}_{\mathcal{I}sm},\forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{s}; w\in {AW}_{s}$$
(13)

wherever jobs are pre-processed and there are preceding jobs on the machine, the completion time when Constraints (14) and (15) are true should be computed using Eq. (16). Constraint (14) requires that the completion time of job \({O}_{j(s-1)}\) is greater than the availability time of the assigned machine and worker. According to Constraint (15), the completion time of job \(s-1\) is less than or equal to the summation of setups and availability time of the assigned machine.

$${C}_{j\left(s-1\right)}>{C}_{ms} >{C}_{ws}$$
(14)
$${C}_{j\left(s-1\right)}-{C}_{ms} \le {st}_{j,\mathcal{I}s}\times {pf}_{w}$$
(15)
$${C}_{\mathcal{I}sm}={C}_{ms} +{st}_{j,\mathcal{I}s}\times {pf}_{w}+{P}_{\mathcal{I}sm}\times {x}_{\mathcal{I}sm},\forall j=\mathrm{1,2}, \dots , {n}_{j}; m\in {AM}_{s}; w\in {AW}_{s}$$
(16)

In the alternative situation, i.e., when jobs are pre-processed and preceding jobs have been completed on the machine, the completion time can also be defined using Eq. (13) if and only if conditions stated in Constraints (14) and (17) are true.

$${C}_{j\left(s-1\right)}-{C}_{ms} >{st}_{j,\mathcal{I}s}\times {pf}_{w}$$
(17)

In situations when jobs are pre-processed, there were early jobs on the machine, and Constraint (18) applies, Eq. (16) defines the completion time. Constraint (18) implies that the availability time of machines should be greater than the maximum of the completion time of the previous job and the worker’s availability.

$${C}_{ms}>max({C}_{j\left(s-1\right)},{C}_{ws})$$
(18)

Finally, when jobs are processed already, there are preceding jobs on the machine, and Constraint (19) is true, and the completion time can be calculated using Eq. (11). Constraint (19) indicates that the worker’s availability is greater than the maximum between the completion time of the preceding job and the machine availability for the current job.

$${C}_{ws}>max({C}_{j\left(s-1\right)},{C}_{ms})$$
(19)

The remainder of the constraints are as follows.

$$\begin{array}{c}{C}_{j\left(s+1\right)}-{C}_{js}\ge {P}_{j\left(s+1\right)m}\times {x}_{j\left(s+1\right)m}+{st}_{j,\mathcal{I}\left(s+1\right)}\times {pf}_{w}\\ \forall j=\mathrm{1,2}, \dots , {n}_{j};s=\mathrm{1,2}, \dots , {n}_{s}-1;m=\mathrm{1,2}, \dots , {n}_{m};w=\mathrm{1,2}, \dots , {n}_{w}\end{array}$$
(20)
$$\sum_{k}\sum_{m}{x}_{jsmk}\le 1, \forall j=\mathrm{1,2}, \dots , {n}_{j};s=\mathrm{1,2}, \dots , {n}_{s}$$
(21)
$$\sum_{s}\sum_{j}{x}_{jsmk}\le 1, \forall m=\mathrm{1,2}, \dots , {n}_{m};k=\mathrm{1,2}, \dots , {n}_{l}$$
(22)
$$\sum_{q}\sum_{w}{Q}_{jsmq}=1 , \forall j=\mathrm{1,2}, \dots , {n}_{j};s=\mathrm{1,2}, \dots , {n}_{s}$$
(23)
$$\sum_{s}\sum_{j}{Q}_{jsmk}\le 1 , \forall w=\mathrm{1,2}, \dots , {n}_{w};q=\mathrm{1,2}, \dots , {n}_{l}$$
(24)

Constraint (20) ensure that the operation sequence is respected, and there is enough time for processing and setups of consecutive jobs considering the performance of the assigned workers. Equation (21) guarantees that each job can be processed by at most one machine at a given time. Constraint (22) is defined to make sure that each machine can process one job at a time. Equation (23) ensures that when setup is required, it must be done by one worker. Constraint (24) ensures that each worker can process a maximum of one operation at a time.

Finally, Eqs. (25)–(31) are used for calculating the cost elements of the objective function. The total electricity consumption (TEC) is incorporated using Eq. (25); this includes the total electricity consumed during the setups, processing, and idle states of machines. The cost terms are defined by Eqs. (26)–(28), respectively; which are adopted from Zhang et al. (2019).

$$TEC={TE}_{setup}+{TE}_{process}+{TE}_{idle}$$
(25)
$${TE}_{setup}=\sum_{j}\sum_{\mathcal{I}}\sum_{w}\sum_{s}\sum_{m}\left\{{OE}_{setup}^{j\mathcal{I}sm} \times {pf}_{w} \times \left[{\int }_{t=0}^{t={C}_{max}}{y}_{j\mathcal{I}smw}\left(t\right).\rho \left(t\right).d(t)\right]\right\}$$
(26)
$${TE}_{process}=\sum_{j}\sum_{s}\sum_{m}\left\{{E}_{process}^{jsm}\times \left[{\int }_{t=0}^{t={C}_{max}}{x}_{jsm}\left(t\right). \rho \left(t\right).d(t)\right]\right\}$$
(27)
$${TE}_{idle}=\sum_{m}\left\{{E}_{idle}^{i}\times \left[{\int }_{t=0}^{t={C}_{max}}{z}_{m}\left(t\right). \rho \left(t\right).d(t)\right]\right\}$$
(28)

\({OE}_{setup}^{j\mathcal{I}sm}\) is the basis for calculating energy consumption per time unit for adjusting from job j to job \(\mathcal{I}\) in stage s on machine m; \({pf}_{w}\) denotes the performance factor of worker \(w\) assigned to undertake the adjustment; \(t=0\) and \(t={C}_{max}\) are the starting and finishing times of the scheduled jobs; and \(\rho \left(t\right)\) counts power cost at time \(t\). In Eq. (27), \({E}_{process}^{jsm}\) is the energy consumption per unit time for processing job \(j\) in stage \(s\) on machine m. In Eq. (28), \({E}_{idle}^{i}\) is the energy consumption per unit time when machine \(m\) is in the idle state.

The total cost of workers (\({TW}_{cost}\)) is defined using Eq. (29), which includes base salary and extra payment per busy time that is calculated by Eqs. (30)–(31), respectively.

$${TW}_{cost}={TW}_{base}+{TW}_{extra}$$
(29)
$${TW}_{base}=\sum_{w}{C}_{max} \times {S}_{w} \times {ActW}_{w}$$
(30)
$${TW}_{extra}=\sum_{j}\sum_{\mathcal{I}}\sum_{s}\sum_{w}\sum_{q}{S}_{w}\times {st}_{j\mathcal{I}s}\times {pf}_{w}\times {\mathrm{Q}}_{\mathcal{I}\mathrm{smq}}$$
(31)

Solution method

This section elaborates on the improved multi-objective optimization algorithm, AMOGA for solving the HFSPs with the time-of-use electricity price model, workforce flexibility, and SDST. The pseudocode of AMOGA is provided in Fig. 2, followed by a detailed explanation of the major computational elements.

Fig. 2
figure 2

Pseudocode of the developed algorithm, AMOGA

Full size image

Encoding, decoding, and initialization

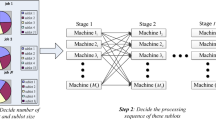
A new scheme using a multi-layer chromosome of length \({n}_{j}\times {n}_{s}\) is proposed to encode the HFSPs with a flexible workforce. As shown in Fig. 3, a vector consisting of job sequence, machine selection, worker assignment, and finish time of job vectors represents a complete solution. In the illustrative example, the number of machines and workers in each stage is (3,1,2) and (2,1,1), respectively. The method introduced by Luo et al. (2013) is applied for decoding, where the optimal selection of resources is made considering both the makespan and total cost computed for different combinations of the available resources. Considering that the precise computation of electricity consumption cost is essential in this application area, the electricity cost of the machine in the idle state is considered in addition to the electricity cost in setup and processing states, as presented in Eq. (25). This technique not only reduces the complexity of the decoding process but also facilitates the generation of high-quality solutions.

Fig. 3
figure 3

Structure of the four-layer chromosome encoding

Full size image

The step-by-step implementation procedure of the proposed scheme is explained below.

  • Step 1. Create a four-level chromosome with empty values.

  • Step 2. Create a job sequence in the first stage using simple permutation.

  • Step 3. Select a prior job in the sequence.

  • Step 4. Assign machine and worker using the resource selection algorithm (RSA) shown in Fig. 4.

  • Step 5. Decode a partial encoding to a partial schedule and record the completion time of the job and indices of selected resources.

  • Step 6. Repeat Steps 3 to 5 for the remaining jobs in this stage.

  • Step 7. Arrange jobs in ascending order of their finish time for processing in the next stage.

  • Step 8. Repeat steps 3 to 7 for the remaining stages.

  • Step 9. Calculate and record start times, as well as the start and finish times of SDST for all jobs/machines in each stage.

  • Step 10. Decode the chromosome to a complete time–cost-efficient schedule and record the objective function values.

Fig. 4
figure 4

Pseudocode of the resource selection algorithm

Full size image

To provide a diverse and high-quality solution population, the sequence of jobs in the first stage is defined by a simple job permutation for every solution followed by the implementation of the RSA algorithm and rearrangement of the jobs in the following stages.

Fitness calculation and Pareto-front generation

In the developed algorithm, individuals with the best fitness value have a greater chance of being selected for reproduction and survival into the next generation. To assign a fitness value, the non-dominated sorting method introduced by Deb et al. (2002) is employed, which exploits the concept of Pareto dominance. This technique consists of pairwise comparisons of all the population members to form the fronts. The solutions that are not dominated by any other solutions belong to the first front (rank one) and represent the (near-)Pareto-optimal solutions. AMOGA tries to find a better set of Pareto-optimal solutions and finds solutions closer to the front (the so-called convergence) across computational generations. In addition to the convergence criterion, the crowding distance of individuals in their rank should be computed, using Eq. (32). It is worthwhile noting that the objective values need to be sorted in ascending order before computing the crowding distance of the solutions.

$${CD}_{r}=\sum_{j=1}^{nOb}\frac{\left({f}_{k}^{r+1}-{f}_{k}^{r-1}\right)}{\left({f}_{k}^{max}-{f}_{k}^{min}\right)}$$
(32)

In this formulation, \({CD}_{r}\) represents the crowding distance of rth individual on the frontier, \(nOb\) is the number of the objectives, \({f}_{k}^{r+1},{f}_{k}^{r-1}\) are the kth objective values of the adjacent solutions, \({f}_{k}^{max},{f}_{k}^{min}\) are the maximum and minimum values of the kth objective. For the boundary solutions in each front, the crowding distance amounts to an infinite value. The solutions can be sorted by classifying them on different fronts and calculating the respective crowding distances. In this definition, the solutions with lower domination rank and higher crowding distance values are preferred. Solutions are first sorted in descending order of their crowding distances and then in ascending order of their front values.

Selection methods

The tournament selection method is used to select parents for reproduction. Choosing the size of the tournament determines whether elitism or diversity received more weight. The larger tournaments reflect the elite-selection policy and the fastest algorithm convergence. However, in smaller tournaments, the diverse-selection policy prevails. In this study, the size of the tournament is \({T}_{size}=2\) individuals from which the one with the lowest rank is selected.

To select the best-ranked individuals from the pool, which contains the old population, \({pop}_{old}\), and the new individuals through the evolutionary phase, \({pop}_{new}\), the truncation function is applied. The population should be updated at the end of every generation to select the best individuals for the next generation. For this purpose, the existing population and the newly generated population from the recombination and mutation phases are first integrated. Then, individuals with the same fitness value (makespan and total cost) are removed. After that, the individuals’ rank and the crowding distance are considered to select \(nPop\) top individuals, which will make it to the next generation(s).

Crossover operators

In the evolutionary phase of AMOGA, crossover operators are used for reproducing new (offspring) solutions from the selected parent solutions. This research considers two crossover operators with equal probability, namely partially mapped crossover (PMX) and uniform crossover. These operators are applied only to the part of the chromosome where the sequence of jobs in the first stage is presented. The machine and worker selection sections are then completed by the RSA algorithm which selects the best resources for the chosen job sequence respecting both objectives. The PMX operator is employed in such a way as to respect both preserves of ordering and information sharing from parents. For this purpose, first, a pair of parents is chosen by tournament selection from the existing population, and two random cut points are selected uniformly. Then the mapping relationship of genes between the cut point is defined, and they are exchanged to form a partial offspring. Eventually, the remaining empty positions are filled by the original parents. In cases of having the same genes, they will be replaced based on the mapping relationship. The illustrative example in Fig. 5 clarifies the PMX procedure.

Fig. 5
figure 5

Illustrative example of the partially mapped crossover (PMX)

Full size image

The uniform crossover begins with selecting two parents using tournament selection. A uniform binary vector, called a mask, with a length equal to the number of jobs (\({n}_{j}\)) is then created. Finally, genes are copied from parents to the offspring as shown in Fig. 6.

Fig. 6
figure 6

Illustrative example of the uniform crossover

Full size image

Mutation operators

The mutation improves search diversity and helps escape premature convergence. This research applies three mutation operators named swap, conversion, and insertion on the job sequence section of the chromosomes for generating a new offspring. For this purpose, an individual is picked from the existing population by tournament selection, and then one of the mutation operators is selected randomly (with an equal probability). The procedure is illustrated in Fig. 7.

Fig. 7
figure 7

Illustration of the mutation operators: (a) swap, (b) insertion, and (c) reversion

Full size image

Overall, the RSA algorithm and a module for discarding duplicate solutions are the major points differentiating AMOGA from the basic multi-objective genetic algorithm. Besides, the encoding, initialization, and genetic operators are tailored for solving HFSPs.

Computational experiments

Benchmark description

To evaluate the performance of the developed algorithm, the state-of-the-art multi-objective evolutionary algorithms are considered benchmarks: SPEA2 (Zitzler et al. 2001) and Pareto envelop-based selection algorithm (PESA2; (Corne et al. 2001)). SPEA2 and PESA2 are selected because they use different approaches for managing the Pareto-front members in comparison with AMOGA; while AMOGA takes advantage of a single-based solution approach, SPEA2 uses K-nearest neighbor(s), and PESA2 uses a region-based approach. These algorithms are most-widely used for solving different classes of multi-objective scheduling problems.

The same solution encoding/decoding and genetic operators are used in all the benchmark algorithms to ensure a fair comparison. Besides, all the algorithms are adjusted for effective handling of discrete problems following (Corne et al. 2001; Zitzler et al. 2001). All the algorithms are coded and compiled on MATLAB R2020a and run on a personal computer with AMD Rayzen 3, 2.60 GHz CPU, and 12 GB Ram.

Test instances

Test data are generated randomly in a way that they can be representative of the shop floor. Table 1 shows the levels and ranges of the factors determining the configuration of the test instances. The test problems are denoted by “number of jobs–number of stages–number of machines in all stages-number of workers in all stages.” For example, a problem with 20 jobs, 3 stages, 10 machines, and 5 workers can be identified by “20–3-10–5.”

Table 1 Summary of the test data
Full size table

The time-of-use plan rates for small and medium-sized enterprises (SMEs) are used in this study, which is illustrated in Fig. 8. According to the figure, the peak electricity demand increases during the summer months (i.e., June to September), as well as the afternoon time (i.e., 4 to 9 pm); hence, the associated energy cost is higher. On this basis, five time-of-use periods are considered for energy cost calculation.where the following rates apply in power cost calculations:

  • \(\rho (t)=0.10497\) if \(24n\le t <24n+14\)

  • \(\rho \left(t\right)=0.12476\mathrm{ if }24n+14 \le t <24n+16\)

  • \(\rho \left(t\right)=0.15311\mathrm{ if }24n+16 \le t <24n+21\)

  • \(\rho \left(t\right)=0.12476\mathrm{ if }24n+21 \le t <24n+23\)

  • \(\rho \left(t\right)=0.10497\mathrm{ if }24n+23\le t <24n+24\)

Fig. 8
figure 8

(Source: Pacific Gas and Electric Company)

Time-of-use plan rates for small-medium business

Full size image

Comparison metrics for algorithm evaluation

To compare the performance of the multi-objective evolutionary algorithms, various metrics should be considered. In this study, five metrics, namely spacing metric (SM), mean ideal distance (MID), diversification metric (DM), quality metric (QM), and inverted generational distance (IGD), are used, as considered in earlier studies (Cheng et al. 2020) to benchmark the performance of AMOGA against SPEA2 and PESA2. These metrics are detailed below.

SM measures the uniformity of the spread of non-dominated schedules, which can be computed using Eq. (33).

$$SM=\frac{{\sum }_{i=1}^{n-1}\left|\overline{d }-{d}_{i}\right|}{(n-1)\times \overline{d} }$$
(33)

In this equation, \({d}_{i}\) is the Euclidean distance between two successive non-dominated schedules in the solution set and \(\overline{d }\) represents the average of Euclidean distances. The smaller value of this metric is preferred (Piroozfard et al. 2018).

MID measures the proximity of the non-dominated solutions \(\left({f}_{1,i},{f}_{2,i}\right)\) from the ideal point \(\left({f}_{1}^{best},{f}_{2}^{best}\right)\) and is calculated by Eq. (34).

$$MID=\frac{{\sum }_{i=1}^{n}\sqrt{{({f}_{1,i}+{f}_{1}^{best})}^{2}+{({f}_{2,i}+{f}_{2}^{best})}^{2}}}{n}$$
(34)

where \({f}_{1,i}\) and \({f}_{2,i}\) denote the fitness function of the ith non-dominated solution found by each algorithm (first and second objectives); \({f}_{1}^{best},{f}_{2}^{best}\) indicate the best fitness function of the first and second objectives among all solutions of the competing algorithms, and \(n\) refers to the total number of Pareto front solution find by each algorithm. A smaller value of MID is desired (Nabipoor Afruzi et al. 2013).

DM determines the extent of heterogeneity in the set of non-dominated schedules for each algorithm, which can be calculated using Eq. (35); higher values of this metric is advantageous (Tavakkoli-Moghaddam et al. 2011).

$$DM=\sqrt{{\sum }_{i=1}^{nOb}{\left(max({f}_{i})+min({f}_{i})\right)}^{2}}$$
(35)

QM shows the percentage of unique non-dominated schedules obtained by each algorithm. To calculate this, a union of obtained Pareto-front solutions of all competing algorithms is first determined to form a new set of non-dominated solutions. Then, the number of solutions obtained by each algorithm in each new Pareto-front is counted and divided by the total number of solutions in the union set. The higher the value of this metric is, the more unique solutions are obtained by the respective algorithm (Moradi et al. 2011).

IGD simultaneously considers both convergence and diversity aspects to measure how far the Pareto-front obtained by an algorithm is from the reference Pareto-front solutions. It is computed by Eq. (36) with the lower value being more desirable (Coello Coello and Reyes Sierra 2004).

$$IGD=\frac{\sqrt{{\sum }_{i=1}^{{n}^{*}}{({d}_{i}^{*})}^{2}}}{{n}^{*}}$$
(36)

In this equation, \({d}_{i}^{*}\) is the Euclidean distance of each Pareto-front solution to the nearest schedule obtained by each algorithm, and \({n}^{*}\) is the number of Pareto-front solutions. It is worth noting that in cases with unknown Pareto-front solutions, IGD can be estimated considering the integrated Pareto-front solutions found by all benchmark algorithms.

Parameter settings

Separate experiments are conducted to calibrate the parameters of each algorithm. For AMOGA, the population size, tournament selection configuration, crossover, and mutation probabilities are tuned. The parameters of SPEA2 include the population size, archive size, crossover probability, and mutation probability. For PESA2, the grid number needs to be considered in addition to the parameters of SPEA2. The Taguchi method is used for determining the optimal level of important known factors while the effects of uncontrollable factors are minimized. For a full description of how to perform the Taguchi method for tuning the algorithm’s parameters, we refer the interested readers to the research conducted by Nabipoor Afruzi et al. (2013).

As a first step, trial-and-error experiments are conducted to determine the initial values for each parameter. Table 2 shows the parameter levels of AMOGA. Considering the number of known parameters, the respective test levels, and the Taguchi method, an orthogonal array L9 then is designed, which consists of different configurations of parameter levels. To assess which combination of parameter values results in the best algorithm performance, four randomly generated test problems of different scales (HS04, HS06, HS10, HS14) are considered. To ensure the reliability of the outcomes, each problem is solved five times, providing a total of 20 results for each trial.

Table 2 Factor levels considered in the calibration of AMOGA
Full size table

Next, the performance metrics explained in the previous section are computed and normalized by the relative deviation index for every instance, calculated using Eq. (37). The average values associated with each trial are then determined. These performance indicators have different degrees of importance based on how they measure the quality and diversity of the Pareto-front solutions for solving a multi-objective optimization problem. SM = 1, DM = 1, MID = 2, QM = 3, and IGD = 4 are considered to measure the weighted average relative deviation index (WARDI; Eq. 38) for every item of the orthogonal array.

$${RDI}_{i}=\frac{\left|\overline{{Pc }_{i}}-{Pc}_{i}^{best}\right|}{\left|{Pc}_{i}^{max}-{Pc}_{i}^{min}\right|}\times 100$$
(37)
$${\mathrm{WA}RDI}_{i}=\frac{{\sum }_{i=1}^{nM}\left({\mathrm{w}}_{i}\times \overline{{RDI }_{i}}\right)}{{\sum }_{i=1}^{nM}{\mathrm{w}}_{i}}\times 100$$
(38)

In these equations, \(\overline{{Pc }_{i}}\) represents the average of performance criterion associated with the ith experiment over 20 runs; \({Pc}_{i}^{best}\) is the best performance metric among all experimental results; \({Pc}_{i}^{max}\) and \({Pc}_{i}^{min}\) denote the maximum (and minimum) values of a certain performance metric among all experiments. It should be noted that \({\mathrm{WA}RDI}_{i}\) is calculated for the ith experiment with \(\overline{{RDI }_{i}}\) representing the average of RDIs of the four test problems, and \(nM\) referring to the number of metrics. The results are used as the response value in the Taguchi design approach, according to which the best combination of parameter values for AMOGA can be obtained.

The same procedure has been implemented for SPEA2 and PESA2. It should be noted that the levels of the common factor of SPEA2 and PESA2 are similar to AMOGA while the archive size levels for these two algorithms are L1(50)-L2(80)-L3(100). For PESA2, the potential levels of the grid’s number are L1(20)-L2(40)-L3(60). The results of the Taguchi experiments for AMOGA, SPEA2, and PESA2 are summarized in Figs. 9, 10, and 11, respectively. Table 3 presents the optimal parameter values for each algorithm.

Fig. 9
figure 9

The mean WARDI plot for each level of the parameters in Taguchi methodology-AMOGA

Full size image
Fig. 10
figure 10

The mean WARDI plot for each level of the parameters in Taguchi methodology-SPEA2

Full size image
Fig. 11
figure 11

The mean WARDI plot for each level of the parameters in Taguchi methodology-PESA2

Full size image
Table 3 Parameter setting of AMOGA, SPEA2, and PESA2
Full size table

Experimental results and discussions

Given the calibration outcomes, this section compares the performance of the algorithms considering a total of twenty-and-four test instances of various scales. Table 4 summarizes the computational results of AMOGA, SPEA2, and PESA2 considering different performance measures, SM, MID, DM, QM, and IGD. The best outcomes in the benchmark are in bold for an easy track.

Table 4 Computational results of AMOGA, SPEA2, and PESA2 based on performance metrics (best in bold)
Full size table

A statistical test of significance is then conducted to confirm if the difference is significant. Looking at the first criterion, SM, it is observed that the PESA2 outperforms both AMOGA and SPEA2 on 19 and 15 out of the 24 test instances, respectively. That is, better uniformity of the spread of non-dominated solutions can be obtained by PESA2. The reason behind the superiority of PESA2 lies in the fact that it benefits from a region-based approach, which leads to yielding results with a more uniform distribution compared with the other two algorithms. However, the difference is not statistically significant (null hypothesis is accepted with statistic = 2.5249 and p-value = 0.0874).

Concerning the second criterion, MID, AMOGA shows a relatively better performance with an average of 235.61 compared with 308.75 and 343.57 of SPEA2 and PESA2, respectively. Considering the number of instances, AMOGA and SPEA2 are comparable and outperform PESA2 in 19 and 16 instances, respectively. Although the statistical test does not confirm a significant difference between the overall performances, AMOGA results are more competitive for large-scale instances (HFSP/W20-24). That is, the proximity of the non-dominated solutions obtained by AMOGA from the ideal point is comparatively better for large-scale instances. The outperformance concerning MID is expected to be even more significant when industry-scale instances are solved.

Concerning the third metric (i.e., DM), it is observed that the diversity of the Pareto-front solution obtained by both AMOGA and SPEA2 is better than PESA2 with 20 and 18 out of the 24 tests being outperformed, respectively. Overall, AMOGA obtained better more diverse solutions with a DM value of 608.12, and it can be confirmed that AMOGA performs significantly better than SPEA2 with statistic = 3.4531, p-value = 0.0012.

Considering the number of unique non-dominated solutions obtained by each algorithm, i.e., the QM indicator, it is evident that AMOGA outperforms both SPEA2 and PESA2. Obtaining better QMs in all 24 test instances proves the superiority of AMOGA for exploring harder solution spaces, like non-convex areas. It is worth noting that an average of about 81% of non-dominated solutions were yielded by AMOGA, compared with only 9 and 11% for SPEA2 and PESA2, respectively. With 99% confidence, a statistic value of 243.5465 and a p-value of 0.0000 the null hypothesis are rejected, confirming that AMOGA performs significantly better in terms of finding unique non-dominated solutions compared to SPEA2 and PESA2.

In terms of the last performance metric, IGD, analysis of the results shows that AMOGA outperforms PESA2 in 23 test instances and SPEA2 yielded better convergence and diversity of solutions only for solving HFSP/W17. Considering the extent of the difference, which is 2.78 against 90.50 and 99.09, one can conclude that AMOGA is also superior considering IGD. Finally, the statistic value of 9.46145 and a p-value of 0.0002 confirm, with 99% confidence, that AMOGA showed better convergence and more diverse solutions compared to SPEA2 and PESA2.

To visually compare the non-dominated solutions obtained by the benchmark algorithms, six test instances of different scales, i.e., HFSP/W03, HFSP/W06, HFSP/W08, HFSP/W12, HFSP/W16, HFSP/W19, and HFSP/W24) are presented in Fig. 12a–f. One can observe that most non-dominated solutions obtained by AMOGA are better than those of SPEA2 and PESA2 in terms of production efficiency and saving total cost. That is, the proposed AMOGA appears to be more effective for solving different scales of the studied problem.

Fig. 12
figure 12

Non-dominated solutions by AMOGA, SPEA2, and PESA2

Full size image

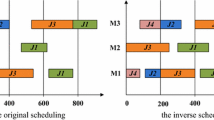
Furthermore, Fig. 13a–b displays the trend of the inverted generational distance of each algorithm for HFSP/W20 and HFSP/W24 instances, which showcases a better convergence give a fixed number of iterations. Finally, sample Gant Charts of the non-dominated solution for HFSP/W08 and HFSP/W11 instances are provided in Fig. 14 to showcase the production schedules obtained by our optimization approach.

Fig. 13
figure 13

Inverse generational distance for AMOGA, SPEA2, and PESA2

Full size image
Fig. 14
figure 14

Visual illustration of a non-dominated solution of HFSP/W08 by AMOGA

Full size image

Given a diverse set of near-optimum non-dominated schedules, production managers can flexibly weigh up between minimizing the total costs and the maximum completion time to select the solution that suits the current operational needs of the company. Taking mandates on the energy consumption and environmental performance as an example, the production manager may choose a schedule with lower energy consumption—but higher makespan—in normal conditions. However, when the delivery time of certain orders is a priority, the production schedule with a minimum makespan may be selected. Workforce productivity is another major consideration; having highly productive workers for the production orders that require substantial setups is one way to reconciliation between cost-effectiveness and responsiveness strategies.

Conclusions

The environmental concerns associated with the growing industrial activities have led to an array of initiatives seeking energy efficiency. As a prime example of net-zero initiatives, the time-of-use electricity policy is pushing manufacturing shop owners to reduce energy consumption. Both value-adding (i.e., production) and non-value-adding operations (i.e., setup and preparation) contribute to energy consumption on the shop floor. Production planning and control methods that address such concerns are of utmost relevance to industrial sustainable development. Besides, the workers’ capabilities impact the energy efficiency of production operations; simultaneously incorporating these features improve the optimization outcomes. This study contributed to the literature by introducing an effective multi-objective optimization approach for scheduling hybrid flow-shops, considering energy consumption under time-of-use pricing models, workers’ flexibility, and SDST features simultaneously. The objective was to minimize total costs comprising electric consumption and worker costs pertinent to the setup operations while minimizing the response time for fulfilling new demands. To the best of the authors’ knowledge, this is the first study that integrates these factors.

To evaluate the performance of the proposed algorithm, different operational parameters and performance measures are considered within a comprehensive computational experiment. Comparing the performance of AMOGA with two state-of-the-art multi-objective evolutionary algorithms, SPEA2 and PESA2, we showed that most of the non-dominated solutions were yielded by AMOGA considering various tradeoffs between the optimization objectives. AMOGA proved to be more effective for solving various scales of HFSP instances considering MID, DM, QM, and IGD measures, which are advantageous for providing wider trade-offs for production planning, while PESA2 showed to perform better in terms of SM.

Future research may extend our study in three directions. First, our study is limited in that it considers a static time-of-use electricity pricing model. Machine learning can be used to predict future power consumption in the region and adjust the production schedules accordingly. Machine learning can also be used for weather forecasting in cases of using renewable energies, like solar panels and wind turbine. Second, the energy pricing model should be incorporated into other classes of scheduling problems, like in unrelated parallel machines. In so doing, situation-specific operational constraints, like a capacitated buffer in each stage, machine failure, and workers’ availability constraints may be considered to explore their impact on the energy consumption factor. The proposed incorporation can also be studied in rescheduling models to reduce energy consumption in times of energy shortage and/or power disruption. In terms of the objective function, a balance of workers’ workload and minimizing earliness/tardiness can be considered to highlight the possible changes in the energy cost in pick hours. Our study focused on the multi-objective feature of managing the Pareto-front members for which AMOGA was compared with SPEA2 and PESA2; the future research may consider comparing other search features to compare AMOGA with the multi-objective evolutionary algorithms based on decomposition (MOEA/D) and multi-objective particle swarm optimization (MOPSO). As a final suggestion for future direction, other methods of dealing with multiple conflicting objectives should be developed and compared with the Pareto-based method developed in our study. For this purpose, some of the properties of multi-objective decision-making models may be inspiring for further development in the multi-objective optimization field.