Designing a sustainable fish closed-loop supply chain network under uncertainty

Abstract

There is increasing attention to the sustainable development of supply chain (SC) and reverse logistics (RL) in the contemporary competitive economy, notably in the food sector, by scholars and stakeholders. This study investigates a sustainable closed-loop supply chain (CLSC) for fish due to its high value in the family food basket, its perishability, and the importance of waste product recycling. A multi-objective mathematical model is developed under uncertainty and sustainability criteria to optimize production rates with the aim of better distribution among different demand markets, total costs, social issues, and negative environmental effects (e.g., CO₂ emissions and unused/waste products). A combination of exact, meta-heuristic, and hybrid meta-heuristic algorithms are used to solve the suggested model. Then, the optimal solutions are found using the Taguchi method by evaluating the best initial replies. The solutions are evaluated based on various performance metrics. The analysis of variance (ANOVA) and the “filtering/displaced ideal solution” methods determine the best solution approach. Moreover, a case study with a trout CLSC in Northern Iran is examined. In addition, the Lingo software utilizes the ε-constraint method to evaluate and check the performance of the algorithms under different levels of uncertainty. Finally, sensitivity analyses are carried out to confirm the efficacy of the proposed algorithms. The findings demonstrate the proposed network’s outstanding consistency with the algorithms used and its application and efficiency.

Introduction

Industries require academia to research innovative extensions and solve problems successfully to develop practical supply chains (SCs) (Naderi et al. 2020). Thus, many researchers’ key goal is to find and develop an effective network to boost customer satisfaction and deliver added value to all SC participants (Salehi-Amiri et al. 2022). Also, a sustainable supply chain network design (SSCND) tries to simulate the best SC network configuration that allows a company to optimize long-term benefits in all three sustainability pillars, namely, environmental, social, and economic aspects (Govindan et al. 2015). Closed-loop supply chains (CLSCs), which bring settings to cover the possible demands of diverse markets in direct flow and use returned products in a reverse route, are a prominent research topic for addressing this issue (Mousavi et al. 2021). Also, managing uncertainty is a major challenge in supply chain management (SCM) (Peidro et al. 2009).

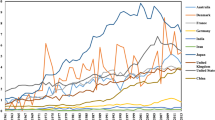
The pressing need for sustainable supplies of nutrients has arisen due to increasing global food consumption, as the world’s population has grown dramatically in recent decades (Yang et al. 2021). To feed the world’s growing population of 9.6 billion people by 2050, the food supply would need to increase by almost 70% from current levels. Food waste is a major threat to global food security, with 20–30% of food loss occurring in developing nations’ post-harvest food supply chain (FSC) (Krishnan et al. 2020). On the other hand, we are experiencing a resource deficit on the planet due to improper land resource consumption in recent years, climate change, and the water issue. Sustainable food production and consumption systems are impossible without considering the entire SC and the individuals involved at each stage along the road. Therefore, to address the increased food demand, it is necessary to change the current food SCs (Desiderio et al. 2021; Govindan 2018), as is reflected in the number of publications in the food SC in recent years (see Fig. 1).¹

Fig. 1

Food SC publication trend: a number and b subject area

The perishable product supply chain (PPSC) is particularly difficult to manage because of demand uncertainty, short shelf-life fluctuation, and high degradation rates, which necessitate unique storage conditions to limit the pace of decay (Van Donselaar et al. 2006).

A large body of research suggests that eating a high-seafood diet has various health benefits. However, global demand for seafood now exceeds the supply from catch fisheries. Hence, aquaculture products have rapidly increased demand (Lund 2013; Yu et al. 2021). Furthermore, by expanding aquaculture farms, the country can develop sustainable foods, and the high effectiveness of aquaculture farms in preserving endangered species has been demonstrated (Dale 2009). The latest report from the Food and Agriculture Organization (FAO) in 2020 revealed an upward trend in production and the number of people involved in fish farming and fishing, as well as a prediction that aquaculture production would increase by 2030 (Fig. 2). Fish farming research has progressed in lockstep with the industry’s expansion (Abedi and Zhu 2017). According to the FAO, as indicated in Fig. 3, Iran has a major part of the aquaculture market in the Middle East. According to statistics from the FAO and the Iranian Fisheries Organization,² Iran’s cold-water fish production rate has been increasing. There are numerous types of fish, the most popular of which is the trout, a cold-water fish.

Fig. 2

Aquaculture and fisheries statista.com

Fig. 3

Aquaculture market share in the Middle East and North Africa in 2015 by country

According to the fish type and processing methods, fish waste (e.g., frame/bone, head, skin, tail, viscera, and fin; see Fig. 4) is estimated to account for more than 30% of total biomass in the fish processing industry (Suwal et al. 2018). Around 40% of the trout is not consumed by humans and is discarded as industrial waste (Fiori et al. 2012). Retailers and consumers also produce a significant amount of waste (Kafa and Jaegler 2021). Most wastes end up in landfills, causing environmental issues, while others are converted into by-products such as aquaculture and animal feed. The aquaculture processing industry’s waste and by-products are receiving more and more attention. In today’s world, the processing of fish waste is extremely valuable. In addition, waste management has a high priority for use because of its freshness and the need to maintain quality. Making fish powder (or fish meal), as shown in Fig. 5, is one of the most common ways to recycle fish waste. If RL is implemented in SC, the network could be considered the CLSC by returning waste and leftover items to the chain as value-added products (i.e., fish powder) (Fig. 6).

Fig. 4

Fish waste

Fig. 5

Fish waste recycling and fish powder production

Fig. 6

Fish CLSC network

The proposed network in this study considers the forward flow of products (e.g., live, fresh, and processed fish) and the reverse flow of returned products (e.g., fish powder). The developed model takes the following sustainability criteria into account, according to the economic (e.g., financial performance), environmental (e.g., pollution and use of resources), and social (e.g., customer issues, fuel saving, and job creation) dimensions in the sustainable supply chain literature (Moreno-Camacho et al. 2019):

• Economic aspects: reducing total costs as the first objective.

• Social aspects: maximizing the responsiveness of both forward and reverse demand (customer satisfaction) as the second objective, reducing fuel consumption, and assisting local businesses by establishing rice farms.

• Environmental aspects: reducing total CO₂ emissions as the third objective, recycling waste and unused products, and considering biodiversity by establishing rice farms.

The remainder of this paper is structured as follows. The “Literature review” section reviews the relevant literature. The definition of the problem and the formulation of the model is presented in the “Describing the model” section. The “Solution approach” section also includes the proposed solution approaches and the encoding and decoding processes. The “Computational results” section includes a case study, sensitivity analysis, computational results, validation, and discussion. The “Conclusions and future directions” section concludes with a few recommendations for future research.

Literature review

RL and CLSC, perishability, sustainability, and uncertainty are all aspects of the problem under consideration. The literature review is thoroughly investigated in the following sub-sections.

RL and CLSC network

The SC performance is one of the most critical factors for firms to survive and prosper in today’s competitive market (Sun et al. 2021). Governments and parliamentarians have been more attentive to manufacturers’ end-of-life (EOL) policies as a result of pressure from numerous stakeholders (Raza 2020; Cheraghalipour et al. 2018). RL/CLSC is widely considered an environmentally friendly technique that can aid in reducing environmental consequences and achieving long-term societal and economic growth. The popular research of RL/CLSC has piqued the interest of both corporate and academic practitioners in recent years (Guan et al. 2020).

Table 1 shows the most recent reviews in RL and CLSC. According to RL/CLSC, researchers should pay more attention to industries like food, healthcare, and steel, which are valued in sustainable SCM (Govindan and Soleimani 2017). Circular economy, CLSC network redesign, and information technology development have been identified as research gaps (Guan et al. 2020).

Table 1 Recent reviews in the fields of RL and CLSC

SC considering uncertainty

Dealing with uncertainty is one of the more difficult jobs in the SCND. In the planning and design phase, it is critical to think ahead and anticipate. The dynamic nature of SCNs and the uncertainty in variables (e.g., demand, capacity, transit times, and manufacturing periods) say that one of the causes of SCN complexity is their complexity (Tordecilla et al. 2021). The uncertainty in demand is a major factor for an RL network design (Mehrbakhsh and Ghezavati 2020). Figure 7 illustrates the uncertainty distribution in CLSC research in the last 8 years (Ropi et al. 2021). The study reveals that the most frequently studied type of uncertainty is multiple uncertainties, accounting for 39%. This is due to the fact that the issues encountered in the CLSC/RL are typically a result of a combination of multiple uncertainties rather than just one. Furthermore, researchers have also considered demand and return rate uncertainties as the second and third most important, respectively, representing 27% and 23%. Quality uncertainty is relatively less studied in the field of CLSC/RL at 5%. On the other hand, uncertainties in inventory, environment, and cost are the least researched areas in this field. However, employing analytical tools (e.g., GAMS, CPLEX, and LINGO) was desirable for solution approaches in this domain. Among the papers that were chosen, MILP was the most popular model. For large-scale issues, heuristic and meta-heuristic algorithms were applied (Ropi et al. 2021; Tordecilla et al. 2021; de Lima et al. 2022).

Fig. 7

Distribution in the analysis of uncertainty in CLSC studies

Sustainable SC

The food industry has prioritized sustainability in recent years. Perishable goods necessitate special handling procedures, which can have socio-environmental and obvious economic consequences. Thus, FSCs have become more sustainable (Jouzdani and Govindan 2021; Shirzadi et al. 2021). The sustainable SCND should be considered by the managers for the sake of competition with other chains (Shakouhi et al. 2022).

Modeling sustainable supply chain and logistics (SSCL) issues can be accomplished using a variety of methods. In SSCL modeling, multi-objective optimization (MOO) is a popular technique. Minimization of costs, maximization of profits, and operational performance were all widely used indicators from an economic standpoint. Most models used greenhouse gas (GHG) minimization, CO₂ emission reduction, or global warming potential reduction in the environmental dimension. The majority of models focused on minimizing or maximizing the social benefit from a social perspective. In terms of optimization approaches and solution methods, most optimization models are deterministic, and most research has employed classical optimization methods with meta-heuristic algorithms (Jayarathna et al. 2021; Tavana et al. 2022; Kumar et al. 2022).

Fish and perishable SC

Because the subject of this research is fish SC and fish is perishable, this section provides an overview of cold and perishable food SC. The design and management of FSCs are significantly influenced by perishability (Tabrizi et al. 2018). The articles are categorized into four areas for a more thorough examination of the literature: perishable product, perishable food, short-life agri-food, and livestock products. As demonstrated in Table 2, a variety of keywords were utilized to collect data. Figure 8 illustrates the classification of different items (Shukla and Jharkharia 2013) to better comprehend the situation of fresh products, particularly fish.

Table 2 Keywords

Fig. 8

Product differentiation

Nahmias (1982) presented the first detailed overview of perishable goods. Also, Goyal and Giri (2001) provided an excellent overview of the classification of perishable products as well as the policies required to manage them. The reader is directed to Karaesmen et al. (2011) for a comprehensive review of papers dealing with perishable inventory management. Chaudhary et al. (2018) looked at perishable inventory models from various perspectives including shelf life, demand, modeling techniques, research gaps, and replenishment policy.

Perishable product supply chain

Due to the uncertainty of demand, the variety of short shelf life, and high degradation rates, PPSC management is particularly challenging (Lusiantoro et al. 2018). Special storage conditions are required to limit the pace of decay. In the first study, Turnbull (1989) suggested that controlling perishable items necessitates a coordinated SC. Perishability considerations in the SC have gained traction in both practice and academic study (Vahdani et al. 2022).

Hiassat et al. (2017) proposed a perishable product location-inventory-routing model. They used a genetic algorithm (GA) to tackle the problem quickly. Vahdani et al. (2017) recommended using a mathematical programming approach to examine the production scheduling and truck routing problems together to maximize product revenues. To overcome the problem, two heuristic and meta-heuristic methods have been developed. Song et al. (2020) investigated a canonical vehicle routing problem (VRP) in the cold chain logistic system. An improved artificial fish swarm (IAFS) algorithm was proposed, and to create early solutions, a canonical put forward insertion heuristic (PFIH)-based initialization heuristic was presented. Biuki et al. (2020) described a two-step process for incorporating the three characteristics of sustainability into SC operations. A multi-objective mixed-integer programming (MIP) model was designed to solve the problem that was solved by employing two-hybrid meta-heuristics. Leng et al. (2020) provided an optimization model for the inclusive low-carbon location-routing problem (LRP) based on a cold chain to reduce overall logistic costs and vehicle and client waiting times. Goli et al. (2020) designed a sustainable, multi-period, multi-product, and multi-level CLSC network for perishable products. Tirkolaee et al. (2020) introduced a novel mixed-integer linear programming (MILP) model for a green VRP with intermediate depots for various urban fuel consumption, traffic conditions, uncertain demand, and time windows of services for perishable products.

Aghighi et al. (2021) studied a location-routing-inventory problem (LRIP) for perishable products, by developing a two-phase hybrid mathematical model. Li and Zhou (2021) proposed an MO location model for distribution centers of chill chain logistics that considered carbon dioxide emissions. The software was designed using a non-dominated sorting genetic algorithm (NSGA-II) through double-layer composite coding. Zhang et al. (2021) presented a model to aid in selecting a location for cold chain logistic facilities. They used the cloud particle swarm optimization algorithm to solve the model and select a viable location for a new center. Li et al. (2022) suggested a carbon transaction-based integrated LRIP model. To solve the model, the NSGA-II was enhanced. Managing the SCs of perishable products has also been the subject of recent review publications (e.g., Amini et al. 2020; Awad et al. 2020; Durán Peña et al. 2021).

Perishable food supply chain

Because of the importance of FSC management, several research studies have been undertaken that propose various methods for increasing food SC efficiency. Taylor coined the phrase “perishable food SC” in his 1994 research (Taylor 1994). We refer to articles in this field of research in the following paragraphs.

Soysal et al. (2014) considered inventory management in a global beef supply chain, including meat production in Brazil and shipment to Europe. They introduced the MILP model, which is a multi-objective model. Mirmajlesi and Shafaei (2016) used meta-heuristic and exact algorithms to solve a multi-period, multi-echelon, multi-product, capacitated SC problem for products with a short lifetime. Lin and Wu (2016) investigated the price scheme and inventory control in a shrimp SC, comparing the performance of a centralized and decentralized SC. Abedi and Zhu (2017) developed an optimization model for fish culture production, the buying of spawn, and the distribution of harvested fish in a fish SC. Tabrizi et al. (2018) explored equilibrium models in the perishable food SC as a case study on the warm-water farmed fish SC using a unique optimization method. Soysal et al. (2018) considered an IRP for food-related environmental issues. The benefits of horizontal collaboration in terms of perishability, logistic costs, and energy use were investigated in their study. Cheraghalipour et al. (2018) studied a citrus CLSC network and proposed a bi-objective, single-product, multi-period mathematical programming model. Allaoui et al. (2018) suggested a novel two-stage hybrid multi-objective decision-making approach for sustainable agro-food SC design. Bottani et al. (2019) studied the resilient food supply chain design (RFSCD) problem, aiming to design an FSC with sufficient resiliency for the continuity of business operations during disruptions. The perishable inventory-routing problem (PIRP) with stochastic demands was studied by Onggo et al. (2019). Their tests showed that the proposed approach can improve the initial solution while still taking a fair amount of time to compute.

Mogale et al. (2020) introduced a multi-period single-objective mathematical model for the green FSC design considering post-harvest losses and risk to facilitate the decision-making process at the administrative level. An expanded model was investigated in the study of Chan et al. (2020), which builds a unified planning issue for effective food logistic operations. The algorithm used was a modified multi-objective particle swarm optimization (MOPSO) algorithm. Masruroh et al. (2020) presented a dairy manufacturing SC network with integrated multi-product production planning and distribution allocation. Therefore, the proposed models significantly lower total costs and increase annual gross profit. Environmental concerns were taken into account in developing a mathematical model for designing and configuring a green meat SC network (Mohebalizadehgashti et al. 2020). They came up with a MILP model that was multi-objective. The proposed model was solved using a solution approach based on the augmented ε-constraint method. Rahbari et al. (2020) considered the multi-period location–inventory–routing problem (LIRP) for the SC of red meat, considering different vehicles with different capacities.

For the data set of the real case, the considered model was solved using GAMS software. Gholami-Zanjani et al. (2021) proposed a two-stage mixed-integer mathematical model to incorporate key features of inventory-replenishment and location-allocation decisions. Mosallanezhad et al. (2021) presented a mathematical model for the shrimp SC, to minimize the total cost through the SC. Goodarzian et al. (2023) expanded a new MILP formulation for the production–distribution-routing problem in an SC network for sustainable agricultural products. Jouzdani and Govindan (2021) devised a multi-objective mathematical programming methodology to reduce the cost, energy use, and traffic congestion associated with SC operations. The results of an investigation into a dairy SC case revealed that decision-makers could dramatically lessen the SC’s environmental and social impacts while maintaining its economic viability. Moreno-Camacho et al. (2022) provided a multi-objective MILP model for an SSCN including four decisions and three sustainable criteria (e.g., total network costs, carbon emissions, and work conditions and societal development) applied to the Colombian dairy sector as a case study. A fish CLSC was designed by Fasihi et al. (2021a). The proposed mathematical model was applied to a single period in this case. The ε-constraint method and the Lp-metric were used, as well as two other exact methods. Fasihi et al. (2021b) investigated a fish CLSC mathematical model that was bi-objective and multi-period. Multi-objective meta-heuristics were used to address the model. The ε-constraint method is used to validate small-scale problems. Fragoso et al. (2021) suggested a multi-objective mixed integer model for a regional fish processing industry SC network. The model and decision-making process was examined using Pareto frontier approximation and visualization.

Zhang et al. (2022b) developed a closed-loop integrated multi-period FSC planning problem with returnable transport items (RTIs). A kernel-search heuristic-based ε-constraint approach was devised to tackle the problem and achieve an approximate Pareto front. Azani et al. (2022) described an MINLP optimization model for dealing with the COVID-19 pandemic’s influence on the food supply network using Food Hubs (FHs). GAMS software was used to solve the proposed model, and GA was used for larger problems. Behzadianfar et al. (2022) presented an SC network to manufacture and distribute a case study’s dairy goods. After that, five MOP approaches from the literature were used to solve the MO crisp formulation obtained. Foroozesh et al. (2022) developed a green and resilient SC network for perishable items with disruption risks and epistemic uncertainty. A new resilient possibilistic programming (RPP) method was introduced to deal with epistemic uncertainty. Kalantari and Hosseininezhad (2022) presented a worldwide FSC model that is sustainable and takes risks into account. A multi-objective cross-entropy (CE) method was developed to tackle huge instances. By constructing a bi-objective model, Salehi-Amiri et al. (2022) designed a CLSC network for the avocado business. To find the best optimum solutions and select the ideal places to open various centers, GAMS software and its CPLEX solver were used. Also, several review studies (Han et al. 2021; Thomé et al. 2021; Mahmoudi et al. 2022) have investigated perishable food SCs.

Discussion and research gap

According to the findings, current FSC optimization strategies mostly focus on food quality, freshness, and distribution planning. They have not considered the farming procedure. Most of the cold chain logistic decision analysis and data analysis articles are about fresh fruits and vegetables in the distribution stage. This suggests that future studies should focus on gathering data and using it to make judgments about distribution and the cold chain from harvest through processing, distribution, and sale. There is limited research on data gathering, mathematical modeling, and decision-making capacities for fish and seafood, regardless of the cold chain stages. Moreover, because each product has its characteristics, managing the SC for each one has its own set of challenges.

Table 3 provides a brief literature evaluation to identify research needs based on perishable food categories. Given the research gap, the proposed mathematical model is comprehensive by taking all decision-making levels into account, as well as decision-making variables (e.g., production, inventory, distribution, location-allocation, sustainability, and multiple vehicles) to compensate for the drawbacks of previous works. In addition, the study represents a first in terms of merging uncertainty and sustainability in a CLFSC by taking CO₂ emission reduction into account as an environmental factor. This model is a multi-period multi-objective MILP that has received little attention in the literature because it considers three objectives via a trade-off between costs, demand fulfillment, and air pollution. Meta-heuristic algorithms and new hybrid algorithms also have been used due to the problem’s complexity, particularly in large dimensions. In brief, the following are our primary contributions and novelties:

• Designing a sustainable multi-period CLSC network for the fish industry in the face of uncertainty.

• Using a MILP model to optimize three fish SC objectives.

• Taking into account forward and RL for delivering products and transporting waste and returned products for reuse.

• Considering the warm chain from the point of origin to the point of sale (live fish sale and holding in the aquarium).

• Taking into account a variety of vehicles to transport products, each of which has a different capacity and uses a different type of fuel to reduce pollution and environmental damage caused by fuel.

• Considering the rate of deterioration in relation to the manner, in which fish is supplied at various levels of the supply chain and the rate of the waste.

• Choosing the best quantities of allocated and inventoried products at each level.

• Investigating whether or not opening potential locations, such as rice farms and sea farms as temporary farms, is economically viable and necessary.

• Using a combination of five tuned meta-heuristic algorithms and a new hybrid meta-heuristic algorithm to find the best solutions.

• Conducting sensitivity analyses to learn more about the model’s results.

• Investigate uncertainty in the model by changing the probabilities for various demand scenarios and comparing several conditions to deterministic demand.

Table 3 Comparison between the current and previous studies

Describing the model

Because this work is an expansion of a recently published study by Fasihi et al. (2021b), all of their assumptions are taken into account and the following changes. This model takes into account uncertainty by assuming that each scenario (U) has a probability (${p}_{u}$) associated with it. Three types of vehicles are considered for product transportation: tanker (v₁: vehicle type 1) for live fish, refrigerated vehicle (v₂: vehicle type 2) for fresh and processed products, and ordinary vehicle (v₃: vehicle type 3) for fish powder. Each of these vehicles runs on a different fuel, such as diesel, gasoline, liquefied petroleum gas (LPG), and compressed natural gas (CNG). Indeed, the amount of CO₂ produced by each of these fuels varies. Hence, the model is enhanced with a third objective function that aims to reduce total CO₂ emissions from these various vehicles. Accordingly, the model is defined as a multi-objective sustainable model with three objective functions: cost minimization (economic aspect), maximizing customer happiness by meeting demand (social aspect), and CO₂ emission minimization (environmental aspect). The cost of carrying a product between network levels is determined by the distance between locations and the type of vehicle used, with three different forms of transport equipment with different capacities and costs assumed.

Figure 9 depicts the proposed network. The enlarged multi-objective mathematical model can be discussed in the following sections by giving the indices, parameters, and decision variables.

Fig. 9

Detailed fish CLSC network structure

Indices
${i}_{1}={1,2},...,{I}_{1}$	Production sites (pool-farm) — established
${i}_{2}={1,2},...,{I}_{2}$	Production sites (rice-farm) — potential
${i}_{3}={1,2},...,{I}_{3}$	Production sites (sea-farm) — potential
$i={i}_{1}+{i}_{2}+{i}_{3}$	Production sites (fish farms)
${j}_{1}={1,2},...,{J}_{1}$	Distribution sites — established
${j}_{2}={1,2},...,{J}_{2}$	Distribution sites — potential
$j={j}_{1}+{j}_{2}$	Distribution sites
${k}_{1}={1,2},...,{K}_{1}$	Market sites — fresh fish
${k}_{2}={1,2},...,{K}_{2}$	Market sites — processed fish
${{k}^{{^{\prime}}}}_{3}={1,2},...,{{K}^{{^{\prime}}}}_{3}$	Market sites — fish meal
${{k}^{^{\prime\prime} }}_{3}={1,2},...,{{K}^{^{\prime\prime} }}_{3}$	Market sites (some of the fish farms) — fish meal
${k}_{3}={{k}^{{^{\prime}}}}_{3}\cup {{k}^{^{\prime\prime} }}_{3}$	Fish meal market sites — all
${l}_{1}={1,2},...,{L}_{1}$	Recycling sites of fish waste — established
${l}_{2}={1,2},...,{L}_{2}$	Recycling sites of fish waste — potential
$l={l}_{1}\cup {l}_{2}$	Recycling sites of fish waste
$m={1,2},\dots ,M$	Processing sites of fish waste
$t={1,2},\dots ,T$	Periods
$u={1,2},\dots ,U$	Scenarios
$f={1,2},...,F$	Fuel types
Parameters
${f}_{i}$	Constant cost for opening the PC i
${f}_{j}$	Constant cost for opening the DC j
${f}_{l}$	Constant cost for opening the FWRC l
${Df}_{ij}$	Distance between PC i and DC j
${Df}_{{ik}_{1}}$	Distance between PC i to market ${k}_{1}$
${Df}_{{jk}_{1}}$	Distance between DC j to market $k_1$
${Dd}_{im}$	Distance between PC i to FPC m
${Dd}_{jm}$	Distance between DC j FPC m
${Dp}_{{mk}_{2}}$	Distance between FPC m to market $k_2$
${Dr}_{{k}_{1}l}$	Distance between market $k_1$ to FWRC l
${Dr}_{ml}$	Distance between FPC m to FWRC l
${Dw}_{{lk}_{3}}$	Distance between FWRC l to fish meal markets $k_3$
${Dq}_{il}$	Distance between PC i to FWRC l
${Dq}_{jl}$	Distance between DC j FWRC l
${Dq}_{{k}_{1}l}$	Distance between market $k_1$ FWRC l
$CTv1$	Freighting cost per unit of products and distance (km) by vehicle type 1
$CTv2$	Freighting cost per unit of products and distance (km) by vehicle type 2
$CTv3$	Freighting cost per unit of products and distance (km) by vehicle type 3
$Ch$	Inventory holding cost per unit of products at DCs for one period
$Cp$	Processing cost per unit of products at FPCs
$Cr$	Fish meal manufacturing cost per unit of products at FWRCs
${Cp}^{{^{\prime}}}$	Production cost per unit of products at PCs
${d}_{{k}_{1}tu}$	Fresh product demand by market $k_1$   at time t for scenario u
${d}_{{k}_{2}tu}$	Processed product demand by market $k_2$   at time t for scenario u
${d}_{{k}_{3}tu}$	Reprocessed product (fish meal) demand by fish meal markets $k_3$   at time t for scenario u
${\lambda c}_{i}$	Maximum manufacturing capacity of PC i
${\lambda h}_{j}$	Inventory holding capacity of DC j
${\lambda r}_{l}$	Fish meal producing capacity of FWRC l
${\lambda r}_{m}$	Processing capacity of FPC m
${\alpha }_{i}$	Percentage of the deteriorating product by PCs
${\alpha }_{j}$	Percentage of the deteriorating product by DCs
${\alpha }_{{k}_{1}}$	Percentage of the deteriorating product by market ${k}_{1}$
${\beta }_{{k}_{1}}$	Percentage of waste product by market ${k}_{1}$
${\beta }_{m}$	Percentage of waste product by FPCs
$\theta$	Minimum rate for capacity utilizing of each DC
$\delta$	Maximum rate for providing customer demand (fresh fish) straight from the PC
$\rho$	Coefficient of importance for responding to the forward flows
$1-\rho$	Coefficient of importance for responding to the reverse flows
$\varphi$	Conversion rate of fish waste to fish meal
${\varphi }^{{^{\prime}}}$	Conversion rate of fish to processed fish
$MM$	A big positive number
${\tau }^{{max}}$	Maximum of consecutive periods for holding the live fish in the aquarium at a DC
${p}_{u}$	Probability of scenario u
CO2f	Factor of CO2 emissions per each kg consumption of fuel f
$RFv{1}_{f}$	Needed fuel f of vehicle type 1 per each km (kg/km)
$RFv{2}_{f}$	Needed fuel f of vehicle type 2 per each km (kg/km)
$RFv{3}_{f}$	Needed fuel f of vehicle type 3 per each km (kg/km)
$F{P}_{f}$	Fuel f price per each kg consumption ($/kg)
$Capv{1}_{f}$	Maximum capacity of vehicle type 1 — transportation capacity for live fish
$Capv{2}_{f}$	Maximum capacity of vehicle type 2 — transportation capacity for fresh or processed fish
$Capv{3}_{f}$	Maximum capacity of vehicle type 3 — transportation capacity for reprocessed fish
Decision variables
$Fv{1}_{ijftu}$	Live fish quantity freighted by vehicle type 1 utilizing fuel f from PC i to DC j at time t in scenario u
$Fv{2}_{i{k}_{1}ftu}$	Fresh fish quantity freighted by vehicle type 2 utilizing fuel f from PC i to market ${k}_{1}$ at time t in scenario u
$Fv{2}_{j{k}_{1}ftu}$	Fresh fish quantity freighted by vehicle type 2 utilizing fuel f from DC j to market ${k}_{1}$ at time t in scenario u
$Rv{2}_{{k}_{1}lftu}$	Fish waste quantity freighted by vehicle type 2 utilizing fuel f from market ${k}_{1}$ to FWRC l at time t in scenario u
$Rv{2}_{mlftu}$	Fish waste quantity freighted by vehicle type 2 utilizing fuel f from FPC m to FWRC l at time t in scenario u
$Dv{2}_{imftu}$	Fresh fish quantity freighted by vehicle type 2 utilizing fuel f from PC i to FPC m at time t in scenario u
$Dv{2}_{jmftu}$	Fresh fish quantity freighted by vehicle type 2 utilizing fuel f from DC j to FPC m at time t in scenario u
$Pv{2}_{m{k}_{2}ftu}$	Processed fish quantity freighted by vehicle type 2 utilizing fuel f from FPC m to market ${k}_{2}$ at time t in scenario u
$Wv{3}_{l{k}_{3}ftu}$	Fish meal quantity freighted by vehicle type 3 utilizing fuel f from FWRCs l to fish meal markets ${k}_{3}$ at time t in scenario u
$Qv{2}_{ilftu}$	Low-quality fish quantity freighted by vehicle type 2 utilizing fuel f from PC i to FWRCs l at time t in scenario u
$Qv{2}_{jlftu}$	Low-quality fish quantity freighted by vehicle type 2 utilizing fuel f from DC j to FWRCs l at time t in scenario u
$Qv{2}_{{k}_{1}lftu}$	Low-quality fish quantity freighted by vehicle type 2 utilizing fuel f from market ${k}_{1}$ to FWRCs l at time t in scenario u
$I{h}_{jtu}$	Fish inventory quantity by DC j at time t in scenario u
${\lambda }_{itu}$	Fish production quantity by PC i at time t in scenario u
${X}_{i}$	1 if PC i is established at the determined site; 0, otherwise
${W}_{j}$	1 if DC j is established at the determined site; 0, otherwise
${Y}_{l}$	1 if FWRC l is established at the determined site; 0, otherwise

1. PC: production center; DC: distribution center; FPC: fish processing center; FWRC: fish waste recycling center

$$Min\;{Z}_{1}={z}_{a}+{z}_{b}+{z}_{c}+{z}_{d}$$

(1)

$${z}_{a}=\sum_{i=1}^{I}{f}_{i}\times {X}_{i}+\sum_{j=1}^{J}{f}_{j}\times {W}_{j}+\sum_{l=1}^{L}{f}_{l}\times {Y}_{l}$$

(1a)

$$ \begin{aligned} {z}_{b}=&\sum_{i=1}^{I} \sum_{j=1}^{J} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{ij}\times (Fv{1}_{ijftu}\times CT{v}_{1}+\frac{Fv{1}_{ijftu}}{capv{1}_{f}}\times RFv{1}_{f}\times F{P}_{f})\\& +\sum_{j=1}^{J} \sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{j{k}_{1}}\times (Fv{2}_{j{k}_{1}ftu}\times CT{v}_{2}+\frac{Fv{2}_{j{k}_{1}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{i=1}^{I} \sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{i{k}_{1}}\times (Fv{2}_{i{k}_{1}ftu}\times CT{v}_{2}+\frac{Fv{2}_{i{k}_{1}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\ &+\sum_{i=1}^{I} \sum_{m=1}^{M} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{d}_{im}\times (Dv{2}_{imftu}\times CT{v}_{2}+\frac{Dv{2}_{imftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{j=1}^{J} \sum_{m=1}^{M} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{d}_{jm}\times (Dv{2}_{jmftu}\times CT{v}_{2}+\frac{Dv{2}_{jmftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{m=1}^{M} \sum_{{k}_{2}=1}^{{K}_{2}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{p}_{m{k}_{2}}\times (Pv{2}_{m{k}_{2}ftu}\times CT{v}_{2}+\frac{Pv{2}_{m{k}_{2}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{m=1}^{M} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{r}_{ml}\times (Rv{2}_{mlftu}\times CT{v}_{2}+\frac{Rv{2}_{mlftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{r}_{{k}_{1}l}\times (Rv{2}_{{k}_{1}lftu}\times CT{v}_{2}+\frac{Rv{2}_{{k}_{1}lftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{l=1}^{L} \sum_{{k}_{3}=1}^{{K}_{3}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{w}_{l{k}_{3}}\times (Wv{3}_{l{k}_{3}ftu}\times CT{v}_{3}+\frac{Wv{3}_{l{k}_{3}ftu}}{capv{2}_{f}}\times RFv{3}_{f}\times F{P}_{f})\\& +\sum_{i=1}^{I} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{il}\times (Qv{2}_{ilftu}\times CT{v}_{2}+\frac{Qv{2}_{ilftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{j=1}^{J} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{jl}\times (Qv{2}_{jlftu}\times CT{v}_{2}+\frac{Qv{2}_{jlftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f})\\& +\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{{k}_{1}l}\times (Qv{2}_{{k}_{1}lftu}\times CT{v}_{2}+\frac{Qv{2}_{{k}_{1}lftu}}{capv{2}_{f}}\times RFv{2}_{f}\times F{P}_{f}) \end{aligned} $$

(1b)

$${z}_{c}=\left(\sum_{j=1}^{J} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times I{h}_{jtu}\times Ch\right)$$

(1c)

$$\begin{array}{c}{z}_{d}=\sum_{m=1}^{M} \sum_{{k}_{2}=1}^{K} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Pv{2}_{m{k}_{2}ftu}\times Cp\\ +\sum_{l=1}^{L} \sum_{{k}_{3}=1}^{{K}_{3}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Wv{3}_{l{k}_{3}ftu}\times Cr\\ +\sum_{i=1}^{I} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times {\lambda }_{itu}\times C{p}^{{^{\prime}}}\end{array}$$

(1d)

$$\begin{array}{c}Max {Z}_{2}=(\rho /2)\times \left((\stackrel{I}{\sum_{i=1}}\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Fv{2}_{i{k}_{1}ftu}+\sum_{j=1}^{J} \sum_{k=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Fv{2}_{j{k}_{1}ftu})/\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times{d}_{{k}_{1}tu}\right)\\ \text{+}(\rho /2)\times \left(\sum_{m=1}^{M} \sum_{{k}_{2}=1}^{{K}_{2}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Pv{2}_{m{k}_{2}ftu}/\sum_{{k}_{2}=1}^{{K}_{2}}\sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times {d}_{{k}_{2}tu}\right)\\ +\left(1-\rho \right)\times \left(\sum_{l=1}^{L} \sum_{{k}_{3}=1}^{{K}_{3}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times Wv{3}_{l{k}_{3}ftu}\right)/\left(\sum_{{k}_{3}=1}^{{K}_{3}}\sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times {d}_{{k}_{3}tu}\right)\end{array}$$

(2)

$$\begin{array}{c}Min{\text{ Z}}_{3}=\\ \sum_{i=1}^{I} \sum_{j=1}^{J} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{ij}\times \frac{Fv{1}_{ijftu}}{capv{1}_{f}}\times RFv{1}_{f}\times CO{2}_{f}\\ +\sum_{j=1}^{J} \sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{j{k}_{1}}\times \frac{Fv{2}_{j{k}_{1}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{i=1}^{I} \sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{f}_{i{k}_{1}}\times \frac{Fv{2}_{i{k}_{1}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{i=1}^{I} \sum_{m=1}^{M} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{d}_{im}\times \frac{Dv{2}_{imftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{j=1}^{J} \sum_{m=1}^{M} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{d}_{jm}\times \frac{Dv{2}_{jmftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{m=1}^{M} \sum_{{k}_{2}=1}^{{K}_{2}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{p}_{m{k}_{2}}\times \frac{Pv{2}_{m{k}_{2}ftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{m=1}^{M} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{r}_{ml}\times \frac{Rv{2}_{mlftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{r}_{{k}_{1}l}\times \frac{Rv{2}_{{k}_{1}lftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{l=1}^{L} \sum_{{k}_{3}=1}^{{K}_{3}} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{w}_{l{k}_{3}}\times \frac{Wv{3}_{l{k}_{3}ftu}}{capv{2}_{f}}\times RFv{3}_{f}\times CO{2}_{f}\\ +\sum_{i=1}^{I} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{il}\times \frac{Qv{2}_{ilftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{j=1}^{J} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{jl}\times \frac{Qv{2}_{jlftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\\ +\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} \sum_{u=1}^{U}{p}_{u}\times D{q}_{{k}_{1}l}\times \frac{Qv{2}_{{k}_{1}lftu}}{capv{2}_{f}}\times RFv{2}_{f}\times CO{2}_{f}\end{array}$$

(3)

The first objective function (Z₁) is utilized to reduce total costs, which include fixed costs for opening farms, distribution centers, and recycling centers, transportation costs based on distance and fuel consumption of the vehicle used, product inventory costs in distribution centers, farm production costs, processing costs in processing centers, and fish powder production costs in recycling centers. Furthermore, the second objective function (Z₂) aims to maximize the reaction time to CLSC demands for forward and reverse flows.

The third objective function (Z₃), as previously stated, reduces the overall quantity of CO₂ emitted by automobiles. There are numerous vehicles for this purpose, each of which utilizes a different type of fuel f and emits a different amount of CO₂ emissions (CO_2f), and consumes a different amount of fuel f ($RFv{1}_{f}$, $RFv{2}_{f}$, and $RFv{3}_{f}$) each kilometer. The capacity of these vehicles varies ($Capv{1}_{f}$, $Capv{2}_{f}$, and $Capv{3}_{f}$), and the number of shipments is defined by the number of items delivered at each step (for example, n times for route i to j;$n={~}^{Fv{1}_{ijftu}}\!\left/ \!{~}_{capv{1}_{f}}\right.$). Therefore, multiplying these values with the distances at each stage (for example, $D{f}_{ij}$ kilometers for the first stage) yields the total CO₂ emissions, considering the scenario’s probability in uncertain conditions.

Subject to:

$$\begin{array}{c}{\lambda }_{itu}\times (1-{\alpha }_{i})-\sum_{m=1}^{M}\sum_{f=1}^{F} Dv{2}_{imftu}=\sum_{j=1}^{J}\sum_{f=1}^{F} Fv{1}_{ijftu}+\sum_{{k}_{1}=1}^{{K}_{1}}\sum_{f=1}^{F} Fv{2}_{i{k}_{1}ftu}\\ \forall i\in I,\forall t\in T,\forall \, {\text{u}}\in U\end{array}$$

(4)

$$\begin{array}{cc}\sum_{i=1}^{I} \sum_{f=1}^{F}\sum_{t=1}^{T}Fv{1}_{ij{f}_{1}tu}\le MM\times {W}_{j}& \forall j\in J,\forall \text{ u}\in U\end{array}$$

(5)

$${\lambda }_{itu}\le \lambda {c}_{i}\forall i\in I,\forall t\in T,\forall \text{ u}\in U$$

(6)

$$\begin{array}{c}I{h}_{j(t-1)u}+\sum_{i=1}^{I} \sum_{f=1}^{F} Fv{1}_{ijftu}=I{h}_{jtu}+\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F}Fv{2}_{j{k}_{1}ftu}+\sum_{m=1}^{M}\sum_{f=1}^{F} Dv{2}_{jmftu}+\sum_{l=1}^{L} \sum_{f=1}^{F} Qv{2}_{jlftu}\\ \forall j\in J,\forall t\in T,\forall \, {\text{u}}\in U\end{array}$$

(7)

$$\begin{array}{cc}I{h}_{j(t-1)u}+\sum_{i=1}^{I} \sum_{f=1}^{F} Fv{1}_{ijftu}\le \lambda {h}_{j}& \forall j\in J,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(8)

$$\begin{array}{cc}I{h}_{j(t-1)u}+\sum_{i=1}^{I}\sum_{f=1}^{F}Fv{1}_{ijftu}\ge \theta *\lambda {h}_{j}& \forall j\in {J}_{1},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(9)

$$\begin{array}{c}I{h}_{jtu}\le \sum_{t}^{t+{\tau }^{{max}}}\sum_{{k}_{1}=1}^{{K}_{1}}\sum_{f=1}^{F}Fv{2}_{j{k}_{1}ftu}+\sum_{t}^{t+{\tau }^{{max}}}\sum_{m=1}^{M}\sum_{f=1}^{F}Dv{2}_{jmftu}+\sum_{t}^{t+{\tau }^{{max}}}\sum_{l=1}^{L}\sum_{f=1}^{F}Qv{2}_{jlftu}\\ \forall j\in J,\forall t\ge T,\forall \text{ u}\in U\end{array}$$

(10)

$$\begin{array}{cc}\sum_{j=1}^{J}\sum_{f=1}^{F} Fv{2}_{j{k}_{1}ftu}+\sum_{i=1}^{I} \sum_{f=1}^{F} Fv{2}_{i{k}_{1}ftu}\le {d}_{{k}_{1}tu}& \forall {k}_{1}\in {K}_{1},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(11)

$$\begin{array}{cc}\sum_{i=1}^{I}\sum_{f=1}^{F}Fv{2}_{i{k}_{1}ftu}\le \delta \times {d}_{{k}_{1}tu}& \forall {k}_{1}\in {K}_{1},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(12)

$$\begin{array}{c}(\sum_{i=1}^{I} \sum_{f=1}^{F}Dv{2}_{imftu}+\sum_{j=1}^{J} \sum_{f=1}^{F} Dv{2}_{jmftu}-\sum_{l=1}^{L} \sum_{f=1}^{F}Rv{2}_{mlftu})\times {\varphi }^{^{\prime}}=\sum_{{k}_{2}=1}^{{K}_{2}} \sum_{f=1}^{F}Pv{2}_{m{k}_{2}ftu}\\ \forall m\in M,\forall t\in T,\forall \, {\text{u}}\in U\end{array}$$

(13)

$$\begin{array}{cc}\sum_{{k}_{2}=1}^{{K}_{2}} \sum_{f=1}^{F}Pv{2}_{m{k}_{2}ftu}\le \lambda {r}_{m}& \forall \text{ m}\in M,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(14)

$$\begin{array}{cc}\sum_{m=1}^{M}\sum_{f=1}^{F} Pv{2}_{m{k}_{2}ftu}\le {d}_{{k}_{2}tu}& \forall {k}_{2}\in {K}_{2},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(15)

$$\begin{array}{cc}\sum_{l=1}^{L} \sum_{f=1}^{F}Qv{2}_{ilftu}\le {\alpha }_{i}\times {\lambda }_{itu}& \forall i\in I,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(16)

$$\begin{array}{cc}\sum_{i=1}^{I}\sum_{f=1}^{F} \sum_{t=1}^{T} Qv{2}_{ilftu}\le MM\times {Y}_{l}& \forall l\in L,\forall \text{ u}\in U\end{array}$$

(17)

$$\begin{array}{cc}\sum_{l=1}^{L}\sum_{f=1}^{F}Qv{2}_{jlftu}\le {\alpha }_{j}\times I{h}_{j(t-1)u}& \forall j\in J,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(18)

$$\begin{array}{cc}\sum_{j=1}^{J} \sum_{f=1}^{F}\sum_{t=1}^{T} Qv{2}_{jlftu}\le MM\times {Y}_{l}& \forall l\in L,\forall \text{ u}\in U\end{array}$$

(19)

$$\begin{array}{cc}\sum_{l=1}^{L} \sum_{f=1}^{F} Qv{2}_{{k}_{1}lftu}\le {\alpha }_{{k}_{1}}\times (\sum_{i=1}^{I}\sum_{f=1}^{F}Fv{2}_{i{k}_{1}ftu}+\sum_{j=1}^{J} \sum_{f=1}^{F}Fv{2}_{j{k}_{1}ftu})& \forall {k}_{1}\in {K}_{1},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(20)

$$\begin{array}{cc}\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F}\sum_{t=1}^{T}Qv{2}_{{K}_{1}lftu}\le MM\times {Y}_{l}& \forall l\in L,\forall \text{ u}\in U\end{array}$$

(21)

$$\begin{array}{cc}\sum_{l=1}^{L}\sum_{f=1}^{F}Rv{2}_{{k}_{1}lftu}\le {\beta }_{{k}_{1}}\times (\sum_{i=1}^{I}\sum_{f=1}^{F}Fv{2}_{i{k}_{1}ftu}+\sum_{j=1}^{J}\sum_{f=1}^{F}Fv{2}_{j{k}_{1}ftu})\times \text{(1-}{\alpha }_{{k}_{1}}\text{)}& \forall {k}_{1}\in {K}_{1},\forall t\in T,\forall \text{ u}\in U\end{array}$$

(22)

$$\begin{array}{cc}\sum_{{k}_{1}=1}^{{K}_{1}}\sum_{f=1}^{F}\sum_{t=1}^{T} Rv{2}_{{k}_{1}lftu}\le MM\times {Y}_{l}& \forall l\in L,\forall \text{ u}\in U\end{array}$$

(23)

$$\begin{array}{cc}\sum_{l=1}^{L}\sum_{f=1}^{F}Rv{2}_{mlftu}\le {\beta }_{m}\times (\sum_{i=1}^{I} \sum_{f=1}^{F} Dv{2}_{imftu}+\sum_{j=1}^{J} \sum_{f=1}^{F}Dv{2}_{jmftu})& \forall m\in M,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(24)

$$\begin{array}{cc}\sum_{m=1}^{M}\sum_{f=1}^{F} \sum_{t=1}^{T} Rv{2}_{mlftu}\le MM\times {Y}_{l}& \forall l\in L,\forall \text{ u}\in U\end{array}$$

(25)

$$\begin{array}{c}(\stackrel{M}{\underset{m=1}{\sum }}\sum_{f=1}^{F} Rv{2}_{mlftu}+\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} Rv{2}_{{k}_{1}lftu}+\sum_{i=1}^{I} \sum_{f=1}^{F} Qv{2}_{ilftu}+\sum_{j=1}^{J} \sum_{f=1}^{F} Qv{2}_{jlftu}+\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F}Qv{2}_{{k}_{1}lftu})\times \varphi =\sum_{{k}_{3}=1}^{{K}_{3}}\sum_{f=1}^{F}Wv{3}_{l{k}_{3}ftu}\\ \forall l\in L,\forall t\in T,\forall \, {\text{u}}\in U\end{array}$$

(26)

$$\begin{array}{cc}\sum_{{k}_{3}=1}^{{K}_{3}} \sum_{f=1}^{F} Wv{3}_{l{k}_{3}ftu}\le \lambda {r}_{l}& \forall l\in L,\forall t\in T,\forall \text{ u}\in U\end{array}$$

(27)

$$\begin{array}{cc}\sum_{l=1}^{L} \sum_{f=1}^{F} Wv{3}_{l{k}_{3}ftu}\le {d}_{{k}_{3}tu}& \forall {k}_{3}\in {K}_{3},t\in T,\forall \text{ u}\in U\end{array}$$

(28)

$$\begin{array}{cc}\sum_{j=1}^{J} \sum_{f=1}^{F} \sum_{t=1}^{T} Fv{1}_{ijftu}\le MM\times {X}_{i}& \forall i\in I,\forall \text{ u}\in U\end{array}$$

(29)

$$\begin{array}{cc}\sum_{{k}_{1}=1}^{{K}_{1}} \sum_{f=1}^{F} \sum_{t=1}^{T} Fv{2}_{i{k}_{1}ftu}\le MM\times {X}_{i}& \forall i\in I,\forall \text{ u}\in U\end{array}$$

(30)

$$\begin{array}{cc}\sum_{m=1}^{M} \sum_{f=1}^{F} \sum_{t=1}^{T} Dv{2}_{imftu}\le MM\times {X}_{i}& \forall i\in I,\forall \text{ u}\in U\end{array}$$

(31)

$$\begin{array}{cc}\sum_{l=1}^{L} \sum_{f=1}^{F} \sum_{t=1}^{T} Qv{2}_{ilftu}\le MM\times {X}_{i}& \forall i\in I,\forall \text{ u}\in U\end{array}$$

(32)

$$\begin{array}{cc}{X}_{i},{Y}_{l},{W}_{j}\in \left\{{0,1}\right\}& \forall i\in I,\forall l\in L,\forall j\in J\end{array}$$

(33)

$$\begin{array}{c}Fv{1}_{ijftu},Fv{2}_{i{k}_{1}ftu},Fv{2}_{j{k}_{1}ftu},Dv{2}_{imftu},Dv{2}_{jmftu},Dv{2}_{jmftu},\\ Rv{2}_{{k}_{1}lftu},Rv{2}_{mlftu},Wv{3}_{l{k}_{3}ftu},Qv{2}_{ilftu},Qv{2}_{jlftu},Qv{2}_{{k}_{1}lftu}\ge 0\\ \forall i\in I,j\in J,{k}_{1}\in {K}_{1},{k}_{2}\in {K}_{2},{k}_{3}\in {K}_{3},m\in M,l\in L,t\in T,\forall \, {\text{u}}\in U,f\in F\end{array}$$

(34)

$$\begin{array}{cc}I{h}_{jtu}\ge 0, {\lambda }_{itu}\ge 0& \forall i\in I,\forall j\in J,\forall t\in T,\forall {\text{u}}\in U\end{array}$$

(35)

Equation (4) compares the quantity of primary product (fish produced less deteriorated fish and amount transported to processing facilities) to the amount of product delivered from aquaculture centers to distribution centers and fish markets. If the possible distribution center is open, Constraint (5) permits the product to be transported there. The output of each fish farming center must be less than or equal to the predicted maximum production capacity, as defined by Constraint (6). Equation (7) demonstrates that the quantity of inventory in each period is equal to the inventory level in the previous period plus the product distributed from aquaculture centers minus the amount moved from distribution centers to processing facilities and customers to recycling locations. The product received from aquaculture centers plus the inventory level in the previous period is less than the holding capacity in distribution centers, according to the Constraint (8). Constraint (9) guarantees that the distribution center’s full capacity is utilized. Constraint (10) states that the inventory retention duration in distribution facilities will never exceed the maximum number of consecutive days that live fish can be kept.

The demand for fresh products is greater than or equal to the total amount of products received from producers and distribution hubs, referred to as Constraint (11). Constraint (12) ensures that the producer supplies the maximum number of fresh fish demanded by the customer directly. Constraint (13) assures that the total processed product provided to the market is the same as a ratio (conversion rate) of the total product received from producers and distribution centers minus waste sent to recycling facilities. Constraint (14) states that the volume of processed goods shipped to markets is less than or equal to the expected maximum processing rate as well as consumer demand (Constraint (15)). Constraint (16) states that returned products shipped to recycling facilities from each manufacturer must be less than or equal to a ratio of production waste. Constraint (17) is related to Constraint (16) and ensures that returned items from production centers will only be transported to a processing center if a potential center for such facilities is opened. Similar Constraints (16)–(25) limit the number of items delivered to the facility’s maximum capacity and treat the facility’s construction as a prerequisite for delivering products.

The entire reprocessed product (fish powder) provided to fish powder markets equals a coefficient (conversion rate) of the total products returned from producers, distribution centers, clients, and processing centers, according to Constraint (26). Constraints (27) and (28) ensure that the amount of fish powder transported to the fish powder markets is less than or equal to their respective production capacity and consumption. Constraints (29)–(32) specify that items are only shipped to a potential location if a manufacturing center has been established there previously. Finally, binary and non-negative variables are shown in Constraints (33)–(35), respectively.

Solution approach

This section delves deeper into the used solution approaches, including the encoding and decoding strategy. It is always difficult to solve large-scaled Np-hard problems with exact methods because they are usually expensive and time-consuming (Amiri et al. 2020; Sadeghi-Moghaddam et al. 2019). This paper solves the given model using well-known and recently developed meta-heuristic algorithms and their hybrids. The main reason for thinking about hybrid metaheuristics is to take advantage of their advantages during the intensification and diversification phases. These phases are amplified when hybrid metaheuristics are used, resulting in a better tradeoff. Furthermore, previous research has shown that using hybrid meta-heuristics can improve the solution process in terms of both time and cost.

In addition, the performance of these algorithms is verified using the ε-constraint method (Paydar et al. 2017). In the ε-constraint method, the first objective function is treated as the primary goal, while two other objects are converted into constraints. To compare evolutionary algorithms and the ε-constraint method for performance, standard measure metrics such as the mean ideal distance (MID), the number of Pareto solutions (NPS), maximum spread (MS), CPU time, and spread of non-dominance solution (SNS) are used. The most important details about these metrics can be found in Fasihi et al. (2021b), and it is worth noting that the third objective function, minimization, should be considered for both MID and SNS metrics.

Meta-heuristic algorithms

NSGA-II (Deb et al. 2002) is a well-known meta-heuristic algorithm, while the multi-objective Keshtel algorithm (MOKA) (Cheraghalipour et al. 2018) and multi-objective social engineering optimizer algorithm (MOSEO) (Fathollahi-Fard et al. 2020) are two new meta-heuristics, and the multi-objective hybrid GA and SEO (MOGASEO) and multi-objective hybrid KA and SEO (MOKASEO) are two new proposed The first three algorithms (MOKA, NSGA-II, and MOSEO) are described in detail in Fasihi et al. (2021b), while the hybrid meta-heuristics are described in the following section.

Multi-objective hybrid GA and SEO: Given that meta-heuristic algorithms have a general state in handling diverse problems, it is preferable to make the necessary adjustments to the problem’s conditions, according to the problem analyst’s judgment. Basic adjustments or a new format combining numerous meta-heuristic methods can improve the problem’s performance. The genetic algorithm has two intensification and diversification operators. MOSEO can be conducted as a series of mutations. MOSEO uses this method to generate rivalry between parents and children by comparing all parents and children initially. If children are more valuable than their parents, they will be accepted.

Multi-objective hybrid KA and SEO

For the intensification phase, the KA has the advantage of using two robust operators: swirling and moving. Although various studies have confirmed the randomization phase in the KA and MOKA, MOSEO can improve this procedure with each iteration. Hence, when new random Keshtels (i.e., solutions) have higher fitness than the previous ones, MOKASEO considers them. The SEO algorithm is used in the KA iteration steps of the MOKASEO algorithm, just as it is in the MOGASEO algorithm. Each solution is compared to MOSEO’s solution, with the best solution being replaced. New Keshtels are replacing the N1 Keshtel group at random. With each iteration of the algorithm, this procedure can produce even better results.

Encoding and decoding scheme

The chromosome in question is a matrix with (3i + 4j + 4k₁ + k₂ + k₃ + 2 m + 2 l + 6f) columns and rows that are counted by the number of periods. The proposed chromosome is depicted schematically in Fig. 10. In reality, the proposed chromosome is made up of two major components. The allocation sequence between the six levels is covered in one section, while the fuel consumption of the vehicles chosen for transmission is covered in the other. The sequence allocation section (the first two columns of each section of this chromosome) is generated randomly with numbers between [0, 1] and arranged in ascending order. The priority of each gene is then used to replace random numbers with discrete numbers. Priority encryption (Gen et al. 2006) is used in these procedures. The section on fuel consumption, on the other hand, is made up of discrete numbers ranging from 1 to F. Columns related to f are single columns in Fig. 10.

Fig. 10

Schematic representation of the proposed chromosome

The following allocation algorithm illustrates the main procedure for calculating allocated quantities and produced CO₂ emissions (Fig. 11). As can be seen, this procedure is followed for each of the proposed network’s six levels, with the only difference being the use of steps 1 and 6. These steps are used if the level has an inventory; otherwise, they are ignored. Fasihi et al. (2021b) provided more details on the constraints taken into account for each segment allocation.

Fig. 11

Primary method for calculating allocated quantities and generated CO₂ emissions

Computational results

Initially, the parameters for both the model and the algorithms are explained in this section. The model is then solved, and the algorithms’ performance is assessed. The results of the computations, as well as sensitivity analysis, a brief discussion, and validation, are presented.

Data generation

Because this study is a follow-up to Fasihi et al. (2021b), some of the repeating values from their work apply to the model parameters reported here as well. Table 4 shows six problems that can be used to evaluate model performance at various sizes. Furthermore, the nodes in Table 4 are cities in Iran’s northern region, and the first issue is that the case study is being conducted in this region. Table 5 shows the model’s other parameters and their values. Table 6 lists all of the parameters related to vehicle capacity, fuel, and CO₂ emissions, as well as the fuel’s CO₂ emission factors (EngineeringToolBox 2009).

Table 4 Suggested data for the test problems

Table 5 Setting other parameters of the model

Table 6 Fuel requirements, prices, and CO₂ emission factors

Algorithm parameter tuning

Tuning the parameters in meta-heuristic algorithms is crucial because if the parameters are not tuned properly, the algorithm’s implementation could result in incorrect results. Thus, the Taguchi experimental design method was adopted (Taguchi 1986). To determine the ideal value for each parameter based on a limited number of encounters. The principle of “smaller is better” is used in this strategy when the problem objective function is minimization. Equation (36) is also provided for calculating the signal-to-noise (S/N) ratio.

$$S/{N}_{smallerisbetter}=-{10}log\left(\frac{1}{k}\sum_{i=1}^{k}{Y}_{i}^{2}\right)$$

(36)

where K stands for the number of orthogonal arrays and Y for the response value. Equation (37) also represents the chosen response. This response is linked to two core concepts (diversity and convergence). The SNS displays the diversity of Pareto solutions, while the MID calculates the algorithm’s convergence rate.

$$MCOV=\frac{MID}{SNS}$$

(37)

This trend must determine the parameters and levels of the algorithm. Each factor (x = i + j + k₁ + k₂ + k₃ + m + l) has three levels, as shown in Table 13. In the next step, Minitab® software is used. NSGA-II and MOSEO will use L₉ orthogonal arrays, while the MOKA, MOGASEO, and MOKASEO will use L₂₇ orthogonal arrays. In addition, Figs. 19, 20, 21, 22, and 23 show the effect plot of these algorithms’ S/N ratio. They can be used to determine the correct levels for all algorithm parameters. Therefore, the optimized algorithm parameters are listed in Table 7’s best-level section.

Table 7 Optimal values for the parameters

Experimental results and discussion

After generating the test problems and tuning the parameters, the algorithms might be implemented and compared for the created issues. Thus, the performance of the five algorithms is evaluated using 24 test problems (i.e., four modes for each of the six test issues, with the likelihood for demand scenarios varying), and the results are compared. The criteria of the four modes are shown in Table 8. Lower and higher demand probabilities are P₂ and P₃, respectively. The criteria listed in the “Solution approach” section are used to evaluate the meta-heuristic algorithms. Table 9 summarizes the findings. The suggested mathematical model is written in the MATLAB R2018b meta-heuristic algorithm program. Under Windows 10, all programs are run on a PC with an Intel® Core™ i7-8750H CPU running at 2.20 GHz. In addition, each test problem was solved for ten trials by utilizing the algorithms developed based on the best parameters according to Taguchi’s experiments.

Table 8 Different scenario probability conditions

Table 9 Algorithm assessment in metrics

Higher NPS, SNS, and MS values correspond to better performance. CPU time and MID should be set to lower values. The MOKASEO, NSGA-II, MOGASEO, MOKA, and MOSEO algorithms have the best performance in terms of the NPS index, as shown in the last three rows of this table. MOKASEO, MOGASEO, MOKA, NSGA-II, MOKASEO, MOKA, and MOSEO algorithms have the best SNS index performance, and MOGASEO, NSGA-II, MOKASEO, MOKA, and MOSEO algorithms have the best MS index performance. MOKASEO, MOGASEO, MOKA, NSGA-II, and MOSEO algorithms have the best performance when the MID index is considered. MOSEO, NSGA-II, MOKA, MOKASEO, and MOGASEO algorithms have the best performance in terms of CPU time index.

Furthermore, the interval plot is utilized to compare the acquired criteria using the analysis of variance (ANOVA) approach (95 percent confidence level). Figures 12, 13, 14, 15, and 16 illustrate the outcomes. It turns out that the outcomes of the algorithms differ statistically. Figure 17 also shows the algorithms’ execution times. Finally, Fig. 18 shows an example of the Pareto front for the first test problem obtained using the MOKASEO algorithm.

Fig. 12

NPS interval plot

Fig. 13

SNS interval plot

Fig. 14

MS interval plot

Fig. 15

MID interval plot

Fig. 16

CPU time interval plot

Fig. 17

Comparing algorithms for CPU time

Fig. 18

The first test problem’s Pareto front

Furthermore, finding the best alternative among the candidate algorithms is difficult due to the wide range of standard measure indicators. Consequently, the “filtering/displaced ideal solution” (F/DIS) approach is used to discover the best algorithm (Pasandideh et al. 2015; Roghanian and Cheraghalipour 2019). Table 10 shows the comparison results of the algorithms using the information from the last two lines of Table 9. MOKASEO is selected as the finest algorithm with the shortest distance to the ideal point because of the direct distance.

Table 10 (F/DIS) method results

Managers are always searching for effective methods for problem-solving and effective decision-making. The administrative bodies and investors in the aquaculture industry can use this model to minimize the negative environmental impacts, lower fixed costs for opening and transportation, and improve the management of production flows and supply chains by aligning production capacities and market demands with the model’s constraints. The results of this model have a significant impact on understanding the requirements for opening new facilities at different levels of the fish industry, taking into account the balance between total cost, customer satisfaction, and environmental concerns.

The proposed model and case study results can be used by fish farm and fish powder factory managers and investors to improve their decision-making. Iran has a significant potential for growth in aquaculture, which if realized, could boost the country’s economy, and protect marine resources. The model looks at potential locations for production, distribution, and recycling centers, and its optimization results can help investors and governors determine the best locations for an efficient distribution and transportation network of fish products in the face of uncertain demand. By utilizing the recycling of fish waste, and by selecting appropriate vehicles, this will also provide environmental management and reducing CO₂ emissions.

Validating and discussing uncertainty

Five cases for the first test problem are considered to investigate the model’s uncertainty by changing the probabilities for various demand scenarios. Table 8 depicts the first four scenarios, with a fifth scenario (P₁ = 1, P₂ = 0, P₃ = 0) depicting situations where uncertainty is not considered.

Lingo software also employs the ε-constraint method to test evolutionary algorithms. It is worth noting that the MID performance measurement criterion is used to compare the performance of the proposed algorithm and the ε-constraint method. Table 11 shows the algorithms’ performance in various probabilities of uncertainty. According to the data, the third, fourth, first, and second cases provide near-optimal answers among the first four cases, respectively. In the many scenarios evaluated, the situation with the highest probability of being attributed to the lower demand scenario produced superior results in the objective functions. In addition, as previously stated, the criteria for not employing the uncertainty scenarios have been studied in case 5, and the results suggest that if the uncertainty is not investigated, the objective functions will have worse values than in cases 3 and 4. The model’s validity is demonstrated by analyzing the generated outcomes. In some circumstances, the proposed algorithms’ outcomes are as good as or better than the ε-constraint method. Equation (38) was used to calculate the gap.

Table 11 Validation results

$$Gap=\left|\frac{Alg-Best}{Best}\right|$$

(38)

Sensitivity analysis

First, sensitivity analysis is conducted under various conditions to further evaluate the proposed model and implement the algorithm in this section. Table 12 summarizes the conditions as well as the findings of the studies. It should be noted that the first problem is subjected to sensitivity analysis, and the MOKASEO solves the proposed MO mathematical model under all conditions. Increasing the rate of deterioration (α) generally lowers overall costs, customer satisfaction, and CO₂ emissions. Similarly, decreasing the rate of deterioration increases costs, satisfaction, and CO₂ emissions. On the other hand, these changes are analyzed for $\rho$ = 0.4 and 0.5, and the prior results were shown to be valid for both of these values. The total cost is decreased by 4% and 7%, respectively; customer satisfaction is reduced by 7% and 16%; and CO₂ emissions are reduced by 23% and 32% with a reduction to 0.5 and 0.4, respectively. Each requirement could be considered based on the decision maker’s priority for the objective functions.

Table 12 Sensitivity analysis results

Conclusions and future directions

Fish is an important source of food and nutritional security for subsistence populations in countries, and it also has connections to the country’s economic and social characteristics. The greatest effectiveness of the utilized network might be guaranteed by using CLSC network design for products such as fish. Furthermore, the industry has made lowering CO₂ emissions a primary priority. As a result of this research, a multi-objective multi-period MILP model for sustainable fish CLSC was developed, which may be used to make strategic decisions on the number of facilities that should be opened. A balance between the chain’s efficiency and responsiveness can be struck by setting consumer demand as a goal and lowering the entire cost of the chain as a goal. On the other hand, environmentalists consider reduced CO₂ emissions from vehicles a third target.

Furthermore, the conditions of uncertainty for demand have been explored to take into account real-world settings. In addition, six test issues in various sizes and situations in terms of probability facing uncertainty have been constructed to demonstrate the model’s robustness. Three well-known meta-heuristics are used, as well as two unique hybrid meta-heuristics, to tackle these challenges. All algorithms are also tweaked using the Taguchi approach to reach optimal performance. The findings of using these meta-heuristics to solve the suggested model are valuable. The statistically significant difference between the techniques’ performances was shown using the ANOVA method. The DIS approach is used to find the optimum algorithm. Finally, the MOKASEO algorithm was chosen as the best for reporting data such as opened locations, assigned values, and saved inventory values. The ε-constraint method of GAMS software was used to analyze the model’s uncertainty and to evaluate evolutionary algorithms using a real-world situation. In addition, a sensitivity analysis under multiple variables is undertaken for the first test problem to better evaluate the planned model. The findings may be beneficial to the appropriate management and organizations.

Other aquaculture products, such as sturgeon and ornamental fish, could be designed using the SC network. Other variables for long-term viability, such as job generation, rumors, and discontent due to foul odors, should be investigated. It is possible to evaluate the impact of the fish farming technique on rice farms’ water pollution or fertilizer enrichment. Other model factors (e.g., fish production) could be unclear; therefore, fuzzy, robust, and stochastic models could be used. More factors (for example, climate change and fish sickness) could raise the uncertainty of model parameters like supply and demand. Operating conditions (such as fish production planning) and the ideal market supply rate could be investigated to improve the model based on the weight of fish to be sold. In this regard, determining the balance in the sale of fish at a specific weight or the provision of production costs (e.g., fish feed) and selling it at a greater weight can be studied. Depending on the trait of cannibalism in trout, several fish farms could be considered based on different production periods. COVID-19’s impact on aquaculture and fish SC might be studied. Coronavirus expansion has had a variety of effects on supply and demand. The significant relationship between the selling price and the product life cycle, as well as its implications for pricing policy, should be investigated. Because fish is perishable, selling prices can be considered a function of time. The high perishability rate could also be considered when planning inventory management.

Appendix

Table 13

Table 13 Algorithm parameters’ ranges and levels

Figures 19, 20, 21, 22, and 23

Fig. 19

NSGA-II S/R plot

Fig. 20

MOKA S/R plot

Fig. 21

MOSEO S/R plot

Fig. 22

MOGASEO S/R plot

Fig. 23

MOKASEO S/R plot