Skip to main content
SpringerLink
Log in

Closing the loop of a global supply chain through a robust optimal decentralized decision support system

  • Recent Advances in Viable and Sustainable Supply Chain Management
  • Published:
Environmental Science and Pollution Research Aims and scope Submit manuscript

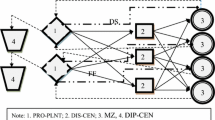
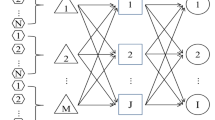
Abstract

This paper presents a novel decentralized decision support system to optimally design a general global closed-loop supply chain. This is done through an original risk-based robust mixed-integer linear programming that is formulated based on an initial uncertain bi-level programming. Addressing the decision-maker’s (DM’s) attitude toward risk, a scenario-based conditional value-at-risk is used to deal with demand and return uncertainty. Also, the Karush–Kuhn–Tucker (KKT) conditions are employed to transform the model into its single-level counterpart. The results obtained from solving a numerical example through the proposed framework are compared with those of the corresponding centralized system, which is formulated through deterministic multi-objective programming and solved by the Lp-metric method. The results show that the use of the proposed framework improves the robustness of profit, income, and cost by about 28%, 34%, and 36% on average. However, a more conservative DM faces a larger cost of robustness than an optimistic DM while experiencing a more significant improvement in the system responsiveness. Using the proposed framework, the manager can measure the advantages, disadvantages, and consequences of their decisions before their actual implementation. This is because the model is capable of establishing fundamental trade-offs among risk, cost, profit, income, robustness, and responsiveness according to the DM’s attitude toward risk.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data availability

I confirm that all relevant data are included in the article and information file.

Abbreviations

RQ:

Research question

SC:

Supply chain

RO:

Robust optimization

CLSC:

Closed-loop supply chain

CLSCND:

Closed-loop supply chain network design

GCLSC:

Global closed-loop supply chain

DSS:

Decision support system

GCLSCND:

Global closed-loop supply chain network design

GSCN:

Global supply chain network

VaR:

Value-at-risk

CVaR:

Conditional value-at-risk

DM:

Decision-maker

MILP:

Mixed integer-linear programming

BLP:

Bi-level programming

KKT:

Karush–Kuhn–Tucker

\(s\in \left\{1,\cdots s,\cdots ,S\right\}\) :

Index of suppliers

\(p\in \left\{1,\cdots p,\cdots ,P\right\}\) :

Index of products

\(f\in \left\{1,\cdots f,\cdots ,F\right\}\) :

Index of manufacturers

\(b\in \left\{1,\cdots b,\cdots ,B\right\}\) :

Index of distribution centers

\(m\in \left\{1,\cdots m,\cdots ,M\right\}\) :

Index of markets

\(g\in \left\{1,\cdots g,\cdots ,G\right\}\) :

Index of collection centers

\(n\in \left\{1,\cdots n,\cdots ,N\right\}\) :

Index of countries

\(t\in \left\{1,\cdots t,\cdots ,T\right\}\) :

Index of times

\(o\in \left\{1,\cdots o,\cdots ,O\right\}\) :

Index of disposal centers

\(\tau \in \left\{1,\cdots o,6\right\}\) :

Index of cost functions

\({q}_{sfpt}^{(1)}\) :

Number of product p purchased for manufacturer f from supplier s at time t

\({q}_{fbpt}^{(2)}\) :

Number of product p produced by manufacturer f for distribution center b at time t

\({q}_{bmpt}^{(3)}\) :

Number of product p distributed from distribution center b to market m at time t

\({q}_{mgpt}^{(4)}\) :

Number of returned product p from market m to collection center g at time t

\({q}_{gopt}^{(5)}\) :

Number of returned product p from collection center g to disposal center o at time t

\({q}_{gfpt}^{(6)}\) :

Number of returned product p from collection center g to manufacturer f at time t

\({X}_{f}\) :

Binary variable to define whether manufacturer f is opened

\({Y}_{b}\) :

Binary variable to define whether distribution center b is opened

\({Z}_{g}\) :

Binary variable to define whether disposal center g is opened

Income:

System’s total income

\({\Psi }_{1}\) :

Facilities’ total opening cost

\({\Psi }_{2}\) :

Products’ total purchasing, transportation, and customs duties cost

\({\Psi }_{3}\) :

Total production and logistics cost from manufacturers to distribution centers

\({\Psi }_{4}\) :

Returned products’ total cost of transportation to collection centers

\({\Psi }_{5}\) :

Products’ total disposal and the relative transportation cost

\({\Psi }_{6}\) :

Sum of saved and transportation costs of returned products to manufacturers

\(\begin{array}{c}{Z}^{leader}\\ {Z}^{lead{er}^{*}}\end{array}\) :

Leader’s objective function/optimal objective function value

\(\begin{array}{c}{Z}^{follower}\\ {Z}^{follow{er}^{*}}\end{array}\) :

Follower’s objective function/optimal objective function value

\(\begin{array}{c}{\gamma }_{leader}\\ {\gamma }_{follower}\end{array}\) :

Objectives’ importance weights

\(Z\) :

The objective function of the mono-objective model resulting from the initial bi-objective one

\({t}_{sfp}^{de}\) :

Delivery time of product p from supplier s to manufacturer f (Month)

\({\rho }_{p}^{se}\) :

The selling price of product p ($)

\({c}_{f}^{mnu}\) :

Opening cost of manufacturer f ($)

\({c}_{b}^{dis}\) :

Opening cost of distribution center b ($)

\({c}_{g}^{col}\) :

Opening cost of collection center g ($)

\({c}_{spn}^{pu}\) :

The unit purchasing cost of product p from supplier s in country n ($)

\({r}_{bspn}^{cd}\) :

Customs duty rate of product p from supplier s in country n

\({c}_{psfn}^{tr (1)}\) :

Unit transportation cost of product p from supplier s to manufacturer f in country n ($)

\({c}_{pfb}^{tr (2)}\) :

Unit transportation cost of product p from manufacturer f to distribution center b ($)

\({c}_{pbm}^{tr (3)}\) :

Unit transportation cost of product p from distribution center b to market center m ($)

\({c}_{pmg}^{tr (4)}\) :

Unit transportation cost of product p from market center m to collection center g ($)

\({c}_{pgo}^{tr (5)}\) :

Unit transportation cost of product p from collection center g to disposal center o ($)

\({c}_{pgf}^{tr (6)}\) :

Unit transportation cost of product p from collection center g to manufacturer f ($)

\({c}_{p}^{pr}\) :

The unit production cost of product p ($)

\({c}_{p}^{o}\) :

Unit disposal cost of product p ($)

\({d}_{sfn}^{(1)}\) :

Distance between supplier s and manufacturer f in country n (× 100 km)

\({d}_{fb}^{(2)}\) :

Distance between manufacturer f and distribution center b (× 100 km)

\({d}_{bm}^{(3)}\) :

Distance between distribution center b and market center m (× 100 km)

\({d}_{mg}^{(4)}\) :

Distance between market m and collection center g (× 100 km)

\({d}_{go}^{(5)}\) :

Distance between collection center g and disposal center o ( x 100 km)

\({d}_{gf}^{(6)}\) :

Distance between collection center g and manufacturer f (× 100 km)

\({a}_{p}\) :

Cost-saving of product p due to its recovery ($)

\({o}_{p}\) :

Minimum disposal fraction of product p

\({{\boldsymbol{v}}}_{fp}^{(1)}\) :

The capacity of manufacturer f for product p

\({{\boldsymbol{v}}}_{bp}^{(2)}\) :

The capacity of distribution center b for product p

\({{\boldsymbol{v}}}_{gp}^{(3)}\) :

The capacity of collection center g for product p

\({r}_{n}^{ex}\) :

Exchange rate of country n

\(\mathcal{X}\) :

Returned products ratio

\({\widetilde{\delta }}_{mpt}\) :

Uncertain demand of product p from market m at time t

References

  • Agrawal VV, Atasu A, Van Wassenhove LN (2019) OM Forum—new opportunities for operations management research in sustainability. Manuf Serv Oper Manag 21(1):1–12

    Article  Google Scholar 

  • Almaktoom AT, Krishnan KK, Wang P, Alsobhi S (2016) Cost efficient robust global supply chain system design under uncertainty. Int J Adv Manuf Technol 85(1–4):853–868

    Article  Google Scholar 

  • Altmann M, Bogaschewsky R (2014) An environmentally conscious robust closed-loop supply chain design. J Bus Econ 84(5):613–637

    Google Scholar 

  • Amin SH, Baki F (2017) A facility location model for global closed-loop supply chain network design. Appl Math Model 41:316–330

    Article  Google Scholar 

  • Amin SH, Zhang G (2012) An integrated model for closed-loop supply chain configuration and supplier selection: multi-objective approach. Expert Syst Appl 39(8):6782–6791

    Article  Google Scholar 

  • Amin SH, Zhang G, Eldali MN (2020) A review of closed-loop supply chain models. J Data Inf Manag 2(4):279–307

    Article  Google Scholar 

  • Amirian J, Amoozad Khalili H, Mehrabian A (2022) Designing an optimization model for green closed-loop supply chain network of heavy tire by considering economic pricing under uncertainty. Environ Sci Pollut Res 29:53107–53120. https://doi.org/10.1007/s11356-022-19578-0

  • Amirtaheri O, Zandieh M, Dorri B, Motameni A (2017) A bi-level programming approach for production-distribution supply chain problem. Comput Ind Eng 110:527–537

    Article  Google Scholar 

  • Asadabadi A, Miller-Hooks E (2018) Co-opetition in enhancing global port network resiliency: a multi-leader, common-follower game theoretic approach. Transp Res B Method 108:281–298

    Article  Google Scholar 

  • Asl-Najafi J, Yaghoubi S, Azaron A (2018) Coordination of a bi-level closed-loop supply chain considering economic and green transportation modes. Int J Ind Eng Prod Res 29(4):429–441

    Google Scholar 

  • Autry CW (2005) Formalization of reverse logistics programs: a strategy for managing liberalized returns. Ind Mark Manag 34(7):749–757

    Article  Google Scholar 

  • Babaveisi V, Paydar MM, Safaei AS (2018) Optimizing a multi-product closed-loop supply chain using NSGA-II, MOSA, and MOPSO meta-heuristic algorithms. J Ind Eng Int 14(2):305–326

    Article  Google Scholar 

  • Baptista S, Barbosa-Póvoa AP, Escudero LF, Gomes MI, Pizarro C (2019) On risk management of a two-stage stochastic mixed 0–1 model for the closed-loop supply chain design problem. Eur J Oper Res 274(1):91–107

    Article  Google Scholar 

  • Battini D, Bogataj M, Choudhary A (2017) Closed loop supply chain (CLSC): economics, modelling, management and control. Int J Prod Econ 183:319–321

    Article  Google Scholar 

  • Ben-Tal A, Bertsimas D, Brown DB (2010) A soft robust model for optimization under ambiguity. Oper Res 58(4-part-2):1220–1234

  • Ben-Tal A, Nemirovski A (1998) Robust convex optimization. Math Oper Res 23(4):769–805

    Article  Google Scholar 

  • Bertsimas D, Brown DB (2009) Constructing uncertainty sets for robust linear optimization. Oper Res 57(6):1483–1495

    Article  Google Scholar 

  • Butner K (2010) The smarter supply chain of the future. Strategy & Leadership 38(1)

  • Cagliano R, Caniato F, Golini R, Kalchschmidt M, Spina G (2008) Supply chain configurations in a global environment: a longitudinal perspective. Oper Manag Res 1(2):86–94

    Article  Google Scholar 

  • Caniato F, Golini R, Kalchschmidt M (2013) The effect of global supply chain configuration on the relationship between supply chain improvement programs and performance. Int J Prod Econ 143(2):285–293

    Article  Google Scholar 

  • Chalmardi MK, Camacho-Vallejo J-F (2018) A bi-level programming model for sustainable supply chain network design that considers incentives for using cleaner technologies. J Clean Prod

  • Chen J, Wang H, Fu Y (2022) A multi-stage supply chain disruption mitigation strategy considering product life cycle during COVID-19. Environ Sci Pollut Res:1–15. https://doi.org/10.1007/s11356-022-18931-7

  • Chen Y-W, Wang L-C, Wang A, Chen T-L (2017) A particle swarm approach for optimizing a multi-stage closed loop supply chain for the solar cell industry. Robot Comput Integr Manuf 43:111–123

    Article  Google Scholar 

  • Cheng X, Yang G, Fan L (2018) Global supply chain network design problem with rules of origin and limited import quotas. Kybernetes. Int J Syst Cyber 48.5:930–948

  • Cheraghalipour A, Roghanian E (2022) A bi-level model for a closed-loop agricultural supply chain considering biogas and compost. Environ Dev Sustain 1–47. https://doi.org/10.1007/s10668-022-02397-1

  • Choi S, RuszczyńSki A (2008) A risk-averse newsvendor with law invariant coherent measures of risk. Oper Res Lett 36(1):77–82

    Article  Google Scholar 

  • Choi TM, Lo CK, Wong CW, Yee RW, Ho HPY (2012) A Five‐R analysis for sustainable fashion supply chain management in Hong Kong: a case analysis. J Fash Mark Manag 16(2):161–175

  • Cohen MA, Lee HL (2020) Designing the right global supply chain network. Manuf Serv Oper Manag 22(1):15–24

    Article  Google Scholar 

  • Collette Y, Siarry P (2013) Multiobjective optimization: principles and case studies: Springer Science & Business Media

  • Crowley J, Fleming C, Cooper C (1982) A computer model for the refraction of non-linear waves. In Coastal Engineering 18:384–403. https://doi.org/10.9753/icce.v18.26

  • Dantzig GB (1955) Linear programming under uncertainty. Manag Sci 1(3–4):197–206

    Article  Google Scholar 

  • Dehghan E, Nikabadi MS, Amiri M, Jabbarzadeh A (2018) Hybrid robust, stochastic and possibilistic programming for closed-loop supply chain network design. Comput Ind Eng 123:220–231

    Article  Google Scholar 

  • Dornier P-P, Ernst R, Fender M, Kouvelis P (2008) Global operations and logistics: text and cases. John Wiley & Sons

  • Du Z-J, Chen Z-X, Yu S-M (2022) Commercial-risk joint analysis with probabilistic linguistic assessments. Knowl-Based Syst 247:108737

    Article  Google Scholar 

  • Duong ATB, Vo VX, Carvalho MDS, Sampaio P, Truong H Q (2022) Risks and supply chain performance: globalization and COVID-19 perspectives. Int J Prod Perform Manag

  • El Ghaoui L, Lebret H (1997) Robust solutions to least-squares problems with uncertain data. SIAM J Matrix Anal Appl 18(4):1035–1064

    Article  Google Scholar 

  • Fallah H, Eskandari H, Pishvaee MS (2015) Competitive closed-loop supply chain network design under uncertainty. J Manuf Syst 37:649–661

    Article  Google Scholar 

  • Fan Y, Zhang X, Zhu L (2010) Estimating the macroeconomic costs of CO2 emission reduction in China based on multi-objective programming. Adv Clim Chang Res 1(1):27–33

    Article  Google Scholar 

  • Fleischmann M, Beullens P, Bloemhof-Ruwaard JM, Van Wassenhove LN (2001) The impact of product recovery on logistics network design. Prod Oper Manag 10(2):156–173

    Article  Google Scholar 

  • Garg K, Kannan D, Diabat A, Jha P (2015) A multi-criteria optimization approach to manage environmental issues in closed loop supply chain network design. J Clean Prod 100:297–314

    Article  Google Scholar 

  • Ghomi-Avili M, Naeini SGJ, Tavakkoli-Moghaddam R, Jabbarzadeh A (2018) A fuzzy pricing model for a green competitive closed-loop supply chain network design in the presence of disruptions. J Clean Prod 188:425–442

    Article  Google Scholar 

  • Goh M, Lim JY, Meng F (2007) A stochastic model for risk management in global supply chain networks. Eur J Oper Res 182(1):164–173

    Article  Google Scholar 

  • Golpîra H (2016) A robust bi-objective uncertain green supply chain network management. Serb J Manag 11(2):211–222

    Article  Google Scholar 

  • Golpîra H (2017a) Robust bi-level optimization for an opportunistic supply chain network design problem in an uncertain and risky environment. Oper Res Decisions 27(1):1–41. https://doi.org/10.5277/ord170102

  • Golpîra H (2017b) Robust bi-level optimization for an opportunistic supply chain network design problem in an uncertain and risky environment. Oper Res Decisions 27(1):21–41

    Google Scholar 

  • Golpîra H (2017c) Supply chain network design optimization with risk-averse retailer. Int J Inform Syst Supply Chain Manag 10(1):16–28

    Article  Google Scholar 

  • Golpîra H (2018) A novel Multiple Attribute Decision Making approach based on interval data using U2P-Miner algorithm. Data Knowl Eng 115:116–128

    Article  Google Scholar 

  • Golpîra H (2020a) Optimal integration of the facility location problem into the multi-project multi-supplier multi-resource Construction Supply Chain network design under the vendor managed inventory strategy. Expert Syst Appl 139:112841. https://doi.org/10.1016/j.eswa.2019.112841

    Article  Google Scholar 

  • Golpîra H (2020b) Smart energy-aware manufacturing plant scheduling under uncertainty: a risk-based multi-objective robust optimization approach. Energy 209:118385

    Article  Google Scholar 

  • Golpîra H, Javanmardan A (2021) Decentralized decision system for closed-loop supply chain: a bi-level multi-objective risk-based robust optimization approach. Comput Chem Eng 154:107472. https://doi.org/10.1016/j.compchemeng.2021.107472

    Article  CAS  Google Scholar 

  • Golpîra H, Javanmardan A (2022) Robust optimization of sustainable closed-loop supply chain considering carbon emission schemes. Sustain Prod Consump 30:640–656. https://doi.org/10.1016/j.spc.2021.12.028

    Article  Google Scholar 

  • Golpîra H, Khan SAR, Safaeipour S (2021) A review of logistics internet-of-things: current trends and scope for future research. J Ind Inf Integr 22:100194. https://doi.org/10.1016/j.jii.2020.100194

    Article  Google Scholar 

  • Golpîra H, Najafi E, Zandieh M, Sadi-Nezhad S (2017) Robust bi-level optimization for green opportunistic supply chain network design problem against uncertainty and environmental risk. Comput Ind Eng 107:301–312. https://doi.org/10.1016/j.cie.2017.03.029

    Article  Google Scholar 

  • Golpîra H, Tirkolaee EB (2019) Stable maintenance tasks scheduling: a bi-objective robust optimization model. Comput Ind Eng 137:106007

    Article  Google Scholar 

  • Govindan K, Fattahi M (2017) Investigating risk and robustness measures for supply chain network design under demand uncertainty: a case study of glass supply chain. Int J Prod Econ 183:680–699

    Article  Google Scholar 

  • Govindan K, Soleimani H, Kannan D (2015) Reverse logistics and closed-loop supply chain: a comprehensive review to explore the future. Eur J Oper Res 240(3):603–626

    Article  Google Scholar 

  • Guan G, Jiang Z, Gong Y, Huang Z, Jamalnia A (2020) A bibliometric review of two decades’ research on closed-loop supply chain: 2001–2020. Ieee Access 9:3679–3695

    Article  Google Scholar 

  • Guan Z, Mou Y, Sun M (2022) Hybrid robust and stochastic optimization for a capital-constrained fresh product supply chain integrating risk-aversion behavior and financial strategies. Comput Ind Eng 169:108224

    Article  Google Scholar 

  • Gupta N, Rajesh R, Daultani Y (2021) Investigation on supply chain vulnerabilities and risk management practices in Indian manufacturing industries. In Computational management. Springer, 535–552

  • Hajipour V, Tavana M, Di Caprio D, Akhgar M, Jabbari Y (2019) An optimization model for traceable closed-loop supply chain networks. Appl Math Model 71:673–699

    Article  Google Scholar 

  • Hammami R, Frein Y (2013) An optimisation model for the design of global multi-echelon supply chains under lead time constraints. Int J Prod Res 51(9):2760–2775

    Article  Google Scholar 

  • Hasani A (2021) Resilience cloud-based global supply chain network design under uncertainty: resource-based approach. Comput Ind Eng 158:107382

    Article  Google Scholar 

  • Hasani A, Khosrojerdi A (2016) Robust global supply chain network design under disruption and uncertainty considering resilience strategies: a parallel memetic algorithm for a real-life case study. Transp Res E Logist Transp Rev 87:20–52

    Article  Google Scholar 

  • Hasani A, Zegordi SH, Nikbakhsh E (2015) Robust closed-loop global supply chain network design under uncertainty: the case of the medical device industry. Int J Prod Res 53(5):1596–1624

    Article  Google Scholar 

  • Hasani A, Zegordi SHJ (2015) A robust competitive global supply chain network design under disruption: the case of medical device industry. Int J Ind Eng Prod Res 26(1):63–84

    Google Scholar 

  • Hassanpour A, Bagherinejad J, Bashiri M (2018) A robust bi-level programming model to design a closed loop supply chain considering government collection’s policy. Sci Iran

  • Huang E, Goetschalckx M (2014) Strategic robust supply chain design based on the Pareto-optimal tradeoff between efficiency and risk. Eur J Oper Res 237(2):508–518

    Article  Google Scholar 

  • Huang L, Murong L, Wang W (2020) Green closed-loop supply chain network design considering cost control and CO2 emission. Modern Supply Chain Research and Applications 2(1):42–59

  • Irawan CA, Akbari N, Jones DF, Menachof D (2018) A combined supply chain optimisation model for the installation phase of offshore wind projects. Int J Prod Res 56(3):1189–1207

    Article  Google Scholar 

  • Jabbarzadeh A, Haughton M, Khosrojerdi A (2018) Closed-loop supply chain network design under disruption risks: a robust approach with real world application. Comput Ind Eng 116:178–191

    Article  Google Scholar 

  • Jalil SA, Hashmi N, Asim Z, Javaid S (2018a) A de-centralized bi-level multi-objective model for integrated production and transportation problems in closed-loop supply chain networks. Int J Manag Sci Eng Manag 14(3):206–217

  • Jalil SA, Javaid S, Muneeb SM (2018b) A decentralized multi-level decision making model for solid transportation problem with uncertainty. Int J Syst Assur Eng Manag 9(5):1022–1033

    Article  Google Scholar 

  • Karakama T, Kainuma Y (2013) Design of a global closed-loop supply chain model. J Jpn Ind Manag Assoc 64(2E):366–375

    Google Scholar 

  • Kaya O, Urek B (2016) A mixed integer nonlinear programming model and heuristic solutions for location, inventory and pricing decisions in a closed loop supply chain. Comput Oper Res 65:93–103

    Article  Google Scholar 

  • Keyvanshokooh E, Ryan SM, Kabir E (2016) Hybrid robust and stochastic optimization for closed-loop supply chain network design using accelerated Benders decomposition. Eur J Oper Res 249(1):76–92

    Article  Google Scholar 

  • Khan SAR, Yu Z, Golpira H, Sharif A, Mardani A (2021) A state-of-the-art review and meta-analysis on sustainable supply chain management: future research directions. J Clean Prod 278:123357

    Article  Google Scholar 

  • Khan SAR, Yu Z, Sharif A, Golpîra H (2020) Determinants of economic growth and environmental sustainability in South Asian Association for Regional Cooperation: evidence from panel ARDL. Environ Sci Pollut Res 27(36):45675–45687

    Article  Google Scholar 

  • Khattry B, Rao JM (2002) Fiscal faux pas?: an analysis of the revenue implications of trade liberalization. World Dev 30(8):1431–1444

    Article  Google Scholar 

  • Kim J, Do Chung B, Kang Y, Jeong B (2018) Robust optimization model for closed-loop supply chain planning under reverse logistics flow and demand uncertainty. J Clean Prod 196:1314–1328

    Article  Google Scholar 

  • Krug Z, Guillaume R, Battaïa O (2021) Exploring the opportunities in establishing a closed-loop supply chain under uncertainty. Int J Prod Res 59(5):1606–1625

    Article  Google Scholar 

  • Kwak D-W, Rodrigues VS, Mason R, Pettit S, Beresford A (2018) Risk interaction identification in international supply chain logistics. Int J Oper Prod Manag 38(2)

  • Li H (2015) A genetic algorithm using a finite search space for solving nonlinear/linear fractional bilevel programming problems. Ann Oper Res 235(1):543–558

    Article  Google Scholar 

  • Li S, Wang L (2010) Outsourcing and capacity planning in an uncertain global environment. Eur J Oper Res 207(1):131–141

    Article  Google Scholar 

  • Liu P, Hendalianpour A, Hafshejani MF, Yaghoobi F, Feylizadeh M (2022) System dynamics model: developing model for supplier selection with a focus on CSR criteria. Complex Intell. Syst. https://doi.org/10.1007/s40747-022-00788-5

  • Longinidis P, Georgiadis MC, Kozanidis G (2015) Integrating operational hedging of exchange rate risk in the optimal design of global supply chain networks. Ind Eng Chem Res 54(24):6311–6325

    Article  CAS  Google Scholar 

  • Lotfi R, Nazarpour H, Gharehbaghi A, Sarkhosh SMH, Khanbaba A (2022) Viable closed-loop supply chain network by considering robustness and risk as a circular economy. 29:70285–70304. https://doi.org/10.1007/s11356-022-20713-0

  • Ma L, Liu Y, Liu Y (2020) Distributionally robust design for bicycle-sharing closed-loop supply chain network under risk-averse criterion. J Clean Prod 246:118967

    Article  Google Scholar 

  • Magazzino C, Alola AA, Schneider N (2021) The trilemma of innovation, logistics performance, and environmental quality in 25 topmost logistics countries: a quantile regression evidence. J Clean Prod 322:129050

    Article  CAS  Google Scholar 

  • MahmoumGonbadi A, Genovese A, Sgalambro A (2021) Closed-loop supply chain design for the transition towards a circular economy: a systematic literature review of methods, applications and current gaps. J Clean Prod 323:129101

    Article  Google Scholar 

  • Mahmud P, Paul SK, Azeem A, Chowdhury P (2021) Evaluating supply chain collaboration barriers in small-and medium-sized enterprises. Sustainability 13(13):7449

    Article  CAS  Google Scholar 

  • Manuj I, Mentzer JT (2008) Global supply chain risk management strategies. Int J Phys Distrib Logist Manag 38.3:192

  • Mao X, Zhang J, Cheng TE, Liu Y (2022) How to choose a downstream partner for a manufacturer considering firms’ personal traits? IEEE Trans Eng Manag. 1–13. https://doi.org/10.1109/TEM.2022.3160279

  • Meixell MJ, Gargeya VB (2005) Global supply chain design: a literature review and critique. Transp Res E Logist Transp Rev 41(6):531–550

    Article  Google Scholar 

  • Mele M, Magazzino C (2021) Pollution, economic growth, and COVID-19 deaths in India: a machine learning evidence. Environ Sci Pollut Res 28(3):2669–2677

    Article  CAS  Google Scholar 

  • Mele M, Magazzino C, Schneider N, Gurrieri AR, Golpira H (2022) Innovation, income, and waste disposal operations in Korea: evidence from a spectral granger causality analysis and artificial neural networks experiments. 39:427–459. https://doi.org/10.1007/s40888-022-00261-z

  • Mirzapour Al-E-Hashem S, Malekly H, Aryanezhad M (2011) A multi-objective robust optimization model for multi-product multi-site aggregate production planning in a supply chain under uncertainty. Int J Prod Econ 134(1):28–42

    Article  Google Scholar 

  • Mishra M, Hota SK, Ghosh SK, Sarkar B (2020) Controlling waste and carbon emission for a sustainable closed-loop supply chain management under a cap-and-trade strategy. Mathematics 8(4):466

    Article  Google Scholar 

  • Nagao T, Ijuin H, Yamada T, Nagasawa K, Zhou L (2021) COVID-19 disruption strategy for redesigning global supply chain network across TPP countries. Logistics 6(1):2

    Article  Google Scholar 

  • Nagurney A, Besik D, Nagurney LS (2019) Global supply chain networks and tariff rate quotas: equilibrium analysis with application to agricultural products. J Glob Optim 75(2):439–460

  • Nakamura K, Ijuin H, Yamada T, Ishigaki A, Inoue M (2018) Modeling of global supply chain network with trans-pacific partnership. J Soc Plant Eng Jpn 30(3):69–81

    Google Scholar 

  • Nakamura K, Yamada T, Tan KH (2019) The impact of Brexit on designing a material-based global supply chain network for Asian manufacturers. Manag Environ Qual Intern J 30(5)

  • Oliveira LS, Machado RL (2021) Application of optimization methods in the closed-loop supply chain: a literature review. J Comb Optim 41(2):357–400

    Article  Google Scholar 

  • Özkır V, Başlıgil H (2013) Multi-objective optimization of closed-loop supply chains in uncertain environment. J Clean Prod 41:114–125

    Article  Google Scholar 

  • Panchal GB, Mirzahosseinian H, Tiwari S, Kumar A, Mangla SK (2022) Supply chain network redesign problem for major beverage organization in ASEAN region. Ann Oper Res 1–32. https://doi.org/10.1007/s10479-022-04571-0

  • Phetsuksiri B, Srisungngam S, Rudeeaneksin J, Boonchu S, Klayut W, Norrarat R, . . . Kasetjaroen Y (2018) QuantiFERON-TB Gold In-Tube test in active tuberculosis patients and healthy adults. Rev Inst Med trop S Paulo 60. https://doi.org/10.1590/S1678-9946201860056

  • Pourjavad E, Mayorga R (2018) Optimization of a sustainable closed loop supply chain network design under uncertainty using multi-objective evolutionary algorithms. Adv Prod Eng Manag 13(2):216–228

    Google Scholar 

  • Prakash S, Kumar S, Soni G, Jain V, Rathore APS (2018) Closed-loop supply chain network design and modelling under risks and demand uncertainty: an integrated robust optimization approach. Ann Oper Res1–28

  • Quintens L, Pauwels P, Matthyssens P (2006) Global purchasing: state of the art and research directions. J Purch Supply Manag 12(4):170–181

    Article  Google Scholar 

  • Rad RS, Nahavandi N (2018) A novel multi-objective optimization model for integrated problem of green closed loop supply chain network design and quantity discount. J Clean Prod 196:1549–1565

    Article  Google Scholar 

  • Rahimi M, Ghezavati V (2018) Sustainable multi-period reverse logistics network design and planning under uncertainty utilizing conditional value at risk (CVaR) for recycling construction and demolition waste. J Clean Prod 172:1567–1581

    Article  Google Scholar 

  • Rahimi M, Ghezavati V, Asadi F (2019) A stochastic risk-averse sustainable supply chain network design problem with quantity discount considering multiple sources of uncertainty. Comput Ind Eng 130:430–449

    Article  Google Scholar 

  • Rahmanzadeh S, Pishvaee MS, Govindan K (2022) Emergence of open supply chain management: the role of open innovation in the future smart industry using digital twin network. Ann Oper Resh 1–29. https://doi.org/10.1007/s10479-021-04254-2

  • Ras PJ, Vermeulen WJ (2009) Sustainable production and the performance of South African entrepreneurs in a global supply chain. The case of South African table grape producers. Sustain Dev 17(5):325–340

  • Reich J, Kinra A, Kotzab H, Brusset X (2021) Strategic global supply chain network design–how decision analysis combining MILP and AHP on a Pareto front can improve decision-making. Int J Prod Res 59(5):1557–1572

    Article  Google Scholar 

  • Rezapour S, Farahani RZ, Fahimnia B, Govindan K, Mansouri Y (2015) Competitive closed-loop supply chain network design with price-dependent demands. J Clean Prod 93:251–272

    Article  Google Scholar 

  • Rockafellar RT, Uryasev S (2002) Conditional value-at-risk for general loss distributions. J Bank Finance 26(7):1443–1471

    Article  Google Scholar 

  • Rogers DS, Tibben-Lembke R (2001) An examination of reverse logistics practices. J Bus Logist 22(2):129–148

    Article  Google Scholar 

  • Rogers L (2009) Going in reverse to move forward. Mod Mater Handl 64(9):28–31

    Google Scholar 

  • Rubio S, Corominas A (2008) Optimal manufacturing–remanufacturing policies in a lean production environment. Comput Ind Eng 55(1):234–242

    Article  Google Scholar 

  • Ruimin M, Lifei Y, Maozhu J, Peiyu R, Zhihan L (2016) Robust environmental closed-loop supply chain design under uncertainty. Chaos Solitons Fractals 89:195–202

    Article  Google Scholar 

  • Saedinia R, Vahdani B, Etebari F, Nadjafi BA (2019) Robust gasoline closed loop supply chain design with redistricting, service sharing and intra-district service transfer. Transp Res E Logist Transp Rev 123:121–141

    Article  Google Scholar 

  • Safaei S, Ghasemi P, Goodarzian F, Momenitabar M (2022) Designing a new multi-echelon multi-period closed-loop supply chain network by forecasting demand using time series model: a genetic algorithm. Environ Sci Pollut Res 1–15. https://doi.org/10.1007/s11356-022-19341-5

  • Sahling F, Kayser A (2016) Strategic supply network planning with vendor selection under consideration of risk and demand uncertainty. Omega 59:201–214

    Article  Google Scholar 

  • Salema MIG, Barbosa-Povoa AP, Novais AQ (2007) An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty. Eur J Oper Res 179(3):1063–1077

    Article  Google Scholar 

  • Saraeian S, Shirazi B, Motameni H (2019) Adaptive control of criticality infrastructure in automatic closed-loop supply chain considering uncertainty. Int J Crit Infrastruct Prot 25:102–124

    Article  Google Scholar 

  • Sharif A, Afshan S, Chrea S, Amel A, Khan SAR (2020) The role of tourism, transportation and globalization in testing environmental Kuznets curve in Malaysia: new insights from quantile ARDL approach. Environ Sci Pollut Res 27(20):25494–25509

    Article  CAS  Google Scholar 

  • Singh AR, Mishra P, Jain R, Khurana M (2012) Design of global supply chain network with operational risks. Int J Adv Manuf Technol 60(1–4):273–290

    Article  Google Scholar 

  • Singh RK, Kumar R (2020) Strategic issues in supply chain management of Indian SMEs due to globalization: an empirical study. Benchmarking Int J 27(3):913–932

  • Soleimani H, Kannan G (2015) A hybrid particle swarm optimization and genetic algorithm for closed-loop supply chain network design in large-scale networks. Appl Math Model 39(14):3990–4012

    Article  Google Scholar 

  • Soyster AL (1973) Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper Res 21(5):1154–1157

    Article  Google Scholar 

  • Srinivasan M, Hamdani M, Ma S (2021) Four supply chain management systems: from supply chain strategies to human resource management. Bus Horiz 64(2):249–260

    Article  Google Scholar 

  • Sun H, Li J, Wang T, Xue Y (2022) A novel scenario-based robust bi-objective optimization model for humanitarian logistics network under risk of disruptions. Transp Res E Logist Transp Rev 157:102578

    Article  Google Scholar 

  • Talaei M, Moghaddam BF, Pishvaee MS, Bozorgi-Amiri A, Gholamnejad S (2016) A robust fuzzy optimization model for carbon-efficient closed-loop supply chain network design problem: a numerical illustration in electronics industry. J Clean Prod 113:662–673

    Article  Google Scholar 

  • Taleizadeh AA, Mamaghan MK, Torabi SA (2018) A possibilistic closed-loop supply chain: pricing, advertising and remanufacturing optimization. Neural Comput Applic 32:1195–1215. https://doi.org/10.1007/s00521-018-3646-3

  • Tan E, Smith G, Saad M (2006) Managing the global supply chain: a SME perspective. Prod Plan Control 17(3):238–246

    Article  Google Scholar 

  • Thiele A (2004) A robust optimization approach to supply chains and revenue management. Massachusetts Institute of Technology. http://hdl.handle.net/1721.1/16693

  • Tosarkani BM, Amin SH (2019) An environmental optimization model to configure a hybrid forward and reverse supply chain network under uncertainty. Comput Chem Eng 121:540–555

    Article  CAS  Google Scholar 

  • Tsiakis P, Papageorgiou LG (2008) Optimal production allocation and distribution supply chain networks. Int J Prod Econ 111(2):468–483

    Article  Google Scholar 

  • Urata T, Yamada T, Itsubo N, Inoue M (2017a) Global supply chain network design and Asian analysis with material-based carbon emissions and tax. Comput Ind Eng 113:779–792

    Article  Google Scholar 

  • Validi S, Bhattacharya A, Byrne P (2014) A case analysis of a sustainable food supply chain distribution system—a multi-objective approach. Int J Prod Econ 152:71–87

    Article  Google Scholar 

  • Vicente LN, Calamai PH (1994) Bilevel and multilevel programming: a bibliography review. J Global Optim 5(3):291–306

    Article  Google Scholar 

  • Wang Q, Chen K, Wang S, Cao X (2022) Optimal decisions in a closed-loop supply chain: fairness concerns, corporate social responsibility and information value. Ann Oper Res 309(1):277–304

    Article  Google Scholar 

  • Wu M, Zhu SX, Teunter RH (2013) The risk-averse newsvendor problem with random capacity. Eur J Oper Res 231(2):328–336

    Article  Google Scholar 

  • Xu Z, Elomri A, Pokharel S, Zhang Q, Ming X, Liu W (2017) Global reverse supply chain design for solid waste recycling under uncertainties and carbon emission constraint. Waste Manag 64:358–370

    Article  Google Scholar 

  • Yang T, Fu C, Liu X, Pei J, Liu L, Pardalos PM (2018) Closed-loop supply chain inventory management with recovery information of reusable containers. J Comb Optim 35(1):266–292

    Article  Google Scholar 

  • Yildizbaşi A, Çalik A, Paksoy T, Farahani RZ, Weber G-WJT, Economy EDo (2018) Multi-level optimization of an automotive closed-loop supply chain network with interactive fuzzy programming approaches. Technol Econ Dev Econ 24(3):1004–1028

  • Yousefi A, Pishvaee M, Teimoury E (2021) Adjusting the credit sales using CVaR-based robust possibilistic programming approach. Iran J Fuzzy Syst 18(1):117–136

    Google Scholar 

  • Yousefi A, Pishvaee MS (2018) A fuzzy optimization approach to integration of physical and financial flows in a global supply chain under exchange rate uncertainty. Int J Fuzzy Syst 20(8):2415–2439

    Article  Google Scholar 

  • Yu Z, Waqas M, Tabish M, Tanveer M, Haq IU, Khan SAR (2022) Sustainable supply chain management and green technologies: a bibliometric review of literature. Environ Sci Pollut Res 29:58454–58470. https://doi.org/10.1007/s11356-022-21544-9

  • Zeballos LJ, Méndez CA, Barbosa-Povoa AP, Novais AQ (2014) Multi-period design and planning of closed-loop supply chains with uncertain supply and demand. Comput Chem Eng 66:151–164

    Article  CAS  Google Scholar 

  • Zeng AZ, Rossetti C (2003) Developing a framework for evaluating the logistics costs in global sourcing processes. Int J Phys Distrib Logist Manag 33(9/10):785

  • Zhang A, Luo H, Huang GQ (2013) A bi-objective model for supply chain design of dispersed manufacturing in China. Int J Prod Econ 146(1):48–58

    Article  Google Scholar 

  • Zhen L, Huang L, Wang W (2019) Green and sustainable closed-loop supply chain network design under uncertainty. J Clean Prod 227:1195–1209

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Sanandaj Branch, Islamic Azad University, Sanandaj, Iran

    Hêriş Golpîra

Authors
  1. Hêriş Golpîra
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The author confirms sole responsibility for the study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.

Corresponding author

Correspondence to Hêriş Golpîra.

Ethics declarations

Ethical approval

The manuscript has not been submitted to any other publication for simultaneous consideration. The submitted work is original and it has not been published elsewhere in any form or language (partially or in full), unless the new work concerns an expansion of previous work. A single study has not been split up into several parts to increase the number of submissions and submitted to various publications or one publication over time. Results have been presented clearly, honestly, and without fabrication, falsification, or inappropriate data manipulation. I adhere to discipline-specific rules for acquiring, selecting, and processing data. No data, text, or theories by others are presented as if they were the author’s own (“plagiarism”).

Conflict of interest

I wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Additional information

Responsible Editor: Arshian Sharif

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Golpîra, H. Closing the loop of a global supply chain through a robust optimal decentralized decision support system. Environ Sci Pollut Res 30, 89975–90005 (2023). https://doi.org/10.1007/s11356-022-23176-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11356-022-23176-5

Keywords

Search

Navigation