Introduction

Recent development in additive manufacturing (AM) technologies has provided increasing applications in functional manufacturing [1]. AM technologies for polymers, particularly powder bed (PB) based processes, are the most widespread and are constantly gaining engineering interest because of easy parts nesting, functional end-use parts, mass production and the absence of support, even for complex geometries [2]. In this regard, lattice structures are a peculiar geometrical feature representing the design freedom possible thanks to the layer-by-layer approach to production [3]. The applications of such structures respond to the intensifying requests of lightweight components with tuned stiffness. From the mechanical point of view, the utilisation of such structures is still confined to products designed under compressive loads, such as impact energy absorbers. The response of lattice structures to a more complex loads system generating, e.g., a tensile stress field, is still a grey area of research, rarely investigated. The main difficulty is designing a suitable specimen geometry that complies with the standard for the bulk specimen. A preliminary approach is to replace the gauge length of a standard specimen with the lattice structures [4]. However, such a sample design introduces discontinuities in the stress distribution along the specimen. This causes a fracture localised at the interface between the lattice and the bulk material, thus out of the controlled region (gauge length) [5]. This result implies a not uniaxial homogeneous stress distribution. Recurrent failures at the transition between the bulk and the cellular material resulted in unreliable mechanical response characterisation, especially in determining the effective tensile strength [5]. In this regard, Drücker et al. [6] also observed a transverse contraction in the transition region due to the ductile material behaviour and the unit cell geometry. Alsalla et al. [5] detected a constraining effect of the full-dense end on the deformation of the cellular solid. Liu et al. [7] proposed an adaption of ASTM-D638-14 which led to the fracture along the rounded transition part between the clamping end and the narrow lattice section. Similar results were presented by Porter et al. [8] and Heiml et al. [9]. Drücker et al. [6] proposed adopting a smooth transition from the lattice to the bulk ends by increasing the strut diameter to avoid this fracture. Drücker et al. [6] applied this method only to a simple elementary cell consisting of three orthogonal struts. However, the transition surface between the bulk and lattice portions was still evident. The fracture was within the lattice portion but localised in different cell rows and planes, which still indicated a non-uniform stress distribution. To eliminate this issue, recently, a modification of the Drücker et al. [6] design has been applied to a non-standard geometry with a lattice structure [10] made by metal additive manufacturing. However, a gap remains in the scientific literature regarding the tensile behaviour and specimen design reliability of polymeric lattice structures. This work proposes a modification of the specimen proposed by Drücker et al. [6] with a new geometry which combines the existing standards with the lattice process/geometry-related limits and constraints. The uniform stress distribution is initially verified by finite element (FE) analysis. Then, the geometry is validated under experimental tensile tests. Three lattice topologies and different strut diameters are tested. The specimens are produced by a laser powder bed fusion process of Polyamide 12. The effect of the part orientation in the build volume on the mechanical performances is investigated by printing replicas of the specimen along different build directions. The boundary effect is analysed by varying the sample thickness. For comparison, the specimens are also tested under compressive loads. The actual cross-section for calculating the mechanical properties is determined using X-ray computed tomography. The tomographs are also used to describe the induced process defects, which were then correlated to the tensile results and the numerical model.

Materials and Methods

Specimen Design

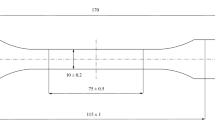
The specimen reported in EN ISO 527–2:2019 [11] (Fig. 1), which covers the tensile properties of plastics, was selected as a starting point to accomplish the standard for the testing. The dimensions proposed by this standard, which fit most of all the industrial AM systems for polymers, are reported in Table 1.

Fig. 1
figure 1

ISO 527 Standard tensile specimen

Full size image
Table 1 Geometric values of the specimen (EN ISO 527–2:2019): specimen type 1A [11]
Full size table

To avoid a fracture out of the gauge length, stress intensification phenomenon and incorrect characterisation of the quantities of interest, the modification of the approach proposed by Drücker et al. [6] method consisted of applying the following measures. Initially, the gauge length of the standard specimen (Fig. 1) was replaced with a repetition of the elementary cell under analysis, then a smooth transition was realized by gradually increasing the diameter of the strut from the end of the gauge length until the complete fusion with the bulk ends. The density gradation was realised in the material portion between the end of the narrow parallel-sided portion (l1 = 80 mm), characterised by the constant nominal relative density of the lattice to be tested and the initial distance between the grips (L = 115 mm). Differently from Drücker et al. [6], the hypothesis is of a density gradation pattern designed to consider a complete fusion between the lattice and the bulk with a final strut diameter corresponding to a relative cell density equal to at least 90% of the bulk value. Considering the size of the unit cell and the space in which this graduation must be realised, it is possible to calculate the number of steps (or the number of cell rows, nsteps) in which the density gradation pattern must be realised to achieve a strut size which leads to at least 90% of relative density. For example, considering l1 = 80 mm and L = 115 mm and a generic cell size of 5 mm, the density gradation must be achieved in a maximum of three steps density gradation. For a cell size equal to 2.5 mm, the maximum number of steps to achieve the desired relative density is 7. In the density gradation region, the strut diameter must vary with a constant percentage increment (Δ%n) calculated according to equation (1).

$${\Delta }_{\%\mathrm{n}}=\sqrt[{\mathrm{n}}_{\mathrm{steps}}]{\frac{{\mathrm{d}}_{\mathrm{f}}}{{\mathrm{d}}_{\mathrm{i}}}}\times 100$$
(1)

where df is the strut diameter corresponding to a cell with at least 90% of relative density and di is the cell diameter to be tested (designed in the gauge length).

Figure 2 shows an example of the gradation pattern for a lattice structure with a cubic primitive (CP) elementary cell with cell size and strut diameter equal to 2.5 mm and 1 mm, respectively. Using the standard specimen reported above, the relative density gradation needs to be realised in 17.5 mm using six steps, up to a strut diameter equal to 2.35 mm, corresponding to a relative density equal to 96%. As can be observed, this approach of relative density gradation gradually reduces the pore size in the elementary cell, allowing a smooth transition between the lattice and the full material density.

Fig. 2
figure 2

Thickness analysis of the six steps density gradation pattern on the 3D model and the mid-plane longitudinal section of the struts of a tensile specimen with two cubic primitive elementary cells in the specimen thickness (cell size and strut diameter equal to 2.5 mm and 1 mm) (CP-2)

Full size image

Topology and Effect of Cell Size and Strut Dimension

This study analyses the behaviour of three different unit cell topologies to validate the design. The three cells were based on a cubic primitive (CP), body-centred based on a cubic primitive (BCC), and face-centred based on a cubic primitive (FCC). In particular, the BCC and FCC structures were combined with CP geometries to avoid bending and misalignment phenomena on the specimen during the tensile tests [12]. According to Maxwell number [13], CP (Maxwell no.—6) and BCC (Maxwell no. -1) are considered slightly bend-dominated structures, while FCC cell (Maxwell no. 0) is stretch-dominated. The cell size and the strut diameters were selected to obtain a width-thickness ratio (i.e. b1/h Fig. 1) equal to about 10:4, according to the standard [11]. Each specimen was designed to have a single elementary cell on the thickness. Therefore, the width and thickness of the specimen were slightly adapted for fitting the lattice cell.

The CP structure was investigated for an elementary cell size of 2.5 mm. Such a small size was selected to verify the design robustness by joining two cells on the specimen thickness. In this case, the mechanical response of the structure is assessed to exclude boundary effects related to the small number of unit cells in the gauge length cross-section. The specimens were named CP-1 and CP-2, respectively.

Different strut diameters, 1 mm and 1.5 mm, were investigated for the BCC structure while keeping constant the cell size (5 mm). The specimens were named BCC1 and BCC1.5, respectively.

The FCC cell size and struts diameter were set equal to 5 mm and 1.25 mm, respectively.

Figure 3 shows the designed structures, and Table 2 summarises the data on each structure design and relative density.

Fig. 3
figure 3

Unit cell of (a) CP, (b) BCC1, (c) BCC1.5 and (d) FCC

Full size image
Table 2 Unit cell dimensions, relative densities and corresponding specimen thickness and width
Full size table

Table 3 reports each structure parameter for the density gradation pattern for the selected geometries. Figure 4 shows an example of the specimen design in the case of the BCC1 structure.

Table 3 Density gradation patterns parameters: di initial diameter, df final diameter, nsteps number of steps to realise the density gradation, and Δ%n the percentage increment of the strut diameter at each increment calculated according to equation (1)
Full size table
Fig. 4
figure 4

BCC1 specimen dimensioning with the detailed view of the three density gradation steps at the lattice-bulk interface

Full size image

For comparison purposes, compression specimens were designed and tested following the ISO 13314 [14]. The lattice portion of the compressive sample (Fig. 5) was designed cubic with a size of 20 mm (referring to the strut middle axis). On the top and the bottom of the lattice portion, two 5 mm thick plates were added to provide a uniform load distribution during the compression tests. The final height of the specimens was 30 mm. Figure 5 shows the specimens and the corresponding nomenclature.

Fig. 5
figure 5

Compression specimen dimensioning (top) applied to the CP structure, followed by BCC1, BCC1.5 and FCC compression samples (bottom)

Full size image

Numerical Modelling, Production and Testing

All the 3D models in STL format are provided as supplementary material. The material selected for the analysis was polyamide-12 (PA12).

After the design and before the production, a 3D finite element model was designed for each designed tensile specimen and solved in ANSYS Workbench 2021 (ANSYS Inc.; Canonsburg, PA). The numerical model aimed to verify the stress distribution homogeneity in the gauge length region. The model has been meshed using a second-order quadratic 10-node tetrahedrons. After a convergence analysis, the element size was set equal to 0.20 mm, which also described well the strut size. A joint constraint was set on all nodes of one of the two end tabs to emulate the clamp. A longitudinal displacement varied linearly from zero to 3 mm on the opposite tab. Figure 6 shows the model schematically in the case of BCC1 structures with the discretisation of a portion of a cell.

Fig. 6
figure 6

Model used for the simulation of the tensile test. BCC1 is reported as an example. Mesh size equal to 0.2 mm

Full size image

The polyamide 12 behaviour was modelled using a multi-linear isotropic hardening (MISO) that simulates plastic yielding and linear-elastic material properties [8]. The properties of the material model (Young Modulus and plasticity) were calculated and tuned from the experimental data extracted from the bulk specimen, while the Poisson ratio has been set accordingly to Ref. [8, 15,16,17].

The samples were manufactured in polyamide-12 (PA12) and using an EOS Formiga P110 Velocis, a laser powder bed fusion system for polymer (PBF-LB/P), also known as selective laser sintering (SLS). The processing chamber and removal chamber temperatures were set to 170 °C and 154 °C, respectively. Table 4 reports the adopted process parameters. During the exposure of each layer, the laser beam scans the contours of all parts before the internal areas.

Table 4 Process parameters for the PBF-LB/P process
Full size table

According to the EOS supplier recommendation, the powder batch was obtained by mixing virgin and recycled in equal portions to emulate a more realistic industrial production.

The specimens were produced along two orientations, horizontal (xy) and vertical (z), within the build volume (Fig. 7) to evaluate the inherent anisotropic behaviour. The specimens in the horizontal position were printed with the thickness of the sample perpendicular to the build direction and axis load along the x-axis (Fig. 7). Specimens z were printed with the load axis along the build direction and the thickness of the specimen along the y-axis (Fig. 7) with the layers perpendicular to the load axis.

Fig. 7
figure 7

Orientations of the samples in the build volume. The primary orientations are xy with the axis load direction of the specimen laid horizontally on the build plane and z with the axis load along the build direction

Full size image

For each specimen, five replicas have been produced and tested. Additional bulk specimens (xy, z orientations) were produced and tested for calibrating the numerical model and for experimental comparison.

After production, the build was cooled to room temperature inside the build chamber. After that, all specimens were cleaned from the residual powders with compressed air. Figure 8(a) shows an example for each xy-oriented produced sample, while Fig. 8(b) depicts the experimental setup in which a BCC1 sample is clamped.

Fig. 8
figure 8

xy specimens manufactured using EOS Formiga P110 Velocis (a) and the experimental setup adopted depicting the clamped BCC1 sample (b)

Full size image

All tensile tests were conducted on an Easydur AURA 10 T equipped with a maximum load equal to 10 tons following EN ISO 527–1 [18], using a crosshead speed of 5 mm/min, machine compliance correction, and an acquisition rate of 500 Hz until the structure collapsed. The stress/strain curves are obtained from the acquired load/displacement counterpart using equations (2) and (3).

$$\upsigma = \frac{P}{{A}_{0}}$$
(2)
$$\upvarepsilon = \frac{\updelta }{{l}_{0}}$$
(3)

where P is the load, δ is the displacement of the crosshead during the tensile test, A0 is the minimal section area measured by CT-scan analysis, and l0 is the initial distance between the two grippers (116 mm).

The elastic modulus was calculated by linear regression as the slope of the stress–strain curve in the interval 0.0005 < ε < 0.0025. The value was expressed in MPa. The transition from linear to non-linear and therefore the yield strength was defined as the stress value corresponding to a deformation equal to 1% [19]. Therefore, the following properties were extracted: tensile strength σm, tensile stress at 1% strain σ1%, tensile modulus Et and elongation at break εtb the stress–strain curve.

After the testing, the fracture surface was observed by a scanning electron microscopy microscope ESEM Quanta 200.

Compression tests were performed according to ISO 13314 [14] standard guidelines with a displacement velocity of 2.5 mm/min up to a total collapse of the structure and an acquisition rate of 100 Hz. The specimens were printed only along the z-direction because of the poorer mechanical performance [20, 21]. The stress/strain curves for the compression test were calculated following the same approach adopted for the tensile test analysis and considering l0 equal to 20 mm. The plateau stress σpl% was calculated as the arithmetical mean of the stresses at 0.1% or smaller strain intervals between 20 and 30% of compressive strain. The area under the curve delimited by the end plateau plastic strain defined the absorbed energy up to failure W*. The compressive Young modulus E* was evaluated by selecting two generic points on the linear part of the curve (equation (4)).

$${E}^{*}= \frac{{\upsigma }_{2}- {\upsigma }_{1}}{{\upvarepsilon }_{2}- {\upvarepsilon }_{1}}$$
(4)

Dimensional Characterisation and Process-Induced Defects

A computed tomography system (CT-scan) (GE Phoenix v|tome|x s) was used to analyse the dimensional, porosity, and pore distribution of the manufactured specimens. The scans were performed using a voltage of 100 kV, a current of 80 μA with a voxel size equal to 16.74 μm. The 3D geometry has been reconstructed using VGStudio Max 3.4. The actual struts diameter was measured in VGStudio Max 3.4 using the cylindrical fitting tool [22]. The measurements have been collected and categorised according to the strut build orientation. From the 3D reconstruction, the section with the minimum area has been extracted and post-processed using ImageJ (an open-source image analysis software). The presence of pores was investigated in different sections of the specimen within the gauge length. The pore diameter was assumed to be the diameter of the maximum sphere containing the pore. The compactness and the sphericity indexes [23] were used to describe the actual shape of the pore. The compactness represents the percentage of the actual volume of the defect compared to the volume of the circumscribed sphere (equation (5)), while sphericity represents the ratio of the defect surface area to the surface area of the equivalent volume sphere (equation (6)).

$$Compactness= \frac{{V}_{defect}}{{V}_{sphere}}= \frac{6{V}_{defect}}{\pi {d}_{defect}^{3}}$$
(5)
$$Sphericity=\Psi = \frac{{A}_{sphere}}{{A}_{defect}}= \frac{\pi {d}_{defect}^{2}}{{A}_{defect}}$$
(6)

Results and Discussion

Preliminary Results of FE Analysis

All topologies were analysed numerically to investigate the uniform load introduction along the lattice portion. The results showed a uniform stress distribution with a gradual decrease toward the bulk section. Figure 9 shows an example of the Von Mises stress distribution for BCC1 at 3 mm of crosshead displacement and a material model from the bulk specimen printed along xy direction. As can be observed, the higher stress regions (in red) are localised and distributed in the gauge length portion in compliance with the standard recommendations and the aim of the design.

Fig. 9
figure 9

Von Mises stress distribution on the BCC1 specimen under tensile load conditions at 3 mm of crosshead displacement: (a) front and (b) mid-plane section views

Full size image

Compression

The compressive behaviour of the tested lattice is shown in Fig. 10. The corresponding mechanical properties are reported in Table 5, in which the cross-section has been extracted from the CT-scan analysis. The curves agree with the compressive mechanisms reported in the literature [9, 13, 24, 25]. Three main stages can be recognised:

  1. 1.

    Elastic region: the stress increases linearly until the yielding region;

  2. 2.

    Progressive collapse of the cells layers at a nearly constant stress level;

  3. 3.

    Densification: the load increases because the lattice collapses, assuming the same behaviour as the bulk material.

Fig. 10
figure 10

Compressive trends of the structures with the corresponding three main deformation stages: elastic region, plateau and densification

Full size image
Table 5 Compression test results. The table values are the average and the standard deviation (SD) of the four replicas for each structure
Full size table

In agreement with the results presented in Ref. [24, 26], no catastrophic failure was observed on the lattice structure. In contrast with the Ashby and Gibson model [27], which correlates the elastic modulus to the relative density, the CP-1 mm and BCC1.5 mm exhibited similar compressive modulus despite having significantly different relative densities (28.67% and 46.84%, respectively). BCC1 showed the lowest compressive modulus value of 751 MPa.

Specimens with struts equal to 1 mm showed a more extended plateau region. In fact, the lower relative density requires a more considerable deformation of the struts to achieve the densification region. The structures with thicker struts were characterised by a positive slope indicating an early densification under the compressive load. This behaviour could be explained by residual un-sintered powder entrapped in the centre of the structure, as visible at the centre of the CT-scan image reported in Fig. 11.

Fig. 11
figure 11

BCC1.5 compression specimen CT-scan section with the residual un-sintered powder noticeable in the centre

Full size image

The extension of the plateau explains the energy absorption values. CP specimens exhibited an absorbed energy value approximately twice BCC1, despite the comparable relative densities (Table 3). The smaller cell size for the CP structure explains the stiffer compressive behaviour with respect to BCC1. The BCC1.5 displayed inferior mechanical performance with respect to FCC, despite the higher relative density. This result could be explained by considering the Maxwell classification. In fact, stretch-dominated topologies like FCC, are usually significantly stiffer than bend-dominated structures (such as the BCC structure) [28].

Tension

The stress–strain curves for the tensile specimens are plotted in Fig. 12, and the cross-section and mechanical properties are reported in Table 6. Figure 13 shows the tested specimens with the corresponding fracture locations in the considered orientations.

Fig. 12
figure 12

Comparison of stress–strain curves of the xy and z specimens

Full size image
Table 6 Tensile test results. The values in the table are the average values and the standard deviations (SD) of the five replicas for each structure
Full size table
Fig. 13
figure 13

Locations of the fracture of the tested tensile specimens built along xy and z orientations

Full size image

The most significant result is that all the fractures occurred within the lattice portion in the gauge length, involving a single lattice row. This confirms a uniform load introduction during the tests, as predicted by the numerical analysis.

All the lattice specimens under tensile load (Fig. 12) showed a first linear zone characterised by Young modulus values comparable to the bulk samples. The plastic region is limited and followed by a brittle fracture of the struts. Because of that, the strain of the lattice specimen is lower than the corresponding bulk specimen. The extension of the plastic region and the tensile strength depended on the topology and the strut size. In fact, the material structure complexity created by the presence of cells produces an inhomogeneous stress distribution within the cell (Fig. 9) that, in turn, inhibits the material elongation. No significant necking has been found, and the SEM inspections (Fig. 14) confirmed the brittle nature of the failure. As an example, Fig. 14 compares the fracture surface of BCC1 xy (Fig. 14(a) and (b)) and BCC1.5 xy (Fig. 14(c)).

Fig. 14
figure 14

SEM images of the strut fracture surfaces of BCC1 xy (a)-(b) and BCC1.5 xy (c) followed by magnifications of (a) representative of different failure surface appearances: lack-of-fusion (detail I), dimpled fracture (detail II) and crazing (detail III)

Full size image

Figure 14(a) shows the fracture mechanisms occurring in the strut. The fracture surface indicates the presence of lack-of-fusion regions (detail I in Fig. 14), typical of the PBF-LB/P, which are characterised by sintered material rather than a full melted [29]. The strut core exhibits a dimpled fracture surface region (detail II in Fig. 14), while the side of the strut shows a region subjected to crazing (detail III in Fig. 14). This region is also visible in Fig. 14(b) and is recognisable by the presence of a fibrillated structure in the entire failed strut cross-section due to the crazing [29]. Some struts displayed a failure characterised by a strained region and a fibrous appearance with visible cavities originated by the initiation and coalescence of micro-voids (detail II in Fig. 14). This type of surface indicates a greater degree of ductility.

Overall, the initial failure of the tested lattice structures under the tensile load is induced by the crazing occurring in some strut, which then led to brittle fractures. Under the increased load due to the partial failure of the structure, the remaining struts exhibited partially ductile fractures, as visible in Fig. 14(a) and (c).

In contrast, neither lack-of-fusion nor crazing phenomenon was observed in BCC1.5 (Fig. 14(c)). Since all the produced specimens were exposed using the same process parameters, the lower number of defects in larger struts indicates a different effect of the process leading to more ductile fractures. Compared to the struts with a diameter of 1 mm, the struts of BCC1.5 also appears more circular.

Regarding testing the specimen geometry robustness using a double cell (CP-2 and CP-1 specimens), the measured mechanical properties were comparable within the calculated standard deviation, validating the specimen design. Thus, the impact of eventual boundary effects on the mechanical characterisation of the structures can be considered negligible.

In agreement with the literature on bulk samples [20, 21, 23], the specimens built along the build direction (z) showed a greater dispersion and lower tensile strength and elongation at break. This behaviour could be explained by the process-induced defects combined with overlapping layers [20, 21, 23]. The different mechanical behaviour among the build direction becomes more marked in the denser structures, such as CP and BCC1. Compared to the magnitude observed in the horizontal (xy) specimens, the elongations at break of the vertical orientation are lower by about 50%. Thinner struts may be less precise, as highlighted by the SEM images, and the porosity may influence mechanical behaviour more [30].

Because of the thicker strut, BCC1.5 specimens exhibited the highest tensile modulus and tensile strength. CP specimens showed a high Young’s modulus and, as expected in comparison with the BCC structure with the same diameter, the lowest tensile strength and elongation at break.

Dimensional Characterisation and the Process-Induced Defects

Figure 13 reports the dimensional characterisation of minimal cross-sectional area and strut diameter for the specimens built along the xy-plane and the vertical orientation, respectively. In addition, the measurements of the strut diameter were grouped according to the direction of the strut in x, y, z and diagonal (diag) according to the machine reference systems reported in Fig. 7.

As can be observed, the highest deviation for the areas compared to the nominal counterpart was detected for the specimen built along the z-direction. All samples geometry differed from the nominal value. For the horizontal, the deviation ranged from -3.2% (CP-2) to -16.5% (BCC1). For the vertical samples, the deviation ranged from -21.2% for CP-1 to -42.6% for BCC1. The deviation, in terms of area, can be explained by observing the strut size (Fig. 15). The measured strut diameter was generally lower than the nominal counterpart along all the considered orientations. The y-oriented struts exhibited the smallest deviations from the nominal counterpart. In contrast, the z-oriented struts showed the highest deviations, reaching the maximum value of -30% for the BCC1 specimens built on the horizontal plane.

Fig. 15
figure 15

Dimensional deviations of the manufactured specimens relative to the CAD nominal. (a) Actual minimal cross-sectional area A0 deviations for the xy and z printing directions and (b) Actual strut diameter deviations along the x,y,z and diag orientations referred to the printer reference axes for both the horizontal and vertical printing directions

Full size image

As regards the effect of the nominal diameter, no significant effect can be detected on the final dimensional deviation. However, as shown in Fig. 15, the deviation measured along two perpendicular diameters is not symmetrical. This identifies an ovalisation of the section, in which the diameter oriented along the vertical building direction is greater than the diameter measured in the horizontal plane (Fig. 16). According to Pavan et al. [31], this effect could be explained by three main factors: the limited fine details capabilities due to the layered construction of the object, the different sintering conditions for the down-facing surfaces (filleting effect [32]) with a resultant higher sintered thickness; and the slicing process performed by the building processor. In addition, gravity could be another influencing factor because the support of the actual sintered region relies only on the previous sintered powder. For this reason, the effect is less evident when the cell is smaller, or the strut diameter is thicker, and the overhang portion becomes shorter, as in the case of CP and BCC1.5, respectively (Fig. 16(c)). This result confirms the observation detected by SEM analysis (Fig. 14).

Fig. 16
figure 16

CT-scans of (a) BCC1 xy, (b) BCC1 z and (c) BCC1.5 z with the ovalisation and strut deflection phenomenon highlighted with red circles. (d) CT-scan section planes scheme of the adopted nomenclature. The reference system reported in the figure corresponds to the production reference system in which the z-axis is the build direction

Full size image

The deviation from an ideal cylinder is higher in the strut built with the axis laying on the xy plane (perpendicular to the build direction) when it creates the bridge of connection (Fig. 16(a)) according to Ref. [31].

The porosity analysis also considered the comparison with data for bulk samples. Table 7 reports the results of the porosity analysis in terms of porosity percentage content.

Table 7 Porosity percentage content analysis results for each structure in the xy and z orientation
Full size table

For the xy direction, in the lattice specimen, the total porosity is lower than the corresponding bulk specimen. For z-oriented specimens, the porosity values are similar to the bulk counterpart. The reason for the lower porosity of the lattice structures compared to the bulk could be found in the laser scanning strategy [31]. As mentioned above, each exposed area is divided into contours and inner area. The contour is the perimeter of the area where the resulting density is higher than the inner part, which is scanned by laser going back and forth continuously. For the bulk specimen, the inner part is predominant, while for the lattice structure, each exposed section is made by numerous small areas (cross-section of the struts) with a size comparable with the beam diameter, and therefore, in most cases, the inner area is absent.

The build direction does not significantly affect the total porosity among the lattice specimens. This fact is explained by considering the exposed area at each layer and the total number of layers. In the case of a bulk specimen, the area of the xy specimen is significantly larger than the corresponding specimen printed along z-direction. The material density within the layer is usually higher than the density created among the layer because of the weak laser penetration through the layers [33]. Since the z-specimen has a smaller exposed area at each layer and a higher number of layers, the porosity of the resulting material is higher [33]. For the lattice structures, the exposed section considers the presence of the struts. Therefore, the section to be scanned by the laser is made of smaller areas that are not connected to each other. With this path of the areas to be scanned, the difference between the build direction becomes negligible.

For a more detailed analysis, the pores were grouped into three classes based on the pore diameter: below 0.2 mm, between 0.2 mm and 0.3 mm, and above 0.3 mm (Table 8). Figure 17 depicts the spatial distribution of the bigger pore size (above 0.3 mm).

Table 8 Porosity analysis results for each structure in the xy and z orientation
Full size table
Fig. 17
figure 17

Spatial distribution of the bigger pore class (d > 0.3 mm) in the the xy and z tensile specimens

Full size image

Regarding the smaller (d ≤ 0.2 mm) and medium (0.2 mm < d ≤ 0.3 mm) pore sizes, the distribution of pores in the bulk and lattice specimens built along the z-axis is comparable. Contrarily, significant differences can be observed for the specimens built along the build direction (z-axis).

The bulk sample showed a higher porosity content for the smallest pores, while the bulk sample showed the lowest porosity content for the medium size.

The percentage of large pores is low. Excluding the CP structure, no significant difference between the bulk and the lattice samples can be detected. A higher quantity of larger pores in the CP structure could also explain the poorest detected mechanical performances. This finding is also confirmed by analysing the sphericity index (Ψ) (Table 9). Compared to spherical pores, irregular ones have a more detrimental effect on the mechanical performance of the manufactured parts, particularly in the stiffness and strength, because these pores are more prone to initiating damage phenomena within the material structure [34]. In the case of the CP specimen, more than 90% of the pores have an irregular shape (Ψ ≤ 0.6). In the xy-oriented specimens, all lattices exhibited a greater presence of irregularly shaped pores (Ψ ≤ 0.5) than in the bulk sample.

Table 9 Analysis of the sphericity index (Ψ) for each structure built along xy and z orientations
Full size table

The difference in the quantity and sphericity of the pores can be explained by a limitation of the process of fabricating such small structures [30]. In particular, regarding xy specimens, pores are primarily distributed along the horizontal struts, which were manufactured with their orientation perpendicular to the build platform (z-oriented struts). In the vertical samples, the porosities are preferentially distributed along the vertical struts printed in the build direction. Consequently, pores with a diameter greater than 0.30 mm tend to cluster along the z-axis (Fig. 15).

BCC1 samples exhibited a more significant number of large pores (d > 0.3 mm) in the z orientation, with a preferential distribution in the nodes and diagonal struts (Fig. 17). In both printing orientations, clusters of pores can be observed, resulting in a low sphericity index compared to the smaller pores. For the BCC1.5, the porosity analysis revealed a preferential concentration of pores in the nodes, with more significant occurrences in the xy specimen than in the vertical counterparts. The central region of the xy specimen contains large, clustered pores (red in the 3D reconstructed section in Fig. 17).

In the FCC specimens, a more significant number of large pores was observed in the vertically printed sample, while both orientations displayed a preferential distribution of porosities along the nodes and the perpendicular struts (Fig. 17).

The porosity morphology and distribution along manufactured porous components affect the mechanical properties strictly. In particular, the porosity is influenced by the strut diameter and relative density from a geometrical point of view and by the printing orientation from a process point of view. The combined effects of these parameters played a crucial role in the exposed surface per layer and the appearance of pores which are detrimental to the mechanical properties. For example, during the testing, the pores aligned in the same direction as the axial load along the z specimens negatively affected the mechanical performance of the z orientation specimen and the perpendicular section relative to the xy orientation.

Comparing Compression and Tensile Properties

PBF-LB/P PA12 specimens exhibited an asymmetric tensile-compression behaviour, with a lower elastic modulus under compression loads with respect to the tensile case of about 85%, which agree with the characterisation of PA12 bulk material performed by Bai et al. [25] and Maskery et al. [35]. This similarity between the lattice and the bulk material behaviours can be explained by considering that bulk polymeric material obtained by PBF-LB is, generally, a sintered artefact. Therefore, despite being considered a bulk material, it behaves as a porous structure at the microscopic point because of a large number of pores.

As regards the lattice structures only, within the standard deviation, Young’s modulus under compression is comparable to the counterpart measured under tensile load. This finding once again validates the robustness of the design.

Numerical Analysis, Model Geometry Correction and Experimental Comparison

The force–displacement curves obtained from the preliminary FE analysis were compared with the actual mechanical response of the structures. The material model was extracted from the data from the bulk material according to the printing orientation. The FE analysis overestimated the resulting force corresponding to a certain displacement in all cases. Therefore, the numerical model is always stiffer than the experimental counterpart. Figure 18 provides an example of this comparison in the case of BCC1 printed along the xy orientation. For a crosshead displacement of 3 mm, the predicted force was roughly 47% higher than the experimental counterpart. This deviation could be explained by the difference between the actual and nominal dimensions, revealed by the X-ray analysis. To consider this effect, the geometry of the numerical model has been corrected according to the dimension of the elliptical geometry of the strut obtained from the CT-scan sections. The adopted modifications are reported in Table 10 according to the strut orientations in the considered x, y, z, and diag orientations and described by the major (a) and minor (b) axes. This means that the geometry of the produced struts deviates systematically from the nominal CAD geometry. Therefore, the model used in the preliminary FE analysis did not represent the actual lattice specimen geometry. Using the modified geometry reduced the deviation between the numerical and experimental results. However, it can be observed (Fig. 18) that the deviation is inverted with respect to the previous comparison. That means the new analysis predicts a weaker mechanical behaviour of the lattice structure. The discrepancy might be because the polyamide 12 material model obtained from the bulk specimen (Sect. 2.3) is not well suited for such a thin lattice. Specifically, this difference could be due to the porosity content of the samples where lattice structures exhibited a lower porosity content than the reference bulk specimen (Table 7). Therefore, in agreement with Ref. [31], the material of such small features, typical of the lattice topologies, behaves differently from the corresponding produced as the bulk sample. Beyond that, a more detailed material model should also consider local differences in the mechanical properties of each strut, according to the orientation of the strut with respect to the build direction, as observed at the specimen level.

Fig. 18
figure 18

BCC1 numerical—experimental force-displacements plot

Full size image
Table 10 BCC1 xy manufactured sample strut’s measurements and standard deviations (SD)
Full size table

Conclusion

This study proposed a novel design for a reliable mechanical characterisation of polymeric lattice structures. The design aimed to localise the sample fracture within the gauge length according to the standard and has been validated by varying the cell topology, the cell size, the strut diameter and the number of cells in the sample thickness. The specimens were produced by PBF-LB/P. The results were also compared with uniaxial compressive tests. The investigation included finite element analysis to verify the load introduction and the stress distribution and CT-scan investigation to analyse the correlation between the porosity morphology and distribution, the inherent anisotropy and the mechanical material behaviour.

The most significant result is the achievement of fracture localisation inside the gauge length in respect of the ISO standard. This result was validated by numerical and experimental analyses. In addition, the comparison between the tensile and the compressive tests also demonstrated the validity of the design.

Apart from that result, it was also shown that the lattice structures produced by PBF-LB/P have some material peculiarity.

Unlike the bulk specimens, lattice specimens showed a lower porosity content but larger percentages of big and irregular pores. A preferential concentration of pores at the nodes and perpendicular struts was observed, especially with respect to the struts aligned along the build direction. This significantly affected the sections of the vertical specimens in which these struts are arranged along the tensile loading axis. The location of these pores clusters reduced the cross-resistance section and promoted fracture initiation.

Vertical specimens exhibited a slight decrease in tensile strength, and the elongation at break was lower than 50% compared to the counterparts built along the xy orientation.

The finite element analyses highlighted the need to account for the actual geometry generated by the process, which systematically differs from the nominal CAD geometry. The modification according to process-related dimensional deviations between the actual and the nominal structures significantly improved the predicting capabilities of the numerical analysis. Despite this correction, the numerical results showed a certain deviation from the experimental counterpart. The discrepancy might be because the material model for the bulk specimen, which was used in the modelling phase, was not well suited for the thin features characterising the lattice structures. The material resulting from processing lattice differs from the bulk counterpart, especially for the porosity content and morphology. In addition, the effect of the strut orientation on the local mechanical performance, which has been neglected in this work, could significantly affect the macroscopic mechanical properties of the structure. While this aspect has been shown to influence the mechanical properties at the macroscopic level, printing specimens in different directions, for lattice structures, single struts should be printed and tested to determine the behaviour of the single struts, also considering the effect of the process on such thin structures.