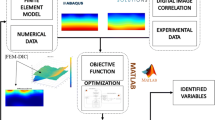
Abstract
Background
Validation of models using full-field experimental techniques traditionally rely on local data comparisons. At present, typically selected data fields are used such as local maxima or selected line plots. Here a new approach is proposed called full-field data fusion (FFDF) that utilises the entire image, ensuring the fidelity of the techniques are fully exploited. FFDF has the potential to provide a direct means of assessing design modifications and material choices.
Objective
A FFDF methodology is defined that has the ability to combine data from a variety of experimental and numerical sources to enable quantitative comparisons and validations as well as create new parameters to assess material and structural performance. A section of a wind turbine blade (WTB) substructure of complex composite construction is used as a demonstrator for the methodology.
Methods
The experimental data are obtained using the full-field experimental techniques of Digital Image Correlation (DIC) and Thermoelastic Stress Analysis (TSA), which are then fused with each other, and with predictions made using Finite Element Analysis (FEA). In addition, the FFDF method enables a new high-fidelity validation technique for FEA utilising a precise full-field point by point similarity assessment with the experimental data, based on the fused data sets and metrics.
Results
It is shown that inaccuracies introduced because of estimation of comparable locations in the data sets are eliminated, The FFDF also enables inaccuracies in the experimental data to be mutually assessed at the same scale regardless of differences in camera sensors. For example, the effect of processing parameters in DIC such as subset size and strain window can be assessed through similarity assessment with the TSA.
Conclusions
The FFDF methodology offers a means for comparing different design configurations and material choices for complex composite substructures, as well as quantitative validation of numerical models, which may ultimately reduce dependence on expensive and time-consuming full-scale tests.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Large composite structures are often certified using the so-called “building block” approach or “testing pyramid” [1] to determine design allowables for components at various length scales, starting at the coupon level for material characterisation to full-scale for complete structural evaluation. The building block approach was developed for validation and certification of composite aerostructures, but other structures including composite wind turbine blades (WTBs) are tested and certified according to this approach (see Fig. 1). Currently the only standardised means of evaluating design allowables is at the coupon scale, as tests between coupon and full-scale may be defined by the manufacturer [1]. Irrespective of the type of structure considered, full-scale testing is becoming ever more time and cost intensive. Therefore, high-fidelity substructure testing methodologies would help to provide structural behaviour based allowables that can be used to inform and validate full-scale design on the basis of performance.
Although sub-structural testing may not fully replace full-scale testing, it will reduce the number of tests required for design developments; in particular cases where the design of a detail or part of a large structure is changed. Examples of substructure testing include detailed examination of sections that involve in-plane and out-of-plane joints, the latter being investigated in the present paper. The concept could be scaled-up to include sections of structures, e.g. across the web and spar-caps of a wind turbine blade or an entire wing box of an aircraft. For such cases, the loads on the section must be defined from a low fidelity global model of the entire structure and fixtures/rigs designed to impart realistic loading scenarios that mimic those experienced in service. Substructural testing enables validation of model predictions at appropriate length scales to capture features in e.g. composite components, which cannot be included at the coupon scale.
To reduce the reliance on physical testing, the concept of “virtual testing” [5] has been introduced. For this to be feasible, high-fidelity simulations must be validated using approaches that provide high levels of confidence in their accuracy and reliability. Such validations can be achieved through quantitative benchmarking using full-field imaging techniques. Thermoelastic Stress Analysis (TSA) [6] and Digital Image Correlation (DIC) [7] are spatially and temporally rich and can be applied to complex component geometries over multiple points to produce full-field representations that are comparable to that generated by models. The spatial resolution of the techniques depend on the camera sensor and lens system, with their temporal resolution dependent on the camera frame rate. Both DIC and TSA rely on image processing approaches that influence the accuracy and precision of the results. In DIC an essential feature of the image processing controls the spatial resolution of the displacements and strains, with the correlation and interpolation dictating the uncertainties in the results associated with data processing. In TSA the raw images retain their spatial resolution but are temporally resolved to reduce uncertainties. Hence, for a quantitative benchmarking based on full-field imaging, the model must be integrated to the same scale and processed using the same algorithms as the experimental data.
The aim of the present paper is to describe the development of a new approach for comparing full-field data quantitively by converting data sets to a common spatial resolution. This means that every individual data point of one data set can be compared with those of another, which allows various full-field comparison and fusion metrics to be applied to discern differences between the data sets, as well as generate valuable performance parameters that cannot be extracted by any single technique, i.e., a combination of strain, stress, and material orientation, may be used to evaluate a metric of stiffness. A further advantage of the data fusion is that the experimental data sets can be mutually assessed to identify regions where the reliability of the measurement is in question. In the paper, examples of fusing TSA, DIC and FEA are provided but the method could be used with any imaging approach, e.g., X-ray computed tomography or computationally derived data sets. The approach is demonstrated on a complex composite hybrid substructure representative of that used in a wind turbine blade. A test rig is designed for the experimental work that provides different loading scenarios. An FEA model of the structure is also developed, and the data fused to provide a series of parameters that can be used for model validation, interpreting the efficacy of the experimental data, and assessing performance parameters. It is demonstrated that full-field data fusion (FFDF) has the potential to provide a direct means of assessing design modifications and material choices.
The paper is based on the 2020 Society for Experimental Mechanics (SEM) Murray Lecture of Professor Janice Dulieu-Barton, entitled “Adventures in thermomechanics: from slow to fast, from expensive to low cost and across length scales”. Hence, it starts with a review of the state of the art on fusing experimental data, citing key publications in the area, including several steps towards the goal of the present paper published by Dulieu-Barton and her co-workers. The following sections cover recent research in more detail than was briefly presented in the Murray Lecture, focusing on the studies of Dr Jack Callaghan, who was awarded a PhD from University of Southampton in May 2022.
Full-Field Imaging Techniques: Background and Progress on Data Fusion
TSA is based on the thermoelastic effect, where the small temperature change that occurs as a result of loading a material in its elastic region is proportional to the change in the sum of the principal stresses [6]. In TSA an infra-red camera is used to obtain the surface temperature change, which in turn is assumed to be related only to stresses on the surface of the component. For orthotropic materials, such as the composite components considered in the present work the following equation relates the surface stresses to the thermoelastic response, \(\Delta T\), as follows [8]:
where \({T}_{0}\) is the absolute temperature of the test specimen, \(\alpha\) is coefficient of thermal expansion, \(\sigma\) is the stress, \(\rho\) is the mass density, and \({C}_{p}\) is the specific heat at constant pressure. Here, the subscripts (\(i,j\)) represent arbitrary coordinates, (\(x,y\)) are the principal stress directions and (\(\mathrm{1,2}\)) are the principal material directions.
A detailed derivation of equation (1) is available in [8], but as \(\Delta T\) is a scalar, the bracketed terms must be equal to each other and are invariant. In the case of the principal stress directions the shear stress is zero, and in the principal material directions \({\alpha }_{6}=0\). The material properties of the plies that comprise a laminated orthotropic composite structure are usually derived in the principal material directions (e.g., elastic moduli, strength, coefficient of thermal expansion, etc.). Hence, it is usual to adopt the principal material directions as the reference axes in TSA of orthotropic composite materials and structures. In deriving equation (1) it is assumed that \(\Delta T\) occurs isentropically. Hence, it is usual to apply a cyclic load in the materials elastic range to achieve reversibility and at a frequency large enough to minimise heat transfer so that the adiabatic assumption satisfied. Recently it has been shown for glass fibre epoxy systems [10], such as those used in the present work, that thermal diffusion is minimised at loading frequencies as low as 2 Hz.
\(\Delta T\) can be extracted from a series of thermal images captured traditionally by either photon detector based thermal cameras [8] or more recently by low-cost microbolometers, e.g. [9]. Typically, in TSA the test specimen is subjected to sinusoidal cyclic loading at a given frequency, \({f}_{0}\), which a measured temperature, \(T\), can be obtained for each pixel (\(x\), \(y\)), and each frame in the thermal image series over the data capture time (\(t\)) as follows:
where \(\phi\) is the phase of \(\Delta T\) with respect to a reference signal usually obtained from the test machine. Equation (2) allows an inverse notch filter or ‘lock-in’ image processing approach based to be applied to extract \({T}_{0}\), \(\Delta T\), and \(\phi\) from the image series. Hence, only the thermal data generated at the loading frequency is used, which allows accurate identification of \(\Delta T\).
In contrast to TSA, Digital Image Correlation (DIC) [7, 11] is a kinematic approach that uses visible light images to evaluate surface displacements from which the component strains are calculated. Images are captured from a test specimen coated with a pattern of randomly positioned greyscale variations (speckles). Typically, images are captured in a reference and deformed state, and the movement of the pattern is tracked in the images through the application of a correlation algorithm. The correlation is facilitated by dividing the images into small subsets of n x n pixels so that the displacement of the central point in each subset can be identified and the deformation between the reference and the deformed state established. DIC is performed using a single camera to obtain in-plane displacements or more usually two cameras in a stereoscopic set-up to accounts for out of plane displacements. Stereo DIC uses approaches founded in photogrammetry, which is essential for assessments of structures with complex geometries, such as the work described in the present paper. Stereo DIC requires camera calibration for triangulation of the relative positions of the cameras [12]. A clear benefit of stereo DIC is that it permits a 3D measure of overall shape changes, i.e. deformations. However it is vital to transform the global co-ordinates into a frame that corresponds to that of the model. Likewise the derived strains will correspond to the projected image plane co-ordinates, which for surfaces that are at an angle to the stereo camera axis, or are not planar, a transformation will be required. DIC is generally applied to test specimens that are quasi statically loaded between two fixed points or over a load ramp. These single correlations often result in very noisy data, which can be spatially smoothed provided the strain is uniform in the region of interest. In the case of complex composite structures containing features and geometry changes, stress concentrations occur that result in heterogeneous strain fields. To capture the strains at features and stress concentrators with any fidelity, small subsets, step size and strain windows are required, all of which reduce precision. The precision can be improved if multiple frames are captured at each load step by introducing pixel by pixel temporal averaging. However, it is often not convenient or even possible to pause tests to capture multiple identical images. To exploit the potential temporal richness of DIC it is possible to apply a cyclic load and to capture multiple images. Then the same image processing procedure used for the TSA, given by equation (2), can be applied by calculating the strains for each image frame using DIC against a single reference image:
where \({\varepsilon }_{0}\) is the mean of the cyclic strain of the specimen, \(\Delta \varepsilon\) is the strain change and \(\phi\) is the phase of \(\Delta \varepsilon\) relative to the load signal and identifies if the strains are positive or negative (i.e., tension or compression) with respect to each other.
The application of DIC to cyclic loading using the lock-in approach is known as Lock-in DIC (LIDIC), which is described in detail in [13]. LIDIC allows TSA and DIC to be combined seamlessly without any need to synchronise image capture. Hence, the infra-red cameras and the visible light cameras can have different frame rates. The approach of combining LIDIC and TSA has been demonstrated in [10] where the stereo LIDIC strain measurements were used to help identify the source of the thermoelastic response in laminated coupon specimens. A simple data fusion was carried out whereby the average \(\Delta \varepsilon\) and \(\Delta T\) were obtained across an area of uniform stress in a strip loaded in uniaxial tension. The identification required a detailed knowledge of the material thermal and mechanical properties so that the strains from the DIC could be converted to \(\Delta T\), to model the response from a laminated orthotropic specimen. A more sophisticated fusion of TSA and DIC data for the same purpose as that of [10] is given in [14], where the thermal data, generated by both DIC and TSA, is interpolated to a common mesh. DIC displacement data were processed using Smoothing Element Analysis (SEA), to create a continuous strain field.
For complex structures, the material coordinate system is not always aligned with the directions of principal stress. Crammond et al. [15] identified this, and used a DIC strain field to determine the stress field by a constitutive relationship with experimentally derived material properties, and then locate the principal stress axes angles which were used to transform the material coefficients of thermal expansion on a point-wise basis for TSA. In [16] LIDIC and TSA were combined to evaluate cracks emanating from a welded structure. The approach used single camera DIC, because the specimens were thin and planar, so that the infra-red camera viewed one side of the specimen and the visible light camera the other. However, the data were not fused, but simply compared using curve fitting. Moreover, full-field images are most often used to validate FEA using colour map/line plot comparisons or by assessing and comparing single values within the field (e.g. local maxima/minima) [9, 15–22]. The approach, although quantitative in the sense that values are compared, may overlook regions where defects are evolving during a test and changes in the strain field are generated away from the points and lines selected for comparison. Hence, comparing single points or lines can only be considered qualitative as spatial quantitative or full-field statistical validations cannot be obtained, justifying the requirement for improved data fusion approaches.
There are multiple data fusion techniques available that combine data from a variety of sensors, numerical modelling, and information from databases in an attempt to improve the accuracy that could be achieved from a single source [23, 24]. Data fusion has been used in non-destructive testing (NDT) applications for materials and structures, whereby pixel-level fusion algorithms have been applied to the detection of a cracks using eddy current, giant magnetoresistance and active thermography testing [25]. The CEN Workshop Agreement CWA 16799 [26] details an approach that incorporates image decomposition methods to validate numerical models from experimental data. Polynomial shape descriptors are used to define the displacement/strain fields across a digital image to ascertain if model predictions fall within experimental uncertainty bounds, hence negating the requirement to determine model uncertainty. It should be noted that a single model output cannot address parametric sensitivity in the prediction. However, the recommendation [26] is that for a model to be deemed a good representation of the reality of the experiment, the model shape descriptors (\({S}_{M}\)) must be within the range
where \({S}_{E}\) is the experimental shape descriptors, and \(u\left({S}_{E}\right)\) is the experimental uncertainty. Examples of the use of this method to validate numerical data from an experiment using full-field imaging can be found in [27–30]. Dvurecenska et al. [27] used image decomposition approach for three different structural test scenarios with a ‘validation metric’. Although the approach may seem quantitative in nature, it should be considered that the scale of the pixels in the images from the techniques are different, and further that the shape and scale of the elements in the model are different. Importantly, model shape functions are often higher order than those used in DIC, which allow linear variation for displacement and give constant strain across subsets and in TSA the temperature is reported as constant across each pixel. This means point comparisons can only be approximate, and the efficacy of line comparisons are highly dependent on how the data is extracted from the FEA. Hence, for a more comprehensive quantitative validation of numerical models for complex structural components, an approach is required that integrates the data sets at the same scale.
A basic example of scale matching model and experimental data fusion is given by Howell [31], who developed a “synthetic reference bitmap” using Finite Element Analysis (FEA) to replicate the thermoelastic response and converted the predicted stress sum to \(\frac{\Delta T}{{T}_{0}}\) using a known values of the thermoelastic parameters. Importantly, instead of comparing data at approximate points, it was converted to the same resolution as experimental TSA data using bi-directional linear interpolation, so that a full-field comparison could be made. Hence, it was possible to subtract the numerical data from the experimental TSA data set to give a residual, which revealed regions of plasticity local to the welds.
Integrated approaches such as that described in [31] enable the variability of material and geometric parameters, as well as any manufacturing inconsistencies, to be assessed in a statistical manner and holistically across the entire field. Thus the effect of discrepancies in material and/or production on the structural response can be obtained. Robust tools are therefore required that can perform quantitative analyses of multi-modal experimental and numerical data, which can provide the basis for further statistically based Design of Experiments (DOE) approaches and other means in which complex structural behaviour can be more comprehensively scrutinised.
Experimental Arrangements
A T-joint substructure was chosen for analysis from an evaluation of cross-sectional strains from the global shell FEA model of a 59 m WTB at 19 m radial distance from the hub, where the strain values were at their maximum (conducted in close collaboration with the project sponsor, Siemens Gamesa Renewable Energy). The location of the T-joint is shown in context to a full WTB in Fig. 2, where the cross-section was defined by radial location, the T-joint specimen was extracted from the cross-section, and the numerical FEA model was built with reference to the specimen, using material properties from the global model. The constituent parts of the T-joint are shown in Fig. 3, along with the composite material coordinate systems. The spar cap (GFRP 1,2,3) and web sheets (GFRP4) are made of a combination of unidirectional (UD) and biaxial glass fibre reinforced polymer (GFRP) composite. Wood 2 is a core region that provides a mould curve for the web face sheets that adhere to the spar cap inner face sheets to form the T-joint. Wood 1 is used as the core material for the web, forming a sandwich panel. Resin pockets are found around the edges of wood 2 and in the centre void.
For the purposes of validating the data fusion process a test case for the T-joint was devised, so that axial compression/tension loading could be combined with bending. The test rig is shown in Fig. 4 and was designed so that it could be clamped to the hydraulic actuator end of a uniaxial servo-hydraulic test machine, and the web of the T-joint specimen clamped to the test machine crosshead via a load cell. The rig is adjustable so that the roller fixtures can be moved horizontally and vertically to accommodate for the complex shape of the specimens, and such that the T-joint specimens can be loaded in both tension and compression. The T-joint substructural samples were cut from actual WTB sections by the manufacturer, and during this process the specimens sustained unexpected damage in the form of cracks in the central core region. To avoid any risk of specimen failure during the cyclic loading tests, a load regime of 5 \(\pm\) 4 kN was selected at 1 Hz load frequency to generate a thermal response (as is required for TSA [6] and LIDIC) and with a positive stress ratio, R, due to the constraints of the rig (i.e. stress reversals are not feasible with the pin contact loading). Due to the geometry and dimension of the test specimens it was necessary to use a servo hydraulic test machine which has a static load capacity of 630 kN. It would normally be preferrable to apply cyclic tests in load control while obtaining full-field data, however due to the low loads and relatively compliant specimens it was not possible to adequately tune the PID control settings. To mitigate this, the cyclic loading tests were executed in displacement control, which meant that the tests had to be manually configured in-situ to ensure that the mean load and load amplitude were maintained throughout by adjusting the displacement amplitude regularly.
The full experimental setup is shown in Fig. 5, with the imaging parameters shown in Table 1. The monochromatic images for DIC (used for LIDIC) were collected using two LaVision Imager E-lite 5 M cameras set up in a stereo configuration using LaVisions’s DaVis StrainMaster software [32]. The DIC measurements yielded 40,632 data points, with a spatial resolution of 0.662 mm/data point. Strains were extracted using a least squares fit to equation (3), i.e., the LIDIC processing [13]. The strain data became consistent (no change in values with increased number of frames used) after 50 frames of capture, and therefore 100 frames in total were used in the analysis for certainty. Thermal images were captured using a FLIR A655sc microbolometer [33] using the camera manufacturer’s proprietary software ResearchIR. A least square curve fitting routine, developed in MATLAB, was used to extract the parameters \({T}_{0}\), \(\Delta T\) and \(\phi\) given in equation (2) from the thermal image series of 8000 frames captured by the microbolometer. A the microbolometer acts as a low pass filter when viewing transient signals [34], such as those obtained for TSA from an object undergoing cyclic loading. Many microbolometer systems have a user selectable inbuilt, software based ‘noise reduction (NR)’ feature. In [34] it was shown that when the NR feature was enabled a pixel-by-pixel rolling temporal average of the number of frames was used to produce the images. In TSA it is usually necessary to have the NR feature enabled [34] as \(\Delta T\) is small and difficult to resolve even with the help of lock-in processing. Hence, in [34] a detailed account of a calibration procedure is provided that is required to account for the attenuation in \(\Delta T\) resulting from the low-pass filter and the NR feature. In the present work the NR feature was activated and even though the loading frequency was low it was necessary to multiply \(\Delta T\) by a calibration parameter for 1 Hz loading frequency given in [34]. This was possible as the microbolometer system used in [34] was the same as that used in present work.
The initial processed data for LIDIC (x-direction strain \({\varepsilon }_{xx}\)) and TSA (temperature change \(\Delta T\)) is shown in Fig. 6. Bending is observed across the spar in both datasets, characterised by the valley-like gradients. High strains are seen within the core material (Fig. 6(a)), highlighting the relative compliance of the material. The fiducial markers can be seen in both data sets as five circles, which will be removed by masking when analysed further using FFDF. It is important to note that the \(\Delta T\) values given in Fig. 6(b) cannot be used to compare the stresses in each of the component materials of the T-joint. Previous work, e.g., [22], has shown that it is necessary to obtain the thermoelastic constants for each material to make a fully quantitative comparison. As the materials for each of the constituent parts were not available to carry out a similar exercise as in [22], the data were normalised appropriately to demonstrate the FFDF. The striations within the \(\Delta T\) data in Fig. 6(b) signifies the bundles of reinforcement glass fibre within the laminates and are not present in the FEA data where the material properties are homogenised across the material regions outlined in Fig. 3.
Numerical Model
To perform the data fusion it is necessary to produce a numerical simulation using 3D FEA; this was developed using the commercial software package ANSYS 17.1 . The FE model was generated by first taking a photographic scan of the cross-section of the T-joint sample, which was used as the basis for the model geometry in SolidWorks [36]. The FE model was meshed in ANSYS with 20-node quadratic brick and 15-node wedge elements (SOLID186 ), shown in Fig. 7(a). The mesh density was chosen so that every material layer region had at-least two elements through the thickness, with further refinement around multiple body boundary interfaces and expected regions of stress concentrations. The material properties are proprietary and cannot be disclosed. To provide the reader with an indication of the different material types these are labelled generically in Fig. 3. The loads were applied by rigidly tying the boundary edges to a fixed remote node that was loaded so that the point of application was in the same location as in the experiment (Fig. 7(b)). The analysis was geometrically nonlinear with eight load steps (one step per every one kN load applied) in a quasi-static regime. This was to simulate the peak-to-peak amplitude of the experimental setup of 8 kN (\(\pm 4\) kN), as the experiments were conducted within the elastic limits of the specimen and measure only the change of state (not absolute values) and a small amount of deformation.
The results from the FEA simulation tension load case are displayed in Fig. 8. It can be seen that the total deformation is quite symmetric about the web, and the greatest contributing component is \({u}_{y}\) (the direction of the actuator). The first and third (maximum and minimum) principal stresses show the regions with the most tension and compression. The curved part of the web sheets are under the highest tension, as they are resisting being opened up, and shows that the inner core materials do not carry much load. The spar is in bending, with tension at the top and compression at the bottom, which is the region of highest stress in the whole T-joint. High compressive stress concentrations are observed around the boundary constraints, just under the fixed nodes of the web and at the pinned nodes on the spar, which are expected due to the singular nature of the constraints.
Full-Field Data Fusion
Full-field data is usually processed in one of two formats: Gridded Array (GA) and Coordinate-based Vector (CV). GA are matrices of field data with units of data point (e.g., pixels)/mm defining the regular spacing between the data points, i.e., the spatial discretisation, which in the case of oblique viewing angles might not be known. The GA is represented by \({\left[{f}_{i,j}\right]}_{1},\dots ,{\left[{f}_{i,j}\right]}_{n}\) for a two-dimensional (planar) data set containing \(n\) fields with resolution \(x\cdot y\) data points. CV data is in tabular form, where one, two, or three columns indicate the data point spatial location (relative to an origin), and the other columns indicate field values. The data point locations can be regular or scattered represented by \(\left[\left\{{x}_{i}\right\}\left\{{y}_{i}\right\}{\left\{{f}_{i}\right\}}_{1},\dots ,{\left\{{f}_{i}\right\}}_{n}\right]\) for a two-dimensional (planar) data set containing \(n\) fields with \(i\) data points. For both GA and CV field data that varies in the time domain, an additional temporal descriptor can be included, thus increasing the dimension of the matrices by one. The two data types are visualised in Fig. 9 for a randomised data set containing 4 fields, with 180 data points in each field, which may be synonymous to DIC (GA) and FEA (CV) data fields (e.g., \(\left[{u}_{x}, {u}_{y}, {\varepsilon }_{xx}, {\varepsilon }_{yy}\right]\)) in (a) and (b) respectively.
The types of numerical and experimental data sets considered are indicated in Table 2. The experimental data sets for LIDIC and TSA are all classified as GA. The data considered are the change of displacement vector (\(\Delta U\)) and plane strain tensor (\(\boldsymbol{\Delta }{\varvec{\varepsilon}}\)) for LIDIC, and the change of temperature (\(\Delta T\)) for TSA.
For the FEA, the data set is classified as CV due to the irregular mesh (Fig. 7a). The data considered are the displacement vector (\(U\)), plane stress tensor (\({\varvec{\sigma}}\)) and plane strain tensor (\({\varvec{\varepsilon}}\)) fields and were exported as the nodal values for the face that represents the imaged surface of the T-joint specimen (Fig. 7(a) ‘Export surface’). The exporting coordinate system (see Fig. 7a) was aligned to the experimental image plane, with \(x\) moving horizontally across the image toward the left, and \(y\) moving vertically across the image toward the top. The FEA data were exported in a coordinate system aligned to the experimental data set plane to ensure there was no disparity between the three different data sets. It should be noted that the FEA model predictions can be used to generate a simulated \(\Delta T\) field using equation (1) if the material properties are known.
The first step in the application of the FFDF methodology is spatial alignment to a common datum. To align GA data sets with unknown discretisation distances, known geometrical feature dimensions are also required. Physical fiducial markers are placed on the specimen inside the imaging field of view, but outside the region of interest, at known locations. As they are positioned outside the region of interest the markers are removed from the data analysis using a spatial mask. For the T-joint specimen considered here, the markers are constructed of reflective tape, which is visible in both the white light and thermal images. The spatial discretisation distance is obtained from the marker dimensions divided by the number of data points it covers and is used to map the GA data to spatial coordinates relative to the datum.
Once the datum and relative spatial coordinates are determined for each data set, they can then be aligned. Figure 10(a) shows the relative positions of the aligned data sets, with a small window (2 mm square) identified for the purpose of visualisation. Figure 9(b) shows the relative positions and number of data points for the LIDIC, TSA and FEA in the window; a common reference grid (0.1 mm square) is shown in the visualisation (NB this is not a representation of the pixels in the GA). For the GA data, each data point represents an average value for each measurement cell, i.e., a square region of each of one spatial discretised distance length. In the case of the TSA the cell is the projected area of a sensor in the infrared detector array, for the DIC the cell is spatial resolution set by the subset and step size used in the analysis. The coordinate location of each data point is the centre of each cell as shown in Fig. 10(b). For the FEA CV data, the data points are the coordinates of the nodal locations, with the connecting lines indicating the element boundaries. When all the data points from the three data sets are shown together it is observed that they are not coincident with each other, due to the differences in resolution and regularity.
An overview of FFDF approach is shown in Fig. 11. For meaningful point-wise comparison and fusion of the data sets they are mapped to a common resolution, so that all data points are aligned spatially and are representative of the same region. The mapping to the target grid requires triangulation-based interpolation for CV data sets, and grid-based interpolation for GA data sets. The target grid is determined by the user and can be defined by a GA data set or manually. Manual grid definition requires selecting a data set, grid increment size, and seed location (plus shrink factor and edge search radius for CV data set). It should be noted that the data can be interpolated to any dimension greater than the lowest resolution data set. Using one of the data sets for the interpolation grid has the advantage that that one original data set is retained resulting in less processing. After interpolation, the fiducial markers used for alignment of the data sets can be removed using a custom mask. Likewise additional masks can be introduced to remove any areas of poor-quality data, e.g., across holes.
Once the data sets are spatially aligned and mapped to a common resolution, they can be fused into two types of metric, named “similarity” and “union” metrics, which are defined in Table 3. Similarity metrics are used to distinguish the difference between data fields, and union metrics describe the combination of data fields into a new parameter field that could be used to evaluate e.g., damage progression or stiffness degradation. For the purposes of comparison, similar data sets with different dimensionality, can be normalised by selecting a normalising point value and dividing the data set by this quantity to provide values between 0 and 1 over the data field. It is critical that the location selected for the normalising value is the same in all data sets so that the field values are scaled identically. Then any differences between the data sets can be attributed to model error, difference in experimental and model boundary conditions and/or departures from linearity. In the present work, normalisation is required to compare the absolute stress sum from FEA with the change in temperature \(\Delta T\) obtained from for TSA. This is permissible as the stress sum and \(\Delta T\) are linearly related and necessary as the thermoelastic properties of the constituent materials of the T-joint were not available. However, it is known that the materials that comprise the T-joint have different thermoelastic properties, and by normalising by a value in one material region, the other regions will become non-comparable. Hence it is necessary to carry out the normalisation within the fields for the different materials. The similarity metric can then be evaluated in a statistical manner and holistically across the entire field, which is necessary for quantitative validation of complex numerical models and in turn for verifying experimental conditions such as the boundary conditions.
A graphical user interface application (GUI app) has been developed using MATLAB [35] that supports the full methodology of FFDF in a user-friendly format to improve bookkeeping and speed of analysis. The processing steps within the GUI app are shown in Fig. 11. All data sets are imported as comma-separated variable (.csv) files for standardisation, where GA data is packaged as one file per field, and CV data can have multiple fields per file. The GUI and the source code are available at (https://doi.org/10.5523/bris.1mj8h85asp70n29097gvz7d155).
Application of FFDF to the WTB Section
The data sets were interpolated to a target grid that was equivalent to the LIDIC data set resolution, i.e., the step size, as was the lowest resolution. A mask was introduced to remove the fiducial markers. The result is 34,389 discrete points with 0.665 mm grid spacing over the imaged surface. The predicted stress and strain field amplitudes for the tension and compression load cases (Fig. 8) gave similar results, hence only the compression case is considered here for the purposes of demonstration. Only the quotient union metric is adopted (see Table 3), as fusing the stress metric from the TSA and the strains from the LIDIC provides an indicator of stiffness or compliance. For individual and residual similarity metric fields the mean (\(\mu\)), standard deviation (\(SD\)), and coefficient of variation (\(CoV\)) are shown, for a full-field data set, \(f\),with \(n\) data points:
Figure 12(a) shows the data generated from the FEA model in the form of the peak-to-peak x-direction normal strain, \({\Delta \varepsilon }_{xx}\), so that is could be qualitatively compared with experimental data from the LIDIC shown in Fig. 12(b). Both data sets capture the bending in the lower flange of the T-joint sample showing a similar magnitude and the large strains in the triangular wood fillet regions (see wood 2, Fig. 3). However, there is a significant difference in the wood 1 core above the fillet, where the FEA predicts a much higher strain concentration than the LIDIC. To make a quantitative comparison the residual similarity metric (Res) is obtained by subtracting the FEA strain from the LIDIC strain and then the percentage error (PE) calculated (see Table 3) to create two new data sets shown in Fig. 13. In both cases the full-field plots should return a value of zero, clearly this is not the case and there are significant departures from the zero condition in both plots. A positive Res is reported that indicates the FEA is under predicting relative to the DIC. Frequency of occurrence histograms of the two plots are provided below the full-field plots in Fig. 13. In the Res histogram of Fig. 13(a) the mean of the difference is determined alongside the standard deviation, which provides the magnitude of the differences. As expected, the greatest difference is observed in the wood 2 region just above the fillet and is the major contributor to the offset of the mean value from zero. Not as apparent in the qualitative comparison of Fig. 12 is that significant differences occur at the boundary of the wood 2 area in the fillet. These differences illustrate the effect of the spatial filtering of the strain calculation in DIC, which is dependent on the number of points used in the strain calculation. To completely remove errors of this nature it is necessary to process the FEA data with the same methods as DIC, e.g., by synthetically deforming experimental images with the FEA displacement field and utilising the DIC algorithm on the synthetic images [38].
The PE similarity metric in Fig. 13(b) demonstrates that the spread of the relative difference between the data sets is large, and as a result of most of the core material in the web (wood 2) displays a percentage difference of greater than 100%, indicating that the material properties for wood 2 assumed in the FEA are incorrect. Another area of high percentage error is around the midplane of the spar where the strain is very small and at the noise floor of the measurements, hence it is expected that this region would yield a high percentage difference. Further, the junction between different materials, e.g. between wood 1 and GRRP 4 (see Fig. 3), indicates that the DIC cannot capture this transition well because of the limitation of the subset size and strain window used. Two other regions of large PE are also noticeable in GFRP 4 in the overlaminate of the fillet and at the junction of wood 2, GFRP 3 and GFRP 4 (see Fig. 3) where there should be adhesive. These regions of large PE are potential indicators of damage. It should be noted that judicious rescaling of the image in Fig. 13(b) may reveal other features that are masked by the presentation.
The FFDF method can also be used to assess the similarity between the FEA with the \(\Delta T\) values extracted from the TSA. Figure 14 shows that in a qualitative sense the distributions match very well even though the scales shown are different demonstrating that equation (1) relates (\({\sigma }_{xx}+{\sigma }_{yy}\)) to \(\Delta T\) by the material thermoelastic properties (\(\alpha ,\rho , {C}_{p}\)). As the TSA processing delivers only the magnitude of \(\Delta T\) (see equation (2)), the FEA data has been plotted as \(\Delta \left|{\sigma }_{xx}+{\sigma }_{yy}\right|\). To make a quantitative assessment of the FEA and TSA data sets it is necessary to calibrate the FEA with values of \({\alpha }_{1},{\alpha }_{2},\rho , {\mathrm{and} C}_{p}\) for each of the component materials in the joint. In [15] and [22] the thermoelastic constant for each of the constituent material was determined experimentally. This required numerous test specimens to be manufactured and tested for each material. It is not usually the case that materials in real components are freely available to manufacture such test specimens, so an alternative procedure was devised to enable comparison. A normalisation routine was adopted by selecting a point at the bottom of the spar cap in the middle of the specimen at location \(x=0\) mm, \(y=2\) mm located in the GFRP 1 material (see Fig. 3). The Res and PE similarity metric fields are shown in Fig. 15, where the agreement is excellent in the spar cap and good in the resin rich regions. As with the LIDIC-FEA fusion, the high PE in the middle of the spar cap is caused by the nominally zero values. However, in the other materials in the joint, i.e., the wood in the fillet the flange, and the fibre bundles in the web sheets, the agreement is poor. The result is expected as the normalisation point in the GFRP is not valid for these regions. Hence, each region with different material requires its own normalisation point.
The normalisation conducted to produce Fig. 15 implies that the thermoelastic equation parameters are homogenised across the structure. Therefore, in regions made of different material to the spar cap, the comparative absolute percentage difference should be proportional to the thermoelastic constant for the spar cap and the fillet. The effect of this is demonstrated by comparing the values along the midline at different material regions. Figure 16(a) shows a line plot through the spar cap and into the web using the same normalisation point in the spar cap used for Fig. 15. Quantitatively, there is good agreement between the FEA and TSA data within the material region where the normalisation is valid, while the other regions are different by a factor of the relative difference between the material thermoelastic constant. In Fig. 16(b) the normalisation point is changed to a position at the base of the web in the fillet resin material. Here the agreement between the data sets is only in the fillet resin material.
The next stage is to make a quantitative similarity assessment between the \(\Delta T\) field (shown in Fig. 14(b)) and the \(\Delta \left|{\varepsilon }_{xx}+{\varepsilon }_{yy}\right|\) fields. As mentioned above the lock-in approach outputs only the magnitude \(\Delta T\) (see equation (2)) and the strains (see equation (3)), so it is not possible to differentiate between positive and negative values of stress and strain without recourse to the phase value, which can be obtained from equations (2) and (3). Figure 17(a, b) shows the phase maps generated for the imaged surface relative to the reference signal (load data) [6], clearly showing the regions in tension and compression, and qualitatively an excellent agreement in the phase derived from the two techniques. Figure 17(c) shows the PE between the two data sets, where, as previously, the greatest differences occur at the neutral axis in the spar cap. Here there is little bias in the mean, indicating that as expected the phase value is independent of the material properties required for the quantitative assessment of the \(\Delta T\) and the stress fields obtained from the FEA.
In Fig. 18, the quotient fusion metric (see Table 2) is applied to the two experimental data sets, dividing the TSA change of temperature \(\Delta T\) by the LIDIC change in sum of strains \(\Delta \left|{\varepsilon }_{xx}+{\varepsilon }_{yy}\right|;\) this metric is related to the material stiffness. Figure 18 clearly shows the two main materials that comprise the joint: the GFRP in the spar cap, the overlaminated fillet and the web face sheets and the wood in the fillet and web core. There is significant noise in the Quo metric in the spar cap. This is because of the inhomogeneous nature of the material and motion correlated in the data. Figure 18 also shows a frequency histogram of the fused union data set, with the two distinct peaks identifying the different materials. Notwithstanding the noise, it would be possible to monitor the changes in the quotient metric using the frequency histogram to identify changes in material performance and progression of damage. Clearly, further investigations are required to ascertain the level of precision required for the quotient metric to be successful in identifying damage progression, which is the object of further work.
An alternative means of full-field data analysis using the CEN methodology is proposed in [26]. In this approach, when one data set value is equal to the other data set value, it is determined how many data points fall within a known error band. In Fig. 19(a) the \(\Delta {\varepsilon }_{xx}\) values obtained from the FEA and LIDIC given in Fig. 12 are plotted against each other; the Res metric given by Fig. 13(a) is used as a comparator. The comparison metric appears in linear bands, with a colour map equivalent to the scale given in Fig. 13(a). The solid red line represents unity (\(x=y\)), and the dashed red lines are the experimental error, which for this case is double the strain resolution (equation (4), [26]), equal to \(\pm 0.0488\; \mathrm{\%\varepsilon }\). All the points from the Res data set were then grouped into bins in both the x and y axes (kernels), which are displayed by colour depending on the number of points within each kernel using the scale to the right of Fig. 19(a); for clarity the kernels that contain only one data point are shown in grey. It is clear that the vast majority of data points are located to the bottom left of the plot in Fig. 19(a) indicating a residual of close to zero. In fact, 10.61% of data points (3648 out of 34389 data points) fall outside the error bounds. The spatial location of the data points is lost in this analysis, but it should be noted that the cluster of points that form vertical branches is from the wood regions of the joint with low LIDIC values compared to the FEA. To retain the spatial meaning of the data in the plot in Fig. 19(a), rather than decomposing the images as in [26], an “error bound overlap” map showing the regions where the data sets fall out of range of the error bounds is shown in Fig. 19(b).
Verification of Model Input Parameters
If the boundary conditions of the model and the experiment are well-matched, as is the case here, the FFDF method can also be used for model validation and in particular assessing the sensitivity of the predictions to model input parameter uncertainties. As the received data regarding the material properties of the wooden material in the fillet and the web core were not reliable, FFDF provides an opportunity to carry out a parametric study to fit the data and identify better properties for this material. Accordingly, the wood elastic properties were adjusted in the FEA model, the FFDF plots of the raw and Res \(\Delta {\varepsilon }_{xx}\) fields are shown in Fig. 20; v1 uses wood elastic properties taken from [39], and v2 is the average of the original values of the assumed wood elastic properties used to create the FEA in Fig. 12 and those taken from [39] to create the v1 FEA. Comparing the new histograms (which should have a zero mean if there is no bias error) to that in Fig. 13, it is clear that the adjustment of the material properties improves the agreement between the data sets, with \(\mu\) reducing from 0.021 (\(SD=\) 0.071) to –0.002 (\(SD=\) 0.31) and 0.007 ( \(SD=\) 0.028) respectively.
From the kernel density plots in Fig. 21 it is clear that the spread of data is much less than for the initial FEA model (see Fig. 19(a)). For material v1 in the central core region, the stiffness has been reduced too much, shown by the cluster of points that drops below the lower error bound. This is corrected for material v2; however, the vertical cluster of erroneous points remains for the core material for the web, which indicates that further investigation is required for full validation of the FEA model. However, the percentage of points outside the error bounds, which was 10.6% for the original material model, has improved to 7.38% and 6.14% for V1 and V2 respectively. This analysis highlights the importance of quantitative full-field analysis for complex structures, as v1 has a mean closer to zero, and v2 has a smaller standard deviation. Moreover, it demonstrates a simple qualitative comparison of the two strain fields is completely insufficient, as none of the original full field data sets appear to match well.
Conclusions
A new approach to full-field data fusion (FFDF) has been proposed and demonstrated by assessing the similarity and discerning differences between experimental full-field data sets and computationally-predicted FEA data sets. FFDF spatially matches the data points of every data set, so that full-field metrics may be applied to assess data sets quantitatively. This approach proposed enables a rigorous comprehensive fusion of the different data fields, which can be utilised aiming to achieve various data analytics tasks, for instance the identification of zones where improvement/refinement of the numerical modelling, as well as the experimental set-up, can be conducted on a statistical basis. Care must be taken when using FEA data in FFDF, as the model zones and elements share nodes, so an unaveraged solution will contain geometrically duplicated values. This is ignored for the current study, but other options will be explored in future work to eliminate this, e.g., exporting results at element centroids. Likewise, misalignments between the data sets will exacerbate errors and methods to improve alignments should be investigated.
In the research presented in the paper the FFDF method was applied to numerical and experimental analyses conducted to evaluate the load response of an industrially relevant load carrying substructure (a composite wind turbine blade internal T-joint) subjected to a simplified uniaxial bend load case. For this example, the validity of the complex FEA model was assessed, where model zones where incorrect material properties were specified were identified in the FFDF analysis process, and the information was subsequently fed back into the model for refinement. Residual and percentage error similarity metrics evaluated the closeness of the data sets. Furthermore, to demonstrate the capabilities of FFDF, material regions were identified from purely experimental data, and load state phase data was evaluated to show significant closeness across multi-modal dissimilar measurements. The presented similarity and union metric data sets have shown that the proposed FFDF methodology can be used as a powerful tool to conduct numerical parametric analyses to assist with the validation of material properties and failure behaviour on the substructural scale. Further, the FFDF procedure presented can used for efficient assessment and quantification of the inherent uncertainties associated with both the experimental and simulation data.
The work described in the paper has formed the basis for the techniques used in the Programme Grant “Certification for Design: Reshaping the testing pyramid” funded by the UK Engineering and Physical Sciences Research Council (www.composites-certest.com). The concepts are being developed so they can be applied to complex 3D geometries used in aerostructures, supported by a wide range of industrial partners seeking to adopt techniques that aid in reducing time to market for new design concepts whilst maintaining safe operations.
Data Availability
Data are available at the University of Bristol data repository, data.bris, at https://doi.org/10.5523/bris.1mj8h85asp70n29097gvz7d155.
Abbreviations
- \({\varvec{\sigma}}\) :
-
Stress tensor
- \(\sigma\) :
-
Stress component
- \({\varvec{\varepsilon}}\) :
-
Strain tensor
- \(\varepsilon\) :
-
Strain component
- \({\varepsilon }_{0}\) :
-
Mean strain component
- \(U\) :
-
Displacement vector
- \(u\) :
-
Displacement component
- \(\alpha\) :
-
Coefficient of thermal expansion
- \(T\) :
-
Temperature
- \({T}_{0}\) :
-
Absolute temperature
- \(\rho\) :
-
Density
- \({C}_{p}\) :
-
Specific heat at constant pressure
- \({f}_{0}\) :
-
Frequency
- \(t\) :
-
Time
- \(\phi\) :
-
Phase
- \(x,y\) :
-
Full-field data set coordinates
- \(f\) :
-
Full-field data set
- \(n\) :
-
Number of data points
- \(\upmu\) :
-
Mean value
- \(SD\) :
-
Standard deviation
- \(CoV\) :
-
Coefficient of variation
- \({S}_{M}\) :
-
Model shape descriptors
- \({S}_{E}\) :
-
Experimental shape descriptors
- \(\overline{u }({S}_{E})\) :
-
Experimental uncertainty
- \(E\) :
-
Young’s modulus
- \(G\) :
-
Shear modulus
- \(\nu\) :
-
Poisson’s ratio
- \(i,j,ij\) :
-
Arbitrary coordinate system
- \(xx, yy, xy\) :
-
Tensorial stress/strain coordinate system
- \(x,y\) :
-
Principal stress coordinate system
- \(\mathrm{1,2}\) :
-
Material coordinate system
- \(\Delta \dots\) :
-
Peak-to-peak amplitude difference (change of value)
- \(|\dots |\) :
-
Absolute value
- WTB:
-
Wind turbine blade
- TSA:
-
Thermoelastic stress analysis
- DIC:
-
Digital image corelation
- LIDIC:
-
Lock-in digital image corelation
- FEA:
-
Finite stress analysis
- NDT:
-
Non-destructive testing
- DOE:
-
Design of experiments
- FFDF:
-
Full-field data fusion
- UD:
-
Uni-directional
- GFRP:
-
Glass fibre reinforced polymer
- CS:
-
Coordinate system
- GA:
-
Gridded array
- CV:
-
Coordinate-based vector
- GUI:
-
Graphical user interface
References
DNV-GL (2015) DNVGL-ST-0376 Rotor blades for wind turbines. https://www.dnv.com/energy/standards-guidelines/dnv-st-0376-rotor-blades-for-wind-turbines.html. Accessed 13 June 2023
MTS Systems Corporation (2012) Wind Turbine Blade Testing Solutions. https://www.mts.com/en/products/energy/wind-turbine-blade-static-systems. Accessed 13 June 2023
Laustsen S, Lund E, Kühlmeier L, Thomsen OT (2014) Development of a high-fidelity experimental substructure test rig for grid-scored sandwich panels in wind turbine blades. Strain 50:111–131. https://doi.org/10.1111/str.12072
Krishnamoorthy K, Sasikumar T (2016) Analysis and characterization of tensile property of the composite specimen using ANSYS. Int J Appl Eng Res 11:380–384
Ostergaard MG, Ibbotson AR, Le RO, Prior AM (2011) Virtual testing of aircraft structures. CEAS Aeronaut J 1:83–103. https://doi.org/10.1007/s13272-011-0004-x
Dulieu-Barton JM (2012) Thermoelastic stress analysis. In: Rastogi P, Hack E (eds) Optical Methods for Solid Mechanics. Wiley, Berlin, pp 345–366
Chu TC, Ranson WF, Sutton MA (1985) Applications of digital-image-correlation techniques to experimental mechanics. Exp Mech 25:232–244. https://doi.org/10.1007/BF02325092
Sambasivam S (2009) Thermoelastic stress analysis of laminated composite materials, PhD Thesis. University of Southampton
Rajic N, Rowlands D (2013) Thermoelastic stress analysis with a compact low-cost microbolometer system. Quant Infrared Thermogr J 10:135–158. https://doi.org/10.1080/17686733.2013.800688
Jiménez-Fortunato I, Bull DJ, Thomsen OT, Dulieu-Barton JM (2021) On the source of the thermoelastic response from orthotropic fibre reinforced composite laminates. Compos Part A Appl Sci Manuf 149. https://doi.org/10.1016/j.compositesa.2021.106515
Pan B, Qian K, Xie H, Asundi A (2009) Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas Sci Technol 20. https://doi.org/10.1088/0957-0233/20/6/062001
Reu P, Sutton MA, Orteu JJ et al (2012) Introduction to digital image correlation: Best practices and applications. Exp Tech 36:3–4. https://doi.org/10.1111/j.1747-1567.2011.00798.x
Fruehmann RK, Dulieu-Barton JM, Quinn S, Tyler JP (2015) The use of a lock-in amplifier to apply digital image correlation to cyclically loaded components. Opt Lasers Eng 68:149–159. https://doi.org/10.1016/j.optlaseng.2014.12.021
de Sá Rodrigues F, Marques R, Tabrizi IE et al (2021) A new methodology for thermoelastic model identification in composite materials using digital image correlation. Opt Lasers Eng 146:106689. https://doi.org/10.1016/j.optlaseng.2021.106689
Crammond G, Boyd SW, Dulieu-Barton JM (2015) A Point-wise Approach to the Analysis of Complex Composite Structures Using Digital Image Correlation and Thermoelastic Stress Analysis. Strain 51:311–323. https://doi.org/10.1111/str.12142
Chen D, Sun S, Dulieu-Barton JM et al (2018) Crack growth analysis in welded and non-welded T-joints based on lock-in digital image correlation and thermoelastic stress analysis. Int J Fatigue 110:172–185. https://doi.org/10.1016/j.ijfatigue.2018.01.020
Crump DA, Dulieu-Barton JM (2012) Assessment of Non-adiabatic Behaviour in Thermoelastic Stress Analysis of Composite Sandwich Panels. Exp Mech 52:829–842. https://doi.org/10.1007/s11340-012-9601-9
Wang W, Martakos G, Dulieu-Barton JM et al (2015) Fracture behaviour at tri-material junctions of crack stoppers in sandwich structures. Compos Struct 133:818–833. https://doi.org/10.1016/j.compstruct.2015.07.060
Laustsen S, Lund E, Kühlmeier L et al (2014) Failure behaviour of grid-scored foam cored composite sandwich panels for wind turbine blades subjected to realistic multiaxial loading conditions. J Sandw Struct Mater 16:481–510. https://doi.org/10.1177/1099636214541367
Chen X, Berring P, Madsen SH et al (2019) Understanding progressive failure mechanisms of a wind turbine blade trailing edge section through subcomponent tests and nonlinear FE analysis. Compos Struct 214:422–438. https://doi.org/10.1016/j.compstruct.2019.02.024
Fernandez G, Usabiaga H, Vandepitte D (2017) Subcomponent development for sandwich composite wind turbine blade bonded joints analysis. Compos Struct 180:41–62. https://doi.org/10.1016/j.compstruct.2017.07.098
Dulieu-Barton JM, Earl JS, Shenoi RA (2001) Determination of the stress distribution in foam-cored sandwich construction composite tee joints. J Strain Anal Eng Des 36:545–560. https://doi.org/10.1243/0309324011514700
Hall DL, Llinas J (1997) An introduction to multisensor data fusion. Proc IEEE 85:6–23. https://doi.org/10.1109/5.554205
Castanedo F (2013) A review of data fusion techniques. Sci World J 2013. https://doi.org/10.1155/2013/704504
Heideklang R, Shokouhi P (2013) Application of data fusion in nondestructive testing (NDT). Proc 16th Int Conf Inf Fusion. FUSION 2013:835–841
National Standards Association of Ireland, Irish Standard Recommendation S.R. CWA 16799:2014 (2014) Validation of computational solid mechanics models. http://www.engineeringvalidation.org/cen-workshop-agreement. Accessed 13 June 2023
Dvurecenska K, Graham S, Patelli E, Patterson EA (2018) A probabilistic metric for the validation of computational models. R Soc Open Sci 5. https://doi.org/10.1098/rsos.180687
Hack E, Lampeas G, Patterson EA (2016) An evaluation of a protocol for the validation of computational solid mechanics models. J Strain Anal Eng Des 51:5–13. https://doi.org/10.1177/0309324715616017
Manta A, Gresil M, Soutis C (2021) Transient conduction for thermal diffusivity simulation of a graphene/polymer and its full-field validation with image reconstruction. Compos Struct 256:113141. https://doi.org/10.1016/j.compstruct.2020.113141
Dvurecenska K, Diamantakos I, Hack E et al (2021) The validation of a full-field deformation analysis of an aircraft panel: A case study. J Strain Anal Eng Des 56:265–272. https://doi.org/10.1177/0309324720971140
Howell G, Dulieu-Barton JM, Achintha M, Robinson AF (2015) A stress-free model for residual stress assessment using thermoelastic stress analysis. Int Conf Exp Mech 2014 9302. https://doi.org/10.1117/12.2083020
LaVision (2020) LaVision Davis 10.0.5. https://www.lavision.de/en/products/strainmaster/index.php. Accessed 13 June 2023
FLIR High-Resolution Science Grade LWIR Camera FLIR A655sc. https://www.flir.co.uk/products/a655sc/. Accessed 2 Apr 2021
Jiménez-Fortunato I, Bull DJ, Thomsen OT, Dulieu-Barton JM (2022) Quantitative Microbolometer-Based Thermoelastic Stress Analysis. Opt Lasers Eng 160:107272. https://doi.org/10.1016/j.optlaseng.2022.107276
ANSYS (2017) ANSYS® Academic Research Mechanical. Release 17:1
Dassault Systèmes (2019) SolidWorks. https://www.3ds.com/newsroom/press-releases/dassault-systemes-introduces-solidworks-2019. Accessed 13 June 2023
MATLAB (2020) 9.9.0.1570001 (R2020b) Update 4. The MathWorks Inc., Natick, Massachusetts. https://www.mathworks.com/company/newsroom/mathworks-introduces-release-2020b-of-matlab-and-simulink.html. Accessed 14 June 2023
Lava P, Jones EMC, Wittevrongel L, Pierron F (2020) Validation of finite-element models using full-field experimental data: Levelling finite-element analysis data through a digital image correlation engine. Strain 56:1–17. https://doi.org/10.1111/str.12350
Foss R J (2010) Wood handbook : wood as an engineering material: USDA Forest Service, Forest Products Laboratory, General Technical Report FPL- GTR-190, 2010: 509 p. 1 v. https://doi.org/10.2737/FPL-GTR-190
Acknowledgements
The experimental work was conducted in Testing and Structures Research Laboratory at University of Southampton and supported by the Principal Experimental Officer, Dr Andrew Robinson. The contributions of the PhD students and co-workers of Professor Dulieu-Barton are acknowledged, in particular, Dr Irene Jimenez-Fortunato for the development of the microbolometer TSA system and Dr Richard Fruehmann for the idea of lock-in processing for DIC.
Funding
The work described in the paper was supported by Siemens Gamesa Renewable Energy (SGRE) as part of the UK Physical and Engineering Science Research Council (EPSRC) Centre for Doctoral Training in Sustainable Infrastructure Systems (CDT-SIS) (EP/L01582X/1). The work forms the basis of techniques developed for the “Structures 2025” facility constructed using an EPSRC Strategic Equipment Grant (EP/R008787/1) and developed for the Programme Grant “Certification for Design: Reshaping the testing pyramid” (EP/S017038/1) led by the University of Bristol.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Callaghan, J.S., Crump, D., Nielsen, A.S. et al. Quantitative Full-Field Data Fusion for Evaluation of Complex Structures. Exp Mech 63, 1095–1115 (2023). https://doi.org/10.1007/s11340-023-00973-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11340-023-00973-8