An Experimental Method to Characterize the Shear Behaviour of Concrete Under High Confinement

Abstract

Background

Shear behaviour of concrete under high confining pressure has not been thoroughly studied despite being widely observed in concrete structures subjected to high blast loading or projectile impact.

Objective

The objective of the present study is to propose an experimental method to investigate the shear behaviour of concrete under high confinement in static conditions.

Methods

This method is based on the Punch-Through Shear testing technique. A specimen with two cylindrical notches is first subjected to an active confinement pressure by means of a triaxial cell and an axial loading is then applied to punch through the central part of the specimen. However, in the previous PTS experiments, the inner cylindrical parts being subjected to uniaxial compression, the level of confining pressure applied in the first stage was usually limited to the sample uniaxial compression strength. In the present work, much higher compression stresses of a few hundreds of MPa are applied to the specimen in both radial and axial directions thanks to the small metallic rings used to confine the inner cylindrical parts of the specimen. A series of numerical simulation based on finite-element method is conducted in order to optimize the notches and sample dimensions.

Results

Experimental tests conducted on a common concrete showed that the confinement rings successfully prevented any compression damage in the central part during sample pressuring and shearing. The experiments conducted at different levels of confining pressure showed that the higher the confinement level the higher the concrete shear strength. Experiments done with a confining pressure of 100 MPa with two different ligament lengths showed that higher nominal shear stress is obtained with a smaller shear surface.

Conclusion

The proposed experimental technique allows reaching confining pressure up to 150 MPa (which corresponds to radial stress of 374 MPa in the ligament) and nominal shear strain of about 38% in the ligament of the concrete sample and confirms that the shear strength increases with the level of normal stress applied to the sheared surface.

Appendices

Appendix A: Design of Specimen Geometries Based on Numerical Simulation

A series of numerical analyses were performed with the commercial finite element software (Abaqus Explicit). The purpose of the numerical simulations was to determine the optimal sample geometry before conducting any experimental test, considering the following requirements: tensile failure in the sample needs to be prevented, at least in the first stage, despite the confining pressure applied to the sample in this stage. Shear stress and confining pressure should be easily deduced from pressure and force measurements. The sample should be compatible with the equipment available in the 3SR laboratory (Giga Press).

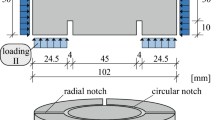
The sample diameter was fixed to 70 mm as recommended for the Giga Press and the notches width were imposed by the drilling tools. Samples having different geometries with respect to the sample length and the notches depth and diameter, have been carried out to study the influence of each parameter on the response of the sample.

Mesh and Loading

In the present work, the Abaqus-explicit FE code was used to decrease the calculation time and considering the high level of deformation reached in the elements belonging to the ligament area. However, the loading was adjusted to make the inertial components negligible. As the constitutive law is non-dependant to strain-rate the same results would have been obtained with Abaqus Standard FE code and considering a static loading.

2D axisymmetric simulations were performed in order to reduce the calculation time and CAX4R elements were used to mesh each part (Fig. 13).

Fig. 13

a Sample geometry, b loading applied in finite element model

Regarding the loading, two steps were created in Abaqus, one for each stage. In the first step, the sample was subjected to a uniform pressure on the top, bottom, and lateral surfaces (pink arrows in Fig. 13(b)). In the second stage a velocity was applied on the central lower part of the specimen and the displacement was blocked on the peripheral upper part in order to produce shear displacement in the ligament. The loadings of the numerical sample are presented in Fig. 13. Dimensions of the samples considered in the present study are reported in the Fig. 14 and in the Table 4.

Fig. 14

Dimensions of the Punch-Through-Shear test specimen

Table 4 Sample dimensions considered in the FE numerical simulation

Constitutive Model and Material Parameters

Steel caps were modelled assuming linear elastic behaviour (Young’s modulus E = 200 GPa and Poisson’s ratio = 0.3). Since the numerical simulation only aims to describe the concrete behaviour until the peak, a pressure-sensitive plasticity model was considered for the concrete sample: the Drucker-Prager model [35]. The linear Drucker Prager criterion is written as:

$$F=q-P\tan\beta -c=0,$$

(4)

where β is the friction angle which reflects the slope of the yield surface in the stress space, q is the equivalent Huber-Mises stress, P is the hydrostatic pressure and c is the cohesion of the material related to the input data as:

$$c=\left(1-\frac{1}{3}\tan\beta \right){\sigma }_{c},$$

(5)

where ${\sigma }_{c}$ is the uniaxial compression strength. In the DP model, the plastic potential function G that governs the flow rule is given by:

$$G=q-P\tan\Psi$$

(6)

where Ψ is the dilation angle. The increments of the plastic strain can be found by:

$$d{\varepsilon }_{ij}=\lambda \frac{\partial G}{\partial {\sigma }_{ij}},$$

(7)

where $\lambda$ is a non-negative scalar parameter. With Ψ = 10°, a dilatancy is imposed during plastic deformation. The parameters considered in the numerical simulation are listed in Table 5. These parameters were identified through an inverse approach by simulating a quasi-static “oedo-PTS test” conducted with a R30A7 concrete sample (cf. Appendix B).

Table 5 Parameters used in the numerical simulations for elasto-plastic Drucker-Prager model

Influence of Confinement Rings

Because of the drilled notches in the specimen, the top and bottom of the inner parts remain unconfined in the radial direction during the test. The axial stress applied on this zone is larger than the compressive strength of concrete. This zone could be damaged under compression before reaching any shear deformation in the ligament. Consequently, two small steel rings were designed to prevent the radial deformation of both unconfined regions. Figure 15 shows the results of two numerical simulations considering a sample subjected to a confining pressure of 100 MPa on its outer surface. This figure illustrates the field of plastic strain without and with the two steel rings in contact with the top and bottom of the inner cylindrical parts. In the first case (no steel rings) the deformation is located in these parts whereas in the second case the deformation is concentrated in the sample ligament.

Fig. 15

Equivalent plastic strain after 1.3 mm of axial displacement at 100 MPa of confinement a without and b with the confinement rings

Mesh Sensitivity

A mesh analysis was conducted to check the influence of mesh size in the ligament region considering three sizes of mesh: 0.15 mm, 1.5 mm and 3 mm and a notch width equal to e = 3 mm (Fig. 16). It was observed that mesh size has a small influence on the shear and radial stresses and a significant effect on the field of the shear strain around the ligament (Fig. 17). For a very fine mesh, an excessive distortion in the smallest elements is noticed and shear deformation is localized in a small area of the ligament.

Fig. 16

Different sizes of mesh studied a 0.15 mm b 1.5 mm c 3 mm

Fig. 17

Shear logarithmic strain after a displacement of 1.5 mm for 3 mesh sizes, a 0.15 mm, b 1.5 mm, c 3 mm. A confining pressure of 100 MPa is considered

For each mesh size, the mean shear stress and strain were calculated in different sets of elements belonging to the ligament and compared to analytical solutions. The selected sets of elements are illustrated in Fig. 18. The thinner mesh is considered in configurations (a) and (b) whereas the rougher mesh is considered in configurations (d) and (e). The intermediate mesh size is used in configuration (c).

Fig. 18

Element sets (a, b, c, d, e) considered with small mesh (SM), normal mesh (NM) and large mesh (LM) sizes to calculate the mean shear stress and strain as plotted in Fig. 10. The mesh size and area width of each element set are given in mm

The mean shear stress is compared to the nominal shear stress in the notch calculated according to:

$${\tilde{\sigma }}_{xy}=\frac{{F}_{y }}{\pi {D}_{lig}{H}_{lig}},$$

(8)

where F_y is the vertical force applied to the sample in stage 2 and D_lig and H_lig are the dimensions defined in Fig. 14. The mean shear strain is compared to a nominal shear strain calculated according to:

$${\overline{\varepsilon }}_{xy}=\frac{{U}_{y\left(imposed\right) }}{2e},$$

(9)

where ${U}_{y(imposed)}$ is the displacement applied to the central part of the specimen and e the notch width. This closed-form solution would correspond to the mean shear strain assuming a homogeneous strain field in the ligament and neglecting the deformation in the x-direction according to:

$${\varepsilon }_{xy}=\frac{1}{2}\left(\frac{\partial {u}_{x}}{\partial y}+\frac{\partial {u}_{y}}{\partial x}\right).$$

(10)

For each mesh size, the nominal shear stress deduced from equation (8) is plotted as a function of nominal shear strain, calculated from equation (9) in the Fig. 19(a).

Fig. 19

a Nominal shear stress plotted as a function of nominal shear strain for three mesh sizes. b Shear stress averaged in different sets of elements (Fig. 18) plotted as function of axial displacement. c, d Shear strain and shear stress averaged in different sets of elements (Fig. 18) plotted as function of, respectively, the nominal shear strain and nominal shear stress defined according to equations (8) and (9)

The averaged shear stress in each set of elements is plotted as function of the applied axial displacement in the Fig. 19(b). The averaged shear strain and stress in each set of elements presented in Fig. 18 are compared respectively to the nominal shear strain and stress calculated according to equations (8) and (9) in Fig. 19(c) and (d).

On the one hand, it is observed that, the larger the mesh size, the higher the axial force so the higher the nominal shear stress (Fig. 19(a)). However, the levels of averaged shear stress in the considered sets of elements are quite similar and reach about 120 MPa in element sets (a) and (b) (small mesh) whereas it tends to 140 MPa in element sets (c) and (e) (normal and large mesh). (Fig. 19(b)).

In addition, when the width of element sets is much larger (element set(e)) or much smaller (element set(a)) than the notch thickness (e = 3 mm), the nominal shear strain is observed to overestimate or underestimate, respectively, the shear strain averaged in the corresponding element set (Fig. 19(c)). This result is not surprising since that, in both element sets (a) and (e), the area of shear (Fig. 17) does not match with the area of element sets (Fig. 18). On the contrary, when the width of element sets is equal to the notch thickness (e = 3 mm) and whatever the mesh size (element sets (b), (c) and (d)) the mean shear strain is close to the nominal shear strain. On the other hand, the mean shear stress matches well with the nominal stress whatever the element set considered (Fig. 19(d)). It is worth noting that the shear strains are quite large (up to 0.5) which suggests that a finite strain model [36, 37] would be more appropriate to describe the behaviour of concrete at the highest level of shear strain.

Finally, it can be observed that the yield shear strength predicted by the numerical simulation of PTS test (about 100 to 110 MPa according to Fig. 19(b)) matches quite well with the experimental value (max shear strength of 94 MPa with a ligament length of 20 mm and a applied pressure of 100 MPa) which validates the set of parameters used in Drucker-Prager model).

Influence of Notch Diameter

To study the influence of the notch diameter (D_lig), a series of numerical simulations were performed considering different notch diameters ranging from 25 to 45 mm, while maintaining the outer diameter constant (70 mm). First, it was noticed that, with a small notch diameter, the axial stress in the central bottom part, as well as the stress concentration in the notch tip increases. Indeed, whereas the ligament surface is proportional to the notch diameter, the cross section of the central bottom part is proportional to the notch diameter square. For this reason, small notch diameter increases the risk of compression failure in the central bottom part. This is the reason why a diameter smaller than 30 mm was not considered. On the other hand, when a large notch diameter is considered (larger than 40 mm), a significant bending deformation of the peripheral part is observed due to the reduction of the peripheral thickness. Thus, a diameter of 35 mm was chosen as a compromise between both cases.

Influence of Self-confinement

Due to the stiffness of the concrete sample, a hoop self-confinement can occur. It is the reason why, in the case of Oedo-PTS experiments conducted with passive confinement cell, four radial notches at 90° were performed to avoid this self-confinement [3, 20, 38]. In that case, the mean radial stress in the ligament can be deduced from the lateral pressure P applied to the sample, knowing the area of the outer lateral surface S_ext of the specimen and the area of the fracture surface S_lig.

$${\sigma }_{rr \left(without\ self-confinement\right)}=\frac{P\times {S}_{ext}}{{S}_{lig}}$$

(11)

In the present case, due to the absence of a radial notch made in the peripheral part of the sample, it is not possible to consider equation (11) to evaluate the radial stress in the ligament as plotted in Fig. 20 (blue curve). It is the reason why, the mean radial stress in the ligament was estimated based on a numerical simulation considering the Drucker-Prager model for concrete and considering an applied displacement of 1.5 mm, which corresponds to the displacement measured at the force peak in PTS-G3 experiment conducted at 100 MPa of confinement. In these numerical simulations, the dilation coefficient Ψ is supposed to be the main parameter that could influence the mean radial stress in the ligament. In addition, this parameter is particularly difficult to characterize. By considering three values for this parameter (5°, 10° and 15°) it was noticed that the mean radial stress in the ligament was very close (dotted, dashed and plain red curves in Fig. 20), so the influence of the dilation angle may be considered negligible.

Finally, a correction coefficient is proposed to calculate the mean radial stress in the ligament from the equation (11) based on the numerical simulations. This coefficient ${\alpha }_{P}$ is defined as:

$${\alpha }_{P}=\frac{{\sigma}_{rr}\ \left(Eq. 11\right)}{{\sigma}_{rr}\ \left(mean\ value\ in\ the\ ligament\right)}$$

(12)

Fig. 20

Estimation of the radial stresses in the ligament for different notch diameters. (Numerical simulations)

It is plotted in black in Fig. 20. For instance, if a lateral pressure of P = 100 MPa is applied to the sample, the radial stress in the ligament without self-confinement would be 400 MPa (with D_sample = 70 mm, H_sample = 40 mm, D_lig = 35 mm, H_lig = 20 mm, equation (11)). However due to the self-confinement, the mean radial stress in the ligament is 400/1.89 = 211 MPa. The radial stress expected in each PTS test is reported in Table 3.

Influence of Ligament Length

The influence of the ligament length was investigated, thanks to numerical simulations considering a sample length fixed to 40 mm. Figure 21 shows the axial force applied in three different configurations: for upper notch length H_t of 10, 15 and 20 mm corresponding to a ligament length H_lig of 20, 15 and 10 mm respectively, under a confining pressure of 100 MPa.

Fig. 21

Axial force applied on the central part of the specimen vs axial displacement for different notch lengths. (Numerical simulations)

It was concluded that the maximum ligament length should not exceed 20 mm to limit the maximum axial stress applied to the bottom central part of the sample. On the other hand, since the press capacity is quite big compared to the axial force, the signal-to-noise ratio is optimized by choosing a higher force and thus a higher ligament length. Furthermore, since the maximum aggregate size of the tested concrete is 8 mm, the choice of the lowest length (10 mm) was not considered to provide a ligament shear surface large enough compared to the largest aggregate cross-section. With a ligament diameter of 35 mm and a ligament length of 15 and 20 mm the shear surface is, respectively, equal to 1650 mm² and 2200 mm² that can be considered large enough compared to the cross-section of the largest aggregates (respectively 33 and 44 times larger than the cross-section of a sphere with diameter of 8 mm). Thus, samples of 15 mm and 20 mm ligament lengths were tested experimentally.

Appendix B: Numerical Simulation of “Oedo-PTS test” with Drucker Prager Model and Comparison with an Experimental Result Obtained with Wet R30A7 Concrete

Oedometric-Punch-Through Shear tests based on the use of a non-pre-stressed confinement were reported in previous paper [3, 15, 23]. The specimen geometry is shown in Fig. 22(a). The axial displacement of the sample middle part with respect to its peripheral part produces a Mode II fracturing in the ligament. Inner diameter of the lower notch and outer diameter of upper notch coincide to obtain a straight cylindrical fracture surface. The metallic confinement cell is not centered toward the symmetry plane of the specimen to get a more uniform pressure between the confinement cell and the concrete sample (Fig. 22(b)) [15]. The gap between the sample and the confinement cell is completely filled with bi-component resin (Chrysor^®) when the sample is introduced in it. Furthermore, as shown in the picture of Fig. 22(b) four radial notches at 90° through the outer part of the specimen are performed in the sample to avoid a self-confinement of the sample during shearing. The cell is instrumented by means of two strain gauges that form an angle of 135°.

Fig. 22

The Oedo-PTS test. a Geometry of the sample used for Oedo-PTS experiments. b Concrete sample after shear testing [15]

Quasi-static experiments are reported in [23]. The mean shear stress in the shear ligament is deduced directly from the axial load that is transmitted onto the shear surface:

$${\sigma }_{shear}=\frac{{F}_{axial}}{{S}_{lig}}\ with\ {S}_{lig}=\pi {D}_{lig}{H}_{lig},$$

(13)

where ${D}_{shear}$ and ${H}_{shear}$ are the diameter and height of the sheared surface (Fig. 22). Sample-self-confinement being suppressed, the mean radial stress in the ligament is deduced from the average contact pressure between the sample and the confinement cell:

$${\sigma }_{radial}= \frac{{S}_{contact}}{{S}_{lig}}{P}_{contact}\ with\ {S}_{contact}=\pi {{D}_{int}}_{cell}{H}_{cell}$$

(14)

${{D}_{int}}_{cell}$ and ${H}_{cell}$ corresponding to the inner diameter and height of the confinement cell (Fig. 22(a)). An experimental result of shear stress and radial stress versus axial displacement is plotted in the Fig. 23.

Fig. 23

Comparison between experimental result and 3D numerical simulation of a “Oedo-PTS” test conducted with wet R30A7 concrete. Strain-rate: 2e-5/s, aluminium confining cell, concrete samples with 4 radial notches

3D numerical simulations of PTS shear tests were conducted with Abaqus FE code. The Drucker-Prager model was used for the specimen to describe the pressure sensitivity and dilation behaviour of concrete. The parameters of DP model are reported in Table 5.

The length of the ligament (10 mm) provides a quite homogeneous shear stress field in the ligament (Fig. 24(b)). Moreover the confining ring is not centred toward the symmetry plane of the specimen to get a uniform pressure between the confining ring and the concrete sample. The change of shear stress and radial stress as function of axial displacement is compared to experimental results in the Fig. 23. A good match is obtained until a displacement of 0.5 mm that would corresponds to a shear strain of 10% (equation (9) with e = 2.5 mm). Beyond a displacement of 2.5 mm due to mode II fracturing in the ligament a softening behaviour is noted that can be captured by the Drucker-Prager constitutive model.

Fig. 24

3D numerical simulation of a “Oedo-PTS” test. a Mesh, b Shear stress field, c Wireframe view