Introduction

The time – dependency of physical parameters, such as mass, damping, stiffness, and rotational speed, may affect the working conditions of a wide variety of dynamical systems. Systems including such time – varying parameters are said to be operating under Parametric Excitation. The existence of parametric excitation can result in responses that are different from the typical resonances, i.e. the system response is unbounded and may have a frequency content different from that of the excitation. Hence, performing a careful dynamic characterization of structures under parametric excitation prior to manufacturing is essential.

In the literature, numerical analyses of systems operating under parametric excitation are numerous. Ghadiri and Hosseini [1] studied the nonlinear dynamic behavior of a nanobeam modeled by Bernoulli–Euler beam theory; in this work, the authors sought the influence of parametric excitation, axially imposed and generated by thermo-magnetic load, on the stability of a beam. Zhang et al. [2] analyzed the stability of a parametrically excited viscoelastic beam. In this study the time – varying axial tension is the source of parametric excitation and its effect on the principal parametric frequencies, close to twice the value of each natural frequency, is investigated. Arvin et al. [3] analyzed the nonlinear behavior of a rotating beam. They studied the stability of the system under parametric excitation resulting from time – varying rotational speed. Karev et al. [4] focused on an asynchronous/out of phase parametric excitation of a disk brake system using a normal form approach. Zhou et al. [5] considered a vertical cantilever beam under different kinds of excitation. They took into account the super periodic and nonlinear periodic parametric excitations and they obtained the boundaries separating chaotic and non-chaotic responses, using Melnikov’s method. Vernizzi et al. [6] studied the influence of parametric excitation on a vertically floated rod in a fluid. In this paper, the authors proposed three types of reduced order models and obtain the stability plots. Here, the results are also verified by FEM of the rod. Sheng and Wang [7] in a part of their research, performed a dynamics analysis of a functionally graded Timoshenko microbeam under parametric excitation. They concluded that the structure would have diverging responses at a parametric frequency equal to twice the natural frequency of specific modes.

In addition to these theoretical studies of parametrically excited systems, few experimental validations can be found in the literature. Hocquet and Devaud [8] investigated parametric resonances of a double coupled pendulum. In this study, the parametric excitation, generated by length modulation, has been tuned around the first and second parametric resonances where the boundaries of stability – instability are obtained. In other studies, an electromagnet is used to generate the time – varying spring. Chen and Yeh [9] studied theoretically and experimentally a parametrically excited cantilever beam. Here, an electromagnet simulates the parametric excitation (time-varying stiffness). The amplitude of the stiffness is computed analytically using the measured natural frequency for a constant gap between the electromagnet and the beam. Han et al. [10] used, as a test rig, a cantilever beam excited by two electromagnets. Two numerical methods were applied to obtain the full stability plot (containing stability boundaries). Furthermore, the instability investigation was performed for a single value of damping based on different gaps, location of the magnets, and excitation phase. Dohnal and Mace [11] demonstrated theoretically and experimentally that at the parametric combination resonance (subtraction kind), a reduction of vibration amplitude would happen. Ecker and Pumhossel [12] worked on the application of parametric excitation to attenuate the unwanted vibration of a torsional system due to self – excitation. In this paper, parametric excitation has been introduced to the experimental model employing a PD controller. Zaghari et al. [13] proposed the application of energy harvesting in a system driven by parametric excitation. The authors demonstrated theoretically and experimentally that at the parametric resonances of the first and second kind, the piezo-electric maximizes energy production.

Whether in a purely numerical context or in an experimental–numerical one, the instability detection of parametrically excited systems is necessary and of interest to a lot of research studies. In this context, Hill’s method which is based on the well – known Harmonic Balance Method, has been applied by numerous researchers. Villa et al. [14] utilized Hill’s method to investigate the stability of a rotor system mounted on rolling element bearings. Detroux et al. [15] proposed the application of Hill’s method, as an alternative to Floquet Theory, to determine the stability of the periodic solution of a SmallSat spacecraft for bifurcation detection. Liao et al. [16] did a comprehensive study on the quasi – periodic solutions of nonlinear systems. They utilized the multi – harmonic Hill’s method to study the stability of nonlinear systems such as a duffing oscillator. Von Groll and Ewins [17] performed the stability analysis of a rotor system in case of rotor–stator contact using Hill’s method.

In the present paper, two numerical methods to identify instability are validated thanks to an experimental test rig which, unlike others in the literature, allows to directly measure the physical parameters of interest. The test rig, used as a demonstrator, is composed of a cantilever beam exited by an electromagnet, serving as a time – varying stiffness. For the first time, to the authors’ knowledge, the amplitude of the time – varying stiffness generated by the magnet is obtained directly from the measured magnetic force. Moreover, an original formulation to quantitively link the physical parameters of the electromagnet to the parametric excitation characteristics is proposed. This formulation is used to build a predictive model of the experimental set-up. In addition, a mathematical formula for the modal damping is derived from the experimental evidence as a function of the gap between the electromagnet and the beam.

Both stable and unstable regimes are investigated experimentally and numerically, with a special reference to the combination resonance. The presence of unstable responses is confirmed not only by the amplitude but also by the frequency content. Instability detection is carried out through two state-of-the-art methods, Hill’s method and the Jacobian Based Approach, recently proposed by the authors [18]. The predictions of the instability detection techniques based on the purposely developed numerical model are validated experimentally. Furthermore, it is shown how, by changing the set-up of the electromagnet, instability can be activated and de-activated, a behavior well predicted by the proposed model.

The “Mathematical Model” section presents the general model of the demonstrator, while the “Stability Analysis” section summarizes the methods used for instability detection. The “Experimental Setup” section is dedicated to the experimental set-up and to the predictive quantitative model of the electromagnet functioning as a time-varying spring. Results are presented and discussed in the “Results and Discussion” section.

Mathematical Model

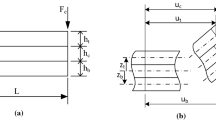
The system here adopted for the stability analysis is a clamped beam attached to a spring with time – varying stiffness introducing parametric excitation into the system. The scheme of the beam with a rectangular cross – section is shown in Fig. 1. The beam is modeled by seven Bernoulli – Euler beam elements (two beams for the length \({L}_{m}\) and five for the remaining length) which have two DOFs (degrees of freedom) for each node (translation along \(Y\) axis and rotation in the \(X\_Y\) plane).

Fig. 1
figure 1

Clamped beam with time-varying stiffness (top view)

Full size image

where \(\left[M\right]\), \(\left[C\right]\) and \(\left[K\right]\) are the mass, damping, and stiffness matrices. The damping matrix is assumed to be proportional and computed as \(\alpha \left[M\right]+\beta \left[K\right]\). \(H\), in equation (1) is a Heaviside function equal to 1 at the DOF \({y}_{E}\) of node \(E\) and zero for the other DOFs. It is used to state that the time – varying stiffness \(k\left(t\right)\) is applied only along the DOF \({y}_{E}\). The mathematical expression of \(k\left(t\right)\) is:

$${\left[M\right]}_{n\times n}{\left\{\ddot{y}\right\}}_{n\times 1}+{\left[C\right]}_{n\times n}{\left\{\dot{y}\right\}}_{n\times 1}+\left({\left[K\right]}_{n\times n }+k\left(t\right)H\right){\left\{y\right\}}_{n\times 1}=0$$
(1)

Equation (2) is periodic with \(T=2\pi /\eta\) and introduces parametric excitation to the system. Here, \({K}_{0}\) denotes the mean value of the stiffness and \(\eta\) represents the parametric excitation frequency. The meaning of this formula will be justified in the “Experimental Setup” section.

$$k\left(t\right)=-{K}_{0}\left(1+\mathrm{cos}\ \eta t\right)$$
(2)

Stability Analysis

Systems under parametric excitation may show unstable (resonance) conditions that are different from the simple resonances caused by an external harmonic excitation. Such instabilities are significant and might occur when the exciting frequency of the time – varying parameter is 1) close to twice each of the natural frequencies or 2) close to their combination [11]. The first condition is known as “primary parametric resonance”, while the second one is the so – called “parametric combination resonance”. The possible instability resonances under parametric excitation can be grouped by the following expression [12]:

The governing equations of motion of the system are:

$$\begin{array}{lc}\begin{array}{ll}\mathrm{Primary\ Parametric\ Resonance\ Frequencies}\\ \mathrm{({1}^{st}\ kind\ Parametric\ Resoance)}\end{array}& \eta =\frac{2{{\omega }_{\mathrm{n}}}_{i}}{r},\ i,r=\mathrm{1,2},\dots \\ \begin{array}{ll}\mathrm{Combination\ Parametric\ Resonance\ Frequencies}\\(\mathrm{{2}^{nd}\ kind\ Parametric\ Resonance})\end{array}& \eta =\frac{\left|{{\omega }_{\mathrm{n}}}_{i}\pm {{\omega }_{\mathrm{n}}}_{j}\right|}{r},\ i,j,r=\mathrm{1,2},\dots \end{array}$$
(3)

where \(r\) is the order of the parametric resonance and \(r=1\) gives the most significant case (primary and combination) [12]. \({{\omega }_{n}}_{i}\) and \({{\omega }_{n}}_{j}\) are the natural frequencies of the system. In particular, the instabilities due to the summation of the natural frequencies are considered the most significant [19]. In this study, only the first two natural frequencies of the beam model given in Fig. 1 are taken into account.

A typical stability plot of a parametrically excited system, in terms of physical parameters, is depicted in Fig. 2. In this case, the stability plot is a space of two parameters \(\left(\eta , {K}_{0}\right)\) divided into regions, whose borders are the so – called Transition Curves where the periodic responses exist. The inside surrounded by the Transition Curves comprises unstable/unbounded responses, while the outside area corresponds to stable/bounded responses.

Fig. 2
figure 2

Schematic of a stability plot with a sample of response

Full size image

Inside and on the boundaries of the combination resonance region, the system’s response has two dominant incommensurable frequencies, \({\omega }_{1}\) and \({\omega }_{2}\), whose summation is equal to the parametric excitation frequency \(\eta\). Moreover from Floquet Theory [20], the unstable regions caused by the primary parametric resonance correspond to periodic responses with frequency content \(\eta /2\) or so – called \(2T\) periodic frequency component.

Hill’s Method

To perform the stability analysis and to obtain the stability plot, here Hill’s method is adopted as an alternative to the classical Floquet method. This method is initiated by perturbing a solution of equation (1), \(\left\{{y}_{p}\left(t\right)\right\}\), as follows [15]:

$${\left\{q\left(t\right)\right\}}_{n\times 1}={\left\{{y}_{p}\left(t\right)\right\}}_{n\times 1}+{\left\{P\left(t\right)\right\}}_{n\times 1}$$
(4)

where \(\left\{P\left(t\right)\right\}\) is a periodic function and is expressed by the Floquet Form [21]:

$$\left\{P\left(t\right)\right\}=\left\{p\left(t\right)\right\}{e}^{\gamma t}$$
(5)

Since the beam vibrates around its equilibrium, \(\left\{{y}_{p}\left(t\right)\right\}=\left\{0\right\}\) which is the trivial solution of equation (1). Hence, the aim is to study the stability of the trivial solution. By substituting equation (4), considering equation (6), in equation (1) following would be derived:

$$\begin{array}{l}E\left(\left\{{y}_{p}\left(t\right)\right\}\right)=\left[M\right]\left\{\ddot{y}\right\}+\left[C\right]\left\{\dot{y}\right\}+\left(\left[K\right]+k\left(t\right)H\right)\left\{y\right\}\\ E\left(\left\{P\left(t\right)\right\}\right)=\left[M\right]\left\{\ddot{p}\right\}+\left[C\right]\left\{\dot{p}\right\}+\left(\left[K\right]+k\left(t\right)H+\left[M\right]{\gamma }^{2}\right)\\\qquad\qquad\qquad \left\{p\right\}+\left(2\left[M\right]\dot{p}+\left[C\right]\left\{p\right\}\right)\gamma \end{array}$$
(6)

where \(E\left(\left\{{y}_{p}\left(t\right)\right\}\right)=0\). The periodic function \(\left\{p\left(t\right)\right\}\) in equation (5) can be expanded by the Fourier series. The frequency components adopted here are \(2T\) periodic and it will be demonstrated that they suffice to obtain the whole unstable regions:

$${p}_{i}\left(t\right)=\sum_{z=0, \mathrm{1,3},\dots }\left({d}_{iz}\mathrm{sin}\frac{z\eta t}{2}+{c}_{iz}\mathrm{cos}\frac{z\eta t}{2}\right)$$
(7)

where \(i\) denotes each node of the FE model of the beam and \(z\) is an odd number except for the zeroth harmonic/static term. By collecting all the \({p}_{i}\left(t\right)\) given by equation (7) in a column vector, substituting the resultant in equation (6) and balancing the resultant equation, the following eigenvalue problem will be obtained [15]:

$${\gamma }^{2}{\mathrm{\rm X}}_{2}+\gamma {\mathrm{\rm X}}_{1}+\mathrm{J}=0$$
(8)

where \(J\) is the Jacobian matrix and the matrices \({\mathrm{\rm X}}_{1}\) and \({\mathrm{\rm X}}_{2}\) can be written as follows:

$$\begin{array}{l}{\mathrm{\rm X}}_{1}=\left[\begin{array}{cccc}\left[C\right]& & & \\ & \ddots & & \\ & & {\left[\begin{array}{cc}\left[C\right]& -2{\Omega }_{z}\left[M\right]\\ 2{\Omega }_{z}\left[M\right]& \left[C\right]\end{array}\right]}_{z}& \\ & & & \ddots \end{array}\right]\\ {\mathrm{\rm X}}_{2}=diag\left(\left[M\right], \dots , \left[M\right]\right)\end{array}$$
(9)

In the present study, the Fourier series is truncated to two harmonics (\({n}_{h}=2\)) i.e. \(z=1, 3\), with corresponding frequencies \(\eta /2\) and \(3\eta /2\) according to equation (7).

To avoid a trivial solution of equation (8) its determinant is set equal to zero:

$$\left|{\gamma }^{2}{\mathrm{\rm X}}_{2}+\gamma {\mathrm{\rm X}}_{1}+\mathrm{J}\right|=0$$
(10)

Equation (10) is a characteristic equation of an eigenvalue problem:

$$\Lambda \overrightarrow{v}=\gamma \overrightarrow{v}$$
(11)

where:

$$\Lambda ={\left[\begin{array}{cc}-{\mathrm{\rm X}}_{2}^{-1}{\mathrm{\rm X}}_{1}& -{\mathrm{\rm X}}_{2}^{-1}J\\ {\mathbb{I}}& 0\end{array}\right]}_{2n\left(2{n}_{h}+1\right)\times 2n\left(2{n}_{h}+1\right)}$$
(12)

then:

$${\gamma }=eig\left(\Lambda \right)$$
(13)

The number of eigenvalues is \(2n\left(2{n}_{h}+1\right)\). The \(2n\) eigenvalues with the smallest imaginary part in modulus, which are the so – called ‘’Floquet Exponents’’, determine whether the perturbing term in equation (5) will grow or decay in time. The system is said to be stable if all the Floquet Exponents in the parameter space are less than zero otherwise the system is unstable.

Instability Detection Using Jacobian Based Approach (JBA)

Jacobian Based Approach (JBA) which is recently developed and explained in detail by the authors in [18], is utilized to exploit the forced response study and locate the instabilities due to the parametric resonances. In [18], it was demonstrated that the HBM can detect an unstable region only if there are force components at the same frequency of the response in the unstable zones. These force components are necessary to trigger and track the unstable regions. Such force components are named “Test Force” components.

In order to implement this approach, the response of each node is expressed by the following Fourier series:

$$\begin{array}{l}{r}_{i}\\\quad =\sum\limits_{z=0, \mathrm{1,3},\dots }\left({a}_{iz}\ \mathrm{sin}\ \frac{z\eta t}{2}+{b}_{iz}\ \mathrm{cos}\ \frac{z\eta t}{2}\right)\\\qquad\quad +\sum\limits_{s=\mathrm{1,2}, \dots }\left(\left({c}_{is}\ \mathrm{sin}\ s{\omega }_{1}t+{d}_{is}\ \mathrm{cos}\ s{\omega }_{1}t\right)\right.\\\qquad\quad \left.+\left({l}_{is}\ \mathrm{sin}\ s{\omega }_{2}t+{o}_{is}\ \mathrm{cos}\ s{\omega }_{2}t\right)\right)\end{array}$$
(14)

where \(s\) and \(z\) are the indices of the Fourier series. In equation (14) the first set of Fourier components corresponds to primary parametric resonance responses (with frequencies \(z\eta t/2\) that are \(2T\) periodic) and the second part (with frequencies \(s{\upomega }_{1}\) & \(s{\omega }_{2}\)) corresponds to the combination parametric resonance responses. It must be noted that the first set of the Fourier series in equation (14), \(z\eta t/2\) frequency component, is truncated to two harmonics i.e. \(z=1, 3\) while the second set is truncated to a single harmonic i.e. \(s=1\). Here, the index \(i\) represents a specific node of the beam. The mathematical expressions of the frequencies \({\omega }_{1}\) and \({\omega }_{2}\) will be presented in the “Stability” section.

In the same way, the “Test Forces” will be expressed in terms of the same harmonic components as equation (14):

$$\begin{array}{l}{f}_{i}\\\quad =F_{TT}\sum\limits_{z=0,\mathrm{ 1,3},\dots }\left(\ \mathit{sin}\ \frac{z\eta t}{2}+\ \mathit{cos}\ \frac{z\eta t}{2}\right)\\\qquad\quad +F_{T}\sum\limits_{s=\mathrm{1,2}, \dots }\left\{\left(\ \mathit{sin}\ s{\omega }_{1}t+\mathit\ {cos}\ s{\omega }_{1}t\right)\right.\\\qquad\quad \left.+\left(\ \mathit{sin}\ s{\omega }_{2}t+\ \mathit{cos}\ s{\omega }_{2}t\right)\right\}\end{array}$$
(15)

Where the values of FTT and FT are arbitrary. By stacking equations (14) and (15) for each node in a column vector, substituting them in equation (1) and balancing the resultant equations for each harmonic term, the following residual equation is obtained:

$$\left\{R\right\}=\left[J\right]\left\{A\right\}-\left\{F\right\}$$
(16)

where \(\left[J\right]\), \(\left\{A\right\}\) and \(\left\{F\right\}\) are the Jacobian matrix and vectors of the harmonic amplitude and the external forces respectively. By minimizing the residual, the frequency response \(\left\{A\right\}\) of the system is computed. It will be shown that the FRF of the system will show local peaks corresponding to the boundaries between stable and unstable zones i.e. Transition Curves.

Experimental Setup

An experimental setup with a parametric excitation is proposed here to experimentally prove the presence of instability in the response. The test rig consists of a cantilever beam excited by an electromagnet. The electromagnet generates a force which corresponds to a time – varying stiffness connected to the beam, thus producing a parametric excitation. Figure 3 displays the scheme of the experimental setup with the generation of the magnetic force and the measurement of the response by means of a laser vibrometer. The picture of the test rig is shown in Fig. 4. The electromagnet is made of two coils of wire wrapped around a U-shaped core of ferromagnetic packed plates. Two prismatic extensions are glued at the two ends of the U – shaped core to be parallel to the beam and to excite the beam from one side. A NI CompactRIO system generates the current which is amplified before being supplied to the electromagnet. Since the beam is in aluminum, a thin steel plate (of mass \({M}_{s}\)) is attached to the part of the beam facing the electromagnet in order to receive the magnetic force. A laser vibrometer Polytec measures the beam response at one point as shown in Fig. 4(b).

Fig. 3
figure 3

Schematic of the test rig and measurement process

Full size image
Fig. 4
figure 4

a Magnet system, b Top view of the test rig

Full size image

The mathematical formula of the magnetic force can be written as [22]:

$$f\left(t\right)=\frac{A}{{\left({L}_{0}-{y}_{m}\right)}^{2}}\left(1-\mathrm{cos}\ \eta t\right)$$
(17)

where \({L}_{0}\) is the initial gap between the electromagnet and the steel plate attached to the beam (as shown in Fig. 3), \({y}_{m}\) represents the displacement amplitude of the beam at a distant time and a distance \({L}_{m}\) from the beam constraint, \(\eta\) is the frequency of the excitation. The coefficient \(A\) is defined as follows [22]:

$$A=\frac{{N}^{2}{\mu }_{air}{S}^{^{\prime}}{I}^{2}}{2}$$
(18)

where \(N\), \({\mu }_{air}\), \({S}^{^{\prime}}\) and \(I\) are respectively: the number of turns of the coils, the air permeability, the area of each coil facing the steel plate, and the amplitude of the current.

Since the beam’s vibration displacement is usually small with respect to \({L}_{0}\), equation (17) can be expanded around \({y}_{m}=0\) by a Taylor series expansion, taking the first order expansion. The force of equation (17) will then become [13]:

$$\begin{array}{l}f\left(t\right)=\frac{A}{{L}_{0}^{2}}\left(1-\mathrm{cos}\ \eta t\right)+\frac{2A}{{L}_{0}^{3}}\left(1-\mathrm{cos}\ \eta t\right){y}_{m}\\\qquad ={F}_{0}\left(1-\mathrm{cos}\ \eta t\right)+{K}_{0}\left(1-\mathrm{cos}\ \eta t\right){y}_{m}\end{array}$$
(19)

From equation (19) it can be observed that the force includes an external force and a time – varying stiffness with a mean value:

$${K}_{0}=2A/{L}_{0}^{3}$$
(20)

The advantage of this system is that the force \({F}_{0}\) exerted by the magnet on the beam can be directly derived from the measurement of a force transducer placed on the magnet itself. The force \({F}_{0}\) is derived by the measurement of the force (\({F}_{m}\)) of the transducer positioned at the base of the electromagnet (see Fig. 5). The electromagnet was calibrated in advance and a calibration curve provides the values of the force exerted on the beam (\({F}_{0}\)) corresponding to the values of the force measured by the transducer (\({F}_{m}\)) for different frequencies [23, 24].

Fig. 5
figure 5

Actual magnetic force generated by the magnet \(\left({F}_{0}\right)\) and the force measured by the transducer \(\left({F}_{m}\right)\)

Full size image

The constant \(A\), which is a function of different parameters, not all known a priori, as shown in equation (18), can be directly derived by the value of the force \({F}_{0}\) at a given exciting frequency. From equations (17) and (19) it can be written:

$$A={F}_{0}{L}_{0}^{2}$$
(21)

Equation (21) will then be substituted in equation (19) for the computation of the magnetic force \(f\left(t\right)\) in the numerical analysis.

Results and Discussion

This section presents an experimental–numerical comparison of the parametrically excited system described in the “Experimental Setup” section and modeled according to the “Mathematical Model” section. A numerical solution of the system is proposed, where stable and unstable regions are identified according to the methods described in the “Stability Analysis” section. The results of the experimental measurements are obtained in one of the unstable regions (corresponding to the combination parametric frequencies). After a modal damping identification of the rig for different gap L0 values, the experimental results are compared to the numerical results on the same stability plot. The values needed to model the test rig, according to the parametrization described in the “Mathematical Model” section, are given in Table 1.

Table 1 system’s parameters
Full size table

Stability

The stability plot is obtained implementing Hill’s method and presented in Fig. 6. Here the results are computed on the \(({K}_{0} , \eta )\) plane where, for each combination of these parameters, the Floquet exponents are computed. The black regions contain unstable responses as at least one Floquet exponent is greater than zero. Three unstable zones are visible in Fig. 6, the first and third are appeared due to the Primary Parametric Resonance while the one in the middle is formed as a result of Combination Parametric Resonance response. According to Fig. 6 and equation (3), the instabilities due to the Primary Parametric Resonance occur when \(\eta\) is around \(2{{\omega }_{n}}_{1}\) (first green dashed line) and \(2{\omega }_{{n}_{2}}\) (last green dashed line), while the instabilities due to the Primary Parametric Resonance takes place when \(\eta\) is around \({\omega }_{{n}_{1}}+{\omega }_{{n}_{2}}\) (middle green dashed line).

Fig. 6
figure 6

Stability plot applying Hill’s method

Full size image

The result of the JBA for \({K}_{0}=800 \mathrm{N}/\mathrm{m}\) is presented in Fig. 7. Since this approach is adopted for a specific value of \({K}_{0}\), it demonstrates “local” stability. The frequency response is obtained for the same range of \(\eta\) as Fig. 6. According to the authors’ observation, for this specific system, the incommensurable frequencies \({\omega }_{1}\) and \({\omega }_{2}\) are linked by the following formula:

Fig. 7
figure 7

JBA results for \({K}_{0}=800\) (N/m)

Full size image
$${\omega }_{1}=\left|\left(\eta +{\omega }_{n1}-{\omega }_{n2}\right)\right|/2,{\omega }_{2}=\eta -{\omega }_{1}$$
(22)

The frequency response shown in the lower portion of Fig. 7 has been obtained by inserting equation (22) in equation (15) and solving equation (16). In this figure the blue curve is the response of the system to the external test force with the frequency associated to \(2T\) periodic responses (primary parametric resonances); conversely, the purple curve corresponds to the system’s response to the external test force having the frequency related to parametric combination resonances. Three sets of dual peaks are visible in Fig. 7, each connected by dashed red lines to the stability plot (obtained according to Hill’s theory) at the corresponding value of \(\eta\). It can be observed how the double peaks efficiently and precisely signal the limits, frequency-wise, of the unstable regions related to \({K}_{0}=800 \mathrm{N}/\mathrm{m}\). In fact, as stated in the “Stability Analysis” section, these local peaks pick up the transition curves, i.e. those curves defined by the parameters combinations giving rise to period responses.

The reader will notice that the JBA response shown in Fig. 7 contains two extra peaks, denoted by ① & ②, which have nothing to do with instability detection. The reason behind these peaks is a by-product of the method itself. The external test force inserted in the system is swept for a range of \(\eta\). It may happen that the exciting frequency \(\eta\) may coincide with one of the natural frequencies and, as the result, cause the resonance. For instance, the first peak of the blue curve at \(\eta =33\ \mathrm{r}/\mathrm{s}\), marked by ①, causes the system to resonate. This is because at \(\eta =33\ \mathrm{r}/\mathrm{s}\) one of the frequencies in equation (15), \(3\eta /2\), will be equal to \({\omega }_{{n}_{1}}\). Accordingly, for the peak ② of the purple curve, when \(\eta =165.9\ \mathrm{r}/\mathrm{s}\), it holds \({\omega }_{1}={\omega }_{{n}_{1}}\) which also causes the resonance of the system. It should be noted that these extra contributions can be easily filtered out a priori and are here shown only to demonstrate a full implementation of the method.

To build the stability plot using JBA, the following procedure must be followed:

  1. (a)

    Perform the JBA for different values of \({K}_{0}\) for an interval of \(\eta\)

  2. (b)

    For each \({K}_{0}\), build a plot like in Fig. 7

  3. (c)

    Collect the frequency values corresponding to the peaks demonstrating the domains of instabilities

  4. (d)

    Plot the collected points from the previous step

Doing so, the stability plot obtained by JBA is given in Fig. 8. In this figure, it can be observed that the transition curves computed by JBA accurately locate all the unstable regions obtained through Hill’s method. Here, the blue transition curves determine the border of the instabilities due to the primary parametric resonances while the purple one characterizes the unstable zone induced by combination parametric resonances. In addition, the first and second lines of simple resonances shown in Fig. 8 (see the labels at the bottom left), are the collection of the peaks ① and ② shown in Fig. 7 for different values of \({K}_{0}\).

Fig. 8
figure 8

Stability plot obtained by employing JBA

Full size image

To make a comparison, in terms of computational time, between JBA and Hill’s method, a portion of the stability plot at \(600\) N/m \(\le {K}_{0}\le 800\) N/m and \(0\) rad/s \(\le \eta \le 700\) rad/s considering 500 values for each parameter, is recomputed where the duration of the computation is presented in Table 2. It must be noted that the reason for choosing this portion of the stability plot is that this part contains just the unstable regions which could be computationally time – consuming to obtain. In this way, the efficiency of the two methods can be examined more precisely. According to Table 2, JBA is almost 45 times faster than Hill in obtaining the stability plot.

Table 2 The computational time for obtaining the complete stability plot via Hill’s method and JBA for \(600\left(\frac{\mathrm{N}}{\mathrm{m}}\right)\le {K}_{0}\le 800\left(\frac{\mathrm{N}}{\mathrm{m}}\right)\) & \(0\left(\frac{\mathrm{rad}}{\mathrm{s}}\right)\le \eta \le 700\left(\frac{\mathrm{rad}}{\mathrm{s}}\right)\)
Full size table

Experimental–Numerical Results

As mentioned in the “Experimental Setup” section, to seek the existence of parametric resonance, a test rig comprising of a cantilever beam excited by an electromagnet is taken into account. In this study, the focus is on the combination parametric resonance response. For this reason, the system will be analyzed at \(\eta \approx {\omega }_{{n}_{1}}+{\omega }_{{n}_{2}}\).

In the first step, in order to make sure that the numerical model matches its experimental counterpart, the natural frequencies corresponding to the free system (i.e. no magnet) are compared. As presented in Table 3, the first two natural frequencies are fairly close.

Table 3 1st two Natural Frequencies
Full size table

In the second step, the experimental results for three values of the gap \({L}_{0}=7 \mathrm{mm},8 \mathrm{mm}, 9 \mathrm{mm}\) are obtained. For each \({L}_{0}\), the system is excited at a frequency equal to the summation of the first two natural frequencies. In each case, the response of the point highlighted in Fig. 4(b) is measured and its FFT is plotted. The numerical calculation is performed for the same nominal conditions. The numerical and experimental results in terms of excitation force and displacement for different \({L}_{0}\) are compared in Fig. 9.

Fig. 9
figure 9

FFT of the force and displacement of the rig and mathematical mode for different values of \({L}_{0}\) where instability is detected

Full size image

For the case \({L}_{0}=7 \mathrm{mm}\), the rig has been excited at the frequency \(\eta =\mathrm{ 58,44}\) Hz \(\approx {\omega }_{{n}_{1}}+{\omega }_{{n}_{2}}\). This is confirmed by the FFT of the measured force shown in Fig. 9(a) where also small extra harmonic contributions are visible. These extra harmonics are due to the response of the beam whose frequency content includes \({\omega }_{{n}_{1}}\) and \({\omega }_{{n}_{2}}\) as shown in the lower portion of Fig. 9(a). At the excitation frequency \(\eta\)= \(\mathrm{58,44}\) Hz, the response, as depicted in the lower portion of Fig. 9(a), not only has a high amplitude but also its frequency content (large peaks at \({\omega }_{{n}_{1}}\) and \({\omega }_{{n}_{2}}\)) is typical of instability due to combination resonance.

To obtain the numerical results at the corresponding gap and exciting frequency, different quantities need to be estimated:

  • the excitation force \({F}_{0}\)

  • the equivalent stiffness \({K}_{0}\)

  • the damping ratio \(\zeta\)

Equation (21) is used to compute the value of the constant \(A\) from the measured force \({F}_{0}\). For this purpose, \({F}_{0}\) is read as the amplitude of the main peak of the FFT of the measured force in Fig. 9. Then \({K}_{0}\) is obtained as a function of \(A\) and \({L}_{0}\) from equation (20). Since the system’s equivalent stiffness changes as \({K}_{0}\) changes and since, in the assumed model, the damping is proportional to the stiffness, its value must be updated for each \({L}_{0}\) as shown in Fig. 10(a). For the damping ratio characterization tests have been performed for three different gap values: \({L}_{0}=7\ \mathrm{mm},\ 8\ \mathrm{mm},\ 9\ \mathrm{mm}\). In all these cases instability has been observed. For each experimental test, a series of numerical simulations are carried out. All the parameters of the numerical model are known but \(\zeta\). The value of \(\zeta\) is obtained as the highest possible value which still ensures the numerical system to reach instability. Repeating this procedure for all three cases, the results are collected and presented in Fig. 10(b). As expected, different values of \({K}_{0}\), produce different values of \(\zeta\). Then, two different fitting curves based on the three sets of values have been obtained. In this paper, the polynomial curve is used to characterize the damping ratio. It is worth mentioning that for \({L}_{0}>9\ \mathrm{mm}\), instability is not observed experimentally. In this case, the corresponding numerical modes adopt the fixed value of \(\zeta \left({L}_{0}=9\ \mathrm{mm}\right)\).

Fig. 10
figure 10

a Effect of gap value \({L}_{0}\) on the mean parametric stiffness \({K}_{0}\) b Modal damping ratio calculation empirically

Full size image

As shown in Fig. 9(a), the FFT of the numerical force has similar components compared to the experimental case. Taking into consideration the FFT of the response, it is observed that the numerical model follows the same behavior as the experimental model but with higher amplitude in the first mode. It must be noted that the response of the numerical model will increase unboundedly at the parametric combination frequency as time passes while the experimental model reaches a high amplitude steady – state response. The bounded response observed during testing is probably due to the additional source of damping provided by the friction of the bolts used to clamp the beam and not taken into account in the model described in the “Mathematical Model” section. The same procedure is followed for \({L}_{0}=8\ \mathrm{mm}\) and \(9\ \mathrm{mm}\).

When the frequency of the electromagnet \(\eta\) is away from resonance frequencies either simple or parametric, the system has infinitesimal displacement and accordingly \({y}_{m}=0\). Therefore, the measured force by the force transducer will be \({F}_{0}\). However, the stiffness – dependent part of the magnetic force given by equation (19) is still available and the Formulas given in equations (20) and (21) can be computed. At the parametric resonance, still the procedure explained above is adopted and since the Experimental and Numerical FFT plots in Fig. 9 overlap each other frequency – wise, it proves that considering the measured force from the transducer, even in case of resonance, to be equal to \({F}_{0}\) is correct.

Considering Fig. 10(a), as the value of the gap increases the value of \({K}_{0}\) decreases and, consequently, the influence of the parametric excitation becomes less significant. This point by the stability plot shown in Fig. 11. This numerical stability plot is obtained applying Hill’s method (see “Stability Analysis” section); the only difference, which has a negligible impact on the final result, is that the damping ratio is modified according to the \({K}_{0}\) values (i.e. Fig. 10(b)). The formula coming from the polynomial fitting curve of the damping ratio is used for a range of \({K}_{0}\) corresponding to \(7\ \mathrm{mm}\le {L}_{0}\le 9\ \mathrm{mm}\) while a fixed value of \(\zeta \left({L}_{0}=9\ \mathrm{mm}\right)\) is applied for \({K}_{0}\) corresponding to \({L}_{0}>9\ \mathrm{mm}\). In order to obtain a complete experimental numerical comparison both stable and unstable responses are shown. As expected stable responses correspond to cases where \({L}_{0}>9\ \mathrm{mm}\). The experimental results match perfectly the numerical stability plot as the \({K}_{0}\) values corresponding to \({L}_{0}>9\ \mathrm{mm}\) lead to \({K}_{0}\) values lower than \(250\ (\mathrm{N}/\mathrm{m})\), for which no instability can be detected, neither numerically nor experimentally.

Fig. 11
figure 11

Stability plot corresponding to the test rig at the combination parametric resonance frequency

Full size image

Conclusion

This paper aims to present an easily attainable experimental test case to study the effect of parametric excitation on the stability of a vibrating system. For this reason, the chosen demonstrator is a cantilever beam mounted on a spring, whose time – varying stiffness can be derived by a measurement of the corresponding force. In this experimental set-up, the time varying stiffness is obtained thanks to an electromagnet. The observation of the experimental results and the subsequent comparison with the numerical simulation results in the following remarks:

  • The experimental set-up is successful in triggering unstable behavior typical of parametric excitation, with a specific reference to the Combination Parametric Resonance.

  • The experimental results obtained by the direct measurement of the magnetic force are in good agreement with the numerical ones.

  • The link between the electromagnet, i.e. source of parametric excitation, and the resulting model form is formulated based on easily controllable physical parameters.

  • The state-of-the-art Hill’s method for the detection of unstable responses, and the one proposed by the authors i.e. JBA, successfully identify the unstable regions of the system. The stability plots thus obtained are confirmed numerically, i.e. through Direct Time Integration, and validated experimentally.

  • The amplitude of the unstable response in the numerical simulation is greater than the experimental one. This may be because the numerical model lacks additional sources of damping, e.g. friction at the bolts, which may limit the amplitude of the response.

  • The multi-functionality of JBA i.e. determining the domain of parametric instabilities in the frequency response plot as well as obtaining accurately the full stability plot in an efficient computational time makes JBA a useful tool for studying a parametrically excited system.

  • The characteristics of the response at combination parametric resonance, i.e. large vibration amplitude and multi –frequency content which is different from the drive frequency, make the experimental setup a good candidate for different applications, e.g. energy harvesting from the high amplitude oscillations, multi-modal investigations, etc.