Introduction

The number of structures close to their design life is increasing, and the increase in maintenance work is becoming a problem. For example, many highway steel bridges, which withstand the heavy traffic of automobiles traveling at high speeds and delivering large loads, were built around the same time. The fatigue cracks in the structure caused during service may lead to serious accidents if the defect is left unaddressed. An efficient non-destructive evaluation method is required for large-scale structures, such as highway steel bridges and airplanes. Contact-type non-destructive inspection methods, such as the ultrasonic inspection method, requires a long period of time for inspection. Infrared thermography enables the remote and non-destructive inspection of cracks and internal defects from thermal images based on heat dissipation using infrared flash and several heating devices [1,2,3]. Furthermore, thermoelastic stress analysis using infrared thermography (TSA) helps obtain a stress amplitude distribution map based on the thermoelastic effect [4,5,6]. The temperature changes due to thermoelastic stress are very small and below the temperature resolution of infrared thermography equipment. Therefore, the lock-in algorithm is utilized for TSA. Lock-in thermography is performed via the frequency analysis of the periodic sinusoidal temperature change measured when a periodic load is applied [7,8,9]. Pitarresi et al. [10] applied low-cost infrared thermography with micro-bolometers and a lock-in algorithm to TSA. When a random or impulse load is applied to the measured structure, TSA based on frequency analysis cannot be applied.

To enable measurement with random load, the random lock-in method has been developed to evaluate the magnitude of temperature change due to the thermoelastic effect using the least squares method for the reference signal obtained from the sensor installed near the measurement site [11]. Furthermore, the self-correlation (self-reference) lock-in TSA method, which uses temperature change at a specific position in a thermal image as the reference signal, has been developed [12, 13]. Since self-correlation lock-in thermography does not require the reference signal from the real sensor installed into the measurement site, this method is suitable for remote field measurements. Sakagami et al. [14, 15] used self-correlation lock-in thermography to evaluate the propagation of fatigue cracks in the welded joints of steel bridges. Galietti et al. [16] proposed another signal processing method for TSA under a random load, where the frequency analysis is performed for the reference signal selected at a certain pixel in the thermal image, and the measured thermographic signal is assumed to be approximated with a harmonic signal based on the results of frequency analysis. However, as shown in this paper, it is found that the quality of the reference signal in self-correlation lock-in thermography affects the stress amplitude distribution.

The self-correlation lock-in thermography in TSA, which uses a dynamic thermographic signal at a specific position or region in the thermal image as a reference signal, is easily affected by the acquisition position of the reference signal. The operator is required to understand the deformation of the measurement structure and component to select the reference point.

This study aims to propose a new TSA method that generates stress distribution and recostructed load signal by singular value decomposition (SVD) from the thermal image sequence without using the reference signal, which is called SVD thermo-component analysis. Rajic [17] developed a pulse thermography inspection using SVD called principal component thermography (PCT) and applied it to the detection of structural defects. When flash heating is applied to a component, the heat conduction behavior is measured in the thickness direction of the component, and the change in heat conduction due to the defect appears as the change in the thermal image. The characteristics of the change in thermal image are extracted using SVD. PCT emphasizes the contrast on the thermal image caused by the defect.

When SVD is applied to an infrared video of an object under loading, it is decomposed into the temperature signal contained in the video and the feature distribution according to the temperature signal. The temperature signal of the first component corresponds to the load signal that is the cause of the thermoelastic effect, and the image is considered to correspond to the stress distribution. SVD extractes various signal components, such as the second and third components, that is considered to reflect temperature signals other than thermoelastic temperature change, such as temperature signals due to other load modes and signals due to energy dissipation. Therefore, developed method is called SVD thermo-component analysis.

In this paper, lock-in thermography and self-correlation thermography are introduced, the problems in self-correlation thermography are discussed, and the principle of SVD thermo-component analysis for TSA is explained. Furthermore, the experiment performed for conducting a basic study on the applicability of SVD thermo-component analysis for TSA is presented. In the experiment, a sinusoidal load was applied to a specimen with a circular hole, and using SVD thermo-component analysis, the load signal was reconstructed, and stress distribution was calculated. The accuracy of the reconstructed signal and calculated stress distribution using SVD thermo-component analysis are verified by comparison with the stress distribution obtained using the conventional lock-in method.

Principal of Svd Thermo-component Analysis

Thermoelastic Stress Analysis

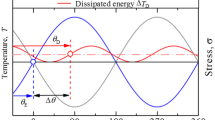
When a load is applied to a material, small temperature changes are observed on the material surface due to the thermoelastic effect. The relation between temperature change \(\Delta T\) and the change in the accumulated stress Δσ can be expressed as:

$$\Delta T = -\frac{\alpha }{\rho C\mathrm{p} }T\Delta \sigma = -kT\Delta \sigma ,$$
(1)

where \(\alpha\) is the coefficient of thermal linear expansion, \(\rho\) is the density, \(C\mathrm{p}\) is the isopiestic specific heat, \(k\) is the thermoelastic modulus, and \(T\) is the absolute temperature of the material [12]. When a sinusoidal load signal with a constant amplitude and frequency fref is applied to the specimen, the sinusoidal surface temperature ψ (p, t) can be measured. The measured dynamic thermal image can be approximated as follows:

$$\psi \left( {p,t} \right) = a\left( p \right) + b\left( p \right)\cos \left( {2\pi t\frac{{f_{{{\text{ref}}}} }}{{f_{{{\text{meas}}}} }} + \theta } \right),$$
(2)

where \(p = (x,y)\) is the pixel position in the thermal image; fmeas is the measurement frequency; a(p) is the mean component of the thermal image at pixel p; b(p) is the magnitude of the sinusoidal temperature change at pixel p, which indicates the stress distribution based on equation (1); and θ is the phase between fref and ψ (p, t).

When the load signal is sinusoidal with constant amplitude, the magnitude of the measured dynamic thermal signal and phase corresponding to the reference signal can be obtained based on Fourier transform. The sine and cosine signals with the same frequency as that of the reference signal measured from the load cell, strain gauge, and testing controller are generated, and signal processing with the measured temperature change is performed as follows [7,8,9]:

$$\begin{gathered} \Delta \psi_{\sin } \left( p \right) = \frac{2}{F}\sum\limits_{t = 1}^{F} {\psi \left( {p,t} \right) \cdot \sin \left( {2\pi t\frac{{f_{{{\text{ref}}}} }}{{f_{{{\text{meas}}}} }}} \right)} \hfill \\ \Delta \psi_{\cos } \left( p \right) = \frac{2}{F}\sum\limits_{t = 1}^{F} {\psi \left( {p,t} \right) \cdot \cos \left( {2\pi t\frac{{f_{{{\text{ref}}}} }}{{f_{{{\text{meas}}}} }}} \right)} , \hfill \\ \end{gathered}$$
(3)

where \(P\) is the number of pixels in the thermal image, and F is the number of measured frames. The b(p) and phase of the sinusoidal signal in ψ can be obtained using the following equation [7,8,9]:

$$b\left( p \right) = \sqrt {\left( {\Delta \psi_{\sin } \left( p \right)} \right)^{2} + \left( {\Delta \psi_{\sin } \left( p \right)} \right)^{2} } ,\quad \theta \left( p \right) = \tan^{ - 1} \left( {\frac{{\left( {\Delta \psi_{\sin } \left( p \right)} \right)^{2} }}{{\left( {\Delta \psi_{\cos } \left( p \right)} \right)^{2} }}} \right).$$
(4)

Since this signal processing is based on Fourier transform, this method is called the frequency analysis method. When a sinusoidal constant stress amplitude fatigue test is performed in a laboratory, the stress distribution acting on the specimen can be accurately evaluated.

If the load signal is a random waveform (variable amplitude and load multi frequency loadings) or only one highly damaging load application, the above frequency analysis method cannot evaluate the magnitude of the load. Therefore, the lock-in method using the least squares method has been developed.

Random Lock-in Thermography using the Original Load Signal

In equation (1), the load is a function of time, and the equation for each pixel on the thermal image is shown below:

$$\psi \left(p,t\right) = a\left(p\right) + b\left(p\right)f\left(t\right), p = 1 - P, t = 1 - F,$$
(5)

where \(a\left(p\right)\) is the stationary component of the infrared thermal image at pixel p. \(a\left(p\right)\) indicates the temperature distribution on the surface of the object when no load is applied (i.e., \(f\left(t\right) = 0\)) and mainly depends on the environmental temperature or emissivity of the surface of the object. b(p) corresponds to the stress distribution in equation (5). If the original load signal \(f\left(t\right)\) in equation (5) is measured using a conventional sensor (e.g., strain gauge) attached to the target object, \(a\left(p\right)\) and \(b\left(p\right)\) can be obtained from the measured thermal image using the least squares method. The sum of the squares of the differences between the measured data and the approximate model can be obtained for the F available frames as follows [13]:

$$\Delta \left(a\left(p\right),b\left(p\right)\right)= {\sum }_{t = 1}^{F}{\left(\psi \left(p,t\right) - a\left(p\right) - b\left(p\right)f\left(t\right)\right)}^{2}$$
(6)

where \(a\left(p\right)\) and \(b\left(p\right)\) minimize \(\Delta (a\left(p\right),b(p))\) and are obtained by differentiating equation (6) with respect to \(a\left(p\right)\) or \(b\left(p\right)\) and setting the result to 0. By solving the simultaneous equations, we can easily obtain \(a\left(p\right)\) or \(b\left(p\right)\) as follows:

$${b}_{L}\left(p\right) = \frac{F{\sum }_{t = 1}^{F}\psi \left(p,t\right)f\left(t\right) - {\sum }_{t = 1}^{F}\psi \left(p,t\right){\sum }_{t = 1}^{F}f\left(t\right)}{F{\sum }_{t = 1}^{F}{f\left(t\right)}^{2} - {\left({\sum }_{t = 1}^{F}f\left(t\right)\right)}^{2}},$$
(7)
$${a}_{L}\left(p\right) = \frac{{\sum }_{t = 1}^{F}\psi \left(p,t\right) - b(p){\sum }_{t = 1}^{F}f(t)}{F},$$
(8)

where subscript \(L\) indicates that \(a\left(p\right)\) and \(b\left(p\right)\) are obtained using the measured load signal \(f\left(t\right)\). This method is called random lock-in thermography [4]. Stress distribution can be obtained even from a random load that is measured separately using a sensor via random lock-in thermography.

Self-correlation Lock-in Thermography

In random lock-in thermography, the reference signal f(t) is obtained using the sensor set near the measurement point. If the sensor cannot be installed near the measurement point, the temperature signal ψ (s, t) near the measurement point can be used as the reference signal f(t). This method is called self-correlation lock-in thermography. By substituting \(\psi (s,t)\) for \(f\left(t\right)\) in equations (7) and (8), \(a\left(p\right)\) and \(b\left(p\right)\) can be obtained as follows:

$${b}_{S}\left(p\right)= \frac{F{\sum }_{t = 1}^{F}\psi \left(p,t\right)\psi \left(s,t\right) - {\sum }_{t = 1}^{F}\psi (p,t){\sum }_{t = 1}^{F}\psi (s,t)}{F{\sum }_{t = 1}^{F}{\psi (s,t)}^{2} - {\left({\sum }_{t = 1}^{F}\psi (s,t)\right)}^{2}},$$
(9)
$${a}_{S}\left(p\right) = \frac{{\sum }_{t = 1}^{F}\psi (p,t) - b(p){\sum }_{t = 1}^{F}\psi (s,t)}{F},$$
(10)

where subscript \(s\) indicates that \(a\left(p\right)\) and \(b\left(p\right)\) are obtained using the self-correlation lock-in method, which provides a stress distribution using only thermal images. The accuracy of stress distribution depends on the position of the reference signal. The temperature change of the reference signal is expressed as:

$$\psi \left(s,t\right) = a\left(s\right) + b\left(s\right)f\left(t\right).$$
(11)

By substituting equation (11) in equation (9), we obtain:

$${b}_{S}\left(p\right) = \frac{F{\sum }_{t = 1}^{F}\psi \left(p,t\right)f\left(t\right) - {\sum }_{t = 1}^{F}\psi (p,t){\sum }_{t = 1}^{F}f(t)}{b(s)(F{\sum }_{t = 1}^{F}{f\left(t\right)}^{2} -{ \left({\sum }_{t = 1}^{F}f\left(t\right)\right)}^{2})}.$$
(12)

By comparing equation (12) with equation (7) and normalizing \({b}_{L}(p)\) with \(b\left(s\right)\) in equation (8), \({b}_{S}(p)\) is obtained. \(\psi \left(s,t\right)\) should follow equation (5) and provide the correct information to replace the input load signal f (t). When f (t) is close to 0, the equation becomes unstable. Consequently, a very small temperature change at the reference position \(s\) with a weak correlation with the load signal provides an incorrect stress distribution.

As the component \(a\left(p\right)\) is not explicitly stated in equation (12), the time average of \(f\left(t\right)\), \(\stackrel{-}{f(t)}{|}_{t}\), cannot be used to calculate \(b(s)\). The fluctuation in the reference signal, \({f}^{*}\left(t\right)\), is expressed as:

$${f}^{*}\left(t\right)= f\left(t\right) -\overline{f(t)}{|}_{t}.$$
(13)

Similarly, fluctuation of the temperature change with respect to the time average \({\psi }^{*}\left(p,t\right)\) is expressed as:

$${\psi }^{*}\left(p,t\right)=\psi \left(p,t\right) -\overline{\psi \left(p,t\right)}{|}_{t},$$
(14)

where \(\stackrel{-}{\psi \left(p,t\right)}{|}_{t}\) is the time average of \(\psi \left(p,t\right)\). By substituting \({f}^{*}(t)\) and \({\psi }^{*}(p,t)\) in equation (9), the time-averaged values, \(\stackrel{-}{f(t)}{|}_{t}\) and \(\stackrel{-}{\psi \left(p,t\right)}{|}_{t}\), disappear, and \({b}_{S}(p)\) can be obtained as follows:

$${b}_{S}\left(p\right) = \frac{{\sum }_{t = 1}^{F}{\psi }^{*}(p,t){f}^{*}(t)}{b(s){\sum }_{t = 1}^{F}{{f}^{*}(t)}^{2}}.$$
(15)

In self-correlation lock-in thermography, each pixel value \(b(p)\) in the stress distribution map involves fluctuations \({f}^{*}(t)\) and \({\psi }^{*}(p,t)\). Similarly, by substituting \({f}^{*}(t)\) and \({\psi }^{*}(p,t)\) in equation (7), \({b}_{L}\left(p\right)\) can be obtained as follows:

$${b}_{L}\left(p\right) = \frac{{\sum }_{t = 1}^{F}{\psi }^{*}(p,t){f}^{*}(t)}{{\sum }_{t = 1}^{F}{{f}^{*}(t)}^{2}},$$
(16)

which is similar to equation (15) but without \(b(s)\) in the denominator. Therefore, \(b(p)\) is related only to \({f}^{*}(t)\) and \({\psi }^{*}(p,t)\) in both random and self-correlation lock-in thermography.

SVD Thermo-Component Analysis

In the field of computer vision, Kanade and Poelman [18] reported that the three-dimensional trajectory of the camera and the three-dimensional shape of the object could be restored by applying SVD to the video sequence. Using a similar idea, we propose a method to reconstruct the load signals and stress amplitude distribution maps from time-vaarying infrared images. If \(\psi \left(s,t\right)\) at pixel \(s\), which shows a large temperature fluctuation, is used as the reference signal instead of the load signal \(f(t)\) in self-correlation lock-in thermography, the correct stress distribution can be obtained. It is not always possible to determine the position where a suitable \(\psi \left(s,t\right)\) can be obtained for correct analysis. Therefore, a method to calculate stress distribution without selecting the reference signal by applying SVD to thermal images is proposed. The proposed method is called “SVD thermo-component analysis.” Thermal image fluctuation \({\psi }^{*}(p,t)\) using equations (5) and (14) is presented as follows:

$$\begin{aligned}{\psi }^{*}\left(p,t\right) &= \psi \left(p,t\right) - \stackrel{-}{\psi \left(p,t\right){|}_{t}}= a\left(p\right) + b\left(p\right)f\left(t\right) - \left(a\left(p\right) + b\left(p\right)\stackrel{-}{f\left(t\right)}{|}_{t}\right)\\ &= b(p)\left(f\left(t\right) - \stackrel{-}{f(t)}{|}_{t}\right)\\ &=b(p){f}^{*}(t)\end{aligned}$$
(17)

Let us define a \(P \times F\) observation matrix \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\), with columns representing the pixel positions of the observed thermal image, rows representing time, and elements being the thermal image fluctuation \({\psi }^{*}(p,t)\).

$${\boldsymbol{\Psi }}^{\boldsymbol{*}}=\left[\begin{array}{c}{\psi }^{*}\left(\mathrm{1,1}\right){ \psi }^{*}\left(\mathrm{1,2}\right) \dots { \psi }^{*}\left(1,F\right)\\ {\psi }^{*}\left(\mathrm{2,1}\right){\psi }^{*}\left(\mathrm{2,2}\right) \dots {\psi }^{*}\left(2,F\right)\\ \vdots \ddots \vdots \\ {\psi }^{*}\left(P,1\right){\psi }^{*}\left(P,2\right) \dots { \psi }^{*}(P,F)\end{array}\right].$$
(18)

The observation matrix \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\) can be represented in terms of equation (14) as follows:

$${\boldsymbol{\Psi }}^{\boldsymbol{*}}= \left[\begin{array}{c}b(1)\\ b(2)\\ \vdots \\ b(P)\end{array}\right]\left[{f}^{*}(1) {f}^{*}(2)\dots {f}^{*}(F)\right] = {\varvec{b}}{{{\varvec{f}}}^{\boldsymbol{*}}}^{T},$$
(19)
$${\varvec{b}}\boldsymbol{ }= \left[\begin{array}{c}b\left(1\right)\\ b\left(2\right)\\ \vdots \\ b(P)\end{array}\right],$$
(20)
$${{\varvec{f}}}^{\boldsymbol{*}}= \left[\begin{array}{c}{f}^{*}(1)\\ {f}^{*}(2)\\ \vdots \\ {f}^{*}(F)\end{array}\right].$$
(21)

As the observation matrix \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\) is the product of b in the \(P \times 1\) matrix and f* in the \(1 \times F\) matrix, its rank must be 1, and its SVD is given by:

$$\mathbf\Psi^\ast=\mathbf U\mathbf\Sigma\mathbf V^T=\left[{\mathbf u}_1{\mathbf u}_2\cdot\cdot\cdot\cdot{\mathbf u}_P\right]\begin{bmatrix}\begin{array}{ccc}\sigma_1&\cdots&0\\\vdots&\ddots&\vdots\\0&\cdots&\sigma_F\end{array}\\O\end{bmatrix}\begin{bmatrix}\mathbf v_1^T\\\mathbf v_2^T\\\vdots\\\vdots\\\mathbf v_F^T\end{bmatrix},$$
(22)

where \({\varvec{U}}\) is the \(P \times P\) vertical eigenvector matrix, \({{\varvec{u}}}_{p}\) is the \(P\)-dimensional unit vector, \({{\varvec{V}}}^{T}\) is the \(F \times F\) horizontal eigenvector matrix, \({{\varvec{v}}}_{t}\) is the \(F\)-dimensional unit vector, \({\varvec{\Sigma}}\) is the \(P \times F\) eigenvalue matrix, and \({\sigma }_{1}\ge \cdots \ge {\sigma }_{F}\ge 0\). As the rank of \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\) is 1, the eigenvalues obtained using SVD should be zero except for \({\sigma }_{1}\). Even if \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\) includes noise, the other eigenvalues should be sufficiently smaller than \({\sigma }_{1}\). Thus, when the eigenvalues other than σ1 are set to 0 in equation (22), the observation matrix becomes:

$${\boldsymbol{\Psi }}^{\boldsymbol{*}}\cong {\sigma }_{1}{{\varvec{u}}}_{1}{{\varvec{v}}}_{1}^{T}.$$
(23)

By comparing the terms in the right hand side of equations (23) and (19), it is evident that vector \({{\varvec{u}}}_{1}\) corresponds to vector \({\varvec{b}}\) and vector \({{\varvec{v}}}_{1}\) corresponds to vector \({{\varvec{f}}}^{\boldsymbol{*}}\):

$$\begin{gathered} {\mathbf{b}} = {\mathbf{u}}_{1} \hfill \\ {\mathbf{f}}^{*} = {\mathbf{v}}_{1} . \hfill \\ \end{gathered}$$
(24)

In the proposed SVD thermo-component analysis, the coefficient proportional to the stress at each pixel \({b}_{V}(p)\) is obtained as \({u}_{1}(p)\), which is an element of the \(p\) th row of vector \({{\varvec{u}}}_{1}\).

$${b}_{V}\left(p\right) ={u}_{1}\left(p\right).$$
(25)

Simultaneously, the fluctuation from the time average of the load signal \(f(t)\), which is the input of equation (7), is recovered using equation (24) of the proposed method. The recovered fluctuation \({f}_{V}^{*}(t)\) is given by:

$${f}_{V}^{*}\left(t\right) ={v}_{1}\left(t\right).$$
(27)

Using SVD, the observation matrix \({\boldsymbol{\Psi }}^{\boldsymbol{*}}\) is decomposed to obtain \({b}_{V}(p)\), which represents the stress distribution map, and \({f}_{V}^{*}\left(t\right)\), which is proportional to the fluctuation of the average load signal. SVD thermo-component analysis provides stress distribution while extracting and recovering the load signal using the temporal information of the thermal image.

For the thermal images with \(P\) pixels and \(F\) measured thermal image frames, equation (5) should be calculated for \(P \times F\) elements. The number of unknown parameters, \({\left\{a(p)\right\}}_{p = 1 - P}, {\left\{b(p)\right\}}_{p = 1 - P}\), and \({\left\{f(t)\right\}}_{t = 1 - F}\), is \(2P + F\). Therefore, if \(F > 2P / (P - 1)\), the corresponding simultaneous equations should be solved, and the proposed method should be stably executed using SVD.

Experiments

The load signal was reconstructed and the stress distribution corresponding to the signal was calculated using SVD thermo-component analysis. To examine the validity of results using SVD thermo-component analysis, as a basic examination, an experiment was conducted wherein a sinusoidal load signal was given to the specimen using a fatigue testing machine. It was also easy to compare the load signal reconstructed using SVD and the input load signal in the graph. The experimental setup and analysis procedure are shown in Fig. 1. A sinusoidal cyclical load was applied to a specimen, and the thermal images of the specimen surface were captured using infrared thermography equipment driven by an external synchronization signal. The control device of the fatigue testing machine supplied a load signal to the load cell and the synchronization signal generator, which related the data of the load signal and the synchronization signal for recording in a computer. The observation matrix of equation (21) was generated from the captured thermal image. Thereafter, the observation matrix was decomposed into a reconstructed load signal and relative stress amplitude distribution using SVD. The stress amplitude of the reference point of the relative stress distribution was obtained by calculating the amplitude of the reconstructed signal from the measured temperature change at the reference point using the least squares method. The relative stress amplitude distribution map was converted into an absolute-value map of stress using the stress amplitude at the reference point. In this study, reduction of computer calculation load of observation matrix ganaration process is introduced. Details of this process is described in Appendix.

Fig. 1
figure 1

Experimental setup and analysis procedure

Full size image

The aluminum alloy (A5052) specimen used in the experiments is shown in Fig. 2. A hole with a diameter of 11 mm was made in the center of the specimen to generate stress concentration. The surface of the specimen was patinted with black heat resistant paint. An area of approximately 30 mm × 30 mm around the hole (red rectangle in Fig. 2) was captured using infrared thermography equipment. The number of pixels of the thermography equipment was 320 × 256 pixels, and one pixel size was approximately 0.094 mm.

Fig. 2
figure 2

Specimen and field of view (red rectangle) for thermography

Full size image

The loading frequency was 5 Hz, stress ratio was − 1, Nominal stress amplitude at the minimum cross section of the specimen without considering stress concentration due to the circular hole was 50 MPa, and frame rate of infrared thermography equipment was 100 fps. The frame rate of the infrared thermography equipment is set high enough to reconstruct the waveform of loading signal with respect to the loading frequency. Tables 1 and 2 list the mechanical and thermal properties of the specimen material and the specifications for infrared thermography equipment, respectively. Two-hundred frames of the thermal image were used for SVD thermal-component analysis. For comparison with the result of SVD thermo-component analysis, stress distribution maps were obtained using conventional lock-in thermography, random lock-in thermography, self-correlation lock-in thermography from the same 200 thermal images.

Table 1 Specimen specifications for the experiment
Full size table
Table 2 Specifications of infrared thermography equipment (FLIR SC7500)
Full size table

Results

Stress Amplitude Distribution

The stress amplitude distribution maps obtained using each method are shown in Fig. 3. The positions \({{\varvec{p}}}_{1}\) and \({{\varvec{p}}}_{2}\) on Fig. 3(a) are used as the reference-signal acquisition position in self-correlation lock-in thermography.

Fig. 3
figure 3

Stress amplitude distribution map. (a) Results of the proposed method showing coefficient \({b}_{V}\left(p\right)\). (b) Results of random lock-in thermography showing coefficient \({b}_{L}\left(p\right)\). (c) Result of self-reference lock-in thermography using \(\psi ({p}_{1},t)\) as reference. (d) Results of self-reference lock-in thermography using \(\psi ({p}_{2},t)\) as reference

Full size image

It can be observed that the map \({b}_{V}(p)\) obtained via SVD thermo-component analysis (Fig. 3(a)) is quite similar to the maps \({b}_{L}(p)\) and bs(p) obtained via random lock-in thermography (Fig. 3(b)) and self-correlation lock-in thermography, respectively, using the reference signal acquired at position \({{\varvec{p}}}_{1}\) (Fig. 3(c)). Figure 3(d) shows the stress amplitude distribution \({b}_{S}(p)\) generated via self-correlation lock-in thermography using the reference signal acquired at position \({{\varvec{p}}}_{2}\). The map in Fig. 3(d) is very different from the other stress distributions.

The horizontal line profiles of the stress distribution obtained using each method are shown in Fig. 4. The position of these profiles is indicated by the horizontal line on Fig. 3(a). The line profile of the stress distribution obtained using SVD thermo-component analysis is similar to that obtained using random lock-in thermography and self-correlation thermography with the reference signal at \({p}_{1}\). However, the line profile obtained using self-correlation lock-in thermography with the reference signal at \({p}_{2}\) is significantly wavy and considerably deviates from that obtained using other method.

Fig. 4
figure 4

Horizontal stress profile of each method

Full size image

Reconstructed Reference Signal

The reconstructed reference signal obtained using SVD thermo-component analysis and the reference signal used in self-correlation lock-in thermography are shown in Fig. 5. In Fig. 5(a), the fluctuation in the reconstructed reference signal is compared with that in the original load signal, which is used as the reference signal in random lock-in thermography. It is observed that SVD thermo-component analysis can restore the fluctuation in the load signal with only infrared images. Figure 5(b) and (c) show the reference signal using the stress distribution of Fig. 3(c) and (d), respectively, obtained using self-correlation lock-in thermography. It is observed that the fluctuation in the reference signal at point p1 is similar to that in the original load signal, while the signal at point p2 is significantly different from the original load signal. It is also observed that the accuracy of stress distribution obtained using self-correlation lock-in thermography is affected by the quality of the reference signal.

Fig. 5
figure 5

(a) Fluctuation in the load signal \({f}^{*}\left(t\right)\) and reconstructed fluctuation in the load signal \({f}_{V}^{*}\left(t\right)\) using the proposed method. (b) Fluctuation in the load signal \({f}^{*}\left(t\right)\) and reference signal \(\psi ({p}_{1},t)\). (c) Fluctuation in the load signal \({f}^{*}\left(t\right)\) and reference signal \(\psi ({p}_{2},t)\)

Full size image

Comparison Between Evaluated Methods

To objectively evaluate the stress distribution calculated using each method, the average error of each pixel d with respect to the reference image was calculated as follows:

$$d = \frac{\sqrt{\sum_{p = 1}^{P}{\left({b}_{1}\left(p\right) - {b}_{2}\left(p\right)\right)}^{2}}}{P},$$
(27)

where \({b}_{1}\left(p\right)\) and b2(p) indicate the stress amplitude distribution. The value d represents the average of the differences between the two maps for each pixel; a lesser value of d indicates that the two maps are close. The stress distribution obtained using random lock-in thermography is used as the reference image. dL-V between \({b}_{L}\left(p\right)\) (shown in Fig. 3(b)) and \({b}_{V}\left(p\right)\)(shown in Fig. 3(a)) and dL-S1 between bL(p) and bS(p) (shown in Fig. 3(c)) were calculated. dL-S1 was 0.033 and dL-V was 0.011. This indicates that SVD thermo-component analysis reconstructed the stress distribution map equivalent to the self-correlation lock-in thermography using a good reference signal.

Self-correlation lock-in thermography and the proposed method use the reference and reconstrution load signals as the input to determine stress distribution, respectively. Therefore, the degree of similarity among the reference signal used in self-correlation lock-in thermography, reconstructed signal used in SVD thermo-component analysis, and original load signal was evaluated. The similarity between the one-dimensional signals \({f}_{1}(t)\) and \({f}_{2}(t)\) can be evaluated by calculating the zero-mean normalized cross-correlation (ZNCC) as follows:

$$ZNCC = \frac{\sum_{t = 1}^{F}\left({f}_{1}\left(t\right) - \overline{{f }_{1}\left(t\right){|}_{t}}\right)\left({f}_{2}\left(t\right) - \overline{{f }_{2}(t){|}_{t}}\right)}{\sqrt{\sum_{t = 1}^{F}{\left({f}_{1}\left(t\right) - \overline{{f }_{1}\left(t\right){|}_{t}}\right)}^{2}\sum_{t = 1}^{F}{\left({f}_{2}\left(t\right) - \overline{{f }_{2}(t){|}_{t}}\right)}^{2}}}, \overline{{f }_{n}(t){|}_{t}}= \frac{\sum_{t = 1}^{F}{f}_{n}(t)}{F}.$$
(28)

Signal similatiry can be evaluated as a number from -1 to 1 by Normalized Cross-Correlation (NCC). However, when the DC component fluctuates, the value of the normalized cross-correlation also fluctuates. ZNCC can stably evaluate the similarity by subtracting the average value of the observation signal value. The ZNCC between the reference signal \(f\left({p}_{1},t\right)\) of self-correlation lock-in thermography, shown as the green line in Fig. 5(b), and the original load signal \(f(t)\), shown as the blue line in Fig. 5, was 0.966, and that between the load signal \(f(t)\) and the reconstructed signal \({f}_{V}^{*}(t)\) using SVD thermo-component analysis, as shown in Fig. 5(a), was 0.993. Therefore, the it can be seen that the signal reconstructed using proposed method resembles the original load signal as much as better than the reference signal used in the self-correlation lock-in thermography. Table 3 shows d (the average of the error for each pixel), the ZNCC between the input load signal and the reconstructed load signal obtained using SVD, and the ZNCC between the input load signal and the reference signal obtained using self-correlation lock-in thermography.

Table 3 Average of the error for each pixel, d, of stress amplitude distribution and the ZNCC value of load and reference signals
Full size table

Table 3 shows that the quality of the reference signal and the reconstructed signal affects the accuracy of the stress distrebution map. The value of d and ZNCC of the self-correlation lock-in thermography using the good quality reference signal \(\psi ({p}_{1},t)\) is equivalent to those of the proposed method, whereas the value of the self-correlation lock-in thermography using the poor quqlity reference signal \(\psi ({p}_{2},t)\) shows the low score. This indicates that the proposed method reconstructs the load signal using only the principal components, so the noise component is removed, and the stress distribution with high accuracy corresponding to the reconstructed load signal can be obtained.

The singular values obtained using SVD on the observation matrix from the captured thermal images is shown in Fig. 6. The singular value \({\sigma }_{1}\), which indicates the principal component in the dynamic thermal images, is sufficiently larger than \({\sigma }_{2}\). The reconstructed signal v2T corresponding to the singular value σ2 is a signal based on other factor unrelated to the load signal. The larger σ1 compared to other singular components implies that the process of SVD gives a good reconstructed signal u1, which is close to the original load, and then provides a stable stress distribution bV (p). Therefore, the SVD process results in noise reduction, and the ratio of the singular values σ1 and σ2 is also effective in confirming the accuracy of TSA.

Fig. 6
figure 6

Singular value distribution in SVD

Full size image

SVD thermo-component analysis does not require prior knowledge of the evaluated mechanical structure to select a suitable reference-signal acquisition position as in self-correlation lock-in thermography.

Conclusion

A new method for TSA using SVD, called SVD thermal-component analysis, was developed. Self-correlation lock-in thermography, which is developed for remote measurements under random loading, uses the temperature change at a specific position as the reference signal. The proposed method restores the signal related to the load signal and generates a stress amplitude distribution related to the reconstructed signal using SVD, which is applied to all thermal images over time. This new method does not need the reference signal.

In this study, a sinusoidal periodic load was applied to the specimen with a circular hole in the center in the laboratory. The load signal was reconstructed and stress amplitude distribution was calculated using SVD thermo-component analysis. The consistency between the reconstructed and original load signals and the accuracy of the obtained stress distribution were compared with those obtained using conventional lock-in methods, such as random lock-in thermography and self-correlation lock-in thermography, and simulated analysis was conducted.

Authors will report the applicability of the proposed method to infrared measurement results for objects under non-sinusoidal loading or random loading, the analysis of mechanical stress and deformation using second and third thermal components in infrared video.