Introduction

Dielectric Elastomers (DEs) represent a type of smart material consisting of a thin elastic film (e.g., acrylic, silicone) surrounded by compliant electrodes [1]. Due to their nature as flexible capacitors, DEs are able to transduce mechanical energy into electrical in both ways. In this way, they can effectively work as sensors as well as actuators. Actuation and sensing effects can be eventually combined and used simultaneously, resulting in the self-sensing operation mode. Self-sensing is attractive, since it allows to monitor the deformation state of a DE transducer while it is being actuated, thus leading to an extremally compact and sensorless device [2].

Due to features such as large deformations, high compliance, high energy density and efficiency, and low cost, DE actuators (DEAs) have found a variety of applications, e.g., as valves [3], pumps [4], loudspeakers [5], and soft robots [6]. The possible fields of use of DEAs range from industry to medicine, and demonstrate the versatility of this technology. It is remarked that most of the current applications make use of DE transducers as stand-alone actuator/sensor elements, embedding them in simple system layouts [3, 7,8,9,10]. Even in the few cases in which multiple active DE elements are used, such as in [6] the individual actuators are completely decoupled from each other, and therefore they can be designed and controlled as if they are independent.

Cooperative systems offer an attractive alternative to stand-alone devices. In the context of actuation, cooperation can be understood in two different ways. On the one hand, a cooperative system may consist of several actuators that physically work together to achieve a common, possibly complex task. Several examples of such systems can be found in the literature. In [11] and [12] multiple identical MEMS actuators are used in a cooperative manner to convey objects via controllable air flows. A camera system is used to determine the position of the object, which is then fed back to a control-loop that adjusts the air flow direction. In [13] an actuator array for tactile displays is presented, based on an electromagnetic actuation principle. The individual actuator elements cooperate on a physical level to reproduce several different shapes. In [14], an inchworm-inspired system based on cooperative actuation cells in proposed. The cells are activated by electrostatic forces, and are supposed to cooperate by using suitable control patterns to move a sliding shaft. On the other hand, cooperation may be implemented through control algorithms. In this case, a complex system-level task is achieved by using local information shared among neighboring actuators, usually in a decentralized fashion [15]. These types of architectures exhibit advantages over centralized controlled systems, e.g., in terms of simplified control hardware, lower real-time computational burden, as well as higher robustness to disturbances and failures [16].

Compared to existing cooperative systems based on alternative technologies, DE transducers are intrinsically capable of features such as large strokes, high energy efficiency, and flexibility, which open up a number of applications in the fields of wearables and soft robotics. Few examples of cooperative DEAs have already been presented in the literature, and are discussed in the sequel. In [17] and [18], a buckling DEA membrane is designed and investigated. Depending on the number of activated DEA elements, the buckling height and its lateral expansion can be controlled, and represent the physical level of cooperation. By considering 7 neighboring DEA elements, each one having a width and distance to its neighbor of 250 µm a maximum deflection of more than 250 µm is achieved at the maximum voltage value. In [19] another example of cooperative DEA is presented for a tactile display application. Here, stack DEAs are used in an array configuration to produce deformations in a surface. Thickness changes of more than 10 µm per layer are achieved. Also, in this case, the individual elements cooperate on a physical level, which allows for a complex surface deformation. A different approach for DEA-based smart surfaces is presented in [20]. A layered membrane consisting of horizontal and vertical heater elements, sandwiched between 2 DEA membranes and 2 shape memory polymer layers, is used to locally deform the stacked membrane, which has an active area of 28 mm × 28 mm and 6 different bending axes. Although no individual DEA elements are used, the combination of local heating and stiffness changing due to activation of the DEA membranes allows for complex surface deformations, by combining different smart material systems. A further array concept is presented in [21], which is based on hydraulically amplified DEA cells. This approach was successfully applied to large 8-by-8 DEA array with individual element sizes of less than 10 mm × 10 mm, which can be used for haptic feedback devices or wearables.

It can be noted how, in most of the cooperative DE-actuator/sensor concepts discussed above, the individual elements are always decoupled from each other both mechanically and electrically, as also shown in [22]. Even though this lack of direct coupling still allows for software-based cooperation, no mutual interference between the elements is present. If this on the one hand simplifies the system control, it introduces on the other hand stiff components which affect the system flexibility and weight. Conversely, if one arranges many DEA onto a common soft substrate without mechanically isolating them, electro-mechanical interactions can be introduced on purpose [23]. In this way, the activation of one actuator element influences its neighboring element actuation and sensing capabilities. If properly exploited, those effects could allow to embed cooperation features within the physical system itself, in a way which is not possible with conventional decoupled designs. The lack of rigid decoupling components also results in a fully polymeric and stretchable design, which opens up new potential applications in the area of soft mechatronics [18, 19], e.g., compliant and energy efficient conveyor systems, haptic wearable wristbands, smart skins with automatic contact detection and embedded actuation functionalities. To effectively exploit the potential and compliance of such cooperative DEA systems in novel applications, innovative design concepts and control algorithms which take advantage of the intrinsic coupling effects need to be developed first. Clearly, the first step towards this goal consists of understanding the complex electro-mechanical coupling existing in fully polymeric DE arrays. Up to date, however, systematic studies aimed at characterizing, designing, modeling, and controlling soft DE arrays have not been conducted in the literature, to the best of our knowledge.

In this work, we present a novel design solution for soft cooperative DEA systems, consisting of a 1-by-3 array of DE elements located onto a common silicone membrane. Each DE can be activated independently of its neighbors, thus allowing to implement complex actuation patterns as well as distributed sensing paradigms. While this design presents a number of advantages, mostly in terms of flexibility, stretchability, lightweight, and simplicity of assembly, it is also affected by strong spatial coupling effects, coming from the electro-mechanical interaction among nearby DE elements. More specifically, displacing one DE in the array unavoidably affects the distribution of stress and electric field within the soft membrane, resulting in a change of force, stroke, and capacitance of its neighboring elements, i.e., a modification of their actuation/sensing characteristics. Those interactions may lead to either beneficial (introduction of coupled actuation/sensing features at hardware level) or detrimental (loss of actuation/sensing functionalities) effects, depending on whether or not they are explicitly accounted for during the system design. To properly understand spatial interactions among DE elements in the 1-by-3 array, a new experimental setup is developed. The test rig allows to measure the force and capacitance characteristics of different DEs in the array, while its neighboring elements are subject to arbitrary electro-mechanical loads defined by the user. By testing different types of electro-mechanical loads and combinations of active neighbors, the sensitivity of the distributed actuation/sensing performance can be systematically understood. In particular, the conducted investigation shows how the electro-mechanical coupling effects have a strong influence on the reaction force and capacitance of nearby DEs, resulting in relative changes up to 9% compared to the reference configuration. We also point out that this paper is an extension of [24], where we presented a preliminary investigation of the passive mechanical coupling in the 1-by-3 array. In the present paper, we expand our previous study by also analyzing the influence of spatial coupling on the array actuation performance and self-sensing capabilities, and by providing a more extensive description of the system design as well as the experimental setup.

The remainder of the paper is structured as followed. In the section Theory, we briefly describe the working principle of DEAs, present a design concept for a compliant DEA array based on a single silicone membrane and clarify the challenges related to the design of such systems. We then propose an experimental investigation to examine the coupling effects within the array in the section Experiments. The results of the experimental characterization, regarding their relevance to the design of a functional array actuator, are presented in Results and Discussion. Finally, the main outcomes of the work are summarized in the section Conclusions.

Theory

Dielectric Elastomer Actuator Principle

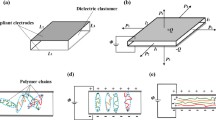
A DE consists of a polymeric membrane coated with a compliant electrode material on both sides. Acrylic-or silicone-based polymers with thicknesses within 10–100 μm are usually adopted as elastomer materials [25], since they are highly flexible and can be strained up to 380% [26]. The compliant electrodes, instead, are typically made of 5–10 μm thick layers of carbon, carbon-grease, or carbon-silicone mixtures [27, 28]. Nano-scaled thin metal films, exhibiting high conductivity and compliance up to strains of 200%, have recently been proposed as alternative electrode material for miniaturized DE applications [29, 30].

On a physical level, a DE is equivalent to a thin capacitor with flexible plates. The capacitance of a DE can be expressed based on the parallel plate capacitor formula, as follows:

$$C= {\varepsilon }_{0}{\varepsilon }_{r}\frac{A}{t},$$
(1)

where A and t are the electrode area and the membrane thickness, respectively. When a DE membrane is stretched, A increases while t is reduced, thus (equation (1)) implies that the electrical capacitance increases as well. This effect represents the basic mechanism which allows using DEs as sensors [31]. The actuation principle of DEs, on the other hand, is based on a mechanical deformation induced by an electrostatic pressure, denoted as Maxwell stress [32]. When opposing charges are stored on the flexible DE electrodes, as a result of an external voltage, the resulting electrostatic forces causes them to attract each other. This result in a compression of the intermediate polymer layer and, in turn, an expansion of the electrode area. Such effect can be used to design DEA systems, capable of providing a stroke/force output in several possible ways. A first actuation mode relies on directly using the thickness reduction of the DE layer, as in [33]. This generally results in relatively large forces, but small displacements. As a second solution, one can couple a DE membrane with a mechanical biasing system, which converts an applied voltage into an area expansion. In this context, different types of biasing systems have been adopted in conjunction with DEs, e.g., pressured air [34], hydrostatic pressure [35], compliant frames [8, 36], permanent magnets [37], or metal springs [38, 39]. The biasing systems strongly affects the type of actuation output (in-plane or out-of-plane), as well as the amount of stroke/force. A particularly attractive type of biasing systems is represented by springs which exhibit an unstable behavior in their force–displacement characteristic. Since this instability manifests itself through a negative slope in the force–displacement curve (i.e., stiffness coefficient), such systems are usually referred to as negative-rate biasing springs (NBS). It has been shown that these types of springs drastically increase the stroke performance of a DEA, compared to usual positive-rate (Hookean) springs [40].

To understand the relationship between the biasing system and the overall DEA stroke performance, a graphical analysis is presented in the following, similarly to [40]. The analysis is based on force equilibrium considerations, and allows determining the theoretically expected stroke based on the characteristics of both DE membrane and biasing element. In case the DEA needs to work against a given external load, the graphical method can be eventually adapted to account for both biasing and external forces, see [41] for details. In Fig. 1(a), a schematic representation of the graphical design method is shown. The intersection between the force–displacement curves of NBS (solid yellow curve) and DE represent the equilibrium points of the system, corresponding to the transducer being subject to low voltage (LV, solid blue curve) or high voltage (HV, solid red curve), respectively. The horizontal distance between these intersection points corresponds to the expected actuator stroke under load-free operations. In this particular case, the shape of the NBS is based on the polymeric dome buckling previously presented in [42], which was proven to represent an effective biasing solution for fully polymeric stand-alone DEAs. To achieve a large stroke, the biasing system curve must be designed in such a way to fit within the gap between DE LV and HV curves. From Fig. 1(a), it is clear that only biasing systems which present a region of positive slope, such as the considered dome-based NBS, can result in a sufficiently large gap between the two equilibrium points (when the NBS force is plotted with respect to the NBS displacement coordinate, rather than the DE one, the positive slope is reverted and corresponds indeed to a negative stiffness). Once the DE and NBS curves are given, the graphical criterion described above can be used to determine the optimal horizontal offset dps that maximizes the resulting stroke. Note that dps physically corresponds to the distance between NBS and DE, measured relatively to the configuration in which contact between both elements is initiated, see the top part of Fig. 1(b). When dps is chosen in a poor way, the stroke of the DEA decreases drastically. One example as indicated by the dashed yellow curve in Fig. 1(a), for which the intersections are located close to each other and thus result in a small stroke. Knowing the characterization DE curves in the LV and HV states is critical for the design high-performance DEAs based on the graphical design methods, especially in conjunction with NBS-type biasing mechanisms.

Fig. 1
figure 1

a Schematic of the graphical design solution b Sketch of a single DEA with a dome based biasing system, before (top) and after (bottom) assembly

Full size image

Single Membrane DEA-Array Concept

In Fig. 2(b), the novel 1-by-3 DE array concept is presented, based on the design initially introduced in [43]. It consists of a single, continuous silicone membrane (depicted in blue) with three circular electrodes screen-printed on it (depicted in grey). In the considered system, each individual DE is mechanically biased with the dome-based NBS elements from [40]. Since this biasing solution is completely based on polymeric materials, it allows the overall actuator array to retain a system-level flexibility, while ensuring at the same time large stroke performance. Differently from other cooperative DEA arrays, our fully polymeric solution allows to retain electro-mechanical coupling between nearby elements, since the silicone membrane is mechanically connected to the underlying biasing array solely at the edges by using a double-sided tape (Nitto P-905), as indicated in Fig. 2(b).

Fig. 2
figure 2

a Schematic of the graphical design soltion for the DE-array. Solid lines schematically represent the characteristics of the DE in the default configuration, whereas dotted lines represent the configuration of the biased membrane b Sketch of the DEA array concept based on a single, continuous DE membrane and dome-based biasing before and after assembly c 3D pictures of the DE-array in the default and biased configuration

Full size image

Within this concept, we expect two kinds of coupling mechanisms existing among DE elements in the array, i.e., electrical and mechanical ones. The electrical coupling arises when the Maxwell pressure acting on a DE, resulting from the application of an external electric field, induces a stress distribution which affects the mechanical response of the neighboring elements. This effect has already been studied experimentally in [43], and also validated with a model-based approach in [44]. In these works, it was shown that the electrical activation of one DE has generally a small influence on the reaction force of its neighbors. Even when reducing the distance among DEs to the minimum possible one to avoid electric arcs, which is dictated by the dielectric strength of air (3 kV/mm), the impact of this electrical coupling is practically negligible. The mechanical coupling, instead, occurs when a biasing force/displacement is applied to one DE. This causes the whole membrane to undergo a complex deformation pattern (see Fig. 2(c)), which affects both the reaction force and capacitance of the neighboring DEs. The mechanical interaction is expected to have a larger influence compared to the electrical coupling, and yields more possibilities to implement cooperative features in the DE array.

On the one hand, this coupling allows to develop new types of cooperative DEAs, in which the motion of a single DEA within the array influences the actuation and sensing behavior of the surrounding elements. As an example, a single DE can automatically detect the motion of its neighbors by monitoring its own capacitance, and use this information as a trigger signal to perform a cooperative actuation task, e.g., propagate a wave pattern. On the other hand, the strong mechanical coupling between the DE makes the design of a functional biasing system significantly more complex. In fact, while a single DE membrane is characterized by a unique pair of HV and LV curves (as in Fig. 1(a)), in case of the actuator in Fig. 2(b) the curves of a DE change depending on the state of deformation of its neighbors.

To better understand the impact of this effect on the system actuation performance, we consider the 1-by-3 DE array in Fig. 2(c). We can characterize the behavior of DE 1 for different combinations of deflections of DEs 2 and 3, and obtain a corresponding family of force–displacement curves. Figure 2(a) qualitatively show the expected curves of DE 1 when its neighbors are undeflected (solid blue and red lines) and displaced (dotted blue and red lines), respectively, corresponding to top and bottom subfigures in Fig. 2(c). A properly designed biasing element should be able to ensure a large stroke to DE 1 independently of the deformation state of its neighbors in the array. An example of such robust design corresponds to the solid NBS curve in Fig. 2(a). In case the mechanical coupling is ignored, and the bias is optimized solely on the basis of the nominal force–displacement DE curves (dash-dotted yellow curve in Fig. 2(a)), a significant drop in performance may be observed when DEs 2 and 3 are deflected. After completing the design of the biasing element for DE 1, the same process must be repeated for the neighbor DEs, based on its corresponding family of force–displacement curves. It should be noted, however, that the process of generating a family of force–displacement curves for a given DE is based on a fundamental assumption, i.e., one must know in advance upper and lower bounds for the neighbors displacement range. As a result, the design of the bias cannot be addressed independently for each element in the array, but it must be performed at system-level by considering how the bias of one DE affects the displacement range of its neighbors. In practice, an optimal biasing system design can be obtained with an iterative design procedure. At each iteration, one estimates the family of force–displacement curve of a given DE, by using the currently available information on its neighbors displacement, and optimizes its biasing element accordingly. This information is then used to update the family of curves of the next DE, on the basis of which its new biasing element is obtained. This process is then repeated several times, until we reach a state in which every DE simultaneously performs a large stroke without the need to further optimize its biasing element. This example clearly illustrates the increased complexity when designing cooperative DEA arrays, compared to the single actuator case.

A further difference, compared to the single actuator case, is related to the sensing property of a DE. In general, measuring the capacitance of a single DE permits to uniquely reconstruct its state of deformation, thus making it possible to implement self-sensing strategies [45]. In case of a DE array, two different self-sensing mechanisms are instead expected. The first one is a capacitance change of a DE due to its own deformation, i.e., a direct self-sensing mechanism. At the same time, a second indirect self-sensing effect can also be observed, occurring when the capacitance of one element in the array is measured while its neighbors are being displaced. In this case, it can be easily understood that the same capacitance value may correspond to a different DE deflection, depending on how much its neighbors are deformed. Therefore, a successful estimation of the array deformation state can only be performed at system-level, by considering the capacitance variations of multiple DE elements at the same time, and interpreting them by means of a suitable model.

To effectively design a robust biasing system for the 1-by-3 DEA array, as well as to practically implement array-level capacitive self-sensing concepts, we need to develop systematic characterization procedure of the existing coupling effects. Specifically, we must be able to apply arbitrary electro-mechanical loads to selected DEs, and measure their impact on the force and capacitance responses of other elements in the array. This experimental setting allows to recreate the configuration of a DEA array in a realistic application, in which every DE element is deflected out-of-plane due to the coupling with the biasing system, as shown in Fig. 2(b) by dbiased. The data obtained with this procedure can be eventually used to calibrate and validate numerical models which, in turn, will enable optimization algorithms for the array biasing system design as well as cooperative self-sensing schemes.

Experiments

Test-Rig Concept

To investigate the coupling among multiple DE elements in the given array, a novel experimental test-rig is developed. The setup allows to perform the following types of experiments:

  • Apply a static pre-deflection to one or more DE elements in the array, and measure at the same time the force of a single DE while it is being dynamically displaced and subject to either LV or HV;

  • Apply a static pre-deflection to one or more DE elements in the array, and measure at the same time the capacitance of a single DE while it is being dynamically displaced and subject to LV;

  • Apply a static pre-deflection to one or more DE elements in the array, and measure the capacitance of one of the statically pre-deflected DEs while a different element in the array is being dynamically displaced and subject to LV.

The basic setup concept is depicted in the sketch in Fig. 3(a). Here, two DEs are statically pre-deflected out-of-plane with respect to the flat default configuration (dotted black line) by an amount dpd. The plane of the flat membrane represents then the zero-reference value for all the applied pre-deflections. Figure 3(b) shows a sketch of how this concept is implemented. During the experiments, the DE array itself is clamped to a 3D-printed rigid frame (Formlabs Clear). Although the final DEA array is supposed to be completely flexible, a rigid frame is necessary to establish a default reference configuration for the systematic characterization. The device that allows to apply the static pre-deflection can then be mounted in front of the DE membrane, clamped by the rigid frame. It consists of a frame, which is used for installation in front of the DE array, and three brackets connected to a removable indenter. Each indenter is connected to a threaded rod, that has a rotary knob on the other end. By rotating the knob, the indenter can be moved relatively to the bracket. In this way, it allows to apply an arbitrary static pre-deflection to the corresponding DE element. A scale located on the knob and bracket allows to achieve an accurate adjustment of the amount of DE pre-deflection.

Fig. 3
figure 3

a Sketch of the basic measuring concept. Two DE elements are statically deflected by a pre-loading of dpl, while the remaining DE is characterized b Sketch of the implementation of the test-rig from both side-view and top-view c Picture of the actual test-rig

Full size image

The device allows to mount an indenter module (consisting of an indenter, a rod, and a knob, shown in the dashed box in Fig. 3(b)) in front of each one of the three DE elements. To measure the force–displacement characteristics of the non-statically pre-deflected DE, its corresponding slot needs to be left free. In this way, another indenter connected to both a linear motor (Aerotech Inc., ANT25-LA) and a load cell (ME-Meßsysteme GmbH, KD40s) can be positioned. While former allows to prescribe a dynamic displacement to the center part of the DE, which can be specified via a LabVIEW controlled user interface, the latter permits to measure the corresponding elastomer reaction force. In this way, each DE can be characterized under different configurations, corresponding of various combinations of static pre-deflections applied to the other two DEs. The same type of experiment can be then repeated by applying different constant voltage values to the dynamically displaced DE. The capacitance measurement is done via an LCR-meter (Rohde & Schwarz GmbH & Co. KG, HM8118), and can either be performed on the dynamically displaced DE, or on a statically pre-deflected one while a neighboring DE is dynamically deformed. A picture of the actual setup is finally shown in Fig. 3(c).

DE-Array

The first design of the device, namely the 1-by-3 DE array, was initially presented in [43]. In the current work, no changes have been made to the array geometry and assembly originally presented in [43]. For reasons of completeness a picture and a sketch of the array is shown in Fig. 4, where all the relevant measures are reported. The used silicone is a 50 µm thick membrane (ELASTOSIL® RT2030/50) from Wacker Chemie AG. The silicone film is biaxially pre-stretched by 10%, before a mixture of carbon black and silicone oil is used for screen-printing the electrodes, and then encapsulated in the rigid frame.

Fig. 4
figure 4

a Sketch of the characterized DE array b Picture of the designed DE array

Full size image

Measurement Concept and Realization

As previously explained, the present study aims at understanding how the deflection of different array elements affects the characterization curves of a given DE. By means of the presented test setup, it is possible to recreate several combinations of pre-deflected/characterized DE elements. Due to the symmetry of the 1-by-3 DE array, only 2 of the 3 elements are explicitly characterized, namely the one in the center and one on the side. In the following, the characterization procedure is described, and also schematically shown in Fig. 5. First, the testing configuration is determined by mounting the indenter modules in front of the DEs that will be statically pre-deflected. In the default position, the indenters are placed in contact with the DE membrane without deflecting it. The combination of DE array and pre-deflection device is then installed in the overall test-rig, where the linear motor and the load cell are located. Then, the array is connected to a motorized XY-stage, that can also be controlled via a LabVIEW user interface. This stage allows to precisely move the complete array, to centrally align the indenter which is attached to the load cell in front of the DE which will be characterized, as shown in Fig. 3(c). The reference position, i.e., d = 0 mm, is determined once for each set of measurements, right after the array is mounted in the test-rig. By moving the indenter on the linear motor close to the membrane (~ 1 mm) and applying a small displacement of 2–3 mm, the resulting contact point is evaluated, and used as the starting position for the following characterization. This starting point corresponds to the plane of the DE membrane, as shown in Fig. 3(b), and is used as the refence position (i.e., d = 0 mm) for the following set of measurements.

Fig. 5
figure 5

Schematic of the measurement concept. After installing the indenter-brackets and aligning the DE array with the load cell indenter, the characterization with different pre-deflection values dpd can be conducted

Full size image

The investigated configurations are illustrated by means of the 3D images in Fig. 6. Each configuration is denoted with a sequence of three digits, which can be equal to 1 or 0 depending on the fact that the corresponding DE is or is not statically pre-deflected, respectively, and a subscript which denotes the DE which is dynamically displaced for characterization. The configurations denoted as 0111, 0101, and 0011 are used to measure the outer left DE, while 1012 and 0012 are set for measuring the center DE, as also indicated by the red colored electrode and the arrow underneath it. For comparison purpose, each DE is initially characterized in the default flat configuration (pre-deflection of 0 mm), corresponding to 0001 and 0002, respectively. Then, measurements in various configurations are performed by increasing the pre-deflection dpd in steps of 1 mm, until a maximum value of 9 mm is reached. To displace the characterized DE, a sinusoidal waveform ranging from 0 to 15 mm at a frequency of 0.1 Hz is applied. The indenters used for the dynamic and static deflection have a radius of 2.5 mm. The displacement test is performed twice, by considering two voltage values of 0 V (LV) and 2750 V (HV) applied to the characterized DE, respectively. The HV value is derived based on a rough estimation, which aims at inducing a maximum electric field of around 80 V/µm when the membrane is at its maximum displacement, see Appendix 1 for details.

Fig. 6
figure 6

3D sketches of the different investigated pre-deflection configurations. The red color and the arrow indicate which DE is characterized in the corresponding configuration

Full size image

To conclude this section, we point out an important difference between the current study and a future cooperative DEA system. In a real actuator array, the biasing elements correspond to a displacement-dependent force boundary condition, while in this study the statically applied pre-deflection is a constant displacement boundary condition. Clearly, a spring- or dome-biased DE element will behave differently than an element which is statically displaced. On the one hand, in the actuator force–displacement diagram, as the one in Fig. 1(a), a constant displacement corresponds to a vertical line at a certain position value. Therefore, when the neighboring element is characterized, the static displacement prevents further out-of-plane movement of the pre-deflected elements. The reaction force of the pre-deflected DEs is expected to change upon activation of the neighbors. On the other hand, in a real actuator array comprising a mechanical biasing system (e.g., made of spring-like elements), this change in force of the neighbors will simultaneously cause their out-of-plane displacement. The softer the biasing elements, the larger the expected change in displacement of the elements nearby the actuated DE. Based on those considerations, we expect that the conducted investigation accurately reflects the behavior of a subset of cooperative actuator systems. Even though this might not necessarily reflect a concrete application or device, our investigation still provides quantitative insights on the coupling effects in such kind of systems by means of a systematic experimental campaign. Being able to simulate force boundary conditions to the neighbors, or even more complex types of loading patterns, would certainly allow to reproduce cooperative effects in DE systems in a more realistic way. Nevertheless, an in-depth systematic investigation of those cases is significantly more challenging to implement in a hardware setup, and thus is omitted from the present investigation since it reaches far beyond our intended scope.

Results and Discussion

In the following, the analysis of the results will be split into 3 main subsections, which investigate the influence of the coupling on the force in general, the influence of the coupling on the gap between the LV and HV curve, and the influence of the coupling on the capacitive behavior. The results are discussed in the context of the actuator and sensor application of the given DE array design. Note that the following experimental results are only conducted with the previously described DE array, characterized by a biaxial pre-stretch of 10% and a fixed electrode spacing. In earlier simulation studies [46], we have studied the effect of membrane pre-stretches and element spacings on the coupling within the array. The simulations revealed that the mechanical coupling is reduced with increasing pre-stretch and increasing element spacing. While validating experimentally those parameter studies would certainly be of interest, we decided to keep the investigation in this paper concise, and focus on a single array prototype. In this way, we are able to test the dependency of the cooperation on a restricted, yet meaningful set of parameters. Increasing the number of elements, and studying the effect on the coupling and the influence on the performance of the final actuator array, will be systematically investigated in future works. Furthermore, we remark how all used indenters had a constant radius of 2.5 mm. From previous studies conducted on cone DEs, we expect the reaction force increases proportionally to the inner diameter of the indenter [47]. However, to keep our study concise, we decided to focus on other parameters related to coupling while keeping the size of the indenter constant.

Coupling Influences on the Force

Figure 7 summarizes the results of the force measurements on the DE array, in case the characterized DE is subject to a LV. For better visualization, the measured force–displacement curves are replaced by polynomial interpolations, in such a way to eliminate the small residual viscoelastic hysteresis. In Fig. 7, the resulting hysteresis-compensated, LV reaction force curves are shown for the configurations 0111 and 1012, for the default flat state as well as 8 different pre-deflected configurations. Figure 7(a) and (b) permit to compare the results of the outer DE and the center DE. A clear influence of the pre-deflection can be observed in those plots, which causes the reaction force to decrease with the pre-deflection values. This effect seems to be smaller for the outer DE, while it is more visible for the center DE where the curves are further spread apart from each other. In addition, the overall force of the center DE appears to be smaller than the outer one. This can be explained by considering the greater proximity of the outer DE to the array frame. In fact, when both DEs are displaced by the same amount with respect to the flat configuration, the membrane region between DEs and frame also undergoes a stretch. The amount of stretch (and thus stress) of this intermediate region turns out to be higher for the outer DE, compared to the center one, causing an overall higher force. In Fig. 7(c) and (d), the peak value of each force curve is plotted as a function of the corresponding pre-deflections. Here, the three additional configurations (0011, 0101, and 0012) are also shown. For the configurations 0111 and 1012, a decreasing trend is clearly visible. This effect becomes less evident when only one direct neighbor is deflected (0101 and 0012). For the 0011 configuration, where the deflected DE is at a distance of 70 mm to the characterized one, the peak force exhibits some irregularities with no clear trend. This effect can be ascribed to small variations of the contact point between the indenter and the DE due to clearance between the threaded rod and the bracket.

Fig. 7
figure 7

a Resulting hysteresis-compensated, LV reaction force curves of the outer left DE, for different values of pre-deflections b Resulting hysteresis-compensated, LV reaction forces of the center DE, for different values of pre-deflections c Maximum values of the LV reaction force curves of the outer left DE plotted against the pre-deflection value, for 3 different pre-deflection configurations d Maximum values of the LV reaction force curves of the center DE plotted against the pre-deflection value, for 2 different pre-deflection configurations

Full size image

Other than that force reduction, there is another phenomenon visible in the force–displacement curves in Fig. 7(a) and (b). With increasing pre-deflection, the 0 N region at the very beginning of the curves also becomes larger. This phenomenon occurs because, due to the pre-deflection of the neighbors, the membrane is no longer in contact with the indenter in the flat configuration, but it is rather pushed slightly away from it. This distance between indenter and deformed membrane increases with the amount of neighbors pre-deflection, and is also visible in the sketch in Fig. 3(a). If we shift horizontally all the curves, thus eliminating the 0 N region, the effective force–displacement behavior of the DE is described. The resulting shifted curves are shown in Fig. 8. With higher pre-deflection, the effective displacement is reduced accordingly, thus reflecting the fact that the contact-free distance between indenter and membrane is also increasing with the pre-deflection. The dashed lines indicate an extrapolation of the curves, and show that the DE reaction force tends to increase when the same effective displacement is considered, instead of the absolute displacement. However, since in a real actuator application the bias is attached to the external frame, the true stroke performance will be determined by the original non-shifted curves in Fig. 7. As a result, we understand that the biasing system offset dps has to be changed according to the amount of neighbor pre-deflection.

Fig. 8
figure 8

Effective displacement as a function of the reaction force of the center DE, in different pre-deflection conifugrations

Full size image

With respect to the overall actuator and biasing design, these results show that the mechanical biasing of one element influences the force characteristic of the neighboring DE by lowering the maximum force of up to 9% for the center DE and up to 5.3% for the outer DEs, given the geometry of the considered 1-by-3 array. This effect must be regarded when designing a suitable biasing element for the overall array.

Coupling Influences on the Gap

When also the HV force–displacement curves are considered, the influence of the coupling on the gap between the LV and HV curve can be investigated. The gap corresponds to the colored area between the DE LV and HV curves in Fig. 2(a). As it is clear from this plot, the larger this gap, the more freedom we have to fit a biasing system to the DE curves, and thus it is easier to achieve a larger actuation stroke. From Fig. 9(a), it can be seen that the gap of the center DE is smaller compared to the one of the outer DE. Both measurements are conducted in the membrane default (flat) configuration. In Fig. 9(b), the computed gap is plotted as a function of the displacement for the outer and center DEs. The pre-deflection was varied from 0 to 8, mm and was applied in the 0111 configuration for the outer DE and 1012 configuration for the center DE. This testing condition corresponds to the setup in a real actuator array, in which the deflected DEs are already biased by a suitable NBS. Despite that the gap of the center DE tends to be slightly lower in general, no clear influence of the pre-deflection on the gap can be observed. All the calculated curves show an overall similar behavior. With respect to the 1-by-3 array actuator design, this result shows that the achievable stroke output is not negatively affected by the coupling, compared to the stroke of a single actuator on the same membrane. With respect to the goal of achieving a high stroke, this is an important finding, as it shows that the array concept itself is not directly restricting the achievable performance. Figure 9(c) shows how an arbitrary calculated slope value k which matches the gap of a given set of DE curves behaves with increasing pre-deflection for the outer (blue line) and center DE (red line). It represents the ideal negative slope that a biasing element should exhibit to produce a large stroke. For actuation purpose, it is crucial to know if the required NBS slope is changing with increasing pre-deflection. The slope is computed by choosing two displacement values, i.e., d1 = 4 mm and d2 = 9 mm, and determining the force values Fc,i which lie in the center between the LV and HV curve, computed as Fc,i = (FHV(di) + FLV(di))/2 for i = 1, 2. The slope of the gap can then be simply determined as k = (Fc,2 – Fc,1)/(d2 – d1). If the coupling in the array affects the ideal slope, this has an impact on the design of the biasing system itself. For both center and outer DEs, the above defined slope value is shown to decrease with increasing pre-deflection. This effect is slightly higher for the center DE than for the outer one. For a correct array design, this means that neighboring actuator elements change the slope of the biasing system required to maintain a high stroke performance. Thus, the value of dbiased of one actuator element influences the NBS slope of its neighbor, or even several neighbors. Nevertheless, since this change is rather small (3.2% and 4.9% deviation compared to the reference configuration, respectively), we expect that using a fixed-slope bias will not introduce dramatic loss in performance in a real array DEA application.

Fig. 9
figure 9

a LV and HV curves of the center and outer DE element b Computed gap between LV and HV curves of the center and outer DE for different per-deflection values c Computed slope of the gap for the center and outer DE as a function of the pre-deflection, together with the corresponding linear fit

Full size image

Coupling Influences on the Capacitance

Finally, we investigate the effects of the coupling on the array capacitive behavior. As previously stated, for the given array we can distinguish between direct and indirect self-sensing effects. In Fig. 10, both effects are shown in comparison. The blue curve shows the capacitance change of the outer DE when it is dynamically deflected at the same time, while the red curve shows the capacitance of the same DE when its neighbor is dynamically deflected instead. Both curves show a distinct capacitance change, with the former being much larger than the latter, as expected. More precisely, the relative change in capacitance is around 45.4% for the direct and 3.1% for the indirect cases, with respect to the initial value. This is clearly due to the spatial coupling among the different DEs, and proves the feasibility of implementing both direct and an indirect self-sensing mechanisms in the array. Note that such effect is intrinsic to the considered array, and has no analogy for a stand-alone DEs.

Fig. 10
figure 10

Comparison of the direct and indirect self-sensing effect. The direct self-sensing effect is measured when the capacitance of the dynamically displaced DE is tracked, while the indirect effect can be observed when the capacitance of the neighbor of the dynamically deflected DE is measured

Full size image

In Fig. 11, the influence of pre-deflection on the direct self-sensing effect of one of the outer DEs is visualized. Here, the DE is deflected by 15 mm while its capacitance is being measured. The experiment is repeated by applying several static pre-deflection values to the two remaining DEs in the array (configuration 0111). A first finding is that the starting value of the capacitance is slightly increasing with the pre-deflection. Another insight is the decrease of the maximum capacitance value with increasing pre-deflection, as shown by the expanded view. The deviation of the capacitance with the maximum pre-deflection of 8 mm applied is about + 1.2% at the beginning and -0.9% in the end, with respect to the capacitance in the flat configuration. The change at the beginning is negligible, since in an application in which every DE is biased this minimum value is never reached.

Fig. 11
figure 11

Influence of the coupling on the direct self-sensing effect

Full size image

Figure 12(a) shows the indirect self-sensing effect of the center DE. In this case, we measure the capacitance of the center DE while a sinusoidal displacement is applied to one of the outer DEs. Between measurements, the pre-deflection is increased stepwise (0111 configuration). Differently from before, in this case the measured DE is the one which is statically pre-deflected. The overall increase in capacitance is caused by the stretching of the electrode area, caused by the directly applied pre-deflection (cf. equation (1)). This is a consequence of the direct self-sensing effect. The experiments also show that the indirect self-sensing effect is overlaying the direct one. Despite the overall increase in capacitance, in fact, the characteristic curves changes with increasing pre-deflection. In particular, a slight decrease of the capacitance in the initial part of the curves can readily be observed. This decrease and its extent in the x-direction are increasing with the pre-deflection. This effect can be explained as follows. The initial displacement of the neighboring DE leads to a strain reduction within the membrane, which results in the initial decrease of the capacitance. The minimum capacitance is obtained when the minimum strain configuration is reached. After this point, a further deflection causes the membrane strain to raise again. This, in turn, results in an increase in the electrode area, which is reflected by the increasing capacitance.

Fig. 12
figure 12

a Effect of the coupling on the indirect self-sensing effect b Normalized capacitance curves of the indirect self-sensing measurements

Full size image

In a future array application, where every DE is biased with a dome-based NBS and thus all DEs are deflected by dbiased, the relevant part of the capacitance curve starts at d = dbiased. If, for example, each element is deflected by 6 mm due to the biasing elements, then the relevant curve corresponds to the portion highlighted in purple in Fig. 13. Figure 12(b) shows the capacitance measurements normalized with respect to the corresponding initial values. The vertical lines are drawn at the positions 4 mm, 6 mm, and 8 mm, and mark the start of the relevant curve part, as also implied by the dotted part and as described above. It is shown that, even if the indirect self-sensing effect is decreasing with increasing pre-deflection, the relevant part of the curve starts close to the global minimum of the graph. In this way, the relative change of the capacitance with respect to the starting value is almost maximized. According to Fig. 12 the capacitance change due to the indirect effect ranges from about 2.7% for 2 mm of pre-deflection to about 1.7% for 8 mm of pre-deflection.

Fig. 13
figure 13

a Sketch of an array actuator, where each DE is biased by 6 mm due to the dome based NBS b Relevant normalized capacitance curve of the 6 mm biased DE

Full size image

Note also that the pre-deflection has a bigger influence on the overall capacitance increase for the outer DE. This happens because the membrane area between the outer DE and the array edges experiences a larger strain than the one around the center DE. As the capacitance is expected to solely depend on the current electrode geometry, a higher strain of the electrode region corresponds to a larger capacitance. The results for the outer DE are similar to those of the center one, and thus are omitted for conciseness.

In general, the results in Fig. 12 show the potential of both direct and indirect self-sensing in a future DE array, where each DE is biased with a dome-based NBS. Similarly to stand-alone DEs, the direct self-sensing can be used to estimate the deformation of a DE by reading its capacitance. At the same time, the indirect effect opens up different self-sensing paradigms which are only possible within cooperative DE systems. As an example, if a change in capacitance of one or more DEs is measured without a high voltage signal being applied to them, then it can be assumed that the effect arises from the deformation of a neighbor (e.g., due to activation of neighbors or even an externally applied force). This information can be used, for instance, to estimate the array state in a decentralized fashion. In principle, direct and indirect effects can be also combined together, since they result in relative capacitance changes differing by one order of magnitude (provided that we know which DE is controlled via high voltage). Combining both effects would lead to a more robust and redundant self-sensing capability, to be exploited in future cooperative control applications.

Conclusions

In this paper, we presented and characterized a novel array actuator concept, consisting of a 1-by-3 array of DE elements sharing a single continuous silicone membrane. Our main focus was the characterization of the electro-mechanical coupling effects among nearby elements, which are of great importance for the future development of cooperative array applications. To systematically study the mutual interactions among the DEs, a novel test rig was developed, and used to perform an experimental campaign which aims at recreating different system configurations commonly observed in an array actuator. With this approach, the effects of the coupling on the actuation and sensing behavior of each element were investigated. More specifically, the test-rig was used to apply different configurations of pre-deflections to one more DEs in the array, while measuring the influence on the reaction force, the LV-HV force gap, and the self-sensing capabilities of the array. This characterization resulted in a detailed understanding of how the permanent deflection of one or more DEs influences the reaction force of another DE, which is expressed in a decrease of the reaction force, compared to the default, undeflected configuration. This effect is stronger for center DE, and results in decrease of the maximum force of up to 9% when both neighbors are pre-deflected by 8 mm. For the outer DEs, the force decrease is up to 5.3% when both neighbors are deflected by 8 mm. Additionally, the impact of the coupling on the actuation potential was investigated. This investigation revealed that, with the proposed array concept, no performance losses must be expected due to the interaction, because both the gap between the DE LV and HV curves and the optimal biasing slope do not significantly depend on the amount of pre-deflection. From those results, we learn that a biasing system optimization algorithm should aim at finding the best offset of each NBS, while their slopes can be safely selected from the start. This represents a fundamental discovery for future studies, aimed at designing large-stroke DEA arrays. Furthermore, the influence of the spatial coupling on the capacitance changes of the DEs was also measured. Other than showing changes in capacitance of about 45% when directly displaced, each DE also exhibits measurable capacitance changes when only its neighbors are directly deformed, whose amount ranges from 1.7% to 2.7% depending on the imposed pre-deflection. Those results confirm the existence of cooperative sensing effects in DE arrays, which open up the possibility of developing cooperative self-sensing algorithms in future studies.

To sum up, the conducted investigation allowed to determine for the first time the performance of DE transducers in continuum cooperative actuator/sensor applications. In future research, the obtained results will be used to calibrate and validate physics-based models of the array, which will then be used to conduct further parameter studies (e.g., array geometry, electrode geometry, DE spacing, membrane pre-stretch, size of the indenter) with the aim of optimizing both the array design as well as the biasing system. Once this model-based optimization procedure is made available, it will be used to design and assemble a first prototype of fully-polymeric cooperative DEA system. Lifetime of the device, as well as effects of fatigue on the coupling, will also be systematically investigated.