Experimental Validation of the Attenuation Properties in the Sonic Range of Metaconcrete Containing Two Types of Resonant Inclusions

Abstract

Background

Metaconcrete is a new concept of concrete, showing marked attenuation properties under impact and blast loading, where traditional aggregates are partially replaced by resonant bi-material inclusions. In a departure from conventional mechanical metamaterials, the inclusions are dispersed randomly as cast in the material. The behavior of metaconcrete at supersonic frequencies has been investigated theoretically and numerically and confirmed experimentally.

Objective

The feasibility of metaconcrete to achieve wave attenuation at low frequencies demands further experimental validation. The present study is directed at characterizing dynamically, in the range of the low sonic frequencies, the—possibly synergistic—effect of combinations of different types of inclusions on the attenuation properties of metaconcrete.

Methods

Dynamic tests are conducted on cylindrical metaconcrete specimens cast with two types of spherical inclusions, made of a steel core and a polymeric coating. The two inclusions differ in terms of size and coating material: type 1 inclusions are 22 mm diameter with 1.35 mm PDMS coating; type 2 inclusions are 24 mm diameter with 2 mm layer natural rubber coating. Linear frequency sweeps in the low sonic range (< 10 kHz), tuned to numerically estimated inclusion eigenfrequencies, are applied to the specimens through a mechanical actuator. The transmitted waves are recorded by transducers and Fast-Fourier transformed (FFT) to bring the attenuation spectrum of the material into full display.

Results

Amplitude reductions of transmitted signals are markedly visible for any metaconcrete specimens in the range of the inclusion resonant frequencies, namely, 3,400-3,500 Hz for the PDMS coating inclusions and near 3,200 Hz for the natural rubber coating inclusions. Specimens with mixed inclusions provide a rather uniform attenuation in a limited range of frequencies, independently of the inclusion density, while specimens with a single inclusion type are effective over larger frequency ranges. With respect to conventional concrete, metaconcrete reduces up to 90% the amplitude of the transmitted signal within the attenuation bands.

Conclusions

Relative to conventional concrete, metaconcrete strongly attenuates waves over frequency bands determined by the resonant frequencies of the inclusions. The present dynamical tests conducted in the sonic range of frequencies quantify the attenuation properties of the metaconcrete cast with two types inclusions, providing location, range and intensity of the attenuation bands, which are dependent on the physical-geometric features of the inclusions.

Introduction

Metaconcrete was proposed in [1] as a new concept of concrete showing marked attenuation properties under explosive or impact loading. In metaconcrete, traditional aggregates (crushed stones and gravel) are partially replaced by spherical inclusions composed of two materials, an internal stiff core and an external compliant coating. Phononic crystals are periodic composite materials exhibiting wave filtering behavior, creating band gaps or stop bands within the frequency spectrum trough the Bragg scattering. Mechanical metamaterials, known as locally resonant phononic crystals, differ from phononic crystals because they show resonance induced band gaps several orders of magnitude lower than the one obtained in the Bragg limit. In a departure from conventional mechanical metamaterials, the engineered inclusions are dispersed randomly as cast in the matrix, instead of in a periodic arrangement. Conveniently, this design permits the use of conventional concrete casting methods in the field. It also departs from Bragg scattering as the means of opening band gaps in traditional metamaterials. Indeed, wave attenuation occurs at frequencies lower than those expected by Bragg scattering, which depends on the distance between regularly arranged inclusions [2], suggesting that the phenomenon is related to the structure of the inclusions. Thus, when inclusions are dynamically excited through waves with frequency content close to their natural frequencies, their cores oscillate around their equilibrium position causing the coating layer to deform, with the result that the inclusions trap part of the mechanical energy of the system and relax the stresses in the mortar matrix. Metaconcrete is a promising material for applications in civil engineering, because inclusions can be tailored to attenuate specific frequencies of interest. For instance, it would be worth to address its effectiveness in seismic applications considering greater inclusions regularly arranged as the periodic pile barriers proposed in [3, 4].

Numerical verification of the attenuation behavior of metaconcrete was originally limited to a three-dimensional model of a metaconcrete slab containing a periodic arrangement of equal inclusions [1]. A modal analysis using finite elements provided an estimate of the lowest eigenfrequencies of the inclusions [5]. The attenuation was evaluated in terms of an energy transmission coefficient, which showed a marked reduction for frequencies around the inclusion eigenfrequencies. A numerical assessment of the attenuation properties of metaconcrete under extreme impact conditions accounting for fracture and fragmentation of the matrix was presented in [6]. These studies suggest that the attenuation efficiency of metaconcrete depends strongly on the geometry, stiffness and weight distribution within the inclusions.

A first experimental validation of metaconcrete in the frequency range 30–90 kHz was reported in [7]. In that study, cylindrical specimens were cast according to the ASTM code using as inclusions commercial mouse balls in a fully random arrangement (cf. type 1 inclusion in the present study). Experimental measurements compared well with numerical predictions [5] and confirmed the theorized strong attenuation of dynamic signals within the resonant frequency range of the inclusions. A second experimental campaign, limited to the range of sonic frequencies (≤ 20 kHz), was conducted with the goal of assessing the effect on attenuation of a periodic ordering of type 1 inclusions with different volume fractions considering cubic specimens [8]. The ratio between the amplitudes of the output signals for metaconcrete and for a reference homogeneous specimen was used as efficiency parameter. The measurements ruled out any significant effect of periodicity and Bragg scattering, thus confirming local resonance of the inclusions as the operative mechanism.

Following the original proposal of [1], metaconcrete has been the focus of a number of recent studies. Using a split Hopkinson bar, Kettenbeil and Ravichandran tested at different impact speeds a manufactured metaconcrete phantom with spherical engineered inclusions embedded in an epoxy matrix [9]. High speed camera images of the transparent specimen during the test confirmed that the signal attenuation is caused by local oscillations of the core of the inclusions. Rubber-coated inclusions set in regular grid arrangements within thin plates were analyzed numerically by Miranda Jr. et al. [10], revealing that spherical shapes result in the lowest resonant frequencies and that coated inclusions lower the eigenfrequencies of plates in bending. The effects on attenuation bands of inclusion shape, size, and volume fraction and the sensitivity to material properties were investigated numerically by Xu et al. [11]. Enriched homogenization techniques to describe the effective behavior of metaconcrete with viscous inclusion coatings have been introduced by Tan et al. [12] as a promising approach for the analysis of large structures. Numerical and experimental tests by Barnhart et al. [13] on an elastic metamaterial containing five-layer spherical resonators demonstrated the possibility of obtaining two attenuation regions that can be combined or overlapped by suitably tuning geometric and material parameters.

In general, interfaces play an important role in wave attenuation. Attenuation properties at ultrasonic frequencies have been observed, indeed, in other innovative types of concrete, where aggregates are replaced by polymeric or rubber materials [14], or by expanded polystyrene beads [15]. Sound attenuation tests conducted in rubberized mortar showed a strong dependence on the longitudinal and shear waves attenuation of the mixture composition [16].

These advances notwithstanding, a thorough experimental understanding of metaconcrete is still lacking in several important respects. Thus, whereas the attenuation capacity of metaconcrete has been assessed both in the sonic and ultrasonic frequency ranges, a characterization of metaconcrete at the relatively low frequencies typical of civil engineering applications is still missing. In addition, there are no direct experimental observations on the effect of combining different types of inclusions. The experimental investigation reported here addresses those gaps. Tests were conducted on cylindrical metaconcrete specimens, cast with two types of randomly arranged inclusions in a mortar matrix, using a mechanical actuator in the sonic range, tuned to numerically estimated inclusion eigenfrequencies. Linear frequency sweeps were applied to the specimens and the transmitted waves were recorded by four piezoelectric acceleration sensors and Fast-Fourier transformed (FFT) to bring the attenuation spectrum of the material into full display. Relative to conventional concrete, metaconcrete strongly attenuates waves over frequency bands determined by the resonant frequencies of the inclusions.

For the applicative point of view, the most interesting comparisons involve metaconcrete and conventional concrete with coarse aggregates instead of mortar. The size of the coarse aggregate of concrete has been shown to be significant in wave propagation and attenuation [17]. Differences between mortar and concrete are observed in experiments at high frequencies (> 100 kHz), and a marked attenuation of the shear waves due to scattering in the high frequency range > 20 kHz was revealed by numerical investigations involving standard concrete [18]. In the present investigation the focus is on the low sonic frequency range, where the differences between concrete and mortar are not relevant.

The paper is organized as follows. Section “Properties of the Resonant Inclusions” presents the aggregate design and the numerical estimation of their eigenfrequencies. Section “Specimen Casting, Experimental Setup, and Test Plan ” describes the specimen casting procedure, the experimental setup and the postprocessing procedures. Section “Results and Discussion” reports the experimental results and “Summary and Concluding Remarks” summarizes the main conclusions.

Properties of the Resonant Inclusions

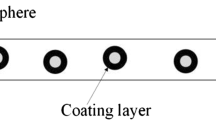
The inclusions used in the metaconcrete specimens are two types of layered spheres made of a steel core of radius r_s and of a polymeric coating of thickness t_c. The two types of inclusions differ in size and coating materials, see Fig. 1.

Fig. 1

Resonant inclusions used in the metaconcrete specimens. a Readily available commercial mouse balls. b Specifically manufactured rubber coated inclusions. Note that the type 2 inclusions present a circular interface due to the manufacturing process

The type 1 inclusions, used also in [8], are common commercial mouse balls readily available from the market. Mouse balls have the same structure of cleaning balls, used to brush off tanks and vessels, and are sold as off-the-shelf components. Fourier transform infrared spectroscopy (FTIR) analysis revealed that the mouse balls consist of a stainless steel core coated with polydimethylsiloxane (PDMS). Type 2 inclusions were manufactured ad hoc by coating AISI 52100 steel spheres with natural rubber (isoprene or 2-methyl-1,3-butadiene) by a local firm (Isopren Srl, Italy), which also provided the mechanical and chemical characterization of the components. The type 2 inclusion coating shows a manufacturing joint, at the equator where two halves of the molded rubber are sealed around the core. The type 1 inclusion steel core shows some roughness associated to the need to improve the adhesion of the coating. The geometrical and approximated mechanical properties of all the components of the inclusions are listed in Table 1. In all the following considerations, materials are considered to be isotropic.

Table 1 Geometry and material data for the two types of inclusions and for the cement matrix

The availability of the mechanical properties of the inclusions used in the experiments permits the accurate determination of the values of the principal eigenfrequencies of the inclusions more accurately than the simplified mass-spring model utilized in [1]. Following [5], a modal analysis by finite elements was conducted on a cubic cell (3 cm side) of metaconcrete with an embedded inclusion using a commercial software¹. To account for the near-incompressibility of coating, and to rule out numerical locking that can occur using the sole interpolation of the displacement field, the model was discretized using two-field hybrid 20-node brick elements with quadratic interpolation of the displacements and linear interpolation of the pressure. The material properties used for mortar were estimated from direct measurements taken during the casting of the specimens (ρ) or on the basis of the chosen mortar mix design (E and ν) [19]. Periodic boundary conditions were applied to the boundary of the cell. The element size ranged from 0.1 mm in the coating to 2.5 mm in the mortar. The total number of nodes was 149,973 and 139,385 for type 1 and type 2 inclusions, respectively. The total number of elements was 39,472 and 39,080 for type 1 and type 2 inclusions, respectively, cf. Fig. 2.

Fig. 2

Finite element models of the two inclusions embedded into a cubic cell (3 cm side) of cement matrix. Elements are hybrid 20 node bricks with quadratic interpolation for displacements and linear interpolation for pressure. a Type 1 inclusion model comprises 149,973 nodes and 39,472 elements. b Type 2 inclusion model comprises 139,385 nodes and 39,080 elements

In order to rule out numerical biases in the results, calculations were repeated using an alternative discretization into 10-node hybrid thetrahedra with quadratic interpolation for the displacements and linear interpolation for the pressure. For this second group of models, the total number of nodes was 301,161 and 314,341 for type 1 and type 2 inclusions, respectively, and the total number of elements was 127,727 and 133,417 for type 1 and type 2 inclusions, respectively.

The modal analysis gave five lowest eigenfrequencies of multiplicity three, due to geometrical symmetry, for both types of inclusion. Table 2 lists the eigenfrequencies, in the second and fourth columns the ones obtained with the brick element discretization, and in the third and fifth columns the ones obtained with the tetrahedral element discretization.

Table 2 First five eigenfrequencies (in Hz) for the unit cell of metaconcrete with different types of inclusions, obtained with two types of finite element discretizations (B bricks, T tetrahedra)

Figure 3 visualizes the eigenfrequencies using bars with different height and shade related to the inclusion type and to the element type used in the finite element discretization.

Fig. 3

Visualization of the eigenfrequencies distribution of the unit cells as obtained with modal analysis, using brick (B) or tetrahedral (T) hybrid finite elements, for the two types of inclusion. The bars have different heights to improve the visualization

A comparison between the results of the two finite-element discretizations shows that, overall, the results are roughly consistent and provides an indication of the accuracy and reliability of the calculations. The first eigenfrequency is well estimated for both inclusion types and is ostensibly independent of the finite element type. The third, fourth, and fifth eigenfrequencies, grouped within a narrow range for each inclusion type, likewise show no strong dependence on the finite element discretization. By way of contrast, the second eigenfrequency depends markedly on the discretization, especially for the type 1 inclusion, characterized by coating with lower density and lower stiffness. Despite the discrepancy in the second eigenfrequency, the two discretizations provide very similar results in terms of eigenshapes.

The color maps in Figs. 4 and 5 show the magnitude of the modal displacements for the brick discretization of type 1 inclusion and type 2 inclusion, respectively. In keeping with the results of [5], for both inclusions the first mode shape corresponds to the rigid rotational oscillation of the core inside the coating, whereas the second mode shape corresponds to the rigid translational oscillation of the core within the coating. Note that the geometrical symmetry of the geometrical model causes an inessential rigid rotation of the eigenmode about the symmetry axes. The third, fourth and fifth mode shapes describe periodic displacements of the coating with four, two, and six stationary nodes, respectively. It bears emphasis that the lowest eigenfrequency, associated with the rotational modes of the core, cannot be activated in standard experiments where waves are primarily one-directional and of low energy content [5, 20, 21]. In fact, the geometric attenuation associated to the spreading of the wavefront crossing a finite size body reduces the available energy [17]. Under a forced vibration with low energy, the stiff cores are more prone to translation than to rotation because their mass participation factors for rotational modes are lower than the ones for translational modes.

Fig. 4

Maps of the displacement magnitude for the first five eigenshapes of the type 1 inclusion modelled with brick elements (or tetrahedra)

Fig. 5

Maps of the displacement magnitude for the first five eigenshapes of the type 2 inclusion modelled with brick elements (or tetrahedra)

Specimen Casting, Experimental Setup, and Test Plan

Cylindric metaconcrete specimens were cast at the Laboratorio Prove Materiali (Material Testing Laboratory) of the Politecnico di Milano [22]. As the most appropriate choice for an isotropic material, the cylindrical shape was chosen in order to minimize the influence of the boundary conditions on signal transmission across the specimen [8]. The size (20 cm height, 10 cm diameter) complies with the Italian code for concrete [19]. By this means, the specimens could be tested for additional mechanical properties with values directly comparable to those of standard concrete. According to the design of the inclusions, the specimens were organized in four groups, Table 3. The maximum number of inclusions (36) was set by the size of the larger inclusion (type 2, 24 mm diameter) and by the need to ensure a minimum coverage preventing the direct exposure of the inclusions on the specimen surfaces.

Table 3 Metaconcrete specimen data (GR, group; SP, specimen identification code; T1, number of type 1 inclusions; T2 number of type 2 inclusions; h_p, height; w_p, weight; t_p, ultrasonic wave crossing time; v_p, ultrasonic wave speed; f_t transversal eigenfrequency and f_l longitudinal eigenfrequency, see “Specimen Experimental Modal Analysis”)

Metaconcrete specimens were cast according to the ASTM C192/C192M code [23] using cylindrical reusable steel molds, nonabsorbent and nonreactive to Portland cement, with a vertical joint to allow removal. Every specimen was cast in a separate batch. The mortar paste was a mix of water and Portland cement (Cement II-A/L 42.5R) in the ratio w/c = 0.6 (according to the mix design chosen to guarantee a minimum compressive strength of 42.5 MPa at 28 days) combined with coarse aggregates (diameter ≤ 0.6 cm). Dry Portland cement, aggregates, and the designated number of inclusions were blended in an electric cement mixer, adding water with equal timing to attain the same density and homogeneity. To facilitate removal, before casting molds were brushed with oil. Molds were set on a horizontal rigid surface and the mixture was poured in six steps, in layers of approximately equal thickness, controlling with a trowel the uniform distribution of the inclusions and the top level of the mixture. Using a tamping rod with rounded ends, each layer was compacted with a few strokes distributed uniformly over the cross section of the mold. Also the external surface of the mold was tapped with a mallet to remove the cavities created by the tamping rod. At the end, the upper surface of the specimen was leveled with a metal ruler to remove the excess of mortar, Fig. 6(a). Specimens were cast as quickly as possible to preserve a uniform density of the mixture.

Fig. 6

Metaconcrete specimens after curing and final polishing.

Specimens were located in a humidity controlled room for 24 hours at 20 ± 2 ^∘C. Removed from the mold and marked permanently with an up-arrow along the removal slot line, specimens were fully immersed in water for 7 days to avoid microcraking due to drying, and subsequently stored for three weeks in a room at controlled humidity for curing. After 28 days, the top and bottom surfaces of the specimens were accurately polished with a diamond disk, and specimens were measured accurately in height and weighted, see Fig. 6(b). The density of the homogeneous specimen was ρ_P1 = 2,368 kg/m³.

Specimen Quality Assessment

The definition of other mechanical parameters, as compressive and flexural strength, was beyond the scope of this study, thus the quality assessment of metaconcrete specimens has been limited to dynamic aspects only. Imperfections alter the speed and the amplitude of the transmitted signal. Voids or inclusions, for example, decrease the pulse velocity with respect to a homogeneous material [14,15,16,17,18]. Ultrasonic tests in direct transmission mode were conducted on all specimens to verify the degree of homogeneity and the presence of cracks or holes. Specimens were removed from the water tank at the fourth day of the week of curing and immersed again after the test in less than 2 hours. Ultrasonic test required the use of a pulse generator, one emitting transducer and one receiver transducer, and a pulse amplifier [7]. The emitting transducer was applied to one base and the receiving transducer to the opposite one. Ultrasonic tests consisted of measuring the time-of-flight t_p for waves to cross the entire length of the specimen. The average speed v_p was computed as the ratio between specimen height h_p and t_p, Table 3. Speeds measured in metaconcrete specimens were always lower than the speed measured in the homogeneous specimen P1, clearly evincing the influence of the resonant inclusions. By observing that the longitudinal wave speed of steel and of polymeric materials are in the range 5,800-5,900 m/s and 2,300-2,400 m/s, respectively, the relatively small reduction of v_p observed in the metaconcrete specimens could be attributed primarily to the presence of inclusions which alter the wave paths, excluding the occurrence of gross imperfections in the specimen manufactoring.

Specimen Experimental Modal Analysis

In order to determine the structural eigenfrequencies, the specimens have been characterized dynamically by means of impact hammer testing. Following ASTM Standard C215 [24], specimens satisfying the requirement of h_p/d_p ≥ 2 (where h_p is the height and d_p the diameter) were supported on rubber squares applied at the position of the nodes of the mode shapes. Specimens were instrumented with receiving piezoelectric acceleration sensors (PCB Piezotronics 353B15 2 g weight, operative frequency range 1-10,000 Hz with sensitivity deviation ± 5 and 0.7-18,000 Hz with sensitivity deviation ± 10, resonance frequency > 70 kHz). Specimens were struck with a metal hammer. Signals were recorded at a sampling frequency of 51,200 measurements per second.

For transversal vibration modes, the specimen in horizontal arrangement was supported on two rubber squares located at a distance 0.224 h_p from each basis, Fig. 7(a). Two sensors were glued, using a special wax provided by the producer, diametrically opposite to the supports, and the hammer strike was imparted at the center of the lateral surface. For longitudinal vibration modes, the specimen in horizontal arrangement was supported on one rubber square equidistant from both bases, Fig. 7(b). One sensor was glued at the center of one of the two bases. For verification purposes, a second sensor was glued slightly displaced from the center of the opposite basis, where the hammer strike was delivered. Signals recorded in the tests were Fast-Fourier transformed in order to identify the transversal and longitudinal modal frequencies.

Fig. 7

Experimental setup used for the characterization of the global vibration modes of the specimens, according to the ASTM Standard C215. (a) Configuration for transversal modes. (b) Configuration for longitudinal modes. (c) Hammer used for the tests

Global frequencies of the specimens are collected in the last two columns of Table 3. For the ten specimens divided in groups (groups are identified by the shade of the symbols), Fig. 8 visualizes the range of the transversal (T1, T2, T3, and T4) and longitudinal (L1, L2, L3, and L4) eigenfrequencies of the specimens as obtained from the impact experiments. Shaded vertical lines in figure locate the inclusion eigenfrequencies estimated numerically, cf. Fig. 3.

Fig. 8

Visualization of the distribution of the global eigenfrequencies of the entire specimens as obtained by the impact experiments. Legenda entries refer to the mode shape (T,L) and to the specimen group (1,2,3,4). Shaded vertical lines visualize the eigenfrequencies of the inclusions, estimated numerically

Bragg Scattering

The relevant component of the frequency spectrum considered in these tests have been bracketed from above by estimating the Bragg frequency. Phononic crystals are characterized by the presence of Bragg band gaps, caused by destructive interference of waves scattered by a periodic arrangement of inclusions, with the result that wave propagation may be inhibited in all directions (full or complete band gaps) or only along certain directions (partial or direction band gaps) [20, 25]. The Bragg’s frequency is defined as

$$ f_{\text{Bragg}} = \frac{v_{p}}{2 a} , $$

(1)

where a measures the lattice parameter (distance between inclusions) and v_p is the velocity of propagation of the waves. For metaconcrete, the average distance between two inclusions estimated in the present batch of specimens is of the order of a = 3 cm (minimum 2.2 cm, maximum 7 cm). In addition, estimating the velocity of propagation longitudinal waves as

$$ v_{p} = \sqrt{\frac{E (1 - \nu)}{\rho_{\text{cls}} (1 + \nu) (1 - 2\nu)}} , $$

(2)

gives v_p = 3,752 m/s, which compares well with the value v_p = 3,729 m/s obtained from ultrasound tests on specimen P1. Inserting these values in Eq. (1), it results $f_{\text {Bragg}} \sim$ 62 kHz (max 82 kHz, min 26 kHz). This frequency is well above the range of frequencies covered in the present dynamic tests, which effectively rules out Bragg scattering as an operative mechanism with respect to the longitudinal waves considered in this work. In the case of transverse waves, the frequency at which Bragg effect occurs can be estimated experimentally, as suggested in [16].

Dynamic Tests

The preceding information has been taken as a basis for designing dynamical tests aimed at assessing the attenuation properties of metaconcrete. Following the approach in [8], one half of the sonic range was explored using a sequence of dynamic excitations covering 13 frequency intervals, partially superposed. Each excitation consisted of applying a sweep in frequency, i. e., a sinusoidal signal with fixed amplitude and linearly growing frequency. Each sweep was centered either at one of the numerically estimated eigenfrequencies of the inclusions, or at one of the additional frequencies covering the half sonic range. The width of each frequency interval was chosen to coincide with its central frequency. The duration of each sweep was different, since a linearly growing sinusoidal excitation produces a steady response only if the acceleration in frequency is inferior to the maximum value [26],

$$ a_{\max} = \frac{54 {f_{c}^{2}}}{Q^{2}} , \qquad Q = \frac{1}{2 \xi} $$

(3)

where f_c is the central frequency of the sweep and ξ is a damping coefficient, here assumed ξ = 0.05 corresponding to standard concrete. The minimum duration in time of the sweep was then defined by dividing the difference between the final angular frequency, ω_end = 3πf_c, and the initial one, ω_begin = πf_c, by the maximum allowable acceleration, with the result

$$ t_{c} = \frac{\omega_{\text{end}} - \omega_{\text{begin}}}{a_{\max}} = \frac{2 \pi}{5400 f_{c}} . $$

(4)

The experimental duration in time of each sweep was then extended by two extra seconds. The plan of the sweeps for each test is tabulated in Table 4, and shown graphically in Fig. 9. Tests were conducted twice on every specimen.

Fig. 9

Visualization of the plan of the dynamical tests in terms of frequency intervals (horizontal axis) and duration (vertical axis). The sweep plan has been applied twice to each of the ten specimens cast. Labels refer to the code in the second column of Table 4

Table 4 Plan of the sweeps in frequency (range and duration) used in each dynamical test

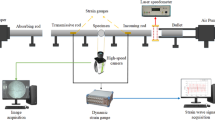
The experimental setup used for the sweep tests consisted of two systems. The first system generated the input signal, and was composed of a PC, an oscilloscope (4-channel Picoscope 2206 PC), an amplifier (Nobsound Mini Bluetooth Power Amplifier) and an actuator (Duokon vibration speaker). The PC activated the oscilloscope, wired to the signal amplifier and to the actuator. The actuator was glued (Loctite Super Attak Precision glue) at the center of one of the bases of the specimen, set in vertical position. The second system recorded the mechanical waves transmitted through the specimens, and it was composed of a PC, four piezoelectric acceleration sensors (PCB cutting Piezotronics 353B15), and a 4-channel 24-bit NI DAQ 9234 acquisition card. The sensors, glued to the specimen, received the attenuated waves. The acquisition card converted the analog signal into a digital signal for the PC. The acquisition of the signal was programmed with the software LabVIEW².

In each test, two sets of 13 sweeps were applied to each specimen, resting on a double support that allowed measurements on the bottom basis, Fig. 10(a). Measurements were taken at four locations, two on the bottom basis (direct wave, DW) and two on the top basis (reflected wave, RW). According to the configuration shown in Fig. 10(b), used in the first test, two acceleration sensors for DW measurements were located at the points A and B, and two for RW measurements at the points C and D. At the end of the first test, sensors were removed and specimens were rotated 90 degrees counterclockwise, Fig. 10(c). The sensors were then glued at the points E, F (DW), and G and H (RW).

Fig. 10

a Experimental setup for the sweep in frequency tests. b Configuration for the first test, with the measurement points, A, B, C and D. c Configuration for the second test, with the measurement points, E, F, G and H

A sampling rate f_camp = 51,200 Hz, larger than twice the maximum experimental frequency (10,500 Hz), was chosen to avoid aliasing effects caused by insufficient sampling (according to the Nyquist’s spatial sampling theorem). The amplitude of the input electric signals, 5.68 V peak-to- peak, the maximum allowed by the used instrumentation, was kept constant for all tests. Output electric signals were transformed into acceleration time histories through the sensitivity of the piezoelectric acceleration sensors, equal to 10/9.81 mV s²/m. Collected experimental data varied from 0.5 to 4.5 MegaBytes per sweep and transducer. Data were Fast-Fourier transformed using a Matlab³ program developed ad hoc.

The attenuation properties were measured by the transmissibility factor, a parameter introduced in the context of operational modal analysis as an application of signal theory that has gained relevance in civil engineering [27]. In the present context the transmissibility T is defined as the ratio between the FFTs of two outputs, i. e., the output obtained from a metaconcrete specimen PM (Y_PM) and the corresponding output of the homogeneous specimen P1 taken as reference (Y_P1). Here, T is estimated as the ratio between the corresponding FFT spectra S, namely,

$$ T = \frac{S_{Y_{PM} Y_{P1}}}{S_{Y_{P1} Y_{P1}}} = \frac{A^{*}_{PM} A_{P1}}{A^{*}_{P1} A_{P1}} , $$

(5)

where A denotes the Fourier transform of the output and A^∗ its conjugate complex. The mean transmissibility $\bar T$ (related either to DW or to RW) of a specimen is defined as the ratio between the averages of the four corresponding measurements

$$ \bar{T} = \frac{{\sum}_{k=1}^{4} S^{k}_{Y_{PM} Y_{P1}}}{{\sum}_{k=1}^{4} S^{k}_{Y_{P1} Y_{P1}}} . $$

(6)

The mean transmissibility accounts for the global response of the specimen and allows for direct comparisons in terms of attenuation effectiveness.

Results and Discussion

An application of the Gabor transform to the experimental data allowed to verify that in all the measurements the signal-to-noise ratio remained larger than 1. For all specimens, observations from FFT spectra are reproducible and consistent. DW (bottom surface in Fig. 10) signals are characterized by larger amplitudes while RW (top surface in Fig. 10) signals are characterized by smaller amplitudes. Amplitude reductions of the RW signals are markedly visible for any metaconcrete specimens in the range of the inclusion resonant frequencies, namely, 3,400-3,500 Hz for the type 1 inclusions and near 3,200 Hz for the type 2 inclusions. A representative example is shown in Fig. 11, which compares the F11 sweep spectra for specimens P1 (homogeneous) and P4 (36 inclusions of mixed type). Interestingly, DW signals (bottom surface) do not show evidence of localized amplitude reduction, but only a uniform reduction of the amplitude in all specimens. A possible explanation of this behavior lies in the intrinsic dissipative properties of mortar, combined with a low-amplitude low-energy signal (5.68 Vpp), which limits the depth of penetration of the waves. The reduction in the RW signals can be explained partly as a result of backscattering from the inclusions and partly as a consequence of resonant wave trapping at the inclusions.

Fig. 11

Frequency spectra of the DW and RW recorded signals relative to the frequency sweep F11, for the homogeneous specimen (P1) and the metaconcrete specimen with highest mixed inclusion content (P4). A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the FFT results

A common feature of both DW and RW frequency spectra for the ten specimens is a marked rattling around the frequencies 500 Hz, 2,000 Hz and 4,000 Hz. The origin of these perturbations can be attributed to resonance at global eigenfrequencies of the specimens, including shear and torsion modes. The rattling around 4,000 Hz, associated to the transversal mode shapes, may mask possible amplitude reductions due to higher natural frequencies of the inclusions, that also fall in this range, see Fig. 8. The rattling around 2,000 Hz, far from resonant frequencies and transversal global eigenfrequencies, is presumably associated with torsion and shear mode shapes. The similarity of the rattling around 500 Hz for all specimens suggests interference with the experimental setup.

The behavior revealed by the frequency spectra is confirmed by the transmissibility diagrams, Eq. (5). As a representative example, Fig. 12 shows the transmissibility coefficient expressed in decibel computed for the RW signals of the sweep F11 applied to the specimen P4. The transmissibility of the specimen P1, taken as reference, is given by a zero constant value.

Fig. 12

Transmissibility (in decibel) of the RW signals relative to the frequency sweep F11, for the metaconcrete specimen with highest mixed inclusion content (P4). The reference transmissibility of the homogeneous specimen is represented by the horizonal line at zero. A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the results

Since the tests involve linear sweeps in frequency, the averaging procedure (XPOW) proposed in [26] can be adopted, i. e., expressing the attenuation properties of metaconcrete at the macroscale in terms of mean transmissibility, Eq. (6). Diagrams of the mean transmissibility $\bar T$ for the three groups of specimens (see Table 3) are shown in Fig. 13.

Fig. 13

Mean Transmissibility (in decibel) of RW recorded signals relative to the frequency sweep F11, for the metaconcrete specimens grouped according to the density and type of inclusions. A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the results

Diagrams in Fig. 13 show that, for all groups of specimens, the range of frequencies where the amplitude attenuation is observed reduces and approaches the numerically estimated eigenfrequency for increasing densities of inclusions. It can been concluded that higher inclusion densities result in a confinement of each inclusion that is increasingly well approximated by the boundary conditions assumed in the numerical model.

There is no obvious pattern to the order of the curves according to the type and the number of inclusions, although some indication can be obtained from the analysis of the minima. Figure 14 shows the minimum values of the mean transmissibility obtained from the plots of Fig. 6 as a function of the frequency, including the error bars, visualized in terms of inclusion type and number.

Fig. 14

Minimum observed values of the Mean Transmissibility (in decibel) of RW recorded signals relative to the frequency sweep F11 and corresponding error. a Visualization in terms of inclusion type. b Visualization in terms of number of inclusions

Data do not reveal a clear dependence of the severity of the attenuation on the inclusion type, probably because of the similarity (both in size and in material properties) of the two inclusions. Specifically, Fig. 14(a) shows that specimens with mixed inclusions (black circles) provide a rather uniform attenuation in a limited range of frequencies, independently of the inclusion density, while specimens with a single type of inclusion (gray and white circles) are effective over larger frequency ranges. Type 2 inclusion specimens reveal the widest range of attenuated frequencies, together with a good efficiency in reducing the minimum value of the mean transmissibility.

Figure 14(b) shows a noticeable effect of the number of inclusion on the magnitude of the minimum mean transmissibility. Low density specimens (20 inclusions, black diamonds) have a reduced influence. High density specimens (36 inclusions, white diamonds) have a more marked effect but comparable with the one of medium density specimens (28 inclusions, gray diamonds). Thus, the attenuation effect increases with the density up to a saturation value, beyond which no further improvement is observed.

The mean transmissibility parameter allows to define the location of attenuation–or attenuation bands–for each metaconcrete specimen. Two types of attenuation bands may be defined in terms of transmissibility reduction: moderate attenuation bands, corresponding to a $\bar T < -7$ dB (80% reduction), and strong attenuation bands, corresponding to a $\bar T < -10$ dB, equivalent to one order of magnitude reduction (90%). Figures 15, 16 and 17 show the attenuation bands for all the specimens divided in groups. The yellow color denotes the moderate attenuation band, while the green color denotes the strong attenuation band. A comparison between specimens of the same group (same type of inclusions) confirms that a tight arrangement of inclusions corresponds to a shift of the attenuation bands towards lower frequencies.

Fig. 15

Mean transmissibility (in decibel) diagrams for the specimens of Group 1 (mixed inclusions). Moderate (in yellow) and strong (in green) attenuation bands of the RW signals relative to the frequency sweep F11. The reference transmissibility of the homogeneous specimen is represented by the horizonal line at zero. A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the results

Fig. 16

Mean transmissibility (in decibel) diagrams for the specimens of Group 2 (type 1 inclusions). Moderate (in yellow) and strong (in green) attenuation bands of the RW signals relative to the frequency sweep F11. The reference transmissibility of the homogeneous specimen is represented by the horizonal line at zero. A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the results

Fig. 17

Mean transmissibility (in decibel) diagrams for the specimens of Group 3 (type 2 inclusions). Moderate (in yellow) and strong (in green) attenuation bands of the RW signals relative to the frequency sweep F11. The reference transmissibility of the homogeneous specimen is represented by the horizonal line at zero. A smoothing process (moving average, a lowpass filter with filter coefficients equal to the reciprocal of the span assumed 1 s) has been applied to the results

Summary and Concluding Remarks

The present study investigated the attenuation properties of metaconcrete cylindrical specimens subjected to mechanical waves in the sonic range. The experimental campaign focused on the effect of combining two types of resonant inclusions in random arrangements, as expected for concrete used in civil engineering applications. The transmissibility factor (a time-honoured parameter employed in the dynamic assessment of the performance of traditional materials) was used as a metric to quantify the attenuation properties of metaconcrete. The present study differs from previous experimental campaigns. The present dynamical tests conducted in the sonic range of frequencies confirm the attenuation properties of the metaconcrete with random arranged inclusions and provide location and range of the attenuation bands, which are dependent on the physical-geometric features of the resonant inclusions.

A noteworthy observation is that the test data shows no significant influence of the type of the inclusions on the magnitude of the attenuation of the specimens. The number of inclusions, instead, affects both the value of the attenuation frequency and the magnitude of the attenuation.

Data shows that, unlike conventional metamaterials, the sought strong attenuation properties do not depend sensitively on the uniformity of the inclusions and their precise periodic arrangement, but, contrariwise, are insensitive to large variations and random placement of the inclusions.