Introduction

Accurate quantification of blast wave parameters remains a significant challenge to the research community, in particular determination of the spatial distribution of pressure imparted to an obstacle located a short distance from the explosive. Semi-empirical methods for predicting blast pressure loads, e.g. the well-established Kingery & Bulmash [1] scaled distance relationships, are largely derived from experiments conducted in the mid-20th century [2]. Whilst these predictive methods have been shown to be highly accurate for geometrically simple far-field situations [3,4,5], blast parameter relationships in the near-field are derived from very few experimental measurements [6] and are not able to accurately represent the complex situation that occurs in the early stages of an explosion [7, 8]. Consequently, numerical analyses in this region demonstrate considerable deviation from semi-empirical predictions [9].

Direct measurement of near-field blast pressures requires robust, hardened apparatus that can survive explosive loading in the order of 100s MPa, yet is sensitive enough to resolve spatial and temporal features that vary in the mm and μ s range respectively. Whilst experimental techniques have recently been developed for measuring surface loads resulting from explosive detonations (e.g. [10], and the apparatus developed by Clarke et al. [11] which provides comparative results in this article), these methods are intrusive. There is still a need to develop non-intrusive methods which do not require sensitive recording equipment to be located close to the source of the explosion, as this may adversely affect the accuracy and longevity of an experimental approach.

Photo-optical techniques have historically been used to record shock front arrival times and velocities, which enabled properties such as pressure and density to be calculated for a freely expanding blast wave [12, 13] by relating particle velocities to shock pressures using the Rankine-Hugoniot jump conditions. Recent advancements in high speed video (HSV) analysis have enabled researchers to further study the properties of blast waves using imaging techniques. Biss and McNesby [14] used schlieren flow visualization and high-speed digital imaging to optically measure the temporal decay of incident blast waves in the 100s kPa range. Hargather & Settles [15] and Hargather [16] used a similar technique to establish the relationship between incident shock pressure and distance for a number of explosive types.

High speed video images are obscured by the intense light released after detonation. Hence, the aforementioned research and other optical-based image tracking studies, e.g. [17] and [18], focus on the intermediate to far-field region where the shock front is freely expanding and has detached from the detonation product fireball. Alternative approaches use pressurised glass spheres [19] or detonation transmission tubing [20] in place of the explosive. In the near-field, however, the detonation product fireball is still rapidly expanding and remains attached to the surrounding layer of compressed air [21]. Thus, in the early stages of fireball expansion, measurement of the velocity of the outer surface of the detonation product fireball equates to measurement of the shock velocity, as is assumed in this article. Schlieren methods are generally not suited for near-field situations as the intensity of light from the fireball is such that the pressure boundary is indistinguishable from the surrounding air [22].

McNesby et al. [23, 24] used a framing camera and streak camera techniques to measure the outer surface of the fireball, and again used the Rankine-Hugoniot jump conditions to determine near-field incident shock pressures. Whilst incident shock pressures accurately describe the properties of a blast wave as it propagates unimpeded through free air, when an incident blast impinges on a notionally rigid reflecting surface its pressure is amplified as a result of conservation of mass, momentum and energy at the interface [25]. The transition from incident to reflected pressure conditions can result in an increase in pressure by up to a factor of 20 for near-field explosions [26]. Reflected blast wave parameters represent the loading an object located in the path of the explosion will be subjected to, and therefore the provision of adequate blast protection systems requires a detailed knowledge of reflected blast pressure conditions and how they are distributed across the face of an obstacle.

To date, there have been no studies which have evaluated near-field reflected blast pressure distributions using non-intrusive image-based techniques. This article presents measurements of reflected blast pressures using high speed video data. A free-air velocity-radius relationship is derived from image tracking of the explosive fireball using numerical edge detection techniques. The velocity relationship is then used to derive reflected pressure predictions on a rigid surface using Rankine-Hugoniot jump conditions. Predictions are compared against directly measured pressure distributions and the method presented herein is shown to be an accurate method for determining reflected blast wave parameters (within 10% of the maximum directly-measured value) through optical measurement of incident conditions only, in the regions of extremely high pressures and shock velocities close to the source of an explosion. The results are also used to make comments on the emergence and growth of turbulent instabilities at the fireball/air interface.

Experimental Work

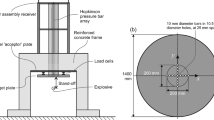
Experiments were performed at the University of Sheffield Blast & Impact Laboratory in Buxton, Derbyshire, UK, using the Characterisation of Blast Loading apparatus [11]. The apparatus comprises a pair of steel fibre and bar reinforced concrete frames, set approximately 1 m apart (Fig. 1(a)). A 1400 mm diameter, 100 mm thick mild steel target spans between the undersides of each frame, and acts as a nominally rigid target to reflect the blast pressures when an explosive charge is detonated some stand-off distance beneath the centre of the plate.

Fig. 1
figure 1

Schematic of Characterisation of Blast Loading apparatus [not to scale]: a) elevation; b detailed plan view of target plate showing bar arrangement (adapted from [27]). Note, camera positioning is indicative

Full size image

The plate is drilled through its thickness, with one 10.5 mm diameter central hole, and four holesFootnote 1 at each radial distance of 25 mm, 50 mm, 75 mm, and 100 mm from the plate centre (Fig. 1(b)). These holes form two orthogonal arrays passing through the centre, and enable pressure to be measured at 17 locations within the central 200 mm diameter region of the target plate. 3.25 m long, 10.0 mm diameter EN24T steel Hopkinson pressure bars (HPBs, after [29]) are suspended from their distal ends and inserted through the holes such that their faces lie flush with the face of the target plate.

Kyowa KSP-2-120-E4 semi-conductor strain gauges mounted in pairs on the perimeter of each HPB allow axial strain to be recorded and thus the reflected pressure history at the bar face to be calculated. HPB strain data were recorded using 14-Bit digital oscilloscopes at a sample rate of 3.12 MHz, although only peak pressure values are required in this study.

100 g PE4 charges (24.6 mm radius) were formed into spheres using bespoke 3D printed charge moulds and were suspended on a glass-fibre weave fabric ‘drumskin’ (25 g/m2 area density), held taught in a steel ring and suspended from the test frame on adjustable screws. The charges were aligned with the centre of the plate using an alignment laser, and were centrally detonated using Nitronel MS 25 non-electronic shock-tube detonators (0.7 g PETN) inserted through the bottom face of the charge. PE4 is an RDX-based plastic explosive comprising 87% RDX and 13% mineral oil binder [30], and is the UK equivalent of C4 [31].

A Photron FASTCAM SA-Z high speed video camera was situated in a protective housing, located a short distance from the test apparatus. The camera was fitted with a 105 mm Nikon lens and an infra-red filter was attached to the inner surface of a polycarbonate window through which the tests were filmed. The tests were self-illuminated by the incandescence of the detonation product cloud, and were recorded at 160,000 fps with 280×256 pixel resolution, f/8 aperture and 0.25 μ s shutter speed. The camera was positioned approximately level in height with the centre of the charge, with the vertical field-of-view set between the charge centre and the underside of the target plate (160,000 fps is the maximum frame rate achievable with this field-of-view). Video recording was synchronised with the detonation by triggering the camera off a voltage drop in a breakwire wrapped around the detonator. Post-processing of preliminary video data confirmed that lens distortion was negligible for the current test setup.

Three tests were performed as part of this study, with the explosive placed at a stand-off (distance from the charge centre to the plate) of 380 mm. All tests were conducted on the same day, under the same lighting conditions, and the camera was only moved for small field-of-view adjustments. Additionally, results from the three 100 g spherical PE4 tests at 80 mm stand-off in [32] are used for comparative purposes.

High Speed Video Edge Detection

Edge Detection Algorithms

Canny [33] devised a numerical algorithm particularly suited for edge detection in images with high levels of background noise [34]. This is available in MatLab as the (pre-existing) edge function. A low-pass Gaussian filter (default standard deviation \(\sigma =\sqrt 2\)) is first applied to the image to remove noise. Following this, intensity gradients are calculated through convolution of four filters used to detect horizontal, vertical and diagonal edge locations. Finally, a two-stage subroutine is implemented. In the first stage, a non-maxima suppression algorithm is applied, which ensures that the central pixel (of the detected edge) has a gradient magnitude larger than the pixels adjacent to the edge. In the second stage, hysteresis thresholding is used to remove noise and suppress weak edges that are not connected to strong edges: a high threshold first identifies strong edges, and a low threshold removes low gradient value pixels that are not attached to the strong edge. Any remaining pixels are assigned the value of 1 and comprise an edge, with the remaining pixel values set to 0. In this study, the user-controlled high and low threshold values were determined iteratively for each frame to ensure the entire edge was detected.

In addition to the Canny [33] algorithm, a binarisation technique was used for the first two frames post-detonation where parts of the image were obscured by the intense flash of light, and reflections of the flash from neighbouring surfaces corrupted the Canny edge detection. This was achieved by modifying the imbinarize MatLab function to apply a threshold to the image. A purpose-written code then located the first pixel above the threshold (when reading from top to bottom) and assigned this a value of 1 to denote the detected edge (with all other pixels in that column set to zero). Edge detection was terminated immediately before the fireball impinged on the target plate, giving a maximum measurable fireball radius of 380 mm. Typically 20–25 frames were analysed at an inter-frame rate of 6.25 μ s.

Figure 2 shows the raw HSV images and Fig. 3 shows the corresponding frames with edge detection algorithms applied. Note: at t = 0 the binarisation routine was implemented, whereas for all other frames in this figure the Canny approach was used.

Fig. 2
figure 2

Raw high speed video stills

Full size image
Fig. 3
figure 3

High speed video stills with edge detection algorithm applied

Full size image

Determining Fireball Radius and Velocity

The pixel height and width was calculated for each image using the known distance between the centre of the charge and the underside of the target (380 mm). This was calibrated separately for each test to account for slight changes in charge placement and camera positioning, with the centre of the charge calculated by taking the average centre point of the fireball for the first three frames after detonation. Since the tests were self-illuminated by the brightness of the fireball the charge was not visible prior to detonation, and calibrating off a static image taken by a different camera would have introduced errors induced by placement. The average pixel dimension was 1.836 mm with an associated error of ± 0.035 mm/pixel, i.e. ± 4 pixels along the 380 mm calibration length. At the maximum fireball radius, the maximum error is approximately ± 7.5 mm, i.e. ± 2.0%, which is comparable to the calibration uncertainty in previous published work [20].

The fireball radius was calculated using an in-house code developed by the authors (illustrated in Fig. 4) by discretising the domain into 1° increments along virtual ‘spokes’ emanating from the charge centre. First, the centroids of the two edge pixels nearest the spoke were determined by identifying the two minimum values of |ϕ − ψ|, where ϕ is the angle between the vertical line intersecting the centre of the explosive and the spoke, and ψ is the angle between the vertical and the line connecting the pixel centroid to the charge centre. In Fig. 4, the nearest edge pixels are identified by the angles ψ1 and ψ2. The position of the fireball edge for that value of ϕ is then defined as the point where the spoke and the line connecting the two pixel centroids intersect.

Fig. 4
figure 4

Method for detecting location of fireball edge along a virtual ‘spoke’ by identifying neighbouring pixel centroids

Full size image

The radial discretisation of Δϕ = 1°, for − 90°≤ ϕ ≤ 90°, was judged to provide sufficiently accurate measurements of the outer surface of the fireball given the resolution of the images. A subroutine was written to eliminate any spoke once the fireball surface had reached the edge of the image along that spoke, or if the fireball was judged to have impacted the target between the previous frame and the current one. This provided measurements of the fireball surface for slant distances up to 400 mm from the charge centre. The velocity along each spoke was determined at the inter-frame midpoint though linear central differencing of the displacement data.

Results and Discussion

Fireball Radius and Velocity Measurements

Figures 5 and 6 show fireball surface radius and fireball surface velocity measurements for Tests 1–3 respectively. The mean displacements and velocities for each individual test are represented by the solid black line, and each spoke is represented by the grey lines in order to provide qualitative information on the degree of spread in the results. Mean fireball surface radius and velocity measurements are compiled in Figs. 5d and 6d.

Fig. 5
figure 5

Fireball radii for Tests 1–3 (a–c) and compiled mean comparison (d)

Full size image
Fig. 6
figure 6

Fireball surface velocity measurements for Tests 1–3 (a–c) and compiled mean comparison (d)

Full size image

The fireball radius measurements can be seen to form a tight banding around the mean in the early stages of expansion (t < 30 μ s). After the fireball has expanded approximately 150 mm, i.e. 6 charge radii or a scaled distance of Z = 0.150/(0.11/3) = 0.32 m/kg1/3, the spread in the measured data begins to increase, albeit gradually, and the data continues to become more widespread until the outer limits of the fireball have propagated 380 mm and impact the target plate. It should be noted that measurements of decreased velocity are hypothesised to be as a result of light obscuration rather than being a genuine feature of fireball expansion. Given that 180 spokes were analysed in each test, a single spoke being obscured for a single frame is likely to have a minimal effect on the mean velocity.

At the moment of first impact of any part of the fireball on the target plate, the fireball radius typically varies between 300–380 mm, suggesting that there are regions of the fireball/air interface that propagate at considerably higher velocities than the main body of the fireball, which leads to a slight skew in the mean velocity. The velocity data shows sporadic, short duration increases in velocity which then appear to decrease, stabilise, and remain at some value above the mean thereafter. This behaviour is illustrated in Fig. 6b, where the trajectory of a single ‘spoke’ has been highlighted. It is suggested that this shows evidence of the emergence and growth of Rayleigh-Taylor [35, 36] and Richtmyer-Meshkov [37, 38] surface instabilities (RT and RM respectively). RT instabilities develop when the density gradient and the pressure gradient are in opposite directions, which occurs when the detonation products expand and compresses the surrounding air to the point at which the local air pressure exceeds that in the fireball (which itself remains denser than the air). RM instabilities are generated when a shock passes through inhomogeneous media, e.g. localised inhomogeneities initially caused by RT instabilities [39]. Such instabilities have previously been observed to significantly influence the localised load on a reflecting surface [40, 41].

These variations in fireball surface velocity are further examined in Fig. 7. Here, the relative standard deviation (RSD = σ/μ) of surface velocity has been calculated at each instant in time using velocity data from all available spokes, and is plotted for each test. It can be seen that the relative standard deviation increases gradually from an initial average value of 8% at 20 μ s, to an average value of 12% at 60 μ s after detonation (corresponding to 3–10 charge radii, with reference to Fig. 5d). Beyond this point the curves begin to rapidly increase and diverge.

Fig. 7
figure 7

Variation of velocity with time for all test showing emergence and growth of fireball surface instabilities

Full size image

It is hypothesised that we are observing two distinct stages of emergent instabilities, which we term: emergence and growth. In the first stage, the emergence of early-time instabilities gives rise to turbulent features which induce low-level and largely deterministic/repeatable variations in fireball surface velocities. This behaviour persists up to a fireball radius of approximately 10 charge radii. Beyond 10 charge radii the second stage is entered, where late-time growth of instabilities gives rise to turbulent features which influence fireball surface velocity in a less deterministic manner. Hence, there is an increased level of inherent stochasticity (i.e. increased and less predictable relative standard deviation) during the growth phase. 10 charge radii corresponds to a scaled distance of Z = 0.246/(0.11/3) = 0.53 m/kg1/3. This closely matches the value of Z = 0.50 m/kg1/3 proposed by Tyas [30] as the transition from ‘extreme’ to ‘late’ near-field regions, based on a collation of data on directly measured peak reflected pressure and peak specific impulse in experiments conducted over a range of scaled distances. Here, loading is described as “relatively consistent” in the extreme near-field, with “large variations in loading” in the late near-field, which appears to be similar to the observations of increased variability of fireball surface velocities (for Z > 0.53 m/kg1/3) in this article.

Reflected Pressure Calculations from Fireball Velocity

The radius–time and velocity–time plots in 5d and 6d were combined to generate the velocity–radius plot shown in Fig. 8, assuming that any error as a result of averaging the data over inter-frame times is minimal. A third-order polynomial equation was fit to the relationship (coefficient of determination, R2 = 0.998), as this curve type has previously been shown to most accurately represent experimentally recorded near-field blast wave radius-time data [42].Footnote 2 Note that this fit type was selected based on its ability to best represent the data rather than being physics-based. Also shown on the secondary y-axis of Fig. 8 is the relative error of the curve fit. Between a fireball radius of 50 and 150 mm the maximum relative error is 5.2%, whereas from 150 to 400 mm radius the relative error is within 0.8%.

Fig. 8
figure 8

Velocity–radius relationship and third order polynomial fit to data (equation (2)), with relative error plotted on secondary y-axis

Full size image

The polynomial curve fit presented in Fig. 8 provides a relationship to calculate the mean fireball surface velocity, v (mm/μ s), as a function of fireball radius, r (mm), for 25 < r < 400 mm:

$$ v = -39.54\text{E-9}r^{3} + 60.47\text{E-6}r^{2} -32.22\text{E-3}r + 7.079 $$
(1)

Dividing through by ambient sonic velocity (0.34mm/μs) gives an expression for the incident Mach number, Mi, as a function of fireball radius:

$$ M_{i} = -116.3\text{E-9}r^{3} + 177.8\text{E-6}r^{2} -94.76\text{E-3}r + 20.82 $$
(2)

Consider reflection of a blast wave after it strikes a rigid target, Fig. 9a. The angle of incidence, θ, at a point on the surface (denoted by the letter A in this figure) is defined as the angle between the outward normal of the surface and the direct vector from the explosive charge to that point [43]. Accordingly, \(\tan (\theta ) = x/y\), where x is the distance along the target to the point of impingement, and y is the distance from the centre of the explosive to the point of impingement (termed stand-off distance).

Fig. 9
figure 9

a formation of the Mach Stem following impingement of an incident wave on a rigid reflecting surface, and definition of angle of incidence θ; b steady-flow counterpart of oblique shock reflection; c oblique reflected Mach number as a function of angle of incidence, with discontinuities showing transition from regular to Mach reflection. (a) adapted from [43], (b) and (c) adapted from [44]

Full size image

Kinney and Graham [44] outline an analytical procedure based on the Rankine-Hugoniot jump conditions to determine the oblique reflected pressure, pr,θ, acting on a rigid surface following impingement of an incident shock propagating at Mach number Mi. In the limiting case of normal reflection, i.e. θ = 0°, the reflected Mach number is given as

$$ M_{r,\theta = 0} = \sqrt{\frac{7{M_{i}}^{2} - 1}{{M_{i}}^{2} + 5}} $$
(3)

and the normally reflected overpressure (where the term ‘overpressure’ refers to the increase in pressure above atmospheric conditions):

$$ p_{r,\theta = 0} =p_{a} \left[\frac{(4{M_{i}}^{2} - 1)(7{M_{i}}^{2} - 1)}{3({M_{i}}^{2} + 5)} -1\right], $$
(4)

where pa is ambient pressure. In the limiting case of θ = 90°, the blast propagates parallel to the surface and incident conditions are maintained: Mr,θ= 90 = Mi and pr,θ= 90 = pi, where pi is overpressure of the incident wave and is a function of incident Mach number only,

$$ p_{i} = p_{a} \frac{7({M_{i}}^{2} - 1)}{6}. $$
(5)

Considering impingement of an incident shock non-normal to a rigid surface (0° < θ < 90°), as a steady-flow counterpart (see Fig. 9b), oblique reflection generates an intermediate flow stream, such that

$$ \frac{\tan(\theta-\alpha)}{\tan\theta} = \frac{5 + {M_{i}}^{2}}{6{M_{i}}^{2}} $$
(6)

where α is the stream deflection angle, and M2 is the stream Mach number, given by

$$ {M_{2}}\sin(\theta-\alpha) = \sqrt{\frac{{M_{i}}^{2} + 5}{7{M_{i}}^{2} - 1}} $$
(7)

This intermediate stream instantaneously enters the reflected region at an angle β. Noting that the corresponding stream deflection angle is α, the angle of entry, β, can be determined through iteration of the following relation

$$ \frac{\tan(\upbeta-\alpha)}{\tan\upbeta} = \frac{5 + ({M_{2}}\sin{\upbeta})^{2}}{6({M_{2}}\sin{\upbeta})^{2}} $$
(8)

The oblique reflected Mach number, Mr,θ, is thus given as

$$ M_{r,\theta} = {M_{2}}\sin{\upbeta} $$
(9)

which can be used to determine the oblique reflected overpressure:

$$ p_{r,\theta} = p_{a} \left[\frac{(7{M_{r,\theta}}^{2} - 1)(7{M_{i}}^{2} - 1)}{36} - 1\right] $$
(10)

Equation (2) can be used in conjunction with equations (6–10) to provide pressure predictions along a rigid reflecting surface at any distance (25 < r < 400 mm) from the centre of a 100 g spherical PE4 explosive.

The relationship for oblique reflected Mach number is a non-continuous function of angle of incidence, and is shown in Fig. 9c. A discontinuity occurs at angles of incidence between 40–48°, with the exact value a function of incident Mach number. This point marks the transition from regular to Mach reflection (or ‘irregular reflection’), as approximately indicated in Fig. 9a. Mach reflection occurs when the higher pressure (and hence higher velocity) reflected wave coalesces with the incoming incident wave and forms the Mach Stem. The Mach Stem connects the reflecting surface with the point where the incident and reflected waves meet, known as the triple point. Note: the analytical work of [44] described above holds for both regular and Mach reflection.

The previous expressions assume ideal gas behaviour, that is the ratio of specific heats, γ, remains constant at a value of 1.4. Real gas behaviour begins to deviate from ideal gas behaviour at incident pressures greater than 2 MPa (300 psi), where dissociation and ionisation can lead to a decrease in γ [39], however this effect is expected to be minimal in the current study where incident pressures are not expected to exceed 25 MPa (\(\sim \)200 MPa reflected pressure, assuming a reflection coefficient of 8.0 after [44], where the reflection coefficient is defined as the ratio of the peak magnitudes of reflected and incident pressures). Thus, the simplified constant-γ relations are used in this article.

Comparison to Directly Measured Peak Pressures

Directly measured overpressure distributions from the HPB tests described in “Experimental Work” are used to assess the veracity of the HSV overpressure predictions, determined from the experimentally derived velocity-radius relationship and the [44] analytical framework outlined above in “Reflected Pressure Calculations from Fireball Velocity”. Two configurations are compared: 100 g PE4 spheres detonated at 80 mm and 380 mm measured orthogonally from the charge centre to the centre of the rigid reflecting surface. It is worth reiterating that reflected pressure distributions are derived from incident Mach number measurements only, through interpolation of the derived velocity-radius relationship.

HPB measurements for each individual bar, and the mean value at each measurement location, are shown graphically alongside the HSV predictions in Fig. 10a and b for the 80 mm and 380 mm tests respectivelyFootnote 3, allowing for a more direct comparison between peak pressure distributions [27, 28]. HSV predictions were evaluated at 1 mm increments along the target surface. Whilst it is not possible to provide error bars of the HSV experimental measurement technique in isolation, pressure predictions are also provided by assuming incident velocities ± 1σ and ± 2σ from the mean at each gauge location, using an aggregate of the time-varying relative standard deviations of each test, as presented in Fig. 7. It is suggested that this envelope primarily encapsulates the intrinsic variability in near-field blast events, i.e. it is a measure of the typical experimental spread of results due to physical features of the fireball as it expands. This is perhaps best illustrated with reference to the right-hand column of Fig. 3, where features at the fireball/air interface are considerably larger than a single pixel and hence any calibration or tracking inaccuracies will be second order.

Fig. 10
figure 10

Comparison of measured pressure distributions using Hopkinson pressure bar (HPB) and high speed video (HSV) predictions: a 80 mm stand-off distance; b 380 mm stand-off distance. Shaded regions indicate ± 1σ and ± 2σ bounds

Full size image

Generally the HSV pressure distributions closely follow those from the HPB measurements, with the magnitude and shape of the pressure distribution curve being well predicted. In the 80 mm stand-off tests, 50 of the 51 HPB peak pressures lie within ± 2σ of the HSV predictions, whereas in the 380 mm tests 41 out of 51 of the HPB peak pressures lie within ± 2σ of the HSV predictions.

Localised increases in reflected pressure can be seen in the HSV predictions for the 80 mm tests at a distance from the plate centre, x, of approximately 65 mm (θ = 40°) as a result of the Mach stem. The pressure increase caused by the Mach Stem persists only for a short duration before being followed by a marked temporal decrease in pressure and rapid return to regular reflection conditions thereafter [43]. The disagreement between HPB and HSV pressures at 75 mm from the plate centre in Fig. 10a is likely due to a limitation of the HPB technique. Propagating pressure signals will exhibit a slight loss of definition of transient pressure features as a result of Pochhammer-Chree dispersion [45, 46], and hence peak pressures recorded using the HPB technique may be a slight underestimation of the true peak reflected pressure at that angle of incidence, i.e. in the region of Mach reflection. In a recent study, dispersion was shown to affect peak pressure recordings by up to 5% for normal reflection [47], and it is suggested that this loss could be greater for irregular/Mach reflection on account of the transient, high-frequency components of the Mach Stem.

The HSV predictions appear to match the upper bound of the HPB pressure measurements for the 380 mm tests in Fig. 10b. It is likely that the mean velocity-radius relationship in Fig. 8 has been slightly skewed by the growth of instabilities and turbulent features as discussed in “Fireball Radius and Velocity Measurements”. However, the results still compare well to the general range of peak pressures recorded at any distance from the plate centre, albeit the HSV technique is generally less able to match the bottom-end of the HPB data.

The results presented in Fig. 10 are compiled in Table 1 along with incident (measured) and reflected (calculated) Mach numbers. As previously, y, x, and r are stand-off distance, distance from the plate centre, and slant distance to the measurement point, which is assumed to be exactly equal to the fireball radius at the moment of impingement after [21]. Maximum and mean HPB peak pressures are provided for comparative purposes. For the 80 mm stand-off tests, the HSV data all lie within 10% of the mean HPB data at each measurement location, with the exception of the x = 75 mm data on account of the Mach Stem as discussed previously. Conversely, the HSV data lie within 10% of the maximum recorded HPB data at each measurement location and are typically 15–20% greater than the mean.

Table 1 Compiled peak oblique reflected pressures, pr,θ, from Hopkinson pressure bar (HPB) measurements and high speed video (HSV) predictions with associated input values
Full size table

Peak incident pressures determined from equation (5) are also provided in Table 1. Taking the ratio of calculated reflected and incident pressures from analysis of the HSV data allows the reflection coefficient to be calculated. Here, the reflection coefficient ranges from 7.82–3.30 for the 80 mm stand-off case, and ranges from 6.41–6.08 for the 380 mm case, which would be expected since it is a function of both angle of incidence and incident shock strength. Remembering that the velocity-radius relationship was derived for incident conditions, the values of reflection coefficient provide further insight into the accuracy of the HSV method: this article has demonstrated that it is possible to use empirical measurement and Rankine-Hugoniot theory to accurately predict distributed pressures up to a factor of ∼8 greater than the incident pressure of the propagating blast wave. Whilst the pressure predictions may be improved by taking real gas effects into account, the assumption of ideal gas behaviour for the range of pressures in this article has been shown to be sufficiently accurate.

Outlook

The results presented in this article have potentially significant implications for the measurement of extremely high pressure near-field blast loads, in that it has been shown that there is no longer the requirement to locate an obstacle in the path of a blast wave in order to measure the pressure distribution that the obstacle will be subjected to.

The HSV analysis, previously conducted for 80 mm and 380 mm, was extended to study the distribution of reflected pressure for stand-off distances, y, of 50–300 mm at increments of 5 mm, for distances out to 250 mm from the plate centre, x, again at 5 mm increments, following detonation of a 100 g spherical PE4 explosive. The results are shown in Fig. 11. This analysis enables reflected pressure distributions to be estimated for a range of target sizes and stand-off distances (scaled target sizes of up to 0.54 m/kg1/3 and scaled distances 0.11–0.65 m/kg1/3) by reading reflected overpressure values off for a given value of stand-off. Hopkinson-Cranz scaling [25] can be used to express the results at a different scale. It should be noted that the effects of blast wave clearing around the target edge have not been included in this analysis [48], however clearing is negligible in the near-field and can be neglected without a significant loss of accuracy [49].

Fig. 11
figure 11

Variation of peak reflected pressure (in MPa) with stand-off and distance from plate centre for a 100 g spherical PE4 explosive, through solution of equations (2) and (6–10): a contour plot; b surface

Full size image

Pressure distribution charts of this nature can be generated for any type and shape of explosive, provided the velocity-radius relationship is known, i.e. determined from high speed video analysis as in this article. This will allow the analyst to generate a suite of empirical loading distributions for any number of stand-off distances and target sizes from only a single test or a small number of repeat tests.

When evaluating structural response to blast loads it is often necessary to quantify the distribution of peak specific impulse (integral of the pressure history with respect to time) in addition to peak pressure distribution. Whilst quantification of specific impulse from HSV is an active area of research for the current authors and others [14], there are many applications where peak pressure is dominant. In particular, peak pressure distributions can provide validation data for numerical modelling, as well as being used to inform experimentalists of the typical pressures they should design their recording equipment to withstand. For example, a HPB with perimeter-mounted strain gauges should remain elastic (to facilitate repeat use, and to ensure the entire signal propagates as an elastic wave), and the gauges should operate within their calibrated range and remain bonded to the HPB. Clearly, these are all dictated by the magnitude of peak pressure, and therefore the methods presenting in this article could be used by researchers to provide a benchmark prior to additional experimental work.

Summary and Conclusions

This article presents the results from high speed video analysis of near-field explosive detonations. Edge detection algorithms were used to track the outer surface of the explosive fireball in order to determine a relationship between fireball surface velocity (i.e. attached shock wave velocity) and fireball radius. The measured velocity behaviour showed two clear stages of Rayleigh-Taylor [35, 36] and Richtmyer-Meshkov [37, 38] surface instabilities: emergence and growth. The emergence stage persists up to a distance of approximately 10 charge radii, and is characterised by low-level and largely deterministic/repeatable variations in fireball surface velocities. At distances greater than 10 charge radii the growth stage is entered, which is characterised by a divergence in fireball surface velocities and higher variability in blast pressures.

Rankine-Hugoniot theory was used to convert the measured incident shock wave velocities into reflected pressure distributions. Whilst image tracking techniques have been used previously to measure variations in incident blast pressures with stand-off distance, this technique has not previously been used to evaluate near-field reflected pressures, nor how they are distributed along a target surface.

Two test cases were considered: 100 g PE4 spheres detonated at stand-off distances (from the centre of the charge) of 80 mm and 380 mm. The results compared well with directly measured pressure distributions using the apparatus described by [11], and were typically within 10% of the mean experimental value at each measurement location on the surface of a nominally rigid target.

The analysis method was extended to develop estimations of peak reflected pressure distribution for a range of near-field stand-off distances (scaled target sizes of up to 0.54 m/kg1/3 and scaled distances 0.11–0.65 m/kg1/3). Using this technique, it is possible to evaluate the blast loading on a structure using a single velocity-radius relationship. The results herein demonstrate that it is possible to accurately estimate reflected pressure distributions (pr > 180 MPa) for situations where the blast wave possesses only free-air incident blast conditions (pi < 25 MPa). Thus, it is no longer necessary to locate sensitive recording equipment close to the source of the explosion in order to accurately measure the peak pressure acting on a surface.