Abstract
In this study, pressure distributions were reconstructed from phase-locked surface deformation measurements on a thin plate. Slope changes on the plate surface were induced by an external flow interacting with the specimen and measured with a highly sensitive deflectometry setup. The Virtual Fields Method (VFM) was used to obtain pressure reconstructions from the processed surface slopes and the plate material constitutive mechanical parameters. The applicability of the approach in combination with phase-locked measurements is demonstrated using a synthetic jet setup generating a periodic flow in air. Phase-averaging slope data allows mitigating random noise effects and resolving low-range differential pressure amplitudes despite the turbulent flow. The size of the spatial structures of the investigated low amplitude flow events identified in full-field with the present method are \(\mathcal {O}(1)~\text {mm}\), which is beyond the capabilities of other available surface pressure measurement techniques. Challenges and limitations in achieving the metrological performance for resolving the observed surface slopes of \(\mathcal {O}(0.1)~\text {mm km}^{-1}\) are described and improvements for future applications are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Full-field surface pressure information is required for the research of flow-structure interactions, the design of aerodynamic components, and applications for heat and mass transfer. Extant techniques are limited in terms of the differential pressure amplitude ranges that can be resolved and in terms of the achievable spatial resolutions. Particle Image Velocimetry (PIV) is a technique that allows full-field investigations of pressure in the flow field, e.g. [13, 14], but cannot be applied directly on a surface. Pressure sensitive paints, e.g. [28, chapter 4.4], yield full-field surface pressure information directly on surfaces, but are typically restricted to limited ranges of large differential pressure amplitudes. Pressure transducers allow accurate measurements for low-range differential pressures. They can be integrated into the investigated surface by drilling holes into the specimen. This can however change the material response. In order to investigate surface pressure distributions, a large number of pressure transducers is required, which then still yield very limited spatial resolution. A number of studies have focused on obtaining pressure information from optical deformation measurements on surfaces instead. This was achieved by solving the mechanical equilibrium equations of the investigated specimen. A common problem of these approaches is that regularization is necessary in order to mitigate the influence of experimental noise. E.g. in [7], deflections measured with 3D-Digital Image Correlation on a flexible Kevlar wind tunnel wall section were projected onto polynomial basis functions to reconstruct pressure using the equilibrium equation. In other studies, surface deformation measurements on thin plates were used as basis for force and pressure reconstruction. The local equilibrium equation for a thin plate in pure bending, which can be obtained using the Love-Kirchhoff theory, requires fourth-order deflection derivatives to calculate pressure. This leads to an amplification of the experimental noise and thus increases the need for regularization. In [17, 19], noise amplification was addressed using wave number filters on the deformation data, which was obtained with Laser Doppler Vibrometer (LDV) measurements. These were used to solve the equilibrium equation and identify external mechanical vibration sources, as well as the acoustic component of a turbulent boundary layer.
To address the issues of experimental noise and noise amplification due to differentiation, the Virtual Fields Method (VFM), which is based on the principle of virtual work, has been used in a series of studies. In case of the problem of a thin plate in pure bending, the principle of virtual work only requires second order spatial derivatives of the surface deflections to calculate pressure. It was used in combination with LDV measurements to reconstruct spatially-averaged sound pressure levels in [23], transverse loads and vibrations in [6], random external wall pressure excitations in [5] and sound transmission of plates in [23]. These studies used piecewise virtual fields, which allow pressure reconstructions over subdomains and act as as a spatial low-pass filter. In the above studies, numerical simulations and microphone measurements revealed that the performance of the method varies with the chosen size of the subdomains and that it can be affected by the structural resonance frequencies of the thin plate specimen.
In order to acquire time-resolved full-field pressure information, the VFM was combined with optical measurements using deflectometry in recent studies. Since deflectometry is a technique for the measurement of surface slopes [27], this combination reduces the order of derivatives of experimental data for calculating pressure with the principle of virtual work to two. Dynamic mechanical point loads were measured this way in [18]. In [15], pressure reconstructions of an impinging air jet on a flat plate were obtained for mean distributions. The study also addressed the accuracy and systematic processing error of the approach, as well as a procedure to mitigate the latter. Dynamic loads of the same impinging jet were reconstructed in [16]. The slope resolution in these experiments were of the order of \(\mathcal {O}(1)~mm\cdot km^{-1}\). The surface slopes caused by dynamic flow events were well below this limit, such that they could not be measured directly. Instead, the spatio-temporal evolution of low differential pressure events in the flow were extracted using a temporal filter and Dynamic Mode Decomposition (DMD).
The present study explores an alternative approach for obtaining low-range differential pressure amplitudes in dynamic flows. It further aims at resolving flow events on small spatial scales of \(\mathcal {O}(1)~mm\). Phase-locked deflectometry measurements were used to measure pressure distributions caused by an impinging synthetic air jet. This allowed implementing changes in the deflectometry setup that improve the metrological performance to resolve the surface slopes caused by the low differential pressure events.
The dynamic range and signal-to-noise ratio in grid images was improved by using a flash light to achieve an optimal illumination. This was a shortcoming in [16], where continuous lighting was required for the time-resolved measurements. Since camera storage is not an issue for phase-locked measurements, it was further possible to use higher camera resolutions. These allowed using smaller pitches for the hatched grid which was used as spatial carrier signal in the deflectometry setup. Smaller grid pitches increase the spatial resolution as well as the resolution in slope, allowing measurements of the extremely small deformations associated with the investigated flow events.
This study demonstrates the feasibility of the approach as well as its limitations and discusses possible improvements for future applications.
Deflectometry
Deflectometry is an optical full-field slope measurement technique [27]. Figure 1 shows a schematic of the setup. It requires a periodic spatial signal, here a cross-hatched grid with printed pitch pG, a specular reflective specimen, a camera and a light source. The printed grid is placed at a distance hG from the specimen surface. The camera is placed at an angle next to the grid, such that it records the reflected grid in normal incidence. The angle 𝜃 should be minimized to avoid distortions in the recorded image.
Top view of deflectometry setup and working principle (redrawn from [15])
The principle of deflectometry is also visualized in Fig. 1. In an unloaded specimen configuration, a camera pixel records the reflected grid point P when directed at point M on the specimen surface. In a loaded configuration, deformations cause local changes of the surface slopes, dα. Neglecting rigid body movements and out-of-plane deflections, this means that the pixel directed at point M records the reflected grid point P\(^{\prime }\) after the surface deformation.
Recorded grid images can be used to extract phase information and thus the phase shift induced by applying a load to the specimen. Here, a spatial phase-stepping algorithm was employed to obtain phase maps [21, 24]. In order to suppress some harmonics and errors from miscalibration, a detection algorithm featuring a windowed discrete Fourier transform algorithm with triangular weighting was used [2, 25]. The chosen detection kernel size was two grid pitches, here 18 pixels.
The phase maps obtained from the unloaded reference configuration and the deformed configuration allow calculating the displacement, u, between P and P\(^{\prime }\). To account for the physical displacement of the point on the specimen surface, an iterative procedure is employed, which is described in [11, section 4.2]:
where the subscripts def and ref refer to a deformed and a reference configuration respectively, as the phase difference between a loaded and unloaded configuration is of interest. A linear approximation of the slopes dα corresponding to u can be derived using geometrical considerations, assuming that dα is small, hG ≫ u, 𝜃 is negligible and that the camera records images in normal incidence (e.g. [22]):
If the assumptions are not met, a more complicated full calibration is required [3, 26]. The printed grid pitch pG drives the spatial resolution. The slope resolution is driven by measurement noise, the printed grid pitch pG and the distance hG, the spatial resolution by pG.
Pressure Reconstruction
Assuming that the plate material is linear elastic, isotropic and homogeneous, the principle of virtual work is expressed by:
where S denotes the surface area, p the investigated pressure, Dxx and Dxy the plate bending stiffness matrix components, κ the curvatures, ρ the plate material density, tS the plate thickness, a the acceleration, w∗ the virtual deflections and κ∗ the virtual curvatures. In the present study Dxx, Dxy, ρ and tS were known from the plate manufacturer. κ and a were obtained from deflectometry measurements. The virtual fields w∗ and κ∗ have to be chosen according to theoretical as well as practical restrictions of the problem such as continuity, boundary conditions and sensitivity to noise.
Assuming pressure to be constant over the investigated area yields a simplified equation. Approximating the integrals with discrete sums yields:
where N is the total number of discrete surface elements. By defining this equation over subdomains of the total surface area, pressure distributions can be reconstructed iteratively. These subdomains are referred to as pressure reconstruction windows (PRW) in the following. In the present study, the spatial data was oversampled by overlapping these windows.
Virtual Fields
Virtual fields were defined with 4-node Hermite 16 element shape functions, which are used in FEM, [32]. Example fields are shown in Fig. 2. The full formulation of these fields as well as an implementation example can be found in [20]. They yield the required C1 continuous virtual deflections and continuous virtual slopes. They further allow eliminating the unknown contributions of virtual work over the plate boundaries because the obtained virtual displacements and curvatures vanish at the borders. Here, 9 nodes were defined for one PRW. All degrees of freedom were set to zero except for the virtual deflection of the center node, which was set to 1. The chosen size of the PRW is an important processing parameter. Larger PRW can be used to average out the effect of random noise on the pressure value within the window. In order to capture small spatial structures however, smaller PRW are required because large windows may average out amplitude peaks. It should be noted that the systematic processing error varies with the PRW size. In order to determine what size to choose and to estimate what systematic error this results in, the experimental parameters can be used to simulate the experiment. A methodology using finite element simulations and artificial grid deformation for this purpose is introduced in [15].
Experimental Methods
Setup
Figure 3 shows a schematic of the experimental setup. A first-surface glass mirror was used as specimen. It was glued onto a 1 cm thick perspex frame around the edges, resulting in simply supported boundary conditions. The grid was printed on transparency and fixed between two glass plates. A flash light and an optical diffuser were placed behind the grid to achieve homogeneous illumination of the latter. The camera was placed next to the grid at the same distance from the specimen, recording images at normal incidence. The distance between the sample and grid was chosen to be as large as possible in order to minimise the angle 𝜃.
A synthetic jet was used to generate the flow impinging on the specimen. It was generated using a driver connected to a cavity with orifice. Here, the jet was driven by a speaker which was actuated using a sinusoidal signal, generating a continuous train of vortices. The cavity was milled out of aluminium plates and had a volume of approximately 1.85 10− 5 m3. The nozzle was 3D printed with a neck length of approximately 19.5 mm. The jet was directed at the flat plate specimen. The driver changes the cavity volume, inducing a pressure difference which results in fluid being either sucked in or ejected through the orifice.
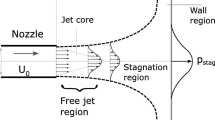
During ejection, vortical structures form around the edges of the nozzle exit due to shear. For sufficiently small Strouhal numbers St < π− 1, the fluid forming the vortices around the edge of the orifice is not sucked back into the cavity but convects downstream [12]. If the actuator is operated continuously, this leads to a train of vortices [10]. Here, a rectangular nozzle was used as orifice. For such nozzle symmetries, the vortices form structures with a major and a minor axis upon formation, which deform after some distance downstream and switch axes (e.g. [1, 8, 29]). They eventually break down entirely and form a turbulent jet [10]. Depending on the distance between nozzle and plate, either the described vortical structures or a circular turbulent jet impinge on the plate, leading to an increase of static pressure and a subsequent diversion of the flow along the wall, e.g. [30].
All relevant experimental parameters are listed in Table 1. The jet amplitude is given in terms of the peak-to-peak input voltage amplitude of the speaker, Upp, as well as the peak velocity at the nozzle exit, vpeak, which was determined using hot wire anemometry measurements. Two jet setups were used to investigate the capabilities in resolving high and low differential amplitudes, as well as different spatial shapes. Since the sample plate was found to deform over time, e.g. due to temperature fluctuations, a set of images for unloaded and loaded configuration was taken for each phase sample.
Data Processing
Each phase map was calculated from a set of grid images taken in an unloaded and a loaded configuration. The slope maps were calculated from phase maps which were averaged from approximately 500 snapshots. Slope maps were smoothed using a 2D Gaussian filter. This was necessary in order to mitigate an amplification of noise in later processing steps, particularly spatial differentiation. The filter kernel is characterised by its side length, which is given in terms of the standard deviation σα. Here, the side length was truncated at 3σα in both directions. This low-pass filter reduces the effect of both random noise and high-frequency bias, but also leads to a reduction of the signal amplitude. Note that this Gaussian filter leads to a loss of data points around the borders, depending on the filter kernel size.
Three-point centered finite differences were used to differentiate slope maps and calculate curvatures. Using geometrical considerations, one can determine that the distance between two data points on the specimen surface, which is required for the finite differences, is pG/2 if the camera is positioned at the same distance hG from the specimen surface as the printed grid. Deflections were obtained from the slope maps using an inverse (integrated) gradient based on a sparse approximation [9]. Accelerations were then obtained from the second temporal derivative of the deflection maps. The acquired deflections and accelerations did however show unexpected distributions for a number of phase points. It is possible that the number of acquired phase points were insufficient to resolve accelerations accurately. Further, since the integration constant for calculating deflections was unknown and set to 0, a comparison with an established measurement technique was necessary. Accelerations were however found to be below the noise level of 0.3 m s− 2 found for the Polytec PDV 100 laser Doppler vibrometer which was used for reference measurements. Figure 4 shows deflections and accelerations obtained from slope measurements using a high amplitude jet setup with Upp = 23 V and hN = 10 mm. Higher acceleration amplitudes of up to 0.4 m s− 2 were observed for different phase points, but with unexpected and asymmetric distributions. Since LDV measurements did not confirm these values and due to the potential inaccuracy of the results, accelerations were not taken into account and set to 0 in the following. The resulting error in pressure amplitude from neglecting accelerations can be estimated to up to 35 Pa.
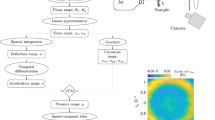
Pressure maps were reconstructed using the curvatures and the material constitutive mechanical parameters as described in “Pressure Reconstruction”. The results were oversampled by shifting the reconstruction window by one data point in both directions until the full field of view was covered. The reconstruction steps are summarised in Fig. 5.
Processing Parameters
The chosen processing parameters, in particular the slope filter kernel size, σα, and the PRW size, significantly impact the pressure reconstruction outcome. Large PRW sizes act as more efficient low-pass filter, but can lead to an underestimation of pressure amplitude and average out small-scale spatial distributions. [15] introduced a methodology for selecting optimal processing parameters in terms of local pressure amplitudes. It addresses the complex interactions between pressure signal, random noise and systematic processing errors. In the present study however, random noise is averaged out reasonably well due to the large number of snapshots, while systematic experimental error sources significantly impact the pressure reconstructions. These errors cannot be modelled because of their unknown distribution and magnitude. Further, in this work the identification of flow structures with small spatial scales of \(\mathcal {O}(1)~\text {mm}\) is more relevant than the accuracy in pressure amplitude. It was therefore necessary to determine the optimal reconstruction parameters empirically. The potential increase in the systematic processing error of the pressure amplitude associated with non-optimal parameters was addressed using the finite element correction procedure described in [15].
Experimental Results
Pressure Reconstructions
Figures 6a-b and 7a and b show averaged slope maps obtained from phase-locked measurements for one phase and for both investigated jet setups. These were used to calculate the corresponding curvature maps (Figs. 6c-e and 7c-e). The noise patterns found in curvature maps indicate the presence of systematic experimental error sources. Without slope smoothing, they can overwhelm the signal from the impinging jet. Pressure reconstructions for 2 different phases for a nozzle exit velocity of 31 m s− 1 and a distance of 10 mm between nozzle and sample, hN, are shown in Fig. 8. σα = 8 and PRW = 12 were used as reconstruction parameters. Due to experimental noise, differential pressure amplitudes below approximately 1 Pa could not be resolved here and were set to 0 to mitigate noise patterns. Figure 8a shows the phase with the highest observed peak pressure amplitude for this setup. The elongated shape of the vortex structure, which originates from the rectangular nozzle, is clearly visible. The orientation of the long and short axis is switched compared to the nozzle orientation (see “Setup”). Since the dynamic pressure decreases with the downstream distance due to entrainment and turbulent decay, the reconstructed peak amplitude of 450 Pa is consistent with the approximately 1200 Pa dynamic pressure that corresponds to the peak velocity at the nozzle exit.
Pressure reconstructions for the second jet setup with nozzle exit velocity of 19 m s− 1 and hN = 25 mm are shown in Fig. 9. Due to the low signal-to-noise ratio, σα = 7 and PRW = 42 were used as reconstruction parameters. The position of the jet impinging in the center of the specimen was identified for both presented phase points. Due to the large downstream distance, the pressure amplitude is significantly reduced compared to the 540 Pa peak dynamic pressure at nozzle exit, and the vortical structure with minor and major axes has decayed into a turbulent jet with approximately Gaussian profile. The negative differential pressure region identified around the center indicates the presence of a vortex ring entraining fluid while moving along the specimen surface, which is consistent with the findings of studies focusing on the flow field, e.g. [31]. Figure 9b shows the phase with the lowest reconstructed pressure amplitude for which the position of the impinging jet could be identified.
Pressure maps for the remaining phase points yield similar results, depending on the pressure amplitudes during the respective phase. The position of the impinging jet could not be identified for a number of phase points, indicating that the amplitudes encountered in these cases are too low to be detected with the present setup. The pressure reconstruction results for all phases and both setups can be found in Appendix A.
It should be noted that the observed spatial distributions and pressure amplitudes could not be validated with any established measurement techniques. Pressure transducers, which are often used to measure low differential pressure amplitudes, do not only provide an insufficient amount of data points, but also average over too large of an area due to their surface diameter of typically 2 − 3 mm. Other full-field techniques cannot resolves the low differential pressure amplitudes or are not applicable to surfaces.
Finite Element Correction
Due to systematic errors in data processing, VFM pressure reconstruction can lead to underestimations of the local pressure amplitudes. In [15] it was shown that the resulting error can be mitigated using a finite element correction procedure, which is employed in the following. In a first step, slope maps are simulated based on an experimentally obtained VFM pressure reconstruction, prec, using a finite element simulation. This was realized using the software ANSYS APDLv181. To simulate the investigated case of a thin plate in pure bending, SHELL181 elements were chosen [4]. The experimental test plate was simulated as homogeneous with the parameters detailed in Table 1. All degrees of freedom were prescribed to be zero along the edges. Processing the thus obtained slope maps with the VFM yields a new pressure distribution, pit,1. The difference between prec and pit,1 reflects the systematic processing error for this particular distribution. It can be interpreted as a first estimate for the systematic error between the real distribution and prec. Adding this difference to prec yields a corrected pressure distribution, pcor, which is closer to the real distribution. The process can be repeated by using pcor as input to the simulation to obtain the next iteration:
where n is the number of iterations. Here the convergence criterion was set as:
In [15] numerical data was used to show that the original load distribution can be approximated very closely for noise-free data with this procedure. The procedure can however significantly amplify noise patterns, in which case spatial filters should be used before the first iteration.
Figure 10 shows an example input pressure distribution and the corrected distribution for a high amplitude case. Here, only one iteration was performed because the correction procedure was found to amplify noise patterns which affect the lower amplitude region of the vortex shape. The peak pressure amplitudes of the shown corrected distribution is approximately 25% higher than that of the original reconstruction. Note that the field of view is reduced around the borders with each iteration, depending on the size of the spatial slope filter kernel and the PRW.
For cases with low signal-to-noise ratio, it was necessary to address the noise patterns found in pressure maps, since they are were amplified by the procedure. Since the pressure distributions found for large distances between nozzle and sample are approximately symmetric, this was achieved by averaging the pressure values for each radial distance from the stagnation point. Figure 11a shows the original pressure reconstruction from experimental data, and Fig. 11b the averaged and corrected distribution. The peak pressure amplitudes of the corrected distribution are 10% − 35% higher than that of the original reconstructions, depending on the investigated phase point.
Error Sources
This section discusses experimental and data processing errors affecting the obtained pressure amplitudes and distributions, as well as the origin of the observed noise patterns. First, systematic errors resulting from phase detection and VFM should be considered. They depend on the chosen reconstruction parameters, particularly the size of the slope filter kernel σα and PRW, the investigated load distribution as well as the signal-to-noise-ratio. In [15] the systematic error was investigated in detail for Gaussian pressure distributions and for different signal-to-noise ratios. In the present study it is difficult to quantify the amount of random noise because slopes were calculated from sets of reference and deformed grid images and averaged, and because the noise patterns stemming from systematic error sources cannot be reliably distinguished from random noise patterns. However, the results of the finite element correction (see “Finite Element Correction”) can be interpreted as an estimate for the systematic processing error (see also [15, chapters 5-6]). It can be estimated to be up to 35% of the local amplitude for uncorrected pressure reconstructions.
In order to estimate the error associated with neglecting inertia (quasi-static plate behaviour), acceleration measurements were conducted using a LDV. The accelerations on the specimen surface were however found to be below the noise level of 0.3 ms− 2. As a worst case estimate, a value of 0.3 ms− 2 can be assumed for the accelerations at every data point. The corresponding dynamic pressure value depends on the PRW window size and is 5 − 35 Pa in the present case. Note that since the accelerations could not be resolved for any setup with the LDV, this is an estimate of the error for the high-amplitude jet setup using Upp = 23 V and hN = 10 mm. The worst-case error estimate is therefore below 8% of the observed peak amplitude. However, if these acceleration were to occur at phases with low pressure amplitude, the associated error in pressure would be of the order of the identified pressure amplitudes. For the lower amplitude jet setup, accelerations can be assumed to be far lower and thus negligible.
Finally, experimental error sources need to be considered. The deflectometry setup is susceptible to misalignments between printed grid and camera sensor, miscalibration, as well as grid defects and damages on the reflective surface. All of these can lead to errors in phase detection. Misalignment is the likely cause for the vertical stripes observed in several pressure maps. Note that the acquisition time for each phase point was more than \(30~{\min \limits } \), such that factors like temperature fluctuations and strained cables may have caused small displacements during measurements. As the investigated printed grid pitch was very small with 0.3 mm and 9 pixels were used to record one reflected grid pitch, these would be sufficient to cause the observed misalignment, despite careful initial arrangement. It should also be noted that the Young’s modulus of the specimen, which is s a linear factor in pressure calculation, was only measured to within 10% [15].
Even though the accumulated potential uncertainty in the identified pressure amplitudes is relatively high, the overall results agree with the magnitudes expected from the applied nozzle exit velocities and downstream distances. The identified spatial distributions correspond to the expected shapes of the vortical structures for the investigated downstream distances.
Limitations and Future Work
The presented VFM pressure reconstructions show that it is possible to obtain high resolution pressure measurements of low-range differential amplitudes with phase-locked deflectometry measurements. Even lower pressure amplitudes can potentially be resolved in future studies by addressing experimental error sources, thus mitigating noise patterns. This could be achieved by using translation stages for the positioning of grid, specimen and camera to address the issue of misalignment. Smaller grid pitches would further increase slope resolution and spatial resolution. Since not all available camera pixels were used in the present study, this would be relatively easy to achieve by changing the printed grid and the camera lens. Slope resolution can also be improved by choosing a larger distance between grid and specimen. However, the availability of suitable camera lenses is a restricting factor. Improving the performance of the VFM by optimising the virtual fields or the pressure determination with higher order approaches could reduce the systematic processing error. These could also allow using smaller PRW sizes, effectively increasing the spatial resolution.
Conclusion
This study presents an approach for full-field pressure reconstructions from phase-locked optical surface slope measurements. A highly sensitive deflectometry setup was used to obtain slopes on a specular reflective specimen. The VFM was used to reconstruct surface pressure from the experimental data and the material mechanical constitutive parameters of the flat plate specimen. It was shown that it is possible to obtain physically meaningful pressure distributions with amplitudes of \(\mathcal {O}(1)~\text {Pa}\) - \(\mathcal {O}(100)~\text {Pa}\) and spatial extent of \(\mathcal {O}(1)~\text {mm}\) - \(\mathcal {O}(10)~\text {mm}\) with this approach. The identification of lower surface pressure amplitudes was limited by noise patterns originating from experimental error sources. Possible improvements for addressing this issue in future studies were discussed. The results are outstanding in terms of the small spatial scales and surface pressure amplitudes which were identified in full-field.
Data Provision
All relevant data produced in this study is available under the DOI https://doi.org/10.5258/SOTON/D1166.
References
Amitay M, Cannelle F (2006) Evolution of finite span synthetic jets. Phys Fluids 18(5):054,101
Badulescu C, Grédiac M, Mathias JD (2009) Investigation of the grid method for accurate in-plane strain measurement. Measur Sci Technol 20(9):095,102
Balzer J, Werling S (2010) Principles of shape from specular reflection. Measurement 43(10):1305–1317
Barbero E (2013) Finite element analysis of composite materials using ANSYS®;, 2nd edn, Composite Materials. CRC Press
Berry A, Robin O (2016) Identification of spatially correlated excitations on a bending plate using the virtual fields method. J Sound Vib 375:76–91
Berry A, Robin O, Pierron F (2014) Identification of dynamic loading on a bending plate using the virtual fields method. J Sound Vib 333(26):7151–7164
Brown K, Brown J, Patil M, Devenport W (2018) Inverse measurement of wall pressure field in flexible-wall wind tunnels using global wall deformation data. Exp Fluids 59(2):25
Chen N, Yu H (2014) Mechanism of axis switching in low aspect-ratio rectangular jets. Comput Math Appl 67(2):437–444. mesoscopic Methods for Engineering and Science (Proceedings of ICMMES-2012, Taipei, Taiwan, 23-27.07.2012)
D’Errico J (2009) Inverse (integrated) gradient. https://de.mathworks.com/matlabcentral/fileexchange/9734-inverse-integrated-gradient https://de.mathworks.com/matlabcentral/fileexchange/9734-inverse-integrated-gradient (accessed on 12.06.2019)
Glezer A, Amitay M (2002) Synthetic jets. Ann Rev Fluid Mech 34(1):503–529
Grédiac M, Sur F, Blaysat B (2016) The grid method for in-plane displacement and strain measurement: a review and analysis. Strain 52(3):205–243
Holman R, Utturkar Y, Mittal R, Smith B, Cattafesta L (2005) Formation criterion for synthetic jets. AIAA J 43:2110–2116
Jaw Y, Chen JH, Wu PC (2009) Measurement of pressure distribution from PIV experiments. J Vis 12:27–35
de Kat R, van Oudheusden BW (2012) Instantaneous planar pressure determination from piv in turbulent flow. Exp Fluids 52(5):1089–1106
Kaufmann R, Pierron F, Ganapathisubramani B (2019) Full-field surface pressure reconstruction using the Virtual Fields Method. Experimental Mechanics 59(8):1203–1221
Kaufmann R, Pierron F, Ganapathisubramani B (2019) Reconstruction of surface pressure fluctuations using deflectometry and the Virtual Fields Method. Experiments in Fluids. Accepted November 2019
Lecoq D, Pézerat C, Thomas JH, Bi W (2014) Extraction of the acoustic component of a turbulent flow exciting a plate by inverting the vibration problem. J Sound Vib 333(12):2505–2519
O’Donoughue P, Robin O, Berry A (2017) Time-resolved identification of mechanical loadings on plates using the virtual fields method and deflectometry measurements. Strain 54(3):e12,258
Pezerat C, Guyader JL (2000) Force Analysis Technique: Reconstruction of force distribution on plates. Acta Acust United Acust 86(2):322–332
Pierron F, Grédiac M (2012) The virtual fields method. Extracting constitutive mechanical parameters from full-field deformation measurements. Springer, New York
Poon CY, Kujawinska M, Ruiz C (1993) Spatial-carrier phase shifting method of fringe analysis for moiré interferometry. J Strain Anal Eng Des 28(2):79–88
Ritter R (1982) Reflection moire methods for plate bending studies. Opt Eng 21:21–9
Robin O, Berry A (2018) Estimating the sound transmission loss of a single partition using vibration measurements. Appl Acoust 141:301–306
Surrel Y (1996) Design of algorithms for phase measurements by the use of phase stepping. Appl Opt 35 (1):51–60
Surrel Y (2000) Photomechanics, chap Fringe Analysis. Springer, Berlin, pp 55–102
Surrel Y, Pierron F (2019) Deflectometry on curved surfaces. In: Lamberti L, Lin M T, Furlong C, Sciammarella C, Reu P L, Sutton M A (eds) Advancement of optical methods & digital image correlation in experimental mechanics, vol 3. Springer International Publishing, Cham, pp 217–221
Surrel Y, Fournier N, Grédiac M, Paris PA (1999) Phase-stepped deflectometry applied to shape measurement of bent plates. Exp Mech 39(1):66–70
Tropea C, Yarin A, Foss J (2007) Springer handbook of experimental fluid mechanics. Springer, Berlin
Van Buren T, Whalen E, Amitay M (2014) Vortex formation of a finite-span synthetic jet: effect of rectangular orifice geometry. J Fluid Mech 745:180–207
Xu Y, Wang JJ (2016a) Flow structure evolution for laminar vortex rings impinging onto a fixed solid wall. Exp Thermal Fluid Sci 75:211–219
Xu Y, Wang JJ (2016b) Flow structure evolution for laminar vortex rings impinging onto a fixed solid wall. Exp Thermal Fluid Sci 75:211–219
Zienkiewicz O (1977) The finite element method. McGraw-Hill, New York
Acknowledgments
This work was funded by the Engineering and Physical Sciences Research Council (EPSRC). Girish Jankee has supported this work by providing hot wire data for the nozzle exit velocities.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kaufmann, R., Ganapathisubramani, B. & Pierron, F. Surface Pressure Reconstruction from Phase Averaged Deflectometry Measurements Using the Virtual Fields Method. Exp Mech 60, 379–392 (2020). https://doi.org/10.1007/s11340-019-00564-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11340-019-00564-6