Abstract
Friction joints are one of the fundamental means used for the assembly of structural components in engineering applications. The structural dynamics of these components becomes nonlinear, due to the nonlinear nature of the forces arising at the contact interface characterised by stick-slip phenomena and separation. Advanced numerical models have been proposed in the last decades which have shown some promising capabilities in capturing these local nonlinearities. However, despite the research efforts in producing more advanced models over the years, a lack of validation experiments made it difficult to have fully validated models. For this reason, experimental techniques which can provide insights into the local dynamics of joints can be of great interest for the refinement of such models and for the optimisation of the joint design and local wear predictions. In this paper, a preliminary study is presented where ultrasound waves are used to characterise the local dynamics of friction contacts by observing changes of the ultrasound reflection/transmission at the friction interface. The experimental technique is applied to a dynamic friction rig, where two steel specimens are rubbed against each other under a harmonic tangential excitation. Initial results show that, with a controlled experimental test procedure, this technique can identify microslip effects at the contact interface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Friction joints are one of the main causes of uncertainty for the validation of the structural dynamic performance of built-up structures [1]. Friction joints introduce nonlinearity in the structural dynamics of the components, leading to frequency shifts, changes in damping, and increasing levels of uncertainty due to the poor repeatability in the assembly of these joints, which makes their modelling, analysis and testing particularly challenging [2,3,4]. Advanced modelling approaches have been developed over the years to account for the effect of frictional nonlinearities on the dynamic response of the system [5,6,7,8]. These modelling approaches must be validated against experimental results, to confirm the quality of the models and their reliability for the analysis of complex nonlinear structures. Despite some validations performed on the global scale which looks at the nonlinear dynamic response of the assembled system [9, 10], experimental techniques which can be used to improve the understanding of local joint dynamics are still a rather unexplored field of research. One of the main reasons for this lack of local experiments is the lack of a suitable technique which is able to capture what is happening locally without interfering with the contact itself. A brief overview of possible approaches found in the literature is reported here.
One of the approaches to detect stick-slip relies on the sound waves generated by the frictional energy dissipation at the interface. Previous studies [11,12,13] have used acoustic emissions (AE) measured in the near field around the contact to detect the onset of slipping in a tensile test machine. The main drawback for dynamic applications would be to isolate the frictional noise from other sources of noise in the test (structural vibration, shaker etc.) as well as the challenge for the localisation of the slipping area.
Another way of detecting stick-slip is by measuring the relative displacement between the sliding contact interfaces. Accurate and non-contacting measurements are possible through laser measurements (see e.g. some of the friction rigs for hysteresis loop measurements [14,15,16,17]) or by using digital image correlation (DIC) [18,19,20,21]. In a recent study [18], the authors have used DIC to monitor the local contact interface of a frictional damper. This experimental approach allowed a clear identification of the different phases of stick, slip and separation at the interface level, demonstrating its capabilities for the investigation of friction contacts. However, one of the main limitations of this approach is the need to have a side view access of the interface, which might not always be available. In addition, the information provided is only two-dimensional, and relative to the edge of the contact interface, without providing any insight into the behaviour of the central part of the contact. This is a very limiting factor, especially for interfaces with a large area of contact and a small accessible side edge.
The use of pressure films is an additional technique to measure the contact area, force and pressure at joints. Film sensors have recently been developed [22] that are able to map the joint pressure not only statically, but also dynamically up to 10 kHz. Unfortunately, the thickness of the sensor and its compliance lead to a change of the contact geometry and characteristics such as, friction coefficient, tangential and normal contact stiffness which prevent its use in a sliding contact interface. In addition, these sensors still do not have the capability to detect slip.
The ultrasound technique, which is the focus of this paper, can be also used to monitor the local dynamics of friction joints. This technique is described in detail in the following Section.
Ultrasounds and Contact
Ultrasonic techniques have been used for more than 50 years to study tribological contacts [23,24,25,26]. Ultrasound is an acoustic wave with a frequency above the human audible range (> 20000Hz). When an ultrasonic wave is propagated through two components in contact, a portion of the incident wave is reflected back and is proportional to the contact stiffness. The ratio between the maximum amplitudes of reflected and incident waves is known as reflection coefficient and, for perfectly bonded interfaces, it depends on the relative mismatch between the acoustic impedances of the two materials, Z1,2 = ρc, where ρ is the material’s density and c is the speed of sound in the material. The reflection coefficient is calculated as follows:
If the material of the bonded interfaces is the same, then the signal is fully transmitted. For not perfectly bonded interfaces, i.e. realistic rough contact interfaces, the ultrasonic wave is not fully transmitted through the interface due mainly to the the low acoustic impedance of the air at cavities [25, 26]. In particular, when the acoustic impedances of the materials of the two interfaces are the same, the factor that governs the ultrasound reflection/transmission is the stiffness of the contact interface [25, 27], which can be directly related to the contact stiffness in the nonlinear dynamic models. The most common modelling approach used so far to describe this behaviour is the “spring model” proposed by Tattersall [27], which consists of a set of springs at the interface. In this case the reflection coefficient for two different materials can be described as:
where K is the stiffness of the interface and ω is the frequency of the ultrasonic wave. For the same pair of materials the equation simplifies and, solving it explicitly for the contact stiffness, it becomes:
Therefore, for a given material and ultrasound wave frequency it is possible to obtain the contact stiffness by measuring the experimental reflection coefficient. Additional analytical models have been developed to include features, such as mass at the interface [28], the damping coefficient [29], or continuum models of the interface [30]. However, the basic spring model has been found to be satisfactory for most of the engineering applications, where the ultrasound frequency is not extremely high (few MHz), and for this reason it will be used here.
Several studies investigated the tribological contacts under static conditions [31,32,33,34,35,36,37,38]. Drinkwater et al. [31] have carried out an extensive study for a partially contacting aluminium interface under different loads. Another study between grounded steel pairs with various roughnesses has been carried out by Arakawa [32]. They showed that rough interfaces reflected less of the wave amplitude than smooth interfaces. Dwyer-Joyce et al. [33] have studied the ultrasound reflection with repeated loading and unloading of a flat aluminium plate pressed against a flat circular punch made of steel, showing an hysteretic behaviour at the interface. These techniques have been successfully applied to a variety of engineering problems, like mapping the contact stresses on bolted joints [34] or interference fits, such as bushes on shafts [39, 40].
More complicated is the case of the ultrasound transmission through sliding contacts [21, 25, 41,42,43,44,45,46], with the pioneering work of Kendall and Tabor [25] being one of the most significant. They used a pin on disc rig under steady sliding and a longitudinal ultrasonic transducer. In that study an increase in ultrasound transmission could be observed, which was explained by the local junction growth of the asperities in contact [47]. Recently, Mulvhill et al. [21], have investigated the tangential contact stiffness of a friction contact at a constant normal load and a gradually increasing tangential load. Digital image correlation and ultrasounds have been compared providing interesting insights. It has been confirmed that the DIC technique measures the tangential contact stiffness of the plastic part of the load-deflection plot, whereas the ultrasonic technique always measures an unloading elastic stiffness, which is independent of the sliding condition and always larger than the one obtained from the load-deflection plots. Their results are further described in section “Test 1: Stick/Slip Ultrasound Test”, where the similarities with the current study are discussed.
The present study focuses on variations in the ultrasound reflection/transmission induced by the local dynamics of sliding contacts, which are representative of vibrating structures with frictional joints. A friction rig built in the Dynamics Group of Imperial College London [14, 15] has been upgraded to perform ultrasounds measurements in combination with friction measurements, and is described in the next Section.
1D Friction Rig Application
The test case chosen for the evaluation of the ultrasound-based technique for friction contacts is the 1D friction rig built in the Dynamics Group of Imperial College London [14, 15], since it generates a well understood and controllable unidirectional oscillating sliding motion in a flat-on-flat contact pair. This rig is able to measure the contact hysteresis loop which occurs at frictional interfaces excited by vibrational forces. The hysteresis loop is a load-displacement plot of the friction force occurring between the two oscillating contact interfaces against their relative displacement. An example of a measured hysteresis loop is shown in Fig. 1. From the measured hysteresis loop, contact properties such as friction coefficient, μ, and tangential contact stiffness, kt, are extracted and can then be used to calibrate contact models for nonlinear dynamic analyses. The friction coefficient is obtained by dividing the force required to start to slide, T, by the applied normal load, N, which pushes the contact interfaces together. The contact stiffness is obtained from the slope of the stick portion of the loop, which is due to the elastic deformation of the micro-asperities at the contact interfaces [48, 49] and to the bulk elastic deformation at the macroscopic contact scale [50,51,52].
Example of a measured contact hysteresis loop on the 1D friction rig [14]
In the present paper, the correlation is investigated between the hysteresis loops evolution due to fretting and ultrasounds transmission at the interface. This set up has been chosen because it allows to conduct highly controlled friction tests, in which it is easy to closely monitor and control the sliding distance between the two specimens, the tangential friction force and the applied normal load.
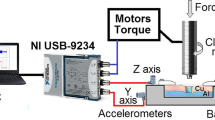
A side view of the 1D friction rig with all its main components is shown in Fig. 2. The rig is composed of a moving block (moving mass and moving arm) that oscillates horizontally under the harmonic excitation of an electrodynamic shaker. The moving specimen, clamped to the moving arm, slides over the static specimen that is clamped to the static arm. The shaker excites the inertia mass (moving mass in Fig. 2), which in turn transmits its motion to the moving arm and the specimen. A close view of the two friction specimens and holding arms is shown in Fig. 3(a), where is also shown the vertical rod that provides the normal load via a pneumatic actuator. The tangential friction force transmitted between the two specimens is measured by means of three force transducers that are placed between the static arm and the static mass. The relative displacement between the two specimens is measured using two Laser Doppler vibrometers (LDVs), which are focused on each specimen less than 1mm far from the contact (see Fig. 3(b)). The friction rig can work at relatively high excitation frequencies, up to 200Hz, compared to the standard tribometers, which work at lower frequencies (< 10 Hz). The maximum normal load is 500N and the maximum tangential relative displacement between the contact surfaces is 25μm. The contact is in a flat-on-flat configuration, with nominal areas of contact variable in the range 1mm2-25mm2. Tests can either be load controlled or displacement controlled. In the present study, sliding tests were conducted in displacement control at 100Hz of excitation frequency, 90N of normal load and a nominal area of contact of 9mm2, resulting in a nominal contact pressure of 10MPa.
In order to perform the ultrasonic tests on the 1D friction rig, new specimens had to be specifically designed to accommodate the ultrasonic transducers. The original specimens were full solid cylinders with a flat area of contact (see Fig. 4(a)). The new specimen is shown in Fig. 4(b), and its concept scheme is shown in Fig. 4(c). This new design is the same for both moving and static specimens. Each specimen is manufactured in two parts, a friction head which is then screwed to a threaded hollow holder, both made of a standard stainless steel AISI 304. This choice allowed the mounting of the ultrasound transducer on the surface opposite and parallel to the friction contact surface, as shown in Fig. 4(c). In addition, with this design choice, the ultrasonic transducer could be mounted relatively close to the contact surface, at a 8mm distance, which is close to the minimum operating distance suggested by the transducer manufacturer. The specimens are mounted on the moving and static arms in the same way as the original ones. They are rotated by 90 degrees with respect to each other, in order to form a square contact patch as shown in Fig. 4(a). The resulting area of contact is a 3 by 3 mm square, which allows a large portion of the ultrasound wave to be transmitted through the contact to the second transducer. Although it could have been possible to operate in a pulse-echo mode, it was preferred to use a second transducer to measure the transmitted signal. This was quite useful at very low normal loads, as its higher percentage variation compared to the reflected signal allowed for more accurate measurements. The chosen ultrasonic transducers were square shear plate Noliac CSAP02, with dimensions 5 by 5 by 0.5 mm, and capable of a maximum free stroke of 1.5μ m. The shear plates were glued to the specimen heads, using a two-parts Loctite Double Bubble epoxy resin capable of a shear strength of 9 MPa.
The contact area (3 by 3 mm) is smaller than the area of the probe (5 by 5 mm) because the friction rig normally works with a 1mm2 contact area since larger areas of contact can lead to difficulties in specimen alignments. Therefore, the chosen compromise to accommodate the transducer was to increase the contact area up to 9mm2.
Static Ultrasounds Tests
Some initial tests were carried out to evaluate the capabilities of this technique in a static configuration. These tests aimed at verifying that changes of contact pressure led to variations in the reflected/transmitted ultrasound signal as shown in previous studies [21, 31,32,33,34,35,36,37,38]. The specimens’ heads with the shear plates attached were mounted on an Instron tensile/compressive machine via a specially designed flange (see Fig. 5(a)). The Instron rig was chosen instead of the 1D friction rig, as it allows to explore a very large range of contact pressure, being able to reach a maximum 5 kN compressive force compared to 0.5 kN on the 1D rig. The full set up and a close up of the specimens are shown in Fig. 5(a). A PC-controlled Handyscope HS3 was used as both excitation source and acquisition device for the piezo shear plates, since it incorporates both an oscilloscope with a sampling rate of 50 MHz at 12 bit and an arbitrary waveform generator (50 MHz sampling rate). The connection scheme used for this test is shown in Fig. 5(b). The output was used to excite the piezo of the specimen 1, and with a split connector, the reflected signal could also be received back and acquired. The second channel (synchronized) was used to acquire the signal transmitted to the piezo attached to the specimen 2, which acted only as a receiver. This transmitted signal is the one passing through the contact interface.
A 3-cycle burst was generated at 2 MHz with a peak to peak amplitude of \(\sim \)10 Volts and was then directly sent to the shear plate, without using an amplifier. The 2 MHz were chosen for the signal generation in order to maximise the ultrasonic wave energy, as this was the resonance frequency of the shear plates attached to the specimens. Once the pulse was sent, only the first reflection was strong enough to be captured by the piezo transducer, and it was around 0.89 V peak to peak when no pressure was applied at the interface. An example of the signal sent and received back at specimen 1 is shown in Fig. 6(a). A Hilbert-envelope of the time domain signal was used to more accurately identify the maximum peak of the burst received (P1 in Fig. 6(a)).
Ultrasound tests were performed for different static normal loadings up to 900 N, corresponding to 100 MPa for this contact interface. Reflected and transmitted signals were recorded at each load:
The signal transmitted to the piezo transducer of the specimen 2 at the various pressure levels is shown in Fig. 6(b). As expected, a strong variation of the transmitted signal amplitude can be observed, which goes from almost zero when no pressure is applied (a tiny signal could be present due to the internal card ’cross-talk’), to the positive max of 0.73 V at 100 MPa. At 5 MPa, the signal acquired was relatively close to the no-load case, having a positive peak at \(\sim \)0.02 V against \(\sim \)0.01 V, but at 10 MPa already, a stronger signal at 0.09 V was measured. This confirms that this technique could be potentially applied to investigate the normal load variation of a joint under dynamic conditions, being only limited by the sensitivity of the measurement system for low variation of the load.
The reflected signal was used to calculate the reflection coefficient, through the ratio R = Ai/A0, where Ai is the acquired amplitude (peak of the Hilbert envelope) of the reflected signal when the load i is applied and A0 is the amplitude of the reference reflected signal obtained when the interfaces are not in contact. Please note that A0 is equivalent to the incident signal in the case of no contact, as the incident signal is almost completey relfected back due to the low acoustic impedance of the air compared to the higher one of the metal. The reflection coefficient was then used to evaluate the tangential contact stiffness through equation (3), where K is the stiffness of the interface expressed in N/mm3, ω is the frequency of the ultrasonic wave (equal to 2MHz), and Z = ρc is the acoustic impedance of the material, where the density ρ for the steel is 7500 kg/m3 and the velocity c of the ultrasonic wave was found to be 2770 m/s after measuring the time taken for the generated signal to be received back. Unlike the application in [25], here a shear wave transducer is used instead of a longitudinal one, and therefore the K measured is actually the tangential stiffness Kt, but no limitations are expected for the model. A significant increase in contact stiffness can be appreciated, which ranges from almost zero at 5 MPa (minimal variation of the reflection coefficient) to a value of 134600 N/mm3 at 100 MPa, as shown in Fig. 7. A trend could be observed, which is in accordance with the results obtained in [49]. These ultrasound results indicate that this approach is a technique well suitable to extract stiffness values for a contact under varying loading condition, with a relatively quick set up.
Dynamic Ultrasounds Tests
After the static tests on the Instron rig, the specimens were mounted on the 1D friction rig for the tests under dynamic conditions. Preliminary 3D interferometry scans were obtained to gain insights on the surface finishing, before wear could occur at the interface during the dynamic tests. A 3D TopMap Polytec interferometer was used to scan the full contact surface, which revealed a roughness Ra between 0.21 and 0.24 μ m that is compatible with the machining process used (milling). However, few machining marks (up to 5 μ m deep) were present on the surface, due to the milling process, as shown by the magnified 3D plot of Fig. 8. As a result of these marks, the contact did not occur over the whole interface, thus probably reducing the interface stiffness and the ultrasonic transmission. However, it is assumed that this condition did not compromise the results of the experimental campaign.
The experimental campaign consisted of four different tests performed under a dynamic oscillating tangential motion and described in the following Sections.
Test 1: Stick/Slip Ultrasound Test
The first tangential test was performed in order to investigate if the ultrasound reflection was affected by changes from stick to slip in the local contact conditions. To this purpose, the Handyscope ultrasound controller was synchronised with the National Instrument PXI controller used to control the 1D friction rig. The goal was to be able to send ultrasonic signals that could reach the contact on demand during either the sticking or sliding phase.
When the friction rig operates, the shaker exerts a harmonic excitation to the top specimen, which enters in a sliding motion with the bottom specimen due to the tangential oscillations. As a result of this sliding motion, hysteresis loops are generated (see Fig. 1). When the excitation force is small, hysteresis loops are fully stick and the tangential friction force transmitted between the two specimens is almost perfectly sinusoidal. As the excitation is increased, specimens start to slide and the friction force signal in time becomes similar to a square wave as it oscillates between positive and negative Coulomb friction limit (± μN). For this reason, the signal of the friction force represents an effective way to evaluate whether the two specimens undergo a relative sliding or not.
After the synchronisation, the control was able to send two ultrasonic bursts during the two different phases of the contact interface (stick, slip) as shown in Fig. 9(a). This was achieved by generating a trigger signal sent to the input trigger channel of the Handyscope controller, which in turn generated the ultrasound burst for the specimens. One trigger was synchronised with the sliding phase of the specimens (black one in Fig. 9(a)), whereas the other trigger was synchronised with the sticking phase (red one in Fig. 9(a)). It should be pointed that the two ultrasound bursts could not be sent within the same hysteresis loop, due to the time needed to initialise the measurement. Therefore two separate tests were required for the stick and sliding triggers.
The results of this investigation are shown in Fig. 9(b), in which no real difference can be noticed for the two different triggers, apart from the scatter of the measurements as confirmed by the three subsequent reflected bursts. These results seem to be in accordance with the findings of Mulvihill et al. [21] obtained with a quasi-static rig, who observed that the reflected signal did not change during the different phases of contact (sticking or sliding). However no conclusive remarks could be made here as the scatter between different measurements was significant and it was not possible to measure the two phases of stick/slip within the same hysteresis loop. Further tests will be required with an improved controller which would allow a much faster synchronization to send and receive multiple ultrasounds measurements within a single hysteresis loop.
During this experimental campaign, a variation of the ultrasound signal was noticed over time. This behaviour was investigated more in detail and a new test was planned (see next Section), in which no synchronization was used between the Handyscope and the 1D rig controller.
Test 2: Effects of Duration Time and Varying Sliding Distances
This test was divided into different steps starting from an initial ramping up of the static normal load (0 N, 45 N, 90 N) with no rig tangential excitation, followed by dynamic tests with increasing tangential relative motion between the two specimens, at a constant pressure of 10 MPa (90 N), and a final unloading static phase. The test sequence is shown in Fig. 10. At the beginning of the dynamic measurement, the two specimens were subjected to a micro sliding of 0.5 μ m, corresponding to a microslip regime of the contact interface, which was then gradually increased up to reaching a full macroslip regime with a sliding distance of approximately 15 μ m. During each step, a series of ultrasound measurements were performed every 40 seconds, with the reflection and transmission signals simultaneously acquired by the Handyscope, while at the same time measuring the contact hysteresis loops with the 1D friction rig (as described in section “1D Friction Rig Application”). To reduce the scatter of the measurement due to noise, each reported ultrasound measurement was the result of an averaging process of 100 bursts sent and received back. A total of 89 ultrasound measurements was performed, resulting in a total running time of the test of 1 hour.
Figure 10 shows the the peak to peak max Hilbert envelope of the transmitted signal (specimen 2) for all the consecutive measurements taken. Although the reflected signal could have been used as well, the choice of using the transmitted signal was due to its higher sensitivity for the post-processing of low loads.
As expected, a significant increase in transmission is observed for the initial static loading, where the signal goes from \(\sim \)0.07 V to \(\sim \)0.25 V. A gradual but clear increase in transmission is also observed when the relative motion is increased, despite keeping the normal load constant at 90 N (10 MPa). An increase in transmission is also observed within the same measurement step at a fixed relative motion, with a growth rate which is increasing at higher relative motions. On the contrary, at lower relative motion levels (low vibration levels), the transmission is not very much affected. The maximum measured transmitted signal is 0.42 V and corresponds to a 5μm relative motion, which is the maximum relative motion achievable in a microslip regime before the gross sliding regime begins. This transmitted value of 0.42 V is approximately 70 % higher than the last static measurement before microslip (0.25 V). When the relative motion is further increased, the specimen goes into a macroslip regime (gross sliding), and the transmitted ultrasound signal drops to a minimum of 0.23 V, before recovering and starting to strongly grow once more and showing also some scatter. During the final unloading, similar transmitted amplitudes are observed compared to the ones of the initial static loading phase.
These findings seem to suggest that some changes occur at the contact interface for higher relative motions within the microslip regime, which lead to an increase of the transmitted signal. A possible reason for this increase in the transmission is the accumulation of debris due to wear, which in fact are generated more easily at larger relative sliding motions. It is therefore possible that, during the macroslip full sliding regime, these debris are washed away, and the signal drops again before an increased wear rate leads to a new rise. This hypothesis is investigated with the following test.
Test 3: Wear Debris Hypothesis
To confirm this hypothesis, a new test was performed, similar to the previous one, but with a sudden change in the relative sliding motion from 0.5 μ m to 4.5 μ m. In fact, it is hypothesised that a sudden change of relative motion should not lead to an immediate increase of transmission if a gradual local accumulation of debris is the key mechanism. However, as shown in Fig. 11, the results obtained do not confirm this hypothesis, since the signal shows a 75% sudden increase, jumping from 0.2V to approximately 0.35V when the sliding distance is increased. Therefore the accumulation of debris due to wear is not a possible explanation for this increase.
Test 4: Plasticity Hypothesis
Another hypothesis, which could explain this behaviour is a change of the real contact area during the microslip regime. To investigate this further, a new test was performed, very similar to the one of Fig. 10, but without reaching the macroslip regime between the two specimens. Instead, after reaching the relative motion of 5 μ m, the contact was brought back to 1 μ m relative motion (step G in Fig. 12). As shown in Fig. 12, a similar trend as before is observed, but the maximum value of transmission is reached with the repeated 1 μ m test, which shows a \(\sim \)0.43 V transmitted signal, 138 % higher than the value of \(\sim \)0.18 V of the precedent similar step B. This seems to indicate that a permanent plastic deformation has occurred at the contact interface, which led to an increase of the real contact area, thus increasing the ultrasonic transmission. A similar behaviour has been observed in [25], where a pin-on-disk sliding test was perfomed with a longitudinal wave transducer, and the increase in transmission has been attributed to the junction growth of contacting asperities [47].
In addition, the comparison between Tests 2 and 4 (respectively Figs. 10 and 12) shows that results are well repeatable, as the values of transmitted signals are comparable. Tests were conducted with the same couple of specimens, but after every test the specimens were disassembled and then reassembled together for the next test. The new assembly lead every time to new contact configurations, which reset the surface condition as a result of new asperities in contact.
Comparison Between Ultrasound and Hysteresis Loops Measurements
Results of Test 4 were compared with the hysteresis loop measurements coming from the 1D friction rig in order to check whether a change of contact stiffness could be observed. It is in fact known from previous studies, such as the one in [25, 52], that an increase of real contact area is linked with an increase of contact stiffness. The hysteresis loops corresponding to the microslip tests with increasing relative motion A to F are shown in Fig. 13(a). For each loop, the tangential contact stiffness of the whole contact was extracted by measuring the slope of the secant between the two extreme points of the hysteresis loop. This represents the equivalent stiffness introduced by the joint under a particular level of excitation amplitude. Figure 13(b) shows that the joint stiffness tends to decrease with increasing relative motion, which is the expected behaviour of a joint progressively starting to slide. In fact, if there is sliding, the frictional joint will not be stuck anymore and it will consequently lose stiffness. However, when comparing steps B and G, which have the same relative motion (and therefore, same loss of stiffness due to the joint microslip), a 18.7 % increase in contact stiffness can be observed which goes from 3210 N/mm3 to 3810 N/mm3. This seems to be an indication that the real contact area has increased due to the plastic deformation of the asperities, as hypothesised with Test 4. The increased area of contact lead to a stiffer joint for the same relative motion of 1 μ m. This behaviour also confirms the idea of the ultrasound transmission driven by the real contact area.
Concluding, these tests suggest that although the joint loses stiffness as it approaches the Coulomb limit (because more sliding leads to a less stiff assembly), a higher ultrasound transmission is measured due to the microslip at the contact interface, which leads to an increase in the real contact area. In addition, this change of contact area caused by microslip is permanent (potentially governed by local plastic deformation) and ultimately leads to a stiffer joint when the excitation amplitude is decreased back from its maximum. The change in the area of contact happens if the relative motion is large enough (> 2μ m) so that asperities can plastically deform and increase their area of contact.
On the contrary, Test 2 also showed that when the joint enters in full sliding (> 15μ m), and macroslip at the contact interface is reached, the transmission drops, probably due to new contacts formed between asperities that did not undergo a plastic deformation yet. This might suggest that the plastic deformation of the asperities can permanently increase the area of contact only until dramatic changes are experienced by the contact interfaces and the asperities reset their contact conditions. However, the scatter of the measurements observed in various tests impedes to draw conclusions for the macroslip regime.
Further tests can be performed in the future to confirm the hypothesis of a growing area of contact due to the plastic deformation of the asperities and to assess its effects on the dynamics of structures with frictional joints. It will also be interesting to further investigate the ultrasound response to full sliding macroslip experiments and to evaluate the possible influence of a modification of contacting surface roughness, topography and area of contact during the test.
Conclusions
In this article, the ultrasound technique is applied to monitor the local dynamics of friction joints. It is found that local contact conditions affect the ultrasonic reflection/transmission signals, which in turn can be analysed to give insights on the frictional behaviour of oscillating contacts.
An ultrasound setup, similar to that used by other authors for static tests, has been applied to a friction rig capable of performing sliding tests with an oscillatory tangential load. These sliding tests are representative of joints of assembled structures that are subjected to structural vibrations. Preliminary experiments have been performed on the static normal contact problem and an increase in transmission has been observed for higher pressures, in accordance with previous studies.
Since these results confirmed the reliability of the chosen experimental setup, novel tests have been performed with a dynamic tangential loading of the contact. A strong increase in the ultrasound transmission over time has been observed, especially as the relative motion between the two metal specimens increased. The authors believe that this increase in transmission is the result of an increase of the real contact area at the interface, probably due to a displacement-induced plasticity of the asperities in contact. An increased transmission is the result of a more conformal and stiffer contact, which might affect the dynamic behaviour of the assembled structure. These findings reveal indeed that a highly controlled test, in which the excitation is gradually increased before approaching macroslip, is needed in combination with ultrasounds measurements to gain useful insights into the joint local dynamics.
These results are promising and could form the basis for the future development of an experimental technique to monitor the behaviour of friction joints for vibrating structures.
References
Gaul L, Nitsche R (2001) The role of friction in mechanical joints. Appl Mech Rev 54(2):93–106
Gaul L, Lenz J (1997) Nonlinear dynamics of structures assembled by bolted joints. Acta Mech 125 (1):169–181
Di Maio D, Schwingshackl C, Sever IA (2016) Development of a test planning methodology for performing experimental model validation of bolted flanges. Nonlinear Dyn 83(1):983–1002
Fantetti A, Gastaldi C, Berruti T (2018) Modeling and testing friction flexible dampers: challenges and peculiarities. Exp Tech 42:407–419
Krack M, Salles L, Thouverez F (2016) Vibration prediction of bladed disks coupled by friction joints. Archives of Computational Methods in Engineering, pp 1–48
Cigeroglu E, An N, Menq CH (2008) Forced response prediction of constrained and unconstrained structures coupled through frictional contacts. J Eng Gas Turbines Power 131(2):919
Pesaresi L, Salles L, Jones A, Green J, Schwingshackl C (2017) Modelling the nonlinear behaviour of an underplatform damper test rig for turbine applications. Mech Syst Signal Process 85:662–679
Gastaldi C, Fantetti A, Berruti T (2017) Forced response prediction of turbine blades with flexible dampers: the impact of engineering modelling choices. Appl Sci 1:8
Berruti T (2010) A test rig for the investigation of the dynamic response of a bladed disk with underplatform dampers. Mech Res Commun 37:581–583
Lacayo R, Pesaresi L, Gross J, Fochler D, Armand J, Salles L, Schwingshackl C, Allen M, Brake M (2019) Nonlinear modeling of structures with bolted joints: a comparison of two approaches based on a time-domain and frequency-domain solver. Mech Syst Sig Process 114:413–438
Ferrer C, Salas F, Pascual M, Orozco J (2010) Discrete acoustic emission waves during stick–slip friction between steel samples. Tribol Int 43:1–6
Emira NA, Mohamad HT, Tahat MS (2011) Stick-slip detection through measurement of near field noise. J Mech Eng Res 3(March):96–102
Geng Z, Puhan D, Reddyhoff T (2019) Using acoustic emission to characterize friction and wear in dry sliding steel contacts. Tribol Int 134:394–407
Fantetti A, Tamatam L, Volvert M, Lawal I, Liu L, Salles L, Brake M, Schwingshackl C, Nowell D (2019) The impact of fretting wear on structural dynamics: experiment and simulation, Tribology International
Schwingshackl CW (2012) Measurement of friction contact parameters for nonlinear dynamic analysis. In: Proceedings of the society for experimental mechanics IMAC conference
Filippi S, Akay A, Gola MM (2004) Measurement of tangential contact hysteresis during microslip. J Tribol 126(3):482
Lavella M, Botto D, Gola MM (2013) Design of a high-precision, flat-on-flat fretting test apparatus with high temperature capability. Wear 302(1-2):1073–1081
Pesaresi L, Stender M, Ruffini V, Schwingshackl CW (2017) DIC measurement Of the kinematics of a friction damper for turbine applications, pp 93–101. Springer International Publishing, Cham
Kartal ME, Mulvihill DM, Nowell D, Hills DA (2011) Measurements of pressure and area dependent tangential contact stiffness between rough surfaces using digital image correlation. Tribol Int 44(10):1188–1198
Kartal ME, Mulvihill DM, Nowell D, Hills DA (2011) Determination of the frictional properties of titanium and nickel alloys using the digital image correlation method. Exp Mech 51(3):359–371
Mulvihill DM, Brunskill H, Kartal ME, Dwyer-Joyce RS, Nowell D (2013) A comparison of contact stiffness measurements obtained by the digital image correlation and ultrasound techniques. Exp Mech 53:1245–1263
Bachus KN, DeMarco AL, Judd KT, Horwitz DS, Brodke DS (2006) Measuring contact area, force, and pressure for bioengineering applications: using Fuji Film and TekScan systems. Med Eng Phys 28:483–8
Krachter H (1958) Ein neuartiges verfahren zur messung von druckkraften mit ultraschall. Werkstatt und Betrieb 5:246–248
Masuko M, Ito Y (1969) Measurement of contact pressure by means of ultrasonic waves, Annals of the CIRP XVII, pp 289–296
Kendall K, Tabor D (1971) An ultrasonic study of the area of contact between stationary and sliding surfaces. Proc R Soc A: Math Phys Eng Sci 323:321–340
Dwyer-Joyce RS (2005) The application of ultrasonic NDT techniques in tribology. J Eng Tribol 219:347–366
Tattersall HG (1973) The ultrasonic pulse-echo technique as applied to adhesion testing. J Phys D: Appl Phys 6:819–832
Baik J-M, Thompson R (1984) Ultrasonic scattering from imperfect interfaces: a quasi-static model. J Nondestruct Eval 4(3-4):177–196
Królikowski J, Szczepek J, Witczak Z (1989) Ultrasonic investigation of contact between solids under high hydrostatic pressure. Ultrasonics 27(1):45–49
Pialucha T, Cawley P (1994) The detection of thin embedded layers using normal incidence ultrasound. Ultrasonics 32(6):431–440
Drinkwater BW, Dwyer-Joyce R, Cawley P (1996) A study of the interaction between ultrasound and a partially contacting solid-solid interface. Proc R Soc London A 452(8):2613–2628
Arakawa T (1983) A study on the transmission and reflection of an ultrasonic beam at machined surfaces pressed against each other. Mater Eval 41:714–719
Dwyer-Joyce RS, Drinkwater BW, Quinn AM (2001) The use of ultrasound in the investigation of rough surface interfaces. J Tribol 123(1):8
Pau M, Baldi a., Leban B (2008) Visualization of contact areas in bolted joints using ultrasonic waves. Exp Tech 32:49–53
Kim JY, Baltazar A, Rokhlin SI (2004) Ultrasonic assessment of rough surface contact between solids from elastoplastic loading-unloading hysteresis cycle. J Mech Phys Solids 52(8):1911–1934
Robinson AM, Drinkwater BW, Dwyer-Joyce RS, Payne JF (2001) Measurement of the stiffness of joints in graphite brick assembly. Proc Inst Mech Eng Part C: J Mech Eng Sci 215(2):167–178
Baltazar A, Rokhlin SI, Pecorari C (2002) On the relationship between ultrasonic and micromechanical properties of contacting rough surfaces. J Mech Phys Solids 50(7):1397–1416
Starzynski G, Buczkowski R (2014) Ultrasonic measurements of contact stiffness between rough surfaces. J Tribol 136(3):034503–1
Marshall MB, Lewis R, Drinkwater BW, Dwyer-Joyce RS (2004) An ultrasonic approach for contact stress mapping in machine joints and concentrated contacts. J Strain Anal Eng Des 39:339–350
Lewis R, Marshall M, Dwyer-Joyce R (2003) Ultrasonic characterisation of an interference fit. In: Tribological research and design for engineering systems proceedings of the 29th Leeds-Lyon symposium on tribology, vol 41 of Tribology Series, pp 449–458, Elsevier
Stancu-Niederkorn S, Engel U, Geiger M (1994) Ultrasonic investigation of friction mechanism in metal forming. J Mater Process Technol 45:613–618
Takeuchi A (2009) Detection of operational abnormality of ball bearing with ultrasonic technique. Key Eng Mater 270–273: 252–257
Ahn H-S, Kim D-I (2001) In situ evaluation of wear surface by ultrasound. Wear 251(1–12):1193–1201. 13th international conference on wear of materials
Kakinoki R, Segawa Y, Marumo Y, Imamura Y, Nonaka T, Sakata Y (2017) Evaluation of wrinkling states using in-process ultrasonic examination during sheet metal forming. Journal of the Japan Society for Technology of Plasticity 58:393–397
Merklein M, Engel U, Vierzigmann U (2009) Novel setup for the investigation of tribological behavior of sheet metal surfaces. Int J Mater Form 2:233–236
Pau M, Leban B, Baldi A (2009) Ultrasonic assessment of wear-induced modifications in engineering contacts. Wear 267:1117–1122
Tabor D (1959) Junction growth in metallic friction: the role of combined stresses and surface contamination. Procedures Royal Society London, Series A 251:378–393
Greenwood J, Williamson JP (1966) Contact of nominally flat surfaces. Proc R Soc London, Ser A Math Phys Sci 295(1442):300–319
Medina S, Nowell D, Dini D (2013) Analytical and numerical models for tangential stiffness of rough elastic contacts. Tribol Lett 49(1):103–115
Hertz H (1882) Ueber die beruhrung fester elastischer korper. J Reine Angew Math 92:156–171
Mindlin RD (1953) Elastic spheres in contact under varying oblique forces. J Applied Mech 20:327–344
O’connor J, Johnson K (1963) The role of surface asperities in transmitting tangential forces between metals. Wear 6(2):118–139
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pesaresi, L., Fantetti, A., Cegla, F. et al. On the Use of Ultrasound Waves to Monitor the Local Dynamics of Friction Joints. Exp Mech 60, 129–141 (2020). https://doi.org/10.1007/s11340-019-00550-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11340-019-00550-y