Introduction

The mechanical properties of materials at the nanoscale have generated considerable recent research interest [1–7]. This is due to the fact that some of these properties can change drastically when the dimensions of the sample decrease towards the atomistic scale. A very popular example of this effect, which has been observed in numerous nano and microindentation experiments, is an increase in hardness with decreasing depth of penetration. This phenomenon is known as the indentation size effect (ISE). Recent studies of ISE have shown that this effect for single crystals is easily observed for depths less than 1 μm [8, 9]. Nix and Gao developed a model, based on geometrically necessary dislocations (GND), which agrees with many microindentation results [10]. According to this model, the dependence between the hardness and the indentation depth can be described as:

$$ {H}^2={H}_0^2\left(1+\frac{h_0}{h}\right), $$
(1)

where H 0 is the hardness for the indefinitely large indentation depth h and h 0 is a length scale which depends on the indenter geometry and the dislocation structure.

Unfortunately, Swadener et al. [11] reported that the Nix-Gao model is in a good agreement with experiments only in the case of micron scale indentations. It overestimates the hardness value for the very small indentation depths. They investigated the ISE using spherical and Berkovich indenters on the iridium alloyed with 0.3 pct W and 60 ppm Th. According to them, the overestimation is due to the fact that the strong repulsion between GNDs at small indentation depths causes an expansion of the GND volume. Feng and Nix also found a similar overestimation for single crystal MgO [12]. They observed that there are a significant number of dislocations spreading out from the plastic zone around the indent. Hence, to relax the NG model’s assumption that all dislocations are in the plastic zone, they presented a new model by defining an effective plastic zone size:

$$ {H}^2={H}_0^2\left(1+{\left(1-r{e}^{-h/h}\right)}^{-3}\frac{h_0}{h}\right), $$
(2)

where r and h 1 are fitting parameters.

The size effect has been analysed in a series of papers by Durst et al. [13–15], where the single crystal CaF2 as well as nanocrystaline and single crystal metals were investigated.

In their modification of the Nix-Gao model they assumed, that geometrically necessary dislocations are stored in a plastic volume (underneath the indenter) having a radius proportional to the contact radius and a proportionality factor depends on tip shape. The proposed model enables a prediction of the indentation behavior of metallic materials from uniaxial stress–strain data. The dislocation density underneath the tip was also discussed.

An analytical model of ISE, based on the maximum allowable GND density, was presented by Huang et al. [16]. An interesting approach to this problem was presented by Wo et al.[17]. In their work, the sizes of the densely dislocated zone created in Berkovich and cube-corner indents on Ni3Al at a range of indentation depths were measured directly from transmission electron microscope micrographs. The expansion of the densely dislocated zone, which they observed, was in a good agreement with the relation proposed by Feng and Nix [12]. There are also other factors, which may contribute to the difference between Eq. (1) and the experimental results gained from the Oliver-Pharr (O-P) method, such as the surface roughness [18], the long-range stress associated with GNDs [9] or the intrinsic lattice resistance [19]. An interesting method to simulate the lattice rotation and an inhomogeneous distribution of the plastic zone under the indenter tip based on the molecular dynamics was presented in [20]. The indentation size effect was also explained using flow theory of mechanism based strain gradient plasticity [21]. In [22] it has been reported that for indentations performed with spherical tips having different radii, the size effect manifested as an increase of stiffness of load-penetration curve (in scaled P/R 2-h/R reference system) when the tip radius decreases. A detailed review of recent achievements in dealing with ISE was described in [23].

It should be noted that in the specification of hardness by means of micro/nanoindentation tests, a fundamental problem is a proper specification of the true contact area between an indenter tip and a sample’s surface. This problem should be analysed more in detail when a precise evaluation of ISE is required.

The methods applied to estimate the contact area can be classified into two subcategories [24]: direct methods where the load-penetration curve is used and post-mortem methods that rely on data extracted from the residual imprint. The direct methods are widely used in the instrumented nanoindentation as they do not need the time-consuming residual imprints measurements. It is worth to note that the investigations of size effects presented above are based on direct methods. The eventual mistakes that may be made when the direct methods are applied, are a source of farther inaccuracies in the estimation of size effect.

On the other hand the post-mortem methods require advanced instruments like atomic force microscope (AFM) and scanning electron microscope (SEM). The development in scanning probe microscopy with the use of indentation tips facilitates the post mortem measurements as it allows the imaging of imprints without manipulating the sample. Nevertheless, these measurements are not so accurate as those performed with the fine AFM tip. Furthermore, there are two different objectives in the topography of residual imprint analysis in post mortem methods: the evaluation of the contact area and the identification of the material’s parameters by the analysis of pile-ups patterns or cracks. In particular, the measurement of the contact area is used to verify the results of direct methods. For instance, in [24] the methodology was proposed that bases on the analysis of profiles extracted from an AFM image to specify the contact boundary of a Berkovich tip in different materials. The residual imprints generated in numerical benchmark (a conical tip) and experimental benchmark (a Berkovich tip) were investigated and a good accuracy of the proposed methodology was shown. In the case of physical experiments the “exact” contact area, considered as a reference one, was estimated through the Sneddon equation

$$ {A}_{c,SN}=\frac{\pi }{4}\frac{S^2}{4{\beta}^2{E}_{eq}^2}, $$
(3)

where S stands for the initial unloading contact stiffness and E eq is estimated from the ultrasonic measurements. Furthermore, Kese and Bergman used AFM to image nanoindents made with a Berkovich indenter in soda-lime glass and then they approximated the pile-up contact perimeter as a semi-ellipse [25]. They finally achieved an empirical relationship for estimating the pile-up contact area from the contact stiffness, S and the contact depth h c . A simple AFM measurements were used to estimate the real contact area by Cao et al. [26]. In their work the effects of film thickness and substrate deformation restraint on the mechanical properties of the electron beam deposited Au and Ag films were examined by using a Berkovich indenter. To examine the residual impression in Au and Al thin films SEM and AFM were used by Zhou et al. [27]. They also applied a quantitative approach to deal with the problems with estimating the real contact area, which was developed by Saha and Nix [28]. It was called ‘the constant modulus assumption analysis’. The basic assumption of this method is that the Young’s modulus is independent of the contact area and the contact depth. The hardness can be determined from a measurement of both the load, P and the contact stiffness, S. Zhou et al. [27] as well as Saha and Nix [28] used a Berkovich indenter in their experiments. Finally, the large review of experimental techniques for the examination of residual imprints was presented in [29]. The authors have concluded that there is a lack of consensus on the methods used to study (analyse) residual imprints generated in the indentation tests.

By contrast, in direct methods the load vs. penetration curve is analysed to determine contact depth h c , that subsequently is used to compute the contact area A c via the tip area function A c (h c ). The area function is specified in a calibration procedure and depends on the theoretical shape of the tip and on its actual defects. The calibration methods can rely on a direct measurement of the tip’s geometry or the residual imprint’s geometry made in a soft material. Generally, the most common approach is to apply a special procedure, in which many indentation tests in a reference material (i.e., fused silica) are performed and the area function is evaluated on the base of the multiple P-h curves analysis. Different forms of area functions were discussed in the literature [30, 31] and similarly different equations (methods) were proposed to compute h c on the base of a P-h curve. One of the difficulties that must be overcome is the pile-up or sink-in pattern that usually occurs. This effect influences the actual contact depth. Hence, Bolshakov and Pharr used Finite Element Method (FEM) to estimate the influence of material’s deformations on the Oliver and Pharr’s hardness measurement method [32] and they reported that the hardness may be overestimated by up to 60 % and Young’s modulus by up to 16 % depending on the extent of the pile-up. Although, already in 2004 Oliver and Pharr, in their review article on nanoindentation [33], discussed the problem with the pile-ups in details and concluded that the issue had to be considered as still unresolved, the problem has not been overcome until now. Nevertheless, Oliver and Pharr described some refinements and changes brought about by the improvements to the testing procedure (i.e., calibration procedure with the use of the continuous stiffness measurement on fused silica). They also conducted some FEM analysis and reported that the fundamental material properties affecting pile-up are the ratio of the effective modulus to the yield stress and the work-hardening behavior. One of the most recent approaches to this problem was presented by Cabibbo and Ricci [34]. They conducted the nanoindentation experiments with a Berkovich tip on deoxidized high phosphorus copper and then they investigated the imprints with AFM. They compared three different AFM-based methods and work of indentation analysis methods and chose one, which showed a good agreement with the literature data and the microhardness tests conducted with a Vickers indenter. Finally, they have developed this technique to make it dependent on load-penetration curve parameters instead of the AFM measurements.

In this paper we present a detailed experimental investigation of the size effect in single crystalline copper specimens having different orientations. We have observed, that for very small indentation depths (<150 nm), after the value of the hardness reached its maximum, it starts to decrease with the decreasing indentation depth. We called this phenomenon the inverse indentation size effect. To confirm these new non-standard, untypical results, besides the well known Oliver-Pharr method (direct method), we applied an AFM-based method (post mortem method) in our investigations of the real contact area and hardness. We also compared the values of hardness specified using both methods and we show that the Oliver-Pharr method overestimates the results at ultra low indentation depths and underestimates at greater indentation depths in single crystal copper.

Experimental

Nanoindentation Setup

A CSM Ultra Nanoindentation Tester was used to carry out the experiments presented in this paper. The device consists of an XYZ sample stage, which is used to precisely position the sample under the indenter, the atomic force microscope (AFM) and the optical microscope. At the beginning of the experiment, the sample is accurately positioned under the indenter tip. Any disturbance of the sample and of the measuring instrument (e.g., resulting from the temperature variations) are avoided due to the fact that the measuring head includes a measuring axis and a reference axis which can be controlled independently. Each axis has its own actuating means, displacement measuring system, and applied force measuring means. The load is measured by a capacitive sensor and it is applied by piezoactuator. The highest load resolution which can be achieved is 10 nN. Displacement is measured by a differential capacitive sensor with 0.001 nm resolution. Typical values of the thermal drift are less than 0.05 nm/min, which enables relatively long dwell time. The indentation was carried out using a Berkovich tip. After the indentation, the sample was positioned under the AFM to imagine the sample surface.

Sample Preparation and Experiments

A copper single crystal was drawn from the melt and cut precisely into samples by spark erosion and a wire saw to give (001)-, (011)-, and (111)-oriented surface planes. The surfaces were polished, then electro-polished, and finally carefully and rigorously cleaned with distilled water and isopropyl alcohol. Next, the electron microscopy methods were used in order to investigate the surface of the Cu sample. The microscope AURIGA (Zeiss) was applied. In the measurement both the secondary electrons (SE) and back scattered electrons (BSE) were detected, that enable an exploration of sample at different depths. For the SE, Everhardt-Thornley SE2 detector (for surface topography) and In-lens electron detector (for surface feature/texture analysis) were used. For the BSE, the Energy selective Backscattered (EsB) detector (suitable for clear compositional contrast) was applied. The measurement was performed with resolution of 1.5 nm, at low primary electron beam energies, equal to 0.5 kV.

The EDS (Energy-dispersive X-ray Spectroscopy) detector of Brucker was used for preliminary chemical analysis of the bulk material. The measurements were carried out in order to ensure that the copper surface is clean. For detection of the chemical composition, the chemical compounds and structure at the surface of the sample the Electron Backscatter Diffraction (EBSD) method was applied with use of Bruker detector. Due to the electrical charge of the surface the EBSD measurements were limited to small regions, about 50 × 2500 nm. The depth (vertical) and the in-plane resolution of the EBSD signal were about 50–100 nm and 4 nm, respectively. Thus the extremely fine structures at a surface of the sample can have been detected.

The indentation tests with a wide range of maximum indentation loads (from 0.1 to 8 mN) were performed on all the above orientations with the aim of investigating the influence of indentation depth on hardness. The experiments were done in the load control mode, which means that the maximum indentation load and the indentation time were set. The load was controlled by the feedback loop. The loading velocity (the increase of load in time) was equal to 50 % of the maximum indentation load per minute. The choice of the unloading velocity was particularly important in these experiments due to the fact that hardness and Young’s modulus are evaluated from the unloading curve. Hence, it was decided that the unloading velocity should be equal to the maximum indentation load per minute. Furthermore, the copper is a material that presents creep behaviour, hence, the 60s dwell time was set. The indentation tests with the same parameters were repeated independently at least five times for the sake of statistical analysis and to avoid random inaccuracies and errors.

The experimental procedure is virtually the same as that used by other researchers. However, the application of small forces (down to 0.1 mN) on copper single crystal and different methods of contact area evaluation revealed an intriguing effect of a hardness decrease for very small indents.

Imprints Imaging and Data Processing

To evaluate the real contact area the AFM was used. After the indentation test, the imprint was precisely positioned under the AFM tip and scanned carefully. The horizontal resolution of the piezoactuators for the smallest imprints was 1 nm/pixel, scanning speed was 0.5 μm s−1, the signal/noise ratio was about 4. It should be noted that due to the convolution the real horizontal resolution was not higher than 10 nm. During the small imprints investigation the digital open feedback loop was used whereas the closed feedback loop in X and Y scanning directions was applied while bigger imprints were scanned. The resolution in the Z-range was 0.01 nm. In order to get the row data the image processing procedures embedded in the software governing the AFM were turned off. The scanned surface topography were next post-processed using the special Hommel Map® software and the contact area was evaluated by methods described further in this paper.

Results

Examination of the Surface with Electron Microscopy Technique

The SEM images (on magnification of 40,000) reveal shallow craters homogeneously distributed on the surface of the sample—dark spots of an irregular oval shape (Fig. 1). The atomic mass of the material located in the craters is lower then the atomic mass of Cu. The dimensions of craters and impurities spots range from 30 up to 60 nm and was measured directly on SEM images. The spots are ordered along regularly spaced lines. The effect of electrical charge of sample surface which was observed during the measurement indicates that the detected nano-regions are not conductive.

Fig. 1
figure 1

SEM images of mono-Cu surface (a) the topography of surface takes with SE2 detector (b) changes in a composition chemical on the surface mono-Cu, and a contour of imprint boundary for the lowest load

Full size image

In the phase maps one can distinguish two phases, Cu and Cu2O. The copper oxide (Cu2O) occurs in a form of separated small spots (clusters). The so called ‘zero solution’ parameter is equal to approximately 0.5 % which signifies a high level of purity of the surface. The CuO oxide was not detected on the investigated surface. The Cu and Cu2O phases constitute 94.5 and 5.1 % of the measured volume, respectively. By combining SEM images and EBSD maps it can be concluded that the craters are constituted by the copper oxides and the remains of the polishing treatment.

Using a special numerical code (Casino) one can estimate that at the applied low level of energy (0.5 kV), the penetration depth of SE and BSE equals about 1.5 and 5.5 nm respectively. As the observed contrast was much better when one used In Lens detector (for SE), than in the case of the EsB detector, it can be concluded that some of detected BSE return from the area situated underneath of Cu2O clusters, thus the thickness of the clusters should be close to 6 nm. On the base of analysis of SEM images one can carefully estimate the clusters thickness as about 8 nm. On the other hand, the dimensions of these clusters (30–60 nm) are much smaller than the dimension of the smallest imprint. Therefore the presence of Cu2O clusters should not influence the results of indentation tests, even those performed with the lowest load.

Preliminary Results of Hardness Measurements

We have carried out the indentation test across the wide range of forces in order to investigate the influence of the indentation load on the hardness value. The examples of force-indentation depth curves are shown in Fig. 2. One has observed, that the creep phenomena influences a form of load-penetration curves, especially at low loads, Fig. 2(a). When the “high speed test” is performed (loading unloading in a few seconds) the unloading curve has a convex shape. Similar observation has been presented in the paper by Feng and Ngan [35], where it has been indicated that the unloading slope would become negative under some operating conditions such that the holding time at the maximum load is too short.

Fig. 2
figure 2

P-h curves for load parameters. (a) In the case of low loads the creep has a significant influence. The values of hardness and Young’s modulus determined from the O-P method in the case of 0 s pause are equal to 775 MPa and 110 GPa, respectively. On the other hand, for 60s pause hardness was 536 MPa and Young’s modulus 72GPa. (b) The creep does not influence the results so strongly in the case of higher loads

Full size image

In such a test, a proper specification of the tangent line that is required to calculate a local derivative would be very difficult. It depends on the test speed. In the direct Olive-Pharr method, as the contact depth is calculated using analysis of unloading curve, the negative slope of this curve can influence the calculated contact area and consequently the value of hardness.

Thus we applied a sufficiently long dwell time, to avoid dependence of results on the test duration. At higher loads the results practically do not depend on the dwell time, nevertheless the 60s dwell time were applied in all the cases. The evolution of the hardness with the increasing load for different indentation directions (001), (011) and close to (111) studied in the present paper is shown in Fig. 3. For each level of load many indentations were performed and a mean value has been calculated. Prior to the experiment the tip was calibrated using standard procedure. The presented results have been obtained using the standard O-P procedure implemented in the commercial software delivered with CSM instrument. The calculations of the hardness were performed using two different area functions: one was specified in the calibration procedure and the second was assumed as a nominal area function of the Berkovich tip. The comparison of both approaches enables to investigate the influence of the calibrated tip area function on the results.

Fig. 3
figure 3

The results of the hardness evaluation. The calculations of the hardness were performed using two different area functions: one was specified in the calibration procedure (HOP) and the second was assumed as a nominal area function of the Berkovich tip (HNOM)

Full size image

One can observe, that with an increase of the load the value of hardness initially increases (the inverse indentation size effect) and reaches a maximum value for the load equal to approximately 0.8mN. Next, for higher loads, up to the value of 8 mN, hardness continuously decreases. Similar character of hardness evolution was observed for all indentation directions. The observed tendency is different than that usually presented in the literature, where only an increase of hardness is described as the load decreases and the maximum hardness value is reached at the lowest applied load. The similar tendency is observed when the calibrated area function is replaced by nominal area, however, the hardness is shifted towards lower values for almost whole range of load. Thus, the values of calibrated area function are smaller than those of nominal one. The greatest discrepancy between both methods of hardness specification is observed at low loads.

It should be noted that only a few have observed the inverse indentation size effect. However, usually they claimed that the strange effect is due to the improper calibration of the tip bluntness. For example, Feng et. all observed a softening phenomenon in the copper single crystal indentation for indentation depths less than 250 nm [36]. They attribute this effect to the non-self-similar expansion of the plastic zone and/or the tip bluntness. Similar effect was reported by Durst et al. but the indentation was done with the cube corner indenter [14]. Furthermore, Liu et al. also presented the results which are in line with the results described in this paper [37]. Therefore, the effect of hardness decrease at low indentation loads was a motivation to see more in detail the specified hardness values and to analyse the influence of the experimental setup and the applied method.

Discussion

Tip Shape and Area Function

In view of a specific shape of the residual imprints and the relatively large range of the load, the problem of proper specification of the contact area has been considered. In the O-P method the area function A c (h) is determined using the calibration procedure, contact depth h c is determined from analysis of a P-h curve and next A c (h c ) is used to calculate hardness. The specification of the area function enables to take into account the actual tip shape.

In Fig. 4 the area function:

$$ \begin{array}{l}{A}_c\left({h}_c\right)=24.5{h}_c^2-6.87034694\cdot {10}^3{h}_c+2.2199921505\cdot {10}^5{h}_c^{1/2}-5.570920137\cdot {10}^5{h}_c^{1/4}\\ {}-9.015398352\cdot {10}^5{h}_c^{1/8}+1.3568625122\cdot {10}^6{h}_c^{1/16}\end{array} $$

resulting from calibration procedure is compared with the theoretical, nominal area function A cT (h) = 24.5 h 2 for the ideal Berkovich tip. One observes that A c (h) > A cT (h) for very low penetration depths (h < 70 nm) and for larger values of h (70–800 nm) A c (h) < A cT (h).

Fig. 4
figure 4

Comparison of calibrated and nominal area functions

Full size image

It should be noted that during the calibration procedure the indentation tests were performed in fused silica, where the penetration depth did not exceed 140 nm. Therefore, the values of A c (h) for h > 140 nm are not reliable. They are only an extrapolation that has not been verified experimentally. The SEM and AFM micrographs, where the angles of the tip in use were measured, indicate that at large penetration depths (h > 200 nm) the theoretical function A cT (h) should properly describe the change of the tip’s area with increasing penetration depth. The shape of the measured tip (inclination of edges) in these micrographs corresponds to the theoretical one. Thus, it must be underlined that the calibrated area function is valid only in a limited range of penetration depth and the value of hardness specified for larger penetration depths should be checked carefully.

On the other hand at small penetration depths the calibrated area function is consistent with the AFM measurements of the indenter tip. The largest difference occurs for ultra-low (smaller than 15 nm) penetration depths. For example, the area of tip cross-section corresponding to the 12 nm penetration depths can be estimated as about 8000 nm2 according to Fig. 5(b), if the influence of AFM tip radius (about 10 nm) is compensated. The calibrated A c (h) for h = 12 nm that equals 8150 nm2, cf. Fig. 4. The difference is equal to approximately 3 % however it should be noted that according to Fig. 4, the real shape of the indenter for the indentation depths lower than 10 nm (that is close to 12 nm) is not properly described by the calibration function. The calibration function below 10 nm starts growing which has no physical meaning. On the other hand, when the AFM measurement is concerned, one can observe a significant deviation of the tip from the pyramidal shape only below 12 nm, Fig. 5(b). It confirms a good quality of the tip. The influence of problems with calibration function and tip bluntness on the results described in this paper are not significant due to the fact that the range of penetration depths applied in our experiments starts from approximately 80 nm that is six time more than 12 nm. In this penetration range, the difference between calibrated area function and the AFM measurements was about 5 % (Fig. 5(c)). It confirms a proper calibration of the area function for the lowest applied indentation depths.

Fig. 5
figure 5

AFM micrographs of the used Berkovich tip. (a) In the microscale the tip is a perfect pyramid. (b) In the nanoscale, 12 nm from the top of the tip, its cross-section still has a triangular shape. (c) When h c equals to 80 nm the area of the tip measured by AFM is about 0.157 μm2 (when the AFM tip radius, about 10 nm, is compensated !), whereas according to the calibration function it is equal to 0.152 μm2—the difference is about 4 %

Full size image

Furthermore, according to the Nix and Gao model of the indentation size effect [10], the hardness of a material should not depend strongly on the depth of indentation if the material is intrinsically hard. Hence, in order to check the correctness of the nanoindentation setup calibration, the tests were performed on the fused silica surface. As anticipated, the hardness, even in the case of the smallest indents (a few tens of nanometers) is equal to approximately 10.5 GPa and does not change with the indentation depth (Fig. 6). This result indicates that the calibration of the nanoindenter’s tip was performed correctly. Additionally, the results gained for single crystal copper at bigger loads are in line with the results presented by other authors [36, 38].

Fig. 6
figure 6

Depth dependence of hardness of fused silica

Full size image

Comparison of the Residual and the Contact Depths

The value of contact depth h c is an important parameter in the specification of contact area accordingly to the O-P procedure as it enables to account for pile-up or sink-in pattern. In Fig. 7 the evolution of h c calculated using the O-P method is presented and compared with h r (residual depth) for different values of load. One can observe that in the whole range of loads h c   > h r , thus the pile ups, visible in AFM images for the lowest loads, are taken into account, at least qualitatively, in the evaluation of the contact area. However, in the case of the highest loads, the relation h c   > h r indicates that the effect of sink-in (Fig. 8) was not taken into account in the O-P procedure.

Fig. 7
figure 7

Measured residual depth, and contact depth calculated with O-P method, indentation in (001) plane

Full size image
Fig. 8
figure 8

Residual imprints for (001) plane: (a) 0.1 mN (b) 8 mN

Full size image

Specification of the Contact Area with Use of Post-Mortem Method

The uncertainty in the estimation of the actual A c and h c values described above may result from an improper account for pile-up and sink-in patterns that lead to an inaccurate specification of the area function. This uncertainty was a motivation to make use of the residual imprint and develop a method to estimate the true contact area in the performed nanoindentation tests.

In the proposed method, classified as a post mortem method, [28], the imprints were measured using AFM and then the Hommel Map commercial software was applied to work out the acquired images. The measured area was leveled using the least squares method—in the first step the reference plane was determined as a best fit to the whole measured area (the points in the imprint were excluded from the best fit procedure). Next the reference plane was subtracted from the raw image, thus the tilt of the initially measured area was removed. Furthermore, for the low load imprints two methods were applied in order to increase the accuracy (reliability) of the contact area estimation. It should be noted that both methods determine precisely the contact area. Due to the fact that the authors cannot state which method is better, both methods are used in this paper. Furthermore, this approach allows to confirm that the findings described here do not depend on the use of a specific post mortem method. In the first method the edge detection filter available in spatial filtering operator in Hommel Map software was used. The filter detects points having most important slope in four directions. The edge detection procedure allows to detect the contact boundary of the imprint and the enclosed area can be estimated. To verify usefulness of this filter it was applied to find the contact area in indentation of fused silica. Figure 9 shows that the detected contact boundary has a convex shape and is enclosed in a triangle resulting from the tip’s cross-section at the level corresponding to the measured penetration depth. Therefore, it lies below the level of an undeformed surface and its shape corresponds to the well known behaviour of fused silica. Similar shape of the contact boundary for fused silica was detected with use of the post-mortem method proposed in [24]. The measurement of residual imprints to estimate the contact area was advised also in [39].

Fig. 9
figure 9

Contact boundary detected using edge detection procedure for fused silica

Full size image

The second approach consisted of fitting a plane to each of the three walls of a residual imprint. In some cases the fit parameters were further precisely adjusted manually. The points less than three standard deviations of the plane fit below the fitted plane were assumed to be in contact with the indenter. However, this approach gives good results only in the case of small indents due to the fact that for bigger indents, the walls of residual imprints are no longer plain. They are bulged in the middle.

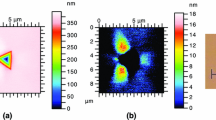
In Fig. 10 is presented an example of both approaches in the detection of contact boundary of the imprint shown in Fig. 8(a) (low load). The contact boundary for the low loads corresponds to material that exhibits low strain hardening (pile-up patterns are visible, Fig. 1(a)). In the case of the low loads the two approaches of contact area specification described above were applied and it was shown that both methods give similar results, Fig. 11. The contact area specified using the proposed post-mortem method is slightly bigger than that resulting from estimation with O-P method. It is an effect of pile-up patterns.

Fig. 10
figure 10

Contact boundaries for imprints in (001) Cu made with low load (0.1 mN) and detected using two methods: (a) edge detection in Hommel Map (b) plane fitting

Full size image
Fig. 11
figure 11

Comparison of the proposed methods of specification of contact area with O-P method at low loads (110 indentation direction)

Full size image

In the case of the higher loads, a specific, more complex behaviour of single crystal can be observed: the sink in occurs in the vicinity of the contact boundary and hillocks are generated at a certain distance from the contact boundary, Fig. 8(b). This sink-in pattern visible close to the contact boundary does not have the three-fold symmetry (tip symmetry), however, it can be qualitatively compared with a sink-in pattern generated in an isotropic material that exhibit high strain hardening e.g., fused silica. We have observed that for such response of material, where the walls of residual imprint are not flat, the first approach (edge detection, Hommel Map) presented in Fig. 12 is better suited to find the contact boundary.

Fig. 12
figure 12

Contact boundaries detected for imprints in Cu made with higher loads (edge detection)

Full size image

In Fig. 13, the contact area specified from residual imprints using the proposed method is compared with that calculated using O-P method for the whole range of applied loads. One can observe that for P < 2 mN, A c specified with use of O-P method is smaller and for P > 2 mN bigger than the A c specified from analysis of residual imprint using the proposed method.

Fig. 13
figure 13

A c PM (proposed method) and A c O-P comparison for one indentation direction (100)

Full size image

The difference between two methods at the lowest loads results from the fact that the presence of pile-up patterns increases the contact area more evident than it is predicted by O-P method. The underestimation of contact area by the OP method is indicated also in other papers, e.g. [40]. However, this difference is smaller than that observed at larger loads. The latter results from an important effect of the reduction of the contact area due to sink-in pattern, cf. Fig. 8(b), that is not taken into account in the OP method. The evolution of the surface topography in the vicinity of residual imprints shown schematically in Fig. 8, was presented more in detail in [41]. In that work the evolution of pile-ups patterns for different directions of indentation performed with Berkovich tip and for large range of loads was studied. It was shown that at low loads the pile-up patterns are generated around the residual imprints, while in the case of higher load the sink-in pattern occurs close to the imprint boundary and relatively small hillocks are formed at a certain distance from the contact area (Fig. 8). Moreover, in the case of small imprints, the pile-up patterns are of random structure (there are one, two or three pile-ups, each of them of a different height). One can summarize, that the character of symmetry of surface topography in a vicinity of residual imprints depends on the tip symmetry at the smallest loads, whereas at higher loads it depends on the indented crystal symmetry. Such a material response influences the value of the contact area and in consequence the hardness specified in the test. It is evident that this phenomena should be taken into account when the indentation size effect is studied. Furthermore, different pile-up patterns for the lowest and the highest loads indicate the different mechanism of its creation. This different mechanism is probably also responsible for the decrease in hardness at the lowest loads shown in this paper.

Comparison of Hardness Values Specified with Different Methods

Once the contact boundaries are specified as a function of load, one can calculate the contact area and consequently the hardness in the whole range of load. Consequently, the values of hardness should change when the proposed method of specification of contact area is applied.

The values of hardness (denoted as PM-hardness) calculated using proposed method are compared with those specified with O-P method (denoted as O-P) in Fig. 14. One can observe that when the proposed method is used the evolution of hardness with an increase of load has different character than that calculated using O-P method. In both cases, for the lowest loads the hardness increases with the load. Next, for the load of about 0.8–1.2 mN, the O-P hardness reaches a local maximum and for bigger loads its value decreases, while the PM hardness reaches an approximately constant value, that next is maintained for up to the highest load. At the loads lower than about 2mN the O-P hardness is higher than the PM-hardness, and when the load increases an inverse relation is observed. In other words, the PM hardness is constant for large range of high loads and decreases at the lowest loads, while O-P hardness first increases and then decreases with the load. The difference of the hardness estimation with these two methods is due to the difference in estimation of the contact area by both methods. The PM hardness is slightly lower for (011) indentation direction than for the remaining (001) and (111) directions.

Fig. 14
figure 14

The comparison between O-P hardness and PM hardness

Full size image

The proposed post-mortem specification of the contact area in the indentation tests leads to a reasonable correction of the values of the hardness. For a relatively large range of loads the value hardness is constant and it decreases for the lowest loads. We tentatively attribute this effect to different mechanisms and modes of deformation that take place at low (down to hundred nanometers) and large (few hundreds nanometers) penetration depths, as it has been mentioned at the end of “Specification of the Contact Area with Use of Post-Mortem Method” section, c.f. [41]. This effect can be explained by the fact, that for the lowest loads the motion of dislocations is rather random and is not restrained by the slip planes. On the other hand, for higher loads when the deformation depends on crystal symmetry, the dislocation motion is more difficult as it takes place only on slip planes.

The EDS measurement confirmed that the layer of the native oxide which creates on the copper surface is no thicker that 5 nm, hence, it does not influence the results significantly—the depth of the shallowest indents was equal to 70 nm. The presented results give a deeper insight into the indentation size effect.

To the best knowledge of the authors, the inverse indentation size effect in experiments performed with sharp tip on single crystals has not been described in details before. Admittedly according to one of latest models the nanoindentation in single crystals [42] the hardness starts decreasing with decreasing load in the lowest load range. However, it is attributed to the imperfect shape (roundness) of indenter tip at smallest depths range. The inverse size effect has been also observed recently in compression tests of nano-crystalline micro-pillars [43] and in nanoindentation tests of nanocrystaline metals [44].

Conclusions

The indentation size effect was investigated in single-crystal copper. Two approaches were applied to specify the hardness evolution with penetration depth: the well known Oliver-Pharr method and a proposed “post-mortem” method, based on a direct measurement of residual imprints. It should be emphasized that in both cases the inverse size effect was observed: at low penetration depth, down to about 150–160 nm, the hardness decreases with the decrease of load. However the absolute value of hardness in this range of loads obtained with PM method is lower, than that calculated using O-P method.

For larger loads, when the load decreases from 8 mN to about 1 mN the hardness calculated with O-P method increases, that is, the “classical” indentation size effect is observed. When the PM method is used in this range of loads the hardness is larger than that specified with O-P method and it is approximately constant—the size effect is not evident.

The analysis of surface of samples with SEM reveals relatively small impurities that cannot influence the presented results of nanoindentation tests.

The different values of hardness specified with both methods is an effect of the difference between estimated areas of contact. This difference is most evident when the pile up or sink in patterns occur. Both patterns are characteristic of single crystal copper indented with Berkovich tip: at low loads the relatively large pile-ups are generated, while at highest loads the pile-ups are at certain distance from contact boundary and close to the contact the sink in patterns occur.

The observed inverse size effect can be a result of long holding time of peaks of load in our experiments. On the other hand, the same holding time was maintained for whole range of loads. It was observed that for shorter holding times at the lowest loads, the results would be rate dependent, the unloading slope would became negative. It can lead to significant errors in analysis with O-P method.

Finally, the observed phenomenon gives a deeper insight into the mechanics of deformation of single crystals. The results presented in this paper may strongly influence the researchers to seek for other examples of the inverse nanoindentation size effect and its explanation.